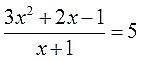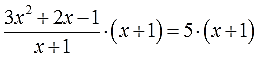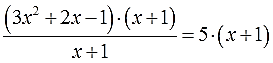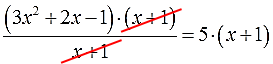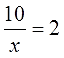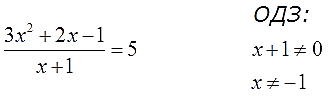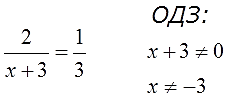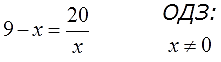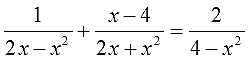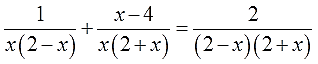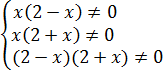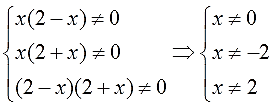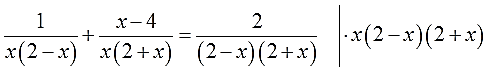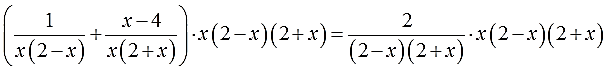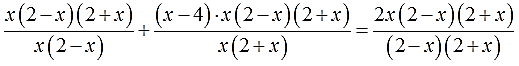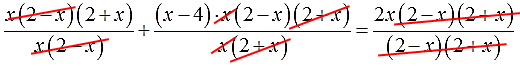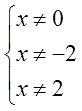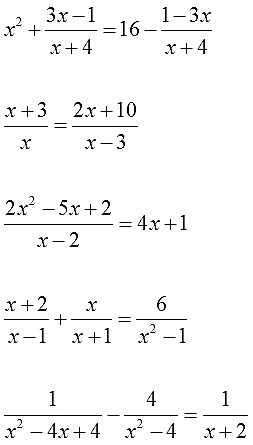Область допустимых значений (ОДЗ) – это все значения переменной, при которых не нарушаются правила математики.
Например:
— если в выражении (frac{x}{x-1}) значение переменной будет равно 1, нарушается правило: на ноль делить нельзя. Поэтому здесь (x) не может быть единицей и ОДЗ записывается так: (xneq1);
— если в выражении (sqrt{x-2}) значение переменной равно (0), нарушается правило: подкоренное выражение не должно быть отрицательно. Значит, здесь (x) не может быть (0), а также (1, -3, -52,7) и т.д. То есть, икс должен быть больше или равен 2 и ОДЗ будет: (xgeq2);
— а вот в выражение (4x+1) мы можем подставить любое число вместо икса, и никакие правила нарушены не будут. Поэтому область допустимых значений здесь — вся числовая ось. В таких случаях ОДЗ не записывают, потому что оно не несет в себе полезной информации.
Как найти ОДЗ?
Если переменная (икс) в уравнении или неравенстве стоит в знаменателе, логарифме, под корнем, в тангенсе или котангенсе ОДЗ записать нужно.
В квадратных и линейных уравнениях
(неравенствах) ОДЗ писать не нужно. В иррациональных, дробно-рациональных, логарифмических, а также тригонометрических
с тангенсом
и котангенсом
— ОДЗ обязательно. В уравнениях с синусом и косинусом — если нет знаменателей или других «отягощающих» функций — ОДЗ не записывают.
Чтобы осознать важность ОДЗ, давайте сравним два решения уравнения: с ОДЗ и без ОДЗ.
Пример: Решить уравнение (frac{x^2-x}{x+3}=frac{12}{x+3})
Решение:
| Без ОДЗ: | С ОДЗ: | |
| (frac{x^2-x}{x+3}=frac{12}{x+3}) | (frac{x^2-x}{x+3}=frac{12}{x+3}) | |
|
ОДЗ: (x+3≠0) (⇔) (x≠-3) |
||
| (x^2-x=12) | (x^2-x=12) | |
| (x^2-x-12=0) | (x^2-x-12=0) | |
| (D=(-1)^2-4·1·(-12)=49) | (D=(-1)^2-4·1·(-12)=49) | |
| (x_1=)(frac{-(-1) + sqrt{49}}{2·1})(=4) | (x_2=)(frac{-(-1) + sqrt{49}}{2·1}) (=4) | |
| (x_1=)(frac{-(-1) — sqrt{49}}{2·1})(=-3) | (x_2=)(frac{-(-1) — sqrt{49}}{2·1})(=-3) — не подходит под ОДЗ | |
| Ответ: (4; -3) | Ответ: (4) |
Видите разницу? В первом решении у нас в ответе появился неверный, лишний корень! Почему неверный? А давайте попробуем подставить его в исходное уравнение.
(frac{(-3)^2-(-3)}{(-3)+3})(=)(frac{12}{(-3)+3})
(frac{12}{0})(=)(frac{12}{0})
Видите, у нас получились и слева, и справа невычислимые, бессмысленные выражения (ведь на ноль делить нельзя). И то, что они одинаковы уже не играет роли, поскольку эти значения — не существуют. Таким образом, «(-3)» – неподходящий, посторонний корень, а область допустимых значений оберегает нас от таких серьезных ошибок.
Именно поэтому за первое решение вы получите двойку, а за второе – пятерку. И это не занудные придирки учителя, ведь неучет одз – не мелочь, а вполне конкретная ошибка, такая же как потерянный знак или применение не той формулы. В конце концов, итоговый ответ-то неверен!
Нахождение области допустимых значений часто приводит к необходимости решать системы неравенств или уравнений, поэтому вы должны уметь это делать хорошо.
Пример: Найдите область определения выражения (sqrt{5-2x}+)(frac{1}{sqrt{14+5x-x^{2}}})
Решение: В выражении два корня, один из которых в знаменателе. Кто не помнит ограничения, накладывающиеся в этом случае, тот смотрит таблицу. Кто помнит, записывает, что выражение под первым корнем больше или равно нулю, а под вторым — больше нуля. Понимаете, почему ограничения именно такие?
| (begin{cases}5-2xgeq0\14+5x-x^{2} > 0end{cases}) |
Дело за малым, нужно решить систему неравенств. |
| (begin{cases}-2xgeq-5\x^{2}-5x-14 < 0end{cases}) |
Поделим первое неравенство на (-2). |
| (begin{cases}xleq2,5\(x-7)(x+2) < 0end{cases}) |
Отметим все корни первого неравенства на числовой оси. |
|
Запишем общий ответ для системы – это и есть допустимые значения для икса. |
Ответ: ((-2;2,5])
Скачать статью
В предыдущем уроке мы с вами освоили основной принцип решения любых дробных уравнений. Это — ликвидация дробей. Кто читал, тот понял, что ничего сложного в этом нет.
Однако, даже в самых простых (казалось бы!) дробных уравнениях нас может поджидать сюрприз не из приятных. С ним, с сюрпризом, надо разобраться! Разберёмся?)
Основная проблема в решении дробных уравнений.
Сейчас мы с вами научимся обходить одну из самых коварных ловушек на ЕГЭ и контрольных! Попадаются в неё все — и троечники и отличники. Я специально поставил её в самое примитивное уравнение, чтобы с ней (с ловушкой) хорошенько разобраться. Но для начала посмотрим, попадёте вы в неё или нет.)
Допустим, надо решить вот такое нехитрое уравнение:
Дело уже привычное и знакомое. Умножаем всё уравнение на знаменатель (х+1) и получаем:
Напоминаю, что со скобками (х+1) работаем целиком, как будто бы это одно число! Производим умножение:
Сокращаем знаменатель и избавляемся от дроби:
3x2 + 2x — 1 = 5(x+1)
Раскрываем оставшиеся скобки, переносим всё влево, приводим подобные:
3x2 + 2x — 1 = 5x + 5
3x2 — 3x — 6 = 0
Делим всё уравнение на 3 и получаем:
х2 — х — 2 = 0
Отлично. Самое обычное квадратное уравнение. Решаем и получаем два корня:
х1 = -1
х2 = 2
Предположим, в задании на ЕГЭ сказано записать в ответ меньший из корней, если корней более одного. Что писать будем?)
Если вы решили, что ответ -1, то вы попали в ловушку. И задание вам не засчитают, да. Зря старались. Правильный ответ был 2… Два, а не минус один.
Так в чём же дело? А вы попробуйте проверку сделать. Подставьте каждый из найденных иксов в исходное уравнение. И, если при х=2 у вас всё славненько срастётся, получится тождество 5=5, то при х=-1 получится деление на ноль! Чего делать нельзя категорически. Нет такой операции ни в природе, ни в математике…
Что это значит? Это значит, что х=-1 — так называемый посторонний корень. Или лишний корень. Он не является корнем нашего дробного уравнения и в ответе никак не учитывается. Ибо его подстановка даёт бессмыслицу. Его мы просто отбрасываем. Окончательный корень один.
А именно: х=2.
Так, стоп, что-то тут не так! Нам же говорили, что всё уравнение можно умножать на одно и то же выражение! Это же тождественное преобразование!
Да, тождественное. Я не спорю. Но при одном маленьком ограничении, которое многие попросту игнорируют. А именно — выражение, на которое умножаем (делим), отлично от нуля! А скобочка (х+1) при х=-1 обращается в ноль! Так что всё честно.
И что нам теперь делать? Совсем не умножать? Тогда мы вообще ничего не решим! Каждый раз проверку делать? Это с ума сойдёшь. Особенно, если уравнение навороченное.
Нет, мы с вами пойдём красивым и элегантным путём. Обратимся за помощью к трём волшебным буквам! Догадались? Да! Это ОДЗ! Область Допустимых Значений.
Что же такое ОДЗ?
Это такие значения икса, которые могут быть в принципе. Или которые разрешены для данного примера.
Например, в уравнении
мы ещё пока не знаем, чему равен икс, верно? Мы уравнение пока не решили. Но зато мы железно знаем, что икс не может равняться нулю ни в коем случае! На ноль делить нельзя. На любое другое число — целое, дробное, отрицательное, иррациональное — ради бога. А вот на ноль — никак. Стало быть, в этом примере ОДЗ:
х — любое число, кроме нуля.
Зато все остальные иксы — абсолютно безопасны. Хоть 41, хоть -17, хоть -1,3 — весь бесконечный набор чисел.
Идея ясна?
Как записывать ОДЗ? Как работать с ОДЗ?
Тоже легко. На первом этапе всегда внимательно осматриваем исходный пример и ищем опасные места. Что значит опасные места?
Это места, где возможны запретные действия. Действия, которые при каких-то иксах могут оказаться недопустимыми с точки зрения математики. В нашей теме такое действие всего одно — деление. Нельзя делить на ноль. Есть ещё запреты в корнях чётной степени, в логарифмах и в тригонометрии. Их мы тоже рассмотрим в соответствующих уроках.
Как только опасные места найдены, рядышком с примером выписываем условия, которые не приводят к бессмыслице. После этого, глядя на эти условия, вычисляем запретные иксы. И исключаем их из ОДЗ. Вот и всё.
Я специально акцентирую внимание на словах «исходный пример». Любое преобразование (сокращение, приведение подобных и т.п.) может изменить ОДЗ, и мы можем получить неверный ответ.
Важно! Для поиска ОДЗ мы не решаем пример! Мы решаем всего лишь маленькие кусочки примера для нахождения запретных иксов.
«Многа букаффф», да. Но на практике вся процедура выглядит до ужаса элементарно.
Итак, берём наше уравнение:
Ничего пока что не трогаем, а внимательно осматриваем исходное уравнение. Осмотрев, мы сразу замечаем операцию деления на х+1.
Это потенциально опасная операция: при каких-то значениях икса выражение х+1 может оказаться равным нулю. На который делить нельзя. Поэтому обезопасим себя вот такой записью:
х+1 ≠ 0
х ≠ -1
Во-о-т. Минус один категорически не подходит нам в качестве ответа. Это и будет ОДЗ для нашего уравнения. Все иксы, кроме минус единички.
На практике запись и нахождение ОДЗ обычно оформляют так:
Иногда ОДЗ записывают и в другой форме, через промежутки. Вот так:
x ∈ (-∞; -1) U (-1; +∞)
Читается эта запись так: «Икс принадлежит интервалу от минус бесконечности до минус единицы (не включая), и от минус единицы (не включая) до плюс бесконечности.»
Перевод с математического на человеческий: «Икс — любое число, кроме минус единицы.»
Вот и всё. Как только мы себя обезопасили такой записью, дальше мы имеем полное право делать с уравнением всё что хотим — переносить члены, домножать, сокращать… Вот и домножаем всё уравнение на (х+1). Дробь-то убирать всё равно надо! Это по-прежнему будет не совсем тождественным преобразованием, но все вредные последствия от нарушения тождественности мы исключим по ОДЗ.
Умножаем:
3x2 + 2x — 1 = 5(x+1)
Как вы думаете, в какой же момент мы с вами попали в ловушку элементарного примера? Как раз в момент домножения всего уравнения на знаменатель дроби! Знаменатель исчез, и вместе с ним исчезли и соответствующие ограничения на иксы. Бесследно. И для нового уравнения, без дроби, на икс уже не накладывается никаких запретов! Любым может быть икс…
В математике это явление называется расширение ОДЗ.
Но теперь мы уже с вами народ бдительный. Исходные ограничения (х≠-1) мы записали и сохранили.
Поэтому дальше спокойно решаем уравнение безо всяких дробей и получаем два корня:
х1 = -1
х2 = 2
А вот теперь стыкуем наши результаты и условия ОДЗ. И видим в наших кандидатах на ответ один из иксов в качестве запретного! Минус один. Это означает, что в окончательный ответ его включать нельзя. Это посторонний корень, появившийся в процессе решения без нашего желания.
Да, это законный корень нашего вспомогательного квадратного уравнения, но никак не корень исходного дробного уравнения!
Стало быть, минус единицу мы безжалостно вычёркиваем и в ответ не включаем. Вот и всё.)
А в других уравнениях прошлого урока? Там что, нет ОДЗ? Есть, разумеется. Есть деление на икс — есть и ОДЗ.
В первом уравнении:
Во втором уравнении:
И так далее.
Я специально в тех примерах ничего не сказал про ОДЗ. Чтобы вас не перегрузить раньше времени.) В всех уравнениях прошлого урока (и домашнего задания к нему) ОДЗ никак не сказывалась на ответе. Так бывает. Но в заданиях ОГЭ и ЕГЭ ОДЗ в 99% случаев влияет на ответ! Так что мы с ОДЗ дружить будем. И во всех темах, где это необходимо, мы будем про ОДЗ вспоминать. Чтобы не упасть лицом в грязь.)
Итак, про ОДЗ поговорили. Убедились, что работать с ней тоже совсем не сложно. Теперь можно перейти и к общему алгоритму решения любого дробного уравнения.
Решаем дробные уравнения по алгоритму!
Для успешного решения любого дробного уравнения необходимо выполнить (правильно) пять пунктов:
1. Разложить знаменатели всех дробей на множители (если требуется). До упора. Переписать уравнение с учётом этого факта.
2. Найти ОДЗ, записать рядышком с уравнением и временно (до конца решения) забыть про неё.
3. Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли полностью.
4. Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Найти решения (кандидаты в ответ).
5. Вспомнить про ОДЗ и состыковать найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.
А теперь, вооружившись таким мощным супероружием, как ОДЗ, и общим алгоритмом, разберём очередной пример. Супердетально разберём!
Решить уравнение:
Решаем строго по пунктам. Выполняем пункт первый:
1. Разложить все знаменатели на множители (если требуется). До упора. Переписать пример с учётом этого факта.
Знаменатели наших дробей НЕ разложены на множители. Вот и приступаем. Вынесение общего множителя за скобки и формула разности квадратов — мощные штуки.)
2x — x2 = x(2-x)
2x + x2 = x(2+x)
4 — x2 = 22 — x2 = (2-x)(2+x)
Вот так. А теперь переписываем уравнение с учётом наших разложений:
Готово. Все знаменатели разложены до упора.) Можно приступать ко второму пункту.
2. Найти ОДЗ, записать рядышком с примером и временно (до конца решения) забыть про неё.
Итак, начинаем осматривать исходный пример на наличие опасных операций.
Внимание! Ничего не трогаем и не решаем! Не складываем дроби, не приводим подобные, не сокращаем!!!
Подобные преобразования запросто могут изменить ОДЗ, что может привести к неверному ответу! Оно нам надо?! Ещё раз напоминаю: ДО поиска ОДЗ с исходным примером мы не делаем НИЧЕГО! Кроме разложения на множители. Оно — безопасно и даже полезно.)
Берём и именно осматриваем исходный пример. И замечаем три опасных места: каждая из дробей таит в себе возможное деление на ноль.
Вот и пишем:
Знак системы (фигурная скобка) здесь не зря поставлен. Она означает, что все три условия должны выполняться одновременно! Мы ведь ОДЗ записываем не для каждой дроби по отдельности, а для всего примера целиком.)
Ну и как? Нашли ОДЗ? Не-а…)
Мы записали кусочек примера, записали три требования, которые должны выполняться железно. Но этого мало. Нужно ещё найти иксы, которые обеспечивают эти железные требования. ОДЗ ведь к иксам относится, а не к кусочкам примера…
Как же найти значения иксов, которые не превращают знаменатели дробей в ноль? Их же очень много? Очень просто! Мы поступим элегантно. Найдём иксы, которые наоборот, превращают знаменатели дробей в ноль. Это и будут запретные иксы.
Вот и решаем эти неравенства методом «от противного». То есть, делаем из неравенств уравнения:
x(2-x) = 0
x(2+x) = 0
(2-x)(2+x) = 0
Именно из этих трёх уравнений мы и будем искать запретные иксы. Уравнения очень простые: произведение равно нулю, когда хотя бы один из множителей равен нулю. Вот и приравниваем (в уме или на черновике) каждый множитель к нулю.
Для первого уравнения получаем: x1 = 0; x2 = 2.
Вспомнив, что это запретные иксы, получим:
х ≠ 0; x ≠ 2.
Точно так же решаем и два оставшихся уравнения.
Для второго уравнения получаем:
x ≠ 0; x ≠ -2.
И, наконец, для третьего уравнения получаем:
x ≠ 2; x ≠ -2.
Видно, что некоторые запретные значения иксов повторяются. Разумеется, для окончательной записи ОДЗ мы их не будем дублировать. Итого ОДЗ для нашего уравнения будет выглядеть вот так:
ОДЗ:
Видите, насколько полезно предварительно раскладывать знаменатели на множители! В уме ОДЗ ищется! Поэтому эта процедура и стоит первым пунктом в алгоритме.)
Можно приступать к третьему пункту.
3. Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли полностью.
И тут разложение на множители тоже здорово играет на руку!
Понятно, что для ликвидации первой дроби, надо её домножать на x(2-x), вторую — на x(2+x) и третью — на (2-x)(2+x).
Но чтобы сразу сократить все дроби, надо скомбинировать такое выражение, которое одинаково хорошо делится и на х(2-х), и на х(2+х), и на (2-х)(2+х).
Вот оно, это выражение:
х(2-x)(2+x)
Как же я до него додумался? Очень просто: составил произведение всех неповторяющихся множителей всех знаменателей. Чтобы ничего не забыть и лишнего не взять.) Приступаем к четвёртому пункту:
4. Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Получить решения (кандидаты в ответ).
Итак, умножаем:
И снова, чтобы не заплутать в трёх соснах, используем скобки:
Производим умножение. Большие скобки раскрываем, малые — не трогаем!
Сокращаем все дроби:
2 + x + (x-4)(2-x) = 2x
Всё. От дробей избавились. Как обычно, раскрываем оставшиеся скобки, приводим подобные и собираем все члены слева:
2 + x + 2x — x2 — 8 + 4x — 2x = 0
–х2 + 5x — 6 = 0
Помним, что минус впереди крайне неудобен, посему умножаем всё на (-1):
x2 — 5x + 6 = 0
Решаем простенькое квадратное уравнение и получаем корни:
x1 = 2
x2 = 3
Нашли кандидатов в ответ. Самое время вспомнить про ОДЗ. Про самый последний пункт:
5. Вспомнить про ОДЗ и состыковать найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.
Итак, наши решения:
x1 = 2
x2 = 3
Условия ОДЗ:
Сопоставляем и… Оп-па! А ведь двойка — запретное значение! Нас не проведёшь! ОДЗ — штука жёсткая. В отвал двойку!
Окончательный ответ: х = 3.
Именно так и решаются все дробные уравнения. В пять шагов. Зачем же я распинался, рассказывая целый урок про избавление от дробей, затем ещё пол-урока про ОДЗ? Мог бы сразу дать общий алгоритм и соответствующий пример!
На этот вопрос отвечу так. Если бы вы знали, сколько народу спотыкается на применении тупо заученного алгоритма! А уж при малейшем отклонении от шаблона простой пример становится вообще нерешаемым… Если понимать смысл, то шанс решить есть всегда. Понимание всегда побеждает механическую память.)
Вот, собственно, и всё, что я хотел сказать. И напоследок очередная порция примеров для самостоятельного решения.
Решить уравнения:
Ответы (по традиции, в беспорядке):
x = 3
x = -1
x = 4
x1 = -1; x2 = -9
x = -2
Всё совпало! Поздравляю! У вас иксов побольше будет? Хм… Про ОДЗ не забыли, случаем? Кое-какие корни выбрасывать надо! ОДЗ учли, а всё равно не выходит? Да-а-а… Проблемка. Такие уравнения надо уметь решать: слишком уж они популярны во многих темах математики. Особенно — в текстовых задачках! Но не отчаивайтесь!
Перечитайте этот и предыдущий уроки ещё раз и прогуляйтесь по смежным темам: разложение на множители, квадратные уравнения, линейные уравнения и (особенно!) тождественные преобразования уравнений. И всё получится. Я в вас верю!)
область определения и область значений функций + ПРИМЕРЫ
Функция-это модель. Определим X, как множество значений независимой переменной // независимая -значит любая.
Функция это правило, с помощью которого по каждому значению независимой переменной из множества X можно найти единственное значение зависимой переменной. // т.е. для каждого х есть один у.
Из определения следует, что существует два понятия- независимая переменная (которую обозначаем х и она может принимать любые значения) и зависимая переменная (которую обозначаем y или f(х) и она высчитывается из функции, когда мы подставляем х).
НАПРИМЕР у=5+х
1. Независимая -это х, значит берем любое значение, пусть х=3
2. а теперь вычисляем у, значит у=5+х=5+3=8. (у зависима от х, потому что какой х подставим, такой у и получим)
Говорят, что переменная y функционально зависит от переменной x и обозначается это следующим образом: y = f (x).
НАПРИМЕР.
1.у=1/х. (наз.
2. (наз. парабола)
3.у=3х+7. (наз. прямая)
4. у= √ х. (наз. ветвь параболы)
Независимая переменная (кот. мы обозначаем х) имеет название аргумент функции.
Область определения функции
Множество всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).
Рассмотрим D (у) для 1.,2.,3.,4.
1. D (у)= ( ∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. D (у)= ( ∞; +∞)//всё мн-во действит.чисел
3. D (у)= ( ∞; +∞)//всё мн-во действит.чисел
4. D (у)= [0; +∞)// мн-во неотрицат.чисел
Зависимая переменная (кот. мы обозначаем у ) имеет название значение функции.
Область значения функции
Множество всех значений, которые может принять зависимая переменная, называется областью значения функции и обозначается E (f) или E (y).
Рассмотрим Е (у) для 1.,2.,3.,4.
1. Е (у)= ( ∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. Е (у)= [0; +∞)// мн-во неотрицат.чисел
3. Е (у)=( ∞; +∞)//всё мн-во действит.чисел
4. Е (у)= [0; +∞)// мн-во неотрицат.чисел
Рассмотрим примеры подробнее
1) Постановка задачи. Найти функции у= 4х/(3+х)
Решение.
1. Найдем D (у)//т.е. какие значения может принимать х. для этого найдем ОДЗ(область допустимых значений дроби)
3+х≠0
х≠-3
значит D (у) данной функции ( ∞; 3) и (3;+∞)// всё множество действительных чисел, кроме 3.
2. Найдем Е (у)//т.е. какие значения может принимать у, при всех возможных х
решаем уравнение вида 4х/(3+х)=А, где А є Е (у)
(3+х)А=4х
3А=4х-хА
3А=х(4-А)
х=3А/(4-А)
значит Е (у) данной функции ( ∞; 4) и (4;+∞)// всё множество действительных чисел, кроме 4.
2) Постановка задачи. Найти D (у)и Е (у) функции, изображенной на графике
Область определения(значения х) смотрим по оси х- это промежуток [ 4; 7],
Областью значения(значения у) смотрим по оси у- это промежуток [ 4; 4].
Нужна помощь в учебе?
Предыдущая тема: Графический способ решения уравнений: алгоритм и примеры графиков
Следующая тема:   Свойства функции: разбираем на примере
Как найти Область Допустимых Значений (ОДЗ)
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
a = 1, b = 2, c = 1.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Запоминаем!
ОДЗ относится к выражениям. Область определения функции относится к функциям и не относится к выражениям.
Пример 2
Рассмотрим выражение
ОДЗ такого выражения выглядит следующим образом: ( — ∞; 3) ∪ (3; +∞).
Читать запись нужно вот так:
Область допустимых значений переменной x для выражения — это числовое множество ( — ∞; 3) ∪ (3; +∞).
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Каждый новый год в школе прибавляет ученикам забот — задачки становятся сложнее, формулы длиннее, а правила — скучнее. В детской онлайн-школе Skysmart ученики занимаются на красочной интерактивной платформе, пользуются электронным учебником и чертят на настоящей онлайн-доске. Такая алгебра не может не понравиться.
Записывайтесь на бесплатный вводный урок и пробуйте новый формат обучения.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения.
Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
- требуется извлечение квадратного корня из отрицательного числа
- присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль)
- отрицательный целый показатель в степени при отрицательном числе
- требуется вычисление логарифма отрицательного числа
- область определения тангенса = π * k, где k ∈ z
- область определения котангенса π * k, где k ∈ z
- нахождение арксинуса и арккосинуса числа, выходящего за пределы числового промежутка [- 1, 1].
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a3 + 4 * a * b − 6.
Как решаем:
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении — пустое множество.
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа.
Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Лайфхак
Чтобы не потратить зря время на решение нерешаемого примера, всегда обращайтесь к списку условий, при которых выражение не может быть решено.
Пример 7
Найдем ОДЗ переменной a в выражении
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a2
+ 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Условие 5: a + 6 ≠ 1.
Определим ОДЗ, опираясь на все означенные условия:
a +1 — 1 0.
Ответ: ОДЗ: [ — 1; 0) ∪ (0; +∞)
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
- Если число входит в ОДЗ, то около числа ставим квадратные скобки.
- Если число не входит в ОДЗ, то около него ставятся круглые скобки.
Например, если х > 6, но х < 8, то записываем интервал [6; 8).
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
- расширить ОДЗ
- никак не повлиять на ОДЗ
- сузить ОДЗ
Рассмотрим каждый случай в отдельности.
Пример 8
Рассмотрим выражение a + 4/a — 4/a
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение
ОДЗ a определяется неравенством (a — 1) * (a — 4) ≥ 0.
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
ОДЗ переменной a для этого выражения определяется неравенствами:
a — 1 ≥ 0
a — 4 ≥ 0
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Тебе следует повторить тему — формулы сокращенного умножения!
В детской школе Skysmart опытные преподаватели научат ребенка решать любые, даже самые сложные, задачки, справляться с формулами и теоремами. На уроках нет скучной зубрежки и непонятных правил — только эффективная подготовка к тестам, контрольными и экзаменам.
Заполнить пробелы в обучении и продвинуться вперед по программе легко и весело со Skysmart. Записывайтесь на бесплатный вводный урок и начните заниматься уже завтра!
Область допустимых значений (ОДЗ): теория, примеры, решения
Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.
В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.
Допустимые и недопустимые значения переменных
Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.
Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1:а, если а=0, тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.
Определение 1
Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.
Определение 2
Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.
То есть отсюда следует полное определение
Определение 3
Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.
Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.
Пример 1
Для примера рассмотрим выражение вида 1x-y+z, где имеются три переменные.
Иначе можно записать, как x=0, y=1, z=2, другая же запись имеет вид (0,1,2). Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 10-1+2=11=1. Отсюда видим, что (1,1,2) недопустимы. Подстановка дает в результате деление на ноль, то есть 11-2+1=10.
Что такое ОДЗ?
Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.
Определение 4
Область ОДЗ – это множество значений, допустимых для данного выражения.
Рассмотрим на примере выражения.
Пример 2
Если имеем выражение вида 5z-3, тогда ОДЗ имеет вид (−∞, 3)∪(3, +∞). Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.
Если имеется выражения вида zx-y, тогда видно, что x≠y, z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.
Область допустимых значений и область определения имеет один и тот же смысл.
Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f(x).
Как найти ОДЗ? Примеры, решения
Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.
Существуют выражения, где их вычисление невозможно:
- если имеется деление на ноль;
- извлечение корня из отрицательного числа;
- наличие отрицательного целого показателя – только для положительных чисел;
- вычисление логарифма отрицательного числа;
- область определения тангенса π2+π·k, k∈Z и котангенса π·k, k∈Z;
- нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [-1; 1].
Все это говорит о том, как важно наличие ОДЗ.
Пример 3
Найти ОДЗ выражения x3+2·x·y−4.
Решение
В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.
Ответ: x и y – любые значения.
Пример 4
Найти ОДЗ выражения 13-x+10.
Решение
Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.
Ответ: ∅.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 5
Найти ОДЗ заданного выражения x+2·y+3-5·x.
Решение
Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю.
При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x+2·y+3≥0. То есть это и есть искомая область допустимых значений.
Ответ: множество x и y, где x+2·y+3≥0.
Пример 6
Определить ОДЗ выражения вида 1x+1-1+logx+8(x2+3).
Решение
По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x+1-1≠0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x+1≥0. Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x2+3>0. Основание логарифма также должно иметь положительное значение и отличное от 1, тогда добавляем еще условия x+8>0 и x+8≠1. Отсюда следует, что искомое ОДЗ примет вид:
x+1-1≠0,x+1≥0,x2+3>0,x+8>0,x+8≠1
Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [−1, 0)∪(0, +∞).
Ответ: [−1, 0)∪(0, +∞)
Почему важно учитывать ОДЗ при проведении преобразований?
При тождественных преобразованиях важно находить ОДЗ.
Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
Тождественные преобразования:
- могут не влиять на ОДЗ;
- могут привести в расширению или дополнению ОДЗ;
- могут сузить ОДЗ.
Рассмотрим на примере.
Пример 7
Если имеем выражение вида x2+x+3·x, тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.
Пример 8
Если взять пример выражения x+3x−3x, то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид (−∞, 0)∪(0, +∞). Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.
Рассмотрим пример с наличием подкоренного выражения.
Пример 9
Если имеется x-1·x-3, тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства (x−1)·(x−3)≥0.
Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид (−∞, 1]∪[3, +∞). После преобразования x-1·x-3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x-1≥0,x-3≥0. При ее решении получаем, что [3, +∞). Значит, ОДЗ полностью записывается так: (−∞, 1]∪[3, +∞).
Нужно избегать преобразований, которые сужают ОДЗ.
Пример 10
Рассмотрим пример выражения x-1·x-3, когда х=-1. При подстановке получим, что -1-1·-1-3=8=22. Если это выражение преобразовать и привести к виду x-1·x-3, тогда при вычислении получим, что 2-1·2-3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.
Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.
Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.
Пример 11
Рассмотрим на примере дроби вида xx3+x. Если сократить на x, тогда получаем, что 1×2+1. Тогда ОДЗ расширяется и становится (−∞ 0)∪(0, +∞).
2$
Функции вида $f(x)=sin x, g(x)=cos x, h(x)=tan x, k(x)=cot x$ называются тригонометрическими функциями. Область определения $f(x)=sin x $ и $g(x)=cos x$ это все действительные числа $mathbb{R}$. А области определения $h(x)=tan x $ и $k(x)=cot x$ следующие:
$h(x)=tan x=dfrac{sin x}{cos x}, cos x=0 rightarrow x=kpi+dfrac{pi}{2} rightarrow$
$D_h=mathbb{R}-lbrace x|x=kpi+dfrac{pi}{2}, k in mathbb{Z} rbrace$
$h(x)=cot x=dfrac{cos x}{sin x}, sin x=0 rightarrow x=kpi rightarrow$
$D_k=mathbb{R}-lbrace x|x=kpi, k in mathbb{Z} rbrace$
Также отметим, что $-1 leq sin x leq 1 $ и $ -1 leq cos x leq 1$. Следовательно,
$R_f=[-1,1] ,,,,,, R_g=[-1,1]$
Множество значений of $h(x)=tan x $ и $k(x)=cot x$ это все действительные числа $mathbb{R}$.
Пример:
Найти область определения и множество значений $f(x)=sin x+cos x$.
Решение:
Область определения $sin x $ и $cos x$ это все действительные числа, следовательно область определения
$f(x)=sin x+cos x$
также все действительные числа.
4 pi x = 0 rightarrow sin pi x=0 rightarrow pi x=k pi rightarrow x=k in mathbb{Z}$
Значит
$D_f=mathbb{Z}$
Согласно $D_f=mathbb{Z}$, можно переписать функцию как
$f(x)=cos pi x=pm 1$
Теперь очевидно, что
$R_f= lbrace pm 1 rbrace$
Пример:
Найти область определения и множество значений $f(x)=sin (log (log x))$.
Решение:
Согласно тому, что уже было сказано относительно логарифмической функции
$D_f= lbrace x| x in mathbb{R}; log x>0,x>0 rbrace$
$= lbrace x| xin mathbb{R}, x>1,x>0 rbrace =(1,+infty)$
Также стоит отметить, что
$|sin (log (log x))| leq 1 rightarrow |y| leq 1 rightarrow -1 leq y leq 1$
Значит
$R_f=[-1,1]$
График $f$ это
Определение:
Пусть $f$ функция, у которой область определения это $D_f$. Функция $f$ является инъективной тогда и только тогда, если для всех $x_1$ и $x_2$ в $D_f$, если $f(x_1)=f(x_2)$, то $x_1=x_2$.
{log x} rightarrow y=(f circ g)_{(x)},,, x in (0,1) rightarrow 0
Теперь, для того, чтобы найти множество значений $g circ f$, отметим, что
$Z=(gcirc f)_{(x)}=x rightarrow x=Zin (1,+infty) rightarrow Z>1 rightarrow R_{g circ f}=(1,+infty)$
Графиком $f$ является
Графиком $g$ является
График $f circ g$ это
График $g circ f$ это
Пример:
Если $f(x)=x-1$ and $(f circ g)_{(x)}=dfrac{1}{x-1}$, то найти область определения и множество значений $g circ f$.
Решение:
Сначала найдем $ g circ f$
$f(x)=x-1 rightarrow f(g(x))=g(x)-1 rightarrow (f circ g)_{(x)}=g(x)-1 rightarrow \ dfrac{1}{x-1}=g(x)-1 rightarrow g(x)=dfrac{x}{x+1}$
Значит
$y=(g circ f)_{(x)}=g(f(x))=dfrac{f(x)}{f(x)-1}=dfrac{x-1}{x+1}$
Следовательно
$D_{g circ f}=lbrace x|x in mathbb{R}, x neq 2 rbrace rightarrow D_{g circ f}=mathbb{R}-lbrace 2 rbrace$
Также
$y=dfrac{x-1}{x-2} rightarrow x=dfrac{2y-1}{y-1}$
$R_{g circ f}=lbrace y | y in mathbb{R}, y neq 1 rbrace rightarrow$
$R_{g circ f}=mathbb{R}-lbrace 1 rbrace$
График $f$ это
График $f circ g$ это
Графиком $g$ является
Графиком $g circ f$ является
Упражнения
1) Если $f(x)=2^{log_2 x}$ and $g(x)=dfrac{x-1}{x^2-x}$, то найти область определения и множество значений $f circ g$.
2 2kx ,,, -1 leq sin 2kx leq 1$
$rightarrow sin 2kx= pm 1 rightarrow y=dfrac{1}{4} , sin 2x=0 rightarrow y=1$
$rightarrow dfrac{1}{4} leq y leq 1 rightarrow R_f=[dfrac{1}{4},1]$
Part 1
Как найти область допустимых значений функции
Область допустимых значений алгебраического выражения (сокращенно ОДЗ) – это множество значений переменной, при которых это выражение определено.
В школьном курсе алгебры есть всего пять элементарных функций, которые имеют ограниченную область определения. Вот они:
1. ОДЗ:
Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
2. ОДЗ:
Выражение, стоящее в знаменателе дроби, не может быть равно нулю.
3. ОДЗ:
Выражение, стоящее под знаком логарифма, должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
4. , ОДЗ:
5. Есть две функции, которые содержат «скрытую» дробь:
и
6. ОДЗ:
Степень корня – натуральное число, отличное от 1.
Таким образом, функции и имеют разную область определения.
Если выражение содержит одну или несколько функций, которые определены на ограниченном множестве значений аргумента, то для того, чтобы найти ОДЗ выражения, нужно учесть все ограничения, которые накладываются этими функциями.
Чтобы найти область допустимых значений выражения, нужно исследовать, присутствуют ли в выражении функции, которые я перечислила выше. И по мере обнаружения этих функций, записывать задаваемые ими ограничения, двигаясь «снаружи» «внутрь».
Поясню на примере:
Найти область определения функции:
Чтобы найти область определения функции, нужно найти область допустимых значений выражения, которое стоит в правой части уравнения функции
Я специально выбрала «страшную», на первый взгляд, функцию, чтобы показать вам, на какие простые операции разбивается процесс нахождения области допустимых значений.
«Просканируем» выражение, стоящее в правой части равенства:
1. Мы видим дробь:
Знаменатель дроби не равен нулю. Записываем:
2. Мы видим в знаменателе логарифм:
Выражение, стоящее под знаком логарифма должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
3.Мы видим квадратный корень:
Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
Теперь запишем все ограничения в систему неравенств:
Решение этой системы неравенств посмотрите в ВИДЕУРОКЕ:
Каждому выражению с переменными соответствует область допустимых значений (ОДЗ) переменных, которую ОБЯЗАТЕЛЬНО нужно учитывать при работе с этим выражением.
Акцент на слове «обязательно» сделан не случайно: при решении примеров и задач халатное отношение к ОДЗ может привести к получению неверных результатов.
Чтобы у нас не возникало подобных проблем, давайте внимательно изучим все, что связано с ОДЗ. Для начала узнаем, что это такое, после этого разберем на характерных примерах, как найти ОДЗ переменных для заданного выражения, а в заключение остановимся на важности учета ОДЗ при преобразовании выражений.
Навигация по странице.
Допустимые и недопустимые значения переменных
Определение области допустимых значений переменных для выражения дается через термин допустимые значения переменной. Введем это вспомогательное определение, для чего проследим, что нас приводит к нему.
На уроках математики в школе вплоть до 7 класса познаются азы работы преимущественно с числами и числовыми выражениями. А с 7 класса начинается изучение такой математической дисциплины как алгебра, и начинается оно с того, что вводится определение выражения с переменными, а также связанное с ним определение значения выражения при выбранных значениях переменных.
Последнее определение нуждается в уточнении следующего плана. Существуют выражения, значения которых при некоторых выбранных значениях переменных вычислить невозможно. Например, невозможно вычислить значение выражения 1:a при a=0 , так как делить на нуль нельзя. Это послужило причиной введения в обиход терминов «выражение, имеющее смысл при данных значениях переменных» и «выражение, не имеющее смысла при данных значениях переменных». Говорят, что
выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение
выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Вот теперь мы обладаем всеми сведениями, позволяющими дать определение допустимых и недопустимых значений переменных:
Допустимые значения переменных – это такие значения переменных, при которых выражение имеет смысл. А значения переменных, при которых выражение не имеет смысла, называют недопустимыми значениями переменных.
Здесь лишь стоит уточнить, что если выражение содержит две, три, и большее число переменных, то речь идет о парах, тройках и т.д. допустимых значений переменных. Приведем пример. Рассмотрим выражение с тремя переменными x , y и z . Тройка значений переменных x=0 , y=1 , z=2 , она же в другой записи (0, 1, 2) , является допустимой, так как при данных значениях переменных мы можем найти значение выражения: . А тройка (1, 2, 1) – недопустимая, так как при подстановке этих значений в выражение мы придем к делению на нуль: .
Определения, озвученные в этом пункте, полностью согласуются с информацией из учебников [1, с. 6; 2, с. 11-12; 3, c. 4] .
Что такое ОДЗ?
Практически у всех, так или иначе имеющих отношение к алгебре, на слуху словосочетание «область допустимых значений», также довольно часто аббревиатуру ОДЗ можно встретить в описаниях решений, но как такового определения области допустимых значений (ОДЗ) нет в основных учебниках, используемых в школе. Поэтому интересно, откуда берет начало этот термин.
Ну а с позиций практики интереснее знать, какой смысл в него вкладывают.
Под областью допустимых значений (ОДЗ) понимают множество всех допустимых значений переменных для данного выражения.
Приведем пример. Допустим, дано выражение , и записано ОДЗ: (−∞, 3)∪(3, +∞) . Последнюю запись стоит понимать так: область допустимых значений переменной z для выражения есть числовое множество (−∞, 3)∪(3, +∞) .
Другой пример. Рассмотрим выражение и относящуюся к нему запись ОДЗ: x≠y , z – любое. Она означает, что ОДЗ переменных x , y и z для данного выражения – это все такие тройки значений переменных x , y и z , для которых выполняются указанные условия x≠y , z – любое.
Завершить этот пункт хочется разговором про область допустимых значений и область определения. Часто между этими терминами стирают различия. Например, говорят про область определения выражения [4, с. 87] , под которой фактически понимают ОДЗ переменных этого выражения. Также можно столкнуться с областью определения уравнения или неравенства [5, с.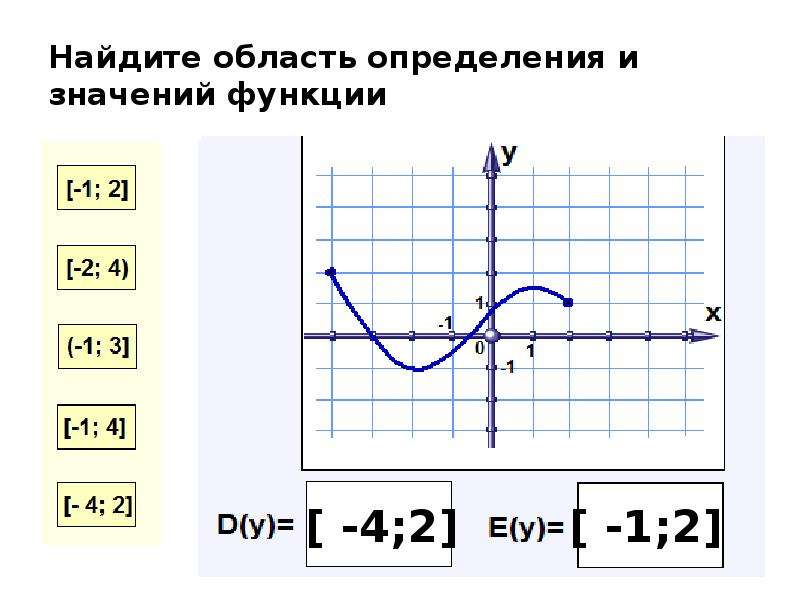
204, 220; 6, с. 188, 190] , под ней подразумевают ОДЗ переменных, на которой одновременно имеют смысл обе части уравнения или неравенства. Как тут не спутать одно с другим? Давайте будем придерживаться следующего подхода: к функциям относить область определения функции, а к выражениям – ОДЗ переменных. И на загладку приведем такое утверждение: область определения функции y=f(x) совпадает с областью допустимых значений переменной x для выражения f(x) .
Как найти ОДЗ? Примеры, решения
Прежде чем обратиться к главной теме этого пункта, нужно понимать, что значит найти ОДЗ, хотя это достаточно отчетливо ясно из определения. Это значит, что надо указать множество всех допустимых значений переменных для заданного выражения. На это можно посмотреть и с другой стороны: найти ОДЗ – это значит указать условия, которые исключают те и только те значения переменных, при которых выражение не имеет смысла. Теперь можно двигаться дальше.
Заданий с формулировкой «найти ОДЗ» не так много.
Однако почти постоянно приходится преобразовывать выражения, а это неявно требует нахождения области допустимых значений для ее контроля. В этом свете вопрос, как найти ОДЗ, очень злободневен.
В поисках ответа на него поразмыслим, значения каких выражений мы не можем вычислить.
Степени с положительным нецелым показателем мы придали смысл лишь для неотрицательных чисел, а с отрицательным нецелым показателем – лишь для положительных чисел. А еще мы не можем вычислить нуль в степени нуль.Что нам это дает? А то, что перечисленные выше моменты и нужно учитывать при поиске ОДЗ. Как это делать, станет понятно из следующих примеров.
Укажите все допустимые значения переменных для выражения x 3 +2·x·y−4 .
Возвести в куб мы можем любое число, также мы умеем умножать любые числа, как и складывать и вычитать. Поэтому, мы можем вычислить значение заданного выражения при любых значениях переменных x и y . А это значит, что выражение x 3 +2·x·y−4 имеет смысл при любых значениях входящих в него переменных. Поэтому, ОДЗ переменных x и y для этого выражения – это множество всех таких пар (x, y) , где x – любое число и y – любое число.
(x, y) , где x – любое, y – любое.
Найти ОДЗ переменной x для выражения .
Мы видим, что данное выражение содержит дробь с нулем в знаменателе. А это значит, что ни при каком значении переменной x мы не сможем вычислить значение этого выражения, так как оно будет содержать деление на нуль. Вывод: это выражение не определено ни при каких значениях переменной x . Другими словами, ОДЗ переменной x для этого выражения есть пустое множество.
Найти ОДЗ .
Здесь нас настораживает присутствие квадратного корня. Чтобы избежать появления под корнем отрицательного числа, надо для переменных x и y потребовать выполнение условия x+2·y+3≥0 .
Оно и задает искомую область допустимых значений.
множество всех пар (x, y) , для которых x+2·y+3≥0 .
В более сложных случаях приходится учитывать одновременно несколько условий из приведенного выше списка. Это дает системы неравенств, задающие ОДЗ.
Определите ОДЗ переменной x для выражения .
Во-первых, выражение в знаменателе дроби не должно обращаться в нуль, это дает первое условие . Во-вторых, выражение под знаком квадратного корня должно быть неотрицательным: x+1≥0 . В-третьих, выражение под знаком логарифма должно быть положительным, это дает третье условие x 2 +3>0 . Наконец, выражение в основании логарифма должно быть положительным и отличным от единицы, так вырисовываются еще два условия x+8>0 и x+8≠1 . Таким образом, искомая ОДЗ определяется системой следующего вида . Это система неравенств с одной переменной, решив ее, записываем ОДЗ: [−1, 0)∪(0, +∞) .
Здесь лишь заметим, что во многих случаях на практике нет необходимости в решении составленных систем.
В заключении остается сказать, что такой подход используется и тогда, когда нужно найти область определения функции.
Почему важно учитывать ОДЗ при проведении преобразований?
Решая различные задачи, нам очень часто приходится проводить тождественные преобразования выражений. Но бывает, что какое-то преобразование в одних случаях допустимо, а в других – нет. Существенную помощь в плане контроля допустимости проводимых преобразований оказывает ОДЗ. Остановимся на этом подробнее.
Суть подхода состоит в следующем: сравниваются ОДЗ переменных для исходного выражения с ОДЗ переменных для выражения, полученного в результате выполнения тождественных преобразований, и на основании результатов сравнения делаются соответствующие выводы.
Вообще, тождественные преобразования могут
- не влиять на ОДЗ;
- приводить к расширению ОДЗ;
- приводить к сужению ОДЗ.
Давайте поясним каждый случай примером.
Рассмотрим выражение x 2 +x+3·x , ОДЗ переменной x для этого выражения есть множество R .
Теперь проделаем с этим выражением следующее тождественное преобразование – приведем подобные слагаемые, в результате оно примет вид x 2 +4·x . Очевидно, ОДЗ переменной x этого выражения тоже является множество R . Таким образом, проведенное преобразование не изменило ОДЗ.
Переходим дальше. Возьмем выражение x+3/x−3/x . В этом случае ОДЗ определяется условием x≠0 , которое отвечает множеству (−∞, 0)∪(0, +∞) . Это выражение тоже содержит подобные слагаемые, после приведения которых приходим к выражению x , для которого ОДЗ есть R . Что мы видим: в результате проведенного преобразования произошло расширение ОДЗ (к ОДЗ переменной x для исходного выражения добавилось число нуль).
Осталось рассмотреть пример сужения области допустимых значений после проведения преобразований. Возьмем выражение . ОДЗ переменной x определяется неравенством (x−1)·(x−3)≥0 , для его решения подходит, например, метод интервалов, в результате имеем (−∞, 1]∪[3, +∞) . А теперь преобразуем исходное выражение к виду , воспользовавшись одним из свойств корней: корень произведения равен произведению корней.
ОДЗ переменной x для этого выражения определяет система линейных неравенств , решение которой дает множество [3, +∞) . Таким образом, в результате проведенного преобразования произошло сужение ОДЗ с множества (−∞, 1]∪[3, +∞) до множества [3, +∞) .
При преобразовании выражений надо строго избегать преобразований, сужающих ОДЗ. Почему? Для пояснения приведем пример.
Допустим нам нужно вычислить значение выражения при x=−1 . Если сразу подставить вместо переменной x число −1 , то мы найдем значение . А теперь представим, что мы из каких-то соображений предварительно преобразовали исходное выражение к виду , сузив тем самым ОДЗ. Вычисляем его значение, для этого подставляем вместо переменной x число −1 , и получаем выражение , которое не имеет смысла, так как под знаком корня оказывается отрицательное число. Такой подход привел нас к проблеме, которая возникла из-за того, что 2 входит в ОДЗ переменной x для исходного выражения, но уже не попадает в «суженную» ОДЗ переменной x для выражения, полученного после преобразования.
Так что надо придерживаться таких тождественных преобразований выражения, которые не изменяют ОДЗ.
А как быть с преобразованиями выражений, при которых расширяется ОДЗ? Их можно проводить, но при этом стоит придерживаться такого взгляда: полученное в результате преобразования выражение рассматривать на ОДЗ переменных исходного выражения.
Например, сокращение алгебраической дроби на x дает дробь и приводит к расширению ОДЗ от множества (−∞ 0)∪(0, +∞) до множества R . При этом можно продолжать работать с полученной дробью , но на ОДЗ переменной x для исходного выражения, то есть, на множестве (−∞ 0)∪(0, +∞) .
Еще пример. При замене суммы логарифмов lnx+ln(x+3) логарифмом произведения ln(x·(x+3)) (см. свойства логарифмов) происходит расширение ОДЗ с (0, +∞) до (−∞, −3)∪(0, +∞) . Поэтому с полученным выражением ln(x·(x+3)) дальше стоит работать на ОДЗ переменной x исходного выражения, то есть, на множестве (0, +∞) .
Итак, на каждом шаге преобразования выражения постоянно спрашивайте себя: «Не изменяет ли это преобразование ОДЗ»? Если не изменяет, то выполняйте его.
Если сужает, то откажитесь от него. А если расширяет, то выполняйте его, но оставайтесь в рамках ОДЗ переменных для исходного выражения.
Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.
В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.
Допустимые и недопустимые значения переменных
Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.
Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1 : а , если а = 0 , тогда оно не имеет смысла, так как делить на ноль нельзя.
То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.
Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.
Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.
То есть отсюда следует полное определение
Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.
Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.
Для примера рассмотрим выражение вида 1 x – y + z , где имеются три переменные. Иначе можно записать, как x = 0 , y = 1 , z = 2 , другая же запись имеет вид ( 0 , 1 , 2 ) . Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1 0 – 1 + 2 = 1 1 = 1 .
Отсюда видим, что ( 1 , 1 , 2 ) недопустимы. Подстановка дает в результате деление на ноль, то есть 1 1 – 2 + 1 = 1 0 .
Что такое ОДЗ?
Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.
Область ОДЗ – это множество значений, допустимых для данного выражения.
Рассмотрим на примере выражения.
Если имеем выражение вида 5 z – 3 , тогда ОДЗ имеет вид ( − ∞ , 3 ) ∪ ( 3 , + ∞ ) . Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.
Если имеется выражения вида z x – y , тогда видно, что x ≠ y , z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.
Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл.
Область определения функции совпадает с областью допустимых значений переменной х к выражению f ( x ) .
Как найти ОДЗ? Примеры, решения
Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.
Существуют выражения, где их вычисление невозможно:
- если имеется деление на ноль;
- извлечение корня из отрицательного числа;
- наличие отрицательного целого показателя – только для положительных чисел;
- вычисление логарифма отрицательного числа;
- область определения тангенса π 2 + π · k , k ∈ Z и котангенса π · k , k ∈ Z ;
- нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [ – 1 ; 1 ] .
Все это говорит о том, как важно наличие ОДЗ.
Найти ОДЗ выражения x 3 + 2 · x · y − 4 .
Решение
В куб можно возводить любое число.
Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.
Ответ: x и y – любые значения.
Найти ОДЗ выражения 1 3 – x + 1 0 .
Решение
Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.
Ответ: ∅ .
Найти ОДЗ заданного выражения x + 2 · y + 3 – 5 · x .
Решение
Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.
Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .
Определить ОДЗ выражения вида 1 x + 1 – 1 + log x + 8 ( x 2 + 3 ) .
Решение
По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 – 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 . Отсюда следует, что искомое ОДЗ примет вид:
x + 1 – 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1
Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0 ) ∪ ( 0 , + ∞ ) .
Ответ: [ − 1 , 0 ) ∪ ( 0 , + ∞ )
Почему важно учитывать ОДЗ при проведении преобразований?
При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
- могут не влиять на ОДЗ;
- могут привести в расширению или дополнению ОДЗ;
- могут сузить ОДЗ.
Рассмотрим на примере.
Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.
Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.
Рассмотрим пример с наличием подкоренного выражения.
Если имеется x – 1 · x – 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства ( x − 1 ) · ( x − 3 ) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) . После преобразования x – 1 · x – 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x – 1 ≥ 0 , x – 3 ≥ 0 .
При ее решении получаем, что [ 3 , + ∞ ) . Значит, ОДЗ полностью записывается так: ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) .
Нужно избегать преобразований, которые сужают ОДЗ.
Рассмотрим пример выражения x – 1 · x – 3 , когда х = – 1 . При подстановке получим, что – 1 – 1 · – 1 – 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x – 1 · x – 3 , тогда при вычислении получим, что 2 – 1 · 2 – 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.
Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.
Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.
Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится ( − ∞ 0 ) ∪ ( 0 , + ∞ ) . Причем при вычислении уже работаем со второй упрощенной дробью.
При наличии логарифмов дело обстоит немного иначе.
Если имеется выражение вида ln x + ln ( x + 3 ) , его заменяют на ln ( x · ( x + 3 ) ) , опираясь на свойство логарифма.
Отсюда видно, что ОДЗ с ( 0 , + ∞ ) до ( − ∞ , − 3 ) ∪ ( 0 , + ∞ ) . Поэтому для определения ОДЗ ln ( x · ( x + 3 ) ) необходимо производить вычисления на ОДЗ, то есть ( 0 , + ∞ ) множества.
При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.
Как найти область определения функции
После этого экскурса в важную составную матанализа многие согласятся, что найти
область определения функции не очень сложно. Ненамного сложнее, чем Московскую область на карте.
Во-первых, нужно различать виды функций (корень, дробь, синус и др.). Во-вторых,
решать уравнения и неравенства с учетом вида функции (например, на что нельзя делить, какое выражение
не может быть под знаком корня и тому подобное). Согласитесь, не так уж много и не так сложно.
Итак, чтобы находить области определения распространённых функций, порешаем
уравнения и неравенства с одной переменной. А в конце урока обобщим понятие на уровне теории. Пока же —
краткое определение. Область определения функции y=f(x)
— это множество значений X, для которых существуют значения Y.
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Приступаем к практике. На рисунке изображён график функции .
Знаменатель дроби не может быть равен нулю, так как на нуль делить нельзя. Поэтому, приравнивая знаменатель
нулю, получаем значение, не входящее в область определения функции: 1. То есть, область определения заданной функции —
это все значения «икса» от минус бесконечности до единицы и от единицы до плюс бесконечности. Это хорошо
видно на графике. Приведённый здесь пример функции относится к виду дробей. На уроке разберём решения
всех распространённых видов функций.
Пример 0. Как найти область
определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять)
()? Нужно всего лишь
решить неравенство
x — 5 ≥ 0,
так как для того, чтобы мы получили действительное значение игрека, подкоренное
выражение должно быть больше или равно нулю. Получаем решение: область определения функции — все значения икса
больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).
На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции
заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.
Постоянная (константа) определена при любых действительных
значениях x, следовательно, данная функция определена на всём
множестве R действительных чисел. Это можно записать и так:
областью определения данной функции является вся числовая прямая ]- ∞; + ∞[.
Пример 1. Найти область определения функции
y = 2.
Решение. Область определения функции не указана, значит, в силу выше приведённого
определения имеется в виду естественная область определения. Выражение
f(x) = 2 определено при любых действительных
значениях x, следовательно, данная функция определена на всём
множестве R действительных чисел.
Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус
бесконечности до плюс бесконечности.
В случае, когда функция задана формулой и n — натуральное число:
Пример 2. Найти область определения функции
.
Решение. Как следует из
определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно, то есть,
если — 1 ≤ x ≤ 1.
Следовательно, область определения данной функции — [- 1; 1].
Заштрихованная область числовой прямой на чертеже сверху — это область определения
данной функции.
Область определения степенной функции с целым показателем степени
В случае, когда функция задана формулой :
если a — положительное, то областью определения функции является множество
всех действительных чисел, то есть ]- ∞; + ∞[;
если a — отрицательное, то областью определения функции является
множество ]- ∞; 0[ ∪ ]0 ;+ ∞[,
то есть вся числовая прямая за исключением нуля.
На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка,
соответствующая нулю, выколота (она не входит в область определения функции).
Пример 3. Найти область определения функции
.
Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором
слагаемом можно представить в виде единицы — так же целого числа.
Следовательно, область определения данной функции — вся числовая прямая, то есть
]- ∞; + ∞[.
Область определения степенной функции с дробным показателем степени
В случае, когда функция задана формулой :
если
— положительное, то областью определения функции является множество [0; + ∞[;
если
— отрицательное, то областью определения функции является множество ]0; + ∞[.
Пример 4. Найти область определения функции
.
Решение. Оба слагаемых в выражении функции — степенные функции с положительными
дробными показателями степеней. Следовательно, область определения данной функции —
множество [0; + ∞[.
На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше,
причём штриховка продолжается вместе с самой прямой до плюс бесконечности.
Пример 5. Найти область определения функции
.
Решение. Дробный показатель степени данной степенной функции — отрицательный.
Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля::
.
Дикриминант получился отрицательный. Следовательно сопряжённое неравенству
квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях
«икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или,
что то же самое — множество R действительных чисел, или,
что то же самое — ]- ∞; + ∞[.
Область определения показательной функции
В случае, когда функция задана формулой ,
областью определения функции является вся числовая прямая, то есть
]- ∞; + ∞[.
Область определения логарифмической функции
Логарифмическая функция
определена при условии, если её аргумент положителен, то есть, областью её определения является множество
]0; + ∞[.
Найти область определения функции самостоятельно, а затем посмотреть решение
Область определения функции y = cos(x) —
так же множество R действительных чисел.
Область определения функции y = tg(x) —
множество R действительных чисел, кроме чисел
.
Область определения функции y = ctg(x) —
множество R действительных чисел, кроме чисел
.
Пример 8. Найти область определения функции
.
Решение. Внешняя функция — десятичный логарифм и на область её определения
распространяются условия области определения логарифмической функции вообще. То есть, её аргумент
должен быть положительным. Аргумент здесь — синус «икса». Поворачивая воображаемый циркуль по
окружности, видим, что условие sin x > 0
нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи»
и любого чётного или нечётного целого числа.
Таким образом, область определения данной функции задаётся выражением
,
где k — целое число.
Область определения обратных тригонометрических функций
Область определения функции y = arcsin(x) —
множество [-1; 1].
Область определения функции y = arccos(x) —
так же множество [-1; 1].
Область определения функции y = arctg(x) —
множество R действительных чисел.
Область определения функции y = arcctg(x) —
так же множество R действительных чисел.
Пример 9. Найти область определения функции
.
Решение. Решим неравенство:
Таким образом, получаем область определения данной функции — отрезок
[- 4; 4].
Пример 10. Найти область определения функции
.
Решение. Решим два неравенства:
Решение первого неравенства:
Решение второго неравенства:
Таким образом, получаем область определения данной функции — отрезок
[0; 1].
Если функция задана дробным выражением, в котором переменная находится в знаменателе
дроби, то областью определения функции является множество R действительных чисел,
кроме таких x, при которых знаменатель дроби обращается в нуль.
Пример 11. Найти область определения функции
.
Решение. Решая равенство нулю знаменателя дроби, находим область определения данной функции — множество
]- ∞; — 2[ ∪ ]- 2 ;+ ∞[.
Пример 12. Найти область определения функции
.
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции —
]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[.
Пример 13. Найти область определения функции
.
Решение. Область определения первого слагаемого — данной функции — множество
R действительных чисел, второго слагаемого — все
действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять
условиями определения обоих слагаемых. Следовательно, область определения данной функции — все
x, кроме -2 и 2.
Пример 14. Найти область определения функции
.
Решение. Решим уравнение:
Уравнение не имеет действительных корней. Но функция определена только на действительных
числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что
то же самое — множество R действительных чисел или,
что то же самое — ]- ∞; + ∞[.
То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не
будет равен нулю.
Пример 15. Найти область определения функции
.
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции —
]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[.
Пример 16. Найти область определения функции
.
Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под
корнем не может быть отрицательным. Сначала решим уравнение:
График квадратичной функции под корнем представляет собой параболу, ветви которой
направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках
1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения
квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена
на отрезке [1; 2].
Найти область определения функции самостоятельно, а затем посмотреть решение
Если функция задана формулой вида y = kx + b,
то область определения функции — множество
R действительных чисел.
А теперь обобщим решения рассмотренных примеров. Каждой точке графика функции соответствуют:
- определённое значение «икса» — аргумента функции;
- определённое значение «игрека» — самой функции.
Верны следующие факты.
- От аргумента — «икса» — вычисляется «игрек» — значения функции.
- Область определения функции — это множества всех значений «икса», для которых существует, то есть может
быть вычислен «игрек» — значение функции. Иначе говоря, множество значений аргумента, на котором
«функция работает».
Весь раздел «Исследование функций»
Реферат по математике «Область определения и область значений функции»
Область определения и область значений функции.
Определение:
Множество первых элементов пары f f называется областью определения , а множество вторых элементов называется множеством значений . Область определения и множество значений функции обозначаются как D f и R f соответственно.
Функция y= f(x) y = f ( x ) — это такая зависимость переменной y от переменной x , когда каждому допустимому значению переменной x соответствует единственное значение переменной y .
Областью определения функции D(f) D ( f ) называют множество всех допустимых значений переменной x .
Область значений функции E(f) E ( f ) — множество всех допустимых значений переменной y .
Область определения функции
Начнем с исследования области определения и области значений функций. Вспомним, что областью определения функции называют все возможные значения аргумента (мы говорим о естественной области определения). Обычно область определения обозначают как . Пока что мы знаем только две недопустимые операции – это деление на ноль и извлечение квадратного корня из отрицательного числа.
Поэтому при нахождении области определения функции ограничения появляются в двух случаях.
-
В функции есть деление на переменные. В этом случае приравниваем знаменатель дроби к нулю. Решая полученное уравнение, получаем недопустимые значения аргумента . Тогда областью определения будут все действительные числа, кроме недопустимых значений.
-
В функции есть операция извлечения корня. Тогда подкоренное выражение должно быть неотрицательным. Записываем соответствующее неравенство. Множество решений этого неравенства и будет областью определения функции.
Краткая запись промежутков
Область определения мы смогли описать словами: все действительные числа, кроме . Но словесное описание в математике редко встречается, ведь обычно оно получается громоздким. Поэтому вводят специальные обозначения.
Так, если мы хотим указать на множество чисел, лежащих в некотором промежутке, то выполняем следующие действия.
-
Через точку с запятой указываем два числа: левую и правую границы промежутка.
-
Если граница входит в промежуток, ставим возле нее квадратную скобку, если не входит – круглую.
-
Если у промежутка нет правой границы, записываем ее как (или ). Если нет левой границы, пишем .
-
Если нужно описать множество, состоящее из нескольких промежутков, ставим между ними знак объединения: .
Например, все действительные числа от до включительно можно записать так: . Все положительные числа можно описать как . Ноль не является положительным числом, поэтому скобка возле него круглая, возле бесконечности скобка всегда круглая.
В примере с областью определения мы получили два промежутка: все числа, большие и все числа, меньшие . Поэтому и записали два соответствующих промежутка , поставив между ними знак объединения.
Область значений функции
Область (или множество) значений функции – это все возможные значения . Область значений принято обозначать .
Вспомним графики базовых функций и их области значений:
-
Линейная функция — это функция вида y=kx+b y = k x + b , где k и b некоторые действительные числа. Если b=0 b = 0 , то функция примет вид y=kx y = k x и будет называться прямой пропорциональностью .x, где a=const, a > 0, , a ≠ 1 D(f) : x ∈ R ; E ( f ) : y ∈ ( 0 ; + ∞ ) . Графиком показательной функции является экспонента.
-
Логарифмическая функция;
-
Тригонометрическая функция;
-
Обратные тригонометрические функции;
Область и диапазон функции
Определения домена и диапазона
Домен
Домен а
функция — это полный набор возможных значений
независимой переменной.
На простом английском языке это определение означает:
Домен — это совокупность всех возможных
x — значения, которые сделают функцию
«работа» и выдаст реальные значения и .
При нахождении домена запомните:
- Знаменатель (внизу) дроби не может быть
ноль - Число под знаком квадратного корня должно быть
положительный в этом разделе
Пример 1а
Вот график y = sqrt (x + 4):
12345-1-2-3-4123xy
Домен: `x> = — 4`
Область определения этой функции — `x ≥ −4`, так как x не может быть меньше, чем` −4`.Чтобы понять, почему, попробуйте в вашем калькуляторе некоторые числа меньше, чем «−4» (например, «−5» или «−10»), и некоторые числа больше, чем «−4» (например, «−2» или «8»). Единственные, которые «работают» и дают нам ответ, — это те, которые больше или равны «−4». Это сделает число под квадратным корнем положительным.
Примечания:
- Закрашенный кружок в точке `(-4, 0)`. Это указывает на то, что домен «запускается» в этот момент.
- Мы видели, как рисовать подобные графики в разделе 4, График функции.2 = х — 2.
Как найти домен
В общем, мы определяем область каждой функции, ища те значения независимой переменной (обычно x ), которые разрешено использовать . (Обычно нам нужно избегать 0 в нижней части дроби или отрицательных значений под знаком квадратного корня).
Диапазон
Диапазон из
функция — это полный набор всех возможных
результирующих значений зависимой переменной ( y, обычно ) после того, как мы подставили домен.
На простом английском языке это определение означает:
Диапазон — это результат
y — значения , которые мы получаем после подстановки всех возможных значений x .
Как найти диапазон
- Диапазон функции — это разброс возможных значений y (от минимального y -значения до максимального y -значения)
- Подставьте различные значения x в выражение для y на
посмотреть, что происходит.(Спросите себя: всегда ли и положительны? Всегда отрицательны? Или, может быть, не равны определенным значениям?) - Убедитесь, что вы ищете минимум и максимум значений y .
- Нарисуйте эскиз ! В математике картина стоит тысячи слов.
Пример 1б
Вернемся к примеру выше, `y = sqrt (x + 4)`.
Мы замечаем, что кривая находится либо на горизонтальной оси, либо над ней.Независимо от того, какое значение x мы попробуем, мы всегда получим нулевое или положительное значение y . Мы говорим, что диапазон в этом случае равен y ≥ 0.
12345-1-2-3-4123xy
Диапазон: `y> = 0`
Кривая всегда продолжается вертикально, за пределы того, что показано на графике, поэтому диапазон — это все неотрицательные значения `y`.
Пример 2
График кривой y = sin x показывает диапазон между -1 и 1.
12345-1-2-3-4-5-6-71-1xy
Диапазон: `-1
Область y = sin x — это «все значения x », поскольку нет никаких ограничений на значения для x . (Введите любое число в функцию «sin» в вашем калькуляторе. Любое число должно работать и даст вам окончательный ответ от -1 до 1.)
Эксперимент с калькулятором и наблюдение кривой показывают, что диапазон составляет y между -1 и 1.Мы могли бы записать это как −1 ≤ y ≤ 1.
Откуда взялся этот график? Мы узнаем о графиках sin и cos позже в Графах греха x и cos x
Примечание 1: Поскольку мы предполагаем, что для значений x должны использоваться только действительные числа, числа, которые приводят к делению на ноль или к мнимым числам (которые возникают при нахождении квадратного корня из отрицательное число) не включаются.В главе «Комплексные числа» подробно рассказывается о мнимых числах, но мы не включаем такие числа в эту главу.
Примечание 2: При выполнении примеров квадратного корня многие люди спрашивают: «Разве мы не получаем 2 ответа, один положительный и один отрицательный, когда мы находим квадратный корень?» Квадратный корень имеет не более одного значения, а не два. См. Это обсуждение: Квадратный корень 16 — сколько ответов?
Примечание 3: Мы говорим о домене и диапазоне функций , которые имеют не более , одно значение y для каждого значения x , а не отношений (которые могут иметь более одного . 2-9),` без использования графика.2-9`, которое, как мы понимаем, можно записать как `(x + 3) (x-3)`. Таким образом, наши значения для `x` не могут включать` -3` (из первой скобки) или `3` (из второй).
В любом случае нам не нужно беспокоиться о «-3», потому что на первом этапе мы решили, что «x> = -2».
Таким образом, домен для этого случая — `x> = -2, x! = 3`, который мы можем записать как` [-2,3) uu (3, oo) `.
Для определения диапазона мы рассматриваем верхнюю и нижнюю части дроби отдельно.
Числитель: Если `x = -2`, верхняя часть имеет значение` sqrt (2 + 2) = sqrt (0) = 0`.2-9) `приближается к` 0`, поэтому `f (x)` переходит в `-oo`, когда приближается к` x = 3`.
Для `x> 3`, когда` x` просто больше, чем `3`, значение дна чуть больше` 0`, поэтому `f (x)` будет очень большим положительным числом.
Для очень большого `x` верхняя часть будет большой, но нижняя будет намного больше, поэтому в целом значение функции будет очень маленьким.
Таким образом, мы можем заключить, что диапазон равен `(-oo, 0] uu (oo, 0)`.
Посмотрите на график (который мы все равно рисуем, чтобы убедиться, что мы на правильном пути):
Показать график
Мы можем видеть на следующем графике, что действительно домен равен «[-2,3) uu (3, oo)» (который включает «-2», но не «3»), а диапазон — «все значения из `f (x)`, кроме `F (x) = 0`.2-9) `.
Сводка
В общем, мы определяем домен по
ищем те значения независимой переменной (обычно x ), которые у нас разрешено использовать . (Мы должны избегать 0 в нижней части дроби или отрицательных значений под знаком квадратного корня).
Диапазон находится путем нахождения результирующих значений y после замены возможных значений x .
Упражнение 1
Найдите домен и диапазон для каждого из следующих.2+ 2`.
Ответ
Домен: Функция
f ( x ) = x 2 + 2
определен
для всех реальных значений x (поскольку нет ограничений на значение x ).
Следовательно, область `f (x)` равна
«все реальные значения x «.
Диапазон: Поскольку x 2 никогда не бывает отрицательным,
x 2 + 2 никогда не меньше `2`
Следовательно, диапазон `f (x)` равен
«все действительные числа` f (x) ≥ 2` «.
Мы видим, что x может принимать любое значение на графике, но результирующие значения y = f ( x ) больше или равны 2.
123-1-2-312345678910-1xf (x)
Диапазон: `y> = 2`
Домен: Все `x`
Примечание
- При построении графиков важно обозначить оси как . Это помогает понять, что представляет собой график.
- Мы видели, как рисовать такие графики в Графике функции.
(б) `f (t) = 1 / (t + 2)`
Ответ
Домен: Функция
`f (t) = 1 / (t + 2)`
не определено для т =
-2, так как это значение приведет к делению на ноль. (Внизу дроби будет 0.)
Следовательно, домен из f ( t ) равен
«все
вещественные числа кроме -2 «
Диапазон: Независимо от того, насколько большим или малым становится т ,
f ( t ) никогда не будет равно нулю.
[ Почему? Если мы попытаемся решить уравнение относительно 0, произойдет следующее:
`0 = 1 / (t + 2)`
Умножаем обе стороны на ( t + 2) и получаем
`0 = 1`
Это невозможно.]
Таким образом, диапазон для f ( t ) равен
«все
вещественные числа кроме нуля ».
На графике видно, что функция не определена для t = -2 и что функция (значения y ) принимает все значения, кроме 0.
1234-1-2-3-4-5-6-712345-1-2-3-4-5tf (t)
Домен: Все `t ≠ -2`
Диапазон: Все `f (t) ≠ 0`
(c) `g (s) = sqrt (3-s)`
Ответ
Функция
`г (т) = sqrt (3-с)`
не определен для реального
числа больше 3, что приведет к мнимым значениям
для г ( с ). 2 + 4` для
`x> 2`
Ответ
Функция `f (x)` имеет область из
«все действительные числа,` x> 2` «, как определено в вопросе.(Здесь не используются квадратные корни из отрицательных чисел или деления на ноль.)
Чтобы найти диапазон :
- Когда `x = 2`,` f (2) = 8`
- Когда x увеличивается с `2`,` f (x) `становится
больше, чем `8` (попробуйте подставить некоторые числа, чтобы понять, почему)
Следовательно, диапазон — это «все действительные числа,` f (x)> 8` »
Вот график функции с белым кружком в «(2, 8)», что указывает на то, что домен не включает «x = 2», а диапазон не включает «f (2) = 8».
123456510152025xf (x) (2, 
Домен: Все `x> 2`
Диапазон:
Все `f (x)> 8`
Функция является частью параболы. [Подробнее о параболе.]
Упражнение 2
Мы запускаем шар в воздух и находим
высота h , в метрах, как функция времени
т , в секундах, равно
ч = 20 т — 4,9 т 2
Найдите домен и диапазон для функции
ч ( т ).
Ответ
Как правило, отрицательные значения времени не имеют
имея в виду. Кроме того, нам нужно предположить, что снаряд попадает в землю, а затем останавливается — он не уходит под землю.
Итак, нам нужно рассчитать, когда он упадет на землю. Это будет, когда h = 0. Итак, решаем:
20 т — 4,9 т 2 = 0
Факторинг дает:
(20 — 4.9 т ) т = 0
Это верно, когда
`t = 0 » s «`,
или
`t = 20/4.9 = 4.082 текст (ы) `
Следовательно, домен функции h равен
«все реально
значения t такие, что `0 ≤ t ≤ 4.082`»
Из выражения функции видно, что это парабола с вершиной вверх. (Это имеет смысл, если вы думаете о подбрасывании мяча вверх. Он поднимается на определенную высоту, а затем падает обратно.)
Какое максимальное значение ч ? Воспользуемся формулой максимума (или минимума) квадратичной функции.
Значение т. дает максимальное значение
.
`t = -b / (2a) = -20 / (2 xx (-4.9)) = 2.041 с`
Таким образом, максимальное значение —
.
20 (2,041) — 4,9 (2,041) 2 = 20,408 м
Наблюдая за функцией h , мы видим, что по мере увеличения t , h сначала увеличивается до максимума.
20,408 м, затем ч снова уменьшается до нуля, как и ожидалось.
Следовательно, диапазон h равен
«все реально
числа, `0 ≤ h ≤ 20,408`»
Вот график функции h :
1234565101520-5-й (t)
Домен: `0
Диапазон:
`0
Функции, определяемые координатами
Иногда у нас нет непрерывных функций. Что нам делать в этом случае? Давайте посмотрим на пример.
Упражнение 3
Найдите область и диапазон функции, заданной координатами:
`{(−4, 1), (−2, 2.5), (2, −1), (3, 2)} `
Ответ
Область — это просто следующие значения x : `x = {−4, −2, 2, 3}`
Диапазон состоит из следующих значений `f (x)`: `f (x) = {−1, 1, 2, 2.5}`
Вот график нашей разрывной функции.
1234-1-2-3-41234-1-2-3-е (т) (3, 2) (2, -1) (- 4, 1)
(-2, 2,5)
Область и диапазон функции — объяснение и примеры
В этой статье объясняется область и диапазон среднего значения функции, а также способы вычисления двух величин. Прежде чем перейти к теме домена и диапазона, давайте кратко опишем, что такое функция.
В математике мы можем сравнить функцию с машиной, которая генерирует некоторый результат в корреляции с заданным входом . На примере машины для чеканки монет мы можем проиллюстрировать значение функции следующим образом.
Когда вы вставляете монету в монетоприемник, в результате получается штампованный и сплющенный кусок металла. Рассматривая функцию, мы можем связать монету и сплющенный кусок металла с доменом и диапазоном.В этом случае функцией считается машина для чеканки монет.
Так же, как станок для штамповки монет, который может производить только один сплющенный кусок металла за один раз, функция работает таким же образом, выдавая один результат за один раз.
История функции
Идея функции появилась в начале семнадцатого века, когда Рене Декарт (1596-1650) использовал эту концепцию в своей книге «Геометрия» (1637) для моделирования математических задач.
Пятьдесят лет спустя, после публикации «Геометрии», Готфрид Вильгельм Лейбниц (1646-1716) ввел термин «функция». Позже Леонард Эйлер (1707-1783) сыграл большую роль, введя технику понятия функции y = f (x).
Реальное применение функции
Функции очень полезны в математике, потому что они позволяют нам моделировать реальные проблемы в математическом формате.
Вот несколько примеров применения функции.
-
Окружность окружности
Окружность окружности зависит от ее диаметра или радиуса. Мы можем математически представить это утверждение как:
C (d) = dπ или C (r) = 2π⋅r
Длина тени объекта является функцией его высоты.
-
Положение движущегося объекта
Местоположение движущегося объекта, например автомобиля, зависит от времени.
Температура тела зависит от нескольких факторов и входных данных.
Сложный или простой процент зависит от времени, основной суммы и процентной ставки.
Высота объекта зависит от его возраста и массы тела.
Теперь, узнав о функции, можно перейти к вычислению области и диапазона функции.
Какова область и диапазон функции?
Область функции — это входные числа, которые при подключении к функции определяют результат. Проще говоря, мы можем определить область определения функции как возможные значения x, которые сделают уравнение истинным.
Некоторые из случаев, когда функция не может быть действительной, — это когда уравнение делится на ноль или отрицательный квадратный корень.
Например, f ( x ) = x 2 является допустимой функцией, потому что независимо от того, какое значение x можно подставить в уравнение, всегда есть правильный ответ. По этой причине мы можем заключить, что область определения любой функции — это действительные числа.
Диапазон функции определяется как набор решений уравнения для заданного входа.Другими словами, диапазон — это результат или значение y функции. Для данной функции существует только один диапазон.
Как использовать обозначения интервалов для указания домена и диапазона?
Поскольку диапазон и область определения функции обычно выражаются в интервальной записи, важно обсудить концепцию интервальной записи.
Процедура записи интервалов включает:
- Запишите числа, разделенные запятой, в порядке возрастания.
- Заключите числа в круглые скобки (), чтобы показать, что значение конечной точки не включено.
- Используйте квадратные скобки [], чтобы заключить числа, когда включено значение конечной точки.
Как найти домен и диапазон функции?
Мы можем определить область определения функции либо алгебраически, либо графическим методом. Чтобы вычислить область определения функции алгебраически, вы решаете уравнение, чтобы определить значения x.
У разных типов функций есть свои методы определения своей области.
Давайте рассмотрим эти типы функций и способы вычисления их области.
Как найти область определения функции без знаменателя и радикалов?
Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.
Пример 1
Найдите область определения f (x) = 5x — 3
Решение
Областью определения линейной функции являются все действительные числа, поэтому
Область: (−∞, ∞)
Диапазон: (−∞, ∞)
Функция с радикалом
Пример 2
Найти область определения функции f (x) = — 2x 2 + 12x + 5
Решение
Функция f (x) = −2x 2 + 12x + 5 является квадратичным многочленом, поэтому область определения (−∞, ∞)
Как найти область для рационального функция с переменной в знаменателе?
Чтобы найти область определения функции этого типа, установите знаменатель на ноль и вычислите значение переменной.
Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.
Пример 3
Определите область значений x − 4 / (x 2 −2x − 15)
Решение
Установите знаменатель равным нулю и решите относительно x
⟹ x 2 — 2x — 15 = (x — 5) (x + 3) = 0
Следовательно, x = −3, x = 5
Чтобы знаменатель не был равен нулю, нам нужно избегать чисел −3 и 5 Таким образом, домен состоит из действительных чисел, кроме −3 и 5.
Пример 4
Вычислить область и диапазон функции f (x) = -2 / x.
Решение
Установите знаменатель на ноль.
⟹ x = 0
Следовательно, домен: все действительные числа, кроме 0.
Диапазон — это все действительные значения x, кроме 0.
Пример 5
Найдите домен и диапазон следующей функции .
f (x) = 2 / (x + 1)
Решение
Установите знаменатель равным нулю и решите относительно x.
x + 1 = 0
= -1
Поскольку функция не определена, когда x = -1, доменом являются все действительные числа, кроме -1. Точно так же диапазон — это все действительные числа, кроме 0
Как определить домен для функции с переменной внутри знака корня?
Для нахождения области определения функции членам внутри радикала задается неравенство> 0 или ≥ 0. Затем определяется значение переменной.
Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.
Пример 6
Найдите область определения f (x) = √ (6 + x — x 2 )
Решение
Чтобы избежать квадратных корней из отрицательных чисел, мы задаем выражение внутри знака корня до ≥ 0.
6 + x — x 2 ≥ 0 ⟹ x 2 — x — 6≤ 0
⟹ x 2 — x — 6 = (x — 3) (x +2) = 0
Следовательно, функция равна нулю, если x = 3 или x = -2
Следовательно, домен: [−2, 3]
Пример 7
Найдите область определения f ( x) = x / √ (x 2 — 9)
Решение
Установите выражение внутри знака радикала равным x 2 — 9> 0
Найдите переменную, чтобы получить;
x = 3 или — 3
Следовательно, домен: (−∞, −3) & (3, ∞)
Пример 8
Найдите область определения f (x) = 1 / √ ( x 2 -4)
Решение
Разложив знаменатель на множители, мы получим x ≠ (2, — 2).
Проверьте свой ответ, подставив -3 в выражение внутри знака корня.
⟹ (-3) 2 — 4 = 5
также попробуйте с нулем
⟹ 0 2 — 4 = -4, поэтому числа от 2 до -2 недействительны
Попробуйте число больше 2
⟹ 3 2 — 4 = 5. Это верно.
Следовательно, домен = (-∞, -2) U (2, ∞)
Как найти область определения функции с помощью натурального логарифма (ln)?
Чтобы найти домен функции с использованием натурального логарифма, установите для членов в круглых скобках значение> 0 и затем решите.
Давайте посмотрим на пример ниже, чтобы понять этот сценарий.
Пример 9
Найти область определения функции f (x) = ln (x —
Решение
⟹ x — 8> 0
⟹ x — 8 + 8> 0 + 8
⟹ x> 8
Домен: (8, ∞)
Как найти домен и диапазон отношения?
Отношение — это актив координат x и y. Чтобы найти домен и диапазон в отношении, просто укажите значения x и y соответственно.
Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.
Пример 10
Укажите область и диапазон отношения {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3) }
Решение
Перечислите значения x. Домен: {2, 3, 4, 6}
Список значений y. диапазон: {–3, –1, 3, 6}
Пример 11
Найдите домен и диапазон отношения {(–3, 5), (–2, 5), (–1, 5), (0, 5), (1, 5), (2, 5)}
Решение
Домен {–3, –2, –1, 0, 1, 2} и диапазон равно {5}
Пример 12
Учитывая, что R = {(4, 2) (4, -2), (9, 3) (9, -3)}, найдите домен и диапазон Р.
Решение
Домен представляет собой список первых значений, поэтому D = {4, 9} и диапазон = {2, -2, 3, -3}
Предыдущий урок | Главная страница | Следующий урок
Домен и диапазон
В
домен
из
функция
ж
(
Икс
)
— это набор всех значений, для которых определена функция, а
диапазон
функции — это набор всех значений, которые
ж
берет.
(В гимназии вы, вероятно, называли домен набором замены, а диапазон — набором решений. Их также можно было назвать входом и выходом функции.)
Пример 1:
Рассмотрим функцию, показанную на диаграмме.
Здесь домен — это множество
{
А
,
B
,
C
,
E
}
.D
не входит в домен, так как функция не определена для
D
.
Диапазон — это набор
{
1
,
3
,
4
}
.
2
не входит в диапазон, так как в домене нет буквы, которая сопоставляется с
2
.
Вы также можете поговорить о домене
связь
, где один элемент в домене может быть сопоставлен более чем с одним элементом в диапазоне.
Пример 2:
Рассмотрим соотношение
{
(
0
,
7
)
,
(
0
,
8
)
,
(
1
,
7
)
,
(
1
,
8
)
,
(
1
,
9
)
,
(
2
,
10
)
}
.
Здесь отношение задано как набор упорядоченных пар. Домен — это набор
Икс
-координаты,
{
0
,
1
,
2
}
, а диапазон — это набор
у
-координаты,
{
7
,
8
,
9
,
10
}
. Обратите внимание, что элементы домена
1
а также
2
связаны с более чем одним элементом диапазона, поэтому это
нет
функция.
Но чаще, особенно при работе с графиками на координатной плоскости, мы имеем дело с функциями, в которых каждый элемент области связан с одним элементом диапазона. (См.
Тест вертикальной линии
.)
Пример 3:
Область определения функции
ж
(
Икс
)
знак равно
1
Икс
все действительные числа, кроме нуля (так как at
Икс
знак равно
0
, функция не определена: деление на ноль недопустимо!).
Диапазон также состоит из действительных чисел, кроме нуля. Вы можете видеть, что на кривой есть точка для каждого
у
-значение кроме
у
знак равно
0
.
Домены также могут быть указаны явно, если есть значения, для которых функция может быть определена, но которые мы не хотим рассматривать по какой-то причине.
Пример 4:
Следующие обозначения показывают, что область определения функции ограничена интервалом
(
—
1
,
1
)
.
ж
(
Икс
)
знак равно
Икс
2
,
—
1
<
Икс
<
1
График этой функции показан на рисунке. Обратите внимание на белые кружки, которые показывают, что функция не определена в
Икс
знак равно
—
1
а также
Икс
знак равно
1
. В
у
-значения варьируются от
0
вплоть до
1
(в том числе
0
, но не включая
1
).Таким образом, диапазон функции
0
≤
у
<
1
.
Домен и Диапазон | Безграничная алгебра
Введение в домен и диапазон
Область функции — это набор всех возможных входных значений, которые производят некоторый диапазон выходных значений
Цели обучения
Определите область и диапазон функции
Ключевые выводы
Ключевые моменты
- Для данной функции [latex] f [/ latex] набор значений [latex] x [/ latex] (входов) является доменом [latex] f [/ latex], а набор [latex] y [/ latex] значения (выходы) — это диапазон [latex] f [/ latex].
- Область определения функции [latex] f [/ latex] — это все значения, для которых функция определена. Например, [latex] frac {1} {x} [/ latex] не определяется, если [latex] x = 0 [/ latex]. Кроме того, [latex] sqrt {x} [/ latex] не определяется, если [latex] x [/ latex] отрицательно.
- Чтобы найти домен функции [latex] f [/ latex], вы должны найти значения, для которых [latex] f [/ latex] не определено. Итак, домен для [latex] sqrt {x} [/ latex] — [latex] x geq 0 [/ latex].
Ключевые термины
- домен : набор всех точек, по которым определяется функция.
- диапазон : набор значений, которые функция принимает в качестве выходных данных.
- функция : отношение между двумя величинами, называемыми входом и выходом; для каждого входа есть ровно один выход.
Каковы область и диапазон функции?
Область функции — это набор входных значений [latex] x [/ latex], для которых определена функция. Домен показан в левом овале на картинке ниже. Функция предоставляет выходное значение [latex] f (x) [/ latex] для каждого члена домена.Набор значений, которые выводит функция, называется диапазоном функции, и эти значения показаны в правом овале на рисунке ниже. Функция — это отношение, которое принимает входные данные домена и выводит значения в диапазоне. Правило для функции состоит в том, что для каждого входа есть ровно один выход.
Отображение функции: Овал слева — это домен функции [latex] f [/ latex], а овал справа — это диапазон.Зеленые стрелки показывают, как каждый член домена сопоставляется с определенным значением диапазона.
Как вы можете видеть на иллюстрации, у каждого значения домена есть зеленая стрелка, указывающая ровно одно значение диапазона. Следовательно, это отображение является функцией.
По набору упорядоченных пар, заданных в этом отображении, мы также можем сказать, что это функция, потому что ни одно из значений [latex] x [/ latex] не повторяется: [latex] (- 1,1), (1,1 ), (7,49), (0,5,0,25) [/ латекс]; поскольку каждый вход соответствует ровно одному выходу.(Обратите внимание, что хотя выходное значение [latex] 1 [/ latex] повторяется, только входные значения не могут повторяться)
Мы также можем сказать это отображение, и набор упорядоченных пар является функцией, основанной на графике упорядоченных пар, потому что точки не образуют вертикальную линию. Если бы значение [latex] x [/ latex] повторялось, были бы две точки, составляющие график вертикальной линии, что не было бы функцией. Давайте посмотрим на это отображение и список упорядоченных пар, построенных на декартовой плоскости.
Упорядоченные пары: Это отображение или набор упорядоченных пар является функцией, потому что точки не образуют вертикальную линию.2 [/ латекс].
Важно отметить, что не все функции имеют набор действительных чисел в качестве своей области. Например, функция [latex] f (x) = frac {1} {x} [/ latex] не определена для [latex] x = 0 [/ latex], потому что вы не можете разделить число на [latex] 0 [/ латекс]. В этом случае домен [latex] f [/ latex] представляет собой набор всех действительных чисел , кроме [latex] 0 [/ latex]. То есть [латекс] х neq0 [/ латекс]. Таким образом, область определения этой функции — [latex] mathbb {R} — {0 } [/ latex].
А как насчет функции [латекс] f (x) = sqrt {x} [/ latex]? В этом случае квадратный корень из отрицательного числа не определен, поэтому домен представляет собой набор всех действительных чисел, где [latex] x geq0 [/ latex].
Поиск домена и диапазона: задана функция
Чтобы найти домен функции, если он не указан с самого начала, нам нужно посмотреть на определение функции, чтобы определить, какие значения не разрешены. Например, мы знаем, что нельзя извлечь квадратный корень из отрицательного числа и нельзя разделить на [латекс] 0 [/ латекс]. Обладая этими знаниями, давайте найдем область определения функции.
Пример 1: Найдите домен:
[латекс] displaystyle f (x) = frac {1} { sqrt {x-1} -2} + x [/ latex]
Во-первых, мы знаем, что не можем разделить на [latex] 0 [/ latex], поэтому любое значение [latex] x [/ latex], которое вызывает деление на [latex] 0 [/ latex], не допускается в домене.В этом примере это происходит, когда:
[латекс] displaystyle sqrt {x-1} -2 = 0 [/ латекс]
Решая для [latex] x [/ latex], это происходит, когда [latex] x = 5 [/ latex], поэтому мы знаем, что [latex] x neq5 [/ latex].
Мы также знаем, что нельзя извлекать квадратный корень из отрицательного числа. Это означает, что:
[латекс] displaystyle x-1> 0 [/ латекс]
После решения для [latex] x [/ latex] мы видим, что [latex] x> 1 [/ latex]. Таким образом, домен этой функции — это набор всех действительных чисел, таких что [latex] x> 1 [/ latex] и [latex] x neq5 [/ latex].
Следовательно, чтобы найти, какие значения отсутствуют в домене, вы должны найти значения, в которых функция не определена.
Визуализация области и диапазона
Все значения в домене отображаются на значения в диапазоне, которые отображаются в виде графиков функций
Цели обучения
Используйте график функции, чтобы определить ее домен и диапазон
Ключевые выводы
Ключевые моменты
- Значения в домене отображаются на значения в диапазоне.
- Тест горизонтальной и вертикальной линии может помочь определить тип связи между доменом и диапазоном.
Ключевые термины
- диапазон : Набор значений (точек), которые может получить функция.
- домен : набор всех точек, по которым определяется функция.
- функция : любая математическая формула, которая дает один и только один результат для каждого ввода.
Обзор домена, диапазона и функций
Как указано в предыдущем разделе, область функции — это набор «входных» значений [latex] (x) [/ latex], для которых функция определена.{2} [/ latex] имеет диапазон [latex] f (x) geq0 [/ latex], потому что квадрат числа всегда дает положительный результат.
С учетом как области, так и диапазона, функция — это любая математическая формула, которая дает один и только один результат для каждого ввода. Следовательно, каждое заданное значение домена в результате имеет одно и только одно значение диапазона, но не обязательно наоборот. Другими словами, два разных значения [latex] x [/ latex] могут иметь одинаковое значение [latex] y [/ latex], но каждое значение [latex] y [/ latex] должно быть объединено с отдельным [ латекс] х [/ латекс] -значение.3 [/ латекс].
Пример 1: Определите область и диапазон каждого графика, изображенного ниже:
Оба графика включают все действительные числа [latex] x [/ latex] в качестве входных значений, поскольку оба графика продолжают влево (отрицательные значения) и вправо (положительные значения) для [latex] x [/ latex] (входные данные) . Кривые уходят в бесконечность в обоих направлениях; поэтому мы говорим, что домен для обоих графов — это набор всех действительных чисел, обозначенных как: [latex] mathbb {R} [/ latex].
Если теперь мы посмотрим на возможные выходы или значения [latex] y [/ latex], [latex] f (x) [/ latex], (глядя вверх и вниз по оси [latex] y [/ latex], обратите внимание, что красный график НЕ включает отрицательные значения [latex] y [/ latex], тогда как синий график включает как положительные, так и отрицательные значения.3 [/ latex] (синий), поскольку все действительные числа могут быть входными значениями. Однако диапазон красного графика ограничен только значениями [latex] f (x) geq0 [/ latex] или [latex] y [/ latex] выше или равными [latex] 0 [/ latex]. Диапазон синего графика — все действительные числа, [latex] mathbb {R} [/ latex].
Пример 2:
Определите область и диапазон каждого графика, изображенного ниже:
График домена и диапазона: Синий график — это тригонометрическая функция [latex] f (x) = sin (x) [/ latex] с доменом [latex] mathbb {R} [/ latex] и ограниченным диапазон [латекс] -1 leq y leq 1 [/ latex] (выходные значения существуют только в диапазоне от [latex] -1 [/ latex] до [latex] 1 [/ latex].Красный график — это функция [latex] f (x) = — sqrt {x} [/ latex] с ограниченным доменом [latex] x geq 0 [/ latex], а также с ограниченным диапазоном [latex] у leq0 [/ латекс].
Области рациональных и радикальных функций
Рациональные и радикальные выражения имеют ограничения на их области, которые можно найти алгебраически или графически.
Цели обучения
Вычислить область определения рациональной или радикальной функции, найдя значения, для которых она не определена
Ключевые выводы
Ключевые моменты
- Рациональное выражение — это отношение двух многочленов.Это может быть выражено как [латекс] displaystyle frac {P (x)} {Q (x)} [/ latex].
- Область рационального выражения установлена так, что знаменатель не может быть равен нулю. Следовательно, учитывая [латекс] displaystyle frac {P (x)} {Q (x)} [/ latex], [latex] Q (x) neq 0 [/ latex].
- Чтобы определить область рационального выражения, установите знаменатель равным нулю, а затем решите относительно [латекс] x [/ латекс]. Все значения [latex] x [/ latex], кроме тех, которые удовлетворяют [latex] Q (x) = 0 [/ latex], являются областью выражения.
- Радикальное выражение выражается как [latex] sqrt x [/ latex] и может иметь другие корни, кроме квадратного.
- Радикальная функция выражается как [latex] f (x) = sqrt x [/ latex] (обычно называемая просто «функцией квадратного корня») — это функция, которая отображает набор неотрицательных действительных чисел на сам.
- Чтобы определить домен радикального выражения, установите подкоренное выражение равным нулю, а затем найдите [латекс] x [/ latex]. Все значения [latex] x [/ latex], кроме тех, которые удовлетворяют [latex] sqrt x = 0 [/ latex], являются областью выражения.
Ключевые термины
- radicand : число или выражение под знаком корня.
- рациональное выражение : выражение, которое можно записать как частное двух многочленов.
Поиск областей рациональных функций
Рациональное выражение — это выражение, которое можно записать как отношение двух полиномиальных функций. Несмотря на то, что это называется рациональным выражением, ни коэффициенты многочленов, ни значения, принимаемые функцией, не обязательно являются рациональными числами.В случае одной переменной, [latex] x [/ latex], выражение называется рациональным тогда и только тогда, когда оно может быть записано в форме:
[латекс] displaystyle frac {P (x)} {Q (x)} [/ латекс]
где [latex] P (x) [/ latex] и [latex] Q (x) [/ latex] являются полиномиальными функциями от [latex] x [/ latex], а [latex] Q (x) [/ latex] равно не нулевой многочлен [латекс] (Q (x) neq 0) [/ latex].
Область рационального выражения — это набор всех точек, знаменатель которых не равен нулю.2-5) = 0 [/ латекс]
Для решения разделите обе стороны на [латекс] 2 [/ латекс], добавьте [латекс] 5 [/ латекс] к обеим сторонам, а затем извлеките квадратный корень из обеих сторон, чтобы получить:
[латекс] displaystyle x = pm sqrt {5} [/ latex].
Следовательно, домен представляет собой набор всех действительных чисел, кроме квадратного корня из пяти или отрицательного квадратного корня из пяти.
Обратите внимание на график функции ниже. При значениях [латекс] x = pm sqrt {5} [/ latex] (что приблизительно равно [латекс] pm 2.2-2 справа)} {x} [/ латекс]
Алгебраически область — это набор всех действительных чисел, кроме нуля, поскольку знаменатель не может быть равен нулю. Один из способов определить это — посмотреть на это графически. Мы можем видеть, что график не является непрерывным при [latex] x = 0 [/ latex], что указывает на то, что домен состоит из всех чисел, кроме [latex] x = 0 [/ latex]. Это имеет смысл, потому что при [latex] x = 0 [/ latex] нам пришлось бы разделить на ноль, который не определен. Линии графика становятся все ближе и ближе к значению [latex] x = 0 [/ latex], но никогда не соприкасаются.2-2 right)} {x} [/ латекс]. Чтобы определить область действия этой функции, мы можем построить график и найти, где функция не существует, в данном случае, когда [latex] x = 0 [/ latex].
Поиск областей радикальных функций
Функция главного квадратного корня [latex] f (x) = sqrt x [/ latex] (обычно называемая просто «функцией квадратного корня») — это функция, которая отображает набор неотрицательных действительных чисел на себя.
Радикальная функция: Функция [latex] f (x) = sqrt x [/ latex] состоит из ограниченной области [latex] x geq 0 [/ latex] или неотрицательных действительных чисел, поскольку мы нельзя извлечь квадратный корень из отрицательного числа.2 [/ latex] будет [latex] sqrt y = pm x [/ latex]). При построении графика корней важно помнить, что отрицательные значения [latex] x [/ latex] не будут давать действительные числа. Это будет объяснено далее в разделе о мнимых числах.
Чтобы определить область определения радикальной функции алгебраически, найдите значения [latex] x [/ latex], для которых подкоренное выражение неотрицательно (установите его равным [latex] geq 0 [/ latex]), а затем решите для [ латекс] х [/ латекс]. Подкоренное число — это число или выражение под знаком корня.Все значения [latex] x [/ latex], кроме тех, которые удовлетворяют [latex] sqrt x geq 0 [/ latex], являются доменом функции.
Пример 3: Область определения радикальной функции:
[латекс] displaystyle f (x) = sqrt {x-3} +4 [/ латекс]
Установите подкоренное выражение больше или равное нулю и решите для [latex] x [/ latex], чтобы найти ограничения для домена:
[латекс] displaystyle {x-3} geq 0 [/ латекс]
Следовательно [латекс] х geq 3 [/ латекс]. Итак, все действительные числа, большие или равные [latex] 3 [/ latex], являются областью определения функции.
Радикальная функция : График уравнения: [латекс] f (x) = sqrt {x-3} +4 [/ latex]. Функция имеет область значений всех действительных чисел, больших или равных [латекс] 3 [/ латекс], как показано на графике выше.
1.3 — Функции
1.3 — Функции
Определения
- Отношение
- Правило, которое связывает значение в домене со значением в диапазоне.
- Функция
- Функция — это отношение (правило), которое присваивает каждому элементу в домене ровно один
элемент в диапазоне. - Домен
- Набор всех значений, которые могут быть введены в функцию. То есть набор всех
значения, которые может принимать независимая переменная. Графически домен — это совокупность всех
x-координаты. - Диапазон
- Набор всех значений, которые выводятся, когда функция оценивается на всех входах.
значения из домена. То есть набор всех значений зависимой переменной может
предполагать. Графически диапазон — это набор всех y-координат. - Независимая переменная
- Обычно независимой переменной является x. Однако независимой переменной является
переменная, которая может принимать разные значения независимо от другой переменной.
Большая часть того, что мы собираемся сделать в этом классе, будет включать только один независимый
переменная, но помните, что возможно иметь более одной независимой переменной. - Зависимая переменная
- Обычно зависимой переменной является y.Однако зависимой переменной является переменная
который определяется на основе значения независимой (ых) переменной (ей). Если функция
записывается как y = 3x + 2, тогда y зависит от x, но x не зависит от y (в виде
написано). Итак, x не зависит от y, но y зависит от x. - Подразумеваемый домен
- Набор всех действительных чисел, для которых определено выражение.
Чем функция отличается от отношения?
Вот несколько рекомендаций по определению, является ли отношение функцией или нет.
- Каждый элемент в домене (x) должен соответствовать элементу
в диапазоне (y). - Каждый элемент в домене (x) может быть сопоставлен только с одним элементом в
диапазон (y). - Различные элементы в домене могут переходить к одному и тому же элементу в
диапазон. Координата Y
может повторяться, но координата x не может. - Некоторые значения в диапазоне не обязательно использовать
Обозначение функций
Обозначение функций используется для именования функций для удобства.Представьте себе, если
каждая функция в мире должна была начинаться с y =. Довольно скоро ты будешь
запутаться в том, какой y = вы
говорили о. Так работают антецеденты в английском языке. Если ты просто
скажи «это» красный, ты
на самом деле понятия не имею, о чем «это» вы говорите. Вам нужен другой
способ называть вещи. Введите обозначение функции.
Определение функции
- f (x) = 3x + 2
- г (x, y) = x 2 + 3y
В этом примере f является функцией x.То есть x — независимая переменная, а значение f
зависит от того, что такое x. Кроме того, g является функцией как x, так и y.
Обозначение f (x) не означает f, умноженное на x. Это означает, что «значение f оценивается
при x «или» значении f
at x «или просто» f of x »
Оценка функций
f (3) = 3 (3) + 2 = 9 + 2 = 11
f (3) не означает f умножить на 3. Это означает «значение f, вычисленное, когда x
составляет 3 дюйма.
f (t) = 3 (t) + 2 = 3t + 2
Все, что указано в скобках в левой части
функция (в данном случае t) подставляется вместо значения независимого
переменная справа.
f (x + h) = 3 (x + h) + 2 = 3x + 3h + 2
Каждое появление независимой переменной заменяется количеством в скобках. А
Распространенная ошибка — взять величину и применить к ней линейные или аффинные преобразования.
ф (х + в)
- f (x + h) не равно f (x) + h = 3x + 2 + h
- f (x + h) не равно f (x) + f (h) = 3x + 2 + 3h + 2 = 3x + 3h + 4
- f (x + h) равно 3 (x + h) + 2 = 3x + 3h + 2
f (3x)
- f (3x) не равно 3 * f (x) = 3 (3x + 2) = 9x + 6
- Это равно 3 (3x) + 2 = 9x + 2
Вы также указываете, какую функцию хотите использовать, когда используете обозначение функций.Рассмотрим
г (2,1) = 2 2 + 3 (1) = 4 + 3 = 7
Поскольку порядок независимых переменных в исходном определении был x, а затем y,
функция g вычисляется, когда x = 2 и y = 1.
г (1,2) — это совсем другое дело. В этом случае x = 1 и y = 2.
г (1,2) = 1 2 + 3 (2) = 1 + 6 = 7
Ладно, это не совсем другое, но обнаруживается по-другому.
Кусочные определения
Иногда функции немного сложнее, чем
простые функции, которые мы описали до сих пор.Если разные правила
используются для разных значений независимой переменной,
тогда мы можем использовать кусочное определение.
Учитывайте показанную функцию и следующие оценки.
f (2,1) = 2 (2,1) = 4,2
Поскольку 2.1 находится в интервале [1,3), мы используем вторую часть определения,
f (х) = 2х.
f (-2) = 3 — (-2) 2 = 3-4 = -1
Поскольку -2 находится в интервале (-∞, -1), мы используем первую часть
определение, f (x) = 3-x 2
f (3) = 5 — (3) = 5 — 3 = 2
Так как 3 не входит во вторую штуку, но входит в третью
пьеса на антракте
[3, + ∞) мы используем третью часть определения, f (x) = 5 — x.
f (0) не определено
Поскольку 0 не попадает ни в один из доменов, функция там не определена.
Когда все области объединены, область определения функции f является множеством
всех действительных чисел, кроме [-1,1). Вы также можете записать его как (-∞, -1) U [1, + ∞).
Символ U обозначает
объединение двух наборов.
Кусочные функции и калькулятор
Вы можете использовать кусочные функции в графическом калькуляторе. Калькуляторы TI82 и TI83
получить ключ [Тест], нажав [2 nd ] [Math].Под этим ключом вы найдете разные
операторы проверки (равно, не равно, больше, больше или равно, меньше и меньше
или равно).
Когда калькулятор оценивает тестовое выражение (x <1), он возвращает значение 1, если оператор
истинно и значение 0, если утверждение ложно. Это действительно хорошо работает с умножением,
потому что умножение на 1 не изменит выражение, а умножение на 0 сделает
выражение 0.
y = (1 — x 2 ) * (x <-1)
Рассмотрим только первую часть кусочного определения сверху.2). Если x не меньше отрицательного,
тогда калькулятор вернет 0. Это
неправильное значение для возврата (оно должно быть неопределенным), но оно будет отображаться на графике
ось x и не будет отображаться, потому что ось уже там. Итак, у него есть
видимость на графике правильно.
Полная кусочная функция может быть определена для калькулятора как:
y = (1-x 2 ) * (x <-1) + 5x * (1≤x и x <3) + (5-3x) * (x≥3)
Ключевое слово «and» можно найти в меню [Test] Logic.Аналогично символы ≤ и ≥
также можно найти в меню [Тест]. Если вы попытаетесь
положить 1≤x <3, как мы
правильно, калькулятор интерпретирует это как 1≤3 и всегда возвращает true.
Обязательно используйте какой-либо десятичный режим или режим точки при просмотре кусочного
функция. В противном случае вы можете получить странные результаты.
В поисках домена
Подразумеваемый домен
Мы определили подразумеваемый домен ранее. Это набор всех действительных чисел, в котором выражение
определенный.
- Начните со всех действительных чисел
- Исключить любые значения независимой переменной, вызывающие деление на ноль
- Исключить любые значения независимой переменной, которые приводят к извлечению квадратного корня из
отрицательное число. Квадратный корень можно заменить любым четным (4 -й , 6 -й и т. Д.) Корнем.
Вам не , а не необходимо указывать ограничения, вытекающие из подразумеваемого домена. Другими словами, если
в знаменателе стоит (x-2), вам не нужно указывать, что x не может быть 2.
Прочие исключения
Иногда вам нужно исключить другие значения.
- Проблемы с ограничениями — они используются в приложениях. вот несколько примеров
- Если
x — длина стороны треугольника, тогда x не может быть отрицательным - Если
x — положение на качелях высотой 12 футов, в котором точка опоры должна
быть позиционированным, то x должен быть в пределах от 0 до 12. - Если x — количество
человек в комнате, то x не может быть отрицательным.
- Если
- Заявленные ограничения — иногда проблема просто выходит и говорит, что вы не можете использовать
определенное значение, или что вы можете использовать только определенные значения. Это не подразумевается,
так что их нужно заявить.
Если вы когда-нибудь упростили функцию, и значение, которое было в подразумеваемой области
больше не находится в подразумеваемой области, тогда это должно стать установленным ограничением.
Например, разделите (x 2 -4) на (x-2).
Подразумеваемая область значений x не может быть равна 2, потому что это приведет к делению на ноль.Однако, если вы разложите числитель на множители как (x-2) (x + 2), то (x-2) в числителе
делится на (x-2) в
знаменатель, и у вас останется только (x + 2). Тот факт, что x не может быть 2
больше не подразумевается простым x + 2 в числителе, поэтому теперь вы должны указать
что x не может быть 2.
Объединение доменов
Когда у вас есть функция, которая представляет собой композицию из нескольких частей, значения в домене
должны быть в состоянии использоваться во всех частях функции.Скажем, в числителе есть квадратный корень из x
в нем (так что x должен быть неотрицательным), а в знаменателе есть x-2 (так что x не может быть 2).
Когда вы объединяете эти домены, вы получаете все неотрицательные значения x, кроме 2.
Другими словами, область действия функции — это пересечение всех областей индивидуальной
части.
Теперь предположим, что в числителе есть квадратный корень из x (так что x должен быть неотрицательным) и
в знаменателе стоит x + 2 (так что x не может быть -2).Когда вы объединяете эти домены, вы получаете
все неотрицательные значения x, кроме -2. Ну, вам не нужно утверждать, что x не может быть -2
поскольку вы уже сказали, что x неотрицательно. Итак, в этом случае доменом будут все неотрицательные значения x.
функций: домен и диапазон | Purplemath
Purplemath
Вернемся к теме доменов и диапазонов.
Когда функции вводятся впервые, вы, вероятно, будете иметь дело с некоторыми упрощенными «функциями» и отношениями, обычно представляющими собой просто наборы точек. Это не будут очень полезными или интересными функциями и связями, но ваш текст хочет, чтобы вы получили представление о том, что такое домен и диапазон функции. Небольшие наборы точек, как правило, являются простейшими видами отношений, поэтому ваша книга начинается с них.
Например:
MathHelp.com
-
Укажите область и диапазон следующего отношения. Отношение — это функция?
{(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}
Приведенный выше список точек, являющийся отношением между определенными x и некоторыми y , является отношением.Домен — это все значения x , а диапазон — все значения y . Чтобы указать домен и диапазон, я просто перечисляю значения без дублирования:
домен: {2, 3, 4, 6}
диапазон: {–3, –1, 3, 6}
(Обычно эти значения перечисляются в числовом порядке, но не требуется . Наборы называются «неупорядоченными списками», поэтому вы можете перечислять числа в любом порядке.Только не дублируйте: технически повторения в подходах допустимы, но большинство инструкторов рассчитывают на это.)
Хотя данный набор действительно представляет отношение (поскольку x и y связаны друг с другом), набор, который они мне дали, содержит две точки с одинаковым значением x : (2, –3) и (2, 3). Поскольку x = 2 дает мне два возможных назначения (то есть два возможных значения y ), то это отношение не является функцией.
Обратите внимание, что все, что мне нужно было сделать, чтобы проверить, является ли отношение функцией, — это найти повторяющиеся значения x . Если вы обнаружите какие-либо повторяющиеся значения x , то разные значения y означают, что у вас нет функции. Помните: чтобы отношение было функцией, каждое значение x должно перейти к одному, и только одному значению , y .
-
Укажите область и диапазон следующего отношения.Отношение — это функция?
{(–3, 5), (–2, 5), (–1, 5), (0, 5), (1, 5), (2, 5)}
Я просто перечислю значения x для домена и значения y для диапазона:
.
домен: {–3, –2, –1, 0, 1, 2}
диапазон: {5}
Это еще один пример «скучной» функции, такой же, как в примере на предыдущей странице: каждое последнее значение x соответствует одному и тому же значению y .Но каждое значение x отличается, поэтому, пока скучно,
это отношение действительно является функцией.
Фактически, эти точки лежат на горизонтальной прямой y = 5.
Между прочим, имя набора, в котором есть только один элемент, как и набор «диапазон» выше, — «singleton». Таким образом, диапазон также может быть указан как «синглтон из 5»
Есть еще один случай нахождения домена и диапазона функций.Они дадут вам функцию и попросят найти домен (и, возможно, диапазон). На этом этапе вашей математической карьеры я видел только (или даже могу придумать) две вещи, которые вам нужно будет проверить, чтобы определить область определения функции, которую они вам дадут, и эти две вещи являются знаменателями и квадратные корни.
-
Определите область и диапазон данной функции:
Домен — это все значения, которые разрешено принимать x .Единственная проблема, с которой я сталкиваюсь с этой функцией, заключается в том, что мне нужно быть осторожным, чтобы не делить на ноль. Таким образом, единственные значения, которые x не могут принять, — это те, которые вызывают деление на ноль. Поэтому я установлю знаменатель равным нулю и решу; в моем домене будет все остальное.
x 2 — x — 2 = 0
( x — 2) ( x + 1) = 0
x = 2 или x = –1
Тогда домен будет «все x не равны –1 или 2».
Диапазон немного сложнее, поэтому они могут не просить об этом. В общем, они хотят, чтобы вы построили график функции и нашли диапазон по картинке. В этом случае:
Как видно из моего рисунка, график «покрывает» все значения и ; то есть график будет идти настолько низко, насколько мне нравится, и также подниматься настолько высоко, насколько мне нравится. Для любой точки оси y , независимо от того, насколько высоко вверх или вниз, я могу перейти от этой точки вправо или влево и, в конце концов, пересечу график.Поскольку в конечном итоге график будет охватывать все возможные значения y , тогда:
диапазон — «все действительные числа».
-
Определите область и диапазон данной функции:
Домен — это все значения, которые могут принимать x .Единственная проблема, с которой я столкнулся с этой функцией, заключается в том, что у меня не может быть отрицательного числа внутри квадратного корня. Итак, я установлю внутренности больше или равными нулю и решу. Результатом будет мой домен:
–2 x + 3 ≥ 0
–2 x ≥ –3
2 x ≤ 3
x ≤ 3/2 = 1,5
Тогда домен будет «все x ≤ 3/2».
Для диапазона требуется график. Мне нужно быть осторожным при построении графика радикалов:
График начинается с y = 0 и идет вниз (направление влево) оттуда. Хотя график идет вниз очень медленно, я знаю, что в конечном итоге я смогу опуститься настолько низко, насколько захочу (выбрав достаточно большой размер x ). Кроме того, по моему опыту работы с графиками я знаю, что график никогда не начнет восстанавливаться. Тогда:
диапазон: «все y ≤ 0».
Партнер
-
Определите область и диапазон данной функции:
y = — x 4 + 4
Это просто многочлен садового разнообразия.Здесь нет знаменателей (поэтому нет проблем с делением на ноль) и нет радикалов (поэтому нет проблем с извлечением квадратного корня из отрицательного числа). С полиномом проблем нет. Нет значений, которые я не могу подключить для x . Когда у меня есть полином, ответ для домена всегда :
Диапазон будет варьироваться от полинома к полиному, и они, вероятно, даже не спросят, но когда они это сделают, я смотрю на картинку:
График идет только до y = 4, но он будет идти настолько низко, насколько мне нравится.Тогда:
Диапазон: «все y ≤ 4».
URL: https://www.purplemath.com/modules/fcns2.htm
Домен и диапазон
Домен и диапазон функции — это все возможные значения независимой переменной x, для которой определено y.Диапазон функции — это все возможные значения зависимой переменной y.
В приведенном ниже примере показаны два различных способа представления функции: в виде таблицы функций и в виде набора координат.
| или | {(2, 4), (3, 8), (5,2), (6,9), (8,3)} |
Несмотря на то, что они представлены по-разному, это одна и та же функция, а область определения функции — x = {2, 3, 5, 6, 8}, а диапазон — y = {4, 8, 2, 9, 3}.Вот как вы можете определить домен и диапазон для дискретных функций. Порядок, в котором вы указываете значения, не имеет значения. Но как определить домен и диапазон для недискретных функций?
Пример:
f (x) = x 2
Функция f (x) = x 2 имеет область значений всех действительных чисел (x может быть любым) и диапазон, который больше или равен нулю.
Два способа записи домена и диапазона функции: интервальная нотация и заданная нотация.
Интервальное обозначение
При использовании обозначения интервалов домен и диапазон записываются как интервалы значений. Для f (x) = x 2 домен в интервальной записи:
D: (-∞, ∞)
D означает, что вы говорите о домене, а (-∞, ∞), читаемое как от отрицательной бесконечности до положительной бесконечности, — это еще один способ сказать, что домен — это «все действительные числа».
Диапазон f (x) = x 2 в интервальной записи:
R: [0, ∞)
R означает, что вы говорите о диапазоне.Обратите внимание, что вместо скобок для 0 используется скобка. Это связано с тем, что диапазон функции включает 0 при x = 0. Диапазон функции исключает ∞ (это делает каждая функция), поэтому мы используем круглую скобку.
На графике вы знаете, когда функция включает или исключает конечную точку, потому что конечная точка будет открытой или закрытой.
Установить обозначение
При использовании обозначения набора мы используем символы неравенства для описания области и диапазона как набора значений. Домены и диапазоны, использованные в примерах дискретных функций, были упрощенными версиями обозначений множеств.В обозначениях множеств используется много разных символов, но здесь будут представлены только самые основные структуры.
Область значений f (x) = x 2 в заданных обозначениях:
D: {x | x∈ℝ}
Опять же, D указывает на домен. Знак «|» означает «такое, что» символ ∈ означает «элемент из», а «ℝ» означает «все действительные числа».
Собирая все вместе, это утверждение может быть прочитано как «домен — это набор всех x таких, что x является элементом всех действительных чисел».
Диапазон f (x) = x 2 в заданных обозначениях:
R: {y | y ≥ 0}
R указывает дальность действия.При использовании обозначения набора символы неравенства, такие как ≥, используются для описания области и диапазона. Следовательно, это утверждение может быть прочитано как «диапазон — это набор всех y таких, что y больше или равно нулю».
Значение области допустимых значений в математике: способы нахождения
Содержание:
- Допустимые и недопустимые значения переменных
- Что такое ОДЗ
-
Как найти ОДЗ: примеры, решения
- Общие принципы нахождения области допустимых значений
- Примеры нахождения ОДЗ
- Почему важно учитывать ОДЗ при проведении преобразований
-
Функции, для которых важна ОДЗ
- ОДЗ обратной зависимости
- ОДЗ степенной функции
- ОДЗ показательной функции
- ОДЗ логарифмической функции
- ОДЗ тригонометрических функций
Допустимые и недопустимые значения переменных
Перед тем, как вводить понятие области допустимых значений функции, необходимо определиться с самим термином «допустимое значение».
Допустимое значение переменной — такое значение переменной, при котором зависимая от нее функция имеет смысл. Это значит, что, подставив данное значение переменной в выражение функции, можно получить конкретный результат. Сама функция в алгебре — это уравнение, в котором каждому значению x соответствует одно значение y.
Например, для функции обратной пропорциональности (y=frac1x) допустимыми значениями для переменной x будут: 1; 2,7; -5, (sqrt{126}), — в общем, все действительные числа. При подстановке их на место x, функция принимает конкретное значение. Исключениями из этого перечня будут 0, (-infty )и (+infty), так как когда x принимает такие значения, функция не имеет смысла.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Что такое ОДЗ
Область допустимых значений (область определения) функции — совокупность всех значений переменных, при которых функция имеет смысл, то есть решается. Для примера из предыдущего пункта, (y=frac1x), область допустимых значений будет иметь следующий вид: ((-infty;;0)cup(0;;+infty)). Это значит, что в область определения функции ( y=frac1x) входят все числа в промежутках от минус бесконечности до нуля и от нуля до плюс бесконечности.
У записи области определения есть некоторые особенности, которые важно иметь в виду. Круглые скобки — () — применяются, когда область допустимых значений заканчивается на данном числе, причем оно не входит в ОДЗ. Квадратные скобки — [] — применяются в ситуациях, когда в область определения входит число, на котором она заканчивается. Знак объединения — (cup) — по сути означает союз «и». Он используется, когда ОДЗ является системой из нескольких числовых промежутков.
Как найти ОДЗ: примеры, решения
Чтобы найти область допустимых значений для какой-либо функции, не имеет смысла перебирать все числа, при подстановке которых ее можно решить. Рациональнее найти те значения, при которых функция не имеет смысла и исключить их из всего множества чисел.
Общие принципы нахождения области допустимых значений
- деление на 0. Практически во всех стандартных математических выражениях такая операция не имеет смысла. У этого действия есть конкретный результат только при нахождении предела последовательности или функции. Пример бессмысленных выражений: (y=frac50;)
- извлечение корня из отрицательного числа. При работе с действительными числами, найти корень любой степени отрицательного числа невозможно. Эта операция приобретает смысл только при переходе к комплексным числам. Пример: (y=sqrt{-11};)
- возведение в степень. У данного действия есть свои ограничения: нельзя возводить 0 в отрицательную и нулевую степень, отрицательные числа в положительную дробную степень и неположительные (отрицательные и 0) в дробную степень со знаком минус. Примеры: (y=0^{-3};;y=0^0;;y=({-7}^{textstylefrac32});;y=({-6}^{-{textstylefrac17}});)
- нахождение логарифма. Так как логарифм равняется степени, в которую необходимо возвести основание, чтобы получить логарифмируемое число, некоторые операции не имеют смысла. К ним относятся логарифмирование неположительного числа, положительного числа по отрицательному основанию или единице. Примеры:( y=log_3left(-9right);;y=log_2left(0right);;y=log_{-4}left(64right);;y=log_1left(5right);)
- тригонометрические функции. Для синуса, косинуса, арктангенса и арккотангенса никаких ограничений нет. Но для тангенса, котангенса, арксинуса и арккосинуса они появляются, исходя из их формул. Так как тангенс является частным при делении синуса на косинус, последний не может равняться нулю. То же самое справедливо и для котангенса, но там уже синус не должен принимать значение 0.
Арксинус и арккосинус могут быть определены только в промежутке от -1 до 1 включительно — (lbrack-1;;1rbrack.)
Примеры нахождения ОДЗ
Пример №1. Найти область определения функции (y=sqrt{1-x^2})
Из обозначенных выше принципов следует, что подкоренное выражение не может быть отрицательным, значит 1-x^2geq0. Приведем данное неравенство к общему виду: (1-x^2geq0Rightarrow1geq x^2Rightarrow x^2leq1)
Вычислим квадратный корень для обеих частей неравенства:
(x^2leq1Rightarrowsqrt{x^2}leqsqrt1Rightarrowleft|xright|leq1)
Раскроем модуль согласно правилу:
(left|xright|leq1Rightarrow-1leq xleq1)
Из этого следует, что область допустимых значений функции (y=sqrt{1-x^2}) лежит в пределах между -1 и 1, включая эти числа. Таким образом, ОДЗ данной функции: (xinlbrack-1;;1rbrack)
Пример №2. Найти ОДЗ функции (y=lgleft(xright))
(lgleft(xright)) является краткой формой записи десятичного логарифма (log_{10}left(xright)). Так как 10 — положительное число, не равное единице, единственным условием остается x>0. Таким образом, область определения функции (y=lgleft(xright)) будет включать в себя все числа в промежутке от нуля до (+infty). Так как неравенство x>0 — строгое, ОДЗ будет иметь следующий вид: (xin(0;;+infty)).
Почему важно учитывать ОДЗ при проведении преобразований
Тождественные преобразования могут приводить к расширению или сужению области допустимых значений. В этом случае значение, подходящее к изначальной функции, после преобразования может оказаться вне области определения. Поэтому стоит избегать сужающих ОДЗ преобразований или находить область допустимых значений уже после них.
Функции, для которых важна ОДЗ
Сама по себе область допустимых значений — важная характеристика для всех функций. Чтобы правильно решать математические задачи, следует всегда находить ее. При этом, для многих, если не большинства, функций она включает в себя все множество действительных чисел. Например, линейная (y=kcdot x+b) или квадратичная (y=acdot x^2+bcdot x+c) функции. Рассмотрим некоторые функции, для которых это не так.
ОДЗ обратной зависимости
Функция обратной пропорциональности (y=frac kx) уже упоминалась выше. Ее область определения содержит все действительные числа, за исключением нуля: (xin(-infty;;0)cup(0;;+infty).)
ОДЗ степенной функции
Для степенной функции y=x^n следует учитывать обозначенные выше принципы нахождения ОДЗ, справедливые для возведения в степень и извлечения корня. Рассмотрим области определения переменной x в зависимости от значения n:
- при n>0 и (ninmathbb{Z}), то есть n — целое положительное число: ( xin(-infty;;+infty);)
- для n>0, причем n — дробное число: ( xinlbrack0;;+infty);)
- для n=0:( xin(-infty;0)cup(0;;+infty);)
- при n<0 и (ninmathbb{Z}: xin(-infty;;0)cup(0;;+infty);)
- для n<0, причем n — дробное число: (xin(0;;+infty).)
ОДЗ показательной функции
Показательная функция y=a^x очень похожа на степенную, но, в отличие от нее, здесь переменная не в основании, а в степени. Область допустимых значений для нее определяется по тем же правилам, что и для степенной функции:
- для a>0: (xin(-infty;;+infty);)
- для a=0: (xin(0;;+infty);)
- для a<0: (xin(-infty;;+infty)), причем x должен быть целым числом.
ОДЗ логарифмической функции
Логарифмическая функция (y=log_aleft(xright)) является обратной для показательной. Согласно свойствам логарифмирования, область определения такой функции будет включать все положительные числа: (xin(0;;+infty).)
ОДЗ тригонометрических функций
Как уже упоминалось выше, для синуса, косинуса, арктангенса и арккотангенса область допустимых значений включает в себя все действительные числа: (xin(-infty;;+infty)). Рассмотрим ОДЗ еще четырех тригонометрических функций:
- тангенс: (xin(-infty;;frac{mathrmpi}2+mathrmpicdotmathrm n)cup(frac{mathrmpi}2+mathrmpicdotmathrm n;;+infty), где ninmathbb{Z};)
- котангенс: (xin(-infty;;mathrmpicdotmathrm n)cup(mathrmpicdotmathrm n;;+infty), где ninmathbb{Z};)
- арксинус и арккосинус: (xinlbrack-1;;1rbrack.)
Как найти область допустимых значений выражения
Определение
Область ОДЗ – это множество простых числовых значений, которые допустимы, для любого данного выражения.
Ограничение области определения:
Область ограничения действительных чисел может быть от [(0 ;+infty)].
Например: [[-4 ; 1) cup[5,7)].
Область определения может указывать на следующие характеристики:
- деление функции как [y=x+frac{2 cdot x}{x^{4}-1}]
- корень четной степени и переменная под корнем:
[=sqrt{x+1} text { или } y=sqrt[n]{2^{2 cdot x+1}} text {; }] - переменная в основании степенного значения
[y=3 cdot(x+1)^{-2}, y=-2+x^{frac{1}{3}} ; y=left(x^{4}-x+2right)sqrt{4}] - логарифмическая переменная [y=ln frac{x^{4}+x}{8} ; quad y=2+].
Значения основания должно быть положительным. Также как и логарифмическое значение. - переменная тангенса и котангенса в виде следующего уравнения: [y=arcsin (x+4)+4 cdot x^{2}]
Если отсутствует хотя бы один из перечисленных характеристик область определения функции определяется иначе.
Пример 1: [y=frac{x^{4}+2 x-x+2}{4}+2 frac{2}{3} cdot x], в данном множестве нет переменной, поэтому и решается оно иначе.
Пример 2: [y=frac{3}{x-1}], нужно вычислить область определения. Обязательно, при решении нужно уделить внимание на знаменатель. Потому что, по законам алгебры деление на ноль запрещено.
Следовательно получаем следующее действие: [frac{3}{x-1}].
Область значения не должна быть равной единице, так как в знаменателе получим нулевое значение. Отсюда область определения будет в пределах [(-infty, 1) cup(1,+infty)].
Область допустимых значений для уравнения
Чтобы правильно уметь определять данную область, нужно знать следующие утверждения:
если функция вычисляется, при помощи суммы: [f_{1}+f_{2}+ldots f_{n} text { или } mathrm{y}=f_{1}+f_{2}+ldots f_{n}].
Область определения будет следующего вида: [mathrm{D}(mathrm{f})=mathrm{D}left(f_{1}right)left(f_{2}right) ldotsleft(f_{n}right)]
Пример суммы числовых значений:
Возьмем уравнение: [y=x^{7}+x+5+operatorname{tg} x]
Решение: уравнение представлено в виде суммы нескольких значений, где степень равна семи, показатель один.
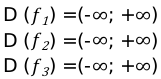
Области определения tg характерны все действительные числа.
Ответ: для заданной функции относится пересечение областей или количество действительных чисел кроме [pi / 2+pi cdot mathrm{n} . mathrm{n} in z]
Пример разности значений:
[y=log _{3} x-4 cdot 2^{x}]
Решение:
[f_{1}(mathrm{x})=log _{3} text { и } f_{2}(mathrm{x})=4 cdot 2^{x}]
Область определения функции разности будет: [(0,+infty)] это для [f_{1} ; text { для } f_{2}(-infty .+infty)]
[y=log _{3} x-4 cdot 2^{x} Rightarrow Dleft(f_{1}right)=(0 ;+infty), quad Dleft(f_{2}right)=(-infty ;+infty)]
Ответ: [(0 ;+infty)].
Пример произведения чисел:
[y=3 cdot operatorname{arctg} x cdot ln x]
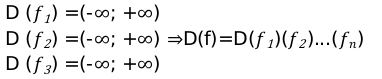
Область допустимых значений для функции
Сложная функция имеет следующий вид: [mathrm{y}=f_{1}left(f_{2}(mathrm{k})right)]
D (f) — множество значений;
Пересечение двух множеств и будет являться областью определения функции сложного типа.
[mathrm{k} in Dleft(f_{2}right) text { и } D f_{2}(x) in Dleft(f_{1}right)]
Пример
[y=ln x^{2}]
Представим функцию в виде: [mathrm{y}=f_{1}left(f_{2}(mathrm{k})right)]
[f_{1}] — логарифм с заданным основанием;
[f_{1}] — степень со значением 2.
Используем изученные в данном уроке области определения:
[Dleft(f_{1}right)=(0 ;+infty)]
[Dleft(f_{2}right)=(-infty ;+infty)]
Исходя из этого получаем систему неравенства: [x in Dleft(f_{2}right) ; f_{2} k in Dleft(f_{1}right) Leftrightarrow k in(-infty ;+infty) k^{2} in(0 ;+infty) Leftrightarrow k in(-infty ;+infty)k^{2}>0 Leftrightarrow k in(-infty ;+infty)]
[ k in(-infty ; 0) cup(0 ;+infty) . Leftrightarrow k in(-infty ; 0) cup(0,+infty)]
Ответ: все действительные числа, кроме нуля.
Область определения функции в виде дробного алгебраического значения
Когда функция задается выражение в виде дроби. Переменная значений находится в знаменателе. Следовательно, область определения являются действительные числа. Исключением служит число, которое приведет знаменатель к нулевому значению.
Пример №1: [y=frac{x-4}{x+4}]. Решив уравнение, определим искомое значение области определения. Которое является [-infty ;-4 cup-4 ;+infty]
Пример №2: [y=frac{1}{x^{2^{2}} 1} ;]
[x^{2-} 1=0 Rightarrow x^{2} Rightarrow x_{1}=-1 x_{2}=1]
Искомая область : [text { — ]- } infty ;-1[cup]-1 ; 1[cup] 1 ;+infty[.]
Пример №3: [y=cos x+frac{3}{x^{2}-4}].
Первое слагаемое имеет область определения множество действительных чисел. Второе — также все числа, кроме -2 и 2, они приведут знаменатель к нулю. Область определения должна соответствовать условиям двух слагаемых и равняться действительным числам, кроме -2 и 2.
Область определения показательной и логарифмической функции
Показательная функция записывается как: [y=k^{x}]
где значение x — показатель степени; k — число, которое обязательно больше нуля и не равно единице. Область определения показательной функции — это множество значений R.
Основные примеры показательных функций:
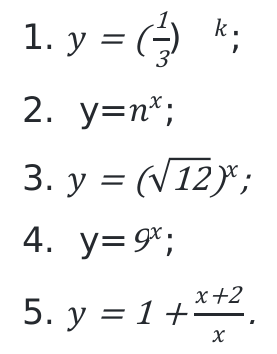
Область определения, для этих функций, записывается следующим образом: [(-infty,+infty)].
Логарифмическая функция выражается как: [y=log n^{k}], где значение n , имеет значение больше нуля и не менее единицы.
Определение
Область определения логарифма и логарифмической функции — это множество положительных значений и действительных чисел.
Рассмотрим на примере, характер решения задачи данной функции.
Пример №1:
[y=ln x], определить область определения натурального логарифма.
[D(y)=(0 ;+infty)]
На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.
[y=ln x=frac{1}{x}]
Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.
[lim _{x rightarrow 0+0} ln x=ln (0+0)=-infty]
[lim _{x rightarrow infty} ln x=ln (+infty)=+infty .]
Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.
Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.
Ответ: множество всех действительных чисел, это и есть область значений функции ln.
Определения области допустимых значений функции
На примерах рассмотрим, как определить области значений функции.
Первоначально, необходимо определить значения непрерывной функции y=f(x).
Известно, что функция непрерывная и достигает своих максимальных max f(x) и минимальных min f(x) значений, на разных периодах. Из этого следует отрезок, где находятся значения исходной функции. Тогда решение состоит в нахождении точек максимума и минимума.
Пример №1 :
Необходимо вычислить область значений уравнения [y=x^{4}-5 x^{3}+6 x^{2}] на отрезке [ 1 ; 4 ] [1; 4].
Для решения задачи необходимо произвести следующие действия:
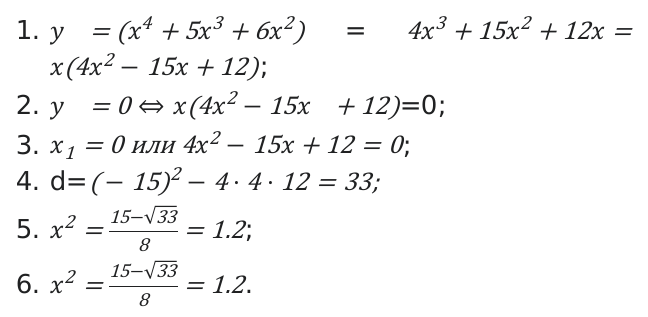
Следующим шагом будет определение значений функции в конечной и начальной точках.
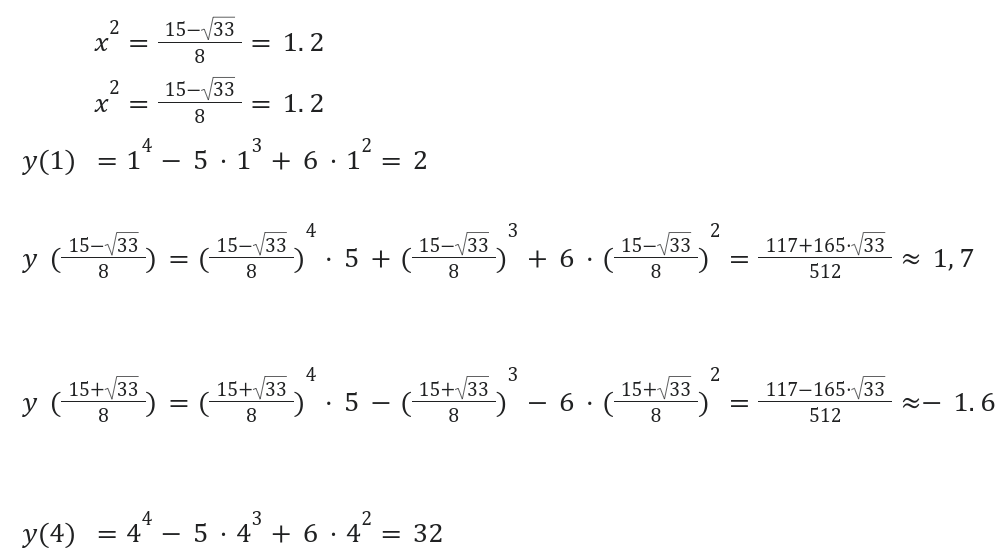
Ответ: [left(frac{117-165 cdot sqrt{33}}{512} ; 32right)].
Нет времени решать самому?
Наши эксперты помогут!
Пример №2.
На этом примере подробно рассмотрим, как вычисляются значения непрерывной функции y= f(x), в определенных промежутках.
Для этого, первоначально вычислим:
- наименьшее и наибольшее значение;
- определим промежуток возрастания и убывания функции;
- односторонние пределы;
- предел бесконечности.
Решение:
Для решения возьмем функцию [y=frac{1}{x^{2}-4}] и вычислим область значений на промежутке (-2;2).
Находим наименьшее и наибольшее значение функции на заданном отрезке.
[y=frac{1}{x^{2}-4}=frac{-2 x}{left(x^{2}-4right)^{2}}]
[mathrm{y}=0 Leftrightarrow frac{-2 x}{left(x^{2}-4right)^{2}}=0 Leftrightarrow x=0 in(-2 ; 2)]
Из данных вычислений видно, что максимальное значение равно 0, так как в этой точке происходит перемена знака функции и соответственно функция начинает убывать.
А именно: [y(0)=frac{1}{0^{2}-4}=-frac{1}{4}]
[-frac{1}{4}] — будет являться наибольшим значение заданной функции.
Следующим шагом в нашем решении, будет выяснение направления функции. Когда x значение стремится к (-2) и (+2).
В алгебре иными словами эти значения называют односторонними пределами.
Решение выглядит следующим образом.
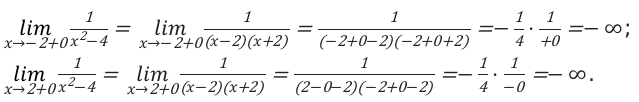
В конечном итоге мы получаем, что в пределах от -2 до 0, функции будут возрастать от [-infty text { до }-frac{1}{4}]. Если аргумент меняется, от 0 до то наоборот будет убывать к [-infty].
Следовательно, необходимое множество значений будет на интервале [-infty text { до }-frac{1}{4}]
Ответ: [left(-infty-frac{1}{4}right)].
Пример №3:
Данная функция имеет определенное значение, только при положительных значениях. [mathrm{D}(mathrm{y})=(0 ;+infty)]
Производная будет иметь следующий вид: [y=(ln x)=frac{1}{x}].
Так как функция имеет положительное значение, то всем промежутке будет наблюдаться ее возрастание. От [-infty text { до } +infty]
Поэтому область значения — это множество всех натуральных значений.
Пример №4:
У функции [y=frac{9}{z^{2}-1}]
Если значение z имеет положительное значение, то функция будет считаться определенной.
Вычислим наибольшее и наименьшее значение, а также промежутки возрастания и убывания.
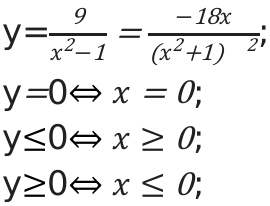
Если значение x будет больше, либо равным 0,то функция будет убывать.
Если значение x будет меньше либо равным нулю , функция будет возрастать.
Затем рассмотрим поведение функции и ее значения на бесконечной прямой.
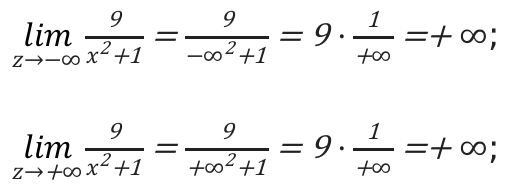
Вывод: если аргумент изменяется от [-infty] до 0, тогда значение функции увеличиваются от 0 до 9 . Когда значения аргумента меняются от 0 до [+infty], значения функции будут уменьшаться от 9 до 0.
Пример №5:
Определить область значений [y=frac{x}{x-2}];
По правилам математики. знаменатель не может равняться нулю. Поэтому: [D(y)=(-infty ; 2)(+infty ; 2)].
Определим множества на первом отрезке. [(-infty ; 2)]. На этом отрезке функция будет убывающей и значение отрицательным.
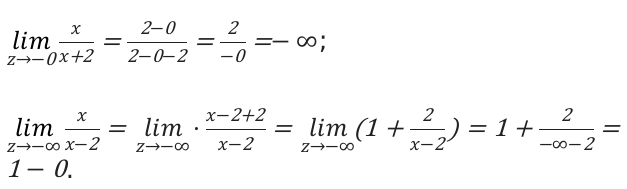
Функция ассиметрично начнет приближаться к 1, когда аргумент будет изменяться к минус бесконечности.
Определим множества на втором отрезке. [(+infty ; 2)]. На этом отрезке функция будет также убывающей.
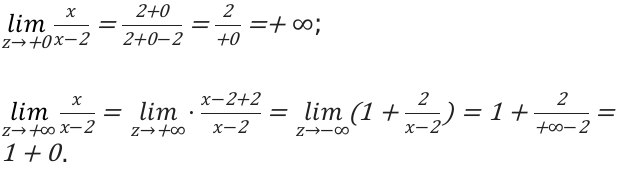
Вывод: [E(y)=(+infty ; 1) cup(1 ;+infty)].