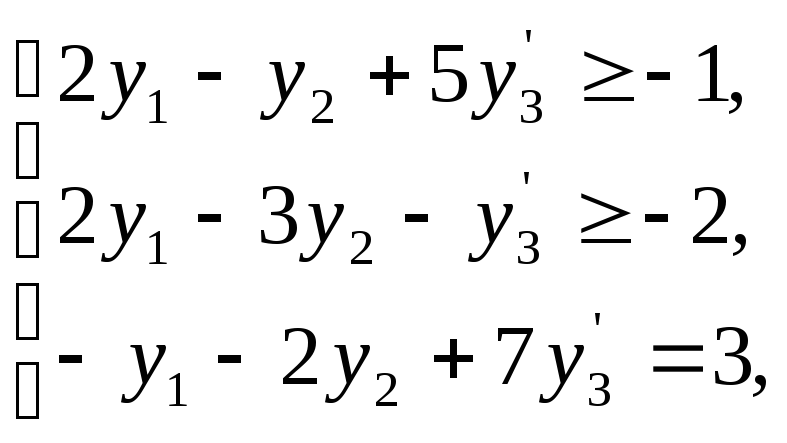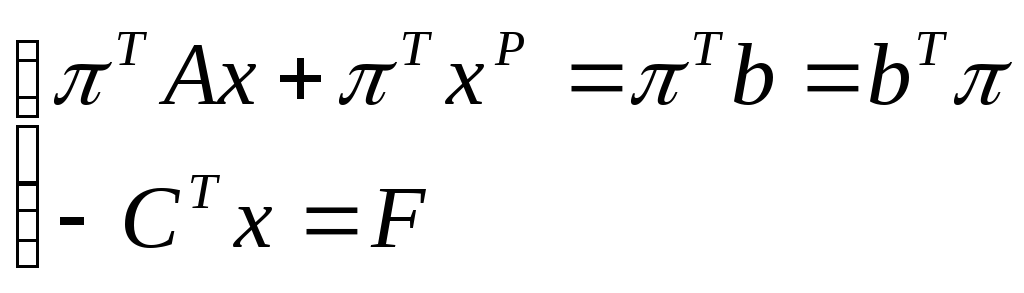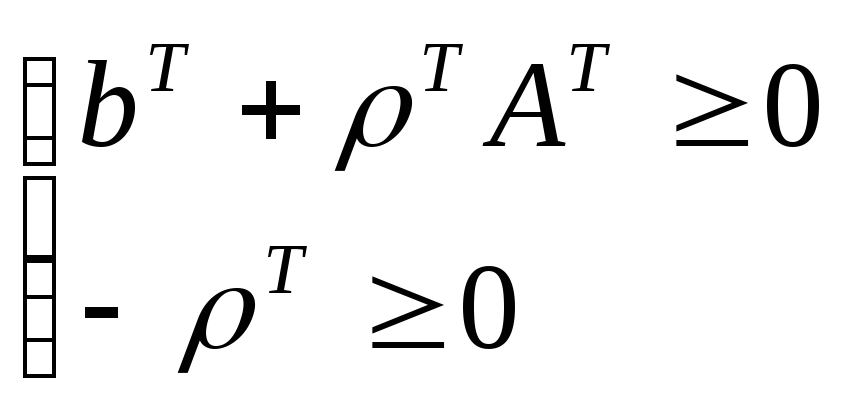Как найти ограничения в двойственной задаче

Двойственная задача линейного программирования

Прочие статьи цикла

Обычно с задачей линейного программирования (ЗЛП) связана другая линейная задача, называемая двойственной. Обе эти задачи можно считать двойственными одну по отношению к другой, считать равносильными. Первая задача называется обычно исходной, или прямой, другая — обратной. Переменные, используемые в двойственной задаче называются двойственными или множителями Лагранжа. На них не накладывается ограничений по знаку. Рассматриваются двойственные критерии оптимальности. Специальные случаи называют симметричными двойственными задачами линейного программирования. Связь между оптимальными решениями двойственных задач устанавливается теоремой двойственности.

Теорема двойственности

Важнейшие свойства пары двойственных задач математического программирования сформулированы в трех основных теоремах.

Теорема двойственности

Допустимый вектор решения прямой задачи программирования оптимален тогда и только тогда, когда существует такой допустимый вектор решения двойственной задачи, что целевые функции прямой и двойственной задачи равны. Допустимый вектор двойственной задачи оптимален тогда и только тогда, когда существует допустимый вектор прямой задачи и целевые функции обеих задач равны.

Теорема существования решения

Если существуют допустимые векторы решений прямой и двойственной задач, то обе задачи имеют оптимальные векторы. Если одна из двух задач не имеет допустимого вектора, то ни одна из них не имеет оптимального вектора решения.

Теорема (принцип) дополняющей нежесткости

1. Если (x_Q , x_L) – оптимальное решение прямой задачи, а (y_Q, y_L) – решение двойственной задачи, то (x_Q , x_L, y_Q , y_L) – решение задачи Лагранжа. В частности, в этом случае удовлетворяются соотношения между переменными прямой и двойственной задач и условия дополняющей нежесткости.

2. Оптимальное решение прямой задачи программирования получается только при одном значении x_Q. Это справедливо и для переменной y_Q в двойственной задаче.

Теоремы двойственности

Основное неравенство двойственности. Для любых допустимых решений Х_<n> и Y_<n>пары двойственных ЗЛП имеет место неравенство

Экономически это означает, что для любого допустимого плана производства и любого дополнительного вектора оценок ресурсов (на складе) стоимость изготовленного продукта не превосходит оценки ресурсов.

Теорема существования (малая тероема двойственности)

Чтобы прямая и двойственная задачи имели opt решения, необходимо и достаточно, чтобы существовали допустимые решения для каждой из них.

Теорема 1 двойственности.

Если одна из пары двойственных задач имеет opt решение, то и другая его имеет. Причем экспериментальные решения их целевых ф. равны; если же ЦФ одной из задач не ограничена, то система ограничений другой противоречива. Интерпретация: оптимальное использование ресурсов – opt план. Суммарная оценка ресурсов = оценке продукта полученного при opt плане. Любой другой план не рентабелен. C_j – стоимость единицы продукции (внешняя оценка) y_i – стоимость единицы ресурса (внутренняя оценка). Эти двойственные оценки выступают как инструменты балансирования затрат и результатов. Имеет место x_j ​<->​ y_m +_j ; x_n+i <-> y_i.

Теорема 2 двойственности (о дополняющей нежесткости)

Для того, чтобы допустимые решения X и Y пары двойственных задач были оптимальными, необходимо и достаточно выполнить условия:

То есть, если какое-либо ограничение одной ЗЛП обращается ее opt планом в строгое равенство, то соответствующая переменная двойственной задачи в ее opt плане равна нулю; если же какая-либо переменная opt-го решения одной ЗЛП положительна, то соответствующее ограничение в двойственной ЗЛП ее opt планом обращается в точное равенство.

Теорема Кёнига хорошо иллюстрирует использование принципа двойственности ЗЛП.

Формулирование теоремы. Максимальное число попарно неколлинеарных единиц любой булевой матрицы равно минимальному числу линий, покрывающих все единицы матрицы.

Доказательство. Для нахождения максимального числа попарно неколлинеарных единиц булевой матрицы достаточно сформулировать и решить линейную задачу:

Минимальное число линий, покрывающих все единицы матрицы [C_ij], найдем, решив линейную задачу:

Оптимальному решению (u*_i, v*_j)  последней задачи отвечает минимальное покрытие, состоящее из множества строк I,  для которых u*_i = 1  и столбцов J, для которых u*_j =1.

Матрицы  А и А^Т коэффициентов (*), (**), (***) являются абсолютно унимодулярными, как матрицы двудольного графа. Поэтому условия целочисленности переменных заменяем  на условие их неотрицательности, и тогда получаем пару двойственных задач линейного программирования и согласно теореме двойственности имеем:

Линией матрицы называется ее строка или столбец. Два элемента матрицы называются неколлинеарными, если они не лежат на одной линии.

Матрица называется абсолютно унимодулярной, если все ее ненулевые миноры равны 1, либо -1.

Следствие. Матрица инциденций неориентированного графа G абсолютно унимодулярна тогда и только тогда, когда G – двудольный граф. В двудольном графе все простые циклы имеют четкую длину                                  

Принцип двойственности в задачах линейного программирования.

Предположим, что руководство предприятия из анализа конъюнктуры рынка продукции приняли решение: производство сократить, а от запасов сырья избавиться, (продать на рынке) и при этом не нанести себе убытков.

С этой целью руководство должно назначить стоимости y_i за единицу сырья вида S_i, стремясь при этом минимизировать общую стоимость сырья (чтобы быстрее продать сырье): Ф = Σ⁴_i=1 b_iy_i

Выручка предприятия от продажи сырья, расходуемого на единицу продукции П_i, составит: Σ⁴_i=1 a_ij y_i

И по условию она не должна быть меньше С_j (в противном случае предприятию выгоднее не продавать сырье, а использовать его для нужд производства, выпуска продукции).

Сформулируем исходную и двойственную задачи:

Обе задачи по отношению друг к другу называются двойственными или сопряженными. Анализ таблицы позволяет сделать выводы:

1. Если первая задача сформулирована на поиск максимума, то вторая формулируется на поиск минимума линейной функции.

2. Коэффициенты ЦФ первой задачи являются свободными членами системы ограничений второй.

3. Свободные члены системы ограничений первой задачи являются коэффициентами линейной системы во второй задаче.

4. Матрица коэффициентов второй задачи является транспонированной к матрице коэффициентов ограничений первой задачи.

5. Знаки неравенств в ограничениях второй задачи противоположны знакам неравенств в ограничениях первой задачи.

Оптимальный план X^opt_<n> одной из задач тесно связан с оптимальным планом Y^opt_<n> другой. Если одна из задач имеет решение, то другая также разрешена, причем для оптимальных клонов X^opt_<n> =<x₁, x₂,…x_n> и Y^opt_<m> =<y₁, y₂,…y_m> справедливо равенство Q( X^opt ) =Q’( Y^opt ). Если линейная форма одной из задач неограниченна, то условия другой задачи несовместны. Если A^-1 обратная матрица к матрице В, состоящей из векторов базиса оптимального плана исходной задачи, то оптимальный план двойственной задачи равен Y^opt_<m> =СВ ^-1, здесь С – вектор базисных переменных. Решение двойственной задачи получается в последней симплексной таблице исходной задачи, в (m+1) строке, в столбцах, соответствующих дополнительным параметрам.

Для того чтобы векторы X^opt_<n> =<x₁, x₂,…x_n> и Y^opt_<m> =<y₁, y₂,…y_m> были решениями пары задач, необходимо и достаточно, чтобы их компоненты удовлетворяли следующим условиям:

Эти условия называют принципом дополняющей нежесткости. Если исходная (прямая) задача задана в канонической форме, то двойственная к ней называется несимметричной. Для несимметричной двойственной задачи соблюдается условие y_i  ≥ 0.

Теория ЗЛП доказывает, что компоненты оптимальных планов взаимно двойственных задач, приведенных к каноническому виду, соответствуют одни другим. То есть базисные переменные основной задачи соответствуют свободным переменным двойственной задачи и наоборот, j = 1(1)n, x*_j ​ y*_{m +j} ; x*_n+i ​ y*_i ; i = 1(1)m.

Размерности в табличке m и n берутся в задаче для y-ков записанной в канонической форме.

Пример. Двойственный симплекс метод.  

Исходная задача. Имеется три вида продуктов П_j, причем единица веса каждого из видов продуктов содержит a_ij  единиц (питательных веществ). Для нормальной жизнедеятельности человек должен потреблять не менее b_i единиц вещества B_i в сутки. Стоимость единицы продукта П_j равняется C_j. Требуется составить оптимальный суточный рацион питания, т.е. найти количество x_j продукта, которое должен потреблять человек, чтобы стоимость питания была бы минимальной, если известно, что

такие значения его компонентов x_j,  j = 1(1)3, которые минимизируют целевую функцию (Ц) Q = 3x₁ + 2x₂ + x₃ и удовлетворяют ограничениям неравенствам

0,3x₁ + 0,2x₂ + 0, 4x₃  ≥ 0,2;

0,4x₁ + 0,3x₂ + 0,45x₃  ≥ 0,5;

0,2x₁ + 0,3x₂  + 0, 1 x₃  ≥ 0,6;

0,1x₁ + 0,2x₂ + 0,05x₃  ≥ 0,1;

x_j ≥ 0; j = 1(1)3 = n

Для приведения задачи к каноническому виду введем дополнительные переменные x₄, x₅, x₆, x₇, переменных стало больше чем уравнений n – m = 7 – 4 = 3, следовательно, части из них (трем любым,) для получения решения можно задать произвольные значения (задают, как правило, нулевые значения), возникает число сочетаний из n по m вариантов. Система ограничений примет вид равенств

0,3x₁ + 0,2x₂ + 0,4x₃ – x₄ = 0,2;

0,4x₁ + 0,3x₂ + 0,45x₃     – x₅ = 0,5;

0,2x₁ + 0,3x₂ + 0,1x₃                     – x₆ = 0, 6;                   

0,1x₁ + 0,2x₂ + 0,05x₃                             – x₇ = 0, 1;

x_j ≥ 0; j = 1(1)3 = n, i = 1(1)4 = m.

Назначаем опорный план. Выбор в качестве базисных переменных x₄, x₅, x₆, x₇ приводит к недопустимому опорному плану. Так как знаки левой и правой частей различны. (Свободные переменные x₁ = x₂ = x₃ = 0) Метод искусственного базиса приводит к увеличению числа неизвестных задач, что нежелательно. Анализ задачи показывает, что число уравнений в системе ограничений больше числа переменных. Поэтому попытаемся применить принцип двойственности, т.е. вначале решим двойственную ЗЛП, а затем найдем решение исходной.

Двойственная задача. Коэффициентами линейной формы в двойственной задаче выступают правые части b_i , i = 1(1)4 = m, исходной основной задачи. Переменные получают другие имена y₁, y₂, y₃, y₄, и формулируется двойственная задача иначе. Найти максимум линейной формы Q’:

Q’=0,2y₁ + 0,5y₂ + 0,6y₃  + 0,1y₄;

при ограничениях

0,3y₁ + 0, 4y₂ + 0,2y₃ + 0,1y₄  ≤ 3;

0,2y₁ + 0, 3y₂  + 0,3y₃ + 0,2y₄  ≤ 2;   

0,4y₁ + 0,45y₂ + 0,1y₃ + 0,05y₄ ≤ 1;

y_i ≥ 0; i = 1(1)4.

Приведем задачу к каноническому виду, вводим дополнительные неотрицательные переменные y₅ , y₆ , y₇ : 

Найти минимум ЦФ (знаки у коэффициентов ЦФ поменяли на противоположные): Q’= — 0,2y₁ — 0,5y₂ — 0, 6y₃  — 0,1y₄;

при ограничениях (в ограничения добавили новые переменные):

 0,3y₁ + 0, 4y₂ + 0,2y₃ + 0, 1y₄ + y₅ = 3;

0,2y₁ + 0, 3y₂ + 0,3y₃ + 0, 2y₄ + y₆ = 2;

0,4y₁ + 0,45y₂ + 0,1y₃ + 0,05y₄           + y₇ = 1,

y_i ≥ 0; i = 1(1)7.

Задача решается симплекс методом. Исходный опорный план в качестве переменных может иметь y₅, y₆, y₇ и свободные переменные y₁ = y₂ = y₃ = y₄ = 0, т.е. Y_<7> = [0, 0, 0, 0, 3, 2, 1] .

Базисные переменные y₅, y₆, y₇ и ЦФ выражаем через свободные переменные, т.е. из свободных членов (правых частей, обозначенных γ_i )  вычитаем левые части ограничений

y₅ = 3 – (0,3y₁ + 0,4y₂ + 0,2y₃ + 0,1y₄);

y₆ = 2 – (0,2y₁ + 0,3y₂ + 0,3y₃ + 0,2y₄);

y₇ = 1 – (0,4y₁ + 0,45y₂ + 0,1y₃ + 0,05y₆);

Q’₁=γ₀ — Σ⁴_i=1 γ_i y_i = 0 -(0,2y₁ + 0,5y₂ + 0, 6y₃  + 0,1y₄);

γ₀ =0, так как ЦФ не содержит свободного члена.

и строим симплекс таблицу с двумя полуклетками. Направляющий столбец y₃, направляющая строка y₆.

Анализ таблицы показывает, что все коэффициенты ЦФ при свободных переменных положительны. Следовательно, план Y_<7> не является оптимальным, ЦФ можно уменьшить, увеличивая значения соответствующих свободных переменных.

Находим γ = max{γ_i} =max {0,2; 0,5; 0,6; 0,1} = 0,6. Переменную y₃ надо ввести в базис. После этого устанавливаем, существует ли оптимальный план. В направляющем столбце все коэффициенты положительны, следовательно, оптимальный план существует. В базисе есть переменные, которые можно уменьшать до нуля увеличивая значения y₃, тем самым минимизируя ЦФ. Раньше других в нуль обратиться переменная y₆ и ее исключаем из базиса.

После замены переменных в базисе переходим к новой симплексной таблице.

Анализ этой таблицы показывает, что все коэффициенты в выражении ЦФ свободных переменных отрицательны. Следовательно, опорный план Y_<7>= [0, 0, 20/3, 0, 5/3, 0, 1/3] является оптимальным. ЦФ при этом Q’₁ = — 4  достигла наименьшего значения. Возвращаемся к двойственной задаче. Используя соответствие между оптимальными планами двойственных задач ЛП, определяем: базисными переменными в оптимальном плане будут x₂ x₄ x₅ x₇; их значения с противоположным знаком записаны в последней строке таблицы. Таким образом, X^opt_<n> =<0; 2; 0; 0; 2; 0; 1; 0; 1/30>, т.е. оптимальный рацион из двух единиц продукта П₂. Стоимость такого рациона минимальна и составляет 4 единицы. Это значение с противоположным знаком записано в той же таблице.

Литература

Двойственная задача линейного программирования

Краткая теория

---

С каждой задачей линейного
программирования тесно связана другая линейная задача, называемая двойственной.
Первоначальная задача называется прямой или исходной. Многие задачи линейного
программирования первоначально ставятся в виде исходных или двойственных задач,
поэтому говорят о паре взаимно двойственных задач линейного программирования.
Пара симметричных двойственных ЗЛП имеет следующий вид:

Прямая задача:

Двойственная задача

Рассмотренная пара взаимно
двойственных задач может быть экономически интерпретирована, например, так.

Прямая задача: сколько и
какой продукции

 надо
произвести, чтобы при заданных объемах имеющихся ресурсов

 и
нормах расходов

 максимизировать
выпуск продукции в стоимостном выражении?

Двойственная задача: какова
должна быть оценка единицы каждого из ресурсов

, чтобы при заданных

 и

 минимизировать
общую оценку затрат на ресурсы?

Для построения двойственной
задачи необходимо пользоваться следующими правилами:

Если прямая задача
решается на максимум, то двойственная — на минимум, и наоборот.
В задаче на максимум
ограничения-неравенства имеют смысл ≤, а в задаче минимизации — смысл ≥.
Каждому ограничению
прямой задачи соответствует переменная двойственной задачи, и наоборот, каждому
ограничению двойственной задачи соответствует переменная прямой задачи.
Матрица системы
ограничений двойственной задачи получается из матрицы системы ограничений
исходной задачи транспонированием.
Свободные члены системы ограничений
прямой задачи являются коэффициентами при соответствующих переменных целевой
функции двойственной задачи, и наоборот.
Если на переменную
прямой задачи наложено условие неотрицательности, то соответствующее
ограничение двойственной задачи записывается как ограничение-неравенство, если
же нет, то как ограничение-равенство.
Если какое-либо
ограничение прямой задачи записано как равенство, то на соответствующую
переменную двойственной задачи условие неотрицательности не налагается.

Основное неравенство теории двойственности

Для любых допустимых планов

 и

 пары
двойственных задач справедливо неравенство

. Его экономическое содержание состоит в
том, что для любого допустимого плана производства

 и
любого допустимого вектора оценок ресурсов

 общая
созданная стоимость не превосходит суммарной оценки ресурсов.

Критерий оптимальности Канторовича (достаточный признак оптимальности)

Если для некоторых
допустимых планов

 и

 пары
двойственных задач выполняется равенство

, то

 и

являются оптимальными планами
соответствующих задач. Экономический смысл критерия следующий: план
производства

 и
вектор оценок ресурсов

 являются оптимальными, если цена всей
произведенной продукции и суммарная оценка ресурсов совпадают.

Теорема существования оптимальных планов пары двойственных задач

Для существования
оптимального плана любой из пары двойственных задач необходимо и достаточно
существования допустимого плана для каждой из них.

Первая теорема двойственности

Если одна из двойственных
задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем
экстремальные значения целевых функций совпадают

. Если одна из двойственных задач
неразрешима вследствие неограниченности целевой функции на множестве допустимых
решений, то система ограничений другой задачи противоречива.

Экономическое содержание
первой теоремы двойственности состоит в следующем: если задача определения
оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима
и задача определения оценок ресурсов. Причем цена продукта, полученного в
результате реализации оптимального плана, совпадает с суммарной оценкой
ресурсов. Совпадения значений целевых функций для соответствующих решений пары
двойственных задач достаточно для того, чтобы эти решения были оптимальными.
Это значит, что план производства и вектор оценок ресурсов являются
оптимальными тогда и только тогда, когда цена произведенной продукции и
суммарная оценка ресурсов совпадают. Оценки выступают как инструмент
балансирования затрат и результатов. Двойственные оценки обладают тем
свойством, что они гарантируют рентабельность оптимального плана, то есть
равенство общей оценки продукции и ресурсов обусловливает убыточность всякого
другого плана, отличного от оптимального. Двойственные оценки позволяют
сопоставлять и балансировать затраты и результаты системы.

Связь между задачами
двойственной пары глубже, чем указано в формулировке теоремы. Решая симплексным
методом одну из них, автоматически получаем решение другой. Для этого
достаточно воспользоваться соответствием переменных прямой и двойственной задач
и оценок в последней симплексной таблице.

Отсюда имеем оптимальный
план двойственной задачи. Если прямая задача решается на максимум, то пользуясь
соответствием переменных:

и так далее.

Если прямая задача решается
на минимум, то:

и так далее.

Вторая теорема двойственности (о дополняющей нежесткости)

Для того, чтобы планы

 и

 пары
двойственных задач были оптимальными, необходимо и достаточно выполнение
условий:

Эти условия называются
условиями дополняющей нежесткости. Из них следует: если какое-либо неравенство
системы ограничений одной из задач не обращается в строгое равенство
оптимальным планом этой задачи, то соответствующая компонента оптимального
плана двойственной задачи должна равняться нулю. Если же какая-либо компонента
оптимального плана одной из задач положительна, то соответствующее ограничение
в двойственной задаче ее оптимальным планом должно обращаться в строгое
равенство.

Экономически это означает,
что если по некоторому оптимальному плану

производства расход i-го ресурса строго меньше его запаса

, то в оптимальном плане соответствующая двойственная
оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане
оценок его i-я компонента строго
больше нуля, то в оптимальном плане производства расход соответствующего
ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить
мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по
оптимальному плану производства) имеет положительную оценку, а избыточный
ресурс (используемый не полностью) имеет нулевую оценку.

Третья теорема двойственности

Двойственные оценки
показывают приращение функции цели, вызванное малым изменением свободного члена
соответствующего ограничения ЗЛП, то есть:

Выясним экономическое
содержание третьей теоремы двойственности. Для этого в последнем выражении
дифференциалы заменим приращениями. Получим:

При

 имеем 

То есть двойственная оценка
численно равна изменению  целевой функции
при изменении соответствующего ресурса на единицу. Двойственные оценки

 часто
называют скрытыми, теневыми или маргинальными оценками ресурсов.

Примеры решения задач

---

Задача 1

Постройте
модель двойственной задачи для данной задачи линейного программирования,
заданной в произвольной форме.

Решение

Воспользуемся правилами для
построения двойственной задачи.Заполним вспомогательную таблицу.

ДЗ/ПЗ				min	СП/ЦФ
	-18	7	-12		-2
	-12	16	-12		3
	-11	3	-7	=	-2
	0	13	-12		-1
max		=
ЦФ/СП	-18	1	-3

Двойственная задача будет
иметь следующий вид:

 –любого
знака,

---

Задача 2

Для приведенной ниже задачи
записать двойственную. Решить одну из них симплексным методом и получить решение
другой.

Решение

Приведем задачу к каноническому виду.

Воспользуемся правилами для
построения двойственной задачи.

Двойственная задача будет иметь следующий вид:

Приведем двойственную задачу к каноническому виду.

Заполняем симплексную таблицу 0-й итерации.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Переходим к таблице 1-й итерации:

В индексной строке все члены неотрицательные, поэтому получено
следующее решение задачи линейного программирования (выписываем из столбца
свободных членов):

Соответствие между переменными исходной и двойственной задачи:

На основании симплексной таблицы получено следующее решение
двойственной задачи линейного программирования:

---

Задача 3

Дана
задача линейного программирования:

Решение прямой задачи:

Найти
оптимальное решение двойственной задачи линейного программирования.

Решение

Исходя из вышеописанных
правил построения модели двойственной задачи, двойственная задача будет иметь
следующий вид:

Найдем оптимальное решение
двойственной задачи:

Условия
дополняющей нежесткости (вторая теорема двойственности): для оптимальных планов
двойственных задач имеют место соотношения:

Так
как для оптимального решения прямой задачи 3-е и 4-е ограничения выполняются
как неравенство, то

Для
нахождения значений

 и

, получаем:

Ответ

Решение двойственной задачи:

1. Правила построения двойственной задачи.

Исходя из
общего вида прямой и двойственной задач
можно установить связь между этими
задачами, позволяющую для любой ЗЛП
строить двойственную ей задачу.

Свойства двойственных задач (правила).

1. Число неизвестных
   двойственной задачи равно числу
   ограничений прямой задачи. Число
   ограничений двойственной задачи равно
   числу неизвестных прямой задачи.

2. Матрица коэффициентов
   двойственной задачи является
   транспонированной матрицей коэффициентов
   прямой задачи.

3. Коэффициенты
   целевой функции двойственной задачи
   являются свободными членами ограничений
   прямой задачи.

4. Свободные члены
   ограничений двойственной задачи
   являются коэффициентами целевой функции
   прямой задачи.

5. Если ограничения
   прямой задачи записаны со знаком меньше
   или равно (),
   то ограничения двойственной задачи
   записываются со знаком больше или равно
   (
   ).

6. Если ограничение
   прямой задачи задано в виде уравнения,
   то соответствующее неизвестное
   двойственной задачи не ограничено
   знаком.

7. Если какое-либо
   неизвестное прямой задачи не ограничено
   знаком, то соответствующее ограничение
   двойственной задачи будет задано в
   виде равенства.

8. Если целевая
   функция прямой задачи сформулирована
   на максимум, то целевая функция
   двойственной задачи будет сформулирована
   на минимум.

Существует
много различных комбинаций ограничений
и целевой функции для записи исходной
задачи. Для упрощения задачи построения
двойственной задачи запишем прямую
задачу в некотором стандартном виде
прямой задачи. Этот вид предполагает,
что:

1. все ограничения
   имеют знак
   ;

2. целевая функция
   сформулирована на максимум;

3. все неизвестные
   неотрицательны.

Чтобы записать
прямую задачу в стандартном виде,
необходимо:

1. неравенство со
   знаком
   
   умножить на (-1);

2. равенство заменить
   на два неравенства противоположных
   знаков, одно из которых следует умножить
   на (-1);

3. формулировку
   целевой функции меняют заменой знаков
   коэффициентов на противоположные;

4. если переменное
   x_j
   не ограничено знаком, его можно
   представить в виде разности двух
   неотрицательных переменных.

Пример.
Составить двойственную задачу к исходной.

.

Решение.
1) Стандартный вид прямой задачи.

2)
Двойственная задача:

Задачу
можно записать в виде, соответствующем
исходной прямой задаче, если заменить:

а)

— не ограничена знаком,

б) два
последних ограничения соответствуют
равенству.

.

1. Основные теоремы двойственности и их экономическое содержание.

Теорема 1.
Двойственная
задача к двойственной есть прямая
задача.

Доказательство:

Пусть имеем
пару двойственных задач в матричном
виде.

Ах


А^Тy


C

F
= C^Tx


Z
=

x


0 y


0

Построим к
двойственной задаче двойственную:

1)
запишем в стандартном виде -А^Тy

—C

Z
= —

2)
-Ах


Ах

F
= — C^Tx


F
= C^Tx

Что
и требовалось доказать.

Теорема 2. Значение
функции F, соответствующее любому
допустимо-

му
решению прямой задачи, не больше значения
функции Z,

соответствующего
любому допустимому решению

двойственной
задачи.

Доказательство:
Пусть X и Y соответственно произвольные
допустимые решения прямой и двойственной
задач. Следовательно,

1) Ах

и Y

Y^Т
,
Y^TAX


Y^Tb
= b^TY
= Z.

2) A^TY

C
и X

0

X^Т
,
X^TA^TY

X^TC
= C^TX
= F.

3) выражение
X^TA^TY
– скалярная величина (число)

она равна

своей
транспозиции, т.е. X^TA^TY
= Y^TAX.
Итак, имеем,

F

X^TA^TY
= Y^TAX

Z

F

Z.

Что и
требовалось доказать.

Следствия:
1) если в прямой задаче допустимая область
не пуста, а целевая функция не ограничена
сверху, то у двойственной задачи
допустимая область пуста;

2) если
в двойственной задаче допустимая
область не пуста, а целевая функция не
ограничена снизу, то у прямой задачи
допустимая область пуста.

Теорема 3. Если
прямая задача имеет конечное оптимальное
решение F
= F_max,
то двойственная задача имеет конечное
оптимальное решение Z = Z_min.
При этом F_max
= Z_min,
а симплекс-множители оптимального
решения прямой задачи являются значениями
переменных в оптимальном решении
двойственной задачи.

Доказательство:

Запишем прямую
задачу Ах
,
x

0 , b
,

F
= C^Tx

.

Запишем задачу
в стандартном виде Ах + х^Р
= b, где

х^Р
= (х₁,…,х_n+m)—
дополнительные, уравновешивающие
переменные,
^Т—
симплекс-множители оптимального решения.
Известно, что прямая задача разрешима,
следовательно, можно определить значения
симплекс-множителей оптимального
решения. Получим оптимальное выражение
целевой функции, то есть

+

(-С^T+)x+=
F
+ b^T.
(*)

Так как это
оптимальный вид целевой функции, то все
коэффициенты неотрицательны.

или

.

Т.о., если y
=
,
то ограничения двойственной задачи
выполняются.

Так как (*) –
оптимальный вид целевой функции, то
коэффициенты перед базисными переменными
равны нулю, а свободные переменные сами
равны нулю

F_min
= —b^T
или F_max
= b^T.
Если y =
,
то это и есть целевая функция двойственной
задачи, то есть Z
= F_max
= Z_min.
Что и требовалось доказать.

Теорема 4. Если
двойственная задача имеет конечное
оптимальное решение Z = Z_min,
то прямая задача имеет конечное
оптимальное решение F
= F_max.
При этом Z_min
= F_max
, а значения симплекс-множителей
оптимального решения двойственной
задачи являются значениями переменных
в оптимальном решении прямой задачи с
противоположными знаками (если обе
задачи решаются прямым симплекс-методом).

Доказательство:
В матричной форме двойственная задача
имеет вид.

А^Тy


C
, y


0, С

0,
Z
=

1) Запишем в
стандартном виде A^Ty
– y^S
= C,
где y^S=
(y_m+1,…,y_m+n)^T

0
– дополнительные, уравновешивающие
переменные,
—
симплекс-множители оптимального решения
двойственной задачи. Для двойственной
задачи
имеют
то же значение, то есть

+

(b^T
+

= Z
+
.
(**)

Так как это
оптимальный вид целевой функции Z,
то все коэффициенты неотрицательны.

или

.

Таким образом,
если
,
то ограничения прямой задачи

удовлетворяются,
значит,
это решение.

2) Так как (**) –
оптимальное решение для целевой функции,
то коэффициенты перед базисными
переменными равны нулю, а свободные
переменные сами равны нулю. Следовательно,

Z_min
= —,
а это есть целевая функция прямой задачи,
если
.
Что и требовалось доказать.

Экономическое
содержание теорем состоит в следующем:
если задача оптимизации плана,
максимизирующего выпуск продукции,
разрешима, то разрешима и задача
определения оценок ресурсов. План
производства и оценки ресурсов являются
оптимальными тогда и только тогда, когда
цена произведенной продукции и суммарная
оценка ресурсов совпадают. Оценки
выступают как инструмент балансирования
затрат и результатов. Так как F

Z,

Z – F =
—
издержки производства, которые равны
нулю
когда
F^*
= Z^*.

Двойственные
оценки обладают тем свойством, что они
гарантируют рентабельность оптимального
плана, то есть равенство общей оценки
продукции и ресурсов, и обуславливают
убыточность всякого другого плана,
отличного от оптимального. Кроме того,
если y_i
> 0, то при
оптимальной производственной программе
этот ресурс используется полностью;
если y_i
= 0, то ресурс
используется не полностью.

Соседние файлы в папке Модуль 1

• #
• #
• #
• #
• #

Двойственная задача линейного программирования. Онлайн калькулятор

С помощю этого онлайн калькулятора можно построить двойственную задачу линейного программирования (ЛП) по отношению к исходной задаче. Для построения двойственной задачи, введите данные исходной задачи и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

1. Построение двойственной задачи к исходной задаче линейного программирования

Пусть задана прямая задача линейного программирования (ЛП) в общем виде:

Задаче (1) соответствует следующая двойственная задача ЛП:

В этих задачах знак ∀ — определяет, что на данную переменную не налагается ограничение в виде неотрицательности, т.е. она произвольная.

Отметим, что если задача ЛП (2) является двойственной к задаче ЛП (1), то задача ЛП (1) является двойственной к задаче ЛП (2). Говорят, что задачи ЛП (1) и (2) взаимно двойственные задачи линейного программирования.

Рассмотрим подробно процесс построения двойственной задачи к исходной задачи линейного программирования. Для построения двойственной задачи:

1. Упорядочивается запись исходной задачи ЛП: если целевая функция исследуется на максимум, то ограничения (1b), (1c) должны иметь знак или «=», или «≤», а если целевая функция исследуется на минимум, то ограничения (1b), (1c) должны иметь знак или «=» , или «≥». Если в исходной задаче ЛП есть ограничения, не удовлетворяющие этим условиям, то это можно исправить, умножая данное ограничение на −1.

2. Каждому ограничению исходной задачи ставится в соответствие переменная . Число переменных двойственной задачи равно числу ограничений исходной задачи, а число ограничений двойственной задачи равно числу переменных исходной задачи.

3. Если в исходной задаче целевая функция исследуется на максимум, то целевая функция двойственной задачи исследуется на минимум.

4. Свободные члены исходной задачи становятся коэффициентами целевой функции двойственной задачи.

5. Коэффициенты целевой функции исходной задачи становятся свободными членами двойственной задачи.

6. Матрица коэффициентов двойственной задачи получается транспонированием матрицы коэффициентов исходной задачи.

7. Если на переменную наложено ограничение в виде неотрицательности, то j-е ограничение двойственной задачи записывается в виде неравенства. Если же переменная исходной задачи произвольная, то j-е ограничение двойственной задачи имеет знак равенства.

8. Если в исходой задаче имеются ограничения в виде равенств, то на соответствующие переменные двойственной задачи не налагаются условия неотрицательности.

Чтобы посмотреть пример построения двойственной задачи воспользуйтесь онлайн калькулятором в начале страницы. Для этого введите коэффициенты исходной задачи в ячейки калькулятора и нажмите на кнопку «Построить».

2. Теория двойственности в задачах линейного программирования

Утверждение 1. Если X и Y − допустимые точки задач (1) и (2), соответственно, то

При этом, если для каких то допустимых точек и выполнено равенство , то и являются решениями задач (1) и (2) соответственно.

Доказательство. Запишем взвимно двойственные задачи (1) и (2) в матричном виде.

Исходная задача:

где ,,,,,,

матрица коэффициентов ограничений исходной задачи, которая разделена на четыре матрицы следующих порядков: ,,,.

Сделаны также следующие обозначения:

Двойственная задача:

где , , .

Имеем:

(5b) и (5c) можно записать так:

Легко показать, что

Действительно:

Множители в правой части выражения (9) неотрицательны. Тогда их произведение не отрицательно, т.е. выполнено условие (8).

Учитывая (7) и (8) упростим выражение 6:

С другой стороны:

(4b) и (4c) можно записать так

Учитывая (12) и Y₁ упростим выражение (11):

Из (9) и (13) получим:

т.е. выполнено условие (3).

Докажем вторую часть утверждения 1. Для любой допустимой точки x задачи (1) в том числе . Тогда

Поэтому наибольшее значение целевой функции задачи (1).

С другой стороны для любой допустимой точки y задачи (2)

т.е. − наименьшее из значений целевой функции задачи (2). Таким образом получили, что является решением задачи (1), а является решением задачи (2).

Теорема 1 (первая теорема двойственности). Если исходная задача имеет решение , то двойственная ей задача также имеет решение , и

Если в исходной задаче целевая функция неограничена, то в двойственной задаче допустимая область пуста.

Отметим, что обратное утверждение неверно. Из несовместности системы системы ограничений одной из задач не следует неограниченность целевой функции для другой. В этом случае системы ограничений обеих задач могут быть несовместными. Приведем пример.

Представленные задачи взаимно двойственные, и в этих задачах допустимые области пусты.

Теорема 2 (вторая теорема двойственности или условие дополняющей нежесткости). Планы и пары двойственных задач (1) и (2) являются решениями этих задач тогда и только тогда, когда выполняются следующие условия:

или выполняется условие:

Докажем эквивалентность условий (15) и (16) с условием (17).

Из (4с) и (5с) имеем:

Откуда:

Из (15) и (16) имеем:

Подставляя (19),(20) в (21),(22) соответственно и упрощая получим:

Выразив, например, через остальные слагаемые из (23) и подставляя в (24) получим:

или

А Запись (25) − это другой вид записи равенства (17).

3. Двойственные к разным формам задач линейного программирования

В статье Формы записи задачи линейного программирования мы рассмотрели различные формы записи задачи линейного программирования. В этом параграфе мы рассмотрим двойственные задачи к задачам ЛП в различных формах.

1) Двойственной к задаче ЛП в канонической форме

является задача ЛП в основной форме

2) Двойственной к задаче ЛП в основной форме

является задача ЛП в канонической форме

3) Двойственной к задаче ЛП в стандантной форме

является задача ЛП также в стандартной форме

Все эти три пары взаимно двойственных задач получаются из пары двойственных задач в общем виде (1) и (2) при различных значениях n₁ и m₁. Первая пара задач получается из (1) и (2) при m₁=0, n₁=n. Вторая пара задач получается из задач (1) и (2) при m₁=m, n₁=0. Третья пара задач получается из (1) и (2) при m₁=m, n₁=n.

Иногда более удобно рассматривать задачи ЛП в векторно-матричной форме. Высше представленные пары двойственных задач представим в векторно-матричной форме записи.

1) Двойственной к задаче ЛП в канонической форме

является задача ЛП в основной форме

2) Двойственной к задаче ЛП в основной форме

является задача ЛП в канонической форме

3) Двойственной к задаче ЛП в стандантной форме

является задача ЛП также в стандартной форме

где векторы строки порядка и соответственно, векторы-столбцы порядка и соответственно, − матрица порядка .

4.Условие дополняющей нежесткости

Равенства (15) и (16) называются условиями дополняющей нежесткости. Рассмотрим уравнение (16). Левая часть уравнения является скалярным произведением неотрицательных векторов и , а это означает, что если один из координат одного из этих векторов больше нуля, то соответствующая координата другого вектора равна нулю (поскольку их скалярное произведение равно нулю). Получается, что если в системе линейных неравенств (4b) некоторое неравенство в точке не удовлетворяется как равенство, то соответствующая координата вектора равна нулю и обратно − если некоторая координата вектора больше нуля, то соответствующее неравенство в системе (4b) в точке удовлетворяется как равенство.

Аналогичные рассуждения можно привести и для равенства (15). Условие дополняющей нежесткости позволяет найти оптимальный план двойственной задачи, если известен оптимальный план исходной задачи. Рассмотрим это на примере пар двойственных задач ЛП записанных в стандартной форме.

Пример 1. Дана следующая задача ЛП:

Решить данную задачу. Построить двойственную задачу и найти ее решение используя решение исходной задачи.

Запишем задачу ЛП в матричном виде:

где

Поскольку задача с двумя переменными, то ее можно решить графически.

Как видно из рисунка, область определения – это желтая область . Вектор целевой функции c={1;2}. Для нахождения оптимального плана нужно прямую, перпендикулярную вектору С перемешать по направлению вектора С , до предельного положения соприкосающаяся с областью определения (точка M). Таким образом точка M является оптимальным решением задачи линейного программирования. Как видно из рисунка, точка M находится на пересечении следующих прямых:

Решая систему линейных уравнений (27) получим координаты точки M, т.е. оптимальный план задачи ЛП (26):

или в векторном виде:

Целевая функция в этой точке равна:

Построим двойственную к (26) задачу ЛП:

В векторно матричном виде задача ЛП (30) будет выглядеть так:

или

где

Условие дополняющей нежесткости (15) и (16) в случае задач ЛП в стандартной форме примут вид:

Условие (32) позволяет найти оптимальный план двойственной задачи ЛП (30). Поскольку все координаты оптимального плана исходной задачи положительны, то из равенства (32) следует, что неравенства (30b) и (30c) в оптимальной точке должны выполняться как равенства, т.е. надо решить систему линейных уравнений

Решив данное уравнение находим оптимальный план

Найдем значение целевой функции в данной точке:

Значение целевых функций в оптимальных точках исходной и двойственной задач равны. Следовательно получено правильное решение.

Графический метод решения задачи ЛП (30) смотрите на Рис.2:

Рассмотрим пример с той же допустимой областью, что и пример 1, но с другой целевой функцией.

Пример 2. Дана следующая задача ЛП:

Решить данную задачу. Построить двойственную задачу и найти ее решение используя решение исходной задачи и условия дополняющей нежесткости.

Запишем задачу ЛП в матричном виде:

где

Поскольку задача с двумя переменными, то ее можно решить графически.

Из Рис.3 видно, что оптимальным является точка

Целевая функция в этой точке равна:

Построим двойственную задачу:

В оптимальной точке ограничение (33b) удовлетворяется как строгое неравенство следовательно исходя из условия дополняющей нежесткости (31), первая координата вектора должна быть равна нулю: . Из равенства (32) следует, что неравенство (34b) в оптимальной точке должно выполняться как равенство, поскольку соответствующая координата опттимального плана исходной задачи больше нуля. Таким образом имеем систему линейных уравнений:

Откуда получим .

В векторном виде оптимальный план двойственной задачи имеет вид:

Найдем значение целевой функции в данной точке:

Значение целевых функций в оптимальных точках исходной и двойственной задач равны. Следовательно получено правильное решение.

Графический метод решения задачи ЛП (34) представлен на Рис.4. Прямая, ортогональная к вектору целевой функции B перемещаем перпендикулярно к вектору целевой функции до соприкосновения к допустимой области задачи ЛП (желтая область). Полученная точка M является решением задачи ЛП.