Определение
Последовательность $left{x_{n}right}$ называется
ограниченной сверху, если существует такое число , что для любого номера $n$ , $x_{n} leq M$
Последовательность $left{x_{n}right}$ называется
ограниченной снизу, если существует такое число
$m in R$ , что для любого номера $n$ , $x_{n} geq m$
Последовательность $left{x_{n}right}$ называется ограниченной , если она ограниченная сверху и ограниченная снизу, то есть существует такое число $M geq 0$ , что для любого номера
$n$ , $left|x_{n}right| leq M$
Последовательность $left{x_{n}right}$ называется
неограниченной, если существует такое число $M geq 0$ ,
что существует такой номер $n$ , что $left|x_{n}right| geq M$
Примеры исследования последовательности на ограниченность
Пример
Задание. Исследовать последовательность $left{x_{n}right}=left{frac{1}{n}right}, n in N$ на ограниченность.
Решение. Заданная последовательность является ограниченной, так как для любого
натурального номера $n$ выполняются неравенства:
$$0 lt frac{1}{n} leq 1, forall n in N$$
То есть последовательность является ограниченной снизу нулем, и вместе с тем является ограниченной сверху единицей,
а значит, является и ограниченной.
Ответ. Последовательность ограничена — снизу нулем, а сверху единицей.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Исследовать последовательность $left{x_{n}right}=left{frac{n+1}{sqrt{n^{2}+1}}right}, n in N$ на ограниченность.
Решение. Рассмотрим $|x_{n}|$ и попробуем его оценить сверху:
$$left|x_{n}right|=left|frac{n+1}{sqrt{n^{2}+1}}right|=left|frac{n}{sqrt{n^{2}+1}}+frac{1}{sqrt{n^{2}+1}}right|$$
Так как модуль суммы меньше либо равен сумме модулей: $|a+b| leq |a|+|b|$ , то получаем, что
$$left|x_{n}right| leqleft|frac{n}{sqrt{n^{2}+1}}right|+left|frac{1}{sqrt{n^{2}+1}}right|=frac{n}{sqrt{n^{2}+1}}+frac{1}{sqrt{n^{2}+1}} lt $$ $$ lt frac{n}{sqrt{n^{2}}}+frac{1}{sqrt{n^{2}+1}}=1+frac{1}{sqrt{n^{2}+1}}$$
Выражение $frac{1}{sqrt{n^{2}+1}}$ принимает свое максимальное
значение, когда знаменатель является наименьшим. Знаменатель будет минимальным при наименьшем значении $n$ , то есть для $m=1$ . А тогда
$$left|x_{n}right|<1+frac{1}{sqrt{1^{2}+1}}=1+frac{sqrt{2}}{2}, forall n in N$$
А таким образом, существует такое число $M=1+frac{sqrt{2}}{2}>0$ , что для любого номера $n$ ,
$|x_{n} leq M|$
. Значит, по определению последовательность ${x_{n}}$ ограничена.
Ответ. Последовательность $left{x_{n}right}=left{frac{n+1}{sqrt{n^{2}+1}}right}, n in N$ ограничена
Читать дальше: бесконечно малые и бесконечно большие последовательности.
Ограниченные последовательности
Последовательность называется ограниченной
сверху,
если существует такое число ,
что для любого номера ,
Последовательность называется ограниченной
снизу,
если существует такое число ,
что для любого номера ,
Последовательность называется ограниченной,
если она ограниченная сверху и ограниченная
снизу, то есть существует такое число ,
что для любого номера ,
Последовательность называется неограниченной,
если существует такое число ,
что существует такой номер ,
что
Примеры исследования последовательности на ограниченность
Пример
Задание. Исследовать
последовательность на
ограниченность.
Решение. Заданная
последовательность является ограниченной,
так как для любого натурального
номера выполняются
неравенства:
То
есть последовательность является
ограниченной снизу нулем, и вместе с
тем является ограниченной сверху
единицей, а значит, является и ограниченной.
Ответ. Последовательность
ограничена — снизу нулем, а сверху
единицей.
Пример
Задание. Исследовать
последовательность на
ограниченность.
Решение. Рассмотрим и
попробуем его оценить сверху:
Так
как модуль суммы меньше либо равен сумме
модулей: ,
то получаем, что
Выражение принимает
свое максимальное значение, когда
знаменатель является наименьшим.
Знаменатель будет минимальным при
наименьшем значении ,
то есть для .
А тогда
А
таким образом, существует такое число ,
что для любого номера ,
.
Значит, по определению
последовательность ограничена.
Ответ. Последовательность ограничена
Монотонные последовательности Основные понятия и определения
Определение
Последовательность называется монотонно
возрастающей,
если для любого ,
Можно
дать еще одно альтернативное определение
возрастающей последовательности.
Определение
Последовательность называется монотонно
возрастающей,
если для любого ,
Определение
Последовательность называется монотонно
убывающей,
если для любого ,
Или,
Последовательность называется монотонно
убывающей,
если для любого ,
Примеры исследования последовательностей на монотонность
Пример
Задание. Исследовать
последовательность на
монотонность.
Решение. Рассмотрим
разность -го
члена последовательности и
ее -го
члена :
а
тогда делаем вывод, что —
возрастающая последовательность.
Ответ. —
возрастающая последовательность.
Пример
Задание. Исследовать
последовательность на
монотонность.
Решение. Найдем
отношение -го
члена последовательности к
ее -му
члену :
Для выражение
,
то есть заданная последовательность является
монотонно убывающей.
Ответ. —
монотонно убывающая последовательность.
Нестрогая монотонность
Последовательность является неубывающей или нестрого
возрастающей (невозрастающей или нестрого
убывающей),
если для ,
Последовательность называется монотонной,
если она убывающая или возрастающая.
Если
все элементы последовательности равны
одному и тому же числу, то последовательность
называетсяпостоянной.
Пример
Последовательность является
постоянной, так для любого натурального :
7 Вопрос. Предел числовой последовательности. Сходящиеся и расходящиеся числовые последовательности. Геометрический смысл сходимости последовательности. Предел числовой последовательности
Определение
Последовательность называется сходящейся,
если существует такое число такое,
что последовательность является бесконечно
малой последовательностью.
Определение
Число называется пределом
последовательности и
обозначается ,
Число называется пределом
последовательности ,
если для любого существует
номер такой,
что для любого выполняется
неравенство :
Определение
Целой
частью некоторого
числа называется
наибольшее целое
число, не превосходящее
Соседние файлы в папке ВМ
- #
12.03.201531.14 Кб218-12_BM.odt
- #
- #
- #
Ограниченные последовательности
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение
Последовательность {an}, n$ in $ N, называется ограниченной, если существуют числа a и b, при которых для каждого номера последовательности n справедливо неравенство (рис.1):
[ale a_{n} le bbegin{array}{cc} {} & {ane b} end{array}]
Например, последовательность вида:
[a_{n} =frac{1}{n^{2} } ]
[frac{1}{n^{2} } =frac{1}{1^{2} } ,frac{1}{2^{2} } ,frac{1}{3^{2} } ,frac{1}{4^{2} } …=1,frac{1}{4} ,frac{1}{9} ,frac{1}{16} …]
Ограничена, т.к. $0le a_{n} le 1$
Определение 2
Последовательность $a_n$, n$ in $ N, называется ограниченной сверху, если существует b, при котором для каждого номера последовательности n справедливо неравенство:
[a_{n} le b]
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Например, последовательность вида:
[a_{n} =100-n^{2} ]
[100-n^{2} =100-1,100-4,…=99,96…]
Ограничена сверху, т.к. $a_{n} le 99$
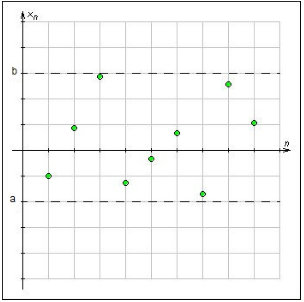
Рисунок 1. Ограничение последовательности
Определение 3
Последовательность $a_n$, n$ in $ N, называется ограниченной снизу, если существует а, при котором для каждого номера последовательности n справедливо неравенство:
[a_{n} ge a]
Например, последовательность вида:
[a_{n} =n^{3} -2]
[n^{3} -2=-1,6,25…]
Ограничена снизу, т.к. $a_{n} ge -1$
Числовые последовательности могут быть неограниченными или постоянными.
Пример 1
Определить вид последовательности:
[a_{n} =left(-1right)^{n} cdot n]
Решение:
[left(-1right)^{n} cdot n=-1,2,-3,4…]
Не является ограниченной, т.к. для любых a и b можно найти большее или меньшее значение.
Пример 2
Определить вид последовательности:
[a_{n} =4]
Решение:
[4=4,4,4…]
Поскольку все члены последовательности равны, числовая последовательность — постоянная.
Пример 3
Определить ограниченность последовательности
[a_{n} =frac{5n-2}{n+1} ]
Решение:
[a_{n} =frac{5n-2}{n+1} =5-frac{7}{n+1} ]
[a_{n} =frac{3}{2} ,frac{7}{3} ,frac{13}{4} …]
Вывод: Функция ограничена и сверху, и снизу, поскольку $a_{n} ge frac{3}{2} $ и $a_{n}
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 17.12.2022

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Ограниченные последовательности
Определения ограниченных последовательностей
Примеры решения задач
ПРИМЕР
| Задание | Исследовать последовательность |
| Решение | Поскольку все члены заданной последовательности являются положительными ( Дробь Итак, имеем, что |
| Ответ | Последовательность ограничена. |
| Понравился сайт? Расскажи друзьям! | |
Нужна помощь с
решением задач?
Более 500 авторов онлайн и готовы помочь тебе прямо сейчас! Цена от 20 рублей за задачу. Сейчас у нас проходит акция, мы дарим 100 руб
на первый заказ.
Предел последовательности
- Определение последовательности
- Предел последовательности
- Как доказать сходимость последовательности к пределу?
- Ограниченные и неограниченные последовательности
- Как доказать неограниченность последовательности?
- Примеры
п.1. Определение последовательности
С понятием «последовательность» мы уже познакомились, когда изучали прогрессии (см. §24 справочника для 9 класса). По определению:
Числовой последовательностью называют функцию натурального аргумента (y_n=f(n), ninmathbb{N}).
Значения (y_1,y_2,…,y_n,…) называют членами последовательности.
В символе (y_n) число (n) называют индексом последовательности.
Т.е., числовая последовательность – это некий набор чисел с присвоенными им порядковыми номерами. Это набор можно задать формулой, описанием или просто перечислением.
Например:
1) Формула (y_n=frac1n, ninmathbb{N}) задает бесконечную последовательность дробей:
| (1,) | (frac12,) | (frac13,) | (…,) | (frac1n,) | (…) |
| 1 | 2 | 3 | … | n | … |
2) Формула (y_n=(-1)^n, ninmathbb{N}) задает бесконечную последовательность «прыгающих» единиц:
| -1, | 1, | -1, | 1, | -1, | 1, | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … |
3) Рекуррентная формула (y_1=1, y_2=1, y_(n+2)=y_(n+1)+y_n) задает бесконечную последовательность чисел Фибоначчи:
| 1, | 1, | 2, | 3, | 5, | 8, | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … |
4) Описание «число π точностью до (10^{-n})» задает бесконечную последовательность все более «подробных» значений числа π:
| 3,1; | 3,14; | 3,141; | 3,1415; | 3,14159; | 3,141592; | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … |
Этот ряд можно также задать формулой (y_n=frac{[picdot 10^n]}{10^n}), где квадратные скобки обозначают целую часть от числа.
п.2. Предел последовательности
Поведение последовательности «на длинных дистанциях» может быть неочевидным. Чтобы лучше понять, возрастает или убывает заданный ряд чисел, ограничен ли он какой-либо величиной или уходит на бесконечность, проще всего построить график.
Например:
В приведенных примерах мы видим, что последовательность (y_n=frac1n) сходится к 0, а приближение числа π (y_n=frac{[picdot 10^n]}{10^n}) конечно же сходится к π.
Говорят, что у таких последовательностей есть конечный предел, и записывают это так: $$ lim_{nrightarrowinfty}frac1n=0, lim_{nrightarrowinfty}frac{[picdot 10^n]}{10^n}=pi $$
Последовательность, имеющая предел, называется сходящейся.
Последовательность, не имеющая предела, называется расходящейся.
Если предел последовательности (lim_{nrightarrowinfty}y_n=0), последовательность называется бесконечно малой.
Число (binmathbb{R}) называют пределом последовательности (left{y_nright}), если последовательность (left{y_n-bright}) является бесконечно малой, т.е. все её элементы, начиная с некоторого номера (N_{varepsilon}), меньше по модулю любого заранее взятого положительного числа (varepsilongt 0): $$ lim_{nrightarrowinfty}y_n=bLeftrightarrow forallvarepsilongt 0 exists N_{varepsilon}inmathbb{N}: ngeq NRightarrow |a_n-b|lt varepsilon $$
Промежуток ((b-varepsilon; b+varepsilon)) $$ b-varepsilonlt y_nlt b+varepsilon $$ называют ε-окрестностью точки b.
п.3. Как доказать сходимость последовательности к пределу?
Разберем данное выше определение предела на конкретном примере.
Пусть (y_n=frac{1}{n+4}). Докажем, что предел этой последовательности b=0.
Найдем номер (N_{varepsilon}) члена последовательности, который первым окажется меньше одной тысячной. Т.е. «заранее взятое число» у нас ε=0,001, а ε-окрестность окружает точку предела (b=0: -varepsilonlt y_nltvarepsilon).
Решаем неравенство (|y_n-b|ltvarepsilon): begin{gather*} left|frac{1}{n+4}-0right|lt 0,001Rightarrow frac{1}{n+4}lt 0,001Rightarrow n+4gt frac{1}{0,001}=1000\ ngt 996Rightarrow N_{varepsilon}=997 end{gather*} Значит, начиная с (N_{varepsilon}=997), все (y_n=frac{1}{n+4}, ngeq N_{varepsilon}=997) будут меньше ε=0,001.
Если попробовать еще больше приблизиться к пределу b=0, например с ε=0,00001, стартовый номер (N_{varepsilon}) для членов последовательности, которые умещаются в 100 раз меньшей ε-окрестности, очевидно, увеличится.
Теперь найдем общую формулу зависимости (N_{varepsilon}) для последовательности (y_n=frac{1}{n+4}) с пределом b=0: begin{gather*} left|frac{1}{n+4}-0right|lt varepsilon Rightarrow frac{1}{n+4}lt varepsilonRightarrow n+4gt frac{1}{varepsilon}\ ngtfrac1varepsilon-4Rightarrow N_{varepsilon}=left[frac1varepsilon-4right]+1 end{gather*} где квадратные скобки обозначают целую часть от числа.
| (varepsilon) | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 7 | 97 | 997 | 9997 | 99997 | 999997 |
| (lg varepsilon) | -1 | -2 | -3 | -4 | -5 | -6 |
| (lg N_{varepsilon}) | 0,845 | 1,987 | 2,999 | 4,000 | 5,000 | 6,000 |
И построим график (в логарифмическом масштабе):
Мы видим, что чем меньше ε, тем больше (N_{varepsilon}). Но главное – мы всегда можем его указать.
Таким образом, мы доказали, что действительно (lim_{nrightarrowinfty}frac{1}{n+4}=0)
Ведь для любого сколь угодно малого (varepsilongt 0) мы можем указать такой номер (N_{varepsilon}=left[frac1varepsilon-4right]+1), начиная с которого, для всех членов последовательности с номерами (ngeq N_{varepsilon}) разность (left|frac{1}{n+4}-0right|), т.е. эти члены не выйдут за переделы ε окрестности предела b=0.
Построенный график интересен еще и тем, что показывает одно из важных практических применений логарифмов: если разбросы по шкалам очень велики, отличаются на порядки, то графики удобней строить в десятичных логарифмах.
Такие графики часто можно увидеть у физиков-ядерщиков, копающих вглубь, от нанометров до планковских длин; или у астрономов, всматривающихся вдаль, от тысяч километров до гигапарсек.
п.4. Ограниченные и неограниченные последовательности
Последовательность (left{y_nright}) называется ограниченной сверху, если существует такое число (Minmathbb{R}), что для любого номера (n, y_nleq M).
Последовательность (left{y_nright}) называется ограниченной снизу, если существует такое число (minmathbb{R}), что для любого номера (n, y_ngeq m).
Последовательность (left{y_nright}) называется ограниченной, если она ограничена сверху и ограничена снизу, т.е. для любого номера (n, mleq y_nleq M).
Последовательность (left{y_nright}) называется неограниченной, если для любого сколь угодно большого (Mgt 0) найдется такой номер (N_M), что для любого (ngeq N_Mcdot|y_n|gt M)
Например:
1) последовательность (y_n=frac1n) ограничена сверху (M=y_1=1) и ограничена снизу (m=lim_{nrightarrowinfty}y_n=0). Т.е. (0lt y_nleq 1, forall n) — последовательность ограничена.
2) последовательность (y_n=(-1)^n) ограничена сверху (M=1) и ограничена снизу (m=-1). Т.е. (-1leq y_nleq 1, forall n) — последовательность ограничена.
3) последовательность чисел Фибоначчи (y_1=1, y_2=1, y_{n+2}=y_{n+1}+y_n) ограничена снизу (m=1), но неограничена сверху. Т.е. последовательность неограничена: (lim_{nrightarrowinfty}=+infty)
Неограниченную последовательность также называют бесконечно большой (стремящейся к бесконечности) и в зависимости от знаков (y_n) при (nrightarrow infty) используют запись: $$ lim_{nrightarrowinfty}y_n=+infty text{или} lim_{nrightarrowinfty}y_n=-infty $$
п.5. Как доказать неограниченность последовательности?
Разберем данное выше определение неограниченности (стремления к бесконечности) на конкретном примере.
Пусть (y_n=n^2). Докажем, что последовательность неограничена.
Найдем номер (N_M) члена последовательности, который первым окажется больше (M=100) — нашего «сколько угодно большого числа».
Согласно определению, подставляем значения в неравенство (|y_n|gt M): begin{gather*} |n^2|gt 100Rightarrow n^2gt 100Rightarrow ngt 10\ N_M=11 end{gather*} Т.е. все (y_n), начиная с 11-го, будут больше 100.
Выведем общую формулу для (N_M): begin{gather*} |n^2|gt MRightarrow n^2gt MRightarrow ngtsqrt{M}\ N_M=[sqrt{M}]+1 end{gather*} где квадратные скобки обозначают целую часть числа.
Например:
| (M) | 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 |
| (N_M) | 4 | 11 | 33 | 101 | 317 | 1001 |
Таким образом, мы доказали, что действительно (lim_{nrightarrowinfty}n^2=+infty)
Ведь для любого сколь угодно большого (Mgt 0) мы можем указать такой номер (N_M=[sqrt{M}]), начиная с которого, для всех членов последовательности с номерами (ngeq N_M, y_n=n^2gt M), т.е. члены последовательности становятся ещё больше.
п.6. Примеры
Пример 1. Используя определение предела последовательности, докажите, что:
a) ( lim_{nrightarrowinfty}frac{n+1}{3-2n}=-frac12 )
По условию: $$ y_n=frac{n+1}{3-2n}, b=-frac12 $$ Находим (N_{varepsilon}) для произвольного ε>0 из неравенства (|y_n-b|ltvarepsilon)
$$ left|frac{n+1}{3-2n}+frac12right|ltvarepsilonRightarrow left|frac{2n+2+3-2n}{2(3-2n)}right| lt varepsilonRightarrow frac52left|frac{1}{3-2n}right|lt varepsilon $$ Знаменатель у дроби под модулем при (ngeq 2) отрицательный . Поэтому, раскрывая модуль, получаем: begin{gather*} frac52left|frac{1}{3-2n}right|=frac{5}{2(2n-3)}lt varepsilonRightarrow 2n-3gt frac{5}{2varepsilon}Rightarrow ngtfrac12left(frac{5}{2varepsilon}+3right)\ N_{varepsilon}=left[frac12left(frac{5}{2varepsilon}+3right)right]+1 end{gather*} Например:
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 15 | 128 | 1253 | 12503 | 125003 | 1250003 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности (N_{varepsilon}=left[frac12left(frac{5}{2varepsilon}+3right)right]+1), начиная с которого
(left|frac{n+1}{3-2n}+frac12right|ltvarepsilon, ngeq N_{varepsilon}geq 2).
Что и требовалось доказать.
б) ( lim_{nrightarrowinfty}frac{n^2+1}{3n^2+n+1}=frac13 )
По условию: $$ y_n=frac{n^2+1}{3n^2+n+1}, b=frac13 $$ Записываем неравенство (|y_n-b|ltvarepsilon):
$$ left|frac{n^2+1}{3n^2+n+1}-frac13right|ltvarepsilonRightarrow left|frac{3n^2+3-3n^2-n-1}{3(3n^2+n+1)}right| lt varepsilonRightarrow frac13left|frac{2-n}{3n^2+n+1}right|lt varepsilon $$ Раскрываем модуль: $$ frac13cdot left|frac{2-n}{3n^2+n+1}right|=frac{n-2}{3(3n^2+n+1)}lt varepsilon $$ Усилим неравенство, чтобы было легче найти (N_{varepsilon}). Заметим, что для (ngeq 3): begin{gather*} frac{n-2}{3(3n^2+n+1)}geqfrac{1}{3(3n^2+n+1)} = frac{1}{9left(n^2+frac n3+frac13right)}gtfrac{1}{9(n^2+2n+1)}=frac{1}{9(n+1)^2}\ frac{1}{9(n+1)^2}ltfrac{n-2}{3(3n^2+n+1)}lt varepsilonRightarrowfrac{1}{9(n+1)^2}lt varepsilonRightarrow (n+1)^2gtfrac{1}{9varepsilon}\ n+1gtfrac{1}{3sqrt{varepsilon}}Rightarrow ngtfrac{1}{3sqrt{varepsilon}}-1\ N_{varepsilon}=left[frac{1}{3sqrt{varepsilon}}-1right]+1 =left[frac{1}{3sqrt{varepsilon}}right], N_{varepsilon}geq 3 end{gather*} Например:
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 3 | 3 | 11 | 33 | 105 | 333 |
Показанный приём с усилением неравенства часто применяется в математическом анализе. Найденное (N_{varepsilon}) немного больше «точного» значения, которое следует из исходной дроби (frac{n-2}{3(3n^2+n+1)}), но наша задача в том, чтобы обоснованно построить любое выражение для стартового номера (N_{varepsilon}) в зависимости от ε.
Если найденный номер будет немного больше исходного – не страшно; главное, чтобы он 1) был обоснован; 2) гарантировал размещение всех последующих (y_n, ngeq N_{varepsilon}) в ε окрестности предела b.
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности (N_{varepsilon}=left[frac{1}{3sqrt{varepsilon}}right]), начиная с которого (left|frac{n^2+1}{3n^2+n+1}-frac13right|ltvarepsilon, ngeq N_{varepsilon}geq 3).
Что и требовалось доказать.
в) ( lim_{nrightarrowinfty}frac{3^n+1}{3^n}=1 )
По условию: $$ y_n=frac{3^n+1}{3^n}, b=1 $$ Записываем неравенство (|y_n-b|ltvarepsilon):
begin{gather*} left|frac{3^n+1}{3^n}-1right|ltvarepsilonRightarrow left|frac{3^n+1-3^n}{3^n}right|ltvarepsilonRightarrow frac{1}{3^n}lt varepsilonRightarrow 3^ngt frac1varepsilon\ ngtlog_3frac1varepsilonRightarrow ngt -log_3varepsilon\ N_{varepsilon}=left[-log_3varepsilonright]+1 end{gather*} Например:
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 3 | 5 | 7 | 9 | 11 | 14 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности (N_{varepsilon}=left[-log_3varepsilonright]), начиная с которого (left|frac{3^n+1}{3^n}-1right|ltvarepsilon, ngeq N_{varepsilon}).
Что и требовалось доказать.
г) ( lim_{nrightarrowinfty}frac{sqrt{n}}{5sqrt{n}+1}=frac15 )
По условию: $$ y_n=frac{sqrt{n}}{5sqrt{n}+1}, b=frac15 $$ Записываем неравенство (|y_n-b|ltvarepsilon):
begin{gather*} left|frac{sqrt{n}}{5sqrt{n}+1}-frac15right|ltvarepsilonRightarrow frac15left|frac{sqrt{n}-sqrt{n}-1}{sqrt{n}+1}right|ltvarepsilon Rightarrow frac{1}{5(sqrt{n}+1)}ltvarepsilonRightarrow sqrt{n}+1gtfrac{1}{5varepsilon}\ sqrt{n}gtfrac{1}{5varepsilon}-1Rightarrow ngtleft(frac{1}{5varepsilon-1}right)^2\ N_{varepsilon}=left[left(frac{1}{5varepsilon}-1right)^2right]+1 end{gather*} Например:
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 2 | 362 | 39602 | 3996002 | 4·108 | 4·1010 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности (N_{varepsilon}=left[left(frac{1}{5varepsilon}-1right)^2right]), начиная с которого (left|frac{sqrt{n}}{5sqrt{n}+1}-frac15right|ltvarepsilon, ngeq N_{varepsilon}).
Что и требовалось доказать.
Пример 2. Используя определения неограниченной последовательности, докажите, что:
a) ( lim_{nrightarrowinfty}2^n=+infty )
По условию: (y_n=2^n)
Записываем неравенство (|y_n|gt M):
begin{gather*} 2^ngt MRightarrow ngt log_2M\ N_M=left[log_2Mright]+1 end{gather*} Например:
| M | 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 |
| NM | 4 | 8 | 11 | 14 | 18 | 21 |
Таким образом, для любого сколь угодно большого (Mgt 0) мы можем указать такой номер (N_M=left[log_2Mright]+1), начиная с которого, для всех членов последовательности с номерами (ngeq N_M, y_n=2^ngt M).
Что и требовалось доказать.
б) ( lim_{nrightarrowinfty}sqrt{n+1}=+infty )
По условию: (y_n=sqrt{n+1})
Записываем неравенство (|y_n|gt M):
begin{gather*} sqrt{n+1}gt MRightarrow n+1gt M^2Rightarrow ngt M^2 -1\ N_M=left[M^2-1right]+1=left[M^2right] end{gather*} знак целой части оставляем, т.к. (Minmathbb{R}) — не обязательно целое.
Например:
| M | 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 |
| NM | 100 | 10 000 | 1 000 000 | 108 | 1010 | 1012 |
Таким образом, для любого сколь угодно большого (Mgt 0) мы можем указать такой номер (N_M=left[M^2right]), начиная с которого, для всех членов последовательности с номерами (ngeq N_M, y_n=sqrt{n+1}gt M).
Что и требовалось доказать.





