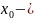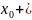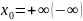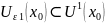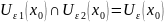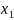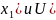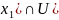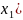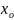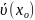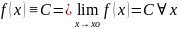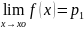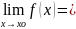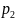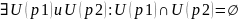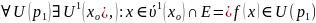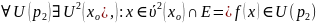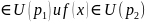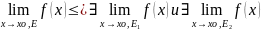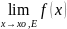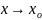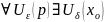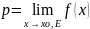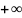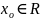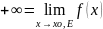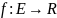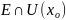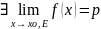Как найти окрестность функции

ε-окрестностью
точки

называется интервал вида (
ε,

ε ) =

(
,
ε>0

Окрестностью
точки

называется
любое множество, содержащее некоторую
ε-окрестность этой точки.

ε-окрестностью
точки

называется интервал вида (ε,

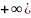
[ (ε,
+

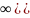
Свойства окрестностей.

1) Любая
окрестность точки содержит эту точку

2) пересечение
двух окрестностей точки снова является
окрестностью этой точки.

Доказательство:

Рассмотрим
любу точку

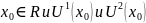
По определению
окрестности существует

и

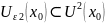
– содержащая точку

3) Свойство
отделимости. Если

и

– произвольные действительные числа
и различны => существует окрестность
U(
)
такие, что пересечение этих двух
окрестностей – не окрестность какой-либо

U(
)
=

Доказательство:

и

— два различных конечных числа. Пусть

<

=> существует a
такое, что:

Возьмем
множество U(

с правым концом a и U(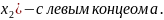

Их пересечение
будет пусто множество.

8. Предельная точка множества. Основное определение предела функции.

Рассмотрим
множество

Точка a
называется предельной для множества
У, если в любой ее окрестности содержится
хотя бы одна точка из E

Теорема.
Если

– предельная для Е точка, то в любой ее
окрестности содержится бесконечное
количество точек из Е.

Доказательство:
пусть

– предельная для Е точка. Рассмотрим
некоторую окрестность U(
)

Предположим,
что в U(
)
содержится конечное число точек из E
– x₁ , x₂
, x₃ … x_k

По свойству
3 окрестностей, существует u¹(x₀)

x₁,
u²(x₀)

x₂,
u³(x₀)

x₃,
… u^k(x₀)

x_k.

Получается,
что пересечение этих окрестностей –
снова окрестность x_o­,
не содержащее ни одну их точек x¹..
x^k. То
есть, x_o
не является предельной для множества
К.

Получаем
противоречие – теорема доказана.
Множество предельных для Е точек будем
обозначать Е¹

Основное определение предела (определение 0 )

Число p

R
называется пределом функции f(x)
при x

,
если значение функции становится как
угодно близким к p лишь
только x ( из области
определения ) становится как угодно
близким к

9. Предел функции. Общие свойства предела (св.1 – св.3).

Определение
предела 1

Пусть есть
функция F: x

Y,

P
называется пределом функции f(x)
при x

на множестве Е, если для любой окрестности
p существует окрестность
точки

,
что как только х попадает в эту окрестность
(проколотую ) —

,
как значение функции попадает в
окрестность точки p.

– проколотая окрестность = U(
)
{
}

Свойства предела :

1)

2) Если
существует предел функции, то он
единственный.

Доказательство:

(1) и

(2)

(1) =>

(2) =>

Тогда для

f(x)

=> не может быть, так как эти две
окрестности не пересекаются.

3) Пусть

Тогда
существование предела

и равенству этих трех пределов.

10. Предел функции. Связь между пределами функции на множестве и на его частях.

Определение
2.

= p

Число

называется
пределом функции f(x)
при

на
множестве Е, если

:

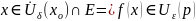
Пользуясь
определением 2 можно дать определение
предела через неравенства для конкретных

.

, если

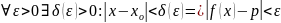
Например
для p =

,

:

, если

Связь между
пределами функции на множестве и его
частях

Пусть

Тогда
существование предела

и равенству этих трех пределов.

11. Ограниченная функция. Ограниченность функции при .

1)

называется ограниченной сверху ( снизу,
просто ограниченной ), если множество
ее значений ограничено сверху ( снизу
, просто ограничено ).

2) Функция
f(x) называется
ограниченной сверху ( снизу, вообще на
Е ) при

,
если

в которой функция ограничена сверху (
снизу, на части

)

Ограниченность
функции при

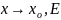
Если

то функция ограничена при

Доказательство:

P
=

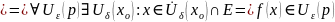
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Математический анализ

ПОНЯТИЕ ОКРЕСТНОСТИ, БЕСКОНЕЧНО МАЛОГО, ПРЕДЕЛА, НЕПРЕРЫВНОСТИ ФУНКЦИИ.

ОКРЕСТНОСТЬЮ ТОЧКИ Хо называется любой интервал, содержащий эту точку.

ПРОКОЛОТОЙ ОКРЕСТНОСТЬЮ т. Хо называется окрестность т. Хо, из которой выброшена сама точка.

ОКРЕСТНОСТЬЮ «+» БЕСКОНЕЧНОСТИ называется любой полубесконечный промежуток вида (а;+) .

ОКРЕСТНОСТЬЮ «-» БЕСКОНЕЧНОСТИ называется любой полубесконечный промежуток вида (- ;b) .

ОКРЕСТНОСТЬЮ БЕСКОНЕЧНОСТИ называется объединение двух любых окрестностей + и — .

Функция f(х) называется бесконечно малой в окрестности т. Хо, если для любого числа >0 существует проколотая окр. т. Хо такая, что для любого числа Х, принадлежащего прокол. окр. т. Хо выполняется неравенство іf(х) і<.

>0 U U => іf(x) і< Число А называется пределом ф-ции f(х) в т. Хо, если в некоторой прок. окр. этой точки ф-цию f(х) можно представить в виде f(х) =А+ (х) , где (х) -бесконечно малое в окрестности т. Хо.

limf(x) =А Ф-ция f(х) называется непрерывной в т. Хо, если в некоторой окр. т. Хо эту ф-цию можно представить в виде: f(х) =f(х) + (х) , где (х) -б. м. в окр. т. Хо.

Иными словами, f(х) -непрерывна в т. Хо, если она в этой точке имеет предел и он равен значению ф-ции.

ТЕОРЕМА: Все элементарные ф-ции непрерывны в каждой точке области определения.

Схема: 1. ф-я элементарна 2. определена 3. непрерывна 4. предел равен значению ф-ции 5. значение ф-ции равно 0 6. можно представить в виде б. м.

СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ:

Теорема#1: Единственная константа, явл-ся б. м.

Теорема#2: Если (х) и (х) -б. м. в окр. т. Хо, то их сумма тоже б. м. в этой окр.

Ф-ция f(х) называется ограниченной в окр. т. Хо, если сущ.

проколотая окр. т. Хо и сущ. число М>0, такие что іf(х) і<М в каждой точке прок. окр. т. Хо.

U M>0: іf(x) і Теорема#3: Если (х) -б. м. в окр. т. Хо, то она ограничена в этой окр.

Теорема#4: О произведении б. м. на ограниченную: Если ф-ция (х) -б. м., а f(х) -ограниченная в окр. т. Хо, то (х) *f(х) -б. м. в окр. т. Хо.

Теорема#5: О промежуточной б. м.: Если (х) и (х) -б. м. в окр. т. Хо и (х) < (х) < (х) — 2 в окр. т. Хо U, то (х) -б. м. в окр. т. Хо.

Две б. м. называются сравнимыми, если существует предел их отношения.

Б. м. (х) и (х) в окр. т. Хо называются одного порядка, если предел их отношений есть число не равное 0.

Две б. м. в окр. т. Хо называются эквивалентными, если предел их отношения равен 1.

Теорема#1: Если и -эквивалентные б. м., то их разность есть б. м. более высокого порядка, чем и чем.

Теорема#2: Если разность двух б. м. есть б. м. более высокого порядка, чем и чем, то и есть эквивалентные б. м.

Определение. Множество вещественных чисел , удовлетворяющих неравенству , называется сегментом или отрезком (обозначается ), а удовлетворяющих строгому неравенству – интервалом (обозначается ). Числа и называются концами, а число – длиной как сегмента , так и интервала .

Определение. Множество вещественных чисел , удовлетворяющих неравенству или , называется полусегментом или полуинтервалом и обозначается соответственно или .

Интервалы и полуинтервалы могут быть и бесконечными. Для обозначения множества вещественных чисел пользуются символом . Знаки и не являются числами, (а являются только символами) и для них нельзя указать соответствующих точек прямой. Поэтому в обозначениях интервалов со стороны таких знаков квадратные скобки не ставят. Сегменты, интервалы и полуинтервалы (конечные и бесконечные) объединяют под общим названием – промежутки.

Определение. Окрестностью точки называется любой интервал, содержащий эту точку.

Часто рассматривают симметричную окрестность точки , то есть интервал , при этом называют радиусом окрестности.

Изобразим на прямой окрестность точки 5 радиуса 3:

Для того, чтобы показать, что точка находится в этой окрестности, воспользуемся неравенством . В общем случае – окрестность точки может быть задана неравенством .

Определение. Окрестностью бесконечно удаленной точки называется внешность некоторого отрезка. Симметричной окрестностью точки называется внешность любого отрезка, симметричного относительно нуля.

С помощью неравенств – окрестность бесконечно удаленной точки записывается в виде , или, объединяя в одно неравенство, .

Определение. Точка называется предельной точкой множества, если в любой ее окрестности содержится, по крайней мере, одна точка данного множества, отличная от .

Из определения следует, что в любой окрестности предельной точки содержится бесконечное число точек данного множества. Предельная точка множества может как принадлежать, так и не принадлежать самому множеству.

Определение. Точка называется внутренней точкой множества, если она принадлежит этому множеству вместе со своей окрестностью.

Определение. Точка называется граничной точкой множества, если в любой ее окрестности есть точки как принадлежащие множеству, так и не принадлежащие ему. Сама граничная точка может как принадлежать множеству, так и не принадлежать ему.

Совокупность граничных точек множества называется его границей.

Определение. Множество, содержащее все свои граничные точки, называется замкнутым, в противном случае – открытым.

Примеры: 1) для множества рациональных чисел граничными являются все точки отрезка как рациональные, так и иррациональные;

2) для множества точек граничными являются сами точки этого множества и нуль.

5.03 Числовая последовательность и ее предел

Если каждому натуральному числу сопоставить вещественное число , тем самым зададим некоторые вещественные числа, определенным образом перенумерованные: имеет номер 1, – номер 2 и т. д. Тогда говорят, что задана последовательность чисел, или числовая последовательность:

, (1)

Которая кратко обозначается .

Числа, составляющие последовательность, называются ее членами, а – общим или -м членом последовательности. В отличие от числового множества, у которого все элементы различны, последовательность может иметь среди своих членов одинаковые, например: или Числовое значение зависит от , то есть является функцией от , поэтому числовая последовательность может рассматриваться как функция натурального аргумента.

Пример 1. Последовательность задана общим членом . Написать члены последовательности.

Решение. , , , .

Для сокращения записей в дальнейшем будем использовать логические символы: квантор общности и квантор существования . Запись означает: любой (всякий) , а – существует (найдется) .

Определение. Последовательность (1) называется ограниченной, если , такое, что выполняется неравенство .

Пример 2. Доказать, что последовательности и – ограниченные, а последовательность — не ограничена.

Решение. Очевидно, что для любого справедливо неравенство . Умножая на 3, получим .

Оценим по модулю общий член последовательности : .

Предположим, что последовательность ограничена сверху, то есть существует число такое, что , тогда или , т. е. неравенство выполняется не для всех , а только для , удовлетворяющих условию , следовательно, не ограничена.

Определение. Число называется пределом числовой последовательности при , если для всякого можно указать номер , такой, что для всех членов последовательности с номерами выполняется неравенство .

Обозначают или и говорят, что последовательность сходится к . Если последовательность не имеет конечного предела, то ее называют расходящейся. Заметим, что величина зависит от , которое выбирается произвольно. Чем меньше , тем , вообще говоря, будет больше (за исключением случая, когда последовательность состоит из одинаковых членов). Очевидно, что если и неравенство выполняется при , то оно подавно будет выполняться при .

Пример 3. Показать, что последовательность имеет своим пределом число 1.

Решение. По определению предела числовой последовательности , .

Будем решать последнее неравенство относительно : . Таким образом, получили, что неравенство выполняется не для всех номеров , а только для тех, которые больше , следовательно, за можно взять целую часть числа , то есть . Если окажется, что , то можно взять равным 1. В определении говорится, что может быть любым положительным числом, в частности, если , то , если , то и т. д.

Пример 4. Показать, что последовательность, заданная общим числом , имеет своим пределом число .

Решение. Возьмем любое . Так как , то из неравенства получим , то есть достаточно взять и тогда при .

Пример 5. Показать, что числовая последовательность с общим членом не имеет предела.

Решение. В подробной записи эта последовательность имеет вид:

Будем рассуждать от противного. Пусть последовательность имеет своим пределом некоторое число . Тогда по определению предела для любого , в том числе и для , найдется , что для . Так как принимает попеременно значения 1 и –1, то должно быть и . Тогда получим , то есть , чего быть не может.

Для доказательства того, что некоторое число не является пределом последовательности, достаточно убедиться, что не все требования, сформулированные в определении предела, выполнены. Допустим, что не является пределом данной последовательности. Это значит, что Нельзя для Любого найти соответствующий , о котором говорится в определении, то есть существует хотя бы одно , для которого невозможно найти такого , чтобы неравенство выполнялось бы для всех . Иначе говоря, найдется хотя бы одно значение , для которого .

Пример 6. Доказать, пользуясь определением предела, что число не является пределом последовательности с общим членом .

Решение. Оценим снизу абсолютную величину разности : , так как при любом . Следовательно, если взять в качестве , то и искать в соответствии с определением бессмысленно.

Дадим геометрическое истолкование предела числовой последовательности.

Числовую последовательность можно рассматривать как последовательность точек прямой и о пределе можно говорить как о точке на прямой. Так как неравенство равносильно неравенству , то определение предела можно сформулировать так: точка будет пределом последовательности точек если, какую бы окрестность точки мы ни задали, найдется такое, что все точки последовательности с номерами попадут в заданную окрестность.

Вне этой окрестности может оказаться лишь Конечное число точек .

Общий член последовательности можно рассматривать как переменную, принимающую эту последовательность значений, поэтому предел последовательности (1) называют также и пределом переменной .

Вопросы для самопроверки и упражнения.

1. Дана последовательность точек Все точки этой последовательности, начиная с пятой, находятся в окрестности нуля . Почему из этого, однако, не следует, что точка нуль является пределом данной последовательности?

2. Пользуясь определением предела числовой последовательности, доказать, что . Начиная с какого , будет ?

3. Доказать, что число 1 не является пределом переменной .

4. Привести пример ограниченной последовательности, не имеющей предела.

< Предыдущая		Следующая >