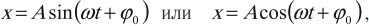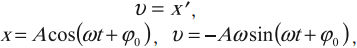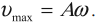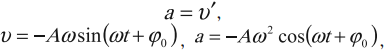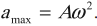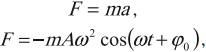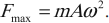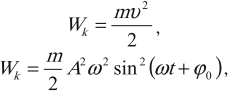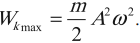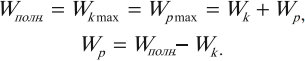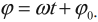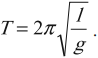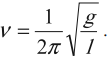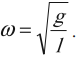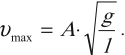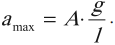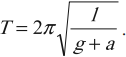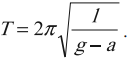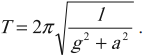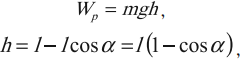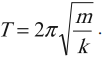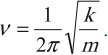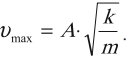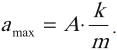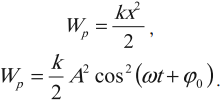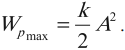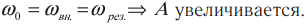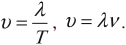Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
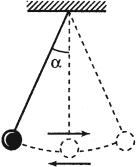
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
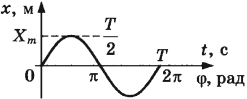
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Амплитуда колебаний – это максимальное значение отклонения от нулевой точки. В физике данный процесс анализируется в разных разделах.
Он изучается при механических, звуковых и электромагнитных колебаниях. В перечисленных случаях амплитуда измеряется по-разному и по своим законам.
Амплитуда колебаний
Амплитудой колебания называют максимальную отдаленную точку нахождения тела от положения равновесия. В физике она обозначается буквой А и измеряется в метрах.
За амплитудой можно наблюдать на простом примере пружинного маятника.
В идеальном случае, когда игнорируется сопротивление воздушного пространства и трение пружинного устройства, устройство будет колебаться бесконечно. Описание движения выполняется с помощью функций cos и sin:
x(t) = A * cos(ωt + φ0) или x(t) = A * sin(ωt + φ0),
где
-
величина А – это амплитуда свободных движений груза на пружине;
-
(ωt + φ0) – это фаза свободных колебаний, где ω — это циклическая частота, а φ0 – это начальная фаза, когда t = 0.
В физике указанную формулу называют уравнением гармонических колебаний. Данное уравнение полностью раскрывает процесс, где маятник движется с определенной амплитудой, периодом и частотой.
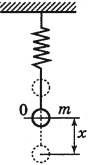
Период колебаний
Результаты лабораторных опытов показывают, что циклический период движения груза на пружине напрямую зависит от массы маятника и жесткости пружины, но не зависит от амплитуды движения.
В физике период обозначают буквой Т и описывают формулами:
Исходя из формул, период колебаний – это механические движения, повторяющиеся через определенный промежуток времени. Простыми словами периодом называют одно полное движение груза.
Частота колебаний
Под частотой колебаний следует понимать количество повторений движения маятника или прохождения волны. В разных разделах физики частота обозначается буквами ν, f или F.
Данная величина описывается выражением:
v = n/t – количество колебаний за промежуток времени,
где
-
n – это единица колебаний;
-
t – отрезок времени.
В Международной системе измерений частоту измеряют в Гц (Герцах). Она относится к точным измеряемым составляющим колебательного процесса.
Например, наукой установлена частота вращения Солнца вокруг центра Вселенной. Она равна -1035 Гц при одинаковой скорости.
Циклическая частота
В физике циклическая и круговая частота имеют одинаковое значение. Данная величина еще называется угловой частотой.
Обозначают ее буквой омега. Она равна числу собственных колебательных движений тела за 2π секунд времени:
ω = 2π/T = 2πν.
Данная величина нашла свое применение в радиотехнике и, исходя из математического расчета, имеет скалярную характеристику. Ее измерения проводят в радианах на секунду. С ее помощью значительно упрощаются расчеты процессов в радиотехнике.
Например, резонансное значение угловой частоты колебательного контура рассчитывают по формуле:
WLC = 1/LC.
Тогда как обычная циклическая резонансная частота выражается:
VLC = 1/2π*√ LC.
В электрике под угловой частотой следует понимать число полных трансформаций ЭДС или число оборотов радиуса – вектора. Здесь ее обозначают буквой f.
Как определить амплитуду, период и частоту колебаний по графику
Для определения на графике составляющих колебательного механического процесса или, например, колебания температуры, нужно разобраться в терминах этого процесса.
К ним относят:
-
расстояние испытываемого объекта от исходной точки – называют смещением и обозначают х;
-
наибольшее отклонение – амплитуда смещения А;
-
фаза колебания – определяет состояние колебательной системы в любой момент времени;
-
начальная фаза колебательного процесса – когда t = 0, то φ = φ0.
Из графика видно, что значение синуса и косинуса может меняться от -1 до +1. Значит, смещение х может быть равно –А и +А. Движение от –А до +А называют полным колебанием.
Построенный график четко показывает период и частоту колебаний. Стоить отметить, что фаза не воздействует на форму кривой, а только влияет на ее положение в заданный промежуток времени.
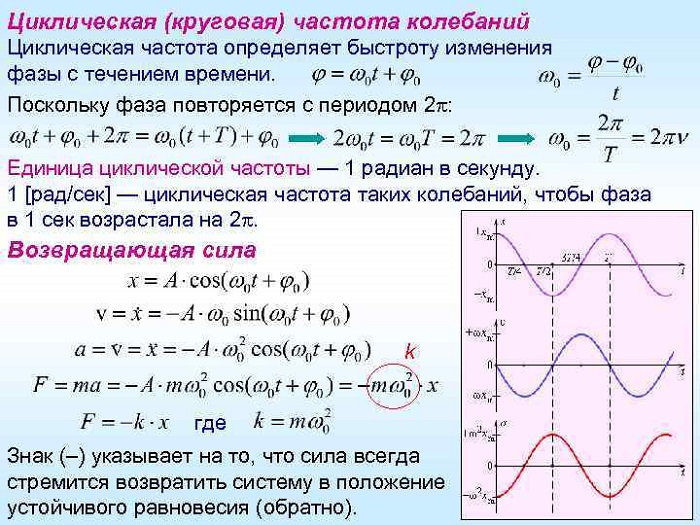
Формула циклической частоты колебаний в физике
Формула циклической частоты колебаний в физике
Определение и формула циклической частоты колебаний
Определение
Циклическая частота — это параметр, характеризующий колебательные движения. Обозначают эту скалярную
величину как $omega $, иногда ${omega }_0$.
Напомним, что уравнение гармонических колебаний параметра $xi $ можно записать как:
[xi left(tright)=A{cos left({omega }_0t+{varphi }_0right) }left(1right),]
где $A={xi }_{max}$ — амплитуда колебаний величины $xi $; $left({omega }_0t+{varphi }_0right)$=$varphi $ — фаза колебаний; ${varphi }_0$ — начальная фаза колебаний.
Циклическую частоту при гармонических колебаниях определяют как частную производную от фазы колебаний ($varphi $) по времени ($t$):
[{omega }_0=frac{?varphi }{partial t}=dot{varphi }left(2right). ]
Циклическая частота колебаний связана с периодом ($T$) колебаний формулой:
[{omega }_0=frac{2pi }{T}left(3right).]
Циклическую частоту с частотой $?$$?$ связывает выражение:
[{omega }_0=2pi nu left(4right).]
Формулы для частных случаев нахождения циклической частоты
Пружинный маятник совершает гармонические колебания с циклической частотой равной:
[{omega }_0=sqrt{frac{k}{m}}left(5right),]
$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.
Гармонические колебания физического маятника происходят с циклической частотой равной:
[{omega }_0=sqrt{frac{mga}{J}}left(6right),]
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.
Частным случаем физического маятника является математический маятник (физический маятник, масса которого сосредоточена в точке), циклическая частота его колебаний может быть найдена как:
[{omega }_0=sqrt{frac{g}{l}}left(7right),]
где $l$ — длина подвеса, на которой находится материальная точка.
Пример 2
Задание. Чему равна циклическая частота гармонических колебаний материальной точки, если амплитуда скорости точки равна ${dot{x}}_{max}=v_0$, амплитуда ее ускорения: ${ddot{x}}_{max}=a_0$? Начальная фаза колебаний равна нулю.
Решение. Из контекста условий задачи понятно, что колебания совершает координата $x$, поэтому уравнение колебаний (в общем виде) запишем как:
[xleft(tright)=A{cos left({omega }_0t+{varphi }_0right)= }A{cos left({omega }_0tright) }left(2.1right),]
По условию задачи ${varphi }_0$=0. Тогда уравнение для скорости изменения параметра $xleft(tright)$ имеет вид:
[dot{x}left(tright)=vleft(tright)=-A{omega }_0{sin left({omega }_0tright)left(2.2right). }]
Из выражения (2.2) следует, что:
[{dot{x}}_{max}=v_0=A{omega }_0left(2.
right.left(2.6right).]
Найдем отношение $frac{a_0}{v_0}$, получим:
[frac{a_0}{v_0}={omega }_0.]
Ответ. ${omega }_0=frac{a_0}{v_0}$
Читать дальше: формула частоты колебаний пружинного маятника.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Омега (значения) | это… Что такое Омега (значения)?
Омега (греч. ὦ μέγα — большое «о») — последняя буква греческого алфавита. А также:
- Омега (кириллица) — буква кириллицы, а также обозначение числа 800 в кириллической системе счисления.
- Альфа и Омега (значения) — первая и последняя буквы греческого алфавита. Словосочетание, буквально означающее «начало и конец», «от и до», «от первой и до последней буквы». Часто применяется в названиях художественных произведений.
Содержание
- 1 «Омега» в музыке
- 2 «Омега» в художественных произведениях, кинематографии и компьютерных играх
- 3 «Омега» как марка технических устройств
- 4 Омега в математике и информатике
- 5 Омега в химии и физике
- 6 Омега в астрономии
- 7 Топонимы
- 8 Другие значения
«Омега» в музыке
- Omega (группа) — венгерская рок-группа.
- Omega — альбом британской рок-группы Asia.
- Deathspell Omega — французская блэк-метал-группа.
«Омега» в художественных произведениях, кинематографии и компьютерных играх
- Omega (Вавилон-5) — вымышленный класс космических кораблей в телесериале «Вавилон-5».
- Омега (Mass Effect) — название космической станции в виде медузы в вымышленной вселенной Mass Effect.
- Вариант «Омега» — советский пятисерийный художественный фильм, снятый в 1975 году режиссёром Антонисом-Янисом Воязосом.
- Омега Суприм (Омегатор) — персонаж-робот из мультсериала «Трансформеры».
- «Человек Омега» — американский фантастический фильм 1971 года режиссёра Бориса Сагала. Одна из экранизаций романа Ричарда Мэтисона «Я — легенда».
- I Am Ωmega, букв. «Я — Омега» (Я воин) — американский художественный фильм 2007 года режиссёра Гриффa Фёрстa, экранизация романа Ричарда Мэтисона «Я — легенда».
- Омега-молекулы — один из видов оружия в вымышленной вселенной «Звёздного пути».
- Миры Омега — один из классов звёздных систем в вымышленной вселенной компьютерной игры Freelancer.
- God of War — используется символ Омега
«Омега» как марка технических устройств
- Opel Omega — марка автомобиля «Опель».
- Омега (самолёт) — советский легкомоторный самолёт конструкции А. Н. Грацианского.
- «Омега» — прототип радиостанции «Север».
- «Омега» — радиоприёмник Р-311.
- Omega (компания) — швейцарская часовая компания, выпускающая часы под одноимённой маркой.
- Омега (компания) — российская компания по разработке и внедрению программного обеспечения для управления предприятиями, комплексной автоматизации бухгалтерского и налогового учета средних и крупных российских предприятий.
- Omega (навигационная система) — система радионавигации.
- Омега — советская программа разработки лазерного оружия высокой мощности для ПВО.
- «Омега» — название советских космических аппаратов типа Космос-14 и Космос-23.
Омега в математике и информатике
- Омега-язык (ω-язык) — это множество бесконечно длинных последовательностей символов.
- Омега-код Элиаса — универсальный код для кодирования положительных целых чисел, разработанный Питером Элиасом.
- Cω (произносится: си́ оме́га, обычно записывается: Cw или Comega) — язык программирования, расширение языка программирования C#, разработанный Microsoft Research.
- Омега-мэппинг — один из способов изображения процесса общего системного мышления с помощью схем, вид диаграммы связей.
Омега в химии и физике
- Знаком Ω обозначают Ом — единицу измерения электрического сопротивления в СИ.
- Омега-3, омега-6, омега-9 — классы полиненасыщенных жирных кислот.
- Омега-гиперон (Ω−-гиперон) — элементарная частица из семейства барионов (Ω-барионы).
Омега в астрономии
- Омега (ω) — обозначение звёзд в некоторых созвездиях в системе обозначений Байера буквами греческого алфавита.
- Омега — туманность в созвездии Стрельца.
- NGC 5139 — ω Центавра, шаровое скопление в созвездии Центавр.
Топонимы
- Бухта Омега — название одной из севастопольских бухт. В бухте находится одноименный пляж «Омега».
Другие значения
- Омега-шахматы — один из вариантов шахмат, изобретённый Дэниелом МакДоналдом в 1992 году.
- Омега (спецподразделение) — спецподразделение внутренних войск МВД Украины.
- Omega (спецподразделение) — спецподразделение Латвии
6.

Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать вращательные кинематические переменные и уравнения и связывать их с их линейными аналогами
- Опишите крутящий момент и плечо рычага
- Решение задач, связанных с крутящим моментом и кинематикой вращения
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
-
(4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением, а также характер пар сил между объектами.
Кроме того, в Руководстве по физике для средней школы рассматривается содержание этого раздела лабораторной работы под названием «Круговое и вращательное движение», а также следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и природу пар сил между объектами.
Основные термины раздела
| угловое ускорение | кинематика вращательного движения | рычаг |
| тангенциальное ускорение | крутящий момент |
Вращательная кинематика
Поддержка учителей
Поддержка учителей
[BL][OL] Повторить уравнения линейной кинематики.
Предупреждение о заблуждении
Студенты могут запутаться между замедлением и увеличением ускорения в отрицательном направлении.
В разделе, посвященном равномерному круговому движению, мы обсуждали движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Однако бывают случаи, когда угловая скорость непостоянна — вращательное движение может ускоряться, замедляться или изменять направление. Угловая скорость не является постоянной, когда вращающийся фигурист тянет руки, когда ребенок толкает карусель, чтобы заставить ее вращаться, или когда компакт-диск останавливается при выключении. Во всех этих случаях угловое ускорение возникает из-за изменения угловой скорости ωω. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение αα – скорость изменения угловой скорости. В форме уравнения среднее угловое ускорение равно
α=ΔωΔt,α=ΔωΔt,
где ΔωΔω — изменение угловой скорости, а ΔtΔt — изменение во времени.
Рисунок
6,9
Фигуристка вращается против часовой стрелки, поэтому ее угловая скорость обычно считается положительной. (Luu, Wikimedia Commons)
Соотношение между величинами тангенциального ускорения, и , и углового ускорения,
α,isa=rαorα=ar.α,isa=rαorα=ar.
6.10
Эти уравнения означают, что величины тангенциального ускорения и углового ускорения прямо пропорциональны друг другу.
Советы для успеха
Тангенциальное ускорение иногда обозначается a t . Это линейное ускорение в направлении, касательном к окружности в интересующей точке при круговом или вращательном движении. Помните, что тангенциальное ускорение параллельно тангенциальной скорости (либо в том же направлении, либо в противоположном направлении).
До сих пор мы определили три вращательные переменные: θθ, ωω и αα. Это угловые версии линейных переменных x, v и a. Следующие уравнения в таблице представляют величину переменных вращения и только тогда, когда радиус постоянен и перпендикулярен переменной вращения. Таблица 6.2 показывает, как они связаны.
| Поворотный | Линейный | Отношения |
|---|---|---|
| θθ | х | θ=xrθ=xr |
| ωω | против | ω=vrω=vr |
| αα | и | α=арα=ар |
Стол
6.
Вращательные и линейные переменные
Теперь мы можем начать понимать, как вращательные величины, такие как θθ, ωω и αα, связаны друг с другом. Например, если колесо мотоцикла, находящееся в состоянии покоя, имеет большое угловое ускорение в течение достаточно долгого времени, оно в конечном итоге начинает быстро вращаться и делает много оборотов. Выражая это в терминах переменных, если угловое ускорение колеса αα велико в течение длительного периода времени t , то конечная угловая скорость ωω и угол поворота θθ велики. В случае линейного движения, если объект находится в состоянии покоя и испытывает большое линейное ускорение, то он имеет большую конечную скорость и пройдёт большое расстояние.
Кинематика вращательного движения описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем. Это только описывает движение — оно не включает никаких сил или масс, которые могут повлиять на вращение (это часть динамики).
Как и в линейной кинематике, мы предполагаем, что a является постоянным, что означает, что угловое ускорение αα также является постоянным, поскольку a=rαa=rα. Уравнение кинематической связи между ωω, αα и т это
ω=ω0+αt(константаα),ω=ω0+αt(константаα),
, где ω0ω0 — начальная угловая скорость. Обратите внимание, что уравнение идентично линейной версии, за исключением угловых аналогов линейных переменных. Фактически все уравнения линейной кинематики имеют аналоги вращения, которые приведены в таблице 6.3. Эти уравнения можно использовать для решения вращательной или линейной задачи кинематики, в которой a и αα являются постоянными.
| Вращательный | Линейный | |
|---|---|---|
| θ=ω¯tθ=ω¯t | х=v¯tx=v¯t | |
| ω=ω0+αtω=ω0+αt | v=v0+atv=v0+at | константа αα, a |
| θ=ω0t+12αt2θ=ω0t+12αt2 | х=v0t+12at2x=v0t+12at2 | константа αα, a |
| ω2=ω02+2αθω2=ω02+2αθ | v2=v02+2axv2=v02+2ax | константа αα, a |
Стол
6.
Уравнения вращательной кинематики
В этих уравнениях ω0ω0 и v0v0 — начальные значения, t0t0 равно нулю, а средняя угловая скорость ω¯ω¯ и средняя скорость v¯v¯ равны
ω¯=ω0+ω2иv¯=v0+v2.ω¯=ω0+ω2иv¯=v0+v2.
6.11
Веселье в физике
Погоня за штормом
Рисунок
6.10
Торнадо спускаются с облаков в виде воронок, которые сильно вращаются. (Дафна Зарас, Национальное управление океанических и атмосферных исследований США)
Охотники за штормами, как правило, попадают в одну из трех групп: любители, гоняющиеся за торнадо в качестве хобби, ученые-атмосферщики, собирающие данные для исследований, наблюдатели за погодой для средств массовой информации или ученые, развлекающиеся под вид работы. Погоня за штормом — опасное времяпрепровождение, потому что торнадо может быстро изменить курс без малейшего предупреждения. Поскольку за разрушениями, оставленными торнадо, следуют охотники за штормами, замена спущенных шин из-за обломков, оставленных на шоссе, является обычным явлением.
Торнадо — прекрасный пример вращательного движения в природе. Они появляются во время сильных гроз, называемых суперячейками, которые имеют столб воздуха, вращающийся вокруг горизонтальной оси, обычно около четырех миль в поперечнике. Разница в скорости ветра между сильными холодными ветрами выше в атмосфере в струйном течении и более слабыми ветрами, движущимися на север от Мексиканского залива, вызывает смещение оси столба вращающегося воздуха по мере продвижения шторма, так что ось становится вертикальной. , создавая торнадо.
Торнадо создают скорость ветра до 500 км/ч (приблизительно 300 миль/ч), особенно в нижней части, где воронка самая узкая, поскольку скорость вращения увеличивается по мере уменьшения радиуса. Они сдувают дома, как если бы они были сделаны из бумаги, и, как известно, протыкают стволы деревьев кусочками соломы.
Крутящий момент
Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила. Чем дальше сила приложена от точки поворота (или точки опоры), тем больше угловое ускорение. Например, дверь открывается медленно, если вы нажимаете слишком близко к петле, но открывается легко, если вы нажимаете далеко от петли. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается; это потому, что угловое ускорение обратно пропорционально массе. Эти отношения очень похожи на отношения между силой, массой и ускорением из второго закона Ньютона. Поскольку мы уже рассмотрели угловые версии расстояния, скорости и времени, вы можете задаться вопросом, что такое угловая версия силы и как она соотносится с линейной силой.
Угловой версией силы является крутящий момент ττ, который представляет собой поворачивающую эффективность силы. См. Рисунок 6.11. Уравнение для величины крутящего момента:
τ=rFsinθ,τ=rFsinθ,
, где r — величина плеча рычага, F — величина линейной силы, а θθ — угол между плечом рычага и силой.
Рисунок
6.11
Человек толкает карусель за ее край и перпендикулярно плечу рычага для достижения максимального крутящего момента.
Применение большего крутящего момента приведет к большему угловому ускорению. Например, чем сильнее человек толкает карусель на рис. 6.11, тем быстрее она ускоряется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Если человек хочет максимизировать воздействие своей силы на карусель, он должен толкнуть ее как можно дальше от центра, чтобы получить наибольшее плечо рычага и, следовательно, наибольший крутящий момент и угловое ускорение. Крутящий момент также максимизируется, когда сила приложена перпендикулярно плечу рычага.
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Продемонстрируйте физические взаимосвязи между крутящим моментом, силой, углом приложения силы и длиной плеча рычага, используя рычаги разной длины. Помогите учащимся установить связь между физическими наблюдениями и математическими соотношениями. Например, крутящий момент максимален, когда сила приложена точно перпендикулярно плечу рычага, потому что sinθ=1sinθ=1 для θ=90θ=90 градусов.
Решение задач кинематики вращения и крутящего момента
Точно так же, как линейные силы могут уравновешиваться, создавая нулевую результирующую силу и линейное ускорение, то же самое верно и для вращательного движения. Когда два крутящих момента одинаковой величины действуют в противоположных направлениях, нет ни чистого крутящего момента, ни углового ускорения, как вы можете видеть в следующем видео. Если нулевой чистый крутящий момент действует на систему, вращающуюся с постоянной угловой скоростью, система будет продолжать вращаться с той же угловой скоростью.
Смотреть физику
Введение в крутящий момент
В этом видео крутящий момент определяется с точки зрения плеча момента (которое совпадает с плечом рычага). Он также охватывает проблему с силами, действующими в противоположных направлениях вокруг точки поворота. (На этом этапе вы можете игнорировать упоминания Сала о работе и механических преимуществах.)
Нажмите, чтобы просмотреть содержимое
Если бы чистый крутящий момент, действующий на линейку из примера, был бы положительным, а не нулевым, что бы это сказало об угловом ускорении? Что произойдет с правителем со временем?
-
Линейка находится в состоянии вращательного равновесия, поэтому она не будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет равно нулю.
-
Линейка не находится в состоянии вращательного равновесия, поэтому она не будет вращаться вокруг своего центра масс.
Таким образом, угловое ускорение будет равно нулю.
-
Линейка не находится в состоянии вращательного равновесия, поэтому она будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет ненулевым.
-
Линейка находится в состоянии вращательного равновесия, поэтому она будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет ненулевым.
Теперь давайте рассмотрим примеры применения вращательной кинематики к рыболовной катушке и концепции крутящего момента к карусели.
Рабочий пример
Расчет времени остановки вращения рыболовной катушки
Глубоководный рыбак использует удочку с катушкой радиусом 4,50 см.
Стратегия
Нас просят найти время t для остановки барабана. Величина начальной угловой скорости ω0=220ω0=220 рад/с, а величина конечной угловой скорости ω=0ω=0 . Величина углового ускорения со знаком равна α=−300α=−300 рад/с 2 , где знак минус указывает на то, что оно действует в направлении, противоположном угловой скорости. Глядя на уравнения кинематики вращения, мы видим все величины, кроме t известны в уравнении ω=ω0+αtω=ω0+αt, что делает его самым простым уравнением для решения этой задачи.
Решение
Используемое уравнение ω=ω0+αtω=ω0+αt .
Алгебраически решаем уравнение для t , а затем подставляем известные значения.
t=ω−ω0α=0−220рад/с−300рад/с2=0,733st=ω−ω0α=0−220рад/с−300рад/с2=0,733с
6.12
Обсуждение
Время остановки катушка довольно мала, потому что ускорение довольно велико. Леска иногда рвется из-за прилагаемой силы, и рыбаки часто позволяют рыбе немного поплавать, прежде чем затормозить катушку. Усталая рыба будет медленнее, ей потребуется меньшее ускорение и, следовательно, меньшая сила.
Рабочий пример
Расчет крутящего момента на карусели
Рассмотрим человека, толкающего игровую карусель на рис. 6.11. Он прикладывает силу 250 Н на краю карусели и перпендикулярно радиусу, который равен 1,50 м. Какой крутящий момент он выдает? Предположим, что трение, действующее на карусель, пренебрежимо мало.
Стратегия
Чтобы найти крутящий момент, обратите внимание, что приложенная сила перпендикулярна радиусу и что трением можно пренебречь.
Решение
τ=rFsinθ=(1,50м)(250Н)sin(π2).=375Н⋅мτ=rFsinθ=(1,50м)(250Н)sin(π2).=375Н⋅м
6,13
Обсуждение
Человек максимизирует крутящий момент, прикладывая силу перпендикулярно плечу рычага, так что θ=π2θ=π2 и sinθ=1sinθ=1 . Мужчина также максимизирует свой крутящий момент, нажимая на внешний край карусели, так что он получает максимально возможное плечо рычага.
Практические задачи
15.
Какой крутящий момент создаст человек, если он приложит силу 12,text{N} на расстоянии 1,0,text{м} от точки вращения, перпендикулярно плечу рычага?
-
frac{1}{144},text{Н-м}
-
frac{1}{12},text{Н-м}
-
12,текст{Н-м}
-
144,text{Нм}
16.
Угловая скорость объекта изменяется с 3 рад/с по часовой стрелке до 8 рад/с по часовой стрелке за 5 с. Каково его угловое ускорение?
- 0,6 рад/с 2
- 1,6 рад/с 2
- 1 рад/с 2
- 5 рад/с 2
Проверьте свое понимание
17.
Что такое угловое ускорение?
-
Угловое ускорение — это скорость изменения углового смещения.
-
Угловое ускорение — скорость изменения угловой скорости.
-
Угловое ускорение — это скорость изменения линейного смещения.
-
Угловое ускорение — скорость изменения линейной скорости.
18.
Какое уравнение для углового ускорения, α ? Предположим, что θ — это угол, ω — угловая скорость, t — время.
- α=ΔωΔtα=ΔωΔt
- α=ΔωΔtα=ΔωΔt
- α=ΔθΔtα=ΔθΔt
- α=ΔθΔtα=ΔθΔt
19.
Что из следующего лучше всего описывает крутящий момент?
-
Это вращательный эквивалент силы.
-
Это сила, влияющая на линейное движение.
-
Это вращательный эквивалент ускорения.
-
Это ускорение влияет на линейное движение.
20.
Какое уравнение для крутящего момента?
-
тау = {F,cosтета},{r}
-
тау = фрак{Fsintheta}{r}
-
тау = rF!cosтета
-
тау = rF!sinтета
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, справляются ли учащиеся с целями обучения этого раздела.
10.1 Угловое ускорение – главы физики колледжа 1-17
10 Вращательное движение и угловой момент
Резюме
- Описать равномерное круговое движение.
- Объясните неравномерное круговое движение.
- Рассчитать угловое ускорение объекта.
- Соблюдайте связь между линейным и угловым ускорением.
Глава 6 Равномерное круговое движение и гравитация обсуждали только равномерное круговое движение, то есть движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Напомним, что угловая скорость[латекс]boldsymbol{omega}[/латекс] определялась как скорость изменения угла[латекс]жирныйсимвол{тета}:[/латекс]
[латекс]boldsymbol{omega:=}[/латекс][латекс]boldsymbol{frac{Deltatheta}{Delta{t}}},[/latex]
, где[латекс]жирныйсимвол{тета}[/латекс] — угол поворота, как показано на рисунке 1.
.
[латекс]boldsymbol{v=romega}[/латекс]
или
[латекс]boldsymbol{omega:=}[/латекс][латекс]boldsymbol{frac{v}{r}},[/латекс]
, где[latex]boldsymbol{r}[/latex] — радиус кривизны, также показанный на рисунке 1. Согласно соглашению о знаках, направление против часовой стрелки считается положительным направлением, а направление по часовой стрелке — отрицательным
Рисунок 1. На этом рисунке показано равномерное круговое движение и некоторые его определяемые величины.
Угловая скорость непостоянна, когда фигурист тянет руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается при выключении. Во всех этих случаях есть угловое ускорение , в котором[латекс]жирныйсимвол{омега}[/латекс]изменяется.
Стратегия для (a)
Угловое ускорение можно найти непосредственно из его определения в [latex]boldsymbol{alpha=frac{Deltaomega}{Delta{t}}}[/latex ]потому что заданы конечная угловая скорость и время. Мы видим, что [латекс]boldsymbol{Deltaomega}[/латекс]составляет 250 об/мин, а [латекс]boldsymbol{Delta{t}}[/латекс]составляет 5,00 с.
Решение для (а)
Вводя известные сведения в определение углового ускорения, получаем 92}[/latex]для углового ускорения нам нужно преобразовать[latex]boldsymbol{Deltaomega}[/latex]из об/мин в рад/с:
[latex]begin{array}{lcl} boldsymbol{Deltaomega} & boldsymbol{=} & boldsymbol{250frac{textbf{rev}}{textbf{min}}cdotpfrac{2pitextbf{rad}}{ textbf{rev}}cdotpfrac{1textbf{ мин}}{60textbf{ сек}}} \ {} & boldsymbol{=} & boldsymbol{26,2textbf{ рад.
Обсуждение
Обратите внимание, что угловое ускорение при вращении девушки колесо маленькое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.
Если бы велосипед в предыдущем примере стоял на колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При движении по окружности линейное ускорение составляет 90 587 по касательной 90 148 к окружности в интересующей точке, как показано на рисунке 2.
Рисунок 2. При круговом движении линейное ускорение a возникает при изменении величины скорости: a касается движения. В контексте кругового движения линейное ускорение также называется тангенциальным ускорением a t .
Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Из главы 6 «Равномерное круговое движение и гравитация» мы знаем, что при круговом движении центростремительное ускорение,[latex]boldsymbol{a_{textbf{c}}},[/latex]относится к изменениям направления скорости, но не ее величины. . Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рис. 3. Таким образом, }}[/latex] перпендикулярны и независимы друг от друга. Тангенциальное ускорение[латекс]boldsymbol{a_{textbf{t}}}[/латекс]прямо связано с угловым ускорением[латекс]жирныйсимвол{альфа}[/латекс]и связано с увеличением или уменьшением скорость, но не ее направление.
Рис. 3. Центростремительное ускорение a c возникает при изменении направления скорости; оно перпендикулярно круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
Теперь мы можем найти точное соотношение между линейным ускорением[latex]boldsymbol{a_{textbf{t}}}[/latex]и угловым ускорением[latex]boldsymbol{alpha}.[/latex]Потому что линейное ускорение пропорциональна изменению модуля скорости, она определяется (как это было в главе 2 «Одномерная кинематика») равной
[латекс]boldsymbol{a_{textbf{t}}:=}[/latex][латекс]boldsymbol{frac{Delta{v}}{Delta{t}}.}[/latex ]
Для кругового движения обратите внимание, что[latex]boldsymbol{v=romega},[/latex], так что
[латекс]boldsymbol{a _{textbf{t}}:=}[/latex][латекс]boldsymbol{frac{Delta(romega)}{Delta{t}}.}[ /латекс]
Радиус[латекс]boldsymbol{r}[/latex]постоянен для кругового движения, поэтому [латекс]boldsymbol{Delta(romega)=r(Deltaomega)}.
[латекс]boldsymbol{a_{textbf{t}}=r}[/latex][латекс]boldsymbol{frac{Deltaomega}{Delta{t}}.}[/latex]
По определению,[латекс]жирныйсимвол{альфа=фракция{Deltaomega}{Delta{t}}}.[/latex] Таким образом,
[латекс]boldsymbol{a_{textbf{t}}=ralpha},[/латекс]
или
[латекс]boldsymbol{alpha:=}[/латекс][латекс]boldsymbol{frac{a _{textbf{t}}}{r}.}[/latex]
Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес автомобиля, тем больше ускорение автомобиля. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении[latex]boldsymbol{alpha}.[/latex]
Пример 2: Расчет углового ускорения колеса мотоцикла
Мощный мотоцикл может разгоняться от 0 до 30,0 м/с (около 108 км/ч) за 4,20 с.
Обсуждение
Радианы безразмерны и появляются в любом соотношении между угловыми и линейными величинами.
На данный момент мы определили три величины вращения — [латекс]boldsymbol{theta,:omega},[/latex]и [латекс]boldsymbol{alpha}.[/latex]Эти величины аналогичны поступательные величины[latex]boldsymbol{x},:boldsymbol{v},[/latex]и[latex]boldsymbol{a}.[/latex]В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.
| Поворотный | Трансляционное | Отношения |
|---|---|---|
| [латекс]boldsymbol{theta}[/латекс] | [латекс]boldsymbol{x}[/латекс] | [латекс] boldsymbol{theta=frac{x}{r}}[/латекс] |
| [латекс]boldsymbol{omega}[/латекс] | [латекс]boldsymbol{v}[/латекс] | [латекс]boldsymbol{omega=frac{v}{r}}[/латекс] |
| [латекс]boldsymbol{alpha}[/латекс] | [латекс]boldsymbol{a}[/латекс] | [латекс] boldsymbol{alpha=frac{a_{textbf{t}}}{r}}[/latex] |
Таблица 1. Вращательные и поступательные величины. Вращательные и поступательные величины. |
СОЗДАНИЕ СОЕДИНЕНИЙ: ЭКСПЕРИМЕНТ НА ДОМУ
Сядьте, поставив ноги на землю, на вращающийся стул. Поднимите одну ногу так, чтобы она была разогнута (выпрямлена). Используя другую ногу, начните вращать себя, отталкиваясь от земли. Прекратите использовать ногу, чтобы отталкиваться от земли, но позвольте стулу вращаться. От исходной точки, с которой вы начали, зарисуйте угол, угловую скорость и угловое ускорение вашей ноги как функцию времени в виде трех отдельных графиков. Оцените величины этих величин.
ИССЛЕДОВАНИЯ PHET: РЕВОЛЮЦИЯ БОЖЬЕЙ КОРОВКИ
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.
Рисунок 5. Революция божьей коровки
- Равномерное круговое движение – это движение с постоянной угловой скоростью[latex]boldsymbol{omega=frac{Deltatheta}{Delta{t}}}.
[/latex]
- При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. углового ускорения) равна [латекс]boldsymbol{alpha=frac{Deltaomega}{Delta{t} }}.[/латекс]
- Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, задается как [латекс]жирныйсимвол{а_{textbf{t}}=frac{Delta{v}}{Delta{t} }}.[/латекс]
- Для кругового движения обратите внимание, что[latex]boldsymbol{v=romega},[/latex], так что
[латекс]boldsymbol{a _{textbf{t}}:=}[/latex][латекс]boldsymbol{frac{Delta(romega)}{Delta{t}}}.[ /латекс]
- Радиус r постоянен для кругового движения, поэтому[латекс]boldsymbol{Delta(romega)=rDeltaomega}.[/latex] Таким образом,
[латекс]boldsymbol{a_{textbf{t}}=r}[/latex][латекс]boldsymbol{frac{Deltaomega}{Delta{t}}}.[/latex]
- По определению,[латекс]жирныйсимвол{Deltaomega/Delta{t}=alpha}.[/latex] Таким образом,
[латекс]boldsymbol{a_{textbf{t}}=ralpha}[/латекс]
или
[латекс]boldsymbol{alpha=}[/латекс][латекс]boldsymbol{frac{a _{textbf{t}}}{r}}.
Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
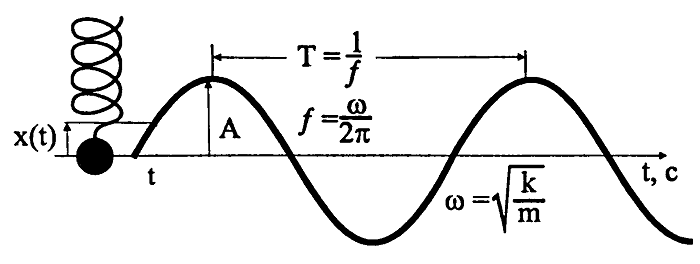
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
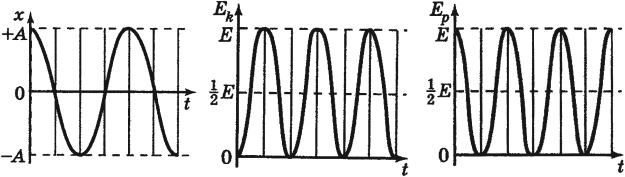
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
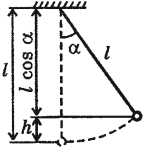
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
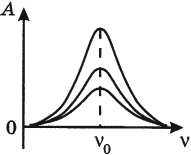
Резонанс
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Механические колебания и волны
3 (59.04%) 146 votes
Механические колебания.
-
Гармонические колебания.
-
Уравнение гармонических колебаний.
-
Пружинный маятник.
-
Математический маятник.
-
Свободные и вынужденные колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний — это величина, обратная периоду:
. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
к оглавлению ▴
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение
. Основная задача механики в данном случае состоит в нахождении функции
, дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому
— амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина
, равная значению фазы при
, называется начальной фазой. Начальная фаза отвечает начальной координате тела:
.
Величина называется циклической частотой. Найдём её связь с периодом колебаний
и частотой
. Одному полному колебанию отвечает приращение фазы, равное
радиан:
, откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить
. Мы получаем закон косинуса:
.
График гармонических колебаний в этом случае представлен на рис. 2.
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить
. Получаем закон синуса:
.
График колебаний представлен на рис. 3.
 |
| Рис. 3. Закон синуса |
к оглавлению ▴
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы
определяются из начальных условий — по начальным значениям координаты и скорости.
к оглавлению ▴
Пружинный маятник.
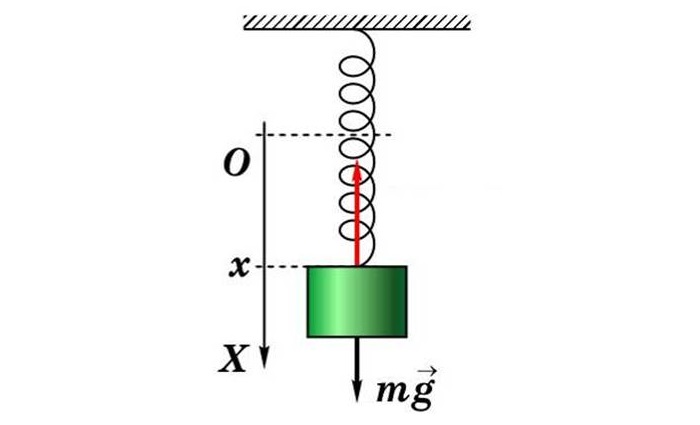
Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна
.
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось
имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и
. Наоборот, если
, то
. Знаки
и
всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
к оглавлению ▴
Математический маятник.
Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство
. Воспользуемся им в формуле (11):
,
или
.
Это — уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
к оглавлению ▴
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы:
, и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний,
, а амплитуда колебаний возрастает до бесконечности при
.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023




















 Таким образом, угловое ускорение будет равно нулю.
Таким образом, угловое ускорение будет равно нулю. 
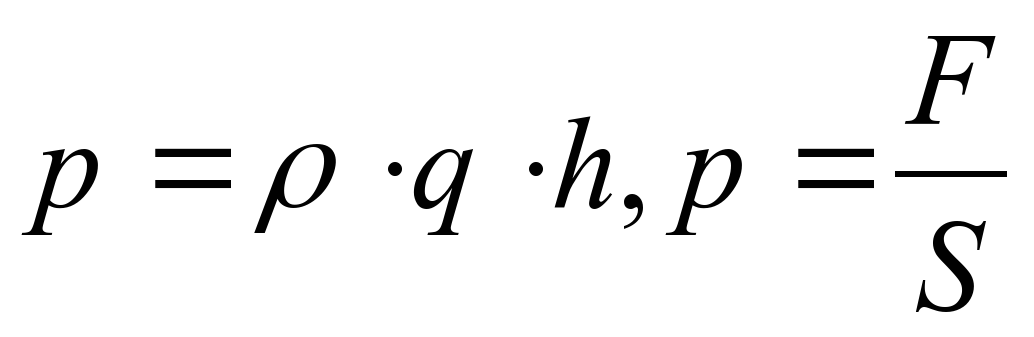
 [/latex]
[/latex]