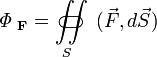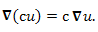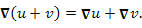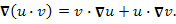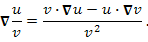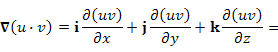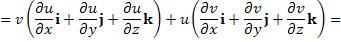Как найти оператор набла - Исправление недочетов и поиск решений вместе с Examum.ru

Опера́тор
на́бла (оператор
Гамильтона) — векторный дифференциальный
оператор,
обозначаемый символом
(набла)
(в ЮникодеU+2207,
∇).
Для трёхмерного евклидова пространства
в прямоугольных декартовых
координатах^[1] оператор
набла определяется следующим образом:

где
—
единичные векторы по осям x, y, z.

Через
оператор набла естественным способом
выражаются основные операции векторного
анализа: grad (градиент), div(дивергенция), rot (ротор),
а также оператор
Лапласа (см.
ниже). Широко употребляется в описанном
смысле в физике и математике (хотя иногда
графический символ
используется
также для обозначения некоторых других,
хотя в некотором отношении не совсем
далеких от рассмотренного, математических
объектов, например, ковариантной
производной).

Под n-мерным
оператором набла подразумевается вектор
с компонентами
в n-мерном
пространстве^[2].

Иногда,
особенно при начертании от руки, над
оператором набла рисуют стрелку:
—
чтобы подчеркнуть векторный характер
оператора. Смысл такого начертания
ничем не отличается от обычного
.

Иногда
(особенно когда речь идет только о
применении к скалярным функциям),
оператор набла называют оператором
градиента,
каковым он в применении к скалярным
функциям (полям) и является.

Замечание:
в физике в наше время название оператор
Гамильтона по
отношению к оператору набла стараются
не употреблять, особенно в квантовой
физике, во избежание путаницы с
квантовым гамильтонианом,
имеющим, в отличие от классического,
операторную природу.

[править]Свойства
оператора набла

Этот
вектор приобретает смысл в сочетании
со скалярной или
векторной функцией, к которой он
применяется.

Если
умножить вектор
на
скаляр
,
то получится вектор

который
представляет собой градиент функции
.

Если
вектор
скалярно
умножить на
вектор
,
получится скаляр

то
есть дивергенция вектора
.

Если
умножить
на
векторно,
то получится ротор вектора
:

Соответственно,
скалярное произведение
есть
скалярный оператор, называемый оператором
Лапласа.
Последний обозначается также
.
В декартовых координатах оператор
Лапласа определяется следующим образом:

Поскольку
оператор набла является дифференциальным
оператором, то при преобразовании
выражений необходимо учитывать как
правила векторной алгебры, так и правила
дифференцирования. Например:

То
есть производная выражения, зависящего
от двух полей, есть сумма выражений, в
каждом из которых дифференцированию
подвергается только одно поле.

Для
удобства обозначения того, на какие
поля действует набла, принято считать,
что в произведении полей и операторов
каждый оператор действует на выражение,
стоящее справа от него, и не действует
на всё, что стоит слева. Если требуется,
чтобы оператор действовал на поле,
стоящее слева, это поле каким-то образом
отмечают, например, ставя над буквой
стрелочку:

Такая
форма записи обычно используется в
промежуточных преобразованиях. Из-за
её неудобства в окончательном ответе
от стрелочек стараются избавиться.

[править]Операторы
второго порядка

Так
как существуют различные способы
перемножения векторов и скаляров, с
помощью оператора набла можно записать
различные виды дифференцирования.
Комбинирование скалярных и векторных
произведений даёт 7 различных вариантов
производных второго порядка:

Для
достаточно гладких полей (дважды
непрерывно дифференцируемых) эти
операторы не независимы. Два из них
всегда равны нулю:

Два
всегда совпадают:

Три
оставшихся связаны соотношением:

Еще
одно может быть выражено через тензорное
произведение векторов:

Градие́нт (от лат. gradiens,
род. падеж gradientis —
шагающий, растущий) — вектор,
показывающий направление наискорейшего
возрастания некоторой величины
,
значение которой меняется от одной
точки пространства к другой (скалярного
поля).
Например, если взять в качестве
высоту
поверхности Земли над уровнем моря, то
её градиент в каждой точке поверхности
будет показывать «направление самого
крутого подъёма». Величина (модуль)
вектора градиента равна скорости
роста
в
этом направлении.

Термин
впервые появился в метеорологии, а в
математику был введен Максвеллом в
1873 г. Обозначение grad тоже предложил
Максвелл.

Определение

Для
случая трёхмерного пространства
градиентом называется векторная функция
с компонентами
,
,
,
где
—
некоторая скалярная функция координат
,
,
.

Если
—
функция
переменных
,
то её градиентом называется
-мерный
вектор

компоненты
которого равны частным
производным
по
всем её аргументам.

Градиент
обозначается
или,
с использованием оператора
набла,
.

Из
определения градиента следует, что

Смысл
градиента любой скалярной функции
в
том, что его скалярное произведение с
бесконечно малым вектором
перемещения
дает полный
дифференциал этой
функции при соответствующем изменении
координат в пространстве, на котором
определена
,
то есть линейную (в случае общего
положения она же главная) часть
изменения
при
смещении на
.
Применяя одну и ту же букву для обозначения
функции от вектора и соответствующей
функции от его координат, можно написать:

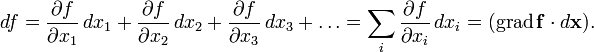
Стоит
здесь заметить, что поскольку формула
полного дифференциала не зависит от
вида координат
,
то есть от природы параметров x вообще,
то полученный дифференциал является
инвариантом, то есть скаляром, при любых
преобразованиях координат, а поскольку
—
это вектор, то градиент, вычисленный
обычным образом, оказывается ковариантным
вектором,
то есть вектором, представленным в
дуальном базисе, какой только и может
дать скаляр при простом суммировании
произведений координат обычного
(контравариантного),
то есть вектором, записанным в обычном
базисе. Таким образом, выражение (вообще
говоря — для произвольных криволинейных
координат) может быть вполне правильно
и инвариантно записано как:

или,
опуская по правилу Эйнштейна знак суммы,

(в
ортонормированном базисе мы можем
писать все индексы нижними, как мы и
делали выше). Однако градиент оказывается
настоящим ковариантным вектором в любых
криволинейных координатах.

[править]Пример

Например,
градиент функции
будет
представлять собой:

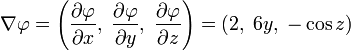
Дивергенция

[править]

Материал
из Википедии — свободной энциклопедии

У
этого термина существуют и другие
значения, см. Дивергенция
(значения).

Дивергенция (от лат. divergere —
обнаруживать расхождение) — дифференциальный
оператор, отображающий векторное
поле наскалярное (то
есть операция дифференцирования, в
результате применения которой к
векторному полю получается скалярное
поле), который определяет (для каждой
точки), «насколько расходится входящее
и исходящее из малой окрестности данной
точки поле» (точнее — насколько
расходятся входящий и исходящий поток).

Если
учесть, что потоку можно приписать
алгебраический знак, то нет необходимости
учитывать входящий и исходящий потоки
по отдельности, всё будет автоматически
учтено при суммировании с учетом знака.
Поэтому можно дать более короткое
определение дивергенции:

дивергенция —
это линейный дифференциальный оператор
на векторном поле, характеризующий поток данного
поля через поверхность малой окрестности
каждой внутренней точки области
определения поля.

Оператор
дивергенции, применённый к полю
,
обозначают как

или

Определение

Определение
дивергенции выглядит так:

где Ф_F — поток
векторного поля F через сферическую
поверхность площадью S,
ограничивающую объём V.
Ещё более общим, а потому удобным в
применении, является определение, когда
форма области с поверхностью S и
объёмом V допускается
любой. Единственным требованием является
её нахождение внутри сферы радиусом,
стремящимся к нулю (то
есть чтобы вся поверхность находилась
в бесконечно малой окрестности данной
точки, что нужно, чтобы дивергенция была
локальной операцией и для чего очевидно
недостаточно стремления к нулю площади
поверхности и объема ее внутренности).
В обоих случаях подразумевается, что

Это
определение, в отличие от приводимого
ниже, не привязано к определённым координатам,
например, к декартовым,
что может представлять дополнительное
удобство в определённых случаях.
(Например, если выбирать окрестность в
форме куба илипараллелепипеда,
легко получаются формулы для декартовых
координат, приведённые в следующем
параграфе).

Определение
легко и прямо обобщается на любую
размерность n пространства:
при этом под объемом понимается n-мерный
объем, а под площадью поверхности
(n-1)-мерная
площадь (гипер)поверхности соответствующей
размерности.

[Править]Определение в декартовых координатах

Допустим,
что векторное поле дифференцируемо в
некоторой области. Тогда в трёхмерном
декартовом пространстве дивергенция
будет определяться выражением

Это
же выражение можно записать с
использованием оператора
набла

Многомерная,
а также двумерная и одномерная, дивергенция
определяется в декартовых координатах
в пространствах соответствующей
размерности совершенно аналогично (в
верхней формуле меняется лишь количество
слагаемых, а нижняя остается той же,
подразумевая оператор набла подходящей
размерности).

[Править]Физическая интерпретация

С
точки зрения физики (и в строгом смысле,
и в смысле интуитивного физического
образа математической операции)
дивергенция векторного поля является
показателем того, в какой степени данная
точка пространства (или очень малая
окрестность точки) является источником
или стоком этого поля:

—
точка
поля является источником;

—
точка
поля является стоком;

—
стоков
и источников нет, либо они компенсируют
друг друга.

Простым,
хоть быть может и несколько схематическим,
примером может служить озеро (для
простоты — постоянной единичной
глубины со всюду горизонтальной скоростью
течения воды, не зависящей от глубины,
давая, таким образом, двумерное векторное
поле на двумерном пространстве). Если
угодно иметь более реалистическую
картину, то можно рассмотреть горизонтальную
проекцию скорости, проинтегрированную
по вертикальной пространственной
координате, что даст ту же картину
двумерного векторного поля на двумерном
пространстве, причём картина качественно
будет для наших целей не сильно отличаться
от упрощённой первой, количественно же
являться её обобщением (весьма
реалистическим). В такой модели (и в
первом, и во втором варианте) родники,
бьющие из дна озера будут давать
положительную дивергенцию поля скоростей
течения, а подводные стоки (пещеры, куда
вода утекает) — отрицательную
дивергенцию.

Дивергенция
вектора плотности тока дает минус
скорость накопления заряда
в электродинамике (так
как заряд сохраняется, то есть не исчезает
и не появляется, а может только
переместиться через границы какого-то
объёма, чтобы накопиться в нём или уйти
из него; а если и возникают или исчезают
где-то положительные и отрицательные
заряды — то только в равных количествах).
(См.Уравнение
непрерывности).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Опера́тор на́бла (оператор Гамильтона) — векторный дифференциальный оператор, обозначаемый символом (набла) (в Юникоде U+2207, ∇).

Под этим оператором подразумевается вектор с компонентами ${displaystyle {partial over partial x_{1}},;{partial over partial x_{2}},;ldots ,;{partial over partial x_{n}}}$ в -мерном пространстве.

Для трёхмерного декартового пространства оператор набла определяется следующим образом

Свойства оператора набла

Этот вектор приобретает смысл в сочетании со скалярной или векторной функцией, к которой он применяется.

Если умножить вектор на скаляр , то получится вектор

{displaystyle nabla phi ={partial phi over partial x}{vec {i}}+{partial phi over partial y}{vec {j}}+{partial phi over partial z}{vec {k}}}

, который представляет собой градиент функции

Если вектор скалярно умножить на вектор , получится скаляр

${displaystyle nabla {vec {a}}=nabla _{x}a_{x}+nabla _{y}a_{y}+nabla _{z}a_{z}={partial a_{x} over partial x}+{partial a_{y} over partial y}+{partial a_{z} over partial z}}$

, то есть дивергенция вектора

Если умножить на векторно, то получится ротор вектора .

Также, произведение ${displaystyle nabla nabla =nabla ^{2}}$ есть оператор Лапласа, и обозначается . В декартовых координатах оператор Лапласа определяется следующим образом:

${displaystyle Delta ={partial ^{2} over partial x^{2}}+{partial ^{2} over partial y^{2}}+{partial ^{2} over partial z^{2}}}$

Поскольку оператор набла является дифференциальным оператором, то при преобразовании выражений необходимо учитывать как правила векторной алгебры, так и правила дифференцирования. Например:

{displaystyle operatorname {grad} (phi psi )=nabla (phi psi )=psi nabla phi +phi nabla psi =psi operatorname {grad} phi +phi operatorname {grad} psi }

{displaystyle operatorname {div} (operatorname {grad} phi )=nabla (nabla phi )=(nabla nabla )phi =Delta phi }

ca:Operador nabla
cs:Nabla
da:Nabla
nl:Nabla
no:Nabla
pl:Nabla
sk:Operátor nabla
sv:Nablaoperatorn
ta:டெல் இயக்கி

Источник

Существуют различные способы задания функций, которые представляет собой те или иные правила сопоставления каждому значению одной величины соответствующее значение другой величины. Например, функция может быть задана графически, параметрически, в явном или неявном виде и т.д.

Один из весьма плодотворных подходов, позволяющих сформулировать соотношения между функциями, основан на использовании понятия оператора, то есть последовательного набора команд, осуществляющих преобразование одной функции в другую.

Например, равенство

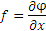можно рассматривать в качестве правила преобразования функции

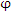в функцию f с помощью оператора дифференцирования

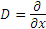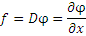
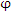
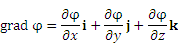
Подобным образом можно интерпретировать формугу для градиента скалярного поля . Напомним, что

где i, j и k – единичные векторы прямоугольной системы координат.

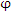
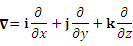Если формально вынести «общий множитель» и определить оператор выражением

(1)

то можно рассматривать как результат действия линейного дифференциального оператора на скалярную функцию :

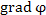
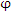
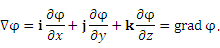
Таким образом,

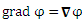
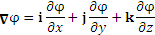
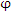
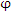
Приведем еще один аргумент в пользу операторной записи. Равенство    справедливо для любой скалярной функции . Поэтому его можно сформулировать в символическом виде (1), убрав упоминание о .


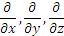
Во многих случаях с оператором    можно обращаться как с обычным вектором, роль координат которого играют операторы
  , преобразующие справа расположенную функцию в соответствующие частные производные от этой функции.


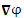
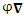
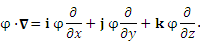
Следует, однако, иметь в виду, что операторная алгебра несколько отличается от векторной. Так, оператор    действует только на функцию, расположенную справа от оператора. Например,    представляет собой векторную функцию, тогда как    – векторный оператор, которому еще предстоит подействовать на ту функцию, которая окажется справа от него:

Свойства оператора .

Для примера докажем справедливость свойства 3:

Источник

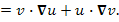
Оператор «набла» в декартовых координатах:

$$
nabla=vec{e}_{x}frac{partial}{partial x}+vec{e}_{y}frac{partial}{partial y}+vec{e}_{z}frac{partial}{partial z}.
$$

Через оператор «набла» записывается градиент:
$$
text{grad } u = nabla u = vec{e}_{x}frac{partial u}{partial x}+vec{e}_{y}frac{partial u}{partial y}+vec{e}_{z}frac{partial u}{partial z},
$$
дивергенция, через скалярное произведение оператора и вектора:
$$
text{div } vec a = (nabla cdot vec a) = frac{partial a_x}{partial x}+frac{partial a_y}{partial y}+frac{partial a_z}{partial z},
$$
ротор, через векторное произведение оператора и вектора:
$$
text{rot } vec a = [nabla times vec a] =
left|begin{array}{ccc}
vec{e}_{x} & vec{e}_{y} & vec{e}_{z}\
frac{partial}{partial x} & frac{partial}{partial y} & frac{partial}{partial z}\
a_x & a_y & a_z
end{array}right|
.
$$

Легко вычисляется действие оператора набла на координаты вектора $vec r$, т.е. когда в качестве скалярной функции рассматривается координата:

$$
nabla x=vec{e}_{x}, , nabla y=vec{e}_{y}, , nabla z=vec{e}_{z},
$$

это приводит к выделению
соответствующих орт. Тогда действие на модуль радиус вектора $r=|vec{r}|=sqrt{x^{2}+y^{2}+z^{2}}$
должен приводить к выделению $vec{n}$ — направления
по этому вектору $vec{r}$, так как мы всегда можем выбрать соответствующую
систему координат, когда некоторая орта будет направлена по $vec{r}=vec{n}cdot r$.
Прямой проверкой это подтверждается:
$$
nabla r=nablasqrt{r^{2}}=left(frac{d}{dleft(r^{2}right)}sqrt{r^{2}}right)nabla r^{2}=
$$
$$
frac{1}{2}frac{1}{sqrt{r^{2}}}cdotleft(vec{e}_{x}2x+vec{e}_{y}2y+vec{e}_{z}2zright)=frac{vec{r}}{r}=vec{n}.
$$
Итак:

$$
nabla r=
frac{vec{r}}{r}.
$$

Градиент от сложной функции

Если рассмотреть вместо скалярной функции — произведение двух функций $u,v, $
тогда действие градиента:
[
nabla uv = u nabla v + vnabla u.
]

Рассмотрим, теперь, скалярную функцию, полученную из скалярного произведения двух векторов:
$$
nabla(vec{a}cdotvec{b})=nabla(a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}).
$$
Пусть вектор $vec{a}$ — постоянный, тогда
$$
nabla(vec{a}cdotvec{b})=vec{i}left(a_{x}frac{partial}{partial x}b_{x}+a_{y}frac{partial}{partial x}b_{y}+a_{z}frac{partial}{partial x}b_{z}right)+
$$
$$
vec{j}left(a_{x}frac{partial}{partial y}b_{x}+a_{y}frac{partial}{partial y}b_{y}+a_{z}frac{partial}{partial y}b_{z}right)+vec{k}left(a_{x}frac{partial}{partial z}b_{x}+a_{y}frac{partial}{partial z}b_{y}+a_{z}frac{partial}{partial z}b_{z}right).
$$
Давайте выделим слагаемые выражения $(vec{a}cdotnabla)vec{b}=left(a_{x}frac{partial}{partial x}+a_{y}frac{partial}{partial y}+a_{z}frac{partial}{partial z}right)vec{b}$,
тогда
$$
nabla(vec{a}cdotvec{b})=(vec{a}cdotnabla)vec{b}+vec{i}left(a_{y}frac{partial}{partial x}b_{y}+a_{z}frac{partial}{partial x}b_{z}-a_{y}frac{partial}{partial y}b_{x}-a_{z}frac{partial}{partial z}b_{x}right)+
$$
$$
vec{j}left(a_{x}frac{partial}{partial y}b_{x}+a_{z}frac{partial}{partial y}b_{z}-a_{x}frac{partial}{partial x}b_{y}-a_{z}frac{partial}{partial z}b_{y}right)+
$$
$$vec{k}left(a_{x}frac{partial}{partial z}b_{x}+a_{y}frac{partial}{partial z}b_{y}-a_{x}frac{partial}{partial x}b_{z}-a_{y}frac{partial}{partial y}b_{z}right)=
$$
$$
(vec{a}cdotnabla)vec{b}+vec{i}left(a_{y}left(frac{partial}{partial x}b_{y}-frac{partial}{partial y}b_{x}right)+a_{z}left(frac{partial}{partial x}b_{z}-frac{partial}{partial z}b_{x}right)right)+
$$
$$
vec{j}left(a_{x}left(frac{partial}{partial y}b_{x}-frac{partial}{partial x}b_{y}right)+a_{z}left(frac{partial}{partial y}b_{z}-frac{partial}{partial z}b_{y}right)right)+
$$
$$
vec{k}left(a_{x}left(frac{partial}{partial z}b_{x}-frac{partial}{partial x}b_{z}right)+a_{y}left(frac{partial}{partial z}b_{y}-frac{partial}{partial y}b_{z}right)right)=
$$
$$
(vec{a}cdotnabla)vec{b}+vec{i}left(a_{y}left(text{rot }vec{b}right)_{z}-a_{z}left(text{rot }vec{b}right)_{y}right)+
$$
$$
vec{j}left(-a_{x}left(text{rot }vec{b}right)_{z}+a_{z}left(text{rot }vec{b}right)_{x}right)+vec{k}left(a_{x}left(text{rot }vec{b}right)_{y}-a_{y}left(text{rot }vec{b}right)_{x}right)=
$$
$$
(vec{a}cdotnabla)vec{b}+left[vec{a}timestext{rot }vec{b}right],
$$
таким образом, если вектор $vec a$ постоянный, то:

$$
nabla(vec{a}cdotvec{b})=
(vec{a}cdotnabla)vec{b}+left[vec{a}timestext{rot }vec{b}right].
$$

Если $vec b = vec r$, то получим

$$
nabla ( vec rcdot vec a ) = vec a,
$$

но в этом можно убедиться и проще — прямым вычислением.

Если, теперь, в выражении $nabla(vec{a}cdotvec{b})$ оба вектора
$vec{a}$ и $vec{b}$ зависят от координат, то действие оператора
набла сводится к поочерёдному действию на скалярное произведение $(vec{a}cdotvec{b})$
так, что сначала один вектор $vec{a}$ постоянный , а потом второй
— $vec{b}$. Тогда:
$$
nabla(vec{a}cdotvec{b})=(vec{a}cdotnabla)vec{b}+left[vec{a}timestext{rot }vec{b}right]+(vec{b}cdotnabla)vec{a}+left[vec{b}timestext{rot }vec{a}right].
$$

Рассмотрим дивергенцию от произведения вектора $vec a$ на скаляр $u$:
$$
text{div } , u vec a=(nablacdot u , vec a)=
frac{partial}{partial x}(u , a_x)+frac{partial}{partial y} (u , a_y)+frac{partial }{partial z} (u , a_z)=
$$
$$
u , frac{partial}{partial x} a_x+ u , frac{partial}{partial y} a_y+ u , frac{partial }{partial z} a_z
+
a_x frac{partial}{partial x}u + a_y frac{partial}{partial y} u + a_z frac{partial }{partial z} u=
$$
$$
u , (nabla cdot vec a ) + (vec a cdot nabla , u)
=
u , text{div } vec a + (vec a cdot text{grad } u)
.
$$

Итак:

$$
bigl(nabla cdot (u ,vec a) bigr) = u , (nabla cdot vec a ) + (vec a cdot nabla , u).
$$

Давайте вычислим и остальные действия оператора $nabla$ на вектор
$vec{r}$:

$$
text{div } vec r=(nablacdotvec{r})=frac{partial}{partial x}x+frac{partial}{partial y}y+frac{partial}{partial z}z=3
$$

$$
text{rot }vec{r}=
left|begin{array}{ccc}
vec{e}_{x} & vec{e}_{y} & vec{e}_{z}\
frac{partial}{partial x} & frac{partial}{partial y} & frac{partial}{partial z}\
x & y & z
end{array}right|
=0,
$$
так как производная берётся всегда не по своей координате, например,
$$
left(text{rot }vec{r}right)_{x}=frac{partial}{partial y}z-frac{partial}{partial z}y=0-0=0.
$$
Итак:

$$
text{rot }vec{r}=0.
$$

Ещё одно важное тождество:

$$
text{rot }(text{rot }vec{A})=text{grad }(text{div }vec{A}) — Delta vec{A}.
$$

Источник

Опера́тор на́бла — векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Обозначается символом ∇ (набла).

Для трёхмерного евклидова пространства в прямоугольной декартовой системе координат^[1] оператор набла определяется следующим образом:

[math]displaystyle{ nabla={partialoverpartial x}vec{i}+{partialoverpartial y}vec{j}+{partialoverpartial z}vec{k} }[/math],

где [math]displaystyle{ vec i, vec j, vec k }[/math] — единичные векторы по осям [math]displaystyle{ x, y, z }[/math] соответственно.

Также используется следующая запись оператора набла через компоненты:

[math]displaystyle{ nabla= left{ {partialoverpartial x}, {partialoverpartial y}, {partialoverpartial z} right} }[/math].

Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div (дивергенция), rot (ротор), а также оператор Лапласа (см. ниже). Широко употребляется в описанном смысле в физике и математике (хотя иногда графический символ [math]displaystyle{ nabla }[/math] используется также для обозначения некоторых других, хотя в некотором отношении не совсем далёких от рассмотренного, математических объектов, например, ковариантной производной).

Под n-мерным оператором набла подразумевается вектор в n-мерном пространстве^[2] следующего вида:

[math]displaystyle{ nabla={partialoverpartial x_1}vec{e}_1+{partialoverpartial x_2}vec{e}_2+…+{partialoverpartial x_n}vec{e}_n }[/math],

где [math]displaystyle{ vec{e}_1, vec{e}_2, …, vec{e}_n }[/math] — единичные векторы по осям [math]displaystyle{ x_1, x_2, …, x_n }[/math] соответственно.

Иногда, особенно при начертании от руки, над оператором набла рисуют стрелку: [math]displaystyle{ vec nabla }[/math] — чтобы подчеркнуть векторный характер оператора. Смысл такого начертания ничем не отличается от обычного [math]displaystyle{ nabla }[/math].

Иногда (особенно когда речь идёт только о применении к скалярным функциям), оператор набла называют оператором градиента, каковым он в применении к скалярным функциям (полям) и является.

Замечание: в физике в наше время название оператор Гамильтона по отношению к оператору набла стараются не употреблять, особенно в квантовой физике, во избежание путаницы с квантовым гамильтонианом, имеющим, в отличие от классического, операторную природу.

Свойства оператора набла

Этот оператор приобретает смысл в сочетании со скалярной или векторной функцией, к которой он применяется.

Если скалярно умножить вектор [math]displaystyle{ nabla }[/math] на функцию [math]displaystyle{ phi }[/math], то получится вектор

[math]displaystyle{ nablaphi={partialphioverpartial x}vec{i}+{partialphioverpartial y}vec{j}+{partialphioverpartial z}vec{k} = mathbf{operatorname{grad}},phi }[/math],

который представляет собой градиент функции [math]displaystyle{ phi }[/math].

Если вектор [math]displaystyle{ nabla }[/math] скалярно умножить на вектор [math]displaystyle{ vec{a} }[/math], получится скаляр

[math]displaystyle{ nablacdotvec{a} = nabla_xa_x+nabla_ya_y+nabla_za_z={partial a_xoverpartial x}+{partial a_yoverpartial y}+{partial a_zoverpartial z} = mathbf{operatorname{div}},vec a }[/math],

то есть дивергенция вектора [math]displaystyle{ vec{a} }[/math].

Если [math]displaystyle{ nabla }[/math] умножить на [math]displaystyle{ vec{a} }[/math] векторно, то получится ротор вектора [math]displaystyle{ vec{a} }[/math]:

[math]displaystyle{ nabla times vec a = begin{vmatrix} vec{i} & vec{j} & vec{k} \ {partialoverpartial x} & {partialoverpartial y} & {partialoverpartial z} \ a_x & a_y & a_zend{vmatrix} = left( {partial{a_z}overpartial y} — {partial{a_y}overpartial z} right)vec{i} + left( {partial{a_x}overpartial z} — {partial{a_z}overpartial x} right)vec{j} + left( {partial{a_y}overpartial x} — {partial{a_x}overpartial y} right)vec{k} = mathbf{operatorname{rot}},vec a }[/math]

Замечание: как и для обозначения скалярного и векторного произведения вообще, в случае их применения с оператором набла, наряду с использоваными выше, часто используются эквивалентные им альтернативные обозначения, так, например, вместо [math]displaystyle{ nabla cdot vec a }[/math] нередко пишут [math]displaystyle{ (nabla, vec a) }[/math], а вместо [math]displaystyle{ nabla times vec a }[/math] пишут [math]displaystyle{ [nabla,vec a] }[/math]; это касается и формул, приводимых ниже.

Соответственно, скалярное произведение [math]displaystyle{ nablacdotnabla=nabla^2 }[/math] есть скалярный оператор, называемый оператором Лапласа. Последний обозначается также [math]displaystyle{ Delta }[/math]. В декартовых координатах оператор Лапласа определяется следующим образом:

[math]displaystyle{ Delta={partial^2overpartial x^2}+{partial^2overpartial y^2}+{partial^2overpartial z^2} }[/math].

Поскольку оператор набла является дифференциальным оператором, то при преобразовании выражений необходимо учитывать как правила векторной алгебры, так и правила дифференцирования. Например:

[math]displaystyle{ mathbf{operatorname{grad}}(phipsi)=mathbf{nabla}(phipsi)=psimathbf{nabla}phi+phimathbf{nabla}psi=psi,
mathbf{operatorname{grad}},phi+phi , mathbf{operatorname{grad}},psi }[/math]

[math]displaystyle{ operatorname{div}(mathbf{operatorname{grad}},phi)=nablacdot(nablaphi)=(nablacdotnabla)phi=nabla^2phi = Deltaphi }[/math]

То есть производная выражения, зависящего от двух полей, есть сумма выражений, в каждом из которых дифференцированию подвергается только одно поле.

Для удобства обозначения того, на какие поля действует набла, принято считать, что в произведении полей и операторов каждый оператор действует на выражение, стоящее справа от него, и не действует на всё, что стоит слева. Если требуется, чтобы оператор действовал на поле, стоящее слева, это поле каким-то образом отмечают, например, ставя над буквой стрелочку:

[math]displaystyle{ nabla cdot vec v = stackrel{downarrow}{vec v} cdot nabla }[/math]

Такая форма записи обычно используется в промежуточных преобразованиях. Из-за её неудобства в окончательном ответе от стрелочек стараются избавиться.

Операторы второго порядка

Так как существуют различные способы перемножения векторов и скаляров, с помощью оператора набла можно записать различные виды дифференцирования. Комбинирование скалярных и векторных произведений даёт 7 различных вариантов производных второго порядка:

[math]displaystyle{ mathbf{operatorname{div}},(mathbf{operatorname{grad}},f ) = nabla cdot (nabla f) }[/math]

[math]displaystyle{ mathbf{operatorname{rot}},(mathbf{operatorname{grad}},f ) = nabla times (nabla f) }[/math]

[math]displaystyle{ Delta f = nabla^2 f }[/math]

[math]displaystyle{ mathbf{operatorname{grad}},(mathbf{operatorname{div}}, vec v ) = nabla (nabla cdot vec v) }[/math]

[math]displaystyle{ mathbf{operatorname{div}},(mathbf{operatorname{rot}},vec v ) = nabla cdot (nabla times vec v) }[/math]

[math]displaystyle{ mathbf{operatorname{rot}},(mathbf{operatorname{rot}},vec v ) = nabla times (nabla times vec v) }[/math]

[math]displaystyle{ Delta vec v = nabla^2 vec v }[/math]

Для достаточно гладких полей (дважды непрерывно дифференцируемых) эти операторы не независимы.
Два из них всегда равны нулю:

[math]displaystyle{ mathbf{operatorname{rot}},(mathbf{operatorname{grad}},f ) = nabla times (nabla f) = (nabla times nabla) f = 0 }[/math]

[math]displaystyle{ mathbf{operatorname{div}},(mathbf{operatorname{rot}},vec v ) = nabla cdot (nabla times vec{v}) = (nabla times nabla) cdot vec{v} = 0 }[/math]

Два всегда совпадают:

[math]displaystyle{ mathbf{operatorname{div}},(mathbf{operatorname{grad}},f ) = nabla cdot(nabla f) = (nabla cdot nabla) f = nabla^2 f = Delta f }[/math]

Три оставшихся связаны соотношением:

[math]displaystyle{ nabla times ( nabla times vec{v} ) = nabla (nabla cdot vec{v}) — nabla^2 vec{v} }[/math]

Ещё одно может быть выражено через тензорное произведение векторов:

[math]displaystyle{ nabla ( nabla cdot vec{v} ) = nabla cdot (nabla otimes vec{v}) }[/math]

Отличия оператора набла от обычного вектора

Хотя большинство свойств оператора набла следуют из алгебраических свойств операторов и чисел и становятся вполне очевидными, если рассматривать его как вектор, нужно соблюдать осторожность. Оператор набла не принадлежит тому же пространству, что и обычные векторы, а говоря точнее, скалярное и векторное произведение для него определено с некоторыми отличиями (в основном сводящимися к тому, что — как это обычно подразумевается — оператор действует на те поля, что стоят от него справа, и не действует на стоящие от него слева, из-за чего скалярное и векторное произведение с участием [math]displaystyle{ nabla }[/math] не коммутативны и не антикоммутативны, как это свойственно для таких произведений обычных векторов), таким образом, оператор набла не обладает некоторыми свойствами обычных векторов, и следовательно не во всём может вести себя в соответствии с геометрическими свойствами обычного вектора. В частности,

он не коммутирует с векторами:

[math]displaystyle{ nabla cdot vec v ne vec v cdot nabla }[/math],

ведь [math]displaystyle{ nabla cdot vec v }[/math] — это дивергенция, то есть в конечном итоге просто скалярная функция координат, а [math]displaystyle{ vec v cdot nabla }[/math] представляет собой нетривиальный оператор дифференцирования по направлению векторного поля [math]displaystyle{ vec {v} }[/math].

Можно дополнительно убедиться в том, что они не совпадают, применив оба выражения к скалярной функции f:

[math]displaystyle{ (nabla cdot vec v) f ne (vec v cdot nabla) f }[/math]

так как

[math]displaystyle{ (nabla cdot vec v) f = left( frac{part v_x}{part x}+frac{part v_y}{part y}+frac{part v_z}{part z} right)f = frac{part v_x}{part x}f+frac{part v_y}{part y}f+frac{part v_z}{part z}f }[/math]

[math]displaystyle{ (vec v cdot nabla) f = left( v_x frac{part}{part x}+v_y frac{part}{part y}+v_z frac{part}{part z} right) f = v_x frac{part f}{part x}+v_y frac{part f}{part y}+v_z frac{part f}{part z} }[/math]

Если бы набла был вектором, то смешанное произведение [math]displaystyle{ (vec v, nabla, vec v) equiv vec v cdot (nabla times vec v) }[/math] было бы всегда равно нулю, однако несложно убедиться, что это неверно.

Кроме того, необходимо помнить, на какие векторы и функции действует каждый оператор набла в написанной формуле, например:

[math]displaystyle{ (nabla x) times (nabla y) = left( vec i , frac{part x}{part x}+vec j , frac{part x}{part y}+vec k , frac{part x}{part z} right) times left( vec i , frac{part y}{part x}+vec j , frac{part y}{part y}+vec k , frac{part y}{part z} right) = }[/math]

[math]displaystyle{ = (vec i cdot 1 +vec j cdot 0+vec k cdot 0) times (vec i cdot 0+vec j cdot 1+vec k cdot 0) = vec i times vec j = vec {k} }[/math]

(здесь первый оператор набла действует только на поле [math]displaystyle{ x }[/math], а второй — только на поле [math]displaystyle{ y }[/math], что как бы жёстко фиксирует порядок действий). Тогда как для обычных векторов:

[math]displaystyle{ (vec u x )times (vec u y) = x y (vec u times vec u) = x y vec 0 = vec {0} }[/math]

поскольку здесь [math]displaystyle{ x }[/math] и [math]displaystyle{ y }[/math] легко выносятся.

Поэтому для удобства, при умножении оператора набла на сложное выражение, обычно дифференцируемое поле обозначают стрелочкой:

[math]displaystyle{ (nabla , [vec u, vec v]) =
(nabla , [stackrel{downarrow}{vec u}, vec v]) + (nabla , [vec u, stackrel{downarrow}{vec v}]) =
(vec v , [nabla , stackrel{downarrow}{vec u}]) — (vec u , [nabla , stackrel{downarrow}{vec v}]) = vec v cdot mbox{rot} , vec u — vec u cdot mbox{rot} , vec v }[/math]

Если оператор не действует на некоторое поле, то вектор поля и оператор коммутируют (для векторного произведения — антикоммутируют). Векторы в смешанных произведениях примера вынесены влево от оператора и конечное выражение записано без стрелочек.

История

В 1853 году В. Р. Гамильтон ввёл этот оператор и придумал для него символ [math]displaystyle{ nabla }[/math] в виде перевёрнутой греческой буквы Δ (дельта). У Гамильтона острие символа указывало налево, позже в работах П. Г. Тэта символ приобрёл современный вид. Гамильтон назвал этот символ словом «атлед» (слово «дельта», прочитанное наоборот), однако позднее английские учёные, в том числе О. Хевисайд, стали называть этот символ «на́бла» из-за сходства с остовом древнеассирийского музыкального инструмента наблы, а оператор получил название оператора Гамильтона, или оператора набла^[3].

Согласно некоторым источникам^[4], [math]displaystyle{ nabla }[/math] — буква финикийского алфавита, происхождение которой связано с музыкальным инструментом типа арфы, так как «ναβλα» (набла) на древнегреческом означает «арфа». Наблий — разновидность арфы^[5].

Примеры

[math]displaystyle{ z = xy, nabla z = {partial zoverpartial x}vec{i}+{partial zoverpartial y}vec{j} = yvec{i} + xvec{j} }[/math]
[math]displaystyle{ z = 30yx^3, nabla z = {partial zoverpartial x}vec{i}+{partial zoverpartial y}vec{j} = 90yx^2vec{i} + 30x^3vec{j} }[/math]

См. также

Оператор Д’Аламбера
Дифференциальные операторы в различных системах координат

Примечания

↑ В других система координат — см. по ссылке ниже.
↑ Эта размерность n, то есть размерность пространства, на поля в котором действует оператор, указывается явно или подразумевается из формулировки соответствующей теории или задачи.
↑ «Кратные и криволинейные интегралы. Элементы теории поля», В. Р. Гаврилом, Е. Е. Иванова, В. Д. Морозова. Математика в техническом университете VII, издательство МГТУ имени Н. Э. Баумана.
↑ Мантуров О. В. и др. Математика в понятиях, определениях и терминах / Под ред. Л. В. Сабинина. — Т. 2. — М.: Просвещение, 1982.
↑ Столяров А. Примечания // Сенкевич Г. Камо грядеши. — Л.: Лениздат, 1990. — С. 692.

Источник