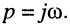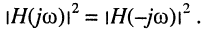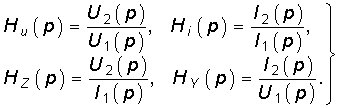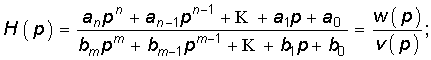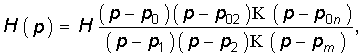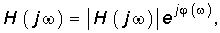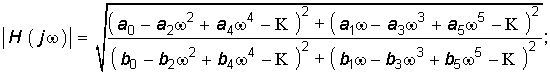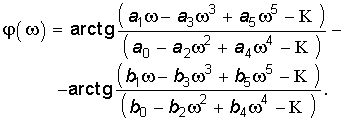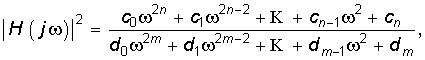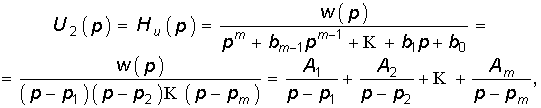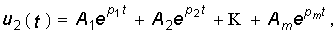Содержание:
Операторные передаточные функции:
Практический смысл и назначение операторного метода в теории электрических цепей состоит, прежде всего, в представлении соотношения вход/выход в операторной форме, что даёт возможность существенно упростить процедуры анализа и синтеза электрических цепей и обеспечить связь между временным и частотным описаниями как колебаний, действующих в цепи, так и самой цепи.
Законы Ома и Кирхгофа в операторной форме
Покажем, что решение задач анализа колебаний в электрической цепи существенно упрощается при использовании операторного метода.
Законы Кирхгофа в операторной форме
Пусть токи
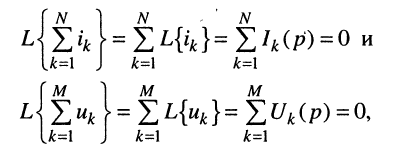
что говорит о формальной справедливости законов Кирхгофа для токов и напряжений, выраженных в операторной форме.
Операторные сопротивления и проводимости элементов электрических цепей
Убедимся в справедливости закона Ома для L-изображений колебаний на зажимах элементов R, L, С при нулевых начальных условиях (см.разд. 15.2) и найдём операторные изображения 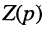
Для элемента активного сопротивления
откуда
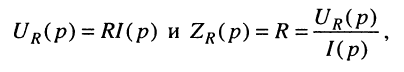
т. е. операторное активное сопротивление равно самому активному сопротивлению, поэтому операторная активная проводимость равна самой активной проводимости
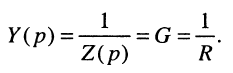
Для элемента индуктивности
правило дифференцирования даёт:
откуда операторные сопротивление и проводимость индуктивности равны:
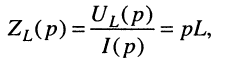
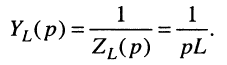
Для элемента ёмкости
правило интегрирования даёт:
откуда операторные сопротивление и проводимость ёмкости равны:
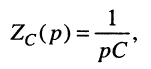
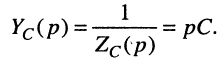
Заметим, что поскольку оператор р согласно (16.2) определён как комплексное переменное
операторные сопротивления и проводимости элементов L и С получаются заменой оператора 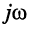
Операторные сопротивление и проводимость последовательного и параллельного двухполюсников
Закон Ома при нулевых начальных условиях формально верен и для сложных двухполюсников, если в числе их элементов не содержатся независимые источники.
Определение:
Операторным сопротивлением 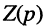
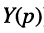
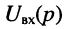
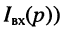
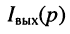
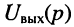
(соответственно 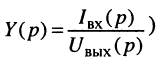
Пример 17.1.
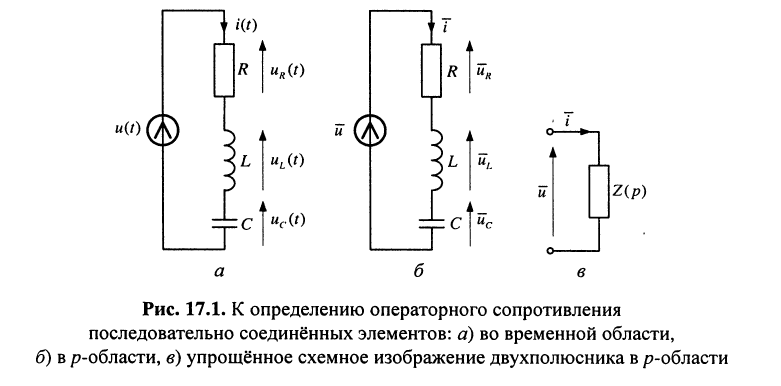
Найти операторное сопротивление двухполюсника (рис. 17.1), состоящего из последовательно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Напряжение на зажимах двухполюсника при нулевых начальных условиях равно
Применим к полученному уравнению преобразование Лапласа:
откуда следует, что при последовательном соединении элементов их операторные сопротивления складываются, как и для комплексных сопротивлений, но оператор 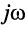
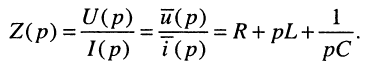
Пример 17.2.
Найти операторную проводимость двухполюсника (рис. 17.2), состоящего из параллельно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Для тока 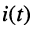
поэтому операторную проводимость заданного двухполюсника можно записать сразу:
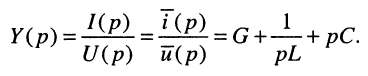
В силу дуальности последовательного и параллельного контуров выражение (17.9) можно было записать сразу на основании формулы (17.8).
Выражения (17.8) и (17.9) представляют собой входные операторные функции цепи. Они дают основания определению операторного сопротивления и проводимости двухполюсника общего вида.
Операторные сопротивление и проводимость двухполюсника общего вида
Закон Ома, при нулевых начальных условиях, формально можно применить и для сколь угодно сложных двухполюсников. Ранее
(см. лекцию 5) было установлено, что если на входе двухполюсника действует источник напряжения с ЭДС 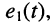
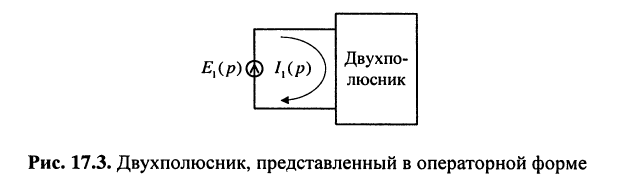
Переходя к L-изображениям напряжений, токов и сопротивлений элементов цепи, получим представление двухполюсника в операторной форме (рис. 17.3), что позволяет записать L-изображение входного тока:
Теперь согласно определению операторной проводимости и операторного сопротивления имеем:
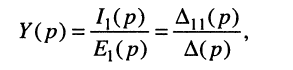
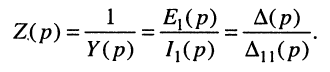
При этом нужно помнить, что определители и алгебраические дополнения в таких формулах записываются с учётом свойств преобразования Лапласа, как это сделано в примерах 17.1 и 17.2.
Определение операторной передаточной функции. Связь с импульсной и переходной характеристиками
В лекции 15 было показано, что во временной области соотношение вход/выход линейной электрической цепи при произвольном воздействии описывается уравнением свёртки:
где h(t) — импульсная характеристика, x(t) — воздействие, y(t) — реакция. При этом воздействие и реакция могут быть напряжениями или токами.
Для описания соотношения вход/выход в операторной форме воспользуемся L-изображением свёртки
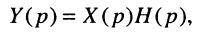
откуда получаем соотношения вход/выход в операторной форме
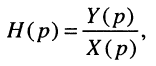
которое называют передаточной функцией.
Определение:
Передаточной функцией линейной электрической цепи называется отношение L-изображения реакции к L-изображению воздействия при нулевых начальных условиях.
Выражение (17.13) говорит о том, что передаточная функция является L-изображением импульсной характеристики, т. е. импульсная характеристика является обратным преобразованием Лапласа передаточной функции:
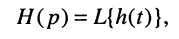
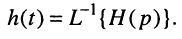
Именно этими зависимостями объясняется содержащееся в определении передаточной функции требование нулевых начальных условий.
Связь между передаточной функцией и переходной характеристикой можно установить, если воспользоваться интегралом Дюамеля (15.20а) при нулевых начальных условиях:
когда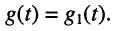
Первый сомножитель правой части полученного уравнения содержит L-изображение производной, поэтому окончательно можно записать:
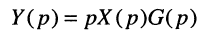
и
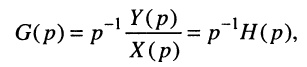
что полностью соответствует связи импульсной и переходной характеристик (15.16).
Обратим внимание на то, что передаточная функция может быть получена из комплексных частотных характеристик формальным образом, а именно — простой заменой в КЧХ 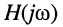
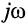
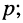
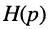
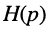
В зависимости от того, какая величина выступает в качестве внешнего воздействия, а какая в качестве реакции цепи, различают четыре вида передаточных функций:
операторное передаточное сопротивление
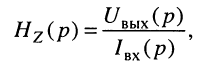
операторную передаточную проводимость
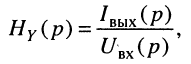
передаточную функцию по току
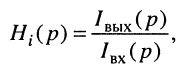
передаточную функцию по напряжению
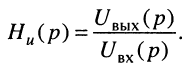
Последние две функции иногда называют операторными передаточными коэффициентами по току и по напряжению соответственно.
По любой из передаточных функций (17.18)—(17.21) нетрудно найти L-изображение реакции цепи, а затем и саму реакцию на заданное воздействие, поскольку любая передаточная функция Н(р) согласно (17.12) может рассматриваться как связующий коэффициент между L-изображения ми воздействия Х(р) и реакции Y(p).
Пример 17.3.
Записать передаточную функцию для последовательного колебательного контура (рис. 17.1, б) относительно напряжения на индуктивности.
Решение. По определению передаточной функции для индуктивности имеем
Но операторное напряжение на индуктивности равно:
поэтому
Подставляя сюда операторное сопротивление (17.8), получаем искомую передаточную функцию:
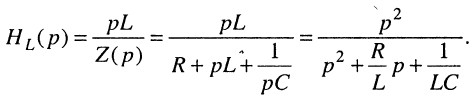
Аналогично можно получить и другие передаточные функции для последовательной, параллельной или более сложной цепи. В последнем случае потребуется составить систему уравнений для L-изображений колебаний, воспользовавшись методом контурных токов или узловых напряжений.
Понятие о нулях и полюсах передаточной функции. Устойчивость передаточной функции
Задача 17.1.
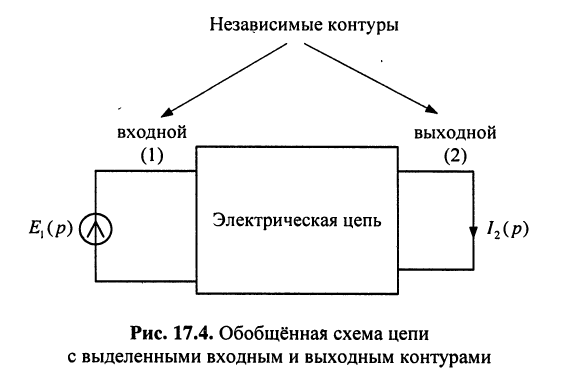
Получить и исследовать общее выражение для передаточной функции цепи, когда воздействие представляет собой ЭДС источника напряжения, а реакцией является ток в выделенной ветви анализируемой цепи (рис. 17.4).
Решение. Выберем независимые контуры в цепи так, чтобы через источник напряжения замыкался ток только одного входного контура, а через интересующую нас ветвь — ток только одного выходного контура. На рис. 17.4 они обозначены индексами 1 и 2 соответственно.
Теперь, как и в задаче 5.2, необходимо положить 
откуда по определению передаточной функции имеем операторную передаточную проводимость
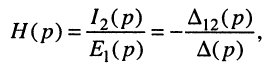
где 
a 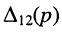
Заметим, что определитель и все его миноры представляют собой рациональные функции оператора р, все коэффициенты которых являются вещественными числами. Это объясняется тем, что при раскрытии определителя над его элементами совершаются только операции умножения, сложения и вычитания, а сами элементы представляют собой простейшие рациональные
функции с вещественными коэффициентами вида (17.11). Раскрывая определитель 
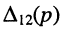
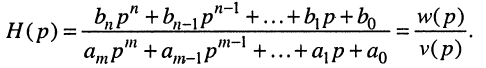
Полиномы числителя 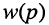
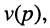
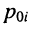
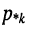
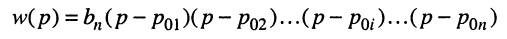
и
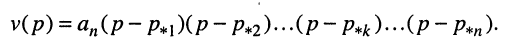
Отсюда передаточная функция (17.24) приобретает вид:
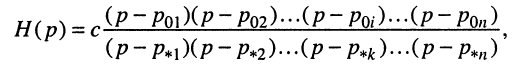
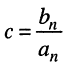
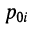
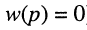
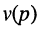
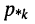
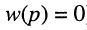
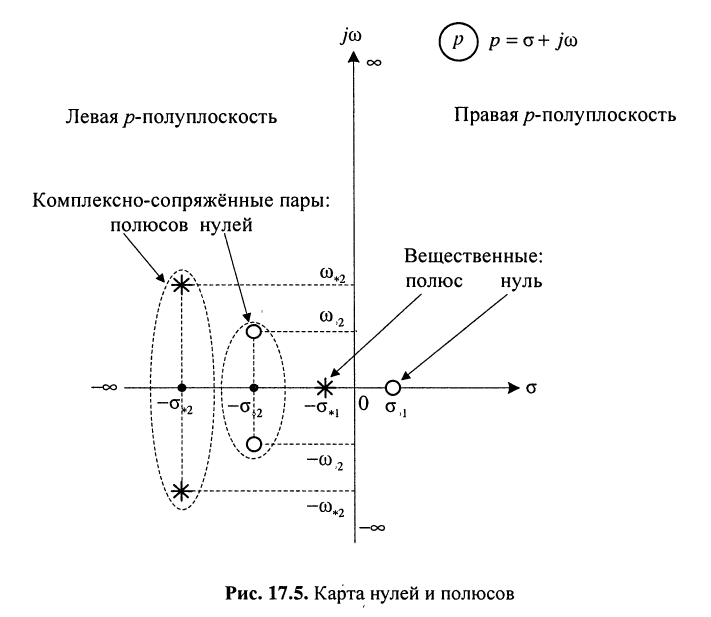
Названия корней уравнения 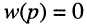
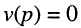
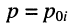
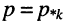
Нули и полюсы наглядно отображаются на комплексной p -плоскости (рис. 17.5) значками ( ° ) и ( * ) соответственно.
На рис. 17.5 показаны:
и 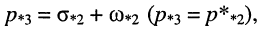
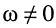
Отображение нулей и полюсов на p-плоскости называют картой нулей и полюсов. Различают левую и правую р-полуплоскости.
Карта нулей и полюсов позволяет оценить ряд свойств электрической цепи и, в частности, определить её устойчивость с точки зрения устойчивости передаточной функции.
Утверждение:
цепь является строго устойчивой тогда и только тогда, когда её передаточная функция имеет, полюсы только в левой р-полуплоскости, исключая мнимую ось.
Доказательство. Напомним, что цепь называется строго устойчивой, если при нулевых начальных условиях ограниченное по величине воздействие
вызывает ограниченную по величине реакцию
Но реакцию y(t) при нулевых условиях можно найти с помощью уравнения свёртки
Отсюда при заданных ограничениях имеем соотношение
из которого следует, что для получения равномерно ограниченной для всех t реакции, т. е. для обеспечения строгой устойчивости цепи должно выполняться условие абсолютной сходимости интеграла от импульсной характеристики:
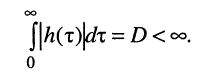
Найдём расположение полюсов, которое соответствует полученному условию. Для этого представим импульсную характеристику h(t) цепи как обратное L-изображение передаточной функции (17.15) путём разложения последней на сумму простых дробей (16.28):
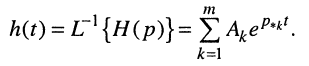
Подставим в интеграл (17.28) правую сумму (17.29)
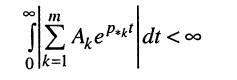
и проведём ряд несложных преобразований.
Поскольку модуль суммы не превосходит суммы модулей, справедливо следующее неравенство:
которое проинтегрируем:
В правой части полученного неравенства поменяем местами знаки суммирования и интегрирования и оставим только знак равенства:
Рассмотрим интеграл в правой части равенства, содержащий модуль экспоненты, при
Здесь, во-первых,
во-вторых, первая экспонента под интегралом всегда неотрицательна, поэтому знак модуля можно опустить:
Остаётся исследовать сходимость интеграла при положительном и отрицательном показателе
Сходимость интеграла при 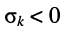
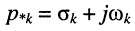
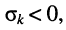
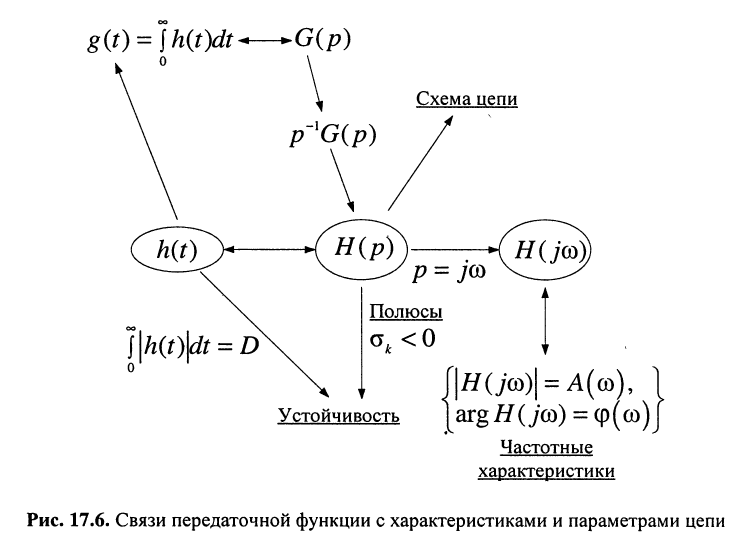
Связь передаточной функции с частотными и временными характеристиками цепи
Как было показано в лекции 10, для определения частотных характеристик АЧХ 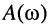
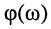
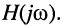
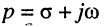
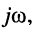
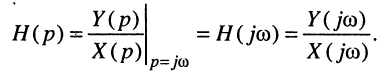
Отсюда имеем:
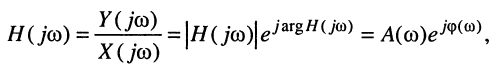
где
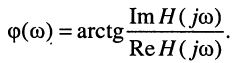
Эквивалентное выражение для КЧХ получается из (17.31), если воспользоваться комплексными функциями числителя и знаменателя:
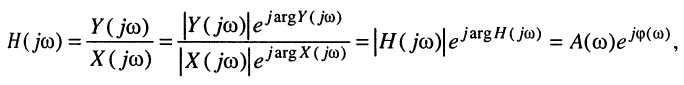
где
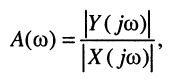
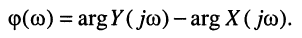
Вследствие того, что функция
является иррациональной, обычно при анализе и синтезе цепей используют квадрат АЧХ:
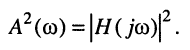
Перечислим основные свойства передаточных функций и квадрата АЧХ пассивных цепей.
- Передаточная функция является L-изображением импульсной характеристики.
- Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами.
- Полюсы устойчивой передаточной функции лежат в левой р-полуплоскости.
- Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей; приневыполнении этого свойства АЧХ на бесконечно больших частотах
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
- Частотные характеристики цепи вычисляются по передаточной функции при подстановке
- Квадрат АЧХ является чётной рациональной функцией переменной с вещественными коэффициентами:
- По передаточной функции можно изобразить схему цепи
Обобщённая схема связи передаточной функции с характеристиками и свойствами цепи представлена на рис. 17.6.
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Колебания в линиях без потерь
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
- Частотные методы анализа и расчёта электрических цепей

|
34 |
||||||||||||||||||||
|
электрических цепей и их свойства |
||||||||||||||||||||
|
I1(p) |
I2(p) |
Операторная |
передаточная |
|||||||||||||||||
|
U1(p) |
H(p) |
U2 (p) |
функция (ОПФ) цепи |
H ( p) |
||||||||||||||||
|
представляет |
собой |
отношение |
||||||||||||||||||
|
изображений |
отклика |
цепи |
к |
|||||||||||||||||
|
Рисунок2.7 – Тракт передачи с |
воздействию (рис. 2.7). |
|||||||||||||||||||
|
операторными параметрами |
Поскольку |
воздействиями |
||||||||||||||||||
|
считают напряжения и токи на |
||||||||||||||||||||
|
входе цепи, а откликами – на выходе, соответственно можно записать четыре |
||||||||||||||||||||
|
вида операторных передаточных функции: |
||||||||||||||||||||
|
1 |
Huu ( p) = U2 ( p) |
– |
операторная |
передаточная |
функция |
цепи |
по |
|||||||||||||
|
U1 ( p) |
||||||||||||||||||||
|
напряжению, это отношение изображения отклика цепи U2(p) в виде |
||||||||||||||||||||
|
напряжения к изображению воздействия U1(p) в виде напряжения; |
(2.33) |
|||||||||||||||||||
|
2 |
Hui ( p) = U2 ( p) |
– операторное |
сопротивление |
цепи |
это |
отношение |
||||||||||||||
|
I1 ( p) |
||||||||||||||||||||
|
изображения отклика цепи U2(p) в виде напряжения к изображению |
||||||||||||||||||||
|
воздействия I1(p) в виде тока; |
(2.34) |
|||||||||||||||||||
|
3 |
Hii ( p) = I2 ( p) |
– |
операторная |
передаточная |
функция |
тока |
это |
|||||||||||||
|
I1 ( p) |
||||||||||||||||||||
|
отношение изображений токов на выходе и входе цепи; |
(2.35) |
|||||||||||||||||||
|
4 |
Hiu ( p) = I2 ( p) |
– операторная |
проводимость |
цепи |
это |
отношение |
||||||||||||||
|
U1 ( p) |
||||||||||||||||||||
|
изображения отклика цепи I2(p) в виде тока к изображению воздействия U1(p) в |
||||||||||||||||||||
|
виде напряжения. |
(2.36) |
|||||||||||||||||||
|
Операторные передаточные функции играют важную роль в методах |
||||||||||||||||||||
|
анализа и синтеза электрических цепей при нулевых начальных условиях. Зная |
||||||||||||||||||||
|
операторную передаточную |
функцию |
цепи H ( p) , с помощью |
выражений |
|||||||||||||||||
|
(2.33…2.35) нетрудно найти изображение отклика цепи, а следовательно и сам |
||||||||||||||||||||
|
отклик цепи на заданное воздействие. |
||||||||||||||||||||
|
Операторную передаточную функцию H ( p) для пассивной цепи можно |
||||||||||||||||||||
|
представить как дробно-рациональную функцию с вещественными |
||||||||||||||||||||
|
коэффициентами. |
pm |
p(m−1) +… +b p +b |
||||||||||||||||||
|
b |
+b |
|||||||||||||||||||
|
m |
(m−1) |
1 |
0 |
|||||||||||||||||
|
Н( p) = a |
n |
pn |
+ a |
(n−1) |
p(n−1) +… + a p + a |
0 |
(2.37) |
|||||||||||||
|
1 |
||||||||||||||||||||
|
или в виде |
( p − p01 )( p − p02 )………..( p − p0m ) , |
|||||||||||||||||||
|
Н( p) = Н |
(2.38) |
|||||||||||||||||||
|
( p − p )( p − p |
2 |
)………..( p − p |
n |
) |
||||||||||||||||
|
1 |

35
где р01, р02,…., р0m – нули операторной передаточной функции H ( p) . При
подстановке нулей в выражение (2.38) операторная передаточная функция H ( p) обращается в ноль; р1, р2,…., рn – полюсы операторной передаточной
функции H ( p) . При подстановке полюсов в выражение (2.38) значение H ( p)
стремится к бесконечности.
В выражении (2.38) коэффициент
H = bm . an
Степень полинома числителя „m” и знаменателя „n” зависят от числа реактивных элементов цепи.
Заменив в (2.33…2.35) оператор „р” на „jω”, получим комплексную передаточную функцию цепи H ( jω) . Таким образом, заменяя „jω” на „р”,
можно автоматически получить законы теории электрических цепей и методы расчета в операторной форме.
Свойства операторных передаточных функций:
1Операторная передаточная функция является дробно-рациональной функцией с вещественными коэффициентами (2.37). Вещественность коэффициентов объясняется тем, что они определяются элементами цепи.
2Степень полинома числителя не превышает степень полинома
≤n .
3 Нули и полюсы операторной передаточной функции H ( p) являются либо вещественными числами, либо комплексно-сопряженными.
|
4 |
Полюсы |
операторной |
переда- |
j |
|
|
точной |
функции |
пассивной |
цепи |
||
|
располагаются |
в |
левой полуплоскости |
jω0 |
||
|
p2 |
|||||
|
комплексной |
плоскости |
р. |
На |
jω2 |
|
|
расположение нулей ограничений нет. |
|||||
|
Последнее |
свойство |
затрагивает |
σ |
||
|
вопросы устойчивости ЛЭЦ. Для |
p1= – σ1 – σ2,3 |
0 |
|||
|
устойчивых ЛЭЦ |
полюсы |
операторной |
|||
|
передаточной функции находятся в левой |
–jω3 |
||||
|
полуплоскости (рис. 2.8). |
p3 |
||||
|
Цепь является устойчивой, если |
–jω0 |
||||
|
после прекращения действия |
источника |
Рисунок 2.8 – Расположение |
|||
|
свободные колебания затухающие: |
e pt , |
полюсов устойчивой цепи |
где p = −σ± jω.
Если полюсы операторной передаточной функции находятся в правой
полуплоскости рисунка 2.8, то такая цепь является неустойчивой: e pt , где p = +σ± jω.
При чисто мнимых полюсах (полюсы расположены на оси мнимых чисел), состояние цепи называют условно устойчивой: e pt , где p = ± jω.

36
Для выявления устойчивости цепей существуют методы, которые называют критериями устойчивости. Они изложены в п. 2.6.
Алгоритм анализа электрических цепей операторным методом
1Определяются независимые начальные условия цепи до коммутации iL(0–), uC(0–).
2Составляется операторная схема замещения цепи после коммутации.
3Находятся изображения исходных токов и напряжений, используя при этом законы Ома и Кирхгофа в операторной форме, а также любые известные методы расчета (метод законов Кирхгофа, метод узловых напряжений и т. д.) в операторной форме.
4По полученным изображениям определяются оригиналы (искомые токи и напряжения). Чаще всего при этом используются таблицы соответствий по Лапласу. Если же изображение представляет собой дробно-рациональную функцию и отсутствует в таблицах, то для перехода к оригиналу следует применить теорему разложения (2.23), (2.24).
2.5 Связь временных‘ , частотных и операторных функций цепей и сигналов
1. По определению операторная передаточная функция:
H ( p) = X 2 ( p) ,
X1 ( p)
где Х2(р) – изображение отклика цепи (U2(р) или I2(р)); Х1(р) – изображение воздействия цепи (U1(р) или I1(р)).
Из (2.39) следует, что:
X 2 ( p) =X 1( p) H ( p) .
Если в качестве воздействия на цепь подать единичную ступенчатую функцию 1(t), то ее изображением будет F(p), которое согласно (2.2) F( p) = 1p .
При этом откликом цепи будет переходная функция h(t), а ее изображением h(р).
Тогда согласно (2.5) и таблице преобразований Лапласа имеем:
|
h(t) h( p) = |
1 |
H ( p) . |
(2.41) |
|
|
p |
||||
Формула (2.41) выражает связь между переходной функцией цепи h(t) и операторной передаточной функцией H ( p) , а также позволяет определять
переходную функцию цепи h(t) по известной операторной передаточной функции H ( p) . Применяя теорему дифференцирования (2.7), можно получить
изображение импульсной характеристики цепи g(t). Если

37
|
′ |
h(t) |
1 |
H ( p) |
, |
|
|
g(t) = h (t) , а |
p |
||||
|
то |
|||||
|
′ |
1 |
H ( p) = H ( p) , |
|||
|
h (t) p |
p |
||||
|
таким образом: |
|||||
|
g(t) H ( p) . |
(2.42) |
Выражение (2.42) позволяет определить импульсную функцию цепи g(t) по известной операторной передаточной функции H ( p) . Для этого достаточно
перейти от изображения H ( p) к оригиналу g(t).
|
Комплексная и операторная функции |
f(t) |
|||||||||
|
связаны |
операторными p ≡ jω. |
Если |
в |
|||||||
|
КПФ |
заменить |
jω |
на |
p, |
то |
Лаплас |
Фурье |
|||
|
H ( jω) |
jω= p |
= H ( p) . Например, |
для цепи |
F(p) |
F(jω) |
|||||
|
Рисунок 2.9 – Связь функций |
||||||||||
|
первого порядка КПФ H ( jω) имеет вид: |
||||||||||
|
сигнала |
||||||||||
|
H |
( jω) = jωb1 + b0 . |
f1(t) |
h(t) |
f2(t) |
||||||
|
jω+ a0 |
H(p) |
|||||||||
|
Для |
этой |
же цепи |
ОПФ |
H ( p) |
F1(p) |
F (p) |
||||
|
F1(jω) |
H(jω) |
2 |
||||||||
|
имеет вид: |
F2(jω) |
|||||||||
|
Рисунок 2.10 – Связь функций |
||||||||||
|
H ( p) = pb1 + b0 . |
||||||||||
|
сигналови цепи |
||||||||||
|
p + a0 |
Таким образом частотные, операторные и временные функции цепей связаны между собой, рис. 2.9 и 2.10.
Применив прямое преобразование Фурье можно получить спектральную плотность единичной ступенчатой функции 1(t):
1( jω) = j1ω +πδ(ω),
а согласно обратному преобразованию Фурье:
1(t) = 1π ∞∫1( jω)e jωt dω.
2 −∞
Если подставить (2.43) в (2.44) то получим:
|
1 |
∞ |
1 |
||||
|
1(t) = |
+πδ(ω) e jωt dω. |
|||||
|
2π−∞∫ |
jω |
|||||
Выражение (2.45) можно преобразовать в другое:
|
38 |
|||||||
|
1 |
1 |
∞ |
1 |
e jωt dω. |
|||
|
1(t) = |
2 |
+ |
∫ |
(2.46) |
|||
|
2π |
jω |
||||||
|
−∞ |
Тогда согласно принципу суперпозиции (наложения) и выражению (2.46) получим связь между переходной функцией цепи h(t) и комплексной передаточной функцией H(jω):
|
1 |
1 |
∞ |
H ( jω) |
e jωt dω. |
|||
|
h(t) = |
2 |
H (0) + |
∫ |
(2.47) |
|||
|
2π |
jω |
||||||
|
−∞ |
Используя связь между единичной ступенчатой функцией 1(t) и функцией Дирака δ(t) можно показать, что:
|
1 |
∞ |
|||
|
δ(t) = |
∫e jωt dω. |
(2.48) |
||
|
2π |
||||
|
−∞ |
Согласно принципу суперпозиции можно доказать связь между импульсной функцией g(t) и комплексной передаточной функцией H(jω):
|
1 |
∞ |
|||
|
g(t) = |
∫H ( jω)e jωt dω. |
(2.49) |
||
|
2π |
||||
|
−∞ |
Выражение (2.49) представляет собой обратное преобразование Фурье, где H(jω) является спектральной плотностью импульсной характеристики цепи.
На основании прямого преобразования Фурье:
|
∞ |
|
|
H ( jω) = ∫g(t)e jωt dt . |
(2.50) |
−∞
Выражения (2.47)…(2.50) показывают связи между временными и частотными функциями цепи.
2.6 Анализ цепей с обратной связью. Критерии устойчивости
Анализ цепей с обратной связью
Рассматриваемые ранее методы анализа электрических цепей (суперпозиции, узловых напряжений, эквивалентного генератора и др.) хорошо “работают” в цепях, представленных в виде соединений двухполюсников. Для цепей, составленных из четырехполюсников, удобно пользоваться матричными методами анализа.
В телекоммуникационных системах прохождение сигналов часто происходит таким образом, что часть сигнала с выхода какого либо блока подается обратно на вход. Эта операция производится с целью изменения свойств устройств передачи и улучшения качества передаваемых сигналов. Цепи с такими свойствами называются цепями или системами с обратной связью. Теория этих цепей весьма обширна и разрабатывается давно [4]. Наша задача дать краткое представление этой теории. Чтобы проанализировать

39
работу системы с обратной связью необходим метод. Рассмотрим взаимодействие двух четырехполюсников: активного, усилитель с коэффициентом усиления К(р), и пассивного (R, L, C) с передаточной функцией Т(р). Соединим эти два четырехполюсника так, чтобы часть энергии с выхода усилителя попадала на вход пассивного четырехполюсника. Способы соединения четырехполюсников между собой были рассмотрены в первом модуле, в разделе матричные методы анализа цепей. С выхода пассивного четырехполюсника часть энергии в зависимости от коэффициента передачи Тср поступает обратно на вход усилителя. Получили своеобразное кольцо. На рис. 2.11, а изображена функциональная схема описанной системы с обратной связью.
|
U1(p) |
+ |
U1K(p) |
U2(p) |
|||||||||
|
К(р) |
U1K |
K(p) |
||||||||||
|
U |
1 |
U2 |
||||||||||
|
+ 1 |
||||||||||||
|
– 1 |
Т(p) |
|||||||||||
|
RLC |
||||||||||||
|
U |
Т(р) |
|||||||||||
|
2(p)Т(p) |
||||||||||||
|
a) |
б) |
|||||||||||
|
Рисунок 2.11 –Цепь с обратной связью: |
||||||||||||
|
функциональная схема (а) и сигнальный граф |
||||||||||||
|
этой системы (б) |
На рис. 2.11, а, изображены два функциональных блока: верхний усилитель с усилением К(р), нижний – пассивный блок с передаточной функцией Т(р). На схеме условно изображен сумматор в виде кружочка, в котором происходит суммирование входного напряжения U1(р) с выходным напряжением пассивного блока U2(р)Т(р). Это суммарное напряжение поступает на вход усилителя.
Опишем данную схему с помощью параметров, которые были получены ранее. Передаточная функция усилительного блока записывается
|
U2 |
( p) |
= K( p), |
передаточная функция пассивного блока записывается |
|
|
U1K ( p) |
||||
|
U2 ( p)T ( p) |
=T ( p), где воздействием является U2(р), а откликом U2(р)Т(р). На |
||||
|
U2 ( p) |
|||||
|
сумматор поступают два напряжения U1( p) +U2 ( p)T( p) =U1K ( p). |
Эта сумма |
||||
|
является воздействием на усилительный блок с усилением К(р) |
и откликом |
||||
|
U2(р). На |
основании этого можно записать: |
U2 |
( p) |
= K( p), откуда |
|
|
U1K ( p) |
|||||
U2 ( p) = K( p)U1K ( p) = K( p)(U1 ( p) +U2 ( p)T ( p))= K( p)U1 ( p) + K( p)U2 ( p)T ( p).
Из этого выражения можно вывести передаточную функцию всей системы
Н(р): так как U2 ( p) − K ( p)U2 ( p)T ( p) = K ( p)U1 ( p), то

|
40 |
||||||||||||||||||||
|
H ( p) = U2 ( p) |
= |
K( p) |
= |
M ( p) . |
(2.51) |
|||||||||||||||
|
U1 ( p) |
1− K( p)T ( p) |
N( p) |
||||||||||||||||||
|
Цепь вида рис. 2.11, а называется системой с замкнутым контуром, а |
||||||||||||||||||||
|
передаточная функция К(р)Т(р) – передаточной функцией разомкнутой |
||||||||||||||||||||
|
системы, где К(р) называют усилением в прямом направлении, Т(р) – |
||||||||||||||||||||
|
передаточной функции цепи обратной связи. |
||||||||||||||||||||
|
При соединении четырехполюсников между собой необходимо соблюдать |
||||||||||||||||||||
|
правило “регулярности” соединения. Например, при последовательно- |
||||||||||||||||||||
|
параллельном соединении двух четырехполюсников рис. 2.12 необходимо |
||||||||||||||||||||
|
общие “заземленные” зажимы четырехполюсников соединить вместе [5]. |
||||||||||||||||||||
|
+ |
+ |
+ |
Из рис. 2.12 видно, что |
|||||||||||||||||
|
К |
U1 =U1K −U2T . |
|||||||||||||||||||
|
U1 |
U1K |
U2 |
||||||||||||||||||
|
Функция вида (2.51) – функция |
||||||||||||||||||||
|
изображения. Система рис. 2.11, а |
||||||||||||||||||||
|
+ |
Т |
+ |
может |
быть |
представлена |
в |
виде |
|||||||||||||
|
U2Т |
U2 |
функции частоты или времени. В |
||||||||||||||||||
|
+ |
анализе цепей с обратной связью |
|||||||||||||||||||
|
Рисунок 2.12 – Регулярное соединение |
можно |
использовать |
теорию |
|||||||||||||||||
|
двух четырехполюсников |
сигнальных |
линейных |
графов. |
|||||||||||||||||
|
Функциональная |
схема |
системы |
с |
|||||||||||||||||
|
обратной связью в виде сигнального графа изображена на рис. 2.11, б. Более |
||||||||||||||||||||
|
подробно о применении сигнальных линейных графов в системах с обратной |
||||||||||||||||||||
|
связью читатель найдет в соответствующей литературе [6]. |
||||||||||||||||||||
|
Попытаемся проанализировать выражение (2.51). Для этого перейдем от |
||||||||||||||||||||
|
операторных функций к комплексным: |
K ( jω) |
|||||||||||||||||||
|
H ( jω) = |
||||||||||||||||||||
|
1 − K ( jω)T ( jω) . |
(2.51а) |
|||||||||||||||||||
|
Если |
1− K( jω)T( jω) >1, то говорят, |
что |
система |
с |
отрицательной |
|||||||||||||||
|
обратной связью (ООС). В этом случае |
H (ω) < K (ω) , |
обратная |
связь |
|||||||||||||||||
|
уменьшает модуль передаточной функции системы (амплитуды выходного |
||||||||||||||||||||
|
сигнала уменьшаются). |
||||||||||||||||||||
|
Если |
1− K( jω)T ( jω) <1, имеет |
место положительная |
обратная |
связь |
||||||||||||||||
|
(ПОС). В этом случае |
H (ω) > K (ω) . |
Обратная |
связь увеличивает |
модуль |
||||||||||||||||
|
передаточной функции системы. Положительная обратная связь может |
||||||||||||||||||||
|
являться причиной неустойчивости системы (может появиться сигнал на |
||||||||||||||||||||
|
выходе при отсутствии сигнала на входе). |
||||||||||||||||||||
|
В случае, когда 1− K( jω)T( jω) =1, возникают автоколебания. |
||||||||||||||||||||
|
Отрицательная обратная связь используется для улучшения |
||||||||||||||||||||
|
характеристик и параметров схем: стабилизация усиления, увеличение |
||||||||||||||||||||
|
входного |
и |
выходного |
сопротивлений, расширение |
полосы |
пропускания |

41
активных фильтров и т.д. Положительная обратная связь, в основном, используется в схемах автогенераторов.
Критерии устойчивости
Для определения электрической устойчивости цепей существуют методы, с помощью которых можно определить где располагаются корни характеристического уравнения системы с обратной связью N(p) = 0.
Критерий Рауса-Гурвица (алгебраический) позволяет, не решая характеристическое уравнение по его виду и величине коэффициентов при членах с разной степенью р сделать вывод о наличии мнимых или комплексносопряженных корней с положительными вещественными составляющими. Иными словами найти корни, лежащие на мнимой оси или в правой
|
полуплоскости. Если передаточная функция |
цепи |
H ( p) = |
U2 |
( p) |
= |
M ( p) |
, |
то |
|
|
U1 |
|||||||||
|
( p) N( p) |
|||||||||
|
характеристическое уравнение записывается |
N(p) =a pn +a |
pn−1 +…+a p+a |
=0 |
||||||
|
n |
n−1 |
1 |
0 |
(1). Для того чтобы корни этого уравнения располагались в левой полуплоскости (условие устойчивости) все коэффициенты an,…а0 должны быть не нулевыми и иметь одинаковый алгебраический знак. Коэффициенты характеристического уравнения выписываются в такой последовательности:
|
an |
an−2 |
an−4 |
……..a1 |
||
|
an−1 |
an−3 |
an−5 |
…….a0 |
||
|
b1 |
b2 |
b3 |
, |
(2.52) |
|
|
c1 |
c2 |
c3 |
|||
|
d1 |
d2 |
d3 |
|||
|
….. |
….. |
….. |
где коэффициенты bi, ci, di образуются по правилу:
|
b |
= |
a |
n−1 |
a |
n−2 |
− a |
n |
a |
n−3 |
; |
b |
2 |
= |
an−1an−4 |
− anan−5 |
; |
|||
|
1 |
an−1 |
an−1 |
|||||||||||||||||
|
с = |
b1an−3 − an−1b2 |
; |
с |
= |
b1an−5 |
− an−1b3 |
; |
(2.53) |
|||||||||||
|
1 |
b1 |
1 |
b1 |
||||||||||||||||
d1 = c1b2 c−b1c3 ……..
1
Если знак членов первой колонки (2.52) не изменяется, все корни уравнения (2.51) лежат в левой полуплоскости и цепь устойчива. Критерий утверждает, что передаточная функция цепи имеет столько полюсов в правой полуплоскости, сколько раз изменяется знак в ряде an, an-1, b, c, d,…
Критерий Михайлова (частотный). Суть метода заключается в том, что на основе характеристического уравнения цепи N(р) = 0 строится частотный годограф. Цепь будет устойчива, если годограф при изменении частоты ω от 0
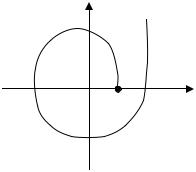
42
до ∞ последовательно пройдет n квадрантов против часовой стрелки, начиная с положительной вещественной оси, где n – степень характеристического уравнения. На рис. 2.13 приведен годограф Михайлова для устойчивой цепи пятого порядка.
|
Im |
Критерий легко доказывается на |
|
|
основе векторного метода построения |
||
|
ω2 |
амплитудно- и фазо-частотных харак- |
|
|
ω5 Re |
теристик по карте нулей и полюсов. |
|
|
ω3 |
Если функция Т(р) имеет n корней, |
|
|
ω1 = 0 |
лежащих в левой полуплоскости, то |
|
|
ω4 |
суммарный фазовый сдвиг на частоте |
|
|
ω → ∞ будет равен n π . Если корни |
||
|
Рисунок 2.13 – Годограф Михайлова |
2 |
|
|
попадают на мнимую ось или в |
||
|
для устойчивой цепи пятого порядка |
правую полуплоскость, то монотон- |
ный характер характеристики функции N(р) нарушится и ход годографа Михайлова изменится. Для устойчивой цепи частоты, при которых годограф пересекает вещественную и мнимую оси рис. 2.13, должны удовлетворять неравенству:
|
ω1 < ω2 < ω3 < ω4 < ω5 . |
(2.54) |
Критерий устойчивости Найквиста. В литературе по автоматическому управлению критерий Найквиста называют амплитудно-фазовым критерием. Данный критерий может быть применен только тогда, когда предварительно проверено отсутствие полюсов в правой полуплоскости возвратной разности N( p) =1 − K( p)T ( p) знаменателя передаточной функции системы.
Критерий устойчивости Найквиста служит для проверки устойчивости системы (предложен в 1930 г.) Он позволил разработать различные способы анализа и синтеза систем. Хорошо работает в тех случаях, когда частотные характеристики системы заданы графически. Критерий основан на теореме функции комплексного переменного о комформном преобразовании замкнутых кривых из р-плоскости в плоскость функции N(р).
Строгий вывод критерия Найквиста можно выполнить с помощью теории вычетов.
Критерий корневого годографа. Корневым годографом называют траекторию перемещения корней характеристического уравнения системы с обратной связью N ( p) =1− K ( p)T ( p) в комплексной плоскости при
изменении коэффициента усиления К(р) от 0 до ∞. Для устойчивой системы траектория корней лежит в левой полуплоскости при всех заданных значениях. Передаточные функции усилителя К(р) и цепи обратной связи Т(р) можно записать в виде:
|
K( p) = K1 |
P1( p) |
, |
(2.55) |
|
Q ( p) |
|||
|
1 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Важную роль в методах анализа и синтеза электрических цепей при нулевых начальных условиях играют операторные передаточные функции, которые определяются как отношение изображения выходной реакции цепи к изображению входного воздействия. В соответствии с этим определением различают четыре вида передаточных функций:
где Ни(р), Hi(p) имеют смысл операторных передаточных функций по напряжению и току; НL(р); НY(р) —операторные передаточные сопротивление и проводимость соответственно.
Если в (7.40) заменить оператор р на jw, то получим уравнение комплексных передаточных функций Н(jw), широко используются при частотных методах анализа электрических цепей.
Зная передаточную функцию цепи Н(р), с помощью (7.40) нетрудно найти изображение реакции цепи, а следовательно, и саму реакцию на заданное воздействие.
Операторную передаточную функцию Н(р) для пассивной цепи можно представить как дробно-рациональную функцию с вещественными коэффициентами:
или в виде
где p01, p02, …, p0n — нули; p1, p2, …, pm — полюсы передаточной функции; Н = аn/bm.
Степени полиномов числителя п и знаменателя т зависят от числа реактивных элементов пассивной цепи.
Заменив в (7.41) оператор р на jw, получим комплексную передаточную функцию цепи
где АЧХ цепи
ФЧХ цепи
Учитывая, что согласно (7.43) |H(jw)| является иррациональной, обычно при анализе и синтезе цепей имеют дело с квадратом АЧХ:
где коэффициенты сk и dk получаются путем объединения коэффициентов при одинаковых степенях переменной w.
Перечислим основные свойства операторных передаточных функций и квадрата АЧХ пассивных цепей:
1. Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами. Вещественность коэффициентов объясняется тем, что они определяются элементами схемы.
2. Полюсы передаточной функции располагаются в левой полуплоскости комплексной переменной р. На расположение нулей ограничений нет. Докажем это свойство на примере передаточной функции Ни(р) = U2(р)/U1(р). Выберем входное воздействие u1(t) = d(t) или в операторной форме U(р) = l. Изображение выходного напряжения U2(р) = U1(р)Ни(р) в этом случае численно равно Ни(р), т. е.
где w(p) — полином числителя передаточной функции; A1, A2, …, Am, —коэффициенты разложения дробно-рациональной функции на сумму простых дробей.
Перейдем от изображения U2(p) к оригиналу u2(t):
где в общем случае pi = ai + jwi.
В пассивных и устойчивых активных четырехполюсниках колебания на выходе четырехполюсника после прекращения воздействия должны иметь затухающий характер. Это означает, что в (7.46) вещественные части полюсов pi должны быть отрицательными (ai < 0), т. е. полюсы должны находиться в левой полуплоскости переменной р.
3. Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей, т. е. п < т. Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимала бы бесконечно большое значение (так как числитель рос бы с увеличением частоты быстрее знаменателя), т. е. цепь обладала бы бесконечным усилением, что противоречит физическому смыслу.
4. Квадрат АЧХ является четной рациональной функцией переменной w с вещественными коэффициентами. Это свойство с очевидностью вытекает из способа получения квадрата АЧХ по передаточной функции.
5. Квадрат АЧХ не может принимать отрицательных и бесконечно больших значений при w > 0. Неотрицательность 
Операторные передаточные функции
Содержание:
Операторные передаточные функции:
Практический смысл и назначение операторного метода в теории электрических цепей состоит, прежде всего, в представлении соотношения вход/выход в операторной форме, что даёт возможность существенно упростить процедуры анализа и синтеза электрических цепей и обеспечить связь между временным и частотным описаниями как колебаний, действующих в цепи, так и самой цепи.
Законы Ома и Кирхгофа в операторной форме
Покажем, что решение задач анализа колебаний в электрической цепи существенно упрощается при использовании операторного метода.
Законы Кирхгофа в операторной форме
Пусть токи
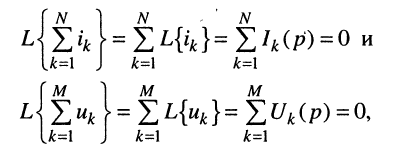
что говорит о формальной справедливости законов Кирхгофа для токов и напряжений, выраженных в операторной форме.
Операторные сопротивления и проводимости элементов электрических цепей
Убедимся в справедливости закона Ома для L-изображений колебаний на зажимах элементов R, L, С при нулевых начальных условиях (см.разд. 15.2) и найдём операторные изображения 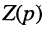
Для элемента активного сопротивления
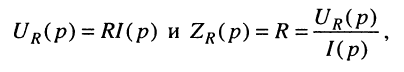
т. е. операторное активное сопротивление равно самому активному сопротивлению, поэтому операторная активная проводимость равна самой активной проводимости
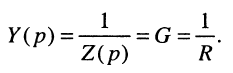
Для элемента индуктивности
правило дифференцирования даёт:
откуда операторные сопротивление и проводимость индуктивности равны:
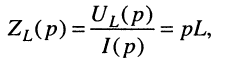
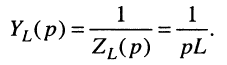
Для элемента ёмкости
правило интегрирования даёт:
откуда операторные сопротивление и проводимость ёмкости равны:
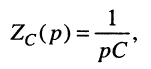
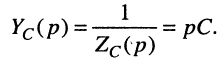
Заметим, что поскольку оператор р согласно (16.2) определён как комплексное переменное
операторные сопротивления и проводимости элементов L и С получаются заменой оператора 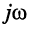
Операторные сопротивление и проводимость последовательного и параллельного двухполюсников
Закон Ома при нулевых начальных условиях формально верен и для сложных двухполюсников, если в числе их элементов не содержатся независимые источники.
Определение:
Операторным сопротивлением 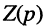
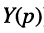
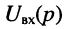
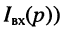
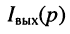
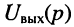
(соответственно 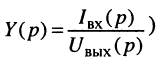
Найти операторное сопротивление двухполюсника (рис. 17.1), состоящего из последовательно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Напряжение на зажимах двухполюсника при нулевых начальных условиях равно
Применим к полученному уравнению преобразование Лапласа:
откуда следует, что при последовательном соединении элементов их операторные сопротивления складываются, как и для комплексных сопротивлений, но оператор 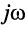
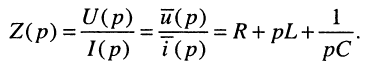
Пример 17.2.
Найти операторную проводимость двухполюсника (рис. 17.2), состоящего из параллельно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Для тока 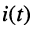
поэтому операторную проводимость заданного двухполюсника можно записать сразу:
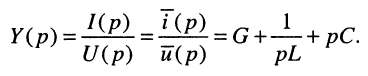
В силу дуальности последовательного и параллельного контуров выражение (17.9) можно было записать сразу на основании формулы (17.8).
Выражения (17.8) и (17.9) представляют собой входные операторные функции цепи. Они дают основания определению операторного сопротивления и проводимости двухполюсника общего вида.
Операторные сопротивление и проводимость двухполюсника общего вида
Закон Ома, при нулевых начальных условиях, формально можно применить и для сколь угодно сложных двухполюсников. Ранее
(см. лекцию 5) было установлено, что если на входе двухполюсника действует источник напряжения с ЭДС 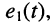
Переходя к L-изображениям напряжений, токов и сопротивлений элементов цепи, получим представление двухполюсника в операторной форме (рис. 17.3), что позволяет записать L-изображение входного тока:
Теперь согласно определению операторной проводимости и операторного сопротивления имеем:
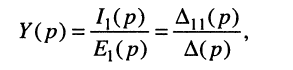
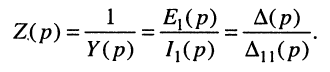
При этом нужно помнить, что определители и алгебраические дополнения в таких формулах записываются с учётом свойств преобразования Лапласа, как это сделано в примерах 17.1 и 17.2.
Определение операторной передаточной функции. Связь с импульсной и переходной характеристиками
В лекции 15 было показано, что во временной области соотношение вход/выход линейной электрической цепи при произвольном воздействии описывается уравнением свёртки:
где h(t) — импульсная характеристика, x(t) — воздействие, y(t) — реакция. При этом воздействие и реакция могут быть напряжениями или токами.
Для описания соотношения вход/выход в операторной форме воспользуемся L-изображением свёртки
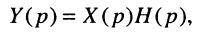
откуда получаем соотношения вход/выход в операторной форме
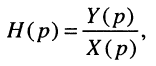
которое называют передаточной функцией.
Определение:
Передаточной функцией линейной электрической цепи называется отношение L-изображения реакции к L-изображению воздействия при нулевых начальных условиях.
Выражение (17.13) говорит о том, что передаточная функция является L-изображением импульсной характеристики, т. е. импульсная характеристика является обратным преобразованием Лапласа передаточной функции:
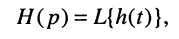
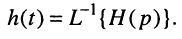
Именно этими зависимостями объясняется содержащееся в определении передаточной функции требование нулевых начальных условий.
Связь между передаточной функцией и переходной характеристикой можно установить, если воспользоваться интегралом Дюамеля (15.20а) при нулевых начальных условиях:
когда 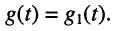
Первый сомножитель правой части полученного уравнения содержит L-изображение производной, поэтому окончательно можно записать:
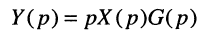
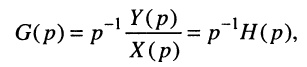
что полностью соответствует связи импульсной и переходной характеристик (15.16).
Обратим внимание на то, что передаточная функция может быть получена из комплексных частотных характеристик формальным образом, а именно — простой заменой в КЧХ 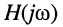
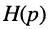
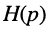
В зависимости от того, какая величина выступает в качестве внешнего воздействия, а какая в качестве реакции цепи, различают четыре вида передаточных функций:
операторное передаточное сопротивление
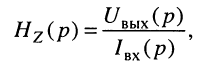
операторную передаточную проводимость
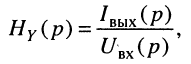
передаточную функцию по току
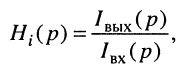
передаточную функцию по напряжению
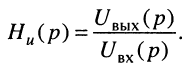
Последние две функции иногда называют операторными передаточными коэффициентами по току и по напряжению соответственно.
По любой из передаточных функций (17.18)—(17.21) нетрудно найти L-изображение реакции цепи, а затем и саму реакцию на заданное воздействие, поскольку любая передаточная функция Н(р) согласно (17.12) может рассматриваться как связующий коэффициент между L-изображения ми воздействия Х(р) и реакции Y(p).
Пример 17.3.
Записать передаточную функцию для последовательного колебательного контура (рис. 17.1, б) относительно напряжения на индуктивности.
Решение. По определению передаточной функции для индуктивности имеем
Но операторное напряжение на индуктивности равно:
Подставляя сюда операторное сопротивление (17.8), получаем искомую передаточную функцию:
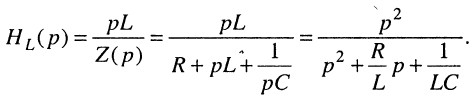
Аналогично можно получить и другие передаточные функции для последовательной, параллельной или более сложной цепи. В последнем случае потребуется составить систему уравнений для L-изображений колебаний, воспользовавшись методом контурных токов или узловых напряжений.
Понятие о нулях и полюсах передаточной функции. Устойчивость передаточной функции
Задача 17.1.
Получить и исследовать общее выражение для передаточной функции цепи, когда воздействие представляет собой ЭДС источника напряжения, а реакцией является ток в выделенной ветви анализируемой цепи (рис. 17.4).
Решение. Выберем независимые контуры в цепи так, чтобы через источник напряжения замыкался ток только одного входного контура, а через интересующую нас ветвь — ток только одного выходного контура. На рис. 17.4 они обозначены индексами 1 и 2 соответственно.
Теперь, как и в задаче 5.2, необходимо положить 
откуда по определению передаточной функции имеем операторную передаточную проводимость
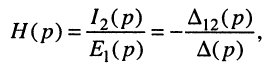
где 
a 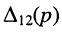
Заметим, что определитель и все его миноры представляют собой рациональные функции оператора р, все коэффициенты которых являются вещественными числами. Это объясняется тем, что при раскрытии определителя над его элементами совершаются только операции умножения, сложения и вычитания, а сами элементы представляют собой простейшие рациональные
функции с вещественными коэффициентами вида (17.11). Раскрывая определитель 
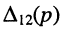
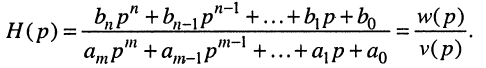
Полиномы числителя 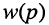
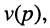
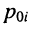
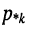
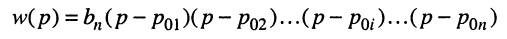
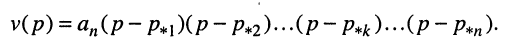
Отсюда передаточная функция (17.24) приобретает вид:
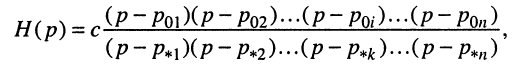
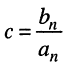
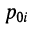
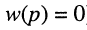
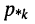
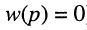
Названия корней уравнения 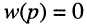
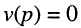
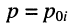
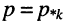
Нули и полюсы наглядно отображаются на комплексной p -плоскости (рис. 17.5) значками ( ° ) и ( * ) соответственно.
На рис. 17.5 показаны:
и 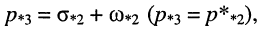
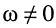
Отображение нулей и полюсов на p-плоскости называют картой нулей и полюсов. Различают левую и правую р-полуплоскости.
Карта нулей и полюсов позволяет оценить ряд свойств электрической цепи и, в частности, определить её устойчивость с точки зрения устойчивости передаточной функции.
Утверждение:
цепь является строго устойчивой тогда и только тогда, когда её передаточная функция имеет, полюсы только в левой р-полуплоскости, исключая мнимую ось.
Доказательство. Напомним, что цепь называется строго устойчивой, если при нулевых начальных условиях ограниченное по величине воздействие
вызывает ограниченную по величине реакцию
Но реакцию y(t) при нулевых условиях можно найти с помощью уравнения свёртки
Отсюда при заданных ограничениях имеем соотношение
из которого следует, что для получения равномерно ограниченной для всех t реакции, т. е. для обеспечения строгой устойчивости цепи должно выполняться условие абсолютной сходимости интеграла от импульсной характеристики:
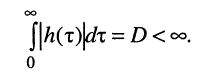
Найдём расположение полюсов, которое соответствует полученному условию. Для этого представим импульсную характеристику h(t) цепи как обратное L-изображение передаточной функции (17.15) путём разложения последней на сумму простых дробей (16.28):
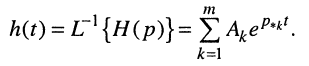
Подставим в интеграл (17.28) правую сумму (17.29)
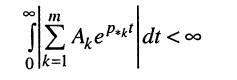
и проведём ряд несложных преобразований.
Поскольку модуль суммы не превосходит суммы модулей, справедливо следующее неравенство:
В правой части полученного неравенства поменяем местами знаки суммирования и интегрирования и оставим только знак равенства:
Рассмотрим интеграл в правой части равенства, содержащий модуль экспоненты, при
во-вторых, первая экспонента под интегралом всегда неотрицательна, поэтому знак модуля можно опустить:
Остаётся исследовать сходимость интеграла при положительном и отрицательном показателе
Сходимость интеграла при 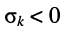
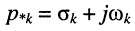
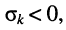
Связь передаточной функции с частотными и временными характеристиками цепи
Как было показано в лекции 10, для определения частотных характеристик АЧХ 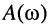
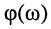
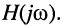
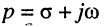
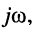
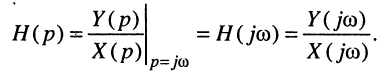
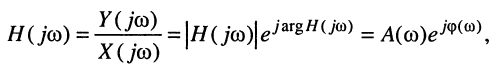
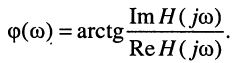
Эквивалентное выражение для КЧХ получается из (17.31), если воспользоваться комплексными функциями числителя и знаменателя:
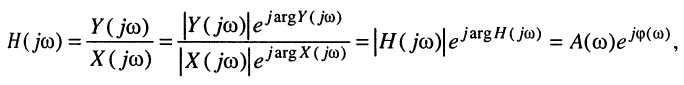
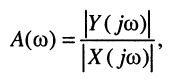
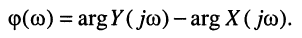
Вследствие того, что функция
является иррациональной, обычно при анализе и синтезе цепей используют квадрат АЧХ:
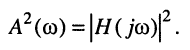
Перечислим основные свойства передаточных функций и квадрата АЧХ пассивных цепей.
- Передаточная функция является L-изображением импульсной характеристики.
- Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами.
- Полюсы устойчивой передаточной функции лежат в левой р-полуплоскости.
- Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей; приневыполнении этого свойства АЧХ на бесконечно больших частотах
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
- Частотные характеристики цепи вычисляются по передаточной функции при подстановке
- Квадрат АЧХ является чётной рациональной функцией переменной с вещественными коэффициентами:
- По передаточной функции можно изобразить схему цепи
Обобщённая схема связи передаточной функции с характеристиками и свойствами цепи представлена на рис. 17.6.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Колебания в линиях без потерь
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
- Частотные методы анализа и расчёта электрических цепей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Контрольная работа: Передаточные функции одноконтурной системы
Практическая работа № 1
1. По заданным дифференциальным уравнениям определить операторные уравнения при нулевых начальных условиях, передаточные функции, структурные схемы звеньев, характеристические уравнения и их корни. Показать распределение корней на комплексной плоскости.
Оценить устойчивость каждого из звеньев.
а) ; б).
2. По заданной передаточной функции записать дифференциальное уравнение:
.
1. а). Дифференциальное уравнение можно записать в виде:
.
Обозначим Y(s) и F(s) как изображения сигналов соответственно y и f , тогда операторное уравнение (при нулевых начальных условиях) примет вид:
1,25s3Y(s) – 4s2Y(s) + 5sY(s) = 3F(s) – sF(s).
Данное уравнение можно преобразовать, вынеся Y(s) и F(s) за скобки:
Y(s). (1,25s3 – 4s2 + 5s) = F(s). (3 – s).
.
Очевидно, что входной сигнал x отсутствует, и выходной сигнал у определяется только внешним воздействием f (система, действующая по возмущению): , то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.
Передаточная функция имеет знаменатель, называемый характеристическим выражением:
A(s) =.
Если приравнять данное выражение к нулю, то образуется характеристическое уравнение , корни которого:
, и .
Распределение корней на комплексной плоскости показано на рис. 2. По рисунку видно, что корни лежат в правой полуплоскости, следовательно, объект неустойчив.
б) Дифференциальное уравнение можно записать в виде:
.
Обозначим Y(s), X(s) и F(s) как изображения сигналов соответственно y , x и f , тогда операторное уравнение (при нулевых начальных условиях) примет вид:
2s2Y(s) + 4sY(s) + 10Y(s) = 3X(s) + 4sF(s).
Данное уравнение можно преобразовать, вынеся Y(s) и X(s) за скобки:
Y(s). (5s2 + 4s + 10) = 3X(s) + 4sF(s).
.
Если обозначить передаточные функции объекта как
и ,
то получается уравнение Y(s) = Wx(s).X(s) + WF(s).F(s). Структурная схема объекта приведена на рис. 3.
Характеристическая функция имеет вид:
,
а характеристическое уравнение:
.
Корни этого уравнения равны:
и .
Распределение корней на комплексной плоскости показано на рис. 4:
Все корни характеристического уравнения лежат в левой полуплоскости, очевидно, что объект устойчив.
2. Дана передаточная функция вида:
Зная, что по определению, , получим:
, тогда:
.
Применяя к полученному выражению обратное преобразование Лапласа, находим искомое дифференциальное уравнение:
.
Практическая работа № 2
Дана одноконтурная АСР, для которой определена передаточная функция регулятора (Р) с настройками и дифференциальное уравнение объекта управления (ОУ). Требуется определить:
— передаточную функцию разомкнутой системы W∞(s),
— характеристическое выражение замкнутой системы (ХВЗС),
— передаточные функции замкнутой системы Фз(s) – по заданию, Фв(s) – по возмущению, ФЕ(s) – по ошибке,
— коэффициенты усиления АСР,
Р — ПИ-регулятор с ПФ вида ;
дифференциальное уравнение объекта управления:
.
Определим передаточную функцию объекта:
W об( s ) .
Передаточная функция разомкнутой системы имеет вид:
Характеристическое выражение замкнутой системы:
;
Передаточные функции замкнутой системы:
— по заданию;
— по ошибке;
— по возмущению.
По передаточным функциям определим коэффициенты усиления путем подстановки в них s = 0:
К3 = Ф3(0) = 1 – по заданию;
КЕ = ФЕ(0) = 0 – по ошибке;
Кв = Фв(0) = 0 – по возмущению.
Определим устойчивость АСР по критерию Гурвица.
Так как коэффициенты ХВЗС а3 = 4, а2 = 6, а1 = 18, а0 = 4 (степень полинома n = 3), то матрица Гурвица имеет вид:
Диагональные миноры матрицы равны соответственно:
Поскольку все определители положительны, то АСР является устойчивой.
Практическая работа № 3
По табличным данным построить переходную кривую объекта, определить параметры передаточной функции объекта, рассчитать настройки ПИД-регулятора, обеспечивающие 20%-е перерегулирование.
DXвх = 5,5 кПа; DY = 0,149 %; tзап = 40 сек
Операторное уравнение по передаточной функции
Понятие линейного динамического звена
САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов динамических звеньев.
Под динамическим звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис. 1.
Подробное изучение свойств реальных объектов управления и систем автоматического управления приводит к описанию динамических звеньев в виде нелинейных дифференциальных уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах. Тем самым осуществляется декомпозиция задач анализа и синтеза систем, то есть первоначально используют линейное представление, а затем осуществляют учет вносимых нелинейностями особенностей. Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются. В дальнейшем мы будем рассматривать преимущественно аппарат изучения линейных систем, а особенности систем других классов: нелинейных, импульсных, цифровых и стохастических, будут излагаться позднее в других учебных дисциплинах.
Если уравнение, связывающее сигналы и , линейно, то говорят о линейном динамическом звене
Уравнение линейного динамического звена имеет следующий общий вид:
где — постоянные коэффициенты, .
Использовать такое описание динамического звена в задачах анализа и синтеза систем и объектов управления не рационально, поэтому существуют и иные формы описания и представления динамических звеньев и систем в целом.
Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу
.
Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов
Преобразуем уравнение (2) к следующему виду
Получим из (3) отношение изображений выходного и входного сигналов
Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена (), имеет вид дробно-рациональной функции.
Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена
.
,
называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции это характеристический полином дифференциального уравнения, описывающего динамическое звено.
Определим передаточную функцию динамического звена по его принципиальной электрической схеме
По второму закону Кирхгоффа запишем уравнения описывающие схему
С учетом того, что
,
Получим операторные уравнения
Из второго уравнения выразим значение изображения тока
Подставим полученное выражение в первое уравнение системы
.
В итоге получаем искомую передаточную функцию
.
Графически передаточные функции динамического звена представляют в следующем виде:
Если известно изображение входного сигнала и передаточная функция динамического звена, всегда можно найти изображение выходного сигнала при нулевых начальных условиях
.(5)
В общем случае САУ состоит из множества динамических звеньев, сигналы с выходов звеньев могут суммироваться или вычитаться, суммироваться с внешними для САУ сигналами. Суммирование и вычитание изображений сигналов могут быть представлено графически с помощью суммирующих звеньев:
Показанная выше неоднозначность графического представления вычитания изображений на суммирующем элементе связана с различием в стандартах разных стран.
Используя графическое представление передаточных функций звеньев и суммирующие звенья, можно в графической форме представить операторные уравнения, описывающие САУ. Такое графическое представление операторных уравнений в ТАУ называют структурной схемой.
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
Получим систему операторных уравнений, подвергнув исходную систему дифференциальных уравнений преобразованию Лапласа и заменив оригиналы изображениями,
Из первого уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим
.
Тогда передаточная функция этого звена имеет вид
,
а выражение описывает суммирующее звено . Таким образом, получены два фрагмента структурной схемы
Из второго уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим, вводя обозначение,
.
Тогда передаточная функция этого звена имеет вид
,
а выражение описывает суммирующее звено . Таким образом, получены еще два фрагмента структурной схемы
Соединим все фрагменты структурной схемы объекта управления, объединяя одноименные сигналы, либо разветвляя их с помощью точек ветвления , показанных на схеме. В результате получим
Временные характеристики динамического звена
Временной или импульсной характеристикой динамического звена называют реакцию звена на , обозначая ее как . При этом схема эксперимента имеет вид
Выясним, что представляет собой временная характеристика, то есть почему ее называют характеристикой динамического звена?
Для этого рассмотрим динамическое звено с передаточной функцией
В этом случае, в соответствии с (5), имеем
.
Получаем, что передаточная функция звена это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции
,
при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа.
Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы.
Для динамического звена с передаточной функцией преобразуем (5), используя теорему об умножении изображений преобразования Лапласа,
,
а если легко получить , тогда
.
Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на , обозначая ее как . При этом схема эксперимента имеет вид
Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией
В этом случае, в соответствии с (5), имеем
.
По теореме об интегрировании оригинала имеем
Переходная функция является интегралом по времени от импульсной характеристике и наоборот
.
Переходная характеристика динамического звена может быть определена по передаточной функции
Контрольные вопросы и задачи
Что такое линейное динамическое звено?
Как определить передаточную функцию линейного динамического звена?
Перечислите основные элементы структурных схем систем управления.
Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную?
Как по переходной характеристике определить импульсную характеристику динамического звена?
Определите передаточную функцию динамического звена по его принципиальной электрической схеме
.
Определите передаточную функцию динамического звена по его принципиальной электрической схеме
.
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
http://www.bestreferat.ru/referat-292845.html
http://drive.ispu.ru/elib/lebedev/3.html
| Название: Передаточные функции одноконтурной системы Раздел: Рефераты по математике Тип: контрольная работа Добавлен 21:52:15 24 декабря 2010 Похожие работы Просмотров: 508 Комментариев: 14 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать |

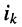
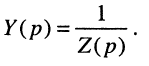
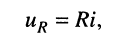
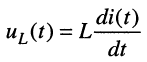
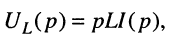
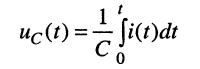
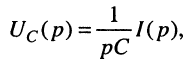
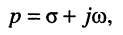
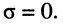
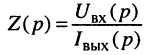
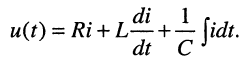
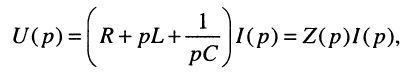
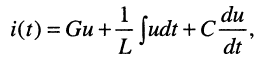
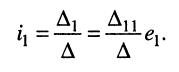
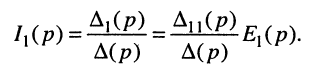
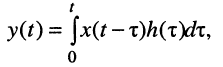
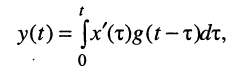
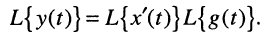
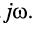
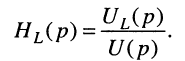
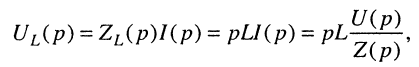
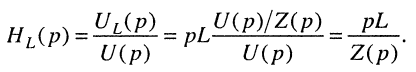
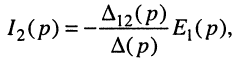
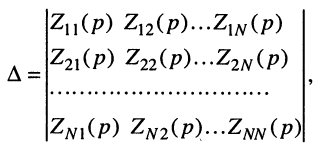
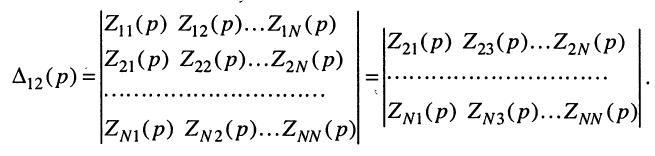
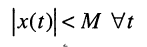
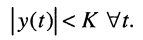
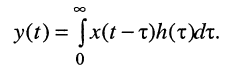
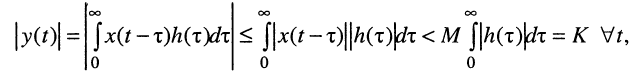
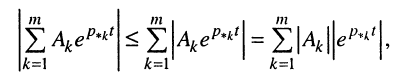
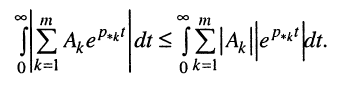
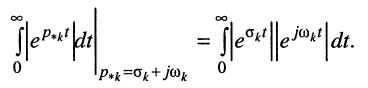
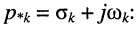
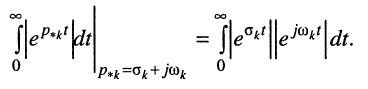
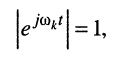
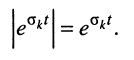
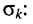
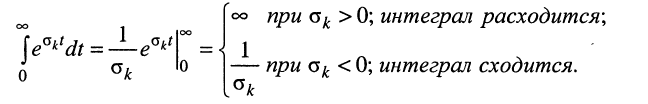
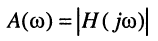
 должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.