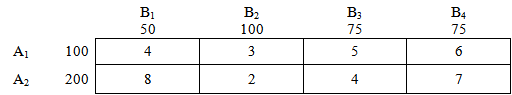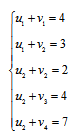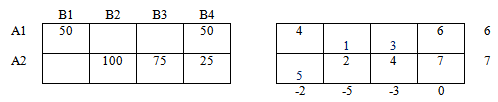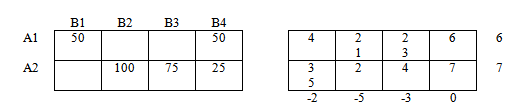Транспортная задача линейного программирования
Время на прочтение
11 мин
Количество просмотров 28K

Транспортная задача линейного программирования относится к перечню классических задач, решаемых в практике деятельности людей. Эта задача методами классической математики не решается. В задаче необходимо отыскивать экстремум целевой функции. В задаче целевая функция – линейная. Ограничения на переменные (их может быть очень много) описываются также линейными зависимостями. Казалось бы чего проще. Но как раз ограничения и порождают трудности, связанные не просто с поиском max и min при отсутствии ограничений, а с необходимостью учета таких ограничений. Искать требуется не просто экстремум, а условный экстремум. Методы решения задачи позволяют учитывать особенности структуры задачи и даже отказаться от симплексного метода решения в чистом виде.
I. Основные параметры, термины и обозначения
Для ощущения масштаба задачи приведу парочку изображений того, что рассматривается в транспортной задаче линейного программирования.
Зеленый цвет — пассажирские суда, желтые — грузовые, розовый — частные яхты, оранжевый — танкеры и др. Аналогичная картина наблюдается и для авиационных перевозок, перевозок по железной дороге или автотранспортом. Изображения получены в начальном периоде Пандемии короновируса, что привело к огромным пробкам в узостях мирового Океана (Панамский, Суэцкий и др. каналы). Танкеры отправили отстаиваться на рейде, экипажам судов на берег сойти не разрешалось. Это форс-мажорные обстоятельства, которые в теории должны рассматриваться и учитываться специальным образом, что пока к сожалению перевозчиков не сделано.
В теории в тексте задачи Хичкока ничего не говорится о равенстве имеющегося общего запаса судов в портах отправления и общей потребности в судах в портах прибытия (назначения). Если такого равенства нет, то система ограничений несовместна. В случае равенства
транспортная задача называется «сбалансированной». Задачи, в которых условие баланса не задано, должны быть приведены к «сбалансированному» виду. Это можно выполнить использованием «фиктивных» перевозок. Рассматриваем два случая:
Поэтому ранг системы равен не n+m, а n+m – 1, т.е с mn неизвестными. Общее число опорных планов равно числу сочетаний из mn по n+m – 1.. Применение симплекс метода для решения задачи возможно, но требует большого объема вычислений уже при n и m ≈ 10 -15. Заметим также, что каждая неизвестная входит лишь в два уравнения системы (матрица коэффициентов системы ограничений имеет в каждой строке и каждом столбце только два ненулевых элемента). Более того, транспортная задача всегда имеет допустимое решение. Все сказанное вызвало потребность попытаться учесть специфику задачи и создать метод ее решения более простой, чем симплекс метод. Такие методы были найдены и получили названия метода потенциалов и распределительного метода. Это разновидности симплексного метода. Они удобно реализуются, если условие задачи представлено в виде таблиц.
ТАБЛИЦА 1 — Вид данных транспортной задачи линейного программирования
Метод содержит три последовательных этапа:
-
Формирование опорного плана;
-
Проверка опорного плана на оптимальность;
-
Переход к новому опорному плану, если предыдущий не оптимален.
II. Формирование опорного плана перевозок
Рассмотрим способ получения начального опорного плана транспортной задачи, названный способом северо-западного (С-З) угла. Способ заключается в заполнении ячеек таблицы m×n значениями переменной xij, таким образом, чтобы удовлетворялись условия задачи. При этом план решения Х[m, n] может быть и не оптимальным, но обязательно должен быть допустимым.
В этом способе формируют опорный план, двигаясь по таблице: сверху вниз по строкам и слева направо вдоль строки. Начинают с левого верхнего угла (ячейки), куда вписывают значение x11 =min{a1, b1}.Первые строка и столбец из рассмотрения далее исключаются.
Затем, если a1 > b1, то определяется остаток (a1 – b1) продукта на первом пункте отправления и его запас реализуется на 2-м пункте назначения. Остаток потребностей 2-го пункта назначения удовлетворяется за счет 2-го пункта отправления, остатки которого направляются в 3-й пункт назначения и т.д. Ниже метод будет иллюстрирован числовым примером.
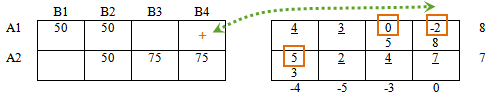
Пример 1. Построение опорного плана методом Северо-Западного угла
Заданы значения: m = 3, n = 4; a1 = 60, a2 = 80, a3 =100, b1 = 40,b2 = 60, b3 = 80, b4 = 60. Слева в таблице приведены dij удельные стоимости перевозок; справа — Вij стоимости совместно с предложениями ai и потребностями bj .
Требуется найти план Х [m,n] перевозок, удовлетворяющий условиям на целевую функцию Q и переменные хij задачи Q.
РЕШЕНИЕ Построить исходный опорный план способом северо-западного угла. Строим симплексную таблицу: Таблица 3. Опорный план задачи
В таблице способом северо-западного угла получен опорный план. Базисные переменные (их число = 6): x11 = 40, x12= 20, x22= 40, x23= 40, x33= 40, x34= 60. Свободные переменные: x13= x14= x21= x24= x31= x32= 0 (их число равно 6).
Ячейки таблицы, соответствующие базисным переменным, называют базисными, остальные – свободными. Далее в алгоритме будем следовать идее симплекс метода. Суммарная стоимость перевозок Q, соответствующая плану Х[m,n], получает представление
Q = d11∙x11 + d12∙x12 + d22∙x22 + d23 ∙x23+ d33 ∙x33+ d34 ∙x34 = = 5∙40 + 2∙20 + 10∙40 + 2∙40 + 8∙40 + 5∙60 = 200+40+400 + 80 + 320+ 300 = 1340 ед
Коэффициенты dij называются фиктивными или косвенными стоимостями; их выражают через косвенные величины α и β, d’ij = αi +βj . Здесь параметры αi и ( — βj ), по аналогии с механикой называют потенциалами i-го пункта отправления и j-го пункта прибытия. Значения потенциалов определяется из системы линейных уравнений: αi + βj = dij Каждому из таких уравнений соответствует какая-либо базисная переменная хij Система уравнений с потенциалами содержит m+n неизвестных потенциалов, число же уравнений равняется числу базисных ячеек таблицы, т.е. (m + n – 1). Следовательно, один из потенциалов можно задать произвольно, положив его равным, например, нулю.
Решая далее систему уравнений для потенциалов, находим значения потенциалов строк и столбцов, все фиктивные стоимости dij и коэффициенты γij. Если для всех свободных клеток γrs ≤ 0, то перевод в базис любой свободной переменной не уменьшит значения целевой функции и, следовательно, выбранный опорный план не является оптимальным. Если же некоторые γrs >0, то данный план можно улучшить путем перевода в базис свободной переменной, соответствующей max γrs, а также путем исключения из базиса, принадлежащей ему переменной, первой обращающейся в нуль. Переход к новому опорному плану и поиск оптимального плана рассмотрим на примере. Другой способ формирования опорного плана предложен Фогелем. Этот способ при первом чтении можно пропустить, так как дальше он в тексте не используется.
Пример 2. Способ аппроксимации Фогеля
В большинстве случаев этот способ дает опорный план наиболее близкий к оптимальному. Удобен для матриц большой размерности. Используется концепция штрафов, взимаемых за выбор не самого оптимального с точки зрения транспортных издержек маршрута. Штраф по каждой строке и каждому столбцу определяется из анализа маршрутов с различными показателями издержек (как разность двух различных уровней транспортных издержек). Первой заполняется клетка матрицы (таблицы), в которой фиксируется самый крупный штраф. После заполнения клетки штрафы пересчитываются и так до тех пор, пока все ресурсы не будут распределены. Исходные данные для этого примера заполняют таблицу слева вверху.
Этапы алгоритма: 1. Вычисление разностей в каждой строке и в каждом столбце между наименьшей стоимостью и ближайшей к ней по величине. Разности по строкам записываются справа в столбце разностей, разности по столбцам – внизу в строке разностей. Например, для строк А1 разность равна А1В2 – А1В3 = 38 – 24 = 14 и т. д.
ТАБЛИЦА 2 — Метод Фогеля для получения опорного плана транспортной задачи
2. Поиск из всех разностей, как по строкам, так и по столбцам максимальный. В нашем примере максимальная разность равна 38 и находится в строке А2. Обведем максимальную разность рамкой.
3. Размещение в клетку, где находится наименьшая стоимость (А2В2 = 18) (строка с наибольшей разностью), максимально возможного количества ресурсов. Оно равно 20, т.е. всему ресурсу отправителя А2. Поскольку все ресурсы отправителя А2 исчерпаны, строку А2 исключаем из дальнейших расчетов, для чего отметим все клетки этой строки точками.
4. Вычисление разностей столбцам и строкам, не принимая во внимание стоимость в клетках, имеющих ресурсы и клетках с точкой (исключенную строку или столбец) и определение максимальной разности в строке или столбце (В3 = 76).
5. Поиск минимального элемента в строке или в столбце с максимальной разностью (А1В3 = 24) и размещения в данную клетку максимально возможного количества ресурса, возвращение к этапу №4 и т.д. Окончательно
ЦФ Q=23∙19 + 7∙3 + 20∙18 + 2∙10 + 14∙24 + 1∙100 +3∙48 = = 437 + 21 + 360 + 20 +3 36 + 100 + 272 =1546 ед. Это значение соответствует опорному плану Фогеля.
III. Транспортная задача линейного программирования
Как основной метод решения транспортной задачи – используется метод потенциалов. Ни симплексный метод, ни распределительный метод здесь не рассматриваются. У них имеются свои плюсы и минусы, но объем изложения достаточно велик. Возможно этому позднее я уделю внимание и время, но пока отвечаю на пожелание читателя Хабра.
Пример 3 — Транспортная задача. Метод потенциалов
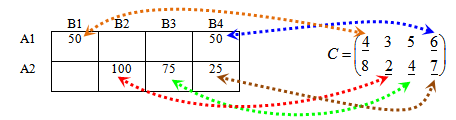
Исходные данные задачи удобно представить двумя матрицами.
ТАБЛИЦА — Исходные данные
Требуется найти план Х [m,n] перевозок, удовлетворяющий условиям на целевую функцию Q и переменные хij задачи
Решение задачи:
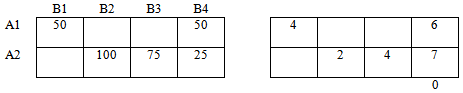
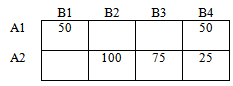
1. Формирование начального опорного плана способом Северо-Западного угла.
Базисные n + m – 1 = 3 + 4 – 1 = 6 переменные:
x11 =70, x12 = 20, x22 = 10, x23 = 20, x24 = 0, x34 = 40.
Остальные переменные nm – n + m – 1 = 12 – 6 = 6 свободные:
x13 = x14 = x21 = x24 = x31= x32 = 0 .
Суммарная стоимость перевозок для опорного плана получает представление:
Q = d11 ∙x11 + d12∙x12 + d22∙x22 + d23∙x23+ d24∙x24+ d34∙x34 =
=2∙70 + 3∙20 + 3∙10 + 1∙20 + 2∙0 + 2∙40 = 140 + 60 + 30 + 20 + 0 +80 = 330 ед.
2. Проверка опорного плана на оптимальность
Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов. Определим систему уравнений для потенциалов и вычислим их значения:
α1 + β1 = d11 = 2;
α1 + β2 = d12 = 3;
α2 + β2 = d22 = 3;
α2 + β3 = d23 = 1;
α2 + β4 = d24 = 2;
α3 + β4 = d34 = 2.
Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пусть β1 = 0. Тогда после решения системы получены значения потенциалов: α1= 2, α2= 2, α3= 2, β1 =0, β2=1, β3 =–1, β4 =0,
Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].
Выделяем в Г [m, n] свободные ячейки, содержащие γrs. Проверяем наличие положительных переменных γi,j > 0. Так как в матрице (в свободных ячейках) имеем γ32 = 2 > 0, то исходный опорный план может быть улучшен, он не является оптимальным.
3. Переход к новому (улучшенному) опорному плану
Переменную x32 =x следует ввести в базис. Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок
Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок Очевидно, что наибольшее x определяется теми xij в базисных клетках, из которых этот х вычитается. Следовательно, x11 = min{х22, х34} = {10, 40} = 10. При x >10 перевозка х22 становится отрицательной. Переменную х22 исключаем из базиса и переводим ее в разряд свободных переменных. Далее повторяются рекурсивно три пункта алгоритма.
-
Получаем из модифицированного плана новый опорный план
В нем объемы перевозок распределены иначе чем в начальном опорном плане.
Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d11 ∙x11 + d12∙x12 + d23∙x23 + d32∙x32 + d24∙x24+ d34∙x34 =
=2∙70 + 3∙20 + 2∙10 + 1∙20 + 1∙10 + 2∙30 = 140 + 60 + 20 + 20 + 10 + 60 = 310 ед. Затраты на перевозки при этом плане уменьшились на 330 – 310 = 20 ед.
Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.
2. Проверка опорного плана на оптимальность
Определим систему уравнений для потенциалов и вычислим их значения:
α1 + β1 = d11 = 2;
α1 + β2 = d12 = 3;
α2 + β3 = d23 = 1;
α2 + β4 = d24 = 2;
α3 + β2 = d32 = 1;
α3 + β4 = d34 = 2.
Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пустьα1 = 0. Тогда после решения системы получены значения потенциалов: α1= 0, α2= – 2, α3= –2, β1 =2, β2=3, β3 = 3, β4 =4.
Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].
Свободные ячейки матрицы Г [m, n] содержат γi,j > 0 (γ14 = 1>0). План не оптимален.
3. Переход к новому (улучшенному) опорному плану
Из свободных переменных с xij > 0, выбираем одну x14 для введения ее в базис. Обозначим ее как и ранее через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся очередным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок
Очевидно, что наибольшее x определяется теми xij в базисных клетках, из которых этот х вычитается. Следовательно, x11 = min{х12, х34} = {20, 30} = 20. При х12 >20 перевозка х12 становится отрицательной. Переменную х12 исключаем из базиса и переводим ее в разряд свободных переменных. Переходим к новой итерации
1. Получаем из модифицированного плана новый опорный план.
В нем объемы перевозок распределены иначе чем в предшествующем опорном плане.
Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d11 ∙x11 + d14∙x14 + d23∙x23 + d32∙x32 + d24∙x24+ d34∙x34 =
=2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 140 + 60 + 20 + 20 + 30 + 20 = 290 ед. Затраты на перевозки при этом плане уменьшились на 310 – 290 = 20 ед. Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.
2. Проверка опорного плана на оптимальность
Определим систему уравнений для потенциалов и вычислим их значения:
α1 + β1 = d11 = 2;
α1 + β4 = d14 = 3;
α2 + β3 = d23 = 1;
α2 + β4 = d24 = 2;
α3 + β2 = d32 = 1;
α3 + β4 = d34 = 2. Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пусть β1 = 0. Тогда после решения системы получены значения потенциалов: α1= 2, α2= 2, α3= 2, β1 =0, β2=1, β3 =–1, β4 =0.
Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].
При переходе к новому опорному плану проверяем наличие положительных свободных переменных γi,j >0. Но таких переменных не оказалось. Отсюда следует вывод, что полученный последним модифицированный план является оптимальным и ему соответствует значение линейной формы
Q’= 2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 290.
Заключение
Вся теория исследования операций с позиций математики решает неклассические задачи оптимизации целевых функций. Отличие от классики в том, что те ограничения на переменные, которые исследователи вынуждены накладывать в рамках моделей, созданы и вызваны реальностью. Отыскивать требуется экстремумы функций при многих ограничениях, так называемые условные экстремумы. Классика не позволяет этого делать. Взятие производных и приравнивание их нулю «не видит» ограничений. Лучшее, что там имеется это функция Лагранжа, но ее использование также весьма ограничено. Транспортные задачи – частный, но важный случай в исследовании операций. Надеюсь, что читатель разобравшись в приведенных примерах, лучше стал понимать логику задачи и сумеет самостоятельно постигать интересующие его вопросы по другим публикациям в учебниках и журнальных статьях.
Литература
-
Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.
-
Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.
-
Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.
-
Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.
-
Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.
-
Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.
-
Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.
Транспортная задача. Методы решения
Транспортная задача, это специальный вид задачи линейного программирования. Для решения транспортной задачи можно использовать методы решения задач линейного программирования, однако ввиду специфического вида задачи, были построены алгоритмы специально для решения этой задачи. Для решения транспортной задачи в онлайн режиме с подробными пояснениями пользуйтесь калькулятором транспортная задача онлайн.
- Содержание
- 1. Математическая постановка транспортной задачи
- 2. Определение опорного плана. Предварительные сведения
- 3. Метод северно-западного угла
- 4. Метод минимального элемента
- 5. Метод аппроксимации Фогеля
- 6. Метод потенциалов
- 7. Метод дифференциальных рент
1. Математическая постановка транспортной задачи.
Общая постановка транспортной задачи заключается в определении оптимального плана перевозок некоторого однородного груза из пунктов отправления A1, A2,…, Am в пункты назначения B1, B2,…, Bn. Критерий оптимальности берется минимальная стоимость перевозки или минимальное время доставки груза.
Рассмотрим транспортную задачу, где в качестве критерия оптимальности взята минимальная стоимость перевозок всего груза. Обозначим через Сij тарифы перевозки единицы груза из пункта отправления i в пункт назначения j. Обозначим через Ai запасы груза i-м пункте отправления, а через Bj потребности груза j-м пункте назначения, а через Xj количество единиц груза переводимого из пункта отправления i в пункт назначения j.
Тогда математическая модель транспортной задачи состоит в определении минимального значения функции
 |
(1.1) |
при условиях
 |
(1.2) |
 |
(1.3) |
 |
(1.4) |
Поскольку удовлетворяется условия (1.2)−(1.4), то обеспечивается доставка необходимого количества груза в каждый из пунктов назначения, вывоз груза из всех пунктов отправления, а также исключаются обратные перевозки.
Определение 1. Любое неотрицательное решение Xij=∥xij∥ (i=1,..,m; j=1,…,n) систем (1.2) и (1.3) называется допустимым планом транспортной задачи.
Определение 2. План 
Если сумма груза у поставщиков равно общей сумме потребностей в пунктах назначения:
 |
(1.5) |
то модель транспортной задачи называется закрытой (или сбалансированной). Если (1.5) не удовлетворяется, то модель транспортной задачи называется открытой (или несбалансированной).
Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось условие (1.5).
В случае превышения запаса над потребностью, т.е. при
 , , |
вводится фиктивный (n+1)-ый пункт назначения с потребностью
 . . |
Соответствующие тарифы считаются равными нулю: ci n+1=0 (i=1,…,m). После этих преобразований получим закрытую модель транспортной задачи.
Аналогично, при 

Мы будем рассматривать закрытую модель транспортной задачи. Если же модель транспортной задачи является открытой, то с помощью вышеизложенных преобразований строим закрытую модель транспортной задачи.
Обычно данные транспортной задачи записывают в виде таблицы:
Число переменных Xij равно mn, где m число пунктов отправнения , а n число пунктов назначения. Число уравнений в (1.2) и (1.3) равно m+n. Так как мы рассматриваем закрытую модель транспортной задачи (выполняется равенство (1.5)), то число линейно независимых уравнений равно m+n−1. Следовательно опорный план транспортной задачи может иметь не более m+n−1 отличных от нуля неизвестных.
Если в опорном плане количество отличных от нуля компонентов равно в точности m+n−1, то опорный план называется невырожденным, а если меньше − то вырожденным.
Для решения транспортной задачи сначала определяется начальный опорный план, а затем определяется оптимальный план путем улучшения текущего опорного плана.
Для определения начального опорного плана существует несколько методов. Мы рассмоьтрим три метода. Метод северно-западного угла, метод минимального элемента и метод аппроксимации Фогеля.
2. Определение опорного плана. Предварительные сведения
Опорный план транспортной задачи находим следующим образом. На каждом шаге в таблице условий задачи заполняем одну клетку, которая называется занятой. Обозначим через Kij клетку, где i -номер пункта отправления (строка), j-номер пункта назначения (столбец). Клетку Kij заполняем так, чтобы удовлетворялись полностью потребности пункта назначения j, либо обеспечивался полный вывоз груза из пункта отправления i.
В первом случае временно исключаем из рассмотрения столбец j и изменяем запас груза пункта отправления i. Во втором случае временно исключаем из рассматрения строку i и изменяем потребность груза пункта назначения j. Далее повторяем процедуру с таблицей условий с исключенной строкой или столбцом.
В m+n−1-ом шаге получаем задачу с одним пунктом отправления и одним пунктом назначения. Остается свободной одна клетка. Запасы оставшегося пункта отправления будут равны потребностям пункта назначения. Заполнив эту клетку заканчиваем m+n−1-ый шаг и получаем опорный план.
Если на некотором шаге (но не на последнем) потребности очередного пункта назначения равны запасам пункта отправления, то временно исключаем из рассмотрения либо столбец, либо строку (только одно из двух). Тогда либо запасы данного пункта отправления, либо потребности данного пункта назначения считаем равным нулю. Этот нуль при очередном шаге записываем в очередную заполняемую клетку. Данный подход обеспечивает ровно m+n−1 занятых клеток, что обеспечивает возможность проверки полученного опорного плана на оптимальность и нахождение оптимального плана.
Для нахождения опорного плана транспортной задачи в онлайн режиме тремия методами с подробными пояснениями пользуйтесь калькулятором транспортная задача онлайн.
3. Метод северно-западного угла
При нахождении опорного плана транспортной задачи методом северно-западного угла, заполнене клеток таблицы условий начинают с верхней левой клетки K11 поэтому метод и называется «метод северно западного угла»).
Рассмотрим метод на конкретном примере.
Пример 1. На три базы A1, A2, A3 поступил очередной груз в количествах равных 140, 160, 120 ед. Этот груз требуется перевезти в четыре пунктов назначения B1, B2, B3, B4 в количествах 150, 90, 100, 80. Тарифы перевозок представлена матрицей
 . . |
Найти план перевозок даной транспортной задачи методом северно-западного угла.
Решение. Запишем все данные в таблицу условий:
Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы.
Наличие груза у поставщиков равно: ∑Ai=140+160+120=420.
Общая потребность в грузе в пунктах назначения равна: ∑Bj=150+90+100+80=420.
∑Ai=∑Bj. Модель транспортной задачи является закрытой. Следовательно она разрешима.
Найдем опорный план задачи методом северно-западного угла.
A1≤B1. Следовательно в клетку (A1, B1 ) помещаем число min(A1, B1)=140. Запасы пункта A1 полностью исчерпаны. Поэтому исключаем из рассмотрения строку A1 и будем считать потребности пункта B1 равными 150−140=10.
A2>B1. Следовательно в клетку (A2, B1) помещаем число min(A2, B1)=10. Потребности пункта B1 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B1 и будем считать запасы пункта A2 равными 160−10=150.
Таким образом, продолжая процедуру в m+n−1-ом шаге получим:
Запишем полученный опорный план:
При этом плане стоимость перевозок вычисляется так:
F=2·140+8·10+4·90+ 1·60+3·40+6·80=1380.
4. Метод минимального элемента
В отличие от метода северно-западного угла, в методе минимального элемента выбор пунктов отправления и пунктов назначения производится ориентируясь на тарифы перевозок, т.е. в каждом шаге нужно выбрать клетку с минимальным тарифом перевозок. Если таких клеток несколько, то выбираем один из них. Надо отметить, что при данном методе определения заполняемой клетки, стоимость перевозок как правило бывает меньше, чем при методе северно западного угла. Поэтому целесообразно начальный опорный план найти методом минимального элемента.
Рассмотрим метод минимального элемента на примере.
Пример 2. Найти опорный план транспортной задачи представленной в таблице условий ниже методом минимального элемента:
Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы. Тарифы перевозок единицы груза из кажного пункта отправления во все пункты назначения задаются матрицей
Наличие груза у поставщиков равно: 
Общая потребность в грузе в пунктах назначения равна: 

Минимальный тариф равный 1 находится в клетке (A1, B3). Поэтому заполняем эту клетку.
A1>B3. Следовательно в клетку (A1, B3) помещаем число 70. Потребности пункта B3 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B3 и будем считать запасы пункта A1 равными 150−70=80.
Минимальный тариф равный 1 находится в клетке (A2, B4). Поэтому заполняем эту клетку.
A2>B4. Следовательно в клетку (A2, B4) помещаем число 40. Потребности пункта B4 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B4 и будем считать запасы пункта A2 равными 100−40=60.
Таким образом, продолжая процедуру в m+n−1-ом шаге получим:
Запишем полученный опорный план:
При этом плане стоимость перевозок вычисляется так:
5. Метод аппроксимации Фогеля
Суть метода аппроксимации Фогеля заключается в следующем. Для каждой строки и для каждого столбца находим разности между двумя записанными в них минимальными тарифами. Полученные разности записываем в специально отведенные для этого столбце и в строке в таблице условий задачи.
Среди указанных разностей выбираем максимальную. В строке (или в столбце), которой данная разность соответствует, определяем минимальный тариф. Клетку, в которой он записан заполняем на данной итерации.
Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбираем ту клетку, которая соответствует наибольшей разности между двумя минимальными тарифами в данном столбце (строке).
Применение метода аппроксимации фогеля позволяет получить либо опорный план, близкий к оптимальнму, либо сам оптимальный план.
Рассмотрим метод аппроксимации Фогеля на примере 2, рассмотренной выше.
Пример 3. Найти опорный план транспортной задачи представленной в таблице условий ниже методом аппроксимации Фогеля:
Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы. Тарифы перевозок единицы груза из кажного пункта отправления во все пункты назначения задаются матрицей
Наличие груза у поставщиков равно: 
Общая потребность в грузе в пунктах назначения равна: 

Для каждой строки Ai найдем разности между двумя минимальными тарифами, записанными в данной строке и поместим их в соответствующем дополнительном столбце.
В строке 1 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1. В строке 2 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В строке 3 минимальный тариф равен 3, а следующий за ним равен 3, разность между ними 3−3=0.
Для каждого столбца Bj найдем разности между двумя минимальными тарифами, записанными в данном столбце и поместим их в соответствующей дополнительной строке.
В столбце 1 минимальный тариф равен 2, а следующий за ним равен 3, разность между ними 3−2=1. В столбце 2 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1. В столбце 3 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В столбце 4 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1.
Вычислив все разности выберем наибольшую из них. В данном случае наибольшая разница равна 2. В этом столбце минимальный тариф равен 1 и находится в пересечении строки A 1 и столбца B3. Следовательно заполняем эту клетку.
A1>B3. Следовательно в клетку помещаем число 70. Потребности пункта B3 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B3 и будем считать запасы пункта A1 равными 150−70=80.
Для каждой строки Ai найдем разности между двумя минимальными тарифами, записанными в данной строке и поместим их в соответствующем дополнительном столбце.
В столбце 1 минимальный тариф равен 2, а следующий за ним равен 3, разность между ними 3−2=1. В столбце 2 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1. В столбце 3 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В столбце 4 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1. В строке 1 минимальный тариф равен 2, а следующий за ним равен 2, разность между ними 2−2=0. В строке 2 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В строке 3 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1.
Для каждого столбца Bj найдем разности между двумя минимальными тарифами, записанными в данном столбце и поместим их в соответствующей дополнительной строке.
В столбце 1 минимальный тариф равен 2, а следующий за ним равен 3, разность между ними 3−2=1. В столбце 2 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1. В столбце 4 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1.
Вычислив все разности выберем наибольшую из них. В данном случае наибольшая разница равна 2. В этой строке минимальный тариф равен 1 и находится в пересечении строки A2 и столбца B4. Следовательно заполняем эту клетку.
A2>B4. Следовательно в клетку помещаем число 40. Потребности пункта B4 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B4 и будем считать запасы пункта A2 равными 100−40=60.
Таким образом, продолжая процедуру в m+n−1-ом шаге получим:
Запишем полученный опорный план:
При этом плане стоимость перевозок вычисляется так:
F=2·40+3·40+1·70+ 4·60+1·40+3·100=850.
Для определения оптимального плана транспортной задачи разработано нескольно методов. Мы расмотрим метод потенциалов и метод дифференциальных рент.
6. Метод потенциалов
Процедура нахождения оптимального плана транспортной задачи имеет два этапа. На первом этапе находят опорной план транспортной задачи. Далее последовательно улучшают найденный опорный план до получения оптимального плана.
Для определения опорного плана будем пользоваться методом северно-западного угла, методом минимального элемента или методом аппроксимации Фогеля рассмотренных выше.
Для онлайн решения задачи методом потенциалов пользуйтель калькулятором транспортная задача онлайн.
При применении этих методов получаем m+n−1 занятых клеток в исходном плане. Отметим, что в некоторых клетках могут стоять нули. Полученный план следует проверить на оптимальность.
Теорема. Если для некоторого опорного плана 
для всех i=1,..,m; j=1,…,n, то 
Определение 6.1. Числа αi и βj (i=1,..,m; j=1,…,n) называются потенциалами пунктов отправления и пунктов назначения, соответственно.
Вышеизложенная теорема позволяет построить алгоритм нахождения оптимального плана транспортной задачи.
Алгоритм состоит в следующем. Предположим, что одним из рассмотренных выше методов найден опорный план транспортной задачи. Для каждого из пунктов отправления и назначения определяют потенциалы αi и βj (i=1,..,m; j=1,…,n) из системы уравнений
где сij − тарифы транспортной задачи в заполненных клетках.
Так как число заполненных клеток равно m+n−1, то система (6.1) с m+n неизвестными содержит m+n−1 уравнений. Для решения данной задачи одно из неизвестных можно сделать равным нулю и найти остальные неизвестные. После этого, для свободных клеток определяем числа
Если среди чисел αij нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клетки αij>0, то данный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых αij>0 и среди данных чисел выбирают максимальное. Клетку с данным числом следует заполнить.
Надо учитывать, что при заполнении данной клетки необходимо изменить объем поставок в нескольких других клетках.
Определение 6.2. Циклом в таблице условий транспортной задачи называется ломанная линия, вершины которой расположены в занятых клетках таблицы, а звеня расположены вдоль строк и столбцов. В каждой вершине цикла встречается два звена, одно из которых находится в строке, а другой в столбце.
Если ломаннная линия, образующая цикл, самопересекается, то место пересечения не является вершиной. Некоторые циклы представлены на рисунке Рис.6.1.
При правильном строении опорного плана для любой свободной клетки можно построить только один цикл. После построения цикла следует перейти к новому опорному плану. Для этого в каждой из клеток, находящихся на вершине цикла записывают определенный знак «+» или «−» . В свободной клетке записывают знак «+» и поочередно проходя по циклу записывают знаки «−» и «+». Назовем клетки с записанными в них знаками плюсовыми и минусовыми.
Далее в свободную клетку переносят меньшее из чисел xij, находящихся в минусовых клетках. Это число прибавляют к числам, стоящим в плюсовых клетках а вычисляют из чисел, стоящих в минусовых клетках. Клетка, которая была свободной, становится занятой, а минусовая клетка с минимальным из чисел xij, находящихся в минусовых клетках считается свободным.
В результате вышеуказанных перемещений груза по циклу, получим новый опорный план транспортной задачи. Описанный переход от одного опорного плана транспортной задачи к другому опорному плану называется сдвигом по циклу пересчета.
При сдвиге по циклу пересчета число занятых клеток не изменяется и равно m+n−1. Если в минусовых клетках имеется два и более одинаковых минимальных числа xij, то освобождают только одину, о остальные оставляют занятыми с нулевыми значениями.
Далее полученный опорный план проверяют на оптимальность. Для этого определяют потенциалы пунктов отправления и назначения и находят числа αij=βj−αi−cij для всех свободных клеток. Если среди них не окажется положительный, то получен оптимальный план. Если же среди них есть положительный, то нужно перейти к новому опорному плану. После конечнего числа шагов получяют оптимальный план.
Таким образом алгоритм нахождения оптимального плана содержит следующие этапы:
1. Нахождение опорного плана. При этом число заполненных клеток должно быть равным m+n−1.
2. Нахождение потенциалов αi и βj (i=1,..,m; j=1,…,n) пунктов отправления и назначения соответственно.
3. Определение числа αij для каждой свободной клетки. Если среди αij нет положительных, то получен оптимальный план транспортной задачи. Если же они имеются, то делается переход к новому опорному плану.
4. Выбор максимального среди положительных чисел αij . Определение свободной клетки, которую нужно заполнить. Построение цикла пересчета для выбранной свободной клетки. Сдвиг по циклу пересчета.
5. Проверка полученного опорного плана на оптимальность, т.е. переход к пункту 2.
Отметим, что в некотором шаге опорный план может стать вырожденным. Чтобы избежать зацикливания следует преобразовать вырожденный план в невыроженный путем замены соответствующий нулевых элементов опорного плана на сколь угодно малыми положительными числами δ и решить задачу. После решения, в оптимальном плане нужно заменить δ нулем.
Рассмотрим метод потенциалов на примере.
Пример 6.1. Решить транспортную задачу, заданную в таблице условий методом потенциалов:
Решение. Найдем сначала опорный план с помощью одного из методов описанного выше. Пусть это будет метод минимального элемента. Тогда после m+n−1 шагов получим следующую таблицу с опорным планом:
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
Полагая α1=0, находим β2=2, β3=1, α2=-1, α3=-3, β4=0, β2=5
Для каждой свободной клетки вычисляем число αij=βj−αi−cij. α12=2, α14=-2, α22=2, α23=-3, α33=-1, α34=-3.
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
Среди чисел αij есть положительные. Следовательно данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки A1 и столбца B2. Для данной свободной клетки строим цикл пересчета. Для этого вставим в эту клетку знак «+» а остальные клетки цикла поочередно знаки «−» и «+».
Наименьшее из чисел в минусовых клетках равно 80. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках добавляется 80, а из чисел, находящихся в минусовых клентках вычитается это число.
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
Полагая α1=0, находим β2=3, β3=1, α3=-3, β1=0, α2=-3, β4=-2
Для каждой свободной клетки вычисляем число αij=βj−αi−cij. α11=-2, α14=-4, α22=2, α23=-1, α33=1, α34=-3.
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
Среди чисел αij есть положительные. Следовательно данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки A2 и столбца B2. Для данной свободной клетки строим цикл пересчета. Для этого вставим в эту клетку знак «+» а остальные клетки цикла поочередно знаки «−» и «+».
Наименьшее из чисел в минусовых клетках равно 20. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках добавляется 20, а из чисел, находящихся в минусовых клентках вычитается это число.
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
Полагая α1=0, находим β2=3, β3=1, α2=-1, β1=2, β4=0, α3=-1
Для каждой свободной клетки вычисляем число αij=βj−αi−cij. α11=0, α14=-2, α23=-3, α32=-2, α33=-1, α34=-3.
Среди чисел αij нет положительных. Следовательно данный опорный план является оптимальным.
Ответ. Оптимальный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
7. Метод дифференциальных рент
При нахождении решения транспортной задачи методом дифференциальных рент сначала распределяем часть груза наилучшим образом между пунктами назначения и получаем так называемое условно оптимальное распеделение. На последующих итерациях уменьшаем общий объем нераспределенных поставок. Для решения транспортной задачи методом дифференциальных рент в онлайн режиме с подробными пояснениями пользуйтесь калькулятором метод дифференциальных рент онлайн.
Начальное распределение груза определяется следующим образом. Для каждого столбца определяем минимальный тариф и заключаем в квадрат. Клетки с тарифами в квадратах заполняем максимально возможными числами. В результате получим некоторое распределение поставок груза в пункты назначения. Это распределение в общем случае не удовлетворяет ограничениям транспортной задачи. Далее шаг за шагом нужно постепенно сокращать нераспределенные поставки груза так, чтобы общая стоимисть перевозки оставалась минимальным. Для этого определяем избыточные и недостаточные строки.
Определение 7.1. Строки, соответствующие пунктом отправления, запасы которых полностью распределены а среди пунктов назначения, связанные с этим распределением есть неудовлетворенные потребности называются недостаточными или отрицательными.
Определение 7.2. Строки, запасы которых не распределены полностью называются избыточными или положительными.
После определения недостаточных и избыточных строк, в дополнительном столбце записываем величину избытка или недостатка. Избыток записывается со знаком «+», а недостаток со знаком «-«.
В случае избытка для данной строки в дополнительном столбце записываем разность между запасом груза данного пункта отправления и суммой всех поставок данной строки. Если же данная строка недостаточная, то определяем общий объем поставок, которая недостает для удовлетворения всех потребностей пунктов назначения, связанных с данным распределением груза.
После определения избыточных и недостаточных строк, для каждого столбца находим разности между числом в квадрате и ближащим к нему тарифом, записанным в избыточной строке. Если число в квадрате стоит в избыточной строке, то разность не определяем. Все разности записываем в дополнительной строке. Среди этих разностей находим наимельшее. Это число называется промежуточной рентой. Далее переходим к новой таблице. Эта таблица получается из предыдущей таблицы прибавлением промежуточной ренты к соответствующим тарифам, стоящим в недостаточных строках. Остальные элементы оставляем прежними. Все клетки новой таблицы считем свободными и начинаем их заполнять. В новой таблице число заполненных клеток на одну больше, чем в предыдущей таблице. Эта клетка находится в столбце с промежуточной рентой.
Так как число заполненных клеток больше, чем столбцов, то при заполнении следует соблюдать специальное правило, которое состоит в следующем.
Выбираем некоторый столбец (строку), в котором имеется одна клетка с помещенным в ней квадратом. Эту клетку заполняем и исключаем из рассмотрения данный столбец (строку). После этого берем некоторую строку (столбец), в котором имеется одна клетка с помещенным в ней квадратом. Эту клетку заполняем и исключаем из рассмотрения данную строку (столбец). Продолжая так, после конечного числа шагов заполняем все клетки, в которых помещены квадраты с записанными в них числами.
Если удается распределить весь груз в пунктах отправления между пунктами назначения, то получаем оптимальный план. В противном случае переходим к новой таблице. Для этого находим извыточные и недостаточные строки, прмежуточную ренту и на основе этого строим новую таблицу.
При определении избыточности или недостаточности строк могут возникнуть трудности когда ее нераспределенный остаток равен нулю. Этот вопрос мы рассмотрим ниже на конкретном примере.
После конечного числа итераций распределенный остаток станет равным нулю. В результате получим оптимальный план данной транспортной задачи.
Пример. Найти решение транспортной задачи представленной в таблице условий методом дифференциальных рент:
Решение. Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы. Тарифы перевозок единицы груза из каждого пункта отправления во все пункты назначения задаются матрицей
Наличие груза у поставщиков равно:
Общая потребность в грузе в пунктах назначения равна:

Найдем оптимальный план транспортной задачи методом дифференциальных рент.
Итерация 1:
В каждом из столбцов таблицы находим минимальные тарифы и заключаем в рамки. Если в каком-либо столбце окажется несколько одинаковых минимальных тарифов, то выбираем какой-нибудь из них, причем неважно какой. Заполняем клетки, в которых стоят указанные числа. Сначала находим те столбцы (строки) в которых есть только одна клетка для заполнения. Заполнив ее, исключаем из рассмотрения данный столбец (строку) и переходим к заполнению следующей клетки.
Последовательность заполнения клеток следующее: A1B1, A3B2, A2B3, A2B4.
В результате заполнения отмеченных клеток получен условно оптимальный план.
После получения условно оптимального плана определяем избыточные и недостаточные строки. Строка A1 является недостаточной, поскольку запасы пункта отправления A1 распределены полностью, а потребности пункта назначения B1 удовлетворены частично. При этом величина недостатка равна 20. Строка A3 является недостаточной, поскольку запасы пункта отправления A3 распределены полностью, а потребности пункта назначения B2 удовлетворены частично. При этом величина недостатка равна 20. Строка A2 является избыточным, поскольку запасы пункта отправления A2 распределены не полностью. При этом величина избытка этой строки равна 40.
Нераспределенный остаток равен 40. Суммарный объем поставок равен 150.
После определения избыточных и недостаточных строк, по каждому из столбцов находим разности между минимальными тарифами, записанными в избыточных строках, и тарифами, стоящими в заполненных клетках.
В столбце 1 минимальный тариф в избыточных строках равно 4 а число стоящее в рамке равно 2. Cледовательно, разность для данного столбца равна 4−2=2. В столбце 2 минимальный тариф в избыточных строках равно 3 а число стоящее в рамке равно 2. Cледовательно, разность для данного столбца равна 3−2=1. Для столбца 3 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке. Для столбца 4 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке.
Избыточные и недостаточные оценки помещаем в дополнительный столбец, а разности в дополнительную строку:
Выбираем наименьшую из найденных разностей, которая является промежуточной рентой. В данном случае промежуточная рента равна 1 и находится в столбце B2. Далее переходим к следующей таблице. В этой таблице в строках (являющихся избыточными) переписываем соответствующие тарифы из предыдущей таблицы, а тарифы недостаточных строках получаются в результате прибавления к ним величину промежуточной ренты, т.е. 1.
Итерация 2:
В каждом из столбцов таблицы находим минимальные тарифы и заключаем в рамки. Заполняем клетки, в которых стоят указанные числа. Сначала находим те столбцы (строки) в которых есть только одна клетка для заполнения. Заполнив ее, исключаем из рассмотрения данный столбец (строку) и переходим к заполнению следующей клетки.
Последовательность заполнения клеток следующее: A1B1, A2B3, A2B4, A2B2, A3B2.
В результате заполнения отмеченных клеток получен условно оптимальный план.
После получения условно оптимального плана определяем избыточные и недостаточные строки. Строка A1 является недостаточной, поскольку запасы пункта отправления A1 распределены полностью, а потребности пункта назначения B1 удовлетворены частично. При этом величина недостатка равна 20. Строка A3 является избыточным, поскольку запасы пункта отправления A3 распределены не полностью. При этом величина избытка этой строки равна 20.
Нераспределенный остаток равен 20. Суммарный объем поставок равен 170.
Избыточные и недостаточные оценки помещаем в дополнительный столбец.
Определяем положительность или отрицательность нулевой строки A2. Для этого запасы этой строки увеличиваем на 1 и снова заполняем таблицу. Если суммарный объем поставок не изменится, то строка положительная, в противном случае − отрицательная.
Последовательность заполнения клеток следующее: A1B1, A2B3, A2B4,A2B2, A3B2:
Суммарный объем поставок не изменился (170). Следовательно строка A2 избыточна (положительна).
После определения избыточных и недостаточных строк, по каждому из столбцов находим разности между минимальными тарифами, записанными в избыточных строках, и тарифами, стоящими в заполненных клетках.
В столбце 1 минимальный тариф в избыточных строках равно 4 а число стоящее в рамке равно 3. Cледовательно, разность для данного столбца равна 4−3=1. Для столбца 2 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке. Для столбца 3 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке. Для столбца 4 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке.
Выбираем наименьшую из найденных разностей, которая является промежуточной рентой. В данном случае промежуточная рента равна 1 и находится в столбце B1. Далее переходим к следующей таблице. В этой таблице в строках (являющихся избыточными) переписываем соответствующие тарифы из предыдущей таблицы, а тарифы недостаточных строках получаются в результате прибавления к ним величину промежуточной ренты, т.е. 1.
Итерация 3:
В каждом из столбцов таблицы находим минимальные тарифы и заключаем в рамки. Заполняем клетки, в которых стоят указанные числа. Сначала находим те столбцы (строки) в которых есть только одна клетка для заполнения. Заполнив ее, исключаем из рассмотрения данный столбец (строку) и переходим к заполнению следующей клетки.
Последовательность заполнения клеток следующее: A2B3, A2B4, A1B1, A2B1, A3B1,A2B2, A3B2.
В результате заполнения отмеченных клеток получен условно оптимальный план. После получения условно оптимального плана определяем избыточные и недостаточные строки.
Посмотрев на таблицу выше мы видим, что избыточных и недостаточных строк нет. Нераспределенный остаток равен 0. Суммарный объем поставок равен 190. Все имеющие запасы распределены в соответствии фактическими потребностями пунктов назначения. Следовательно получен оптимальный план.
Ответ.
Оптимальный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
 |
В данной статье разберемся с решением транспортной задачи. Все действия будем выполнять пошагово с очень подробными пояснениями. Дадим определение, аналогичное тому, которое дано в ваших учебниках или лекциях. Определение:Транспортная задача — это математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов с минимизацией затрат на перемещение. |
Чтобы не загромождать страницу большим объемом пояснений, разобью весь материал на несколько частей — блоков.
Ну, начнем! Далее Вводная часть, с которой желательно ознакомиться.
Вводная часть, с которой желательно ознакомиться
Существует несколько методов решения транспортной задачи. Мы будем подробно рассматривать два из них:
- решение транспортной задачи методом потенциалов (рассмотрен в данной статье)
- решение транспортной задачи с использованием симплекс метода.
Решение задачи методом потенциалов происходит в несколько этапов:
- Определение опорного решения.
- Применение к найденному опорному решению самого метода потенциалов.
- Проверка единственности решения.
Определение опорного плана, в свою очередь, можно выполнить несколькими способами. Мы рассмотрим два из них:
- метод северо-западного угла
- метод минимальных стоимостей
(не путать с методами решения самой транспортной задачи!!!)
О чем говорится в определении транспортной задачи?
У нас есть некоторый груз, который находится на складах: склад 1, склад 2, …, склад — это пункты отправления.
Этот груз нам необходимо развести по магазинам: магазин 1, магазин 2, …, магазин k — это пункты назначения.
Нам выгоднее как можно эффективнее выполнить работу, т.е. найти такой вариант перевозки, при котором затраты будут минимальными.
Рассмотрим пример решения транспортной задачи подробно.
Транспортная задача задается следующей таблицей:
Далее, что означают числа в условии транспортной задачи?
Что означают числа в условии транспортной задачи?
Рассмотрим постановку транспортной задачи, т.е. что дано в условии и переведем ее с математического языка на язык, понятный нам.
Это наши «склады» — пункты отправления: два склада с товаром: А1 и А2
Это объем товара — количество груза, соответственно на складах А1 и А2:
Далее имеем дело с пунктами назначения — с «магазинами». В нашем случае их 4 штуки: В1, В2, В3 и В4.
И соответственно потребности каждого из магазинов — потребности пунктов назначения:

Числа внутри таблицы — матрица стоимостей, или по другому, расценки перевозки 1 единицы груза из соответствующих пунктов. Эти значения также могут интерпритироваться как расстояния между соответствующими пунктами. Подробности — в условии решаемой задачи.

Например, для перевозки 1 единицы груза из пункта отправления («склада») А2 в пункт назначения («магазин») В3 надо заплатить 4 условные единицы стоимости, например 4 руб.

Аналогично, мы заплатим 6 рублей за перевозку 1 единицы груза из «склада» А1 в «магазин» В4.

Или та же самая задача может быть задана сразу в более понятном виде:

Возможна текстовая постановка задачи. В этом случае необходимо самим заполнять все ячейки таблицы, исходя из заданных в условии значений.
Далее — Методы определения первоначального плана транспортной задачи.
Методы определения первоначального плана транспортной задачи.
Рассмотрим самый распространенный метод получения опорного плана — метод северо-западного угла.
Называется он так потому, что заполнение таблицы начинается с самой верхней левой (северо-западной) ячейки.
Перед тем, как распределять ресурсы по «магазинам», проверим, равны ли общие потребности имеющимся ресурсам?
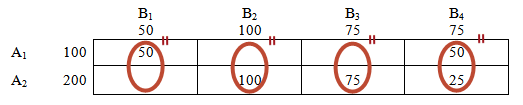
Потребности: 50 + 100 + 75 + 75 = 300
Ресурсы: 100 + 200 = 300
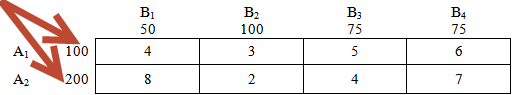
Потребности = Ресурсам
В этом случае говорят, что транспортная задача закрытая. Решение открытой транспортной задачи рассмотрим чуть позже.
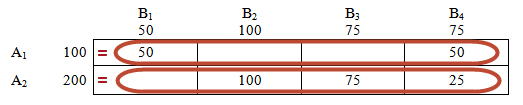
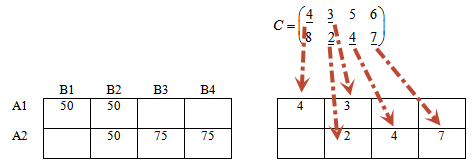
Начнем нахождение опорного решения:
Заполним клетку (1;1).
В магазин В1 требуется 50 единиц товара. Со склада А1 отправим в этот магазин 50 единиц.
Потребности магазина В1 выполнены, следовательно, нет необходимости везти туда груз со склада А2.
На складе А1 еще осталось 50 единиц груза. Эти остатки можем направить в магазин В2. Ресурсы склада А1 исчерпаны.
Переходим к складу А2.
Так как потребности магазина В1 выполнены полностью, рассмотрим магазин В2, которому требуется 100-50=50 единиц товара. Направим их туда.

Заметим, на складе А2 осталось еще 200-50=150 единиц груза, которые мы распределим по магазинам В3 и В4, полностью удовлетворяя и их потребности.
Склады пусты!
Потребности магазинов в товаре полностью выполнены!
Получен опорный (первоначальный) план транспортной задачи.

Рассмотрели северо-западный метод построения первоначального плана (опорного решения).
Далее опишем метод минимальных стоимостей получения опорного плана.
Метод минимальных стоимостей получения опорного плана
Суть метода состоим в том, чтобы в первую очередь направлять груз в те пункты, где «расценки» в матрице стоимостей минимальны. Если клеток с наименьшими тарифами несколько, то заполняется любая из них.

Направляем 100 единиц груза из склада А2 в магазин В2.
Остатки на складе А2 — 100 единиц. Потребности магазина В2 выполнены.
Груз со склада А2 отправим в магазин, у которого стоимость перевозки ниже — магазин В3, так как мин(4;7)=4
Размер поставки равен потребности магазина — 75. Остатки со склада 200-100-75=25 перенесем в магазин В4.

Остается только раскидать груз со склада А1 по магазинам: В1 — 50 единиц, В4 — 75-25=50 единиц.
Получили два опорных плана: методом северо-западного угла и методом минимальных стоимостей.
Первый опорный план (по методу северо-западного угла):
Второй опорный план (по методу минимальных стоимостей):
Далее проверим правильность вычисления первоначального плана.
Проверка правильности вычисления первоначального плана
Перед тем как перейти к дальнейшему решению задачи проверим условие:
Правило:
Количество заполненных клеток (базисных клеток) в первоначальном плане ВСЕГДА должно быть равно m + n — 1, где m — количество строк, n — количество столбцов
В нашем случае условие выполняется: 2 + 4 — 1 = 5
Что же делать, если количество заполненных ячеек меньше необходимого?
Подробно об этом с разбором примеров в статье Вырожденность опорного плана транспортной задачи. Как избавиться?
Во избежании случайных вычислительных ошибок проверим, равны ли суммарные значения каждой строки и каждого столбца соответствующим значениям условия.
100 = 50 + 50
200 = 100 + 75 + 25
По столбцам:
Видим, суммарные значения элементов каждого столбца равны соответствующим потребностям магазинов.
Несмотря на то, что опорные планы разные, оба приведут к одному оптимальному решению или же к решениям, имеющим одну стоимость перевозки.
Далее применим метод потенциалов к обоим опорным планам и сравним получившиеся ответы.
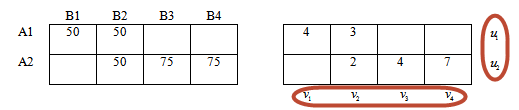
Метод потенциалов решения транспортной задачи — шаг 1.
Описанную ниже последовательность действий будем повторять несколько раз, с каждым шагом приближаясь к оптимальному решению. Начнем с проверки опорного плана на оптимальность.
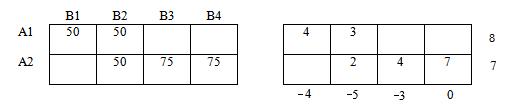
Выпишем матрицу стоимостей, данную в условии задачи.
Далее строим рядом две таблицы. Размерность таблиц как и в матрице стоимостей:
количество строк = количеству складов, количество столбцов = количеству магазинов.
Заполняем первую — левую таблицу в соответствии с полученным опорным планом.

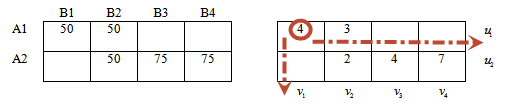
Переходим в правую таблицу.
Переносим из матрицы стоимостей значения, которые соответствуют занятым клеткам левой таблицы.
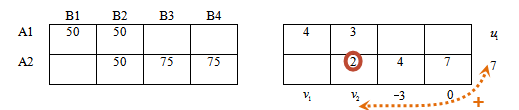
В матрице стоимости эти значения подчеркнуты.
Припишем каждой строке правой таблице потенциалы u1, u2. Каждому столбцу — потенциалы v1, v2, v3, v4.
Для вычисления этих потенциалов в некоторых учебниках составляют систему и из нее определяют неизвестные (покажу на данном шаге).
Мы будем определять значения потенциалов непосредственно из правой таблицы.
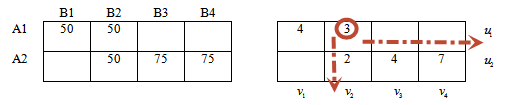
Составим систему уравнений по следующему правилу:
Каждое из значений в ячейке (правая таблица) равно сумме потенциалов соответствующей строки и соответствующего столбца.
Например: значение 4 находится в 1-й строке и 1-м столбце. Тогда сумма потенциалов 1-й строки (u1) и 1-ого столбца(v1) равна 4.
Первое уравнение системы: u1 + v1 = 4
Рассмотрим следующее значение таблицы.
Значение 3 находится в первой строке (потенциал u1), втором столбце (потенциал v2).
Второе уравнение системы: u1 + v2 = 3
Аналогично для каждого значения таблицы составим уравнение.
Получим систему уравнений:
Для того, чтобы система имела единственное решение, примем значение одного из потенциалов равным нулю.
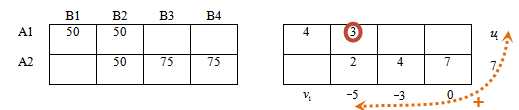
Для удобства в качестве этого потенциала всегда будем брать v4.
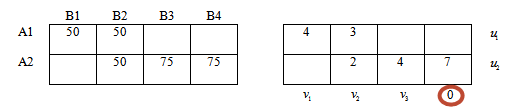
Тогда система уравнений будет выглядеть:
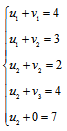
Решим систему уравнений и получим значения потенциалов:
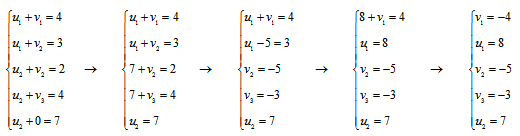
Наглядно:

Так как система очень проста, то значения потенциалов можно получить и устно.
Покажем подробно:
Сумма отмеченных потенциалов равна 7, следовательно, потенциал u2 = 7
Значение 4 базисной ячейки находится во 2-й строке, 3-м столбце, тогда рассмотрим сумму соответствующих потенциалов.
v3 + 7 = 4 откуда v3 = -3
Далее все аналогично:
Значение 2 равно сумме потенциалов 2-й строки и 2-го столбца:
2 = v2 + 7 откуда v2 = -5
u1 — 5 = 3, откуда u1 = 8
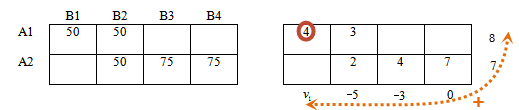
v1 + 8 = 4, откуда v1 = -4
В итоге получили:
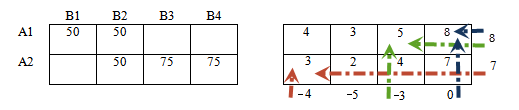
Далее приступим к заполнению пустых ячеек (свободные ячейки) правой таблицы.
Свободные ячейки подчиняются тому же правилу суммирования потенциалов.
Вычислим оценочную матрицу, по которой узнаем, оптимален ли рассматриваемый план.
Из каждого элемента матрицы стоимостей вычтем соответствующий элемент правой таблицы:
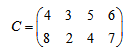 |
— |  |
= |  |
Получили оценочную матрицу. Заметим, что в базисных ячейках всегда получим нули.
Критерий оптимальности:
если в оценочной матрице нет отрицательных элементов, то решение оптимально, в противном случае решение не оптимально.
Согласно критерию оптимальности, решение выше не оптимально, так как в оценочной таблице присутствует отрицательное значение.
Дабы не загромождать решение множеством таблиц, оценочная матрица в нашем решении будет «вписана» в правую таблицу.
Подчеркнутые значения — базисные ячейки, как сказано выше, значения оценочной матрицы в базисных ячейках равны нулю, нули писать не будем. Выделенные значения — значения оценочной матрицы в свободных ячейках, среди них ищем отрицательные значения.
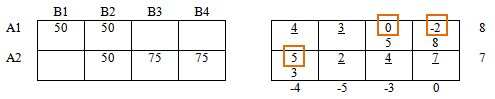
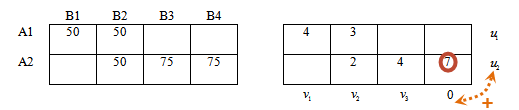
Для перехода к следующему опорному решению выполним следующее (построим цикл пересчета):
— найдем среди отрицательных значений оценочной матрицы максимальный по модулю (или по другому, минимальный среди отрицательных)
— в соответствующей ячейке левой таблицы ставим знак » + «
В нашем примере наименьшее отрицательное значение -2.
Знак » + » ставим в ячейке 1-й строки, 4-го столбца левой таблицы — ячейка соответствующая значению (-2).
Необходимо расставить чередующиеся значения «+ » и » — » в левой таблице так, чтобы получился замкнутый цикл и выполнялись правила:
— остальные знаки цикла (все кроме уже поставленного первого » + «) ставим только в заполненных (базисных) ячейках таблицы,
— если в строке есть «плюс» («минус»), то в этой строке должен быть и «минус» («плюс»),
— если в столбце есть » плюс» («минус»), то в этом столбце должен быть и «минус» («плюс»).
Применим к нашей таблице:
В столбце В4 есть «плюс», следовательно в этом столбце должен быть и «минус».
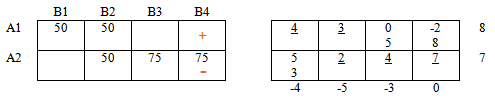
Аналогично, в строке А2 есть «минус», следовательно должен быть и «плюс».
Если мы поставим этот «плюс» в столбце В3, то цепочка порвется, так как в этом же столбце невозможно поставить «минус» — нет заполненной ячейки.
Ставим » + » в столбце В2 и продолжаем чередовать знаки.
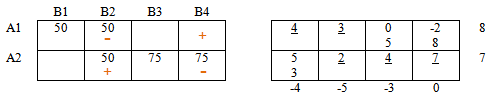
Получили замкнутый цикл чередующихся знаков. Цикл пересчета найден!
Далее обратимся к ячейкам, содержащим «минусы». Среди значений этих ячеек найдем минимальное: Δ = мин {50;75} = 50
К «плюсам» прибавим найденное Δ = 50, в ячейках с «минусами» — вычтем Δ = 50.
Ячейка, в которой находилось значение Δ = 50 останется пустой. В ячейке в которой мы поставили первый плюс появится значение, равное Δ = 50.
Общее количество заполненных (базисных) ячеек при пересчете не должно изменится!
Получили следующий опорный план:
Вычислим стоимость перевозки на первом шаге.
Для этого найдем сумму произведений значений опорного плана и матрицы стоимостей.
S1 = 50 · 4 + 100 · 2 + 75 · 4 + 25 · 7 + 50 · 6 = 1275
На первом шаге решения транспортной задачи получили опорный план:

Общая стоимость перевозки S1 = 1275
Метод потенциалов — шаг 2
Алгоритм проверки плана на оптимальность и построение цикла пересчета очень подробно расписан в шаге 1.
Далее решение задачи будем излагать менее детально.
Для полученного опорного решения строим вспомогательную — правую таблицу и заполняем значениями из матрицы стоимостей базисные ячейки.
Вычисляем потенциалы строк и столбцов:
По правилу суммирования соответствующих потенциалов, заполняем свободные ячейки.
Вычисляем оценочные значения в свободных ячейках.
Для этого из значений матрицы стоимостей вычитаем найденные значения соответствующих свободных ячеек.
Среди оценочных значений нет отрицательных, следовательно план перевозки оптимален.
Получили оптимальный план. Итоговая стоимость перевозки S1 = 1275
Примеры решения транспортных задач:
Закрытая транспортная задача размерностью 2х2
Закрытая транспортная задача размерностью 3х4
Закрытая транспортная задача размерностью 2х3
Закрытая транспортная задача размерностью 4х5

Глава2 ТРАНСПОРТНАЯ ЗАДАЧА
Под транспортной задачей в дальнейшем понимается задача линейного программирования, в которой требуется найти оптимальный (по стоимости) план перевозок некоторого однородного груза от конечного числа поставщиков A1, A2 , , Am с заданными запасами
a1, ,am к конечному числу потребителей B1, B2 , , Bn с потребностями b1, ,bn . Стоимость cij перевозки единицы груза от поставщика Ai к потребителю Bj предполагается известной.
Отметим, что данная постановка задачи может быть значительно расширена или изменена. Например, в приложениях часто рассматриваются задачи перевозки неоднородного груза. Также в качестве критерия оптимальности можно рассматривать время перевозок (транспортная задача по критерию времени). Подобного рода задачи решаются сведением к однородной транспортной задаче, или для них разработаны другие методы, изложение которых остается за рамками данной книги.
§ 2.1. Постановка задачи
Итак, пусть X =(xij ) – m ×n матрица, где xij – объем перевозок от i -го поставщика к j -му потребителю. Тогда общие затраты на пе-
|
m |
n |
|
|
ревозку груза определяются функцией |
z(X ) = ∑∑cij xij . Математиче- |
|
|
i=1 |
j=1 |
ская постановка транспортной задачи определяется следующей задачей линейного программирования
m n
z(X ) = ∑∑cij xij → min
i=1 j=1
при условиях
23
|
∑xij =bj , |
j =1, ,n, |
||
|
m |
|||
|
i=1 |
|||
|
n |
i =1, ,m, |
(2.1) |
|
|
∑xij = ai , |
|||
|
j=1 |
|||
|
x |
≥ 0. |
||
|
ij |
|||
Первая часть нетривиальных ограничений означает, что все потребности удовлетворены, вторая часть – то, что весь груз вывезен от поставщиков.
Замечание 2.1. Если запасы и потребности задаются целыми числами, то транспортная задача имеет целочисленное оптимальное решение, поэтому транспортную задачу относят формально к задачам целочисленного линейного программирования.
Можно показать, что число базисных переменных в системе ограничений (2.1) равно m + n −1.
|
Поставщики |
Потребители |
Запасы |
|||||||||
|
B1 |
B2 |
… |
Bj |
… |
Bn |
||||||
|
A1 |
c11 |
c12 |
… |
c1 j |
… |
c1n |
a1 |
||||
|
x11 |
x12 |
x1 j |
x1n |
||||||||
|
A |
c |
с |
… |
с |
… |
c |
a |
||||
|
2 |
21 |
22 |
2 j |
2n |
2 |
||||||
|
x21 |
x22 |
x2 j |
x2n |
||||||||
|
… |
… |
… |
… |
… |
… |
… |
… |
||||
|
Ai |
ci1 |
ci2 |
… |
cij |
… |
cin |
ai |
||||
|
xi1 |
xi2 |
xij |
xin |
||||||||
|
… |
… |
… |
… |
… |
… |
… |
… |
||||
|
Am |
cm1 |
cm2 |
… |
cmj |
… |
cmn |
am |
||||
|
xm1 |
xm2 |
xmj |
xmn |
||||||||
|
Потребности |
b1 |
b2 |
… |
bj |
… |
bn |
|||||
|
Таблица 2.1 |
Определение 2.1. Решение X =(xij ) (оптимальное решение X * =(xij* )) транспортной задачи, удовлетворяющее условиям (2.1) и
имеющее не более m + n −1 занятой клетки (ненулевой перевозки), бу-
дем называть опорным планом (оптимальным опорным планом)
транспортной задачи.
Исходные данные задачи представляют в виде таблицы 2.1.
m
Общие запасы определяются суммой ∑ai , а общая потребность –
i=1
24
n
∑bj . Транспортная задача называется задачей с правильным балан-
j=1
|
m |
n |
|
|
сом, а ее модель закрытой, если ∑ai |
= ∑bj , то есть суммарные запа- |
|
|
i=1 |
j=1 |
|
|
сы |
поставщиков равны суммарным |
запросам потребителей. Если |
|
m |
n |
|
|
∑ai ≠ ∑bj , то такая задача называется задачей с неправильным ба- |
||
|
i=1 |
j=1 |
лансом, а ее модель – открытой.
§ 2.2. Построение начального опорного плана транспортной задачи
Алгоритм решения транспортной задачи с правильным балансом излагается в курсе «Линейная алгебра». В этом параграфе мы напомним основные методы построения начального опорного плана и метод потенциалов решения транспортной задачи.
Первым этапом решения является построение начального опорного плана, т.е. плана перевозок, удовлетворяющего всем ограничениям конкретной транспортной задачи. Сущность методов состоит в том, что начальный опорный план находят за не более чем m + n −1 шагов (по числу базисных переменных), на каждом из которых в транспортной таблице заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз
груза из одного из пунктов
|
B1 |
B2 |
B3 |
B4 |
ai |
|
|
A1 |
1 |
11 |
3 |
13 |
140 |
|
A2 |
12 |
4 |
8 |
2 |
160 |
|
A3 |
3 |
5 |
14 |
6 |
100 |
|
bj |
80 |
40 |
150 |
130 |
400 |
|
Таблица 2.2 |
оптимального.
отправления (из того, в строке которого находится заполняемая клетка). Различаются эти планы по принципам выбора заполняемых клеток и, в зависимости от этого, могут давать планы,
более или менее отличные от
Пример 2.1. Рассмотрим транспортную задачу, заданную таблицей 2.2. В правом нижнем углу стоит сумма запасов (и, одновременно, сумма потребностей, так как модель закрытая)
140+160+100=80+40+ +150+ 130=400.
25
|
Напомним |
сначала |
метод северо-западного |
угла. Заполнение |
|||||||
|
таблицы начинаем с левого |
||||||||||
|
B1 |
B2 |
B3 |
B4 |
ai |
верхнего (северо-западного) |
|||||
|
A1 |
1 |
40 |
11 |
3 |
13 |
140 |
угла таблицы. Так как по- |
|||
|
80 |
20 |
|||||||||
|
требности первого потреби- |
||||||||||
|
A2 |
12 |
4 |
8 |
2 |
160 |
|||||
|
теля В1 равны 80, а запасы |
||||||||||
|
130 |
30 |
|||||||||
|
A3 |
3 |
5 |
14 |
6 |
100 |
первого поставщика A1 |
рав- |
|||
|
100 |
ны 140, то в клетку |
A1B1 |
||||||||
|
bj |
80 |
40 |
150 |
130 |
400 |
|||||
|
вписываем |
максимально |
|||||||||
|
Таблица 2.3 |
возможную перевозку |
80. |
||||||||
|
Потребности В1 |
полностью удовлетворены, поэтому первый столбец |
исключаем из рассмотрения, а оставшиеся запасы первого поставщика, т.е. 60, переносим следующим потребителям. Мы можем 40 записать потребителю В2 (столбец В2 исключается), а оставшиеся 20 – В3
и исключить первую строку из дальнейшего рассмотрения.
Далее, так как потребности В3 равны 150, а 20 единиц груза ему
уже доставлены, то оставшиеся 130 единиц доставляются от второго поставщика A2 (заполняем клетку A2B3 ) . С толбец В3 исключаем из
рассмотрения, а оставшиеся запасы второго поставщика (30 единиц) записываем потребителю В4 . Окончательно потребности последнего
удовлетворяются за счет поставщика A3 : вписываем в клетку A3B4 пе-
ревозку 100. Заметим, что, так как исходная задача — с правильным балансом, то потребности последнего потребителя B4 равны запасам по-
ставщика A3 , т.е. 100. Получаем таблицу 2.3 с начальным опорным планом
|
80 |
40 |
20 |
0 |
||
|
0 |
0 |
130 |
30 |
||
|
X = |
. |
||||
|
0 |
0 |
0 |
100 |
||
Суммарная стоимость перевозок равна
z(X ) =1 80 +11 40 +3 20 +8 130 + 2 30 +6 100 = 2280.
Из решения видно, что метод северо-западного угла, с одной стороны, достаточно прост с точки зрения построения, а с другой стороны, не учитывает стоимость перевозок. Поэтому опорный план, построенный методом северо-западного угла, как правило, далек от оптимального.
26

Построим теперь для этой же задачи начальный опорный план методом минимального тарифа. Суть этого метода состоит в том, что в клетки с наименьшими тарифами помещают максимально возможные перевозки. Итак, в таблице исходной задачи выбираем клетку с минимальным тарифом, т.е. клетку A1B1 с тарифом 1. Запасы постав-
щика A1 равны 140, а потребности В1 – 80, поэтому в клетку A1B1 вписываем максимально возможную перевозку 80, и потребителя В1 ис-
ключаем из рассмотрения. В оставшейся части таблицы выбираем минимальный тариф, т.е.
|
B1 |
B2 |
B3 |
B4 |
ai |
клетку A B с тарифом 2. За- |
||||
|
1 |
11 |
3 |
13 |
||||||
|
A1 |
140 |
2 |
4 |
||||||
|
80 |
60 |
пасы поставщика A2 |
равны |
||||||
|
A |
12 |
4 |
8 |
2 |
160 |
140, а потребности В4 |
— 130, |
||
|
2 |
30 |
130 |
поэтому в клетку A2B4 |
запи- |
|||||
|
A3 |
3 |
5 |
14 |
6 |
100 |
||||
|
10 |
90 |
сываем перевозку 130 и по- |
|||||||
|
bj |
80 |
40 |
150 |
130 |
400 |
требителя |
В |
исключаем из |
|
|
4 |
|||||||||
|
Таблица 2.4 |
рассмотрения. |
У оставшихся |
потребителей В2 , В3 выбираем клетку с минимальным тарифом. Это A1B3 с тарифом 3. Запасы (оставшиеся) поставщика A1 равны 60, а по-
|
требности В3 – 150, поэтому в клетку |
A1B3 |
записываем максимально |
|||||
|
возможную перевозку 60 и исключаем поставщика A1 из дальнейшего |
|||||||
|
рассмотрения. Далее, аналогично в клетку |
A2B2 записываем 30 и ис- |
||||||
|
ключаем второго поставщика. |
|||||||
|
В оставшиеся две клетки A3B2 |
и A3B3 |
последовательно вписыва- |
|||||
|
ем перевозку 10 в A3B2 |
и 90 в A3B3 . Получаем таблицу 2.4 с начальным |
||||||
|
80 |
0 |
60 |
0 |
||||
|
опорным планом X = |
0 |
30 |
0 |
130 |
|||
|
. Суммарная стоимость пере- |
|||||||
|
0 |
10 |
90 |
0 |
||||
возок равна
z(X ) =1 80 +3 60 + 4 30 + 2 130 +5 10 +14 90 =1950 < 2280.
Таким образом, опорный план, построенный методом минимального тарифа, лучше, чем план, полученный методом северо-западного угла.
Применим, наконец, к исходной задаче метод аппроксимации Фогеля. Для этого найдем разность между двумя минимальными тарифами для каждой строки и столбца таблицы и запишем их в дополнительно образованные строки и столбцы (см. таблицу 2.5). В строке A1 минимальный тариф равен 1, а следующий за ним 3, поэтому раз-
ность между ними 4-2=2; в строке A2 минимальный тариф равен 2, а следующий за ним 4, поэтому разность между равна 2; аналогично,
27
для строки A3 разность между минимальным тарифом 3 и следующим
за ним 5 равна 2. Итак, три двойки записываем в первый дополнительный столбец.
Аналогично для столбцов разности 3-1=2, 5-4=1, 8-3=5 и 6-2=4 записываем в первую дополнительную строку. Теперь из всех разностей выбираем максимальную, т.е. 5 в столбце B3 , и в клетку A1B3 с
минимальным тарифом в этом столбце записываем максимально возможную перевозку 140. При этом поставщика A1 исключаем из рас-
смотрения. Теперь аналогично вычисляем разности между оставшимися минимальными тарифами и заполняем вторые дополнительные столбец и строку, не учитывая тарифы в строке A1 . Видим, что теперь
максимальная разность получается в столбце B1 и перевозку 80 записываем в клетку A3B1 с минимальным тарифом 3 в этом столбце (первую строку мы исключили из рассмотрения). Столбец B1 аналогично исключаем из рассмотрения. Как видно из таблицы, на следующем
|
B1 |
B2 |
B3 |
B4 |
ai |
Разности по строкам |
||||||||
|
A1 |
1 |
11 |
3 |
13 |
140 |
2 |
– |
– |
– |
– |
– |
||
|
140 |
|||||||||||||
|
A2 |
12 |
4 |
8 |
2 |
160 |
2 |
2 |
2 |
2 |
0 |
– |
||
|
20 |
10 |
130 |
|||||||||||
|
A3 |
3 |
5 |
14 |
6 |
100 |
2 |
2 |
1 |
1 |
0 |
0 |
||
|
80 |
20 |
||||||||||||
|
bj |
80 |
40 |
150 |
130 |
400 |
||||||||
|
2 |
1 |
5 |
4 |
||||||||||
|
9 |
1 |
6 |
4 |
||||||||||
|
Разности |
|||||||||||||
|
– |
1 |
6 |
4 |
||||||||||
|
по |
|||||||||||||
|
– |
1 |
– |
4 |
||||||||||
|
столбцам |
|||||||||||||
|
– |
1 |
– |
– |
||||||||||
|
– |
0 |
– |
– |
||||||||||
Таблица 2.5
шаге вписываем перевозку 10 в клетку A2B3 и исключаем столбец B3 , затем – максимально возможную перевозку 40 в клетку A2B4 и исключаем из рассмотрения столбец B4 . Теперь для вычисления дальнейших разностей остается единственный столбец B2 , поэтому в качестве разностей по строкам записываем нули. Далее, в клетку A2B2 записываем 20, а на последнем шаге записываем перевозку 20 в клетку A3B2 . По-
28
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #