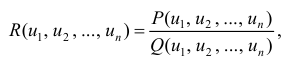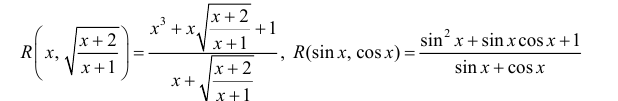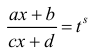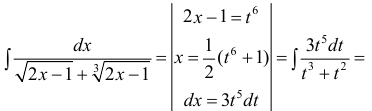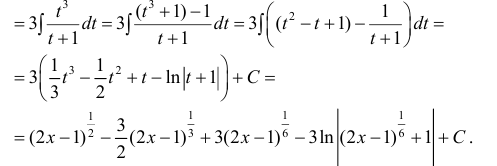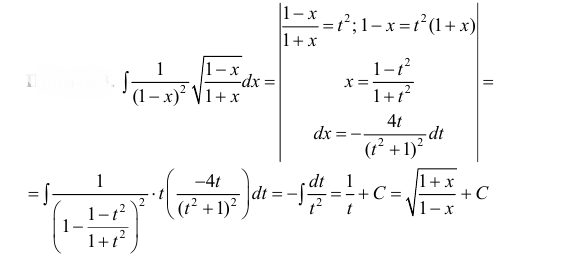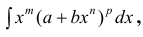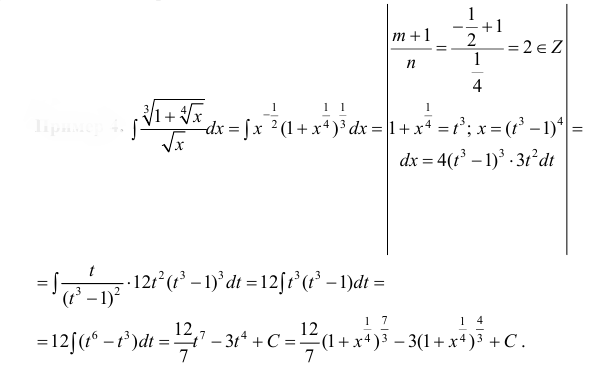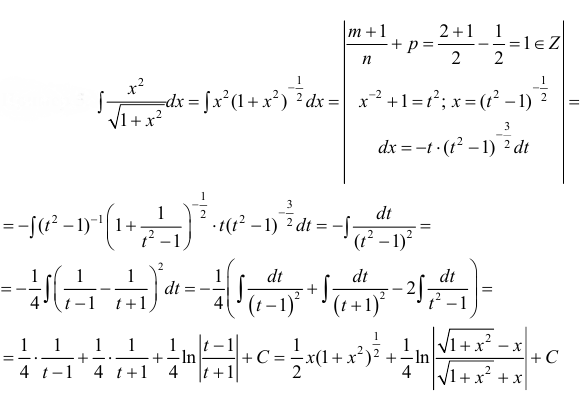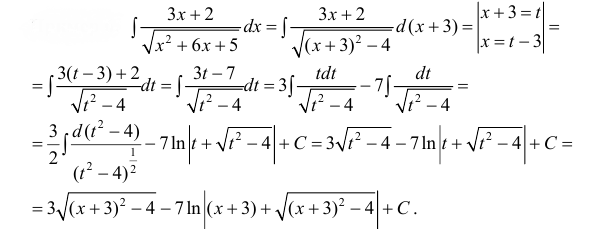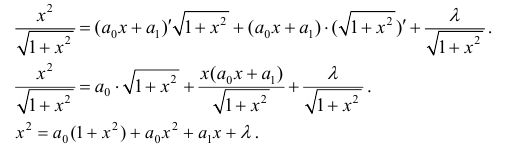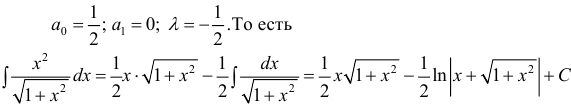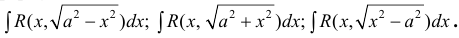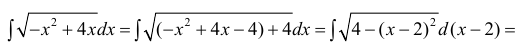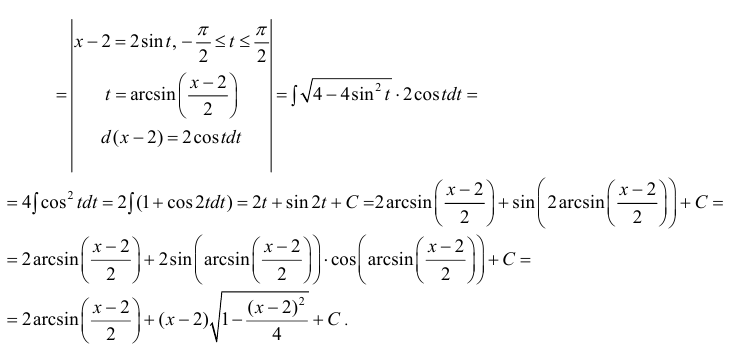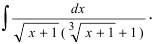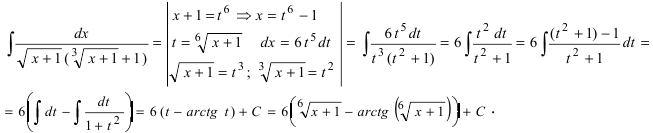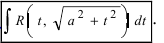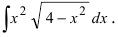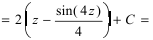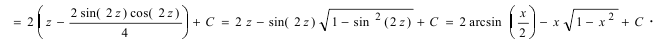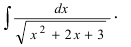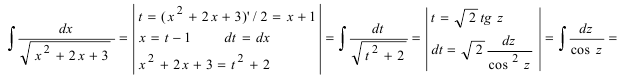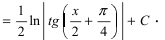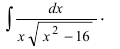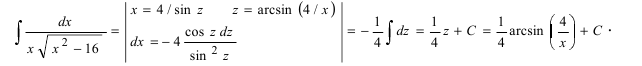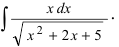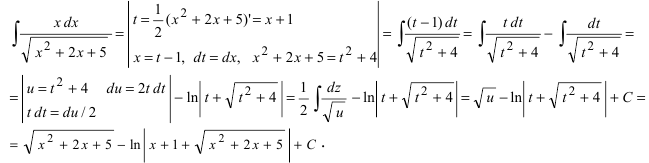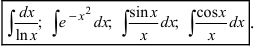Recall that for $alpha neq -1$, we have
$$int (ax+b)^{alpha}dx = dfrac1a cdot dfrac{(ax+b)^{alpha+1}}{alpha+1} + text{ constant}$$
A way to see the above is as follows. Let $y = ax+b$. We then have $dy = adx$. Hence for $alpha neq -1$,
$$int (ax+b)^{alpha}dx = int y^{alpha} dfrac{dy}a = dfrac1a dfrac{y^{alpha+1}}{alpha+1} + text{ constant} = dfrac1a dfrac{(ax+b)^{alpha+1}}{alpha+1} + text{ constant}$$
If $alpha = -1$, we then have
$$int dfrac{dx}{ax+b} = dfrac{log(ax+b)}a + text{ constant}$$
In general, there is no easy way to get $$int sqrt{P(x)} dx,$$ if degree of $P(x)$ is greater than $2$.
If $P(x)$ is linear, i.e., has degree $1$, I have mentioned above how to proceed.
Below we will see how to proceed if $P(x)$ is quadratic, i.e., $$P(x) = ax^2 + bx + c = a ((x+b_1)^2 + c_1).$$
$$b_1=frac{a}{2b}$$ $$c_1=frac{c}{a}-b_1^2$$
We now have the following
$$sqrt{P(x)} = sqrt{a} sqrt{(x+b_1)^2 pm c_1}$$
which gives us that
$$int sqrt{P(x)} dx = sqrt{a} int sqrt{(x+b_1)^2 + c_1} dx$$
and
$$int sqrt{(x+b_1)^2 + c_1} dx = dfrac{(b_1+x)sqrt{P(x)} + c_1 log left(b_1 + x + sqrt{P(x)}right)}2 + text{constant}$$
Интеграл от корня
Интеграл от корня в таблице интегрирования записан как: $$ int sqrt{x} dx = frac{2}{3}sqrt{x^3} + C $$
Словами это звучит как интеграл от корня равен две трети от квадратного корня из икс в кубе плюс постоянная. Далее в примере сделаем вывод данной формулы с помощью интегрирования показательной функции.
| Пример 1 |
| Найти интеграл корень из икс: $ int sqrt{x} dx $ |
| Решение |
|
Вспомним, что такое квадратный корень. Это степень $frac{1}{2}$ при $ x $. Записывается следующим образом: $$ sqrt{x} = x^{frac{1}{2}} $$ Подставляем в интеграл эту формулу и интегрируем уже как показательную функцию по правилу: $$ int x^{p} dx = frac{x^{p+1}}{p+1} + C $$ $$ int sqrt{x} dx = int x^{frac{1}{2}} dx = frac{x^{frac{1}{2}+1}}{frac{1}{2}+1} + C = $$ $$ = frac{x^{frac{3}{2}}}{frac{3}{2}} + C = frac{2}{3} x^frac{3}{2} + C = frac{2}{3} sqrt{x^3} + C $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ int sqrt{x} dx = frac{2}{3}sqrt{x^3} + C $$ |
Содержание:
- Формула
- Примеры вычисления интеграла корня
Формула
$$int frac{d x}{sqrt{x}}=2 sqrt{x}+C$$
Интеграл от единицы, деленной на корень, равен двум таким же корням плюс константа интегрирования.
$$int sqrt{x} d x=frac{2}{3} sqrt{x^{3}}+C$$
Заметим, что данные формулы сводятся к
интегралу от степенной функции при помощи следующих свойств:
$sqrt[m]{x^{n}}=x^{frac{n}{m}}$ и $frac{1}{x^{n}}=x^{-n}$
Примеры вычисления интеграла корня
Пример
Задание. Найти неопределенный интеграл $int frac{d x}{2 sqrt{x}}$
Решение. Согласно
свойствам неопределенного интеграла, константу можно выносить за знак интеграла, то есть получим:
$$int frac{d x}{2 sqrt{x}}=frac{1}{2} int frac{d x}{sqrt{x}}$$
А тогда, согласно формуле, будем иметь:
$$int frac{d x}{2 sqrt{x}}=frac{1}{2} int frac{d x}{sqrt{x}}=frac{1}{2} cdot 2 sqrt{x}+C=sqrt{x}+C$$
Ответ. $int frac{d x}{2 sqrt{x}}=sqrt{x}+C$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание.$int 2 sqrt{x} d x$
Решение. Константу выносим за знак интеграла:
$$int 2 sqrt{x} d x=2 int sqrt{x} d x$$
Далее интеграл находи по формуле:
$$int 2 sqrt{x} d x=2 int sqrt{x} d x=2 cdot frac{2}{3} sqrt{x^{3}}+C=frac{4 sqrt{x^{3}}}{3}+C$$
Ответ. $int 2 sqrt{x} d x=frac{4 sqrt{x^{3}}}{3}+C$
Читать дальше: интеграл обратной функции.
Преподаватель который помогает студентам и школьникам в учёбе.
Интегрирование иррациональных функций с примерами решения
Содержание:
Интегрирование иррациональных функций.
Определение 1. Функция вида
Пример 1.
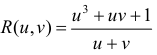
п.1. Интегралы вида:
Пусть s – общий знаменатель дробей 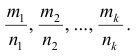
делает подинтегральную функцию рациональной.
Пример 2.
Пример 3
п.2. Интегралы вида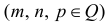
Интегралы вида (1) выражаются через элементарные функции в следующих случаях:
а) p∈Z — интегралы рассмотрены в п.1.
б) 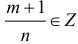
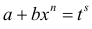
в) 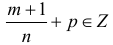
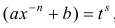
Во всех других случаях интегралы (1) выразить через элементарные функции нельзя (теорема Чебышева).
Пример 4.
Пример 5.
п.3. Интегралы вида 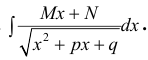
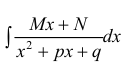
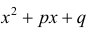
Пример 6.
п 4. Интегралы вида 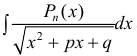
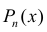
Для вычисления интегралов используют равенство:
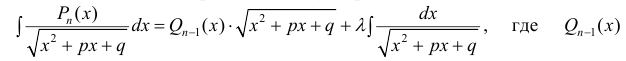
- Заказать решение задач по высшей математике
Пример 7.
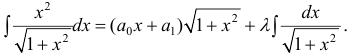
Приравниваем друг к другу коэффициенты при одинаковых степенях х в правой и левой частях.
Решив систему (3), получим :
(сравни с примером 5).
п.5. Интегралы вида
В данных интегралах можно избавиться от иррациональности, если применить подходящую тригонометрическую или гиперболическую подстановку.
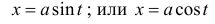
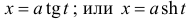
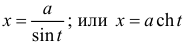
Пример 8.
Пример 9.
Интегрирование некоторых иррациональных функций
1. Интегралы вида 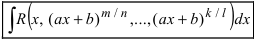
Интегралы такого типа вычисляются по следующей схеме:
В результате приведенных действий данный интеграл переходит в неопределенный интеграл от рациональной функции.
Пример:
Вычислить
Решение:
В данном примере 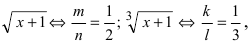
2. Интегралы вида 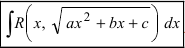
Такие интегралы путем замены 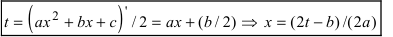
1. 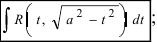
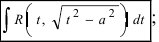
Для вычисления этих интегралов применяют следующие тригонометрические замены
1. 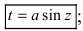
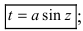
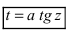
Пример:
Вычислить
Решение:
Данный интеграл соответствует интегралам типа 1., поэтому
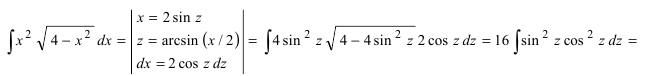
Пример:
Вычислить
Решение:
Воспользуемся указанной выше заменой
(интеграл вычислен в п. 2а)
Пример:
Вычислить
Решение:
Пример:
Вычислить
Решение:
Воспользуемся указанной выше заменой
Понятие о неберущихся интегралах
Определение: Интегралы, первообразные которых не выражаются через элементарные функции, называются неберущимися:
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
- Полярные координаты
- Непрерывность функции
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений