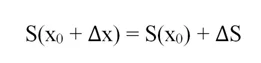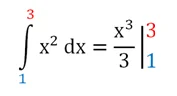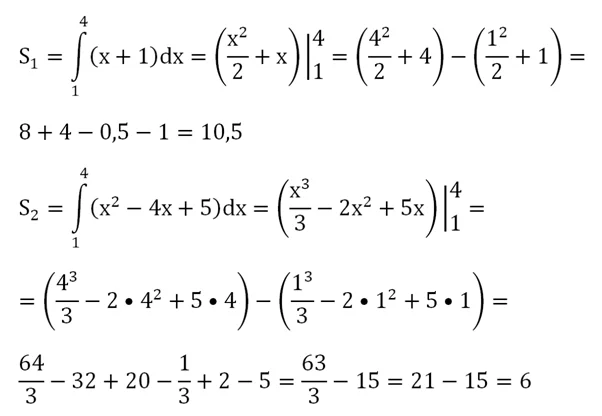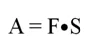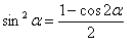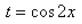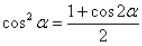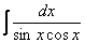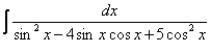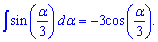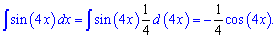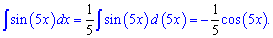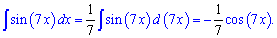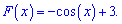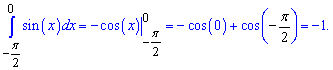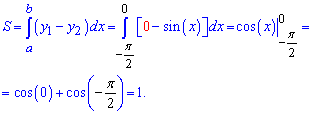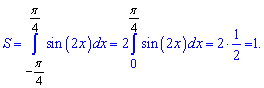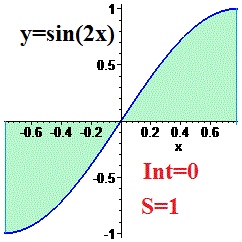Заказать задачи по любым предметам можно здесь от 10 минут
Интеграл от синуса
Интеграл от синуса по таблице интегрирования равен: $$ int sin x dx = — cos x + C $$
Словами это читается так: интеграл от синуса равен сумме отрицательного косинуса и произвольной постоянной.
| Пример 1 |
| Найти интеграл от синус 2x: $$ int sin 2x dx $$ |
| Решение |
|
Напрямую интеграл взять не получится, так как аргумент синуса и знака дифференциала отличаются. Выполняем подведение под дифференциал $ 2x $ и добавляем перед интегралом дробь $ frac{1}{2} $: $$ int sin 2x dx = frac{1}{2} int sin 2x d(2x) = -frac{1}{2} cos 2x + C $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ int sin 2x dx = -frac{1}{2} cos 2x + C $$ |
| Пример 2 |
| Найти интеграл от синуса в квадрате: $$ int sin^2 x dx $$ |
| Решение |
|
В данном случае необходимо воспользоваться одной из тригонометрических формул. Конкретно формулой понижения степени синуса: $$ sin^2 x = frac{1-cos 2x}{2} $$ Заменяем выражение под интегралом: $$ int sin^2 x dx = int frac{1-cos 2x}{2} dx = frac{1}{2} int (1-cos 2x) dx = $$ $$ = frac{1}{2} int 1dx — frac{1}{2} int cos 2x dx = frac{1}{2}x — frac{1}{2}cdotfrac{1}{2}int cos 2x d(2x) = $$ $$ = frac{1}{2}x — frac{1}{4}sin 2x + C $$ |
| Ответ |
| $$ int sin^2 x dx = frac{1}{2}x — frac{1}{4}sin 2x + C $$ |
| Пример 3 |
| Найти интеграл от синуса в кубе: $$ int sin^3 x dx $$ |
| Решение |
|
Здесь нужно вспомнить свойство степеней и учесть: $$ sin^3 x = sin x cdot sin^2 x $$ Подставляем, полученное выражение в интеграл и заносим $ sin x $ под знак дифференциала: $$ int sin^3 x dx = int sin x sin^2 x dx = — int sin^2 x d(cos x) = $$ Далее используем свойство $ sin^2 x = 1 — cos^2 x $: $$ = -int (1-cos^2 x) d(cos x) = -int d(cos x) + int cos^2 x d(cos x) = $$ $$ = — cos x + frac{cos^3 x}{3} + C = frac{1}{3} cos^3 x — cos x + C $$ |
| Ответ |
|
$$ int sin^3 x dx = frac{1}{3} cos^3 x — cos x + C $$ |
| Пример 4 |
| Вычислить определенный интеграл от синуса: $$ int_0^pi sin x dx $$ |
| Решение |
|
Вычисление начнем как в случае с неопределенным интегралом и в конце используем формулу Ньютона-Лейбница $ int_a^b f(x) dx = F(x) bigg |_a^b = F(b)-F(a) $: $$ int_0^pi sin x dx = -cos x bigg |_0^pi = -cos pi + cos 0 = -(-1) + 1 = 1+1=2 $$ |
| Ответ |
| $$ int_0^pi sin x dx = 2 $$ |
План урока:
Криволинейная трапеция и понятие определенного интеграла
Формула Ньютона-Лейбница
Задачи, связанные с определенным интегралом
Криволинейная трапеция и понятие определенного интеграла
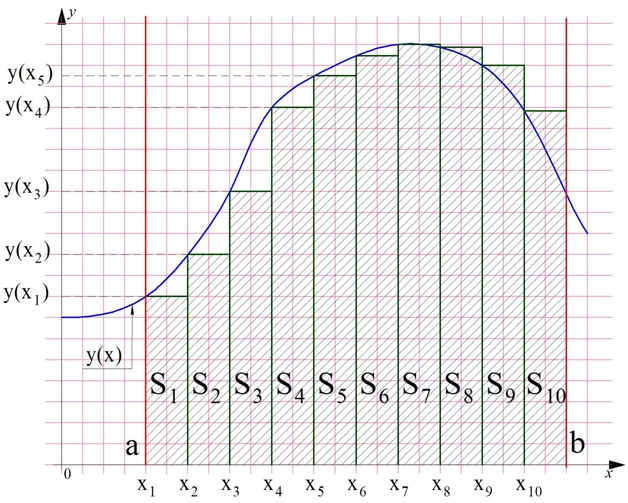
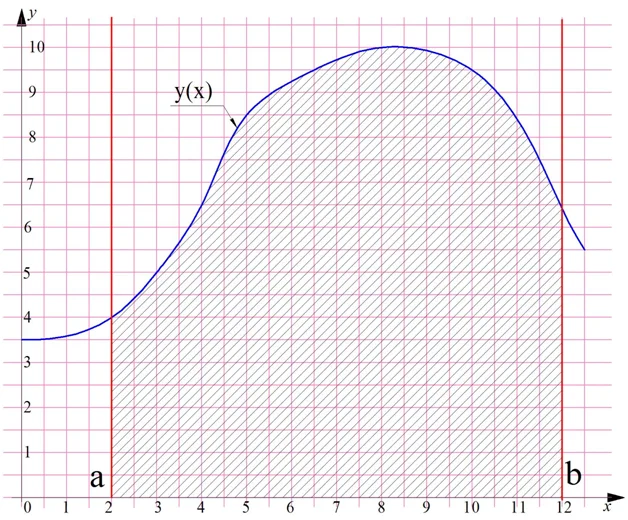
Построим на плоскости график произвольной функции у(х), который полностью располагается выше горизонтальной оси Ох. Далее проведем две вертикальные линии, пересекающие ось Ох в некоторых точках a и b. В результате мы получим интересную фигуру, которая на рисунке показана штриховкой:
Особенностью этой фигуры является то, что одна из ее сторон (верхняя) – это не прямая линия, а какая-то произвольная кривая. Условно будем считать эту фигуру четырехугольником, ведь у нее действительно четыре угла и четыре стороны. Две из них (вертикальные красные линии), очевидно, параллельны друг другу. Две другие стороны (кривую линию и участок оси Ох) параллельными назвать никак нельзя.
Напомним, что в геометрии четырехугольник, у которого две стороны параллельны друг другу, а две другие не параллельны, называют трапецией. Поэтому полученную нами фигуру мы также назовем трапецией. Но так как одна из ее сторон кривая, то мы будем использовать термин «криволинейная трапеция», чтобы отличать ее от трапеции «настоящей».
У каждой плоской фигуры есть площадь, и криволинейная трапеция – не исключение. Но как ее подсчитать? Есть приближенный способ подсчета. Разобьем отрезок [a; b] на несколько более мелких отрезков, и построим на каждом из них прямоугольник:
Обозначим площадь первого прямоугольника как S1, площадь второго прямоугольника – как S2 и т. д. Мы строим прямоугольники таким образом, что их левая сторона в точности равна значению функции в соответствующей точке. Обозначим те точки, на которых стоят стороны прямоугольника, как х1, х2, х3 и т. д. Тогда значения функции в этих точках будут соответственно равны у(х1), у(х2) и т. д.:
Площадь каждого полученного прямоугольника подсчитать несложно – она равна произведению его высоты на ширину. Мы организовали разбиение на прямоугольники таким образом, что ширина у них одинакова. Обозначим ее как ∆х. Тогда площадь каждого отдельного прямоугольника равна
Тогда общая площадь криволинейной трапеции приближенно будет равна сумме площадей всех треугольников:
где n – это количество прямоугольников (на рисунках мы выбрали n = 10).
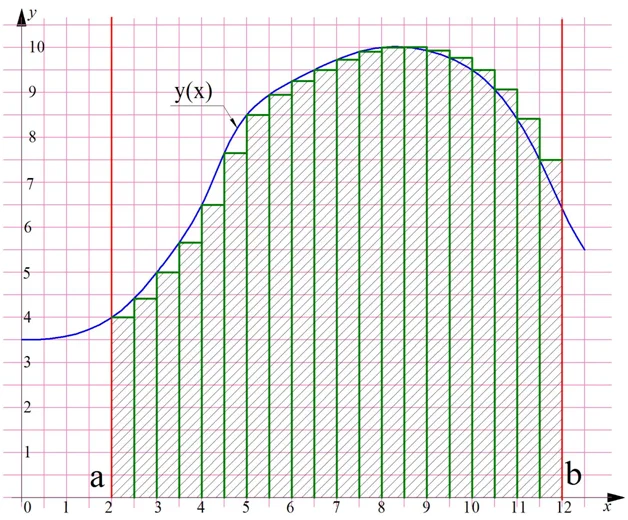
Ясно, что чем больше число n, тем более точное приближение мы получим. Например, если разбить трапецию уже не на 10, а на 20 прямоугольников, то получим такую картинку:
Обратите внимание, что ширина каждого прямоугольника, то есть величина ∆х, уменьшилась.
При росте числа n ошибка при оценке площади трапеции будет уменьшаться и стремится к нулю. Поэтому в предельном случае, когда n стремится к бесконечности, в формуле (1) вместо знака приближенного равенства «≈» можно поставить знак «=». При этом величина ∆х также будет стремится к нулю, то есть становится бесконечно малой. В математике для таких величин вместо символа ∆ принято использовать букву d, то есть вместо ∆х мы напишем dx. С учетом всего этого формула (1) примет вид:
В правой части стоит сумма бесконечного числа слагаемых. У нее есть специальное название – определенный интеграл. Ясно, что величина этой суммы, то есть площадь трапеции, зависят от чисел а и b (боковых границ трапеции). Поэтому обозначение интеграла выглядит так:
Обозначение очень похоже на неопределенный интеграл. Единственное отличие – это появление чисел а и b, которые определяют боковые границы трапеции. Число b называют верхним пределом интегрирования, а число a– нижним пределом интегрирования. Дадим более строгое определение понятию определенного интеграла.
Геометрический смысл определенного интеграла заключается в том, что он равен площади криволинейной трапеции, ограниченной графиком функции у(х) и вертикальными прямыми, проходящими через точки а и b.
Формула Ньютона-Лейбница
Изначально мы хотели научиться вычислять площадь криволинейной трапеции, однако пока что мы лишь придумали, как ее обозначать – через определенный интеграл. Но как вычислить значение его значение? Оказывается, определенный интеграл очень тесно связан с неопределенным интегралом, и эта связь описывается формулой Ньютона-Лейбница.
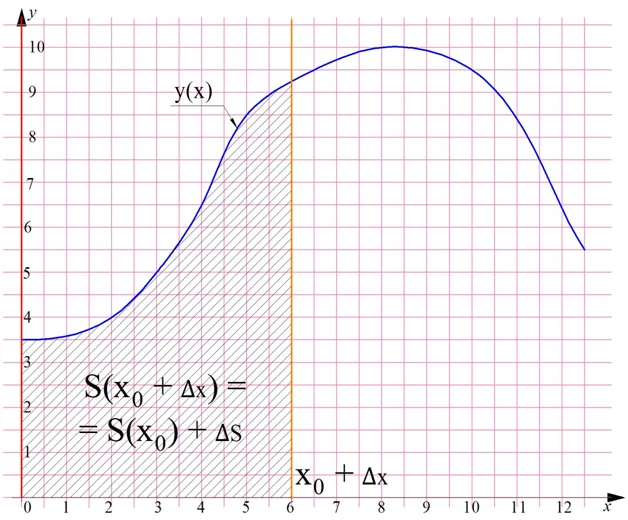
Ещё раз построим криволинейную трапецию, а ее площадь обозначим как S. Пусть ее левая граница совпадает с осью Оу, а правая будет равна некоторому значению х0. Дело в том, что нас будет интересовать зависимость площади трапеции от значения ее правой границы, то есть некоторая функция S(x). Обозначим площадь получившейся трапеции как S(x0):
Теперь сдвинем правую границу вправо на величину ∆х. В итоге получим новую трапецию, площадь которой можно записать как S(x0 + ∆x). При этом ее площадь увеличилась на некоторую величину ∆S:
Получается, что мы дали некоторое приращение аргумента ∆х, и получили приращение функции ∆S. Мы уже выполняли похожие действия в рамках предыдущих уроков, изучая понятие производной.
Итак, мы можем записать, что
Оценим величину ∆S. Если заменить соответствующую площадь прямоугольником, то его площадь окажется равной произведению ширины прямоугольника (она равна ∆x) на высоту, которая равна у(х0):
Поделим обе части равенства (2) на величину ∆х и получим:
А теперь устремим величину ∆х к нулю. В результате в равенство (2), а значит, и (3) будет становиться все более точным. В итоге мы можем написать, что
Хорошо подумайте, что мы получили. Вспомните определение производной. Оказывается, в левой части равенства (4) стоит не что иное, как производная функции S! То есть мы можем написать, что
Получается, что производная функции S на равна значению функции у(х). А это значит, что она является ее первообразной:
Здесь F(x) – первообразная функции у(х), а F(x0) – конкретное значение этой первообразной в точке х0.
Теперь рассмотрим более привычную криволинейную трапецию, у которой правой и левой границей являются числа а и b:
Как найти ее площадь? С помощью формулы (5) мы можем найти две площади:
Из рисунков очевидно, что площадь интересующей нас трапеции равна разности величин S(b) и S(a):
Эту площадь мы и обозначаем определенным интегралом. То есть можно записать, что
Таким образом, чтобы найти площадь криволинейной трапеции, необходимо проинтегрировать функцию у(х), а потом в полученную первообразную подставить числа а и b вычесть один результат из другого.
Для примера вычислим площадь криволинейной трапеции, ограниченной линией у = х2 и вертикальными прямыми х = 1 и х = 3.
Сначала находим первообразную функции у = х2, взяв от нее интеграл (неопределенный):
Отметим, что в обоих случаях речь идет об одной и той же первообразной, поэтому значения констант С у них одинаковы. Теперь вычитаем из F(3) величину F(1):
Константы интегрирования сократились. Для простоты решение записывают в несколько более короткой форме. Сначала сразу после определенного интеграла пишут первообразную (то есть находят неопределенный интеграл), причем без константы интегрирования
Далее ставят вертикальную черту и пишут пределы интегрирования, которые надо подставить в первообразную:
Потом ставят знак равно и подставляют в первообразную верхнее и нижнее число, после чего выполняют оставшиеся арифметические действия:
Задание. Вычислите
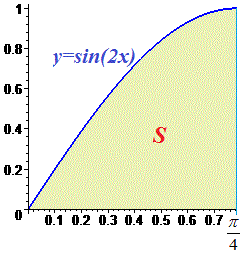
Задание. Найдите площадь фигуры, ограниченной полуволной синусоиды и осью Ох.
Решение. Сначала построим схематичный график у = sinx, чтобы понять, что именно нам надо вычислить:
Теперь ясно, что надо произвести вычисление определенного интеграла синуса на отрезке [0; π]:
Итак, мы теперь знаем и про определенный, и про неопределенный интеграл. Хотя они и очень похожи, между ними есть большая разница, и ее важно понимать. Определенный интеграл – это число, а именно величина площади криволинейной трапеции. Неопределенный интеграл – это функция (точнее, семейство функций), которая является первообразной для интегрируемой функции. Формула Ньютона-Лейбница как раз и показывает ту связь, которая есть между двумя этими различными понятиями.
Может ли определенный интеграл быть отрицательным числом? Кажется, что нет, ведь площадь фигур не бывает отрицательной. Но не всё так просто. Рассмотрим случай, когда график функции является не верхней, а нижней границей трапеции. Например, пусть трапеция образована функцией
Просто надо найти определенный интеграл:
Получили отрицательное значение. Дело в том, что фигура располагается под осью Ох. Из-за этого ее площадь получается со знаком минус.
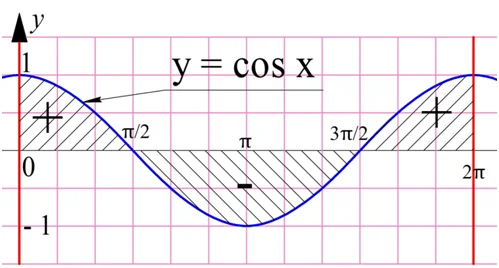
Рассмотрим ещё один пример. Найдем интеграл косинуса на промежутке от 0 до 2π:
Получился ноль. Посмотрим на графике, какую же площадь мы посчитали:
Оказывается, график на отрезке дважды пересекает ось Ох. В результате получается сразу три криволинейных трапеции. Две из них расположены выше оси Ох, а потому из площади считаются со знаком «+». Третья трапеция лежит ниже оси Ох, а потому ее площадь считается со знаком «–». То, что интеграл оказался равным нулю, означает, что площадь нижней трапеции в точности равна сумме площадей двух верхних фигур, поэтому в сумме они и дали ноль.
Отметим важное свойство определенного интеграла:
Проиллюстрируем это правило графически. Каждый из этих интегралов равен площади соответствующих криволинейных трапеций:
Задачи, связанные с определенным интегралом
Определенный интеграл помогает находить и площади более сложных фигур, которые получаются при пересечении нескольких различных графиков.
Рассмотрим задачу на интеграл. Пусть требуется найти площадь фигуры, полученной при пересечении параболы
Сначала найдем точки пересечения графиков. Для этого приравняем функции:
Корнями этого квадратного уравнения являются числа 1 и 4. Именно в этих точках и пересекаются графики (это и так видно из графика). Площадь интересующей нас фигуры можно получить вычитанием из одной криволинейной трапеции другой:
Величины S1и S2 можно вычислить через определенный интеграл. Обратите внимание, что найденные нами корни являются пределами интегрирования:
Тогда искомая нами площадь составит
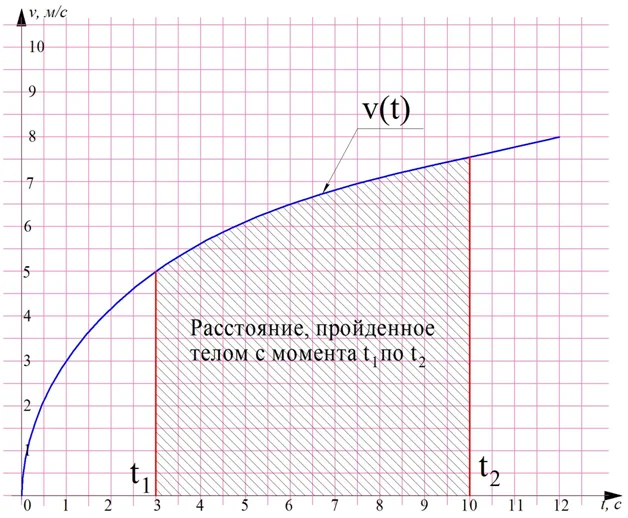
Ошибочно думать, что определенные интегралы нужны только для расчета площадей. С их помощью можно и решать ряд физических задач. Пусть известен закон изменения скорости тела v(t). Можно доказать, что путь, пройденный этим телом за период времени с t1по t2, будет равен интегралу
Задание. Самолет разгоняется, однако из-за сопротивления воздуха он набирает скорость не равномерно. Скорость самолета в момент времени t может быть вычислена по формуле
Определите, какое расстояние пролетит самолет в период времени между 16-ой и 25-ой секундой разгона.
Решение. Задача сводится к простому вычислению интеграла:
Ответ: 610 метров.
Этот пример показывает важную зависимость между скоростью тела и путем, который она преодолевает. Если есть график изменения скорости тела, то площадь под этим графиком равна тому пути, которое проходит тело:
Действительно, если тело двигается равномерно (то есть с постоянной скоростью), то путь, пройденный им, может быть вычислен по известной формуле
Но если построить для такого случая график v(t), то он будет выглядеть как горизонтальная прямая линия. Тогдафигура под графиком окажется прямоугольником, чья площадь равна произведению длины и ширины:
Заметим, что зависимость между путем, скоростью временем носит линейный характер, и именно поэтому здесь может быть использован неопределенный интеграл. Но ведь в физике очень много линейных зависимостей! И во всех этих случаях интегралы играют огромную роль!
Рассмотрим задачу. Есть пружина, которая изначально находится в нерастянутом состоянии. Потом человек начинает медленно и с постоянной скоростью, растягивать пружину, увеличивая ее длину на 0,5 метра. Жесткость пружины (ее коэффициент упругости) равна 100 Н/м. Какую работу совершил человек при растягивании пружины?
Из средней школы известна следующая формула для вычисления работы:
где F– сама сила, а S– путь, пройденный телом под действием этой силы. Легко заметить, что эта формула похожа на ранее рассмотренную зависимость пути от скорости и времени (они обе являются линейными). Сначала рассмотрим простой случай, когда сила остается неизменной. Тогда можно построить график F(S). Окажется, что площадь под графиком как раз равна работе, совершенной силой:
Случай с пружиной сложнее, ведь сила при растяжении пружины не остается неизменной. Чем сильнее растянута пружина, с тем большей силой ее приходится тянуть. Известен закон Гука, связывающий удлинение пружины с силой ее натяжения:
где k – коэффициент жесткости пружины, а x– ее удлинение. По смыслу задачи максимальное удлинение известно и равно 0,5 м. Можно нарисовать такой график зависимости силы натяжения пружины от ее удлинения (он будет выглядеть как прямая линия, так как эта зависимость является прямой пропорциональностью):
И в данном случае работа также будет равна площади под графиком функции, то есть ее можно посчитать с помощью определенного интеграла! В качестве пределов интегрирования надо взять крайние значения удлинения пружины (это 0 и 0,5 м), а качестве интегрируемой функции – F(t), которая равна
Существует и много других примеров приложений определенного интеграла. С его помощью можно находить объемы сложных фигур (конуса, пирамиды, тел вращения), определять центр масс тел сложной формы. Следует отметить и использование интегралов в механике при решении задач, в которых сила действует не на конкретную точку, а на площадь (задачи на распределенную нагрузку). В качестве примера можно привести расчет прочности крыши, на которой лежит слой снега.Но для их рассмотрения необходим более высокий уровень математических и физических знаний, который можно получить уже в рамках не среднего, а высшего образования.
Представлены основные тригонометрические формулы и основные подстановки.
Изложены методы интегрирования тригонометрических функций – интегрирование рациональных функций, произведение степенных функций от sin x и cos x, произведение многочлена, экспоненты и синуса или косинуса, интегрирование обратных тригонометрических функций.
Методы интегрирования тригонометрических функций
Затронуты нестандартные методы. Ниже приведены некоторые тригонометрические формулы, которые могут понадобится при интегрировании тригонометрических функций:
sin2 a + cos2 a = 1 sin (a+b) = sin a cos b + cos a sin b cos (a+b) = cos a cos b – sin a sin b sin 2a = 2 sin a cos a cos 2a = cos2 a – sin2 a = 2 cos2 a – 1 = 1 – 2 sin2 a
Стандартные подстановки при интегрировании тригонометрических функций
Здесь мы рассмотрим стандартные подстановки, с помощью которых, в большинстве случаев, выполняется интегрирование тригонометрических функций.
Подстановка t = sin x
Преобразование выполняется по формулам:
cos x dx = dt; sin x = t; cos2 x = 1 – t2;
Подстановка t = cos x
sin x dx = – dt; cos x = t; sin2 x = 1 – t2;
Интегрирование обратных тригонометрических функций
Интегралы, содержащие обратные тригонометрические функции arcsin φ, arctg φ, и т.д., где φ – некоторая алгебраическая функция от x, нередко интегрируются по частям, полагая u = arcsin φ, u = arctg φ, и т.д.
Стандартные методы интегрирования тригонометрических функций
Общий подход
Вначале, если это необходимо, подынтегральное выражение нужно преобразовать, чтобы тригонометрические функции зависели от одного аргумента, который совпадал бы с переменной интегрирования.
Например, если подынтегральное выражение зависит от sin(x+a) и cos(x+b), то следует выполнить преобразование: cos (x+b) = cos (x+a – (a–b) ) = cos (x+a) cos (b–a) + sin ( x+a ) sin (b–a). После чего сделать замену z = x+a. В результате, тригонометрические функции будут зависеть только от переменной интегрирования z.
Когда тригонометрические функции зависят от одного аргумента, совпадающим с переменной интегрирования (допустим это z), то есть подынтегральное выражение состоит только из функций типа sin z, cos z, tg z, ctg z, то нужно сделать подстановку .
Такая подстановка приводит к интегрированию рациональных или иррациональных функций (если есть корни) и позволяет вычислить интеграл, если он интегрируется в элементарных функциях.
Однако, часто можно найти другие методы, которые позволяют вычислить интеграл более коротким способом, основываясь на специфике подынтегрального выражения. Ниже дано изложение основных таких методов.
Методы интегрирования рациональных функций от sin x и cos x
Рациональные функции от sin x и cos x – это функции, образованные из sin x, cos x и любых постоянных с помощью операций сложения, вычитания, умножения, деления и возведения в целочисленную степень.
Они обозначаются так: R(sin x, cos x). Сюда также могут входить тангенсы и котангенсы, поскольку они образованы делением синуса на косинус и наоборот. Методы интегрировании рациональных тригонометрических функций следующие:
- Подстановка всегда приводит к интегралу от рациональной дроби. Однако, в некоторых случаях, существуют подстановки (они представлены ниже), которые приводят к более коротким вычислениям.
- Если R(sin x, cos x) умножается на –1 при замене cos x → – cos x, то выполняется подстановка t = sin x.
- Если R(sin x, cos x) умножается на –1 при замене sin x → – sin x, то выполняется подстановка t = cos x.
- Если R(sin x, cos x) не меняется как при одновременной замене cos x → – cos x, и sin x → – sin x, то применяется подстановка t = tg x или t = ctg x.
Произведение степенных функций от cos x и sin x
Интегралы вида являются интегралами от рациональных тригонометрических функций. Поэтому к ним можно применить методы, изложенные в предыдущем разделе. Ниже рассмотрены методы, основанные на специфике таких интегралов. Если m и n – рациональные числа, то одной из подстановок t = sin x или t = cos x интеграл сводится к интегралу от дифференциального бинома.
Разложение дроби из синусов и косинусов на более простые дроби
Рассмотрим интеграл . Наиболее простой способ интегрирования заключается в разложении дроби на более простые, применяя преобразование:
- sin(a – b) = sin(x + a – (x + b) ) = sin(x+a) cos(x+b) – cos(x+a) sin(x+b)
Интегрирование дробей первой степени
При вычислении интеграла , удобно выделить целую часть дроби и производную знаменателя:
- a1sin x + b1cos x = A (a sin x + b cos x) + B (a sin x + b cos x)′ .
Постоянные A и B находятся из сравнения левой и правой частей.
Источник: https://1cov-edu.ru/mat_analiz/integrali/neopredelennie/trigonometricheskie/
Интегрирование тригонометрических функций
На практике часто приходится вычислять интегралы трансцендентных функций, которые содержат тригонометрические функции. В рамках этого материала мы опишем основные виды подынтегральных функций и покажем, какие методы можно использовать для их интегрирования.
Интегрирование синуса, косинуса, тангенса и котангенса
Начнем с методов интегрирования основных тригонометрических функций – sin, cos, tg, ctg. Используя таблицу первообразных, сразу запишем, что ∫sin xdx=-cos x+C, а ∫cos xdx=sin x+C. Для вычисления неопределенных интегралов функций tg и ctg можно воспользоваться подведением под знак дифференциала:
- ∫tg xdx=∫sin xcos xdx=d(cos x)=-sin xdx==-∫d(cos x)cos x=-lncos x+C∫ctg xdx=∫cos xsin xdx=d(sin x)=cos xdx==∫d(sin x)sin x=lnsin x+C
Как же у нас получились формулы ∫dxsin x=ln1-cos xsin x+C и ∫dxcos x=ln1+sin xcos x+C, взятые из таблицы первообразных? Поясним только один случай, поскольку второй будет понятен по аналогии.
Используя метод подстановки, запишем:
- ∫dxsin x=sinx=t⇒x=arcsin y⇒dx=dt1-t2=dtt1-t2
Здесь нам нужно интегрировать иррациональную функцию. Берем тот же метод подстановки:
- ∫dtt1-t2=1-t2=z2⇒t=1-z2⇒dt=-zdz1-z2==∫-zdzz1-z2·1-z2=∫dzz2-1=∫dz(z-1)(z+)==12∫dzz-1-12∫dzz+1=12lnz-1-12z+1+C==12lnz-1z+1+C=lnz-1z+1+C
Теперь производим обратную замену z=1-t2 и t = sin x:
- ∫dxsin x=∫dtt1-t2=lnz-1z+1+C==ln1-t2-11-t2+1+C=ln1-sin2 x-11-sin2 x+1+C==lncos x-1cos x+1+C=ln(cos x-1)2sin2x+C==lncos x-1sin x+C
Отдельно разберем случаи с интегралами, которые содержат степени тригонометрических функций, таких, как ∫sinn xdx, ∫cosn xdx, ∫dxsinn x, ∫dxcosn x.
О том, как их правильно вычислять, можно прочесть в статье об интегрировании с использованием рекуррентных формул. Если вы знаете, каким образом выведены эти формулы, то легко сможете брать интегралы вроде ∫sinn x·cosm xdx с натуральными m и n.
Если у нас имеется комбинация тригонометрических функций с многочленами или показательными функциями, то их придется интегрировать по частям. Советуем прочесть статью, посвященную методам нахождения интегралов ∫Pn(x)·sin (ax)dx, ∫Pn(x)·cos (ax)dx, ∫ea·x·sin (ax)dx, ∫ea·x·cos (ax)dx.
Наиболее сложными являются задачи, в которых подынтегральная функция включает в себя тригонометрические функции с разными аргументами. Для этого нужно пользоваться основными формулами тригонометрии, так что желательно помнить их наизусть или держать запись под рукой.
Пример 1
Найдите множество первообразных функции y=sin (4x)+2cos2 (2x)sin x·cos (3x)+2cos2x2-1·sin (3x).
Решение
Воспользуемся формулами понижения степени и запишем, что cos2x2=1+cos x2, а cos22x=1+cos 4×2. Значит:
- y=sin (4x)+2cos2 (2x)sin x·cos (3x)+2cos2x2-1·sin (3x)=sin (4x)+2·1+cos 4x2sin x·cos (3x)+2·1+cos x2-1·sin (3x)==sin (4x)+cos(4x)+1sin x·cos (3x)+cos x·sin (3x)
В знаменателе у нас стоит формула синуса суммы. Тогда можно записать так:
- y=sin (4x)+cos(4x)+1sin x·cos (3x)+cos x·sin (3x)=sin (4x)+cos(4x)+1sin(4x)==1+cos (4x)sin (4x)
У нас получилась сумма 3-х интегралов:
- ∫sin (4x)+cos(4x)+1sin x·cos (3x)+cos x·sin (3x)dx==∫dx+cos(4x)dxsin (4x)+∫dxsin (4x)==x+14ln∫d(sin(4x))sin(4x)+14lncos (4x)-1sin (4x)==14lnsin (4x)+14lncos (4x)-1sin (4x)+C=x+14·lncos4x-1+C
В некоторых случаях тригонометрические функции, находящиеся под интегралом, можно свести к дробно рациональным выражениям с использованием метода стандартной подстановки. Для начала возьмем формулы, которые выражают sin, cos и tg через тангенс половинного аргумента:
- sin x=2tgx21+tg2x2, sin x=1-tg2x21+tg2x2, tg x=2tgx21-tg2x2
Также нам нужно будет выразить дифференциал dx через тангенс половинного угла:
Поскольку dtgx2=tgx2’dx=dx2cos2x2, то dx=2cos2x2dtgx2=2dtgx21cos2x2=2dtgx2cos2x2+sin2x2cos2x2=2dtgx21+tg2x2
Таким образом, sin x=2z1+z2, cos x1-z21+z2, tg x2z1-z2, dx=2dz1+z2 при z=tgx2.
Пример 2
Найдите неопределенный интеграл ∫dx2sin x+cos x+2.
Решение
Используем метод стандартной тригонометрической подстановки:
- 2sin x+cos x+2=22z1+z2+1-z21+z2=z2+4z+31+z2⇒dx2sin x+cos x+2=2dz1+z2z2+4z+31+z2=2dzz2+4z+3
Получим, что ∫dx2sin x+cos x+2=2dzz2+4z+3. Теперь мы можем разложить подынтегральную функцию на простейшие дроби и получить сумму двух интегралов:
- ∫dx2sin x+cos x+2=2∫2dzz2+4z+3=2∫121z+1-1z+3dz==∫dzz+1-∫Cz+3=lnz+1-lnz+3+C=lnz+1z+3+C
Далее производим обратную замену z=tgx2:
- ∫dx2sin x+cos x+2=lnz+1z+3+C=lntgx2+1tgx2+3+C
Ответ: ∫dx2sin x+cos x+2=lntgx2+1tgx2+3+C
Важно отметить, что те формулы, которые выражают функции через тангенс половинного аргумента, не являются тождествами, следовательно, получившееся в итоге выражение lntgx2+1tgx2+3+C – это множество первообразных функции y=12sin x+cos x+2 только на области определения. Для решения других типов задач можно использовать основные методы интегрирования.
Источник: https://Zaochnik.com/spravochnik/matematika/integraly-integrirovanie/integrirovanie-trigonometricheskih-funktsij/

Подставим все в формулу интегрирования по частям и приведем интеграл к табличному, тогда будем иметь:
Методы не применяются для интегрирования функций вида




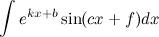

умноженных на многочлен. Такие интегралы интегрируются по частям.
При нахождении интегралов от тригонометрических функций используется ряд методов:
Использование тригонометрических формул Понижение степени подынтегральной функции Метод замены переменной Универсальная тригонометрическая подстановка
При работе с тригонометрическими функциями следует помнить, что:
Косинус – это четная функция, то есть 
Синус – функция нечетная: 
Использование тригонометрических формул
Пример34
Найти интеграл.
Используем формулу: 

Пример 35
Найти интеграл
Для упрощения подынтегральной функции воспользуемся тригонометрическими функциями. Затем с помощью свойств интеграла приведем данный интеграл к табличному виду.
Пример 36
Найти интеграл.
Используем формулу: 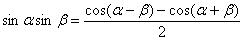
Пример 37
Найти интеграл.
Используем формулу:

Пример 38
Найти неопределенный интеграл
Используем формулы преобразования произведения функций сначала для произведения 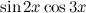
В результате искомый интеграл будет равен
Понижение степени подынтегральной функции
Данный приём используют, когда в подынтегральных функциях присутствуют синусы и косинусы в чётных степенях. Для понижения степени используют
тригонометрические формулы 
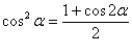
направлении:

Интеграл вида ʃ sinn (x) cosm (x), где n и m – чётные числа, решается методом
понижения степени подынтегральной функции.
Пример 39
Найти интеграл
|
∫cos2xdx = ∫1+cos2x2 |
dx = |
21 |
∫(1 + cos2x)dx = 21 x + 21 sin2x + C |
|
|
Используем формулу: |
||||
|
Пример 40 |
||||
|
Найти интеграл |
dx = |
21 ∫(1 −cos3x)dx = 21 x −31 sin3x + C |
||
|
∫sin2 23 xdx = ∫1−cos3x2 |
||||
|
Используем формулу: |
Пример 41
Найти интеграл
Выражаем sin4 x как (sin2 x)2 и применяем формулу
Используем формулу
В третьем слагаемом снова понижаем степень с помощью формулы 

Пример 42
Найти интеграл
Метод замены переменной
Данный приём используют, когда в подынтегральных функциях присутствуют синусы и косинусы в нечётных степенях.
Общие рекомендации :
1.за t нужно обозначить функцию, которая находится в знаменателе.
2.за t нужно обозначить ту функцию, которая, является более сложной.
3.Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится в нечетной степени, то нужно от нечетной степени «откусить» одну функцию, а за t – обозначить другую функцию
Интеграл вида ʃ sinn (x) cosm (x), где n или m – нечётные числа, решается методом замены переменной
Пример 43
Найти интеграл
Проведем замену:
Примечание: здесь можно было сделать замену 


Пример 44
Найти интеграл 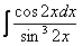
Пример 45
Найти интеграл 
Пример 46
Найти интеграл
Представляем cos3 x dx как cos2 x cos x dx, а cos2x выражаем через синус с помощью основного тригонометрического тождества:
Делаем замену:

Пример 47
Найти интеграл 
Проведем замену:
Пример 48
Найти интеграл 
Пример 49
Найти неопределенный интеграл 
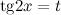
Подставляя это в искомый интеграл, получим

Сделаем обратную замену
Пример 50
Найти неопределенный интеграл 
Введем замену 
Сделаем обратную замену и окончательно получим
Пример 51
Найти неопределенный интеграл 
а затем, формулу для понижения степени

Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка 
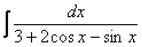



Указанная замена позволяет свести интеграл от тригонометрической функции к интегралу от рациональной функции.
При этом следует учесть, что из равенства 
;
Обратите внимание, что аргумент под тангенсом должен быть в два раза меньше, чем под синусом и косинусом, т.е., в общем виде, если присутствуют функции вида:
sin(kx), cos(kx), делается подстановка tg(kx/2) = t. Еще раз, при sin2x ‒ tg(2x/2), при sin3x ‒ tg(3x/2) и т.д.
Пример 52
Найти неопределенный интеграл 

Пример 53
Найти неопределенный интеграл 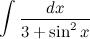

то есть 
Сделаем обратную замену
Пример 54
Найти неопределенный интеграл 
Для нахождения первого интеграла будем использовать универсальную тригонометрическую замену

Тогда первый интеграл преобразуется следующим образом
Разложим подынтегральную функцию полученного интеграла на элементарные дроби:
Приведем к общему знаменателю дроби в правой части равенства и приравниваем числители:
Приравнивая коэффициенты при соответствующих степенях, получим такую систему для нахождения 
Тогда подынтегральная функция имеет следующее разложение на простые дроби
а соответствующий интеграл равен
Делаем обратную замену
Окончательно искомый интеграл равен:

Пример 55
Найти неопределенный интеграл. 

Универсальная тригонометрическая подстановка:
Применение универсальной тригонометрической подстановки часто приводит к длинным и трудоемким вычислениям. Поэтому на практике универсальной тригонометрической подстановки стараются избегать (если возможно).
В ряде случаев целесообразно свести подынтегральное выражение, содержащее sinn(α) и cosm(α), к tg(α) и ее производной 1/cos2(α) т.е. произвести замену:



Метод работает, если сумма показателей степеней n+m ‒ целое четное отрицательное число .

Пример56
Найти неопределенный интеграл
Пример57
Найти неопределенный интеграл
Замена tgх =t (чтобы не запутаться)
Пример58
Найти неопределенный интеграл
Пример59
Найти неопределенный интеграл

Пример60
Найти неопределенный интеграл
|
Пример61 |
||||||||||||||
|
Интеграл из примера55 |
||||||||||||||
|
= |
= |
= |
||||||||||||
|
4 2 − 5 2 |
(4 2 − 5 2 ) 2 |
(4 2 − 5) 2 |
||||||||||||
|
( ) |
= |
2 |
1 |
2 |
1 |
1 |
2 − √5 |
|||||||
|
= |
4 2 − 5 |
= |
= 4 2 − 5 = |
2 |
(2 )2 − (√5)2 |
= 2 |
2√5 |
2 + √5 + = |
||||||
|
= 4√1 |
5 22 +−√√55 + |
Решение значительно быстрее и проще.

6.Интегралы от дробей
Суть методов решения интегралов от дроби сводится к преобразованию дроби в сумму элементарных дробей табличного вида:
1.
2.
3.
4.
5.
6.
Для преобразования дроби используется комплекс приемов, основными из которых будут выделение полного квадрата, подстановка, разложение на множители, с дальнейшим преобразованием в сумму элементарных дробей.
Для решения интегралов от дроби можно придерживаться следующего алгоритма:
|
Определяем тип подынтегрального выражения. |
||||||
|
1. |
Для простейших дробей вида |
применяется способ подведения функции |
||||
|
под знак дифференциала с дальнейшим интегрированием с помощью таблицы. |
||||||
|
( + ) |
||||||
|
( + ) |
( + )−+ |
, |
||||
|
∫( + ) = ∫( + ) |
= |
−+ |
+ |
Примеры:

|
2. Для дробей вида |
, |
, |
, |
(коэффициенты |
a и c не равны нулю) также применяется способ подведения функции под знак дифференциала с дальнейшим интегрированием с помощью таблицы. (Формулы 2 — 6, см. выше).
Примеры:
|
3. Для дробей вида |
сначала представляем |
|
интеграл в виде суммы: |
Первый интеграл берем методом подведения под знак дифференциала:

|
В интегралах вида |
выделяем в знаменателе полный квадрат и приводим |
||||
|
выражение к табличному виду. |
|||||
|
В ряде случаев, неразложимый многочлен |
целесообразно представить в |
||||
|
необходимо вынести коэффициент за знак интеграла, |
|||||
|
виде полного квадрата (перед этим |
( |
+ + ) |
|||
|
поделив все выражение на ) по формуле: |
и свести интеграл к виду:
,
или
Пример62
Найти неопределенный интеграл 
раскладывается на множители 
Пример63
Найти неопределенный интеграл 

т.е. вида
В подкоренном выражении выделяем полный квадрат:
Поэтому
Пример64
4. Для дробей вида
используют метод интегрирования по частям n раз, каждый раз понижая степень знаменателя и применяя предыдущие способы. Вычисления получаются очень длинные и долгие. Или пользуемся рекуррентными формулами.
5. Дроби( ) , у которых многочлены и в числителе и в знаменателе,
( ) , где Pn(x) и Pm(x) многочлены степени n и m соответственно, перед
собственно взятием интеграла необходимо разложить на множители, а затем, преобразовать в сумму элементарных дробей.
Определяем что дробь правильная. Правильной называется дробь, у которой степень числителя меньше степени знаменателя. Если дробь неправильная, то выделяем целую часть, с оставшейся частью работаем как с правильной дробью.
Раскладываем знаменатель правильной дроби на множители и преобразуем дробь в сумму элементарных дробей.
Для преобразования дроби в сумму элементарных дробей в большинстве случаев используют метод неопределенных коэффициентов.

Метод неопределенных коэффициентов.
|
т.е. |
|||||
|
Любую дробь вида |
( + )( + )( + ) |
можно представить в виде |
|||
|
2+ + |
|||||
|
2 + + |
|||||
|
( + )( + )( + ) = |
+ + + + + , |
+ ++ + +
|
где A, B, C неизвестные коэффициенты. |
|||||||||||||||||||||||
|
Приводим правую часть уравнения к общему знаменателю: |
|||||||||||||||||||||||
|
+ |
= |
( + )( + ) + ( + )( + ) ( + )( + ) |
, |
||||||||||||||||||||
|
+ |
+Тогда |
+ |
( + )( + )( + ) |
||||||||||||||||||||
|
+ |
|||||||||||||||||||||||
|
2 |
+ + |
( + )( + ) + ( + )( + ) + ( + )( + ) |
|||||||||||||||||||||
|
( + )( + )( + ) |
( + )( + )( + ) |
||||||||||||||||||||||
|
2 |
+ + = ( + )( + ) + ( + )( + ) ( + )( + ) |
||||||||||||||||||||||
|
Если дроби равны= и равны их знаменатели, то должны быть равны и их числители, |
: |
||||||||||||||||||||||
|
+ + = |
|||||||||||||||||||||||
|
= 2 |
Раскрываем скобки |
( + ) + + 2 + |
( + ) + = |
||||||||||||||||||||
|
+ |
( + ) + + 2 + |
||||||||||||||||||||||
|
= ( + + ) |
+ |
( + + + + + ) + ( + + ) |
|||||||||||||||||||||
|
= + + |
|||||||||||||||||||||||
|
Приравниваем коэффициенты в выражениях: |
|||||||||||||||||||||||
|
= ( + ) |
+ ( + ) + ( + ) |
||||||||||||||||||||||
|
= + + |
|||||||||||||||||||||||
|
Решая систему уравнений, находим неизвестные коэффициенты A, B, C и раскладываем |
|||||||||||||||||||||||
|
2 |
+ + |
||||||||||||||||||||||
|
дробь на сумму элементарных дробей: |
+ |
||||||||||||||||||||||
|
( + )( + )( + ) |
+ |
+ |
|||||||||||||||||||||
|
он приравнивается к |
( |
+ + ) |
квадратный. |
многочлен вида: |
|||||||||||||||||||
|
Если в знаменателе встречается= |
+неразложимый+ |
||||||||||||||||||||||
|
( + )( |
+ |
1 + ) |
2 |
+ |
|||||||||||||||||||
|
12 |
, где |
— неразложимый квадратный многочлен (D<0), то |
|||||||||||||||||||||
|
( + )( |
сумме дробей по формуле: |
||||||||||||||||||||||
|
+ + ) |
+ |
( |
+ + ) |
||||||||||||||||||||
|
Если в знаменателе2 |
встречаются= |
+кратные2 |
множители. |
вида: |
|||||||||||||||||||
|
1 |
, |
1 |
2 |
1 |
2 |
||||||||||||||||||
|
( 1+ ) |
то они раскладываются по формуле: |
||||||||||||||||||||||
|
( + ) = |
+ |
2 + + |
+ ( + ) + |
( + )2 |
+ + |
( + ) |

Пример65
Найти неопределенный интеграл 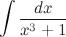
Тогда интеграл примет вид:
Далее разложим подынтегральную функцию на простые дроби с неопределенными коэффициентами. В нашем случае имеет место следующее разложение:
Найдем неопределенные коэффициенты, для этого приведем к общему знаменателю дроби в правой части равенства, а затем приравняем соответствующие числители
Далее приравняем коэффициенты при соответствующих степенях
Подставим, выраженные через 





|
1 |
1 |
(2 − 1) − 3 |
|||||||
|
= 3 |
| + 1| − 6 |
2 − + 1 |
= |
||||||
|
1 |
1 |
2 − 1 |
−3 |
= |
|||||
|
= 3 |
| + 1| − 6 |
2 |
− + 1 − |
6 |
2 − + 1 |
||||
|
1 |
1 |
| |
2 |
1 |
|||||
|
= 3 |
| + 1| − 6 |
− + 1| + 2 |
2 − + 1 |

Квадратный трехчлен, стоящий в знаменателе последнего интеграла, не раскладывается на
|
множители |
1 |
1 |
2 |
. Поэтому для его нахождения выделим в |
||||||||
|
1 |
||||||||||||
|
знаменателе полный квадрат: |
||||||||||||
|
3 + 1 |
= = 3 |
| + 1| − 6 |
| |
− + 1| + |
2 2 − + 1 = |
|||||||
|
1 |
| + 1| − |
1 |
| |
2 |
1 |
+ 3 = |
||||||
|
= 3 |
6 |
2 |
− + 1| + 2 |
( − 1)2 |
||||||||
|
1 |
| + 1| − |
1 |
| |
1 |
1 |
2 |
4 |
|||||
|
= 3 |
6 |
− + 1| + 2 |
3 |
3 |
+ = |
|||||||
|
1 |
| + 1| − |
1 |
| |
2 |
1 |
4 |
2 |
4 |
||||
|
= 3 |
6 |
− + 1| + √3 |
√3 + |
Пример66
Найти неопределенный интеграл 
Раскладываем знаменатель на множители, используя формулу сокращенного умножения
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Приводим дробь к общему знаменателю:
Составим и решим систему:
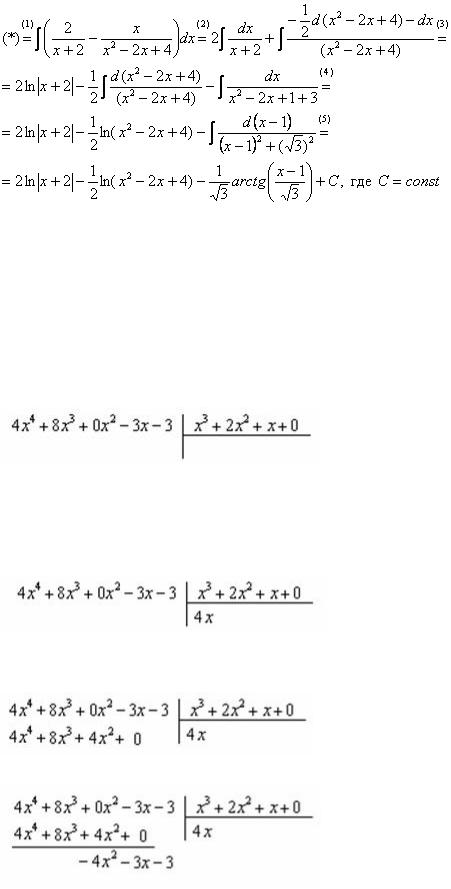
Пример67
Найти неопределенный интеграл 
Основной метод решения интеграла с неправильной дробно-рациональной функцией – это
деление числителя на знаменатель.
Сначала рисуем «заготовку» для деления:
ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами
Теперь маленькая задачка, на какой множитель нужно умножить 

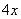
Далее умножаем 



Проводим черточку и производим вычитание (из верха вычитаем низ):
Старшая степень остатка 


изначально унас был в числителе многочлен пятой степени, то алгоритм деления увеличился бы на один шаг.
Итак, у нас получилась целая часть плюс остаток:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
6. Неопределенные интегралы иррациональных функций вида 
В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:
|
1. |
Если p — целое число, то принимают |
, где N — общий знаменатель чисел m и n. |
||||||||||
|
2. |
— целое число, то |
, где N — знаменатель числа p. |
||||||||||
|
Если + |
||||||||||||
|
знаменатель |
+ p |
— целое число, то вводят новую переменную |
, где N — |
|||||||||
|
3. |
Если |
+ |
||||||||||
|
числа . |
||||||||||||
|
привести к виду: |
± |
, |
− |
которые можно |
||||||||
|
Очень часто в вычислениях встречаются дроби вида |
||||||||||||
|
+ − |
+ |
|||||||||||
|
+ = |
+ |
= + |
− + = − + |
|||||||||
|
+ − |
− |
− |
||||||||||
|
− = |
− |
= − |
+ − = − − |
+ − = −1 + − = − − |
||||||||
|
+ − |
− |
|||||||||||
|
− = |
− |
= − |
+ − = + − |

Пример68
Найти неопределенный интеграл
То есть, m = -1, n = 1, p = 1/2. Так как 
переменную 
Выполняем подстановку в исходный интеграл:
Пример 69
Найти неопределенный интеграл 

Вот почему дифференциалы нужно именно НАВЕШИВАТЬ на обе части и добросовестно
раскрывать эти дифференциалы. Немало чайников здесь формально напишет 
Пример70
Найти неопределенный интеграл

Проведем замену: 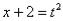
С числителем разобрались. Что делать с 

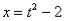

Пример71
Найти неопределенный интеграл 
Когда даны разные корни удобно придерживаться следующей схемы решения. Сначала выписываем на черновике подынтегральную функцию, при этом все корни представляем в
виде 
Теперь нужно найти наименьшее общее кратное чисел 2, 3, 3 – такое число, чтобы оно делилось и на 2 и на 3 (в данном случае), кроме того, это число должно быть как можно меньше.
Очевидно, что наименьшим общим кратным является число 6. Оно делится и на 2 и на 3, кроме того, меньше шестерки ничего не придумать.
Замена в рассматриваемом интеграле будет следующей: 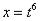
Проведем замену:
Согласно формулам интегрирования интеграл от синуса sin (x) равен косинусу, причем со знаком минус. Многие часто допускает ошибки потому что не может запомнить, что производная от синуса равна минус косинусу, а от косинуса — синусу со знаком плюс.
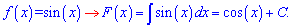
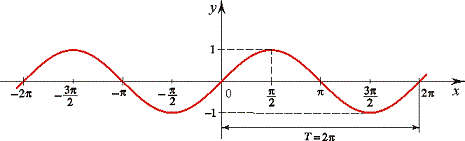
График синуса имеет вид
Синус нечетная, а косинус — четная функция, поэтому при интегрировании появляется знак минус. В начале всем кажется все простым и понятным. Но рано или поздно наступает время усложнять интеграл, то есть интегрировать синус двойного угла, тройного аргумента и т.д. И во многих возникают трудности с интегрированием. Для вывода формулы интеграла для sin (k*x) проведем все выкладки сначала. Для того чтобы свести интеграл к табличной формулы надо внести коэффициент под дифференциал, но это изменит сам интеграл. Поэтому одновременно делим на коэффициент
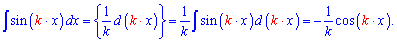
Зная эту формулу, интеграл от синуса двойного угла записываем одной строкой
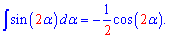
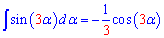
int(sin(k*x)=-1/k*cos(k*x).
По такой же формуле выводят интеграл от синуса половины угла, который равен минус 2 косинус половины угла.
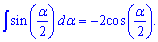
Распространенные примеры интегрирования синуса
Пример 1. Найти интеграл от sin(4*x).
Решение: По формуле интегрирования находим
Пример 2. Вычислить интеграл от sin(5*x).
Решение: Выполняем интегрирования
Пример 3. Проинтегрировать выражение sin(7*x).
Решение: Находим неопределенный интеграл
Пример 4. Найти интеграл функции y=sin(x/5).
Решение: Находим неопределенный интеграл
Как только Вы научитесь вычислять простые интегралы от синуса можете переходить к определенному интегралу
Пример 5. Найти первоначальную от sin(x) которая в нуле равна 2.
Решение: Вычисляем первоначальную
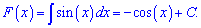
Из условия на первоначальную находим постоянную
-cos(0)+C=2;
C=2+cos(0)=3.
Возвращаемся к первоначальной и подставляем найденную постоянную
Это и есть ответ к задаче.
Пример 7. Проинтегрировать синус двойного угла y=sin(2*x) от 0 до 45 градусов.
Решение: Записываем интеграл от синуса и подставляем пределы интегрирования
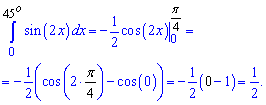
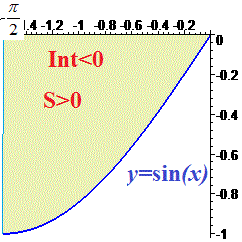
По физическому содержанию определенный интеграл равен площади фигуры ограниченной функцией sin (x) и осью абсцисс.
Но определенный интеграл и площадь, это не одно и то же. Интеграл может быть отрицательным, а площадь нет. Если функция большую площадь имеет под осью абсцисс, то ее определенный интеграл отрицательный.
Площадь криволинейной трапеции равна интегралу от разницы уравнения верхней кривой и нижней.
В данном случае верхняя кривая это ось абсцисс или y = 0. Нижняя — это график синуса. Поэтому формула площади синус функции равна 1, или определенному интегралу по модулю.
Если функция антисимметрична относительно оси абсцисс то ее интеграл равен нулю, а площадь равна двойному интегралу графика над осью абсцисс. Например, интеграл синуса двойного угла от -45 до 45 градусов равен нулю
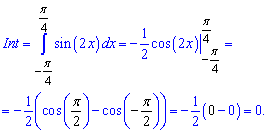
В то же время площадь заштрихованной фигуры равна единице.
На графике это будет выглядеть.
Из следующих материалов Вы узнаете, как найти интеграл от функции вида
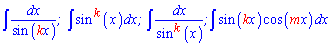

На этом знакомство с интегрированием синуса завершается. Интегралы от других тригонометрических и обратных к ним функций Вы найдете на страницах категории «Интегрирование функций«.