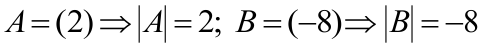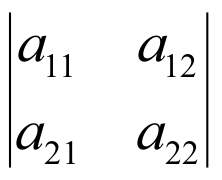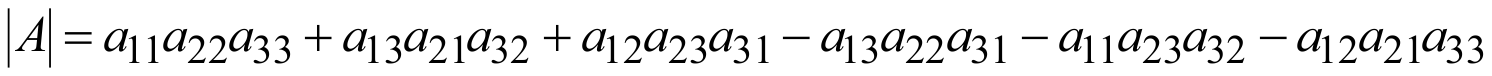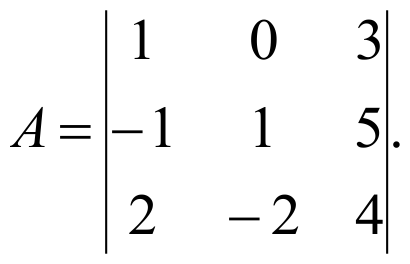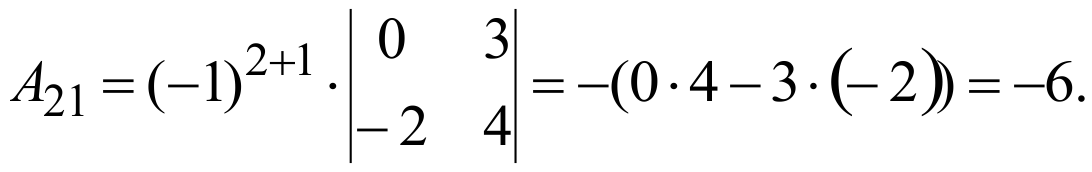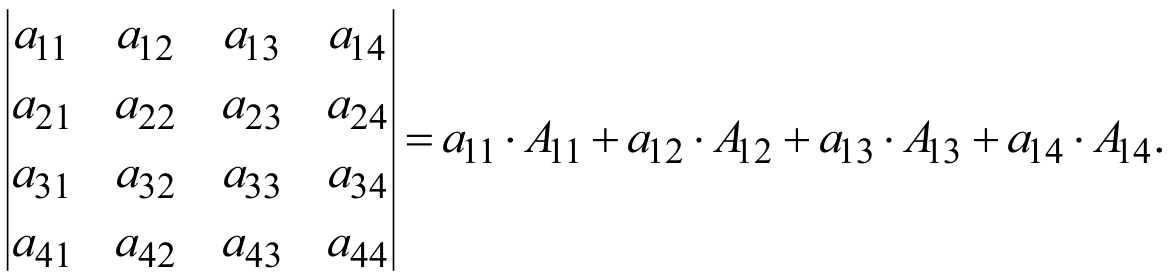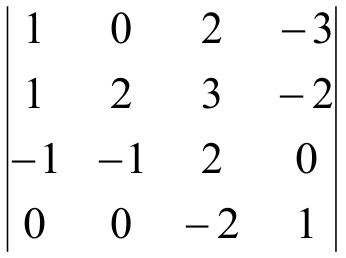Как найти определитель 4 порядка пример

Основные определения и формула для нахождения определителя матрицы четвертого порядка

Часто в математических и прикладных задачах возникает необходимость использовать матрицы. Дадим определение матрицы.

Выделяют разные матрицы. Нам пригодятся понятие следующих:

• если матрица имеет единственный элемент, то она является совпадающей со своим единственным скаляром;
• квадратной матрицей называют такую матрицу, у которой количество столбцов совпадает с количеством строк.

Алгебраические операции над матрицами имеют свой алгоритм и порядок, отличающийся от тех же операций над обычными числами. Помимо алгебраических операций, существуют и другие операции над матрицами. Например, операция транспонирования матрицы.

Часто учащиеся сталкиваются с задачами по нахождению определителя матриц разных порядков. Под матрицами первого, второго, третьего, четвёртого и т.д. порядка понимаются квадратные матрицы. Дадим определение определителю.

Определитель первого порядка равен скаляру данной матрицы. Определители второго и третьего порядка высчитываются в определённом порядке, то есть по известным формулам.

Для вычисления определителя больше третьего порядка, необходимо понимание минора матрицы.

«Найти определитель матрицы четвертого порядка» 👇

Формула для определителя четвёртого порядка:

$|A|=a_{11}M_{11}-a_{12}M_{12}+a_{13}M_{13}-a_{14}M_{14}$.

Пример решения

Решим пример.

В рамках учебной программы принято использовать однотипные примеры с действительными числами. Зная формулу, очевидно, что все примеры будут аналогичны друг другу.

Теорема Лапласа

Существует также метод нахождения определителя четвертого порядка по теореме Лапласа. Тогда понадобится следующее понятие:

Эта теорема распространяется на матрицы любого порядка.

При ручном решении подобных задач главное помнить о внимательности и сосредоточенности, а также уметь проявлять терпение, когда дело касается большой матрицы или матрицы с большими значениями элементов. На практике в современных условиях для решения подобных задач применяют вычислительные машины.

Уважаемые студенты,

каждый месяц у вас есть возможность попасть на бесплатный вебинар по высшей математике. Темы предстоящих вебинаров выбираем все вместе в Телеграм-канале (ТК). Переходите, кликнув по иконке

Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.

Определители.

С каждой квадратной матрицей связывают число. Это число называется определителем матрицы. Определитель вычисляется по особым правилам и обозначается |A|, det A, ΔA.

Число строк (столбцов) определителя называется его порядком.

Определитель первого порядка матрицы 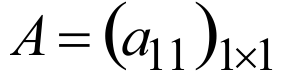равен элементу a₁₁: |A|=a₁₁

ПРИМЕРЫ:

Не путать определитель первого порядка с модулем.

Определитель второго порядка обозначается символом

и равен |A|=a₁₁a₂₂-a₁₂a₂₁

ПРИМЕРЫ:

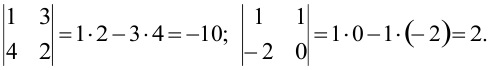
Определитель 3-го порядка обозначается символом

Для запоминания этой формулы используют схематические правила (правило треугольника или Саррюса)

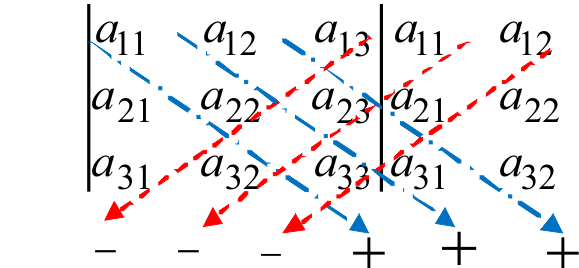
Правило Саррюса.

Правило треугольника.

Посмотрим на примере, как используются эти правила.

ПРИМЕР:

Правило Саррюса

Допишем к определителю два первых столбца.

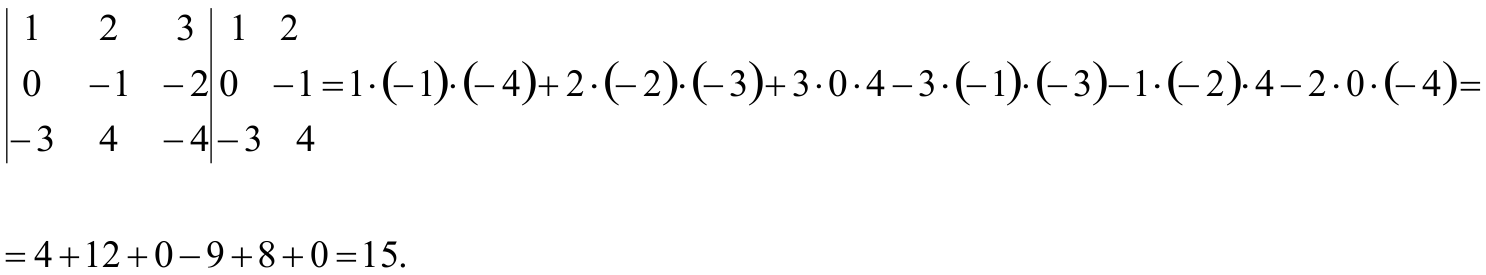
Правило треугольника

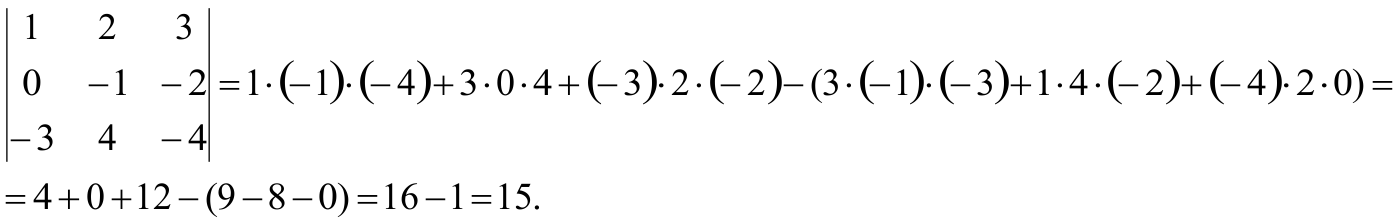
Такой способ вычисления определителей не подходит для определителей 4-го порядка и выше. Прежде чем указать правило, которое позволяет находить определители любого порядка, рассмотрим понятие алгебраического дополнения элемента матрицы.

Алгебраическим дополнением (А_ij ) элемента а_ij определителя матрицы А называется число, равное произведению (-1)^i+j (в степени номер строки плюс номер столбца этого элемента) на определитель, который получается из данного в результате вычеркивания строки и столбца, где стоит этот элемент.

ПРИМЕР:

Вычислить алгебраическое дополнение А₂₁ элемента а₂₁ .

РЕШЕНИЕ:

По определению алгебраического дополнения

Вычисление определителя произвольного порядка.Определитель равен сумме произведений элементов любой его строки (или столбца) на соответствующие алгебраические дополнения.

Например, разложение определителя 4-го порядка по первой строке выглядит следующим образом:

ПРИМЕР: Вычислить определитель

РЕШЕНИЕ: Разложим определитель по второму столбцу (Выбирать лучше ту строку (или тот столбец), где больше нулей, если они есть).

Упражнения к уроку:

Показать ответ

Если вы приступили к изучению данной темы, то вы уже знакомы с понятием определителя матрицы и умеете находить определители первого, второго и третьего порядка.

Прежде чем начать рассмотрение новой темы, рекомендуется повторить правило вычисления определителя по строке и столбцу, рассматривающееся в теме «Как вычислить определитель матрицы третьего порядка», свойства определителей, а также нахождение миноров и алгебраических дополнений.

Разложение определителей по строкам или столбцам

Для вычисления определителей высших порядков применяется способ разложения определителя по строке или столбцу. Это позволяет представить детерминант в виде суммы произведений элементов какой-либо его строки или столбца на соответствующие этим элементам алгебраические дополнения. В таком случае вычисление определителя nn-го порядка сводится к вычислению определителей n−1n-1-го порядка.

Пример 1

Найти определитель ∣32454−32−45−2−3−7−3429∣begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix} двумя способами:

1. по 2-й строке;
2. по 3-у столбцу.

1 способ. Разложим определитель 4-го порядка по строке №2 и вычислим его:

∣32454−32−45−2−3−7−3429∣=4(−1)2+1∣245−2−3−7429∣+(−3)(−1)2+2∣3455−3−7−329∣+2(−1)2+3∣3255−2−7−349∣+(−4)(−1)2+4∣3245−2−3−342∣=begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix}=4(-1)^{2+1}begin{vmatrix}2&4&5\-2&-3&-7\4&2&9end{vmatrix}+(-3)(-1)^{2+2}begin{vmatrix}3&4&5\5&-3&-7\-3&2&9end{vmatrix}+2(-1)^{2+3}begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}+(-4)(-1)^{2+4}begin{vmatrix}3&2&4\5&-2&-3\-3&4&2end{vmatrix}=

=−4∣245−2−3−7429∣−3∣3455−3−7−329∣−2∣3255−2−7−349∣−4∣3245−2−3−342∣=−4(−54−20−112+60+28+72)−3(−81+50+84−45+42−180)−2(−54+100+42−30+84−90)−4(−12+80+18−24+36−20)=−4(−26)−3(−130)−2⋅52−4⋅78=104+390−104−312=78=-4begin{vmatrix}2&4&5\-2&-3&-7\4&2&9end{vmatrix}-3begin{vmatrix}3&4&5\5&-3&-7\-3&2&9end{vmatrix}-2begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}-4begin{vmatrix}3&2&4\5&-2&-3\-3&4&2end{vmatrix}=-4(-54-20-112+60+28+72)-3(-81+50+84-45+42-180)-2(-54+100+42-30+84-90)-4(-12+80+18-24+36-20)=-4(-26)-3(-130)-2cdot52-4cdot78=104+390-104-312=78.

2 способ. Разложим определитель 4-го порядка по 3 столбцу и вычислим его:

∣32454−32−45−2−3−7−3429∣=4(−1)1+3∣4−3−45−2−7−349∣+2(−1)2+3∣3255−2−7−349∣+(−3)(−1)3+3∣3254−3−4−349∣+2(−1)4+3∣3254−3−45−2−7∣=begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix}=4(-1)^{1+3}begin{vmatrix}4&-3&-4\5&-2&-7\-3&4&9end{vmatrix}+2(-1)^{2+3}begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}+(-3)(-1)^{3+3}begin{vmatrix}3&2&5\4&-3&-4\-3&4&9end{vmatrix}+2(-1)^{4+3}begin{vmatrix}3&2&5\4&-3&-4\5&-2&-7end{vmatrix}=

=4∣4−3−45−2−7−349∣−2∣3255−2−7−349∣−3∣3254−3−4−349∣−2∣3254−3−45−2−7∣=4(−72−80−63+24+112+135)−2(−54+100+42−30+84−90)−3(−81+80+24−45+48−72)−2(63−40−40+75−24+56)=4⋅56−2⋅52−3⋅(−45)−2⋅90=224−104+138−180=78=4begin{vmatrix}4&-3&-4\5&-2&-7\-3&4&9end{vmatrix}-2begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}-3begin{vmatrix}3&2&5\4&-3&-4\-3&4&9end{vmatrix}-2begin{vmatrix}3&2&5\4&-3&-4\5&-2&-7end{vmatrix}=4(-72-80-63+24+112+135)-2(-54+100+42-30+84-90)-3(-81+80+24-45+48-72)-2(63-40-40+75-24+56)=4cdot56-2cdot52-3cdot(-45)-2cdot90=224-104+138-180=78.

Метод понижения порядка

Для упрощения расчетов при вычислении определителей рекомендуется применять их свойства. Рассмотрим примеры вычисления определителей с применением их свойств.

Пример 1

Вычислить определитель

∣638−45642034241−46∣begin{vmatrix}6&3&8&-4\5&6&4&2\0&3&4&2\4&1&-4&6end{vmatrix}.

Вынесем из столбца №3 множитель 4:

∣638−45642034241−46∣=4⋅∣632−45612031241−16∣begin{vmatrix}6&3&8&-4\5&6&4&2\0&3&4&2\4&1&-4&6end{vmatrix}=4cdotbegin{vmatrix}6&3&2&-4\5&6&1&2\0&3&1&2\4&1&-1&6end{vmatrix}.

Вынесем из столбца №4 множитель 2:

4⋅∣632−45612031241−16∣=4⋅2⋅∣632−25611031141−13∣=8⋅∣632−25611031141−13∣4cdotbegin{vmatrix}6&3&2&-4\5&6&1&2\0&3&1&2\4&1&-1&6end{vmatrix}=4cdot2cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}.

Прибавим к строке №1 строку №2, умноженную на -2:

8⋅∣632−25611031141−13∣=8⋅∣−4−90−45611031141−13∣8cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}.

Прибавим к строке №3 строку №2, умноженную на -1:

8⋅∣−4−90−45611031141−13∣=8⋅∣−4−90−45611−5−30041−13∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\4&1&-1&3end{vmatrix}.

Прибавим к строке №4 строку №2, умноженную на 1:

8⋅∣−4−90−45611−5−30041−13∣=8⋅∣−4−90−45611−5−3009704∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\9&7&0&4end{vmatrix}.

Разложим определитель по столбцу №3:

8⋅∣−4−90−45611−5−3009704∣=8⋅1⋅(−1)2+3∣−4−9−4−5−30974∣=8⋅(−1)5∣−4−9−4−5−30974∣=−8∣−4−9−4−5−30974∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\9&7&0&4end{vmatrix}=8cdot1cdot(-1)^{2+3}begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=8cdot(-1)^{5}begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=-8begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}.

Прибавим к строке №1 строку №3, умноженную на 1:

−8∣−4−9−4−5−30974∣=−8∣5−20−5−30974∣-8begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=-8begin{vmatrix}5&-2&0\-5&-3&0\9&7&4end{vmatrix}.

Разложим определитель по столбцу №3 и вычислим его:

−8∣5−20−5−30974∣=−8⋅4⋅(−1)3+3∣5−2−5−3∣=−32⋅(−1)6∣5−2−5−3∣=−32∣5−2−5−3∣-8begin{vmatrix}5&-2&0\-5&-3&0\9&7&4end{vmatrix}=-8cdot4cdot(-1)^{3+3}begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32cdot(-1)^{6}begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32begin{vmatrix}5&-2\-5&-3end{vmatrix}.

Прибавим к строке №2 строку №1, умноженную на 1:

−32∣5−2−5−3∣=−32∣5−20−5∣-32begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32begin{vmatrix}5&-2\0&-5end{vmatrix}.

Разложим определитель по столбцу №1 и заменим определитель 1-го порядка единственным его элементом:

−32∣5−20−5∣=−32⋅5⋅(−1)1+1⋅(−5)=−32⋅5⋅1⋅(−5)=800-32begin{vmatrix}5&-2\0&-5end{vmatrix}=-32cdot5cdot(-1)^{1+1}cdot(-5)=-32cdot5cdot1cdot(-5)=800.

Пример 2

Вычислить определитель

∣44−10−18237523325732122112176657211221∣begin{vmatrix}4&4&-1&0&-1&8\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №1 строку №4, умноженную на -4:

∣44−10−18237523325732122112176657211221∣=∣0−4−9−4−50237523325732122112176657211221∣begin{vmatrix}4&4&-1&0&-1&8\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №2 строку №4, умноженную на -2:

∣0−4−9−4−50237523325732122112176657211221∣=∣0−4−9−4−500−1330−1325732122112176657211221∣begin{vmatrix}0&-4&-9&-4&-5&0\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №3 строку №4, умноженную на -3:

∣0−4−9−4−500−1330−1325732122112176657211221∣=∣0−4−9−4−500−1330−10−4−140−4122112176657211221∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №5 строку №4, умноженную на -1:

∣0−4−9−4−500−1330−10−4−140−4122112176657211221∣=∣0−4−9−4−500−1330−10−4−140−4122112054545211221∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №6 строку №4, умноженную на -2:

∣0−4−9−4−500−1330−10−4−140−4122112054545211221∣=∣0−4−9−4−500−1330−10−4−140−41221120545450−3−300−3∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\0&-3&-3&0&0&-3end{vmatrix}.

Разложим определитель по 1 столбцу:

∣0−4−9−4−500−1330−10−4−140−41221120545450−3−300−3∣=1⋅(−1)4+1∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣=−∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\0&-3&-3&0&0&-3end{vmatrix}=1cdot(-1)^{4+1}begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.

Прибавим к строке №1 строку №3, умноженную на -1:

−∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣=−∣0−8−8−54−1330−1−4−140−454545−3−300−3∣-begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.

Прибавим к строке №3 строку №2, умноженную на -4:

−∣0−8−8−54−1330−1−4−140−454545−3−300−3∣=−∣0−8−8−54−1330−10−13−80054545−3−300−3∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.

Прибавим к строке №4 строку №2, умноженную на 5:

−∣0−8−8−54−1330−10−13−80054545−3−300−3∣=−∣0−8−8−54−1330−10−13−8000192040−3−300−3∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\-3&-3&0&0&-3end{vmatrix}.

Прибавим у строке №5 строку №2, умноженную на -3:

−∣0−8−8−54−1330−10−13−8000192040−3−300−3∣=−∣0−8−8−54−1330−10−13−80001920400−12−900∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\0&-12&-9&0&0end{vmatrix}.

Разложим определитель по 1 столбцу:

−∣0−8−8−54−1330−10−13−80001920400−12−900∣=−(−1)⋅(−1)2+1∣−8−8−54−13−800192040−12−900∣=(−1)3∣−8−8−54−13−800192040−12−900∣=−∣−8−8−54−13−800192040−12−900∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\0&-12&-9&0&0end{vmatrix}=-(-1)cdot(-1)^{2+1}begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=(-1)^{3}begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=-begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}.

Вынесем множитель -3 из строки №4:

−∣−8−8−54−13−800192040−12−900∣=−(−3)∣−8−8−54−13−8001920404300∣=3∣−8−8−54−13−8001920404300∣-begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=-(-3)begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}=3begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}.

Разложим определитель по 4 столбцу:

3∣−8−8−54−13−8001920404300∣=3⋅4⋅(−1)1+4∣−13−8019204430∣=12⋅(−1)5∣−13−8019204430∣=−12∣−13−8019204430∣3begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}=3cdot4cdot(-1)^{1+4}begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=12cdot(-1)^{5}begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=-12begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}.

Разложим определитель по столбцу №3 и вычислим его:

−12∣−13−8019204430∣=−12⋅4⋅(−1)2+3∣−13−843∣=−48⋅(−1)5∣−13−843∣=48∣−13−843∣-12begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=-12cdot4cdot(-1)^{2+3}begin{vmatrix}-13&-8\4&3end{vmatrix}=-48cdot(-1)^{5}begin{vmatrix}-13&-8\4&3end{vmatrix}=48begin{vmatrix}-13&-8\4&3end{vmatrix}.

Прибавим к строке №1 строку №2, умноженную на 3:

48∣−13−843∣=48∣−1143∣48begin{vmatrix}-13&-8\4&3end{vmatrix}=48begin{vmatrix}-1&1\4&3end{vmatrix}.

Прибавим к строке №2 строку №1, умноженную на 4:

48∣−1143∣=48∣−1107∣48begin{vmatrix}-1&1\4&3end{vmatrix}=48begin{vmatrix}-1&1\0&7end{vmatrix}.

Разложим определитель по столбцу №1 и заменим определитель 1-го порядка единственным его элементом:

48∣−1107∣=48⋅(−1)⋅(−1)1+1⋅7=48⋅(−1)⋅1⋅7=−33648begin{vmatrix}-1&1\0&7end{vmatrix}=48cdot(-1)cdot(-1)^{1+1}cdot7=48cdot(-1)cdot1cdot7=-336
.

Приведение к треугольному виду

Данный метод состоит в том, чтобы привести определитель к треугольному виду, а затем вычислить произведение элементов, стоящих на главной диагонали.

Пример 1

Вычислить определитель ∣4−20532−21−213−123−6−3∣begin{vmatrix}4&-2&0&5\3&2&-2&1\-2&1&3&-1\2&3&-6&-3end{vmatrix}.

Поменяем местами строки №1 и №3:

∣4−20532−21−213−123−6−3∣=−∣−213−132−214−20523−6−3∣begin{vmatrix}4&-2&0&5\3&2&-2&1\-2&1&3&-1\2&3&-6&-3end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\2&3&-6&-3end{vmatrix}.

Прибавим к строке №4 строку №1, умноженную на 1:

−∣−213−132−214−20523−6−3∣=−∣−213−132−214−20504−3−4∣-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\2&3&-6&-3end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\0&4&-3&-4end{vmatrix}.

Прибавим к строке №3 строку №1, умноженную на 2:

−∣−213−132−214−20504−3−4∣=−∣−213−132−21006304−3−4∣-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\0&4&-3&-4end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\0&0&6&3\0&4&-3&-4end{vmatrix}.

Умножим строку №2 на 2:

∣−213−132−21006304−3−4∣=−12∣−213−164−42006304−3−4∣begin{vmatrix}-2&1&3&-1\3&2&-2&1\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}begin{vmatrix}-2&1&3&-1\6&4&-4&2\0&0&6&3\0&4&-3&-4end{vmatrix}.

Прибавим к строке №2 строку №1, умноженную на 3:

−12∣−213−164−42006304−3−4∣=−12∣−213−1075−1006304−3−4∣-frac{1}{2}begin{vmatrix}-2&1&3&-1\6&4&-4&2\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&4&-3&-4end{vmatrix}.

Умножим строку №4 на 7:

−12∣−213−1075−1006304−3−4∣=−12⋅17∣−213−1075−10063028−21−28∣-frac{1}{2}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&28&-21&-28end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на -4:

−12⋅17∣−213−1075−10063028−21−28∣=−12⋅17∣−213−1075−1006300−41−24∣-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&28&-21&-28end{vmatrix}=-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&0&-41&-24end{vmatrix}.

Поменяем местами столбцы №3 и №4:

−12⋅17∣−213−1075−1006300−41−24∣=12⋅17∣−21−1307−15003600−24−41∣-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&0&-41&-24end{vmatrix}=frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&-24&-41end{vmatrix}.
Прибавим к строке №4 строку №3, умноженную на 8 и вычислим определитель:

12⋅17∣−21−1307−15003600−24−41∣=12⋅17∣−21−1307−1500360007∣=12⋅17⋅(−2)⋅7⋅3⋅7=−21frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&-24&-41end{vmatrix}=frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&0&7end{vmatrix}=frac{1}{2}cdotfrac{1}{7}cdot(-2)cdot7cdot3cdot7=-21.

Пример 2

Вычислить определитель

∣7694−410−266789−1−61−1−245−70−92−2∣begin{vmatrix}7&6&9&4&-4\1&0&-2&6&6\7&8&9&-1&-6\1&-1&-2&4&5\-7&0&-9&2&-2end{vmatrix}.

Поменяем местами строки №1 и №4:

∣7694−410−266789−1−61−1−245−70−92−2∣=−∣1−1−24510−266789−1−67694−4−70−92−2∣begin{vmatrix}7&6&9&4&-4\1&0&-2&6&6\7&8&9&-1&-6\1&-1&-2&4&5\-7&0&-9&2&-2end{vmatrix}=-begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\7&8&9&-1&-6\7&6&9&4&-4\-7&0&-9&2&-2end{vmatrix}.

Поменяем местами строки №3 и №5:

−∣1−1−24510−266789−1−67694−4−70−92−2∣=∣1−1−24510−266−70−92−27694−4789−1−6∣-begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\7&8&9&-1&-6\7&6&9&4&-4\-7&0&-9&2&-2end{vmatrix}=begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\-7&0&-9&2&-2\7&6&9&4&-4\7&8&9&-1&-6end{vmatrix}.

Поменяем местами столбцы №4 и №5:

∣1−1−24510−266−70−92−27694−4789−1−6∣=−∣1−1−25410−266−70−9−22769−44789−6−1∣begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\-7&0&-9&2&-2\7&6&9&4&-4\7&8&9&-1&-6end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\1&0&-2&6&6\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}.

Прибавим к строке №2 строку №1, умноженную на -1:

−∣1−1−25410−266−70−9−22769−44789−6−1∣=−∣1−1−25401012−70−9−22769−44789−6−1∣-begin{vmatrix}1&-1&-2&5&4\1&0&-2&6&6\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}.

Прибавим к строке №4 строку №3, умноженную на 1:

−∣1−1−25401012−70−9−22769−44789−6−1∣=−∣1−1−25401012−70−9−22060−66789−6−1∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\7&8&9&-6&-1end{vmatrix}.

Прибавим к строке №5 строку №3, умноженную на 1:

−∣1−1−25401012−70−9−22060−66789−6−1∣=−∣1−1−25401012−70−9−22060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.

Прибавим к строке №3 строку №1, умноженную на 7:

−∣1−1−25401012−70−9−22060−66080−81∣=−∣1−1−254010120−7−233330060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&-7&-23&33&30\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.

Прибавим к строке №3 строку №2, умноженную на 7:

−∣1−1−254010120−7−233330060−66080−81∣=−∣1−1−2540101200−234044060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&-7&-23&33&30\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.

Вынесем из строки №4 множитель 6:

−∣1−1−2540101200−234044060−66080−81∣=−6∣1−1−2540101200−234044010−11080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&8&0&-8&1end{vmatrix}.

Прибавим к строке №5 строку №4, умноженную на -8:

−6∣1−1−2540101200−234044010−11080−81∣=−6∣1−1−2540101200−234044010−110000−7∣-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&8&0&-8&1end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&0&0&0&-7end{vmatrix}.

Прибавим к строке №4 строку №2, умноженную на -1 и вычислим определитель:

−6∣1−1−2540101200−234044010−110000−7∣=−6∣1−1−2540101200−234044000−2−10000−7∣=−6⋅1⋅1⋅(−23)⋅(−2)⋅(−7)=1932-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&0&0&0&-7end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&0&0&-2&-1\0&0&0&0&-7end{vmatrix}=-6cdot1cdot1cdot(-23)cdot(-2)cdot(-7)=1932.

Мы рассмотрели наиболее распространенные методы вычисления определителей высших порядков. Каждый из них может применяться для их нахождения.

Онлайн-помощь с решением контрольных работ на бирже Студворк!

Тест по теме «Как вычислить определитель матрицы высших порядков»

Содержание:

• Вычисления определителей второго порядка
• Методы вычисления определителей третьего порядка
• Приведение определителя к треугольному виду
• Правило треугольника
• Правило Саррюса
• Разложение определителя по строке или столбцу
• Разложение определителя по элементам строки или столбца
• Теорема Лапласа

В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.

Вычисления определителей второго порядка

Чтобы вычислить определитель матрицы второго порядка, надо от произведения
элементов главной диагонали отнять произведение
элементов побочной диагонали:

$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$

Методы вычисления определителей третьего порядка

Для вычисления определителей третьего порядка существует такие правила.

Правило треугольника

Схематически это правило можно изобразить следующим образом:

Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.

$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$

$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:

$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.

Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.

Разложение определителя по элементам строки или столбца

Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.

Теорема Лапласа

Читать дальше: обратная матрица.

Задача 1.

Вычислить определитель

.

Указание

Воспользуйтесь либо правилом треугольников, либо разложением определителя по 2-й строке или 2-му столбцу, содержащим нулевой элемент.

Решение

1-й способ (правило треугольников).

Вычислим определитель 3-го порядка, используя его определение:

Δ = 2·0·(-1) + (-3)·(-4)·2 + 5·1·1 — 2·0·5 -1·(-4)·2 – (-1)·1·(-3) =

= 0 + 24 + 5 – 0 + 8 – 3 = 34.

2-й способ (разложение по строке).

Применим свойство определителя:

.

Для удобства вычисления выберем 2-ю строку, содержащую нулевой элемент (А22 = 0), поскольку при этом нет необходимости находить А22, так как произведение А22 А22 = 0. Итак,

(напомним, что определитель второго порядка, входящий в алгебраическое дополнение Aij, получается вычеркиванием из исходного определителя I-й строки и J-го столбца).

Тогда Δ = А21 А21 + А23 А23 = 1·2 + (-4)(-8) = 34.

Ответ: Δ = 34.

Задача 2.

Используя свойства определителя, вычислить определитель

.

Указание

Вычитая из 2-й и 3-й строк определителя соответствующие элементы 1-й строки, добьемся того, что в 1-м столбце останется только один ненулевой элемент. Далее можно разложить определитель по 1-му столбцу.

Решение

Поскольку все элементы первого столбца равны 1, вычтем из 2-й и 3-й строк определителя соответствующие элементы 1-й строки (при этом величина определителя не изменится – свойство 6):

.

Заметим, что теперь все элементы 2-й строки кратны двум, а элементы 3-й строки кратны трем. По следствию 2.2 соответствующие множители можно вынести за знак определителя:

.

Вычтем из элементов 3-й строки полученного определителя соответствующие элементы 2-й строки:

И разложим определитель по 1-му столбцу:

Ответ: Δ = 6.

Задача 3.

Используя свойства определителей, вычислить определитель

.

Указание

Прибавьте к элементам 2-й строки соответствующие элементы 1-й строки, а из элементов 3-й строки вычтите удвоенные элементы 1-й строки. Затем вынесите за знак определителя все общие множители элементов какой-либо строки или столбца.

Решение

Прибавим к элементам 2-й строки соответствующие элементы 1-й строки, а из элементов 3-й строки вычтем удвоенные элементы 1-й строки:

Вынесем за знак определителя множитель -1 из 2-й строки и 3 – из 3-й:

Теперь из 3-го столбца вынесем множитель -2:

Вычтем из элементов 2-го столбца элементы 3-го столбца и разложим полученный определитель по 3-й строке:

Ответ: Δ = 306.

Задача 4.

Решить уравнение

Указание

Разложив определитель, стоящий в левой части равенства, по первой строке, и приравняв его 40, вы получите квадратное уравнение для Х.

Решение

Разложим определитель, стоящий в левой части равенства, по первой строке. Предварительно найдем соответствующие алгебраические дополнения:

Тогда

И требуется решить квадратное уравнение

.

Ответ:

Задача 5.

Решить неравенство

Указание

Раскройте определитель, стоящий в левой части неравенства, по 1-й строке.

Решение

Раскроем определитель, стоящий в левой части неравенства, по 1-й строке:

3(10 — 12) – X(2X – 9) + 4X – 15 > — 3;

-2X2 + 13X – 18 > 0;

2X2 – 13X + 18 < 0;

2 < X < 4,5.

Ответ: (2; 4,5).

Задача 6.

Используя свойства определителей (не раскрывая определитель), вычислить определитель

Указание

Используйте тригонометрическую формулу cos 2A = cos2A — sin2A и свойство определителя с двумя равными столбцами.

Решение

Из тригонометрии известно, что cos 2A = cos2A — sin2A. Вычтем из элементов

2-го столбца определителя соответствующие элементы 1-го столбца:

У полученного определителя, равного исходному (свойство 6), два столбца одинаковы, поэтому он равен нулю (следствие 2.1).

Ответ: 0.

Задача 7.

Вычислить определитель 4-го порядка

.

Указание

Преобразуйте определитель так, чтобы три из четырех элементов какой-либо строки или столбца стали равными нулю. Для этого воспользуйтесь свойством 6.

Решение

Преобразуем определитель так, чтобы три из четырех элементов какой-либо строки или столбца стали равными нулю. Для этого воспользуемся свойством 6. Его особенно удобно применять, если в определителе существует элемент, равный +1. Выберем в качестве такого элемента А13 = 1 и с его помощью обратим все остальные элементы 3-го столбца в нуль. С этой целью:

А) к элементам 2-й строки прибавим соответствующие элементы 1-й строки;

Б) из элементов 3-й строки вычтем элементы 1-й строки, умноженные на 2;

В) из элементов 4-й строки вычтем элементы 1-й строки

(напомним, что при этом величина определителя не изменится). Тогда

Разложим полученный определитель по 3-му столбцу:

Вычтем из элементов 1-й строки нового определителя удвоенные элементы 2-й строки:

И разложим этот определитель по 1-й строке:

Ответ: Δ = -9.

Задача 8.

Вычислить определитель 4-го порядка

Указание

Разложите определитель по 1-й строке, а затем полученный определитель 3-го порядка вновь разложите по 1-й строке.

Решение

Разложим определитель по 1-й строке:

Полученный определитель 3-го порядка вновь разложим по 1-й строке:

Ответ: Δ = 24.

Ответ: Δ = 24.

< Предыдущая		Следующая >