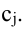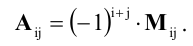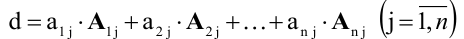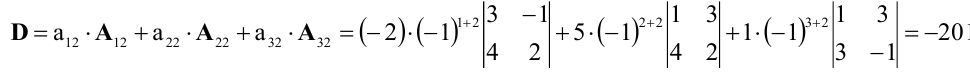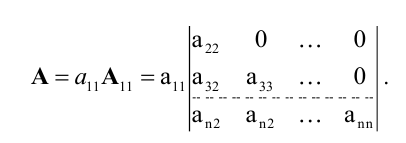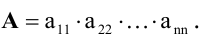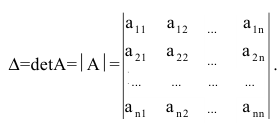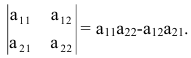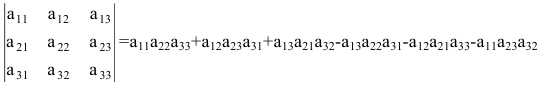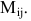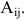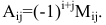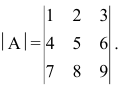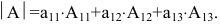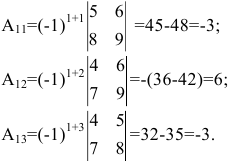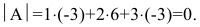Понятие минора и алгебраического дополнения было рассмотрено нами в теме «Как вычислить определитель матрицы третьего порядка». В данной статье разберем тему более подробно, а также научимся вычислять миноры и алгебраические дополнения матриц высших порядков.
Сначала рекомендуется повторить вычисление определителей второго, третьего и высших порядков.
Минор
Минором MijM_{ij} к элементу aija_{ij} определителя nn-го порядка называется определитель (n−1)(n-1)-го порядка, который получается из исходного определителя вычеркиванием ii-той строки и jj-того столбца.
Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M12M_{12} получается вычеркиванием 1-й строки и 2-го столбца, M34M_{34} — вычеркиванием 3-й строки и 4-го столбца.
Алгоритм нахождения миноров
- вычеркиваем i-ю строку;
- вычеркиваем j-й столбец;
- записываем определитель, который получили в результате действий 1 и 2.
Пример 1
Найти минор M34M_{34} к элементу a34a_{34} определителя ∣21−23−121213−1543−31∣begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
M34=∣21−23−121213−1543−31∣=∣21−2−12143−3∣=2⋅2⋅(−3)+1⋅1⋅4+(−2)⋅3⋅(−1)−(−2)⋅2⋅4−1⋅(−3)⋅(−1)−2⋅1⋅3=−12+4+6+16−3−6=5M_{34}=begin{vmatrix}2&1&-2&color{green}3\-1&2&1&color{green}2\color{green}1&color{green}3&color{green}-1&color{green}5\4&3&-3&color{green}1end{vmatrix}=begin{vmatrix}2&1&-2\-1&2&1\4&3&-3end{vmatrix}=2cdot2cdot(-3)+1cdot1cdot4+(-2)cdot3cdot(-1)-(-2)cdot2cdot4-1cdot(-3)cdot(-1)-2cdot1cdot3=-12+4+6+16-3-6=5.
Пример 2
Найти миноры матрицы K=(03−122100−2−102−5711)K= begin{pmatrix}0&3&-1&2\2&1&0&0\-2&-1&0&2\-5&7&1&1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
M11=(03−122100−2−102−5711)=∣100−102711∣=1⋅(−1)1+1∣0211∣=1⋅(−1)2∣0211∣=∣0211∣=1⋅(−1)2+1⋅2=1⋅(−1)3⋅2=−2M_{11}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\color{green}2&1&0&0\color{green}-2&-1&0&2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=1cdot(-1)^{1+1}begin{vmatrix}0&2\1&1end{vmatrix}=1cdot(-1)^{2}begin{vmatrix}0&2\1&1end{vmatrix}=begin{vmatrix}0&2\1&1end{vmatrix}=1cdot(-1)^{2+1}cdot2=1cdot(-1)^{3}cdot2=-2,
M12=(03−122100−2−102−5711)=∣200−202−511∣=2⋅(−1)1+1∣0211∣=2⋅(−1)2∣0211∣=2∣0211∣=2⋅(−1)2+1⋅2=2⋅(−1)3⋅2=−4M_{12}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&color{green}1&0&0\-2&color{green}-1&0&2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=2cdot(-1)^{1+1}begin{vmatrix}0&2\1&1end{vmatrix}=2cdot(-1)^{2}begin{vmatrix}0&2\1&1end{vmatrix}=2begin{vmatrix}0&2\1&1end{vmatrix}=2cdot(-1)^{2+1}cdot2=2cdot(-1)^{3}cdot2=-4,
M13=(03−122100−2−102−5711)=∣210−2−12−571∣=2⋅(−1)⋅1+0⋅7⋅(−2)+1⋅2⋅(−5)−0⋅(−1)⋅(−5)−2⋅2⋅7−1⋅1⋅(−2)=−2−10−28+2=−38M_{13}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&1&color{green}0&0\-2&-1&color{green}0&2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=2cdot(-1)cdot1+0cdot7cdot(-2)+1cdot2cdot(-5)-0cdot(-1)cdot(-5)-2cdot2cdot7-1cdot1cdot(-2)=-2-10-28+2=-38,
M14=(03−122100−2−102−5711)=∣210−2−10−571∣=1⋅(−1)3+3∣21−2−1∣=0M_{14}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&1&0&color{green}0\-2&-1&0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=1cdot(-1)^{3+3}begin{vmatrix}2&1\-2&-1end{vmatrix}=0,
M21=(03−122100−2−102−5711)=∣3−12−102711∣=3⋅0⋅1+2⋅1⋅(−1)+(−1)⋅2⋅7−2⋅0⋅7−(−1)⋅1⋅(−1)−3⋅2⋅1=−2−14−1−6=−23M_{21}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&color{green}1&color{green}0&color{green}0\color{green}-2&-1&0&2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=3cdot0cdot1+2cdot1cdot(-1)+(-1)cdot2cdot7-2cdot0cdot7-(-1)cdot1cdot(-1)-3cdot2cdot1=-2-14-1-6=-23,
M22=(03−122100−2−102−5711)=∣0−12−202−511∣=0⋅0⋅1+(−1)⋅2⋅(−5)+2⋅1⋅(−2)−2⋅0⋅(−5)−(−1)⋅1⋅(−2)−0⋅2⋅1=10−4−2=4M_{22}= begin{pmatrix}0&color{green}3&-1&2\color{green}2&color{green}1&color{green}0&color{green}0\-2&color{green}-1&0&2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=0cdot0cdot1+(-1)cdot2cdot(-5)+2cdot1cdot(-2)-2cdot0cdot(-5)-(-1)cdot1cdot(-2)-0cdot2cdot1=10-4-2=4,
M23=(03−122100−2−102−5711)=∣032−2−12−571∣=0⋅(−1)⋅1+3⋅2⋅(−5)+2⋅7⋅(−2)−2⋅(−1)⋅(−5)−3⋅1⋅(−2)−0⋅2⋅7=−30−28−10+6=−62M_{23}= begin{pmatrix}0&3&color{green}-1&2\color{green}2&color{green}1&color{green}0&color{green}0\-2&-1&color{green}0&2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=0cdot(-1)cdot1+3cdot2cdot(-5)+2cdot7cdot(-2)-2cdot(-1)cdot(-5)-3cdot1cdot(-2)-0cdot2cdot7=-30-28-10+6=-62,
M24=(03−122100−2−102−5711)=∣03−1−2−10−571∣=0⋅(−1)⋅1+3⋅0⋅(−5)+(−1)⋅7⋅(−2)−(−1)⋅(−1)⋅(−5)−3⋅1⋅(−2)−0⋅0⋅7=14+5+6=25M_{24}= begin{pmatrix}0&3&-1&color{green}2\color{green}2&color{green}1&color{green}0&color{green}0\-2&-1&0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=0cdot(-1)cdot1+3cdot0cdot(-5)+(-1)cdot7cdot(-2)-(-1)cdot(-1)cdot(-5)-3cdot1cdot(-2)-0cdot0cdot7=14+5+6=25,
M31=(03−122100−2−102−5711)=∣3−12100711∣=1⋅(−1)2+1∣−1211∣=1⋅(−1)3∣−1211∣=−∣−1211∣=−(−1−2)=3M_{31}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&1&0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=1cdot(-1)^{2+1}begin{vmatrix}-1&2\1&1end{vmatrix}=1cdot(-1)^{3}begin{vmatrix}-1&2\1&1end{vmatrix}=-begin{vmatrix}-1&2\1&1end{vmatrix}=-(-1-2)=3,
M32=(03−122100−2−102−5711)=∣0−12200−511∣=2⋅(−1)2+1∣−1211∣=2⋅(−1)3∣−1211∣=−2∣−1211∣=−2(−1−2)=6M_{32}= begin{pmatrix}0&color{green}3&-1&2\2&color{green}1&0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=2cdot(-1)^{2+1}begin{vmatrix}-1&2\1&1end{vmatrix}=2cdot(-1)^{3}begin{vmatrix}-1&2\1&1end{vmatrix}=-2begin{vmatrix}-1&2\1&1end{vmatrix}=-2(-1-2)=6,
M33=(03−122100−2−102−5711)=∣032210−571∣=0⋅1⋅1+3⋅0⋅(−5)+2⋅7⋅2−2⋅1⋅(−5)−0⋅0⋅7−3⋅1⋅2=28+10−6=32M_{33}= begin{pmatrix}0&3&color{green}-1&2\2&1&color{green}0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=0cdot1cdot1+3cdot0cdot(-5)+2cdot7cdot2-2cdot1cdot(-5)-0cdot0cdot7-3cdot1cdot2=28+10-6=32,
M34=(03−122100−2−102−5711)=∣03−1210−571∣=0⋅1⋅1+3⋅0⋅(−5)+(−1)⋅7⋅2−(−1)⋅1⋅(−5)−3⋅1⋅2−0⋅0⋅7=−14−5−6=−25M_{34}= begin{pmatrix}0&3&-1&color{green}2\2&1&0&color{green}0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=0cdot1cdot1+3cdot0cdot(-5)+(-1)cdot7cdot2-(-1)cdot1cdot(-5)-3cdot1cdot2-0cdot0cdot7=-14-5-6=-25,
M41=(03−122100−2−102−5711)=∣3−12100−102∣=1⋅(−1)2+1∣−1202∣=1⋅(−1)3∣−1202∣=−∣−1202∣=−(−1)⋅(−1)1+1⋅2=1⋅(−1)2⋅2=2M_{41}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&1&0&0\color{green}-2&-1&0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=1cdot(-1)^{2+1}begin{vmatrix}-1&2\0&2end{vmatrix}=1cdot(-1)^{3}begin{vmatrix}-1&2\0&2end{vmatrix}=-begin{vmatrix}-1&2\0&2end{vmatrix}=-(-1)cdot(-1)^{1+1}cdot2=1cdot(-1)^{2}cdot2=2,
M42=(03−122100−2−102−5711)=∣0−12200−202∣=2⋅(−1)2+1∣−1202∣=2⋅(−1)3∣−1202∣=−2∣−1202∣=−2⋅(−1)⋅(−1)1+1⋅2=2⋅(−1)2⋅2=4M_{42}= begin{pmatrix}0&color{green}3&-1&2\2&color{green}1&0&0\-2&color{green}-1&0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=2cdot(-1)^{2+1}begin{vmatrix}-1&2\0&2end{vmatrix}=2cdot(-1)^{3}begin{vmatrix}-1&2\0&2end{vmatrix}=-2begin{vmatrix}-1&2\0&2end{vmatrix}=-2cdot(-1)cdot(-1)^{1+1}cdot2=2cdot(-1)^{2}cdot2=4,
M43=(03−122100−2−102−5711)=∣032210−2−12∣=0⋅1⋅2+3⋅0⋅(−2)+2⋅(−1)⋅2−2⋅1⋅(−2)−3⋅2⋅2−0⋅0⋅(−1)=−4+4−12=−12M_{43}= begin{pmatrix}0&3&color{green}-1&2\2&1&color{green}0&0\-2&-1&color{green}0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=0cdot1cdot2+3cdot0cdot(-2)+2cdot(-1)cdot2-2cdot1cdot(-2)-3cdot2cdot2-0cdot0cdot(-1)=-4+4-12=-12,
M44=(03−122100−2−102−5711)=∣03−1210−2−10∣=0M_{44}= begin{pmatrix}0&3&-1&color{green}2\2&1&0&color{green}0\-2&-1&0&color{green}2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0.
Алгебраическое дополнение
Алгебраическим дополнением AijA_{ij} к элементу aija_{ij} определителя n-го порядка называется число Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}, где i,ji, j — соответствующие строка и столбец, а MijM_{ij} — минор к элементу aija_{ij}.
Алгоритм нахождения алгебраических дополнений
- найти сумму номеров строки (i)(i) и столбца (j)(j);
- найти минор MijM_{ij} по алгоритму нахождения миноров, который представлен выше;
- подставить значения, полученные на шагах 1 и 2, в формулу Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}.
Пример 1
Найти алгебраическое дополнение A34A_{34} к элементу a34a_{34} определителя
∣21−23−121213−1543−31∣begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}.
A34=(−1)3+4⋅M34=(−1)7⋅∣21−23−121213−1543−31∣=−∣21−2−12143−3∣=−(2⋅2⋅(−3)+1⋅1⋅4+(−2)⋅3⋅(−1)−(−2)⋅2⋅4−1⋅(−3)⋅(−1)−2⋅1⋅3)=−(−12+4+6+16−3−6)=−5A_{34}=(-1)^{3+4}cdot M_{34}=(-1)^{7}cdot
begin{vmatrix}2&1&-2&color{green}3\-1&2&1&color{green}2\color{green}1&color{green}3&color{green}-1&color{green}5\4&3&-3&color{green}1end{vmatrix}=-begin{vmatrix}2&1&-2\-1&2&1\4&3&-3end{vmatrix}=-(2cdot2cdot(-3)+1cdot1cdot4+(-2)cdot3cdot(-1)-(-2)cdot2cdot4-1cdot(-3)cdot(-1)-2cdot1cdot3)=-(-12+4+6+16-3-6)=-5.
Пример 2
Найти алгебраические дополнения матрицы K=(03−122100−2−102−5711)K= begin{pmatrix}0&3&-1&2\2&1&0&0\-2&-1&0&2\-5&7&1&1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
A11=(−1)1+1⋅M11=(−1)1+1⋅∣100−102711∣=(−1)2∣100−102711∣=∣100−102711∣=−2A_{11}=(-1)^{1+1}cdot M_{11}=(-1)^{1+1}cdotbegin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=(-1)^{2}begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=-2,
A12=(−1)1+2⋅M12=(−1)1+2⋅∣200−202−511∣=(−1)3⋅∣200−202−511∣=−∣200−202−511∣=−(−4)=4A_{12}=(-1)^{1+2}cdot M_{12}=(-1)^{1+2}cdotbegin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=(-1)^{3}cdotbegin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=-begin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=-(-4)=4,
A13=(−1)1+3⋅M13=(−1)1+3⋅∣210−2−12−571∣=(−1)4⋅∣210−2−12−571∣=∣210−2−12−571∣=−38A_{13}=(-1)^{1+3}cdot M_{13}=(-1)^{1+3}cdot begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=(-1)^{4}cdot begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=-38,
A14=(−1)1+4⋅M14=(−1)1+4⋅∣210−2−10−571∣=(−1)5⋅∣210−2−10−571∣=−∣210−2−10−571∣=0A_{14}=(-1)^{1+4}cdot M_{14}=(-1)^{1+4}cdotbegin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=(-1)^{5}cdot begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=-begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=0,
A21=(−1)2+1⋅M21=(−1)2+1⋅∣3−12−102711∣=(−1)3⋅∣3−12−102711∣=−∣3−12−102711∣=−(−23)=23A_{21}=(-1)^{2+1}cdot M_{21}=(-1)^{2+1}cdotbegin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=(-1)^{3}cdotbegin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=-begin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=-(-23)=23,
A22=(−1)2+2⋅M22=(−1)2+2⋅∣0−12−202−511∣=(−1)4⋅∣0−12−202−511∣=∣0−12−202−511∣=4A_{22}=(-1)^{2+2}cdot M_{22}=(-1)^{2+2}cdotbegin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=(-1)^{4}cdotbegin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=begin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=4,
A23=(−1)2+3⋅M23=(−1)2+3⋅∣032−2−12−571∣=(−1)5⋅∣032−2−12−571∣=−∣032−2−12−571∣=−(−62)=62A_{23}=(-1)^{2+3}cdot M_{23}=(-1)^{2+3}cdotbegin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=-begin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=-(-62)=62,
A24=(−1)2+4⋅M24=(−1)2+4⋅∣03−1−2−10−571∣=(−1)6⋅∣03−1−2−10−571∣=∣03−1−2−10−571∣=25A_{24}=(-1)^{2+4}cdot M_{24}=(-1)^{2+4}cdotbegin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=begin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=25,
A31=(−1)3+1⋅M31=(−1)3+1⋅∣3−12100711∣=(−1)4⋅∣3−12100711∣=∣3−12100711∣=3A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{3+1}cdotbegin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=(-1)^{4}cdotbegin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=begin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=3,
A32=(−1)3+2⋅M32=(−1)3+2⋅∣0−12200−511∣=(−1)5⋅∣0−12200−511∣=−∣0−12200−511∣=−6A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{3+2}cdotbegin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=-begin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=-6,
A33=(−1)3+3⋅M33=(−1)3+3⋅∣032210−571∣=(−1)6⋅∣032210−571∣=∣032210−571∣=32A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{3+3}cdotbegin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=begin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=32,
A34=(−1)3+4⋅M34=(−1)3+4⋅∣03−1210−571∣=(−1)7⋅∣03−1210−571∣=−∣03−1210−571∣=−(−25)=25A_{34}=(-1)^{3+4}cdot M_{34}=(-1)^{3+4}cdotbegin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=(-1)^{7}cdotbegin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=-begin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=-(-25)=25,
A41=(−1)4+1⋅M41=(−1)4+1⋅∣3−12100−102∣=(−1)5⋅∣3−12100−102∣=−∣3−12100−102∣=−2A_{41}=(-1)^{4+1}cdot M_{41}=(-1)^{4+1}cdotbegin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=-begin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=-2,
A42=(−1)4+2⋅M42=(−1)4+2⋅∣0−12200−202∣=(−1)6⋅∣0−12200−202∣=∣0−12200−202∣=4A_{42}=(-1)^{4+2}cdot M_{42}=(-1)^{4+2}cdotbegin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=begin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=4,
A43=(−1)4+3⋅M43=(−1)4+3⋅∣032210−2−12∣=(−1)7⋅∣032210−2−12∣=−∣032210−2−12∣=−(−12)=12A_{43}=(-1)^{4+3}cdot M_{43}=(-1)^{4+3}cdotbegin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=(-1)^{7}cdotbegin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=-begin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=-(-12)=12,
A44=(−1)4+4⋅M44=(−1)4+4⋅∣03−1210−2−10∣=(−1)8⋅∣03−1210−2−10∣=∣03−1210−2−10∣=0A_{44}=(-1)^{4+4}cdot M_{44}=(-1)^{4+4}cdotbegin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=(-1)^{8}cdotbegin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0.
Задачи на заказ недорого по любому предмету от наших экспертов!
Тест по теме «Минор матрицы и алгебраическое дополнение матрицы»
Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.
В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме «Матрицы. Виды матриц. Основные термины». Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.
Содержание темы:
- Минор $M_{ij}$ элемента $a_{ij}$.
- Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$.
- Минор k-го порядка матрицы $A_{mtimes n}$. Главный минор, базисный минор, окаймляющий минор.
- Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Минор $M_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).
Минором $M_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ именуют определитель матрицы, полученной из матрицы $A$ вычёркиванием i-й строки и j-го столбца (т.е. строки и столбца, на пересечении которых находится элемент $a_{ij}$).
Для примера рассмотрим квадратную матрицу четвёртого порядка:
$A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$. Найдём минор элемента $a_{32}$, т.е. найдём $M_{32}$. Сперва запишем минор $M_{32}$, а потом вычислим его значение. Для того, чтобы составить $M_{32}$, вычеркнем из матрицы $A$ третью строку и второй столбец (именно на пересечении третьей строки и второго столбца расположен элемент $a_{32}$). Мы получим новую матрицу, определитель которой и есть искомый минор $M_{32}$:
Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$
M_{32}=left| begin{array} {ccc}
1 & -3 & 9\
2 & 11 & 5 \
3 & -5 & 58 end{array} right|=
1cdot 11cdot 58+(-3)cdot 5cdot 3+2cdot (-5)cdot 9-9cdot 11cdot 3-(-3)cdot 2cdot 58-5cdot (-5)cdot 1=579.
$$
Итак, минор элемента $a_{32}$ равен 579, т.е. $M_{32}=579$.
Часто вместо словосочетания «минор элемента матрицы» в литературе встречается «минор элемента определителя». Суть остается неизменной: чтобы получить минор элемента $a_{ij}$ нужно вычеркнуть из исходного определителя i-ю строку и j-й столбец. Оставшиеся элементы записывают в новый определитель, который и является минором элемента $a_{ij}$. Например, найдём минор элемента $a_{12}$ определителя
$left| begin{array} {ccc}
-1 & 3 & 2\
9 & 0 & -5 \
4 & -3 & 7 end{array} right|$. Чтобы записать требуемый минор $M_{12}$ нам понадобится вычеркнуть из заданного определителя первую строку и второй столбец:
Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:
$$
M_{12}=left| begin{array} {cc}
9 & -5\
4 & 7 end{array} right|=9cdot 7-(-5)cdot 4=83.
$$
Итак, минор элемента $a_{12}$ равен 83, т.е. $M_{12}=83$.
Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).
Алгебраическое дополнением $A_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ находится по следующей формуле:
$$
A_{ij}=(-1)^{i+j}cdot M_{ij},
$$
где $M_{ij}$ – минор элемента $a_{ij}$.
Найдем алгебраическое дополнение элемента $a_{32}$ матрицы $A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$, т.е. найдём $A_{32}$. Ранее мы уже находили минор $M_{32}=579$, поэтому используем полученный результат:
Обычно при нахождении алгебраических дополнений не вычисляют отдельно минор, а уж потом само дополнение. Запись минора опускают. Например, найдем $A_{12}$, если $A=left( begin{array} {ccc}
-5 & 10 & 2\
6 & 9 & -4 \
4 & -3 & 1 end{array} right)$. Согласно формуле $A_{12}=(-1)^{1+2}cdot M_{12}=-M_{12}$. Однако чтобы получить $M_{12}$ достаточно вычеркнуть первую строку и второй столбец матрицы $A$, так зачем же вводить лишнее обозначение для минора? Сразу запишем выражение для алгебраического дополнения $A_{12}$:
Минор k-го порядка матрицы $A_{mtimes n}$
Если в предыдущих двух пунктах мы говорили лишь о квадратных матрицах, то здесь поведём речь также и о прямоугольных матрицах, у которых количество строк вовсе не обязательно равняется количеству столбцов. Итак, пусть задана матрица $A_{mtimes n}$, т.е. матрица, содержащая m строк и n столбцов.
Минором k-го порядка матрицы $A_{mtimes n}$ называется определитель, элементы которого расположены на пересечении k строк и k столбцов матрицы $A$ (при этом предполагается, что $k≤ m$ и $k≤ n$).
Например, рассмотрим такую матрицу:
$$A=left( begin{array} {cccc}
-1 & 0 & -3 & 9\
2 & 7 & 14 & 6 \
15 & -27 & 18 & 31\
0 & 1 & 19 & 8\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$
Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:
$$
left( begin{array} {cccc}
-1 & 0 & -3 & 9 \
boldblue{2} & boldblue{7} & 14 & boldblue{6} \
15 & -27 & 18 & 31\
boldblue{0} & boldblue{1} & 19 & boldblue{8}\
0 & -12 & 20 & 14\
boldblue{5} & boldblue{3} & -21 & boldblue{9}\
23 & -10 & -5 & 58 end{array} right);;
M=left|begin{array} {ccc}
2 & 7 & 6 \
0 & 1 & 8 \
5 & 3 & 9 end{array} right|.
$$
Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.
Минор k-го порядка матрицы $A_{mtimes n}=(a_{ij})$ называется главным, если на главной диагонали данного минора находятся только главные диагональные элементы матрицы $A$.
Напомню, что главными диагональными элементами именуют те элементы матрицы, у которых индексы равны: $a_{11}$, $a_{22}$, $a_{33}$ и так далее. Например, для рассмотренной выше матрицы $A$ такими элементами будут $a_{11}=-1$, $a_{22}=7$, $a_{33}=18$, $a_{44}=8$. На рисунке они выделены зелёным цветом:
$$left( begin{array} {cccc}
boldgreen{-1} & 0 & -3 & 9\
2 & boldgreen{7} & 14 & 6 \
15 & -27 & boldgreen{18} & 31\
0 & 1 & 19 & boldgreen{8}\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$
Например, если в матрице $A$ мы вычеркнем строки и столбцы с номерами 1 и 3, то на их пересечении будут расположены элементы минора второго порядка, на главной диагонали которого будут находиться только диагональные элементы матрицы $A$ (элементы $a_{11}=-1$ и $a_{33}=18$ матрицы $A$). Следовательно, мы получим главный минор второго порядка:
$$
M=left|begin{array} {cc}
boldgreen{-1} & -3 \
15 & boldgreen{18} end{array} right|
$$
Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.
Пусть некий минор $M$ k-го порядка матрицы $A_{mtimes n}$ не равен нулю, т.е. $Mneq 0$. При этом все миноры, порядок которых выше k, равны нулю. Тогда минор $M$ называют базисным, а строки и столбцы, на которых расположены элементы базисного минора, именуют базисными строками и базисными столбцами.
Для примера рассмотрим такую матрицу:
$$A=left( begin{array} {ccc}
-1 & 0 & 3 & 0 & 0 \
2 & 0 & 4 & 1 & 0\
1 & 0 & -2 & -1 & 0\
0 & 0 & 0 & 0 & 0 end{array} right)
$$
Запишем минор этой матрицы, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов с №1, №3, №4. Мы получим минор третьего порядка (его элементы выделены в матрице $A$ фиолетовым цветом):
$$
left( begin{array} {ccc}
boldpurple{-1} & 0 & boldpurple{3} & boldpurple{0} & 0 \
boldpurple{2} & 0 & boldpurple{4} & boldpurple{1} & 0\
boldpurple{1} & 0 & boldpurple{-2} & boldpurple{-1} & 0\
0 & 0 & 0 & 0 & 0 end{array} right);;
M=left|begin{array} {ccc}
-1 & 3 & 0 \
2 & 4 & 1 \
1 & -2 & -1 end{array} right|.
$$
Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$
M=left| begin{array} {ccc}
-1 & 3 & 0\
2 & 4 & 1 \
1 & -2 & -1 end{array} right|=4+3+6-2=11.
$$
Итак, $M=11neq 0$. Теперь попробуем составить любой минор, порядок которого выше трёх. Чтобы составить минор четвёртого порядка, нам придётся использовать четвёртую строку, однако все элементы этой строки равны нулю. Следовательно, в любом миноре четвёртого порядка будет нулевая строка, а это означает, что все миноры четвёртого порядка равны нулю. Миноры пятого и более высоких порядков составить мы не можем, так как матрица $A$ имеет всего 4 строки.
Мы нашли минор третьего порядка, не равный нулю. При этом все миноры высших порядков равны нулю, следовательно, рассмотренный нами минор – базисный. Строки матрицы $A$, на которых расположены элементы этого минора (первая, вторая и третья), – базисные строки, а первый, третий и четвёртый столбцы матрицы $A$ – базисные столбцы.
Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.
Введём ещё одно понятие – окаймляющий минор.
Пусть некий минор k-го порядка $M$ матрицы $A_{mtimes n}$ расположен на пересечении k строк и k столбцов. Добавим к набору этих строк и столбцов ещё одну строку и столбец. Полученный минор (k+1)-го порядка именуют окаймляющим минором для минора $M$.
Для примера обратимся к такой матрице:
$$A=left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & 12 & 20 & 21 & 54\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$
Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:
$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & -3 & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M=left|begin{array} {ccc}
-17 & 19 \
12 & 21 end{array} right|.
$$
Добавим к набору строк, на которых лежат элементы минора $M$, ещё строку №1, а к набору столбцов – столбец №5. Получим новый минор $M’$ (уже третьего порядка), элементы которого расположены на пересечении строк №1, №2, №5 и столбцов №2, №4, №5. Элементы минора $M$ на рисунке выделены красным цветом, а элементы, которые мы добавляем к минору $M$ – синим:
$$
left( begin{array} {ccccc}
-1 & boldblue{2} & 0 & boldblue{-2} & boldblue{-14}\
3 & boldred{-17} & -3 & boldred{19} & boldblue{29}\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & boldblue{54}\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M’=left|begin{array} {ccc}
2 & -2 & -14 \
-17 & 19 & 29 \
12 & 21 & 54 end{array} right|.
$$
Минор $M’$ является окаймляющим минором для минора $M$. Аналогично, добавляя к набору строк, на которых лежат элементы минора $M$, строку №4, а к набору столбцов – столбец №3, получим минор $M»$ (минор третьего порядка):
$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & boldblue{-3} & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & boldblue{11} & boldblue{19} & boldblue{-20} & -98\
6 & boldred{12} & boldblue{20} & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M»=left|begin{array} {ccc}
-17 & -3 & 19 \
11 & 19 & -20 \
12 & 20 & 21 end{array} right|.
$$
Минор $M»$ также является окаймляющим минором для минора $M$.
Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.
Пусть задан некий минор $M$ k-го порядка матрицы $A_{ntimes n}$. Определитель (n-k)-го порядка, элементы которого получены из матрицы $A$ после вычеркивания строк и столбцов, содержащих минор $M$, называется минором, дополнительным к минору $M$.
Для примера рассмотрим квадратную матрицу пятого порядка:
$$
A=left( begin{array}{ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$
Выберем в ней строки №1 и №3, а также столбцы №2 и №5. На пересечении оных строк и столбцов будут элементы минора $M$ второго порядка. Эти элементы выделены в матрице $A$ зелёным цветом:
$$
left(begin{array}{ccccc}
-1 & boldgreen{2} & 0 & -2 & boldgreen{-14}\
3 & -17 & -3 & 19 & 29\
5 & boldgreen{-6} & 8 & -9 & boldgreen{41}\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M=left|begin{array}{cc}
2 & -14 \
-6 & 41 end{array} right|.
$$
Теперь уберём из матрицы $A$ строки №1 и №3 и столбцы №2 и №5, на пересечении которых находятся элементы минора $M$ (элементы убираемых строк и столбцов показаны красным цветом на рисунке ниже). Оставшиеся элементы образуют минор $M’$:
$$
left( begin{array}{ccccc}
boldred{-1} & boldred{2} & boldred{0} & boldred{-2} & boldred{-14}\
3 & boldred{-17} & -3 & 19 & boldred{29}\
boldred{5} & boldred{-6} & boldred{8} & boldred{-9} & boldred{41}\
-5 & boldred{11} & 16 & -20 & boldred{-98}\
-7 & boldred{10} & 14 & -36 & boldred{79} end{array} right);;
M’=left|begin{array} {ccc}
3 & -3 & 19 \
-5 & 16 & -20 \
-7 & 14 & -36 end{array}right|.
$$
Минор $M’$, порядок которого равен $5-2=3$, является минором, дополнительным к минору $M$.
Алгебраическим дополнением к минору $M$ квадратной матрицы $A_{ntimes n}$ называется выражение $(-1)^{alpha}cdot M’$, где $alpha$ – сумма номеров строк и столбцов матрицы $A$, на которых расположены элементы минора $M$, а $M’$ – минор, дополнительный к минору $M$.
Словосочетание «алгебраическое дополнение к минору $M$» часто заменяют словосочетанием «алгебраическое дополнение минора $M$».
Для примера рассмотрим матрицу $A$, для которой мы находили минор второго порядка
$
M=left| begin{array} {ccc}
2 & -14 \
-6 & 41 end{array} right|
$ и дополнительный к нему минор третьего порядка:
$M’=left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|$. Обозначим алгебраическое дополнение минора $M$ как $M^*$. Тогда согласно определению:
$$
M^*=(-1)^alphacdot M’.
$$
Параметр $alpha$ равен сумме номеров строк и столбцов, на которых находится минор $M$. Этот минор расположен на пересечении строк №1, №3 и столбцов №2, №5. Следовательно, $alpha=1+3+2+5=11$. Итак:
$$
M^*=(-1)^{11}cdot M’=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|.
$$
В принципе, используя формулу №2 из темы вычисления определителей второго и третьего порядков, можно довести вычисления до конца, получив значение $M^*$:
$$
M^*=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|=-30.
$$
Миноры
матрицы
Пусть
дана квадратная матрица
А, n — ого порядка. Минором
некоторого элемента аij
, определителя матрицы
n — ого порядка называется определитель
(n — 1) — ого порядка, полученный из исходного
путем вычеркивания строки и столбца,
на пересечении которых находится
выбранный элемент аij.
Обозначается Мij.
Рассмотрим
на примере определителя
матрицы 3 — его
порядка:
, тогда
согласно определению минора,
минором
М12,
соответствующим элементу а12,
будет определитель:
При
этом, с помощью миноров
можно облегчать задачу вычисления
определителя матрицы.
Надо разложить определитель
матрицы по некоторой
строке и тогда определитель
будет равен сумме всех элементов этой
строки на их миноры. Разложение
определителя матрицы
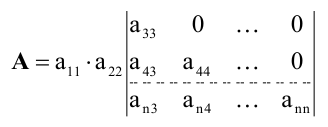
3 — его порядка будет выглядеть так:
|
|
|
, знак
перед произведением равен (-1)n,
где n = i + j.
Алгебраические
дополнения:
Алгебраическим
дополнением элемента
аij
называется его минор,
взятый со знаком «+», если сумма (i
+ j) четное число, и со знаком «-«,
если эта сумма нечетное число. Обозначается
Аij.
Аij
= (-1)i+j
× Мij.
Тогда
можно переформулировать изложенное
выше свойство. Определитель
матрицы равен сумме
произведение элементов некторого ряда
(строки или столбца) матрицы
на соответствующие им алгебраические
дополнения. Пример:
4. Обратная матрица и её вычисление.
Пусть
А — квадратная матрица
n — ого порядка.
Квадратная
матрица
А называется невырожденной, если
определитель
матрицы (Δ = det A) не
равен нулю (Δ = det A ≠ 0). В противном случае
(Δ = 0) матрица
А называется вырожденной.
Матрицей,
союзной к матрице
А, называется матрица
, где
Аij
— алгебраическое
дополнение элемента
аij
данной матрицы
(оно определяется так же, как и
алгебраическое
дополнение элемента
определителя матрицы).
Матрица
А-1
называется обратной
матрице А, если
выполняется условие:
А × А-1
= А-1
× А = Е
, где Е — единичная матрица
того же порядка, что и матрица
А. Матрица
А-1
имеет те же размеры, что и матрица
А.
Обратная
матрица
Если
существуют квадратные матрицы
Х и А, удовлетворяющие условию:
X × A =
A × X = E
, где Е — единичная матрица
того же самого порядка, то матрица
Х называется обратной
матрицей к матрице А
и обозначается А-1.
Всякая невырожденная матрица
имеет обратную
матрицу и притом
только одну, т. е. для того чтобы квадратная
матрица
A имела обратную
матрицу, необходимо
и достаточно, чтобы её определитель
был отличен от нуля.
Для
получения обратной
матрицы используют
формулу:
, где
Мji
дополнительный минор
элемента аji
матрицы
А.
5. Ранг матрицы. Вычисление ранга с помощью элементарных преобразований.
Рассмотрим
прямоугольную матрицу mхn. Выделим в
этой матрице какие-нибудь k строк и k
столбцов, 1 £ k £ min (m, n) . Из элементов,
стоящих на пересечении выделенных строк
и столбцов, составим определитель k-го
порядка. Все такие определители называются
минорами матрицы. Например, для матрицы
можно
составить миноры второго порядкаи
миноры первого порядка 1, 0, -1, 2, 4, 3.
Определение.Рангом матрицы называется наивысший
порядок отличного от нуля минора этой
матрицы. Обозначают ранг матрицы r (A).
В
приведенном примере ранг матрицы равен
двум, так как, например, минор
Ранг
матрицы удобно вычислять методом
элементарных преобразований. К
элементарным преобразованиям относят
следующие:
1)
перестановки строк (столбцов);
2)
умножение строки (столбца) на число,
отличное от нуля;
3)
прибавление к элементам строки (столбца)
соответствующих элементов другой строки
(столбца), предварительно умноженных
на некоторое число.
Эти
преобразования не меняют ранга матрицы,
так как известно, что 1) при перестановке
строк определитель меняет знак и, если
он не был равен нулю, то уже и не станет;
2) при умножении строки определителя на
число, не равное нулю, определитель
умножается на это число; 3) третье
элементарное преобразование вообще не
изменяет определитель. Таким образом,
производя над матрицей элементарные
преобразования, можно получить матрицу,
для которой легко вычислить ранг ее и,
следовательно, исходной матрицы.
Определение.
Матрица
,
полученная из матрицыпри
помощи элементарных преобразований,
называется эквивалентной и обозначаетсяА
В.
Теорема.Ранг матрицы не изменяется при элементарных
преобразованиях матрицы.
С
помощью элементарных преобразований
можно привести матрицу к так называемому
ступенчатому виду, когда вычисление ее
ранга не представляет труда.
Матрица
называется
ступенчатой если она имеет вид:

где
,
,
.
Очевидно,
что ранг ступенчатой матрицы равен
числу ненулевых строк
,
т.к. имеется минор
-го
порядка, не равный нулю:
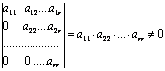
Пример.Определить ранг матрицы с помощью
элементарных преобразований.
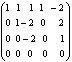
Ранг матрицы равен
количеству ненулевых строк, т.е.
.
Соседние файлы в папке Шпоры ИУП_1сессия
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
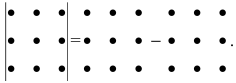
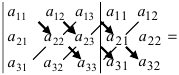
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
Содержание:
Определители II и III порядка
Определение: Определителем порядка n называется число (выражение), записанное в виде квадратной таблицы, имеющей n строк и n столбцов, которая раскрывается по определенному правилу.
Числа
Определение: Определителем II порядка называется число (выражение), записанное в виде квадратной таблицы размером 2×2, т.е. имеющая 2 строки и 2 столбца.
Определение: Определитель II порядка вычисляется по правилу: из произведения элементов, стоящих на главной диагонали, надо вычесть произведение элементов, стоящих на побочной диагонали:
Пример:
Определение: Определителем III порядка называется число (выражение), записанное в виде квадратной таблицы размером 3×3, то есть имеющей 3 строки и 3 столбца.
Определитель III порядка вычисляется по правилу Саррюса: за определителем выписывают первый и второй столбцы, затем из суммы произведений элементов, стоящих на главной диагонали ей параллельных диагоналях, надо вычесть сумму произведений элементов, стоящих на побочной диагонали и ей параллельных:
Пример:
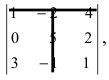
Определение: Минором 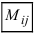
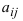
Пример:
Найти миноры элементов 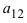
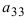
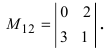
Пример:
Найти миноры элементов 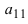
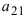
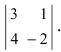
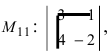
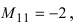
Определение: Алгебраическим дополнением 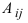
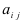
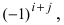
Замечание: Из определения алгебраического дополнения следует, что алгебраическое дополнение совпадает со своим минором, если сумма 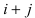
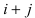
Определение: Транспонированным определителем n-го порядка называется определитель порядка n, полученный из исходного определителя путем замены строк на соответствующие столбцы, а столбцов на соответствующие строки.
Если
Пример:
Найти определитель, транспонированный к определителю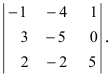
Свойства определителей
1. Величина транспонированного определителя равна величине исходного определителя. Пусть 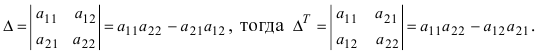
2. Перестановка местами двух строк (столбцов) изменяет знак определителя на противоположный. Пусть
Если поменять местами строки (столбцы) четное число раз, то величина и знак определителя не меняется. Нечетная перестановка местами строк (столбцов) не меняет величину определителя, но изменяет его знак на противоположный.
3. Определитель, содержащий две (или более) одинаковых строки (столбца), равен нулю. Если определитель содержит два одинаковых столбца, то 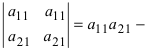
4. Для того чтобы умножить определитель на число k, достаточно умножить на это число все элементы какой-либо одной строки (столбца). Обратно: если все элементы какой-либо строки (столбца) имеют общий множитель k, то его можно вынести за знак определителя.
Докажем это свойство:
5. Если две каких-либо строки (столбца) пропорциональны, то определитель равен нулю.
Пусть в определителе II порядка первая и вторая строки пропорциональны, тогда
6. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю.
Пусть в определителе II порядка все элементы первой строки равны нулю, тогда
7. Если элементы какой-либо строки (или столбца) можно представить в виде двух слагаемых, то сам определитель можно представить в виде суммы двух определителей. Если 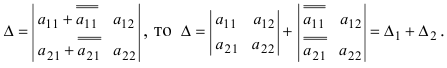
8. Если все элементы какой-либо строки (столбца) умножить на вещественное число к и прибавить k соответствующим элементам другой строки (соответственно, столбца), то величина определителя не изменится.
Умножим элементы второго столбца на вещественное число k и прибавим результат умножения к соответствующим элементам первого столбца, получим
Второй определитель равен нулю по свойству 5.
Замечание: Данное свойство применяется для обнуления всех элементов какой-либо строки (столбца) за исключением одного (метод обнуления), что существенно снижает трудоемкость вычисления определителей порядка выше 3 (см. также свойство 9.).
9. [Метод раскрытия определителя по элементам какой-либо строки (или столбца); универсальный способ вычисления определителя любого порядка]. Определитель любого порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
Пример:
Вычислить определитель 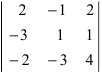
Решение:
Воспользуемся свойством 9.: раскроем определитель по элементам 3 строки 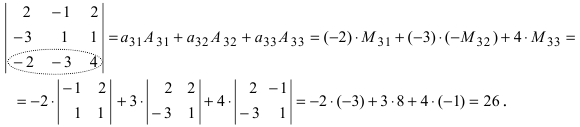
Из полученных результатов видно, что свойство 9. является универсальным методом вычисления любых определителей по элементам любой строки или столбца.
Используя свойство 8. можно обнулить все элементы какой-либо строки (столбца) за исключением одного (метод обнуления), а затем раскрыть определитель по элементам этой строки, воспользовавшись свойством 9.
Пример:
Вычислить определитель
Решение:
Обнулим элементы в третьей строке, для чего выполним следующие действия: 
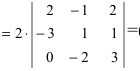
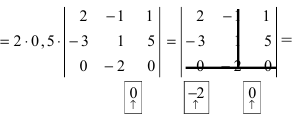
(по свойству 4. из третьего столбца вынесем множитель 0,5, тогда множитель перед определителем станет равным 1)
(раскроем определитель по элементам третьей строки: 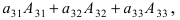
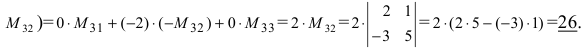
Пример:
Решить уравнение
Решение:
Вычислим определители второго и третьего порядков согласно вышеописанным правилам:
Найденные величины подставим в исходное уравнение
Пример:
Решить неравенство
Решение:
Вычислим определители второго и третьего порядков согласно вышеописанным правилам:
Найденные величины подставим в исходное неравенство
Пример:
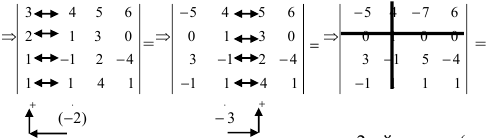
Вычислить определитель четвертого порядка (аналогично выполнить такие же действия с определителем третьего порядка), преобразовав его так, чтобы три элемента некоторого ряда равнялись нулю, и вычислить полученный определитель по элементам этого ряда:
Решение:
Во второй строке исходного определителя присутствуют 1 и 0, поэтому обнуление элементов будем производить в этой строке (при обнулении элементов в строке действия производят со столбцами и наоборот): 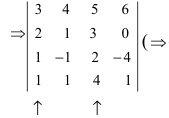
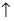
(по методу обнуления раскроем определитель по элементам 2-ой строки (
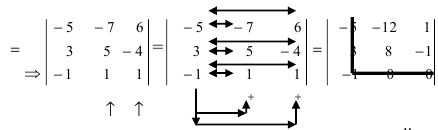
Определители
Перестановкой чисел 1, 2,…, n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12…n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.
Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ 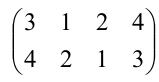
Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде 
Пусть нам дана квадратная матрица порядка n
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
где индексы 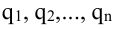
Определителем n-го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ 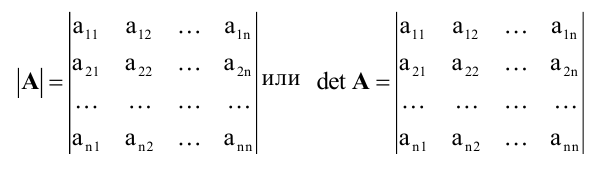
Свойства определителей:
- Определитель не меняется при транспонировании.
- Если одна из строк определителя состоит из нулей, то определитель равен нулю.
- Если в определителе переставить две строки, определитель поменяет знак.
- Определитель, содержащий две одинаковые строки, равен нулю.
- Если все элементы некоторой строки определителя умножить на некоторое число
то сам определитель умножится на
- Определитель, содержащий две пропорциональные строки, равен нулю.
- Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых
то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов
в другом — из элементов
- Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Минором 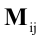
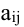
Алгебраическим дополнением элемента 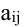
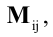
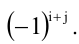
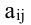
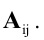
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
- Заказать решение задач по высшей математике
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки 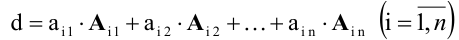
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Пример:
Не вычисляя определителя 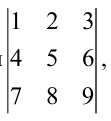
Решение:
Вычтем из второй строки первую, получим определитель 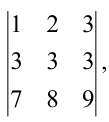
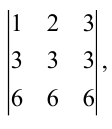
Такой определитель равен нулю.
Пример:
Вычислить определитель 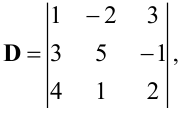
Решение:
Разложим определитель по элементам второго столбца:
Пример:
Вычислить определитель 
Решение:
Разложим определитель А по первой строке:
Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
И так далее. После n шагов придем к равенству
Пример:
Вычислить определитель
Решение:
Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель: 
Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.
——- в вышмате
Определители. Алгебраические дополнения
Внимание! Понятие определителя вводится только для квадратной матрицы.
Матрица называется квадратной порядка n, если количество ее строк совпадает с количеством столбцов и равно n.
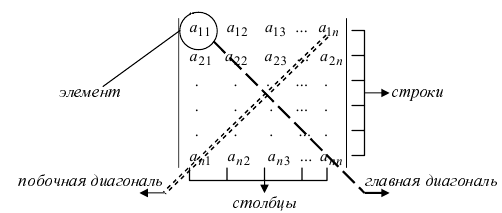
Элементы квадратной матрицы, имеющие одинаковые значения индексов, составляют главную диагональ. Элементы квадратной матрицы порядка n, сумма индексов каждого из которых равна n+1, составляют побочную диагональ.
Определитель матрицы 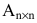
Внимание! Определитель — это число, характеризующее квадратную мат- рицу.
Определитель матрицы второго порядка равен разности элементов главной и побочной диагоналей соответственно:
Определитель матрицы третьего порядка равен сумме элементов главной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали, а также разности элементов побочной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными побочной диагонали.
Схематично это правило изображается так (правило треугольника):
Например,
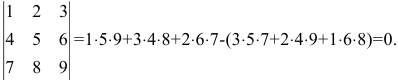
Отметим некоторые свойства определителя.
- Определитель треугольной матрицы равен произведению элементов главной диагонали.
- При транспонировании матрицы ее определитель не изменяется.
- От перестановки двух рядов (строк или столбцов) определитель меняет знак.
- Общий множитель всех элементов некоторого ряда определителя можно выносить за знак определителя.
- Если все элементы какого-нибудь ряда матрицы равны нулю, то определитель равен нулю.
- Определитель, содержащий два пропорциональных ряда, равен нулю.
- Определитель не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы другого ряда, умноженные на одно и то же число.
- Определитель произведения двух матриц одинакового порядка равен произведению определителей этих матриц.
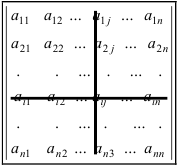
Минором элемента 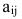
Алгебраическим дополнением элемента 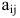
Теорема разложения.
Определитель матрицы равен сумме произведений элементов любого ряда на их алгебраические дополнения.
Пример №2
Вычислить определитель, разлагая его по элементам первой строки:
Решение:
По теореме разложения
Найдем алгебраические дополнения элементов матрицы А:
Следовательно,
Для вычисления определителя порядка выше третьего удобно пользоваться теоремой разложения (метод понижения порядка) или методом приведения определителя к треугольному виду.
Пример №3
Вычислить определитель, приведя его к треугольному виду:
Решение:
Применяя свойство 6 определителей, преобразуем последовательно второй, третий, четвертый столбцы матрицы.
- прибавили ко второму столбцу первый, умноженный на -2;
- прибавили к третьему столбцу первый, умноженный на -3;
- прибавили к четвертому столбцу первый, умноженный на -4;
- применили свойство 1 определителей.
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
- Плоскость и прямая в пространстве





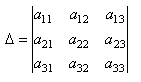
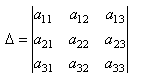
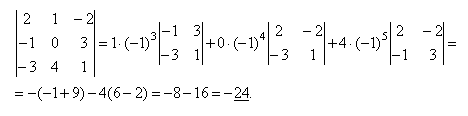
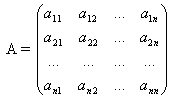

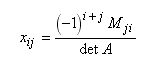
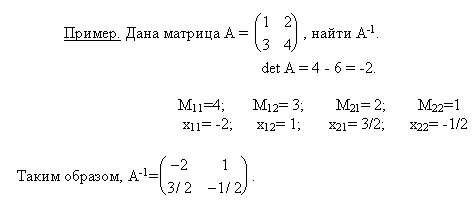
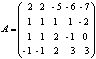
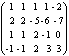
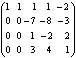
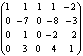
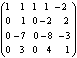
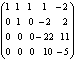
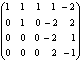
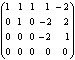



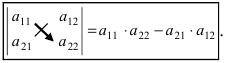
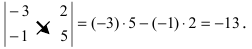
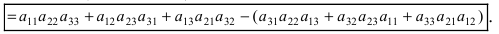
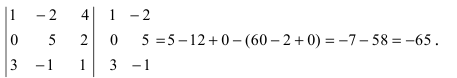
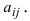
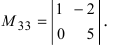
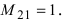
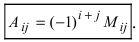

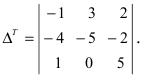
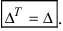
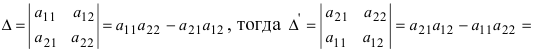
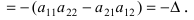
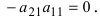
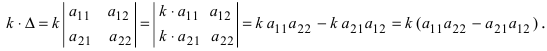
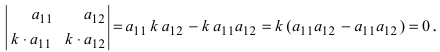
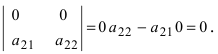
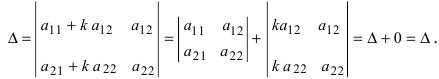
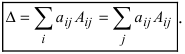
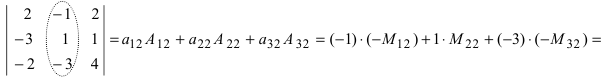
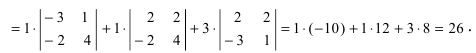
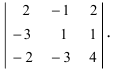
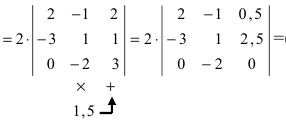
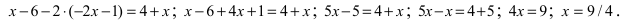

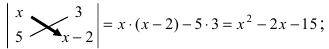
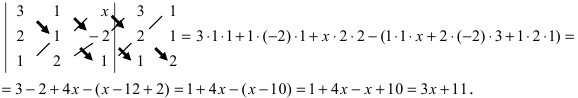
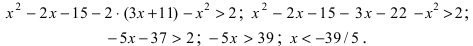

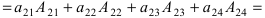
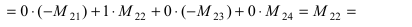
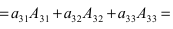
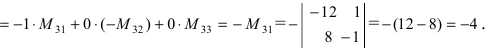


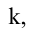 то сам определитель умножится на
то сам определитель умножится на 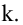
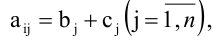 то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов
то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов 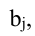 в другом — из элементов
в другом — из элементов