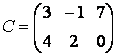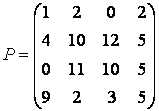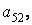Как найти определитель матрицы матлаб - Исправление недочетов и поиск решений вместе с Examum.ru

Syntax

Description

example

d = det(A) returns the determinant of
square matrix A.

Examples

collapse all

Calculate Determinant of Matrix

Create a 3-by-3 square matrix, A.

A = [1 -2 4; -5 2 0; 1 0 3]

A = 3×3

     1    -2     4
    -5     2     0
     1     0     3

Calculate the determinant of A.

Determine if Matrix Is Singular

Examine why the determinant is not an accurate measure of singularity.

Create a 10-by-10 matrix by multiplying an identity matrix, eye(10), by a small number.

The matrix A has very small entries along the main diagonal. However, A is not singular, because it is a multiple of the identity matrix.

Calculate the determinant of A.

The determinant is extremely small. A tolerance test of the form abs(det(A)) < tol is likely to flag this matrix as singular. Although the determinant of the matrix is close to zero, A is actually not ill conditioned. Therefore, A is not close to being singular. The determinant of a matrix can be arbitrarily close to zero without conveying information about singularity.

To investigate if A is singular, use either the cond or rcond functions.

Calculate the condition number of A.

The result confirms that A is not ill conditioned.

Find Determinant of Singular Matrix

Examine a matrix that is exactly singular, but which has a large nonzero determinant. In theory, the determinant of any singular matrix is zero, but because of the nature of floating-point computation, this ideal is not always achievable.

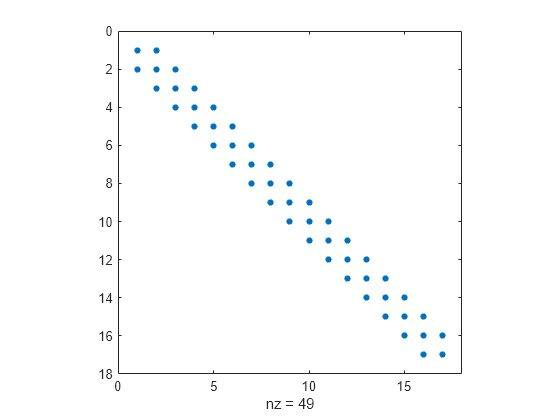
Create a 13-by-13 diagonally dominant singular matrix A and view the pattern of nonzero elements.

A = diag([24 46 64 78 88 94 96 94 88 78 64 46 24]);
S = diag([-13 -24 -33 -40 -45 -48 -49 -48 -45 -40 -33 -24],1);
A = A + S + rot90(S,2);
spy(A)

A is singular because the rows are linearly dependent. For instance, sum(A) produces a vector of zeros.

Calculate the determinant of A.

The determinant of A is quite large despite the fact that A is singular. In fact, the determinant of A should be exactly zero! The inaccuracy of d is due to an aggregation of round-off errors in the MATLAB® implementation of the LU decomposition, which det uses to calculate the determinant. This result demonstrates a few important aspects of calculating numeric determinants. See the Limitations section for more details.

Input Arguments

collapse all

`A` — Input matrix
square numeric matrix

Input matrix, specified as a square numeric matrix.

Data Types: single | double
Complex Number Support: Yes

Limitations

Avoid using det to examine if a matrix is
singular because of the following limitations. Use cond or rcond instead.

Limitation	Result
The magnitude of the determinant is typically unrelated to the condition number of a matrix.	The determinant of a matrix can be arbitrarily large or small without changing the condition number.
`det` uses the LU decomposition to calculate the determinant, which is susceptible to floating-point round-off errors.	The determinant calculation is sometimes numerically unstable. For example, `det` can produce a large-magnitude determinant for a singular matrix, even though it should have a magnitude of 0.

Algorithms

det computes the determinant from the triangular
factors obtained by Gaussian elimination with the lu function.

[L,U] = lu(X)
s =  det(L)      % This is always +1 or -1 
det(X) = s*prod(diag(U))

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

Code generation does not support sparse matrix inputs for this
function.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

Code generation does not support sparse
matrix inputs for this function.

Thread-Based Environment
Run code in the background using MATLAB® `backgroundPool` or accelerate code with Parallel Computing Toolbox™ `ThreadPool`.

This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced before R2006a

Источник

This topic contains an introduction to creating matrices and performing basic matrix calculations in MATLAB^®.

The MATLAB environment uses the term matrix to indicate a variable containing real or complex numbers arranged in a two-dimensional grid. An array is, more generally, a vector, matrix, or higher dimensional grid of numbers. All arrays in MATLAB are rectangular, in the sense that the component vectors along any dimension are all the same length. The mathematical operations defined on matrices are the subject of linear algebra.

Creating Matrices

MATLAB has many functions that create different kinds of matrices. For example, you can create a symmetric matrix with entries based on Pascal’s triangle:

Or, you can create an unsymmetric magic square matrix, which has equal row and column sums:

Another example is a 3-by-2 rectangular matrix of random integers. In this case the first
input to randi describes the range of possible values for the
integers, and the second two inputs describe the number of rows and columns.

A column vector is an m-by-1 matrix, a row vector is a 1-by-n matrix, and a scalar is a 1-by-1 matrix. To define a matrix manually, use square brackets [ ] to denote the beginning and end of the array. Within the brackets, use a semicolon ; to denote the end of a row. In the case of a scalar (1-by-1 matrix), the brackets are not required. For example, these statements produce a column vector, a row vector, and a scalar:

u = [3; 1; 4]

v = [2 0 -1]

s = 7

u =
       3
       1
       4

v =
       2     0    -1

s =
       7

For more information about creating and working with matrices, see Creating, Concatenating, and Expanding Matrices.

Adding and Subtracting Matrices

Addition and subtraction of matrices and arrays is performed element-by-element, or element-wise. For example, adding A to B and then subtracting A from the result recovers B:

Addition and subtraction require both matrices to have compatible dimensions. If the dimensions are incompatible, an error results:

Error using  + 
Matrix dimensions must agree.

For more information, see Array vs. Matrix Operations.

Vector Products and Transpose

A row vector and a column vector of the same length can be multiplied in either order. The result is either a scalar, called the inner product, or a matrix, called the outer product:

u = [3; 1; 4];
v = [2 0 -1];
x = v*u

For real matrices, the transpose operation interchanges a_ij and a_ji. For complex matrices, another consideration is whether to take the complex conjugate of complex entries in the array to form the complex conjugate transpose. MATLAB uses the apostrophe operator (') to perform a complex conjugate transpose, and the dot-apostrophe operator (.') to transpose without conjugation. For matrices containing all real elements, the two operators return the same result.

The example matrix A = pascal(3) is symmetric, so A' is equal to A. However, B = magic(3) is not symmetric, so B' has the elements reflected along the main diagonal:

For vectors, transposition turns a row vector into a column vector (and vice-versa):

If x and y are both real column vectors, then the product x*y is not defined, but the two products

and

produce the same scalar result. This quantity is used so frequently, it has three different names: inner product, scalar product, or dot product. There is even a dedicated function for dot products named dot.

For a complex vector or matrix, z, the quantity z' not only transposes the vector or matrix, but also converts each complex element to its complex conjugate. That is, the sign of the imaginary part of each complex element changes. For example, consider the complex matrix

z = [1+2i 7-3i 3+4i; 6-2i 9i 4+7i]

z =

   1.0000 + 2.0000i   7.0000 - 3.0000i   3.0000 + 4.0000i
   6.0000 - 2.0000i   0.0000 + 9.0000i   4.0000 + 7.0000i

The complex conjugate transpose of z is:

ans =

   1.0000 - 2.0000i   6.0000 + 2.0000i
   7.0000 + 3.0000i   0.0000 - 9.0000i
   3.0000 - 4.0000i   4.0000 - 7.0000i

The unconjugated complex transpose, where the complex part of each element retains its sign, is denoted by z.':

ans =

   1.0000 + 2.0000i   6.0000 - 2.0000i
   7.0000 - 3.0000i   0.0000 + 9.0000i
   3.0000 + 4.0000i   4.0000 + 7.0000i

For complex vectors, the two scalar products x'*y and y'*x are complex conjugates of each other, and the scalar product x'*x of a complex vector with itself is real.

Multiplying Matrices

Multiplication of matrices is defined in a way that reflects composition of the underlying linear transformations and allows compact representation of systems of simultaneous linear equations. The matrix product C = AB is defined when the column dimension of A is equal to the row dimension of B, or when one of them is a scalar. If A is m-by-p and B is p-by-n, their product C is m-by-n. The product can actually be defined using MATLAB for loops, colon notation, and vector dot products:

A = pascal(3);
B = magic(3);
m = 3; 
n = 3;
for i = 1:m
     for j = 1:n
        C(i,j) = A(i,:)*B(:,j);
     end
end

MATLAB uses an asterisk to denote matrix multiplication, as in C = A*B. Matrix multiplication is not commutative; that is, A*B is typically not equal to B*A:

X =
      15    15    15
      26    38    26
      41    70    39

Y =
      15    28    47
      15    34    60
      15    28    43

A matrix can be multiplied on the right by a column vector and on the left by a row vector:

Rectangular matrix multiplications must satisfy the dimension compatibility conditions. Since A is 3-by-3 and C is 3-by-2, you can multiply them to get a 3-by-2 result (the common inner dimension cancels):

However, the multiplication does not work in the reverse order:

Error using  * 
Incorrect dimensions for matrix multiplication. Check that the number of columns 
in the first matrix matches the number of rows in the second matrix. To perform 
elementwise multiplication, use '.*'.

You can multiply anything with a scalar:

When you multiply an array by a scalar, the scalar implicitly expands to be the same size as the other input. This is often referred to as scalar expansion.

Identity Matrix

Generally accepted mathematical notation uses the capital letter I to denote identity matrices, matrices of various sizes with ones on the main diagonal and zeros elsewhere. These matrices have the property that AI = A and IA = A whenever the dimensions are compatible.

The original version of MATLAB could not use I for this purpose because it did not distinguish between uppercase and lowercase letters and i already served as a subscript and as the complex unit. So an English language pun was introduced. The function

returns an m-by-n rectangular identity matrix and eye(n) returns an n-by-n square identity matrix.

Matrix Inverse

If a matrix A is square and nonsingular (nonzero determinant), then
the equations AX =
I and XA =
I have the same solution X. This solution is called
the inverse of A and is denoted A^-1. The inv function and the expression
A^-1 both compute the matrix inverse.

X =

    3.0000   -3.0000    1.0000
   -3.0000    5.0000   -2.0000
    1.0000   -2.0000    1.0000

ans =

    1.0000         0         0
    0.0000    1.0000   -0.0000
   -0.0000    0.0000    1.0000

The determinant calculated by det is a measure of the scaling factor of the linear transformation
described by the matrix. When the determinant is exactly zero, the matrix is
singular and no inverse exists.

Some matrices are nearly singular, and despite the fact that an
inverse matrix exists, the calculation is susceptible to numerical errors. The cond function computes the condition number for
inversion, which gives an indication of the accuracy of the results from
matrix inversion. The condition number ranges from 1 for a
numerically stable matrix to Inf for a singular matrix.

It is seldom necessary to form the explicit inverse of a matrix. A frequent misuse of
inv arises when solving the system of linear equations Ax =
b. The best way to solve this equation, from the standpoint of both
execution time and numerical accuracy, is to use the matrix backslash operator
x = Ab. See mldivide for more information.

Kronecker Tensor Product

The Kronecker product, kron(X,Y), of two matrices is the larger matrix formed from all possible products of the elements of X with those of Y. If X is m-by-n and Y is p-by-q, then kron(X,Y) is mp-by-nq. The elements are arranged such that each element of X is multiplied by the entire matrix Y:

[X(1,1)*Y  X(1,2)*Y  . . .  X(1,n)*Y
                     . . .
 X(m,1)*Y  X(m,2)*Y  . . .  X(m,n)*Y]

The Kronecker product is often used with matrices of zeros and ones to build up repeated copies of small matrices. For example, if X is the 2-by-2 matrix

and I = eye(2,2) is the 2-by-2 identity matrix, then:

ans =

     1     0     2     0
     0     1     0     2
     3     0     4     0
     0     3     0     4

and

ans =

     1     2     0     0
     3     4     0     0
     0     0     1     2
     0     0     3     4

Aside from kron, some other functions that are useful to replicate arrays are repmat, repelem, and blkdiag.

Vector and Matrix Norms

The p-norm of a vector x,

is computed by norm(x,p). This operation is defined for any value of p > 1, but the most common values of p are 1, 2, and ∞. The default value is p = 2, which corresponds to Euclidean length or vector magnitude:

v = [2 0 -1];
[norm(v,1) norm(v) norm(v,inf)]

ans =

    3.0000    2.2361    2.0000

The p-norm of a matrix A,

can be computed for p = 1, 2, and ∞ by norm(A,p). Again, the default value is p = 2:

A = pascal(3);
[norm(A,1) norm(A) norm(A,inf)]

ans =

   10.0000    7.8730   10.0000

In cases where you want to calculate the norm of each row or column of a matrix, you can use vecnorm:

ans =

    1.7321    3.7417    6.7823

Using Multithreaded Computation with Linear Algebra Functions

MATLAB supports multithreaded computation for a number of linear algebra and element-wise numerical functions. These functions automatically execute on multiple threads. For a function or expression to execute faster on multiple CPUs, a number of conditions must be true:

The function performs operations that easily partition into sections that execute concurrently. These sections must be able to execute with little communication between processes. They should require few sequential operations.
The data size is large enough so that any advantages of concurrent execution outweigh the time required to partition the data and manage separate execution threads. For example, most functions speed up only when the array contains several thousand elements or more.
The operation is not memory-bound; processing time is not dominated by memory access time. As a general rule, complicated functions speed up more than simple functions.

The matrix multiply (X*Y) and matrix power (X^p) operators show significant increase in speed on large double-precision arrays (on order of 10,000 elements). The matrix analysis functions det, rcond, hess, and expm also show significant increase in speed on large double-precision arrays.

External Websites

Matrix Methods of Linear Algebra (MathWorks Teaching Resources)

Источник

Определитель и ранг матрицы

Для нахождения
определителя
(детерминанта) и
ранга матриц в MATLAB имеются следующие
функции:

det(X) — возвращает
определитель квадратной матрицы X. Если
X содержит только целые элементы, то
результат — тоже целое число. Использование
det(X)=0 как теста на вырожденность матрицы
действительно только для матрицы малого
порядка с целыми элементами.

Пример:

»
А=[2,3,6;1,8,4;3,6,7]

А
=


2	3	6
1	8	4
3	6	7

»
det(A)

ans
=

-29

Ранг матрицы
определяется количеством сингулярных
чисел, превышающих порог

Для вычисления
ранга используется функция rank:

rank (А) — возвращает
количество сингулярных чисел, которые
являются большими, чем заданный по
умолчанию допуск;
rank(A,tol) — возвращает
количество сингулярных чисел, которые
превышают tol.

Пример:

»
rank(A,1)

ans= 3

Обращение
матриц — функция inv
Обращение матриц — одна из наиболее
распространенных операций матричного
анализа. Обратной
называют
матрицу, получаемую в результате деления
единичной матрицы Е на исходную матрицу
X. Таким образом, Х^-1=Е/Х.
Следующие функции обеспечивают реализацию
данной операции: inv(X) — возвращает
матрицу, обратную квадратной матрице
X. Предупреждающее сообщение выдается,
если X плохо масштабирована или близка
к вырожденной. Пример: »
inv(rand(4,4))
ans
=

2.2631
-2.3495 -0.4696 -0.6631

-0.7620
1.2122 1.7041 -1.2146

-2.0408
1.4228 1.5538 1.3730

1.3075-0.0183-2.54830.6344

На практике вычисление явной
обратной матрицы не так уж необходимо.
Чаще операцию обращения применяют при
решении системы линейных уравнений
вида Ах=b. Один из путей решения этой
системы — вычисление x=inv(A)*b. Но лучшим
с точки зрения минимизации времени
расчета и повышения точности вычислений
является использование оператора
матричного деления х=Аb. Эта операция
использует метод исключения Гаусса без
явного формирования обратной матрицы.
Понятие о
многомерных массивах
В MATLAB двумерный массив является частным
случаем многомерного массива. Многомерные
массивы характеризуются размерностью
более двух. Таким массивам можно дать
наглядную интерпретацию. Так, матрицу
(двумерный массив) можно записать на
одном листе бумаги в виде строк и
столбцов, состоящих из элементов матрицы.
Тогда блокнот с такими листками можно
считать трехмерным массивом, полку в
шкафу с блокнотами — четырехмерным
массивом, шкаф со множеством полок —
пятимерным массивом и т. д.

Соседние файлы в папке Matlab

#
#
20.02.201635.74 Mб80Инженерные расчеты в Mathcad Макаров 2005.djvu

Источник

Determinant of a matrix is calculated using the det function of MATLAB. Determinant of a matrix A is given by det(A).

Example

Create a script file with the following code −

Live Demo

a = [ 1 2 3; 2 3 4; 1 2 5]
det(a)

When you run the file, it displays the following result −

a =
      1     2     3
      2     3     4
      1     2     5
ans = -2

matlab_matrics.htm

Previous Page
Print Page
Next Page

1. Различные способы ввода матриц в пакете MatLab

Вводить небольшие по размеру матрицы удобно прямо из командной строки. Введите матрицу размерностью два на три

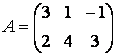
Для хранения матрицы используйте двумерный массив с именем A. При вводе учтите, что матрицу А можно рассматривать как вектор-столбец из двух элементов, каждый из которых является вектор-строкой длиной три, следовательно, строки при наборе отделяются точкой с запятой:

» А = [3 1 -1; 2 4 3]
А =
3 1 -1
2 4 3

Для изучения простейших операций над матрицами приведем еще несколько примеров. Рассмотрим другие способы ввода. Введите квадратную матрицу размера три так, как описано ниже:

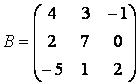
Начните набирать в командной строке

Нажмите клавишу . Обратите внимание, что пакет ничего не вычислил. Курсор мигает на следующей строке без символа ». Продолжите ввод матрицы построчно, нажимая в конце каждой строки . Последнюю строку завершите закрывающей квадратной скобкой, получается:

2 7 0
-5 1 2]
B =
4 3 -1
2 7 0
-5 1 2

Еще один способ ввода матриц состоит в том, что матрицу можно трактовать как вектор-строку, каждый элемент которой является вектор-столбцом. Например, матрицу два на три

можно ввести при помощи команды:

» С = [[3; 4] [-1; 2] [7; 0]]
С =
3 -1 7
4 2 0

Посмотрите переменные рабочей среды, набрав в командной строке whos:

А 2×3 48 double array
В 3×3 72 double array
С 2×3 48 double array

Итак, в рабочей среде содержится три матрицы, две прямоугольные и одна квадратная.

2. Обращение к элементам матриц в пакете MatLab

Доступ к элементам матриц осуществляется при помощи двух индексов — номеров строки и столбца, заключенных в круглые скобки, например

Элементы матриц могут входить в состав выражений:

» С(1, 1) + С(2, 2) + С(2, 3)
ans =
5

Расположение элементов матрицы в памяти компьютера определяет еще один способ обращения к ним. Матрица А размера m на n хранится в виде вектора длины mn, в котором элементы матрицы расположены один за другим по столбцам

[А(1,1) А(2,1) . А(m,1) . А(1,n) А(2,n) . А(m,n)].

Для доступа к элементам матрицы можно использовать один индекс, задающий порядковый номер элемента матрицы в векторе.
Матрица С, определенная в предыдущем подразделе, содержится в векторе

[C(1,1) C(2,1) C(1,2) С(2,2) С(1,3) С(2,3)],

который имеет шесть компонент. Доступ к элементам матрицы осуществляется следующим образом:

3. Операции над матрицами в пакете MatLab: сложение, вычитание, умножение, транспонирование и возведение в степень

При использовании матричных операций следует помнить, что для сложения или вычитания матрицы должны быть одного размера, а при перемножении число столбцов первой матрицы обязано равняться числу строк второй матрицы. Сложение и вычитание матриц, так же как чисел и векторов, осуществляется при помощи знаков плюс и минус. Найдите сумму и разность матриц С и А, определенных выше:

» S = А+С
S =
6 0 6
6 6 3
» R = С — А
R =
0 -2 8
2 -2 -3

Следите за совпадением размерности, иначе получите сообщение об ошибке:

» S = А+В
. Error using ==> ±
Matrix dimensions must agree.

Для умножения матриц предназначена звездочка:

» Р = С*В
P =
-25 9 11
20 26 -4

Умножение матрицы на число тоже осуществляется при помощи звездочки, причем умножать на число можно как справа, так и слева:

» Р = А*3
Р =
9 3 -3
6 12 -3
» Р = 3*А
Р =
9 3 -3
6 12 9

Транспонирование матрицы, так же как и вектора, производится при помощи .’, а символ ‘ означает комплексное сопряжение. Для вещественных матриц эти операции приводят к одинаковым результатам:

» В’
ans =
4 2 -5
3 7 1
-1 0 2

» В.’
ans =
4 2 -5
3 7 1
-1 0 2

Замечание 1

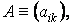
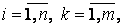
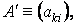
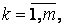
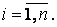
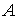
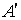
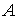
Если матрица есть произвольная матрица размера n m, то матрица, транспонированная по отношению к А,есть матрица размера m n: Таким образом, строки матрицы становятся столбцами матрицы , а столбцы матрицы становятся строками матрицы .
Комплексно-сопряженная матрица получается из исходной в два этапа: выполняется транспонирование исходной матрицы, а затем все комплексные числа заменяются на комплексно-сопряженные.

Сопряжение и транспонирование матриц, содержащих комплексные числа, приведут к созданию разных матриц:

»K= [l-i, 2+3i; 3-5i, l-9i]
К = 1.0000 – 1.0000i 2.0000 + 3.0000i
3.0000 – 5.0000i 1.0000 – 9.0000i
»K’
ans =
1.0000 + 1.0000i 3.0000 + 5.0000i
2.0000 – 3.0000i 1.0000 + 9.0000i

» K.’
ans =
1.0000 — 1.0000i 3.0000 — 5.0000i
2.0000 + 3.0000i 1.0000 — 9.0000i

Замечание 2

При вводе вектор-строк их элементы можно разделять или пробелами, или запятыми. При вводе матрицы К применены запятые для более наглядного разделения комплексных чисел в строке.

Возведение квадратной матрицы в целую степень производится с использованием оператора ^:

» В2 = В^2
B2 =
27 32 -6
22 55 -2
-28 -6 9

Проверьте полученный результат, умножив матрицу саму на себя.
Убедитесь, что вы освоили простейшие операции с матрицами в MatLab. Найдите значение следующего выражения

Учтите приоритет операций, сначала выполняется транспонирование, потом возведение в степень, затем умножение, а сложение и вычитание производятся в последнюю очередь.

»(А+С)*В^3*(А-С)’
ans =
1848 1914
10290 3612

4. Умножение матриц и векторов

Вектор-столбец или вектор-строка в MatLab являются матрицами, у которых один из размеров равен единице, поэтому все вышеописанные операции применимы и для умножения матрицы на вектор-столбец или вектор-строки на матрицу. Например, вычисление выражения

можно осуществить следующим образом:

» a = [1 3 -2];
» B = [2 0 1; -4 8 -1; 0 9 2];
» c = [-8; 3; 4];
» a*B*c
ans =
74

5. Блочные матрицы

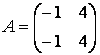
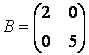
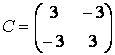
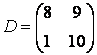
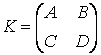
Очень часто в приложениях возникают так называемые блочные матрицы, т.е. матрицы, составленные из непересекающихся подматриц (блоков). Рассмотрим вначале конструирование блочных матриц. Введите матрицы: , , , и создайте из них блочную матрицу .
Учитывая, что матрица К состоит из двух строк, в первой строке матрицы А и B, а во второй — С и D, блочную матрицу можно сформировать следующим образом:

» К = [А В; С D]
K =
-1 4 2 0
-1 4 0 5
3 -3 8 9
-3 3 1 10

Блочную матрицу можно получить и другим способом, если считать, что матрица К состоит из двух столбцов, в первом — матрицы А и С, а во втором — В и D:

Обратной задачей к конструированию блочных матриц является задача выделения блоков. Выделение блоков матриц осуществляется индексацией при помощи двоеточия. Введите матрицу

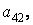
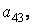
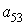
и затем выделите подматрицу с элементами , задав номера строк и столбцов при помощи двоеточия:

»Р1 = Р(2:3,2:3)
Р1 =
10 12
11 10

Для выделения из матрицы столбца или строки (то есть массива, у которого один из размеров равен единице) следует в качестве одного из индексов использовать номер столбца или строки матрицы, а другой индекс заменить двоеточием без указания пределов. Например, запишите вторую строку матрицы Р в вектор р

»p = P(2, 🙂
p =
4 10 12 5

При выделении блока до конца матрицы можно не указывать ее размеры, а использовать элемент end:

»p = Р(2, 2:end)
p =
10 12 5

6. Удаление строк и столбцов

В MatLab парные квадратные скобки [ ] обозначают пустой массив, который, в частности, позволяет удалять строки и столбцы матрицы. Для удаления строки следует присвоить ей пустой массив. Удалите, например, первую строку квадратной матрицы:

» М = [2 0 3
1 1 4
6 1 3];
» M(1,:)=[];
» M
M =
1 1 4
6 1 3

Обратите внимание на соответствующее изменение размеров массива, которое можно проверить при помощи size:

Аналогичным образом удаляются и столбцы. Для удаления нескольких идущих подряд столбцов (или строк) им нужно присвоить пустой массив. Удалите второй и третий столбец в массиве M

Индексация существенно экономит время при вводе матриц, имеющих определенную структуру.

7. Заполнение матриц при помощи индексации

Выше было описано несколько способов ввода матриц в MatLab. Однако часто бывает проще сгенерировать матрицу, чем вводить ее, особенно если она обладает простой структурой. Рассмотрим пример такой матрицы:

Генерация матрицы Т осуществляется в три этапа:
1. Создание массива T размера пять на пять, состоящего из нулей.
2. Заполнение первой строки единицами.
3. Заполнение части последней строки минус единицами до последнего элемента.
Соответствующие команды MatLab приведены ниже.

» A(1:5, 1:5) = 0
A=
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
» A(1, 🙂 = 1
A=
1 1 1 1 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
» A(end, 3:end) = -1
A=
1 1 1 1 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 -1 -1 -1

Создание некоторых специальных матриц в MatLab осуществляется при помощи встроенных функций.

8. Создание матриц специального вида

Заполнение прямоугольной матрицы нулями производится встроенной функцией zeros, аргументами которой являются число строк и столбцов матрицы:

» A = zeros(3, 6)
A =
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0

Один аргумент функции zeros приводит к образованию квадратной матрицы заданного размера:

» A = zeros(3)
A =
0 0 0
0 0 0
0 0 0

Единичная матрица инициализируется при помощи функции eye:

» I = eye(4)
I=
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

Функция eye с двумя аргументами создает прямоугольную матрицу, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю:

» I = eye(4,
I =
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0

Матрица, состоящая из единиц, образуется в результате вызова функции
ones:

» E = ones(3, 7)
E =
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1

Использование одного аргумента в ones приводит к созданию квадратной матрицы, состоящей из единиц.

MatLab предоставляет возможность заполнения матриц случайными элементами. Результатом функции rand является матрица чисел, распределенных случайным образом между нулем и единицей, а функции randn — матрица чисел, распределенных по нормальному закону:

» R = rand(3, 5)
R =
0.9501 0.4860 0.4565 0.4447 0.9218
0.2311 0.8913 0.0185 0.6154 0.7382
0.6068 0.7621 0.8214 0.7919 0.1763

Один аргумент функций rand и randn приводит к формированию квадратных матриц:
Часто возникает необходимость создания диагональных матриц, т.е. матриц, у которых все недиагональные элементы равны нулю. Функция diag формирует диагональную матрицу из вектор-столбца или вектор-строки, располагая их элементы по диагонали матрицы:

» d = [1; 2; 3; 4];
» D = diag(d)
D =
1 0 0 0
0 2 0 0
0 0 3 0
0 0 0 4

Функция diag служит и для выделения диагонали матрицы в вектор, например

» A = [10 1 2; 1 20 3; 2 3 30];
» d = diag(A)
d =
10
20
30

9. Поэлементные операции с матрицами

Поскольку векторы и матрицы хранятся в двумерных массивах, то применение математических функций к матрицам и поэлементные операции производятся так же, как для векторов.
Введите две матрицы

, .

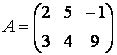
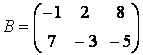
Умножение каждого элемента одной матрицы на соответствующий элемент другой производится при помощи оператора .*:

» С = А.*В
С =
-2 10 -8
21 -12 -45

Для деления элементов первой матрицы на соответствующие элементы второй используется оператор ./, а для деления элементов второй матрицы на соответствующие элементы первой служит .:

» R1 = А./В1
R1 =
-2.0000 2.5000 -0.1250
0.4286 -1.3333 -1.8000
» R2 = А.В1
R2 =
-0.5000 0.4000 -8.0000
2.3333 -0.7500 -0.5556

Поэлементное возведение в степень осуществляется при помощи оператора .^. Показатель степени может быть числом или матрицей того же размера, что и матрица, возводимая в степень. Во втором случае элементы первой матрицы возводятся в степени, равные элементам второй матрицы.

10. Визуализация матриц

Матрицы с достаточно большим количеством нулей называются разреженными. Часто необходимо знать, где расположены ненулевые элементы, т.е. получить так называемый шаблон матрицы. Для этого в MatLab служит функция spy. Посмотрим шаблон матрицы G
.

После выполнения команды spy на экране появляется графическое окно Figure No. 1. На вертикальной и горизонтальной осях отложены номера строк и столбцов. Ненулевые элементы обозначены маркерами, внизу графического окна указано число ненулевых элементов (nz = 19).
Наглядную информацию о соотношении величин элементов матрицы дает функция imagesc, которая интерпретирует матрицу как прямоугольное изображение. Каждый элемент матрицы представляется в виде квадратика, цвет которого соответствует величине элемента. Для того чтобы узнать соответствие цвета и величины элемента следует использовать команду colorbar, выводящую рядом с изображением матрицы шкалу цвета (Insert (в графическом окне Figure No. 1), colorbar). Наконец, для печати на монохромном принтере удобно получить изображение в оттенках серого цвета, используя команду colormap(gray) (Edit (в графическом окне Figure No. 1), Colormap, Colormap Editor, Tools, gray). Мы будем работать с матрицей G. Набирайте команды, указанные ниже, и следите за состоянием графического окна:

» imagesc(G)
» colorbar
» colormap(gray)

В результате получается наглядное представление матрицы.

Работа с матрицами.

Матрица — прямоугольная таблица.

dim A (dimention — размерность) = n*m.

Это означает, что матрица имеет n строк и m столбцов.

1*m — матрица-строка;
n*1 — матрица-столбец;
n*n — квадратная матрица.

Квадратная матрица — важнейший частный случай.

Если элементы главной диагонали равны 1, а остальные равны 0, то такая матрица называется «единичной» (обозначение: E или I).

Пример: определить матрицу для системы MATLAB.

Решение: в системе MATLAB для матриц применяются буквенные обозначения. Множество элементов записывается в квадратных скобках «[]»; элементы одной строки записываются через запятую или через пробел, строки разделяются точкой с запятой «;».

A = [3 2; 1 4];
или
A = [3 2; 1 4]

A = [3, 2; 1, 4];
или
A = [3, 2; 1, 4]

Рассмотрим различия между строками: очевидно, различие между парами строк состоит лишь в использовании запятой или пробела (см. выше). Другой вопрос — использовать ли точку с запятой в конце строки?

Если Вы хотите, чтобы система MatLab отобразила результат операции в рабочем поле, точку с запятой ставить не нужно.

Приведем результаты работы программ:

Без точки с запятой:

С точкой с запятой:

Любое число является матрцей размерностью 1*1.

Действия над матрицами:

A+B — сложение (размерности матиц должны совпадать): A+B = [a_ij+b_ij] — складываются соответственнае элементы. Команда MATLAB: A+B;
c*A — умножение на скаляр (с — скаляр, т.е. какое-то число). Команда MATLAB: 2*A;
A*B — умножение матриц (количество столбцов первой матрицы должно быть равно количеству строк второй). Итоговая матрица имеет размерность: * . Команда MATLAB: A*B;

Внимание! A*B не равно(!) B*A.

Для матриц не определена операция деления (X = b/A). Зато есть операция нахождения обратной матрицы (Команда MATLAB: A -1 ). Тогда X = A -1 *b. Команда MATLAB: X = A^(-1).

Умножение матриц (MATLAB).

Узнать, как математически выполняется умножение матриц, можно в соответствующем разделе: Математика/Умножение матриц.

В MATLAB у множение записывается при помощи оператора * или .* (для поэлементного умножения).

Пример: выполнить умножение матриц в системе MATLAB:

A = [0 1 -1; 0 2 1];
B = [1 2; -1 0; 0 1];
A*B;

Определитель квадратной матрицы.

Естественно, необходимо знать, как математически вычисляется определитель матриц. Почитайте в соответствующем разделе: Математика/Определитель (детерминант) матрицы.

В MATLAB нахождение определителя записывается при помощи команды det( ).

Пример: найти определитель матрицы A = [0 1; 2 0] с помощью MATLAB.

Обратная матрица.

Обязательно прочитайте, как математически вычисляется обратная матрица, в соответствующем разделе: Математика/Нахождение обратных матриц.

В MATLAB нахождение обратных матриц записывается при помощи команды ^(-1).

Пример: найти обратную матрицу для A = [2 3 1; 2 8 0; 5 6 3] с помощью MATLAB.

A = [2 3 1; 2 8 0; 5 6 3];
A^(-1)

Ответ: A -1 =[12 -1.5 -4; -3 0.5 1; -14 1.5 5].

1. Матрица строка. Указывается переменная, ставится знак присвоения и в квадратных скобках через запятую или пробел перечисляются элементы:

2. Матрица столбец. В качестве разделителя элементов применяется символ «;»:

3. Квадратная или прямоугольная матрица:

>> C = [5 6 9; 56 45 73; 15,21,36];

4. Генерация вектора. Синтаксис: = : : . Если не указать шаг, то по умолчанию он принимается за 1.

5. Единичная матрица. Синтаксис: =ones( , ).

6. Нулевая матрица. Синтаксис: =zeros( , );

Доступ к ячейкам матрицы. Синтаксис: ( , ). Необходимо помнить, что нумерация строк и столбцов начинается с 1.

Операции с матрицами:

1. Скалярные операции. Умножение и деление матрицы на число, а также сложение и вычитание матрицы и числа (скаляр) – «.*», «./»,«.+», «.–». Каждая скалярная операция выполняются с каждой ячейкой матрицы отдельно. Любая скалярная (поэлементная) операция, то есть операция сразу над всем массивом, в MatLab обозначаются при помощи точки.

2. Сложение и вычитание матриц. Данная операция выполнима только с матрицами одинакового размера. При выполнении операции действие выполняется с соответствующими друг другу ячейками.

3. Произведение матриц. Производится последовательное умножение строки первой матрицы на столбец второй. Для реализации данной операции необходимо выполнение условия (количество строк первой матрицы ровно количеству столбцов во второй матрице). Матрица результата будет иметь столько же строк сколько и в первой матрице, и количество столбцов равное количеству столбцов во второй матрице.

4. Удаление отдельных столбцов или строк. Для удаления отдельных столбцов или строк матрицы используются: пустые квадратные скобки [] и оператор двоеточие (:).

>> C = [24 33 42; 34 47 60; 44 61 78]

Источник

Syntax

Description

Examples

Calculate Determinant of Matrix

Determine if Matrix Is Singular

Find Determinant of Singular Matrix

Input Arguments

A — Input matrix square numeric matrix

Limitations

Algorithms

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Thread-Based Environment Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Version History

Creating Matrices

Adding and Subtracting Matrices

Vector Products and Transpose

Multiplying Matrices

Identity Matrix

Matrix Inverse

Kronecker Tensor Product

Vector and Matrix Norms

Using Multithreaded Computation with Linear Algebra Functions

Related Topics

External Websites

Определитель и ранг матрицы

Example

1. Различные способы ввода матриц в пакете MatLab

2. Обращение к элементам матриц в пакете MatLab

3. Операции над матрицами в пакете MatLab: сложение, вычитание, умножение, транспонирование и возведение в степень

4. Умножение матриц и векторов

5. Блочные матрицы

6. Удаление строк и столбцов

7. Заполнение матриц при помощи индексации

8. Создание матриц специального вида

9. Поэлементные операции с матрицами

10. Визуализация матриц

Работа с матрицами.

Действия над матрицами:

Умножение матриц (MATLAB).

Определитель квадратной матрицы.

Обратная матрица.

`A` — Input matrix
square numeric matrix

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Thread-Based Environment
Run code in the background using MATLAB® `backgroundPool` or accelerate code with Parallel Computing Toolbox™ `ThreadPool`.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.