Как найти определитель матрицы в matlab

Calculate Determinant of Matrix

Create a 3-by-3 square matrix, A.

A = [1 -2 4; -5 2 0; 1 0 3]

A = 3×3

     1    -2     4
    -5     2     0
     1     0     3

Calculate the determinant of A.

Determine if Matrix Is Singular

Examine why the determinant is not an accurate measure of singularity.

Create a 10-by-10 matrix by multiplying an identity matrix, eye(10), by a small number.

The matrix A has very small entries along the main diagonal. However, A is not singular, because it is a multiple of the identity matrix.

Calculate the determinant of A.

The determinant is extremely small. A tolerance test of the form abs(det(A)) < tol is likely to flag this matrix as singular. Although the determinant of the matrix is close to zero, A is actually not ill conditioned. Therefore, A is not close to being singular. The determinant of a matrix can be arbitrarily close to zero without conveying information about singularity.

To investigate if A is singular, use either the cond or rcond functions.

Calculate the condition number of A.

The result confirms that A is not ill conditioned.

Find Determinant of Singular Matrix

Examine a matrix that is exactly singular, but which has a large nonzero determinant. In theory, the determinant of any singular matrix is zero, but because of the nature of floating-point computation, this ideal is not always achievable.

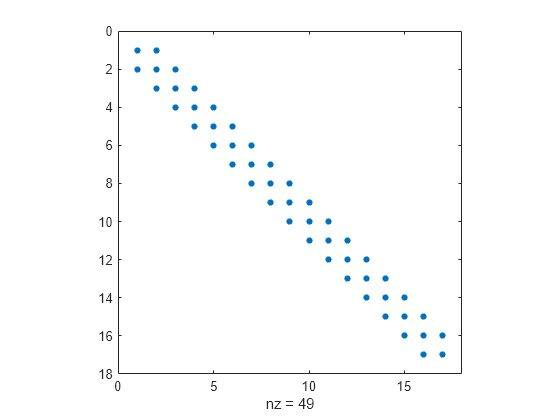
Create a 13-by-13 diagonally dominant singular matrix A and view the pattern of nonzero elements.

A = diag([24 46 64 78 88 94 96 94 88 78 64 46 24]);
S = diag([-13 -24 -33 -40 -45 -48 -49 -48 -45 -40 -33 -24],1);
A = A + S + rot90(S,2);
spy(A)

A is singular because the rows are linearly dependent. For instance, sum(A) produces a vector of zeros.

Calculate the determinant of A.

The determinant of A is quite large despite the fact that A is singular. In fact, the determinant of A should be exactly zero! The inaccuracy of d is due to an aggregation of round-off errors in the MATLAB® implementation of the LU decomposition, which det uses to calculate the determinant. This result demonstrates a few important aspects of calculating numeric determinants. See the Limitations section for more details.

A — Input matrix
square numeric matrix

Input matrix, specified as a square numeric matrix.

Data Types: single | double
Complex Number Support: Yes

• Code generation does not support sparse matrix inputs for this
  function.

• Code generation does not support sparse
  matrix inputs for this function.

Compute Determinant of Matrix with Symbolic Scalar Variables

Compute the determinant of a matrix that contains symbolic scalar variables.

syms a b c d
A = [a b; c d];
B = det(A)

Compute Determinant of Matrix with Symbolic Numbers

Compute the determinant of a matrix that contains symbolic numbers.

A = sym([2/3 1/3; 1 1]);
B = det(A)

Compute Determinant Using Minor Expansion

Create a symbolic matrix that contains polynomial entries.

syms a x 
A = [1, a*x^2+x, x;
     0, a*x, 2;
     3*x+2, a*x^2-1, 0]

A = 
(1a x2+xx0a x23 x+2a x2-10)

Compute the determinant of the matrix using minor expansion.

B = det(A,'Algorithm','minor-expansion')

Compute Determinant of Block Matrix

Compute the determinant of a 4-by-4 block matrix

M=[A02,2CB]

where A, B, and C are 2-by-2 submatrices. The notation 02,2 represents a 2-by-2 submatrix of zeros.

Use symbolic matrix variables to represent the submatrices in the block matrix.

syms A B C [2 2] matrix
Z = symmatrix(zeros(2))

Find the determinant of the matrix M.

Convert the result from symbolic matrix variables to symbolic scalar variables using symmatrix2sym.

D1 = simplify(symmatrix2sym(det(M)))

D1 = A1,1 A2,2-A1,2 A2,1 B1,1 B2,2-B1,2 B2,1

Check if the determinant of matrix M is equal to the determinant of A times the determinant of B.

D2 = symmatrix2sym(det(A)*det(B))

D2 = A1,1 A2,2-A1,2 A2,1 B1,1 B2,2-B1,2 B2,1

Compute Determinant of Matrix Polynomial

Compute the determinant of the matrix polynomial a0 I2+A, where A is a 2-by-2 matrix.

Create the matrix A as a symbolic matrix variable and the coefficient a0 as a symbolic scalar variable. Create the matrix polynomial as a symbolic matrix function f with a0 and A as its parameters.

syms A [2 2] matrix
syms a0
syms f(a0,A) [2 2] matrix keepargs
f(a0,A) = a0*eye(2) + A

Find the determinant of f using det. The result is a symbolic matrix function of type symfunmatrix that accepts scalars, vectors, and matrices as its input arguments.

Convert the result from the symfunmatrix data type to the symfun data type using symfunmatrix2symfun. The result is a symbolic function that accepts scalars as its input arguments.

gInv = symfunmatrix2symfun(fInv)

gInv(a0, A1_1, A1_2, A2_1, A2_2) = A1,1 a0+A2,2 a0+a02+A1,1 A2,2-A1,2 A2,1

Вычисление определителя матрицы

Создайте 3х3 квадратную матрицу, A.

A = [1 -2 4; -5 2 0; 1 0 3]

A = 3×3

     1    -2     4
    -5     2     0
     1     0     3

Вычислим определитель A.

Определите, сингулярна ли Матрица

Исследуйте, почему определитель не является точной мерой сингулярности.

Создайте 10 10 матрица путем умножения единичной матрицы, eye(10), небольшим числом.

Матричный A имеет очень маленькие записи по основной диагонали. Однако A не сингулярно, потому что это является кратным единичной матрице.

Вычислим определитель A.

Определитель чрезвычайно мал. Тест допуска формы abs(det(A)) < tol вероятно, отметит эту матрицу как сингулярную. Несмотря на то, что определитель матрицы близко к нулю, A на самом деле плохо не обусловливается. Поэтому A не близко к тому, чтобы быть сингулярным. Определитель матрицы может быть произвольно близко к нулю, не сообщая о сингулярности.

Заниматься расследованиями если A сингулярно, используйте любого cond или rcond функции.

Вычислим число обусловленности A.

Результат подтверждает тот A плохо не обусловливается.

Нахождение детерминанта сингулярной матрицы

Рассмотрим матрицу, которая точно является сингулярной, но имеет большой ненулевой определитель. В теории определитель любой сингулярной матрицы равен нулю, но из-за особенностей вычислений с плавающей точкой, этот идеал не всегда достижим.

Создайте 13 13 по диагонали доминирующий сингулярный матричный A и просмотрите расположение ненулевых элементов.

A = diag([24 46 64 78 88 94 96 94 88 78 64 46 24]);
S = diag([-13 -24 -33 -40 -45 -48 -49 -48 -45 -40 -33 -24],1);
A = A + S + rot90(S,2);
spy(A)

A сингулярно, потому что строки линейно зависимы. Например, sum(A) дает нулевой вектор.

Вычислим определитель A.

Определитель A является довольно большим несмотря на то, что A сингулярно. На самом деле, определитель A должен быть ниже нуля! Погрешность d происходит из-за накопления ошибок округления в реализации MATLAB® LU-разложения, который det использование, чтобы вычислить определитель. Этот результат демонстрирует несколько важных аспектов вычисления числовых определителей. Дополнительную информацию см. в разделе Limitations.

A — Введите матрицу
квадратная числовая матрица

Введите матрицу в виде квадратной числовой матрицы.

Типы данных: single | double
Поддержка комплексного числа: Да

• Генерация кода не поддерживает входные параметры разреженной матрицы для этой функции.

• Генерация кода не поддерживает входные параметры разреженной матрицы для этой функции.