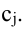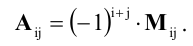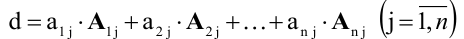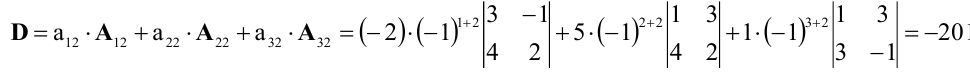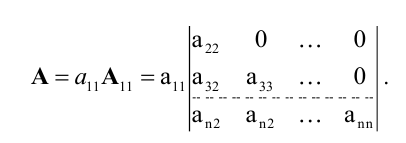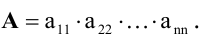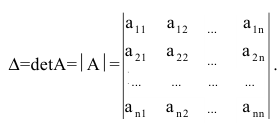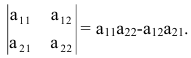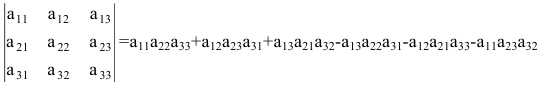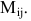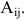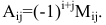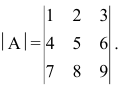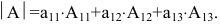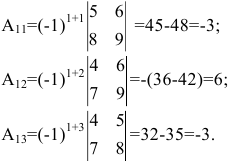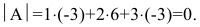Если вы приступили к изучению данной темы, то вы уже знакомы с понятием определителя матрицы и умеете находить определители первого, второго и третьего порядка.
Прежде чем начать рассмотрение новой темы, рекомендуется повторить правило вычисления определителя по строке и столбцу, рассматривающееся в теме «Как вычислить определитель матрицы третьего порядка», свойства определителей, а также нахождение миноров и алгебраических дополнений.
Разложение определителей по строкам или столбцам
Для вычисления определителей высших порядков применяется способ разложения определителя по строке или столбцу. Это позволяет представить детерминант в виде суммы произведений элементов какой-либо его строки или столбца на соответствующие этим элементам алгебраические дополнения. В таком случае вычисление определителя nn-го порядка сводится к вычислению определителей n−1n-1-го порядка.
Пример 1
Найти определитель ∣32454−32−45−2−3−7−3429∣begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix} двумя способами:
- по 2-й строке;
- по 3-у столбцу.
1 способ. Разложим определитель 4-го порядка по строке №2 и вычислим его:
∣32454−32−45−2−3−7−3429∣=4(−1)2+1∣245−2−3−7429∣+(−3)(−1)2+2∣3455−3−7−329∣+2(−1)2+3∣3255−2−7−349∣+(−4)(−1)2+4∣3245−2−3−342∣=begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix}=4(-1)^{2+1}begin{vmatrix}2&4&5\-2&-3&-7\4&2&9end{vmatrix}+(-3)(-1)^{2+2}begin{vmatrix}3&4&5\5&-3&-7\-3&2&9end{vmatrix}+2(-1)^{2+3}begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}+(-4)(-1)^{2+4}begin{vmatrix}3&2&4\5&-2&-3\-3&4&2end{vmatrix}=
=−4∣245−2−3−7429∣−3∣3455−3−7−329∣−2∣3255−2−7−349∣−4∣3245−2−3−342∣=−4(−54−20−112+60+28+72)−3(−81+50+84−45+42−180)−2(−54+100+42−30+84−90)−4(−12+80+18−24+36−20)=−4(−26)−3(−130)−2⋅52−4⋅78=104+390−104−312=78=-4begin{vmatrix}2&4&5\-2&-3&-7\4&2&9end{vmatrix}-3begin{vmatrix}3&4&5\5&-3&-7\-3&2&9end{vmatrix}-2begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}-4begin{vmatrix}3&2&4\5&-2&-3\-3&4&2end{vmatrix}=-4(-54-20-112+60+28+72)-3(-81+50+84-45+42-180)-2(-54+100+42-30+84-90)-4(-12+80+18-24+36-20)=-4(-26)-3(-130)-2cdot52-4cdot78=104+390-104-312=78.
2 способ. Разложим определитель 4-го порядка по 3 столбцу и вычислим его:
∣32454−32−45−2−3−7−3429∣=4(−1)1+3∣4−3−45−2−7−349∣+2(−1)2+3∣3255−2−7−349∣+(−3)(−1)3+3∣3254−3−4−349∣+2(−1)4+3∣3254−3−45−2−7∣=begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix}=4(-1)^{1+3}begin{vmatrix}4&-3&-4\5&-2&-7\-3&4&9end{vmatrix}+2(-1)^{2+3}begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}+(-3)(-1)^{3+3}begin{vmatrix}3&2&5\4&-3&-4\-3&4&9end{vmatrix}+2(-1)^{4+3}begin{vmatrix}3&2&5\4&-3&-4\5&-2&-7end{vmatrix}=
=4∣4−3−45−2−7−349∣−2∣3255−2−7−349∣−3∣3254−3−4−349∣−2∣3254−3−45−2−7∣=4(−72−80−63+24+112+135)−2(−54+100+42−30+84−90)−3(−81+80+24−45+48−72)−2(63−40−40+75−24+56)=4⋅56−2⋅52−3⋅(−45)−2⋅90=224−104+138−180=78=4begin{vmatrix}4&-3&-4\5&-2&-7\-3&4&9end{vmatrix}-2begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}-3begin{vmatrix}3&2&5\4&-3&-4\-3&4&9end{vmatrix}-2begin{vmatrix}3&2&5\4&-3&-4\5&-2&-7end{vmatrix}=4(-72-80-63+24+112+135)-2(-54+100+42-30+84-90)-3(-81+80+24-45+48-72)-2(63-40-40+75-24+56)=4cdot56-2cdot52-3cdot(-45)-2cdot90=224-104+138-180=78.
Метод понижения порядка
Для упрощения расчетов при вычислении определителей рекомендуется применять их свойства. Рассмотрим примеры вычисления определителей с применением их свойств.
Пример 1
Вычислить определитель
∣638−45642034241−46∣begin{vmatrix}6&3&8&-4\5&6&4&2\0&3&4&2\4&1&-4&6end{vmatrix}.
Вынесем из столбца №3 множитель 4:
∣638−45642034241−46∣=4⋅∣632−45612031241−16∣begin{vmatrix}6&3&8&-4\5&6&4&2\0&3&4&2\4&1&-4&6end{vmatrix}=4cdotbegin{vmatrix}6&3&2&-4\5&6&1&2\0&3&1&2\4&1&-1&6end{vmatrix}.
Вынесем из столбца №4 множитель 2:
4⋅∣632−45612031241−16∣=4⋅2⋅∣632−25611031141−13∣=8⋅∣632−25611031141−13∣4cdotbegin{vmatrix}6&3&2&-4\5&6&1&2\0&3&1&2\4&1&-1&6end{vmatrix}=4cdot2cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}.
Прибавим к строке №1 строку №2, умноженную на -2:
8⋅∣632−25611031141−13∣=8⋅∣−4−90−45611031141−13∣8cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}.
Прибавим к строке №3 строку №2, умноженную на -1:
8⋅∣−4−90−45611031141−13∣=8⋅∣−4−90−45611−5−30041−13∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\4&1&-1&3end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на 1:
8⋅∣−4−90−45611−5−30041−13∣=8⋅∣−4−90−45611−5−3009704∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\9&7&0&4end{vmatrix}.
Разложим определитель по столбцу №3:
8⋅∣−4−90−45611−5−3009704∣=8⋅1⋅(−1)2+3∣−4−9−4−5−30974∣=8⋅(−1)5∣−4−9−4−5−30974∣=−8∣−4−9−4−5−30974∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\9&7&0&4end{vmatrix}=8cdot1cdot(-1)^{2+3}begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=8cdot(-1)^{5}begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=-8begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}.
Прибавим к строке №1 строку №3, умноженную на 1:
−8∣−4−9−4−5−30974∣=−8∣5−20−5−30974∣-8begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=-8begin{vmatrix}5&-2&0\-5&-3&0\9&7&4end{vmatrix}.
Разложим определитель по столбцу №3 и вычислим его:
−8∣5−20−5−30974∣=−8⋅4⋅(−1)3+3∣5−2−5−3∣=−32⋅(−1)6∣5−2−5−3∣=−32∣5−2−5−3∣-8begin{vmatrix}5&-2&0\-5&-3&0\9&7&4end{vmatrix}=-8cdot4cdot(-1)^{3+3}begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32cdot(-1)^{6}begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32begin{vmatrix}5&-2\-5&-3end{vmatrix}.
Прибавим к строке №2 строку №1, умноженную на 1:
−32∣5−2−5−3∣=−32∣5−20−5∣-32begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32begin{vmatrix}5&-2\0&-5end{vmatrix}.
Разложим определитель по столбцу №1 и заменим определитель 1-го порядка единственным его элементом:
−32∣5−20−5∣=−32⋅5⋅(−1)1+1⋅(−5)=−32⋅5⋅1⋅(−5)=800-32begin{vmatrix}5&-2\0&-5end{vmatrix}=-32cdot5cdot(-1)^{1+1}cdot(-5)=-32cdot5cdot1cdot(-5)=800.
Пример 2
Вычислить определитель
∣44−10−18237523325732122112176657211221∣begin{vmatrix}4&4&-1&0&-1&8\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №1 строку №4, умноженную на -4:
∣44−10−18237523325732122112176657211221∣=∣0−4−9−4−50237523325732122112176657211221∣begin{vmatrix}4&4&-1&0&-1&8\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №2 строку №4, умноженную на -2:
∣0−4−9−4−50237523325732122112176657211221∣=∣0−4−9−4−500−1330−1325732122112176657211221∣begin{vmatrix}0&-4&-9&-4&-5&0\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №3 строку №4, умноженную на -3:
∣0−4−9−4−500−1330−1325732122112176657211221∣=∣0−4−9−4−500−1330−10−4−140−4122112176657211221∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №5 строку №4, умноженную на -1:
∣0−4−9−4−500−1330−10−4−140−4122112176657211221∣=∣0−4−9−4−500−1330−10−4−140−4122112054545211221∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №6 строку №4, умноженную на -2:
∣0−4−9−4−500−1330−10−4−140−4122112054545211221∣=∣0−4−9−4−500−1330−10−4−140−41221120545450−3−300−3∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\0&-3&-3&0&0&-3end{vmatrix}.
Разложим определитель по 1 столбцу:
∣0−4−9−4−500−1330−10−4−140−41221120545450−3−300−3∣=1⋅(−1)4+1∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣=−∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\0&-3&-3&0&0&-3end{vmatrix}=1cdot(-1)^{4+1}begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.
Прибавим к строке №1 строку №3, умноженную на -1:
−∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣=−∣0−8−8−54−1330−1−4−140−454545−3−300−3∣-begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.
Прибавим к строке №3 строку №2, умноженную на -4:
−∣0−8−8−54−1330−1−4−140−454545−3−300−3∣=−∣0−8−8−54−1330−10−13−80054545−3−300−3∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на 5:
−∣0−8−8−54−1330−10−13−80054545−3−300−3∣=−∣0−8−8−54−1330−10−13−8000192040−3−300−3∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\-3&-3&0&0&-3end{vmatrix}.
Прибавим у строке №5 строку №2, умноженную на -3:
−∣0−8−8−54−1330−10−13−8000192040−3−300−3∣=−∣0−8−8−54−1330−10−13−80001920400−12−900∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\0&-12&-9&0&0end{vmatrix}.
Разложим определитель по 1 столбцу:
−∣0−8−8−54−1330−10−13−80001920400−12−900∣=−(−1)⋅(−1)2+1∣−8−8−54−13−800192040−12−900∣=(−1)3∣−8−8−54−13−800192040−12−900∣=−∣−8−8−54−13−800192040−12−900∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\0&-12&-9&0&0end{vmatrix}=-(-1)cdot(-1)^{2+1}begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=(-1)^{3}begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=-begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}.
Вынесем множитель -3 из строки №4:
−∣−8−8−54−13−800192040−12−900∣=−(−3)∣−8−8−54−13−8001920404300∣=3∣−8−8−54−13−8001920404300∣-begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=-(-3)begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}=3begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}.
Разложим определитель по 4 столбцу:
3∣−8−8−54−13−8001920404300∣=3⋅4⋅(−1)1+4∣−13−8019204430∣=12⋅(−1)5∣−13−8019204430∣=−12∣−13−8019204430∣3begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}=3cdot4cdot(-1)^{1+4}begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=12cdot(-1)^{5}begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=-12begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}.
Разложим определитель по столбцу №3 и вычислим его:
−12∣−13−8019204430∣=−12⋅4⋅(−1)2+3∣−13−843∣=−48⋅(−1)5∣−13−843∣=48∣−13−843∣-12begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=-12cdot4cdot(-1)^{2+3}begin{vmatrix}-13&-8\4&3end{vmatrix}=-48cdot(-1)^{5}begin{vmatrix}-13&-8\4&3end{vmatrix}=48begin{vmatrix}-13&-8\4&3end{vmatrix}.
Прибавим к строке №1 строку №2, умноженную на 3:
48∣−13−843∣=48∣−1143∣48begin{vmatrix}-13&-8\4&3end{vmatrix}=48begin{vmatrix}-1&1\4&3end{vmatrix}.
Прибавим к строке №2 строку №1, умноженную на 4:
48∣−1143∣=48∣−1107∣48begin{vmatrix}-1&1\4&3end{vmatrix}=48begin{vmatrix}-1&1\0&7end{vmatrix}.
Разложим определитель по столбцу №1 и заменим определитель 1-го порядка единственным его элементом:
48∣−1107∣=48⋅(−1)⋅(−1)1+1⋅7=48⋅(−1)⋅1⋅7=−33648begin{vmatrix}-1&1\0&7end{vmatrix}=48cdot(-1)cdot(-1)^{1+1}cdot7=48cdot(-1)cdot1cdot7=-336
.
Приведение к треугольному виду
Данный метод состоит в том, чтобы привести определитель к треугольному виду, а затем вычислить произведение элементов, стоящих на главной диагонали.
Пример 1
Вычислить определитель ∣4−20532−21−213−123−6−3∣begin{vmatrix}4&-2&0&5\3&2&-2&1\-2&1&3&-1\2&3&-6&-3end{vmatrix}.
Поменяем местами строки №1 и №3:
∣4−20532−21−213−123−6−3∣=−∣−213−132−214−20523−6−3∣begin{vmatrix}4&-2&0&5\3&2&-2&1\-2&1&3&-1\2&3&-6&-3end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\2&3&-6&-3end{vmatrix}.
Прибавим к строке №4 строку №1, умноженную на 1:
−∣−213−132−214−20523−6−3∣=−∣−213−132−214−20504−3−4∣-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\2&3&-6&-3end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\0&4&-3&-4end{vmatrix}.
Прибавим к строке №3 строку №1, умноженную на 2:
−∣−213−132−214−20504−3−4∣=−∣−213−132−21006304−3−4∣-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\0&4&-3&-4end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\0&0&6&3\0&4&-3&-4end{vmatrix}.
Умножим строку №2 на 2:
∣−213−132−21006304−3−4∣=−12∣−213−164−42006304−3−4∣begin{vmatrix}-2&1&3&-1\3&2&-2&1\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}begin{vmatrix}-2&1&3&-1\6&4&-4&2\0&0&6&3\0&4&-3&-4end{vmatrix}.
Прибавим к строке №2 строку №1, умноженную на 3:
−12∣−213−164−42006304−3−4∣=−12∣−213−1075−1006304−3−4∣-frac{1}{2}begin{vmatrix}-2&1&3&-1\6&4&-4&2\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&4&-3&-4end{vmatrix}.
Умножим строку №4 на 7:
−12∣−213−1075−1006304−3−4∣=−12⋅17∣−213−1075−10063028−21−28∣-frac{1}{2}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&28&-21&-28end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на -4:
−12⋅17∣−213−1075−10063028−21−28∣=−12⋅17∣−213−1075−1006300−41−24∣-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&28&-21&-28end{vmatrix}=-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&0&-41&-24end{vmatrix}.
Поменяем местами столбцы №3 и №4:
−12⋅17∣−213−1075−1006300−41−24∣=12⋅17∣−21−1307−15003600−24−41∣-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&0&-41&-24end{vmatrix}=frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&-24&-41end{vmatrix}.
Прибавим к строке №4 строку №3, умноженную на 8 и вычислим определитель:
12⋅17∣−21−1307−15003600−24−41∣=12⋅17∣−21−1307−1500360007∣=12⋅17⋅(−2)⋅7⋅3⋅7=−21frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&-24&-41end{vmatrix}=frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&0&7end{vmatrix}=frac{1}{2}cdotfrac{1}{7}cdot(-2)cdot7cdot3cdot7=-21.
Пример 2
Вычислить определитель
∣7694−410−266789−1−61−1−245−70−92−2∣begin{vmatrix}7&6&9&4&-4\1&0&-2&6&6\7&8&9&-1&-6\1&-1&-2&4&5\-7&0&-9&2&-2end{vmatrix}.
Поменяем местами строки №1 и №4:
∣7694−410−266789−1−61−1−245−70−92−2∣=−∣1−1−24510−266789−1−67694−4−70−92−2∣begin{vmatrix}7&6&9&4&-4\1&0&-2&6&6\7&8&9&-1&-6\1&-1&-2&4&5\-7&0&-9&2&-2end{vmatrix}=-begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\7&8&9&-1&-6\7&6&9&4&-4\-7&0&-9&2&-2end{vmatrix}.
Поменяем местами строки №3 и №5:
−∣1−1−24510−266789−1−67694−4−70−92−2∣=∣1−1−24510−266−70−92−27694−4789−1−6∣-begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\7&8&9&-1&-6\7&6&9&4&-4\-7&0&-9&2&-2end{vmatrix}=begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\-7&0&-9&2&-2\7&6&9&4&-4\7&8&9&-1&-6end{vmatrix}.
Поменяем местами столбцы №4 и №5:
∣1−1−24510−266−70−92−27694−4789−1−6∣=−∣1−1−25410−266−70−9−22769−44789−6−1∣begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\-7&0&-9&2&-2\7&6&9&4&-4\7&8&9&-1&-6end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\1&0&-2&6&6\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}.
Прибавим к строке №2 строку №1, умноженную на -1:
−∣1−1−25410−266−70−9−22769−44789−6−1∣=−∣1−1−25401012−70−9−22769−44789−6−1∣-begin{vmatrix}1&-1&-2&5&4\1&0&-2&6&6\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}.
Прибавим к строке №4 строку №3, умноженную на 1:
−∣1−1−25401012−70−9−22769−44789−6−1∣=−∣1−1−25401012−70−9−22060−66789−6−1∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\7&8&9&-6&-1end{vmatrix}.
Прибавим к строке №5 строку №3, умноженную на 1:
−∣1−1−25401012−70−9−22060−66789−6−1∣=−∣1−1−25401012−70−9−22060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.
Прибавим к строке №3 строку №1, умноженную на 7:
−∣1−1−25401012−70−9−22060−66080−81∣=−∣1−1−254010120−7−233330060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&-7&-23&33&30\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.
Прибавим к строке №3 строку №2, умноженную на 7:
−∣1−1−254010120−7−233330060−66080−81∣=−∣1−1−2540101200−234044060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&-7&-23&33&30\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.
Вынесем из строки №4 множитель 6:
−∣1−1−2540101200−234044060−66080−81∣=−6∣1−1−2540101200−234044010−11080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&8&0&-8&1end{vmatrix}.
Прибавим к строке №5 строку №4, умноженную на -8:
−6∣1−1−2540101200−234044010−11080−81∣=−6∣1−1−2540101200−234044010−110000−7∣-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&8&0&-8&1end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&0&0&0&-7end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на -1 и вычислим определитель:
−6∣1−1−2540101200−234044010−110000−7∣=−6∣1−1−2540101200−234044000−2−10000−7∣=−6⋅1⋅1⋅(−23)⋅(−2)⋅(−7)=1932-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&0&0&0&-7end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&0&0&-2&-1\0&0&0&0&-7end{vmatrix}=-6cdot1cdot1cdot(-23)cdot(-2)cdot(-7)=1932.
Мы рассмотрели наиболее распространенные методы вычисления определителей высших порядков. Каждый из них может применяться для их нахождения.
Онлайн-помощь с решением контрольных работ на бирже Студворк!
Тест по теме «Как вычислить определитель матрицы высших порядков»
Определители высших порядков.
Все
перечисленные выше свойства дословно
переносятся на определители любого
порядка. При их вычислении основную
роль играют свойства 7 и 8. С помощью
свойства 7 добиваются того, чтобы в
некоторой строке стояли на всех местах
нули, кроме, может быть, одного. Затем,
применяя свойство 8, разлагают определитель
по этой строке и тем самым сводят его
вычисление к нахождению определителя
меньшего порядка. Повторяя этот прием,
в конце концов, получают определитель
второго или третьего порядка, который
вычисляется непосредственно. Разумеется,
вместо строк можно выбрать столбцы,
используя свойство их равноправности.
Примеры
решения задач
-
Вычислить
определитель четвертого порядка

Решение:
В данном случае удобно из четвертой
строки вычесть
третью,
тогда в ней получится сразу три нуля

Разлагая
теперь определитель по четвертой строке,
мы должны будем умножить ее элементы
на свои алгебраические дополнения и
результаты сложить. Но поскольку три
из четырех этих элементов равны нулю,
то из всей суммы остается лишь второе
слагаемое
Выписанный
минор получен из определителя
вычеркиванием второго элемента четвертой
строки. Алгебраическое дополнение этого
элемента равно минору, умноженному на
(-1)4+2
= 1. Определитель третьего порядка,
который получился, вычислен непосредственно.
Метод
приведения к треугольному виду
заключается в таком преобразовании
определителя, когда все элементы, лежащие
по одну сторону одной из его диагоналей,
становятся равными нулю.
Вычислить
определитель:
Решение:
Вычитая первую строку из всех остальных,
получаем:
Упражнения
Вычислить
определители:
1.

2.
3.
4.

5.
6.
7.


Высшая алгебра.
Матрицы
и определители.
Понятие
матрицы и основанный на нём раздел
математики – матричная алгебра – имеют
чрезвычайно важное значение для
экономистов. Объясняется это тем, что
значительная часть математических
моделей, экономических объектов и
процессов записываются в достаточно
простой, а главное – компактной матричной
форме.
Матрицей
называется система элементов (в частном
случае чисел), находящихся в определённом
порядке и образующих таблицу. Если в
этой таблице m
строк и n
столбцов, а её элементы обозначены через
aij,
где i
– номер строки, а j
– номер столбца, на которых находится
этот элемент, то матрица записывается
в следующем виде:

(1)
Короче
эта матрица может быть записана так: А
= (аij),
(i
= 1, m;
j
= 1, n).
Каждый элемент матрицы называется её
компонентой.
Матрица
(1) имеет размер mn.
Если число строк матрицы m
не равно числу её столбцов n,
то матрица называется прямоугольной.
Если число строк равно числу столбцов,
то матрица называется квадратной, тогда
говорят о порядке матрицы. Матрица, у
которой все элементы равны нулю,
называется нулевой. Квадратная матрица,
у которой равны нулю все элементы, кроме
элементов, стоящих на главной диагонали,
называется диагональной. Диагональная
матрица, у которой все диагональные
элементы равны единице, называется
единичной, и обозначается через I
или Е. Иногда применяется транспонирование
матрицы А, т.е. перемена ролями её строк
и столбцов. Полученную матрицу обозначают
через АТ.
В общем, виде можно написать аТij
=
аji.
Ясно, что (АТ)Т
=
А.
Матрица,
совпадающая со своей транспонированной,
называется симметричной; (такой может
быть только квадратная матрица). Условие
симметричности можно записать в виде
Квадратная
матрица А имеет определитель, который
мы будем обозначать Прямоугольная
матрица определителя не имеет, так как
определители бывают только квадратные
(Определителем n-го
порядка называется число, которое
обозначается:

Если
из определителя квадратной матрицы
порядка n
вычеркнуть i-ую
строку и j-ый
столбец, на пересечении которых стоит
элемент, и составить из оставшихся
элементов определитель порядка n -1,
умножив на (-1)i+j,
где I
+ j
– сумма номеров вычеркнутой строки и
столбца, то полученное произведение
называется алгебраическим дополнением
элемента матрицы и обозначается символом
Aij.
Минором Мij
элемента aij
матрицы n-го
порядка называется определитель матрицы
(n
-1) порядка, полученный из матрицы А
вычёркиванием i-й
строки и j-го
столбца:

т.е.
алгебраическое дополнение совпадает
с минором, когда сумма номеров строки
и столбца (i+j)-чётное
число и не совпадает, когда (i+j)
– нечётное число.
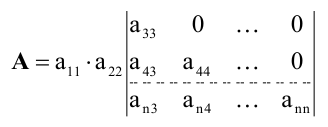
Формула
для вычисления определителей:

(4.14)
Предполагается,
что а11
0, если а11
=
0, то перестановкой строк и столбцов
всегда можно из данного определителя
получить такой, в котором = 0. Эта формула
очень проста в употреблении и позволяет
вычисление определителя порядка n
свести к вычислению определителя порядка
n
— 1.
Действия
над матрицами:
Линейными
действиями над матрицами называется
сложение матриц и умножение их на число.
Оба эти действия определяются поэлементно:
Сложению
матриц имеет обратное действие –
вычитание, которое также осуществляется
поэлементно, например, если А = (аij),
В
= (bij),
то С = А — В = (cij),
где cij.=
aij
– bij
.
Отметим
очевидные формулы:
(А
+ В)T
=
АT
+
ВT;
(kА)T
= kАT;
det(kC)
= kndetC,
где
n
– порядок квадратной матрицы С. При
этом, вообще говоря, det(A+B)
detA
+ detB.
Пример:
,
Умножение
матриц:

Матрица
С называется произведением матрицы В
на матрицу А. С = ВА.
Размер её (sm)
(mn)
= (sn).
Элемент
матрицы С, стоящий в i
–ой строке и j
–ом столбце, равен сумме произведений
элементов i-ой
строки матрицы В на соответствующие
элементы j
–ого столбца матрицы А, т.е.
,
(т.е.
для нахождения элементов произведения
матриц В и А мы находим скалярное
произведение i
строки матрицы В на j
столбец матрицы А).
Пример
,
.
.
Откуда
видно, что ВА
АВ.
Свойства
произведения двух матриц:
А)
Не всякие две матрицы можно перемножить.
Произведение ВА
двух матриц в указанном порядке возможно
в том и только в том случае, если число
столбцов матрицы В равно числу строк
матрицы А (ширина первого сомножителя
должна равняться высоте второго).
Символически это можно записать так:
(mk)
(kn).
Значит,
в матрице, являющейся произведением
двух матриц, число строк равно числу
строк левого сомножителя, а число
столбцов – числу столбцов правого
сомножителя.
Простое
правило, определяющее возможность
матричного умножения и его результат,
можно записать следующим образом (здесь
А – матрица порядка mk,
В — kn):
(mk)*(kn)
(
произведения).
Таким
образом, произведение матрицы определено
только в том случае, когда внутренние
индексы равны. Тогда порядок произведения
получается вычёркиванием внутренних
индексов.
Очевидно,
что порядок, в котором перемножаются
матрицы (здесь мы не можем избежать
использования слова “порядок” в двух
смыслах), имеет решающее значение. В
произведении ВА
тех же матриц А и В мы имели бы (kn)
(mk).
Внутренние индексы здесь не равны, т.е.
произведение ВА
не определено.
Если
А – матрица порядка mn,
а В – порядка nm,
то определены оба произведения АВ и ВА.
Однако АВ будет матрицей порядка mn,
в то время как ВА — nm,
т.е. АВ
= ВА.
Только тогда, когда А и В – квадратные
матрицы одного и того же порядка, возможно
равенство АВ
= ВА,
но даже и в этом случае оно, вообще
говоря, не верно.
Б) Произведение
двух матриц, в общем случае, не обладает
свойством переместительности (т.е. иначе
говорят, что не обладает свойством
коммутативности).
Значит,
в общем случае менять местами матрицы
– сомножители нельзя, не изменив их
произведения. В этом состоит одно из
отличий законов алгебры матриц от
законов элементарной алгебры. Если
изменить порядок сомножителей, может
оказаться, что вообще умножить матрицы
невозможно.
В
произведении ВА
двух матриц В и А мы будем говорить, что
матрица А умножается слева на матрицу
В, или что матрица В умножается справа
на матрицу А.
Правило
умножения матриц на первый взгляд может
показаться громоздким и сложным. Однако,
те кому приходится часто и много работать
с матрицами, очень быстро привыкают
безошибочно это правило применять, и
оно представляется им исключительно
простым; палец левой руки должен скользить
слева направо вдоль строк первой матрицы,
а палец правой руки должен при этом
скользить по столбцам второй матрицы
сверху вниз. Выполнив несколько
упражнений, правило умножения матриц
можно легко освоить.
Если
две матрицы А и В – квадратные одного
и того же порядка, а их произведение АВ
есть единичная матрица АВ=Е, то матрица
В называется матрицей обратной к А и
обозначается символом А-1.
Следует иметь в виду, что квадратная
матрица А и ей обратная А-1
коммутативны, т.е. АА-1
=
А-1А
= Е.
Для
того, чтобы квадратная матрица А имела
обратную, необходимо и достаточно, чтобы
определитель А(detA)
не был равен нулю, т.е. матрица А не должна
быть особенной (вырожденной).
Укажем
основные методы вычисления обратной
матрицы:
А) Метод
присоеднённой матрицы
(если
А невырожденная матрица)
Матрица
,
элементами которой является алгебраические
дополнения оответствующих элементов
матрицы А, называется присоединённой
(в литературе присоеднённую матрицу
называют взаимной, или союзной) к матрице
А
Справедливо
равенство ()ТА
= A()Т
=
detAЕ
Отсюда
следует, что если А – невырожденная
матрица, то
А-1
=
(1/ detA)
()Т.
(2)
Приведём
алгоритм вычисления обратной матрицы.
-
Находим
определитель исходной матрицы. Если
detA
= 0, то матрица А – вырожденная и обратной
матрицы А-1
не существует. Если detA
0, то матрица А – невырожденная и обратная
матрица существует. -
Находим
алгебраические дополнения соответствующих
элементов матрицы А, и составляем из
них присоеднённую матрицу
.
-
Вычисляем
обратную матрицу по формуле (2) -
Проверяем
правильность вычисления обратной
матрицы
А-1,
исходя из её определения А-1А
= AА-1
=
Е.
Найти
матрицу, обратную к данной:
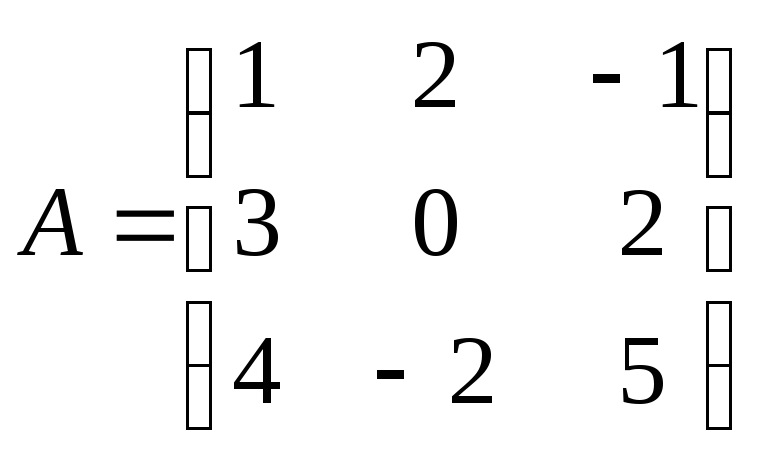
Решение:
-
Определитель
матрицы detA
= — 4
0, значение определителя получено
разложением по первой строке:
2.
Находим алгебраические дополнения
соответствующих элементов матрицы А:
и
составляем из них присоединённую матрицу
:
3. Находим
матрицу (Аv)Т,
транспортированную к Аv
4. Вычисляем
обратную матрицу по формуле

5. Проверяем
правильность вычисления обратной
матрицы по формулам: А-1А
= AА-1
=
Е
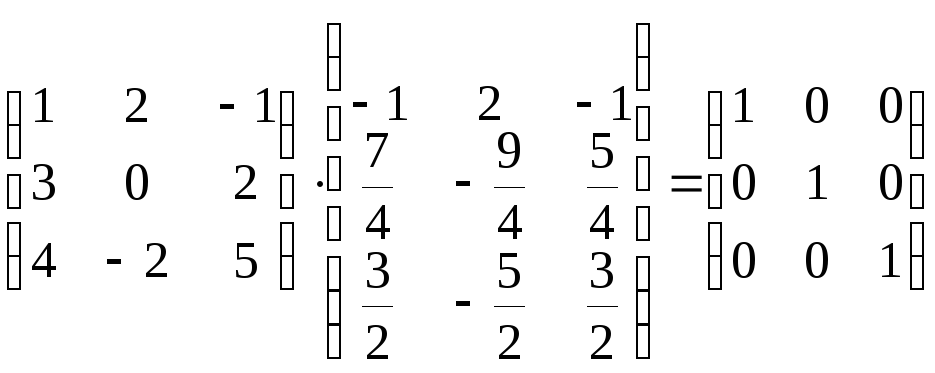
Методом
элементарных преобразований найти А-1
для
заданной
матрицы:
Решение:
образуем матрицу ГА:
Обозначим
через
,
строки матрицы ГА,
произведём над ними следующие
преобразования:
В
результате последовательно получаем
Следовательно,

Для
невырожденных матриц выполняются
следующие свойства:
1.
detА-1
=
(1/ detA); 2. (А-1)-1
= A; 3. (Аm)-1
= (А-1)m;
4.
(АB)-1
=
B-1A-1;
5. (А-1)T
= (АT)-1.
В) Вычисление
обратной матрицы методом элементарных
преобразований (метод Гаусса).
Напомним,
что элементарными преобразованиями
матрицы называются следующие: 1)
перестановка строк (столбцов) 2). Умножение
строки (столбца) на число, отличное от
нуля; 3). Прибавление к элементам строки
(столбца) соответствующих элементов
другой строки (столбца), предварительно
умноженных на некоторое число.
Алгоритм
вычисления обратной матрицы методом
Гаусса состоит в следующем преобразовании:
Для данной матрицы А n-го
порядка построим прямоугольную матрицу
ГА
=
(АЕ)
размера n2n,
приписывая к А справа единичную
матрицу. Далее, используя элементарные
преобразования над , приводим матрицу
ГА
к виду (ЕВ),
что всегда возможно, если А невырождена.
Тогда В=А-1
(коротко, это выглядит так ((АЕ)
(ЕА-1)),
элементарные преобразования осуществляются
только над строками).
Примеры
решения задач
-
Пусть
,
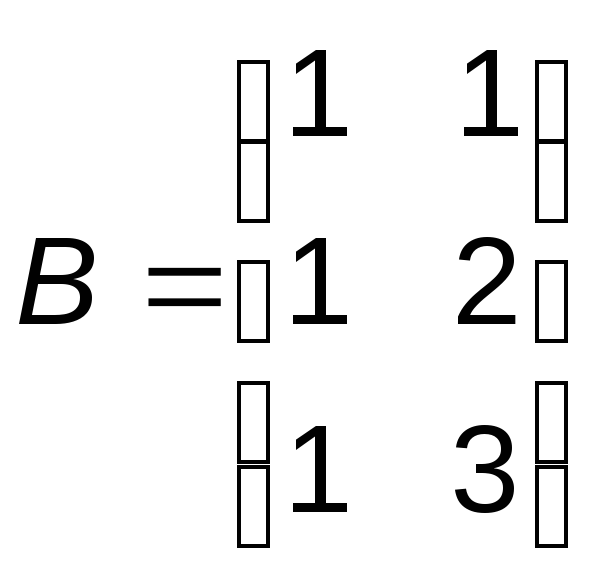

Вычислить
АВ,
ВА,
АС,
ВС
и С2.
Решение:
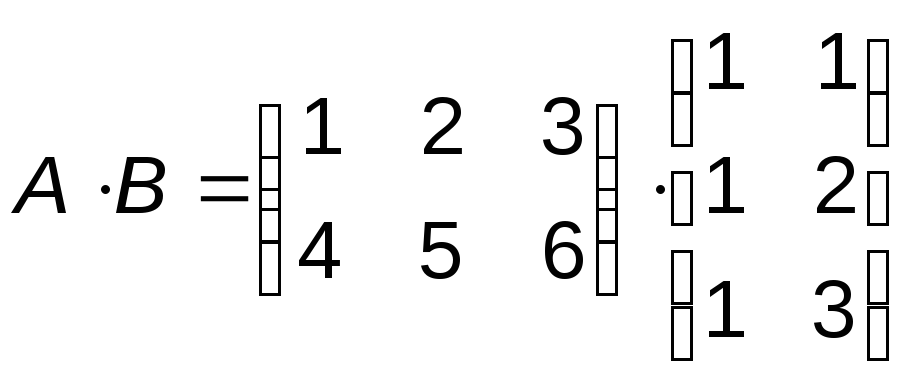
Видим,
что количество столбцов у матрицы А,
равно количеству строк у матрицы В,
следовательно произведение матриц
существует. Найдём рамер этой матрицы:
(23)
(32)
= (22).
Найдём произведение матриц:

Аналогично,

Далее,
и

Произведение
ВС
не определено, так как число столбцов
матрицы В (два) не равно числу строк
матрицы С (три), т.е. ширина матрицы В не
равна высоте матрицы С.
2.
Вычислить произведение матрицы строки
на матрицу столбец:

Очевидно,
правило произведения выполнено и размер
произведения: (15)(51)
= (11)
т. е. получим число:

3. Вычислить:

Решение:
выполняя последовательно произведение
матриц, получим:

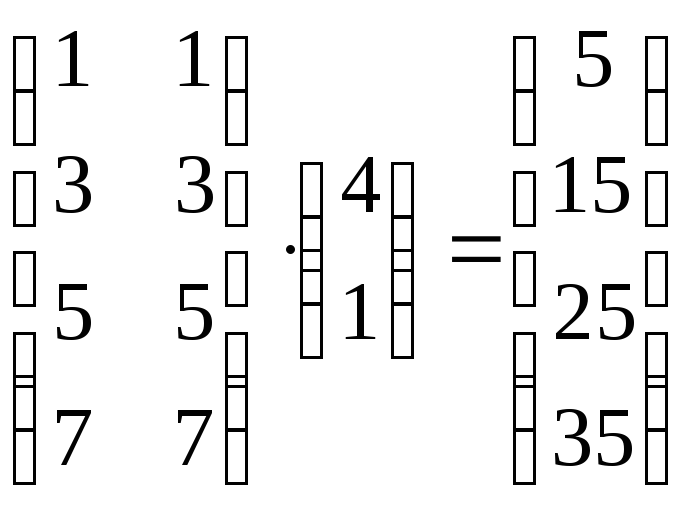
4.
Вычислить обратные матрицы для следующих
матриц:
а)


Решение:
а)
Вычтем
из третьей строки первую и вторую строки
и вычтем из второй строки первую, тогда
Наконец,
вычтем из первой строки вторую и третью,
умноженную на ½, и разделим третью строку
на 2, тогда

Проверка:
А-1А
= АА-1
= Е
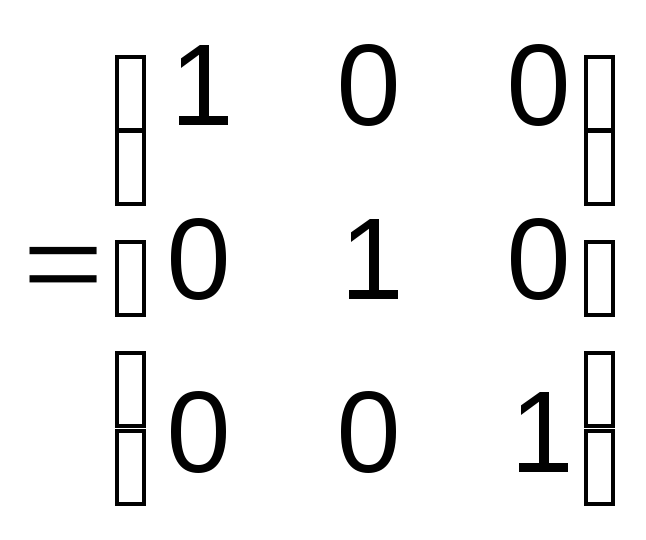
b)
вычтем
четвёртую строку из третьей и разделим
четвёртую строку на 2, тогда
теперь
вычтем из первой строки удвоенную
вторую, а затем третью строку, умноженную
на 6, и вычтем из второй строки удвоенную
третью.

В
справедливости этих выкладок убедиться,
сделав проверку умножением исходной
матрицы на полученную обратную.
5.
Даны матрицы

Решить
уравнения:
а)
AX
= B;
b)
XA
= C
Решение:
-
AX
= B
Выразим из этого уравнения X.
Для этого его слева умножим на А-1.
A-1АX
= A-1B
X = A-1B
(размер
(22)
(23)
= (23)).
Найдём
обратную матрицу А-1,
(А-1
=
(1/ detA)
(Аv)Т!)
согласно
алгоритму вычисления обратной матрицы:
-
detA
= 31
— 21
= 1, так как detA
0, то А-1
существует. -
Находим
алгебраические дополнения соответствующих
элементов матрицы А и составляем из
них присоеднённую матрицу
:
= 1, = -1, = -2, = 3
:
.
3. Находим
матрицу (Т,
транспонированную к
),
.
4. Вычисляем
обратную А-1=(1/
detA)
()Т:
5. Проверяем
правильность вычисления обратной
матрицы
А-1
,
исходя из её определения А-1А
= AА-1
=
Е
.
Матрицу
неизвестных Х найдём, умножая уравнение
слева на А-1:
.
б) Полагая
матрицу А невырожденной, умножим обе
части уравнения XA
= C
справа на обратную матрицу А-1:
(XA)А-1
=
CА-1
. Так как (XA)А-1
=
X(AА-1)
= XE
= X,
то X
= СА-1
и размер матрицы переменных (42);
(так как (42)(22)
= (42)):

Следовательно,
Ответ:

-
Решить
уравнение:
.
Решение:
обозначив:
,
представим
уравнение в виде АXВ
= С. Умножим обе части уравнения слева
на обратную матрицу А-1
и справа на обратную матрицу В-1,
учитывая, что А и В – невырожденные
матрицы:
detA
= 1
0, detB
= -10
0. Получим А-1(АXВ)В-1
=
А-1СВ-1.
Учитывая, что А-1(АXВ)В-1
=
(А-1А)
(XВ)В-1
=
Е(XB)В-1
=
(XB)В-1
=
X(BВ-1)
= XE
= X,
получим X=
А-1СВ-1
Теперь
найдём
.
Поэтому

Ответ:
.
Упражнения
-
Вычислить
линейные комбинации матриц и
3А + 2В; В – 3А; 2(А – В), если
и .
-
Вычислить
произведения матриц:
а)
;
б);
в)

г)
д)

е)
-
Методом
присоедненной матрицы найти обратные
для следующих матриц:
а)
;
б);
в);
г)

д)
-
Методом
элементарных преобразований найти
обратные матрицы для следующих матриц:
а)

б)
в)
г)

5.
Вычислите А-1,
B-1,
AB
и (АB)-1,
если
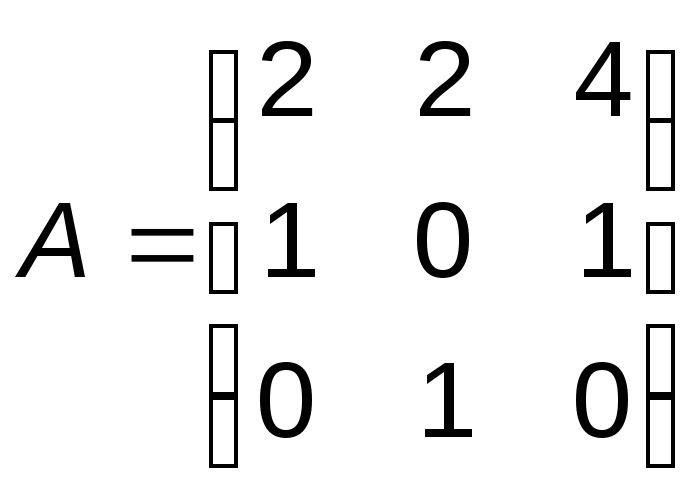

убедитесь
в том, что (АB)-1
=
B-1А-1
.
6.
Решить матричные уравнения:
а)
;б)
;
в)
;
д)

е)

Системы
линейных алгебраических уравнений
(СЛАУ).
Это
один из основных разделов в алгебре.
Нет такой отрасли науки и приложений,
где в том или ином виде не использовались
бы системы линейных алгебраических
уравнений. При решении экономических
и управленческих задач системы линейных
уравнений наиболее употребимы как в
аппарате исследования, так и при
рассмотрении частных проблем.
Система
m
линейных уравнений с n
неизвестными (переменными) x1,
x2,
. . . , xn
имеет вид

(1)
где
(i=1,2…m;
j=1,2…n)
— произвольные числа, называемые
соответственно коэффициентами при
переменных и свободными членами
уравнений.
В
более краткой записи с помощью знаков
суммирования систему можно записать в
виде:
.
Решением
системы называется такая совокупность
n
чисел
(),
при подстановке которых каждое уравнение
системы обращается в верное равенство.
Система
уравнений называется совместной, если
она имеет хотя бы одно решение, и
несовместной, если она не имеет решений.
Совместная система уравнений называется
определенной, если она имеет единственное
решение, и неопределенной, если она
имеет более одного решения.
Две
системы уравнений называются
равносильными, или эквивалентными, если
одно и то же множество решений.
Запишем
систему (1 в матричной форме). Обозначим
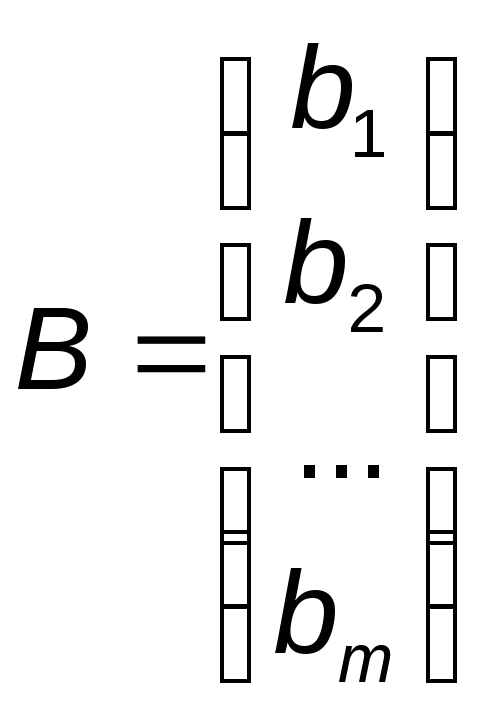
где
А – матрица коэффициентов при переменных,
или матрица системы; Х – матрица-столбец
переменных; В – матрица-столбец свободных
членов.
На
основании определения равенство (1)
можно записать в виде:
AX
= B
(2)
Система
n
линейных уравнений с n
переменными. Метод обратной матрицы и
формулы Крамера.
Пусть
число уравнений системы (1) равно числу
неизвестных, (переменных), т.е. m
= n.
Тогда матрица системы является
квадратной, а ее определитель detA
называется определителем системы.
Для
получения решения системы (1) при m
= n
в общем виде предложим, что квадратная
матрица А невырoждена,
т.е. её определитель detA
0. В этом случае существует обратная
матрица A-1.
Умножая слева обе части матричного
равенства (2) на матрицу A-1,
получим A-1(AX)
= A-1B.
Так как A-1(AX)
= (A-1A)X
= EX
= X,
то решением системы методом обратной
матрицы будет матрица-столбец X
= A-1B.
Пусть
∆ — определитель матрицы системы , а ∆i
— определитель матрицы, получаемой из
матрицы заменой i-го
столбца столбцом свободных членов.
Тогда, если ∆
0, то система имеет единственное решение,
определяемое по формулам
Формулы
получили название формул Крамера.
Пример
1. Решить систему уравнений по формулам
Крамера.

Решение:
Найдём определитель системы
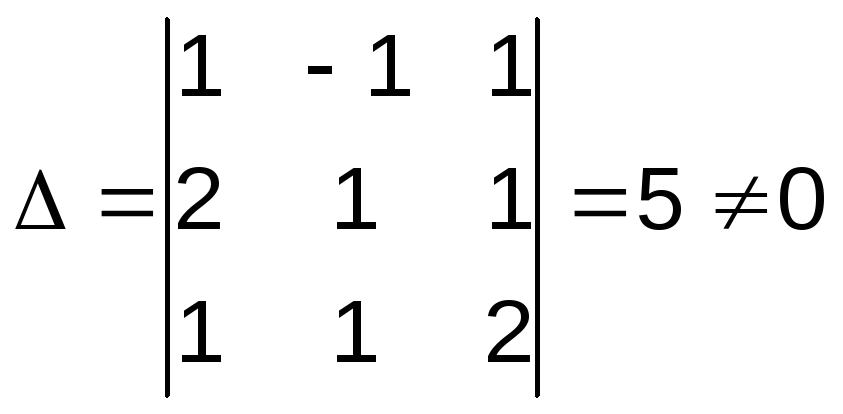
Так
как ∆
0, то по правилу Крамера система имеет
единственное решение. Вычислим
определители матриц ∆, ∆, ∆, полученные
из матрицы А, заменой соответственно
первого, второго и третьего столбцов
столбцом свободных членов:
(рекомендуем
читателю вычислить самостоятельно!).
Теперь по формулам Крамера найдём
решения системы:
.
Ответ:
.
Существенным
недостатком решения систем и линейных
уравнений с n
переменными по формулам Крамера и
методом обратной матрицы является их
большая трудоёмкость, связанная с
вычислением определителей и нахождением
обратной матрицы. Поэтому эти методы
представляют скорее теоретический
интерес и на практике не могут быть
использованы для решения реальных
экономических задач, сводящихся часто
к системам с большим числом уравнений
и переменных.
Метод
Гаусса.
Рассмотрим
решение системы (1) m
линейных уравнений с n
переменными в общем виде.
Метод
Гаусса – метод последовательного
исключения переменных- заключается в
том, что с помощью элементарных
преобразований система уравнений
приводится к равносильной системе
ступенчатого (или треугольного) вида,
из которой последовательно, начиная с
последних (по номеру) переменных,
находятся все остальные переменные.
Предположим,
что в системе (1) коэффициент при переменной
x
в первом уравнении a
0 (если это не так, то перестановкой
уравнений местами добьёмся того, что a
0).
.
Умножая первое уравнение на подходящие
числа (a,
именно, на -a/a,
— a/a,
. . . , a/a),
и прибавляя полученные уравнения
соответственно ко второму, третьему,
…, m-му
уравнению системы (1), исключим переменную
х1
из всех последующих уравнений, начиная
со второго.
Получим:

Где
буквами с верхним индексом (1) обозначены
новые коэффициенты, полученные после
первого шага.
.
Предположим, что
(если
это не так, то соответствующей перестановкой
уравнений или переменных с изменением
их номеров добьёмся того, чтобы).
Умножая
второе уравнение на подходящие числа
(,
,
. . . ,)
и прибавляя полученные уравнения
соответственно к третьему, четвёртому,
… ,m-му
уравнению системы, исключим переменную
x
из всех последующих уравнений, начиная
с третьего.
Продолжая
процесс последовательного исключения
переменных x,
x,
… , x,
после (r-1)-го
шага получим систему

Число
нуль в последних m-r
уравнениях означает, что их левые части
имеют вид 0+
0+…+
0. Если хотя бы одно из чисел b,
…. , не равно нулю, то соответствующее
равенство противоречиво, и система (1)
несовместна.
Таким
образом, для любой совместной системы
числа b,
…. , в системе (4) равны нулю. В этом
случае последние m+r
уравнений в системе (4) являются тождеством
и их можно не принимать во внимание при
решении системы (1). Очевидно, что после
отбрасывания « лишних» уравнений
возможны два случая: а) число уравнений
(4) равно числу переменных, т.е. r
= n
( в этом случае система имеет треугольный
вид); б) r
< n
( в этом случае система (4) имеет ступенчатый
вид).
Переход
системы (1) к равносильной ей системе
(4) называется прямым ходом метода Гаусса,
а нахождение переменных из системы (4)
– обратным ходом.
Преобразования
Гаусса удобно проводить, осуществляя
преобразования не с самими уравнениями,
а с матрицей их коэффициентов. Рассмотрим
матрицу
называемую
расширенной матрицей системы (1), ибо в
неё, кроме матрицы системы А, дополнительно
включен столбец свободных членов.
ПРИМЕРЫ.
2.
Решить систему уравнений
Решение.
Расширенная матрица системы имеет вид:

ШАГ
1. Так как
0 то, умножая первую строку матрицы на
числа (-2), (-3), (-2) и прибавляя полученные
строки соответственно ко второй, третьей,
четвёртой строкам, исключим переменную
. из всех строк, начиная со второй.
Заметив, что в новой матрице = 0, поменяем
местами вторую и третью строки:

ШАГ
2. Так как теперь = — 4
0 то, умножая вторую строку на (-7/4) и
прибавляя полученную строку к четвёртой,
исключим переменную из всех строк,
начиная с третьей:

ШАГ
3. Учитывая, что = -8
0, умножаем третью строку на 13,5 / 8 = 27 / 6,
и, прибавляя полученную строку к
четвёртой, исключим из неё переменную
.
Получим
систему уравнений

Откуда,
используя обратный ход метода Гаусса,
найдём из четвёртого уравнения из
третьего из второго и из первого
уравнения т.е. решение системы (1,2,-1,2).
3. Решить
следующие системы уравнений:
а)

Решение:
а). Расширенная матрица системы имеет
вид:
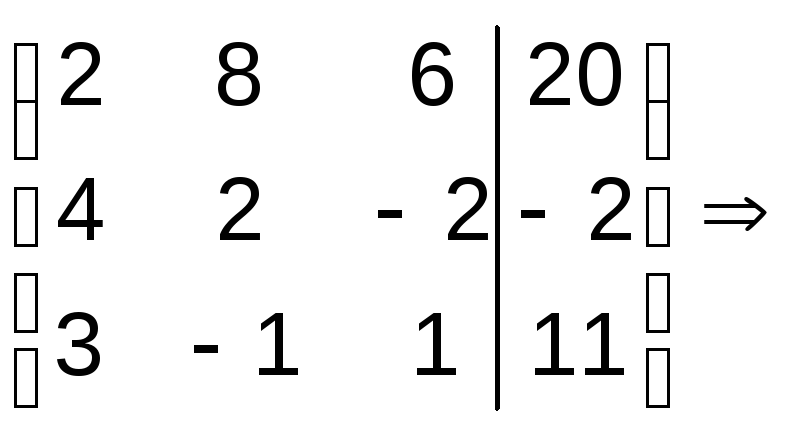
1. Так как
,
то разделим первую строку на вторую,
получим:

Умножая
первую стоку матрицы на числа (-4), (-3) и
прибавляя полученные строки соответственно
ко второй и третьей строке, исключим
переменную х1
из всех строк, начиная со второй, получим:

Шаг
2. Так как = -14
0, то разделим 2-ю и 3-ю строки соответственно
на (–14) и на (–1)
Умножая
2-ю строку на (-13), прибавим к третьей.

Используя
обратный ход метода Гаусса, найдём

Откуда
x3
=
(-20)/(-5) = 4; x2
=
3 — x3
=
— 1; x1
=
10 — 4x2
—
3x3
=
2,
т.е.
наёдено решение системы (2,-1,4)
б)
Здесь = 1, расширенная матрица имеет вид
Шаг
1. Умножим 1-ю строку на (-2) и (-4) и прибавим
ко второй
и
третьей соответственно, получим
Шаг
2. Умножим вторую строку на (-1) и прибавим
к третьей
Ясно,
что эта система уравнений несовместна
и не имеет решения.
в)
Поступая,
как и в предыдущих случаях, получим

Исходная
система сводится к следующей системе:

Существует
бесконечное число решений, причём все
они удовлетворяют соотношениям полагая
, получим (()/3, (c-1)/3,
c),
где с может принимать любое значение.
Для
совместных систем линейных уранений
верны следующие теоремы:
1.
Если ранг матрицы совместной системы
равен числу переменных, т.е. r
= rangA
= n,
то система (2) имеет единственное решение.
2.
Если ранг матрицы совместной системы
меньше числа переменных, т.е. r
= rangA
< n,
то система 2 неопределена и имеет
бесконечное множество решений.
Результаты
исследования системы (1) приведём в виде
следующей схемы (см. стр. 43).
Пусть
rang(A)
= rangA
= r,
т.е. система совместна. Не ограничивая
общности, будем считать, что базисный
минор располагается в первых r
(1
r
min
(m,n))
строках и столбцах матрицы А. Отбросив
последние m
— r
уравнений системы (1), запишем укороченную
систему:

(5)
которая
эквивалентна исходной. Назовем неизвестные
базисными, а свободными и перенесем
слагаемые, содержащие свободные
неизвестные, в первую часть уравнения
(5). Получаем систему относительно
базисных неизвестных:
a11x1+…+a1rxr=
b1-a1,
r+1
xr+1—
… -a1nxn,
которая
для каждого набора значений свободных
неизвестных
b1,…bn,
имеет единственное решение (X1,…,Xn),
находимое по правилу Крамера.
Соответствующее решение укороченной,
а следовательно, и исходной систем имеет
вид:

Формула
(6), выражающая произвольное решение
системы в виде вектор-функции от n
— r
свободных неизвестных, называется
общим решением системы (1).
Схема
исследования системы неоднородных
линейных алгебраических уравнений
Rang
< n
Система
неопределённая (бесконечно много
решений).
Rang
A
Система
несовместная.
Rang
< m
Уравнения
системы зависимые.
Система
m
линейных уравнений с n
переменными.
Rang
= n
Система
определённая (единственное решение).
Rang
= m
Уравнения
системы не зависимые.
Rang
A
=
Система
совместная.
Алгоритм
(правило) для решения системы линейных
уравнений.
1).
Путём вычисления ранга матрицы системы
и расширенной матрицы выясняют вопрос
о совместности системы; если система
совместна, то находят один из гланых
миноров M
порядка r,
равного рангу обеих матриц.
2).
Берут r
уравнений, в которых лежит минор M;
остальные уравнения отбрасывают; r
неизвестные коэффициенты, которые
входят в главный минор M,
обьявляют базисными и оставляют слева,
а остальные n-r
неизвестные обьявляют свободными и
переносят в правую часть.
3).
По правилу Крамера находят выражения
базисных неизвестных через свободные
переменные. Полученные равенства
называют общим решением.
4).
Придавая свободным неизвестным любые
числовые значения, из общего решения
находят соответствующие значения
базисных неизвестных и тем самым находят
решение исходной системы уравнений,
которое в отличие от общего решения
можно назвать частным решением. Указанным
путём можно получить любое решение. Для
этого свободным неизвестным в общем
решении надо придать те значения, которые
они имеют в данном решении.
ПРИМЕР
4. Установить совместность и найти общее
решение системы.
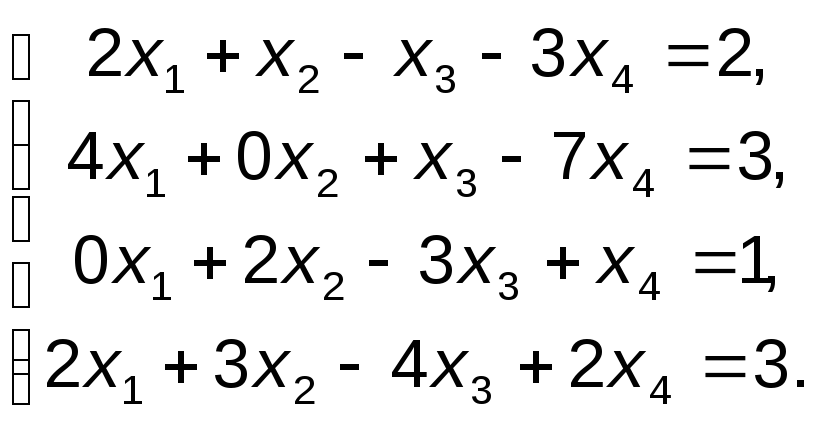
РЕШЕНИЕ:
Выпишем основную и расширенную матрицу
системы:

Так
как, А = rangA
(проверьте!), то исходная система совместна
(так как rangA
= 2 < 4, то система имеет бесконечно много
решений).
Выберем
в качестве базисного м
.
Тогда
неизвестные x,
x
— базисные, x,
x
— свободные, а укороченная система имеет
вид:
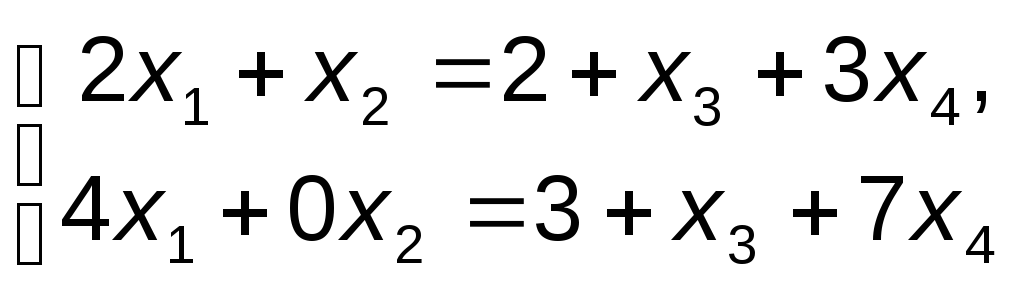
Полагая
x=
с, x=
с, и решая укороченную систему относительно
базисных неизвестных, получаем
Следовательно,
общее решение исходной системы иммет
вид:
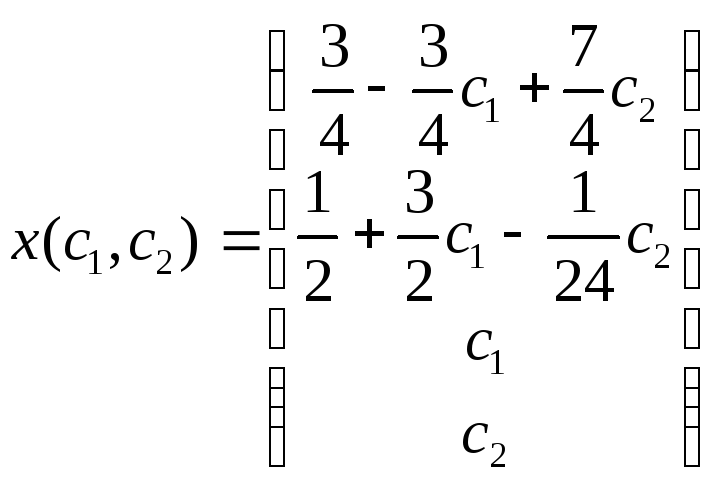
Однородная
система АХ
= 0. Всегда совместна, так как имеет
тривиальное решение Х = 0. Для существования
нетривиального решения однородной
системы необходимо и достаточно, чтобы
r
= rangA
< n
(при m
= n
это условие означает, что detA
= 0).
Пусть
Q
Rn
множество всех решений однородной
системы. Всякий базис во множестве Q
состоит из n
— r
векторов. Соответствующая ему в
каноническом базисе система вектор-столбец
(
Х1…Хn)Т
—
называем фундаментальной системой
решений. Общее решение однородной
системы имеет вид: X
=(c1,…,сn),
где c1,…,сn
– произвольные
постоянные.
Базисные
решения могут быть получены методом,
изложенным в предыдущем пункте, если
свободным неизвестным придавать
поочередно значение 1, полагая остальные
равные 0.
Алгоритм
(правило) для построения фундаментальной
системы решений.
Берут
любой определитель D
порядка n
— r,
отличный от нуля (например, определитель,
у которого элементы главной диагонали
равны единице, а остальные нулю). Свободным
неизвестным придают поочередно значения,
равные элементам первой, второй и т.д.
строк определителя D,
и каждый раз из общего решения находят
соответствующие значения главных
неизвестных. Полученные n
— r
решений составляют фундаментальную
систему. Меняя произвольно исходный
определитель D,
можно получить различные фундаментальные
системы решений.
ПРИМЕР
5. Найти фундаментальную систему решений
и общее решение следующей однородной
системы уравнений:
РЕШЕНИЕ:
Матрица коэффициентов:
имеет
ранг r
= 2 (проверте!).
Выберем
в качестве базисного минора:
Тогда
укороченная система имеет вид:
3x1
+
x2
=
8x3
— 2x4
— x5,
Откуда
находим.
Общее
решение системы:

Из
общего решения находим фундаментальную
систему решений:
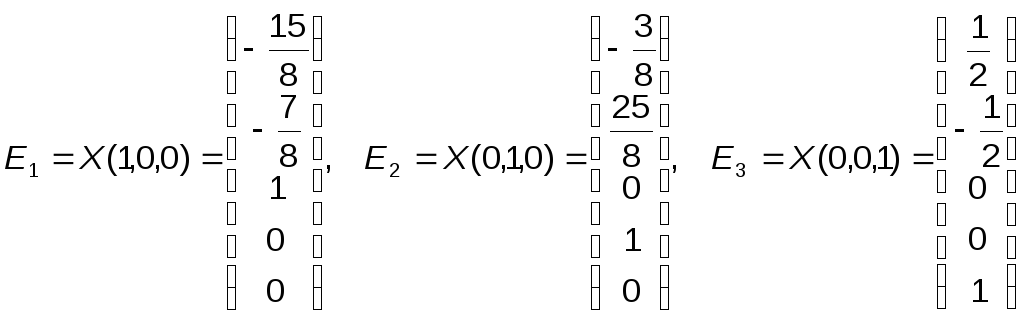
С
использованием фундаментальной системы
общее решение может быть записано в
виде:

ЗАМЕЧАНИЕ:
Если ранг системы однородных линейных
уравнений на единицу меньше числа
неизвестных: r
= n
— 1, то n
— r
= 1 т.е. фундаментальная система состоит
из одного решения и любое ненулевое
решение образует фундаментальную
систему. В этом случае любые два решения
различаются
между
собой лишь числовым множителем.
ПРИМЕР
6. Найти общее решение и фундаментальную
систему решений системы уравнений:
РЕШЕНИЕ:
Составим матрицу системы
поэтому
Так
как это решение не нулевое, то оно
образует фундаментальную систему
решений. Все решения ему пропорциональны.
Значит, общее решение имеет вид:
где
с параметр принимающий любые числовые
значения. С использованием фундаментальной
системы, общее решение может быть
записано в виде:
Если
в неоднородной системе линейных уравнений
заменить все свободные члены нулями,
то получится однородная система,
называемая приведённой системой для
исходной неоднородной системы. Решение
даннорй системы и ситемы соответствующей
ей приведённой системы связаны следующим
образом.
-
Сумма
любого решения неоднородной системы
и любого решения её приведённой системы
является решением неоднородной системы. -
Разность
двух любых решений неоднородной системы
является
решением
её приведённой системы. Из этих двух
свойств следует:Все решения неоднородной
системы можно получить, прибавляя к
одному (любому) её решению поочередно
все решения её приведённой системы.
Иными словами, общее решение неоднородной
системы можно получить, если к любому
частному решению этой системы прибавить
общее решение её приведённой системы.
Найти
общее решение системы уравнений
.
РЕШЕНИЕ:
Эта
система имеет частное решение x
= y
= z
= 1.
Общее
решение её приведённой системы найдено
в предыдущем примере и имеет вид:
X
= 2,
где
параметр, принимающий любые значения.
Поэтому общее решение данной неоднородной
системы уравнений имеет вид x
= 1 + 2, где произвольный параметр.

Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
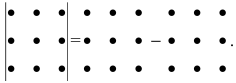
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
Методы вычисления определителей
При вычислении определителей высокого порядка (больше 3-го) определение, как правило, не используется, так как это приводит к громоздким выражениям и требует большого количества арифметических операций. Гораздо эффективнее использовать свойства определителей. Наиболее важными для вычисления определителей являются свойства 3, 6, 9. Эти свойства можно назвать элементарными преобразованиями определителя, что соответствует элементарным преобразованиям матрицы.
I. Перестановка двух столбцов (строк) определителя приводит к изменению его знака на противоположный.
II. Умножение всех элементов одного столбца (строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число.
III. Прибавление к элементам одного столбца (строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.
При помощи элементарных преобразований можно упростить определитель, т.е. привести его к виду, удобному для вычислений.
Метод приведения определителя к треугольному виду
При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Итак, метод состоит из двух шагов.
1. При помощи элементарных преобразований привести определитель к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.
Пример 2.12. Вычислить определитель четвёртого порядка
приводя его к треугольному виду.
Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):
Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.
Умножим элементы второй строки на (-1), а элементы третьей строки — на 0,5, при этом, чтобы не нарушить равенство, надо полученный определитель разделить на , т.е. умножить на (-2):
В полученной матрице нужно сделать равными нулю элементы и
второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента
и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:
Осталось сделать равным нулю элемент . К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):
Получили определитель треугольного вида.
2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали:
Метод понижения порядка определителя
Этот метод также основан на элементарных преобразованиях определителя.
1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.
2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.
Пример 2.13. Вычислить определитель четвёртого порядка методом понижения порядка.
Решение. 1. В качестве ведущего элемента возьмем , а все остальные элементы второй строки при помощи элементарных преобразований сделаем равными нулю. Для этого ко второму столбцу прибавим четвертый, умноженный на (-3):
2. Разложим определитель по второй строке
Получили определитель третьего порядка.
Вынесем за знак определителя множитель (2) из второго столбца (точнее все элементы второго столбца умножим на 0,5 , а получившийся определитель умножим на 2):
Прибавим ко второму столбцу первый
Полученный определитель разложим по второму столбцу
Получили определитель 2-го порядка.
Прибавим ко второй строке первую, умноженную на (-2)
Разложим определитель по второй строке и заменим определитель первого порядка единственным его элементом
Результат совпадает с полученным в примере 2.7.
Метод изменения всех элементов определителя
При вычислении определителей бывает полезно изменить все его элементы, умножив их на одно и то же число, не равное нулю, либо прибавить к каждому элементу одно и то же число. Найдем формулы изменения определителя при этих преобразованиях.
Пусть дана квадратная матрица n-го порядка. Из свойства 6 следует, что при умножении всех элементов определителя n-го порядка на число
определитель умножается на число
.
Рассмотрим теперь определитель матрицы , элементы которой
получены из соответствующих элементов матрицы
прибавлением числа
Применяя свойство 7 к первому столбцу этого определителя, получаем сумму определителей
То же свойство применяем к каждому определителю («раскладывая» второй столбец) и т.д. В итоге получим сумму определителей n-го порядка, причем определители, имеющие по два и более столбцов из элементов, равных
, равны нулю (по свойству 4). Поэтому в сумме остаются только
слагаемых: определитель матрицы
и
определителей вида
отличающихся от определителя матрицы только j-м столбцом. Раскладывая этот определитель по j-му столбцу, получаем сумму алгебраических дополнений элементов этого столбца, умноженную на
Следовательно, сумма всех таких определителей равна сумме алгебраических дополнений всех элементов матрицы
, умноженной на
Окончательно получаем, что при увеличении всех элементов определителя на число , определитель увеличивается на сумму всех алгебраических дополнений, умноженную на число
Пример 2.14. Вычислить определитель n-го порядка
Решение. Рассмотрим определитель диагональной матрицы
Искомый определитель получается прибавлением к каждому элементу определителя матрицы
числа
. Поэтому
Определитель диагональной матрицы равен произведению диагональных элементов:
Осталось вычислить сумму алгебраических дополнений всех элементов матрицы . Заметим, что алгебраическое дополнение недиагонального элемента равно нулю (
при
, так как дополнительный минор содержит нулевой столбец). Дополнительный минор диагонального элемента — это определитель диагональной матрицы, т.е.
Поэтому
Вычисление определителей с помощью рекуррентных уравнений
Этот метод заключается в том, что исходный определитель n-го порядка выражается через определители
того же вида, но меньшего порядка. Получается рекуррентное уравнение
Решая это уравнение, находим формулу, выражающую определитель через определители
и порядок
В последнюю формулу подставляем определители невысокого
порядка, которые нетрудно вычислить каким-либо другим способом.
Замечание 2.6. Рекуррентным уравнением называется равенство вида , выражающее n-й член
искомой числовой последовательности
через
её предыдущих членов
. Методы решения таких уравнений рассматриваются в разд.
Пример 2.15. Вычислить определитель n-го порядка
Решение. Разложим определитель по первой строке
Первый из полученных определителей (n-l)-ro порядка обозначим , так как он имеет такой же вид, что и
. Разложив последний определитель по первому столбцу, получим определитель того же вида, что и
, но (n-2)-го порядка
Следовательно, искомый определитель удовлетворяет рекуррентному уравнению
Решение этого уравнения будем искать в виде , где
и
— неизвестные коэффициенты. Заметим, что эта формула дает решение рекуррентного уравнения при любых коэффициентах
и
. В самом деле, подставляя
в уравнение, получаем тождество
Подберем теперь коэффициенты и
в формуле
так, чтобы при
и
она давала правильные результаты, т.е.
Решая систему уравнений получаем
. Следовательно, искомый определитель равен
Пример 2.16. Вычислить определитель Вандермонда
где
— действительные числа.
Решение. Рассмотрим определитель
который отличается от определителя Вандермонда последним столбцом, но совпадает с ним при . Раскладывая определитель
по последнему столбцу, получаем многочлен (n-1)-й степени действительной переменной
где старший коэффициент равен алгебраическому дополнению элемента
т.е. определителю — определителю Вандермонда (n-l)-ro порядка. Заметим, что при
определитель
равен нулю, так как он имеет два одинаковых столбца (свойство 4). Следовательно,
— корень многочлена
. То же самое можно сказать про числа
. Все они являются корнями многочлена
. Следовательно, этот многочлен имеет вид:
Подставляя в это равенство и учитывая, что
, получаем рекуррентное уравнение
Записывая аналогичным образом и учитывая, что
, получаем
Таким образом, определитель Вандермонда равен произведению всех разностей при
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
Определители II и III порядка
Определение: Определителем порядка n называется число (выражение), записанное в виде квадратной таблицы, имеющей n строк и n столбцов, которая раскрывается по определенному правилу.
Числа
Определение: Определителем II порядка называется число (выражение), записанное в виде квадратной таблицы размером 2×2, т.е. имеющая 2 строки и 2 столбца.
Определение: Определитель II порядка вычисляется по правилу: из произведения элементов, стоящих на главной диагонали, надо вычесть произведение элементов, стоящих на побочной диагонали:
Пример:
Определение: Определителем III порядка называется число (выражение), записанное в виде квадратной таблицы размером 3×3, то есть имеющей 3 строки и 3 столбца.
Определитель III порядка вычисляется по правилу Саррюса: за определителем выписывают первый и второй столбцы, затем из суммы произведений элементов, стоящих на главной диагонали ей параллельных диагоналях, надо вычесть сумму произведений элементов, стоящих на побочной диагонали и ей параллельных:
Пример:
Определение: Минором 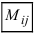
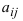
Пример:
Найти миноры элементов 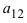
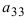
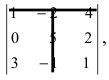
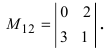
Пример:
Найти миноры элементов 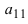
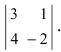
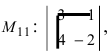
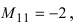
Определение: Алгебраическим дополнением 
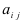
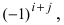
Замечание: Из определения алгебраического дополнения следует, что алгебраическое дополнение совпадает со своим минором, если сумма 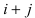
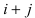
Определение: Транспонированным определителем n-го порядка называется определитель порядка n, полученный из исходного определителя путем замены строк на соответствующие столбцы, а столбцов на соответствующие строки.
Если
Пример:
Найти определитель, транспонированный к определителю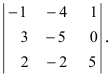
Свойства определителей
1. Величина транспонированного определителя равна величине исходного определителя. Пусть 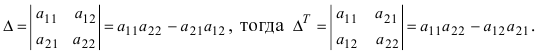
2. Перестановка местами двух строк (столбцов) изменяет знак определителя на противоположный. Пусть
Если поменять местами строки (столбцы) четное число раз, то величина и знак определителя не меняется. Нечетная перестановка местами строк (столбцов) не меняет величину определителя, но изменяет его знак на противоположный.
3. Определитель, содержащий две (или более) одинаковых строки (столбца), равен нулю. Если определитель содержит два одинаковых столбца, то 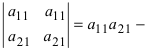
4. Для того чтобы умножить определитель на число k, достаточно умножить на это число все элементы какой-либо одной строки (столбца). Обратно: если все элементы какой-либо строки (столбца) имеют общий множитель k, то его можно вынести за знак определителя.
Докажем это свойство:
5. Если две каких-либо строки (столбца) пропорциональны, то определитель равен нулю.
Пусть в определителе II порядка первая и вторая строки пропорциональны, тогда
6. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю.
Пусть в определителе II порядка все элементы первой строки равны нулю, тогда
7. Если элементы какой-либо строки (или столбца) можно представить в виде двух слагаемых, то сам определитель можно представить в виде суммы двух определителей. Если 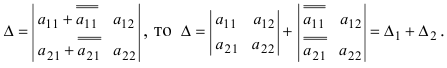
8. Если все элементы какой-либо строки (столбца) умножить на вещественное число к и прибавить k соответствующим элементам другой строки (соответственно, столбца), то величина определителя не изменится.
Умножим элементы второго столбца на вещественное число k и прибавим результат умножения к соответствующим элементам первого столбца, получим
Второй определитель равен нулю по свойству 5.
Замечание: Данное свойство применяется для обнуления всех элементов какой-либо строки (столбца) за исключением одного (метод обнуления), что существенно снижает трудоемкость вычисления определителей порядка выше 3 (см. также свойство 9.).
9. [Метод раскрытия определителя по элементам какой-либо строки (или столбца); универсальный способ вычисления определителя любого порядка]. Определитель любого порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
Пример:
Вычислить определитель 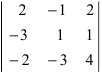
Решение:
Воспользуемся свойством 9.: раскроем определитель по элементам 3 строки 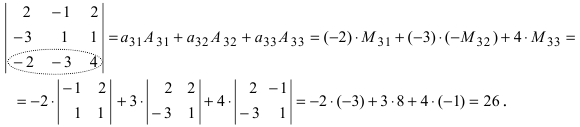
Из полученных результатов видно, что свойство 9. является универсальным методом вычисления любых определителей по элементам любой строки или столбца.
Используя свойство 8. можно обнулить все элементы какой-либо строки (столбца) за исключением одного (метод обнуления), а затем раскрыть определитель по элементам этой строки, воспользовавшись свойством 9.
Пример:
Вычислить определитель
Решение:
Обнулим элементы в третьей строке, для чего выполним следующие действия: 
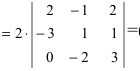
(по свойству 4. из третьего столбца вынесем множитель 0,5, тогда множитель перед определителем станет равным 1)
(раскроем определитель по элементам третьей строки: 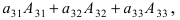
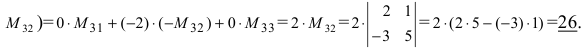
Пример:
Решить уравнение
Решение:
Вычислим определители второго и третьего порядков согласно вышеописанным правилам:
Найденные величины подставим в исходное уравнение
Пример:
Решить неравенство
Решение:
Вычислим определители второго и третьего порядков согласно вышеописанным правилам:
Найденные величины подставим в исходное неравенство
Пример:
Вычислить определитель четвертого порядка (аналогично выполнить такие же действия с определителем третьего порядка), преобразовав его так, чтобы три элемента некоторого ряда равнялись нулю, и вычислить полученный определитель по элементам этого ряда:
Решение:
Во второй строке исходного определителя присутствуют 1 и 0, поэтому обнуление элементов будем производить в этой строке (при обнулении элементов в строке действия производят со столбцами и наоборот): 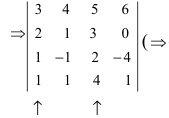
(по методу обнуления раскроем определитель по элементам 2-ой строки (
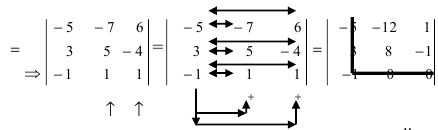
Определители
Перестановкой чисел 1, 2,…, n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12…n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.
Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ 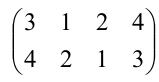
Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде 
Пусть нам дана квадратная матрица порядка n
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
где индексы 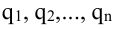
Определителем n-го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ 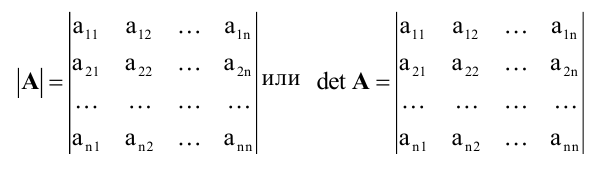
Свойства определителей:
- Определитель не меняется при транспонировании.
- Если одна из строк определителя состоит из нулей, то определитель равен нулю.
- Если в определителе переставить две строки, определитель поменяет знак.
- Определитель, содержащий две одинаковые строки, равен нулю.
- Если все элементы некоторой строки определителя умножить на некоторое число
то сам определитель умножится на
- Определитель, содержащий две пропорциональные строки, равен нулю.
- Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых
то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов
в другом — из элементов
- Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Минором 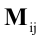
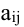
Алгебраическим дополнением элемента 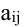
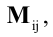
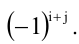
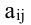
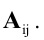
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
- Заказать решение задач по высшей математике
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки 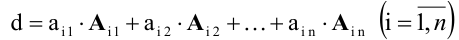
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Пример:
Не вычисляя определителя 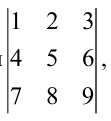
Решение:
Вычтем из второй строки первую, получим определитель 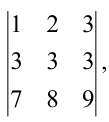
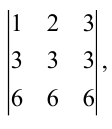
Такой определитель равен нулю.
Пример:
Вычислить определитель 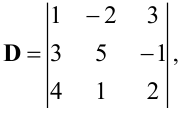
Решение:
Разложим определитель по элементам второго столбца:
Пример:
Вычислить определитель 
Решение:
Разложим определитель А по первой строке:
Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
И так далее. После n шагов придем к равенству
Пример:
Вычислить определитель
Решение:
Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель: 
Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.
——- в вышмате
Определители. Алгебраические дополнения
Внимание! Понятие определителя вводится только для квадратной матрицы.
Матрица называется квадратной порядка n, если количество ее строк совпадает с количеством столбцов и равно n.
Элементы квадратной матрицы, имеющие одинаковые значения индексов, составляют главную диагональ. Элементы квадратной матрицы порядка n, сумма индексов каждого из которых равна n+1, составляют побочную диагональ.
Определитель матрицы 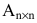
Внимание! Определитель — это число, характеризующее квадратную мат- рицу.
Определитель матрицы второго порядка равен разности элементов главной и побочной диагоналей соответственно:
Определитель матрицы третьего порядка равен сумме элементов главной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали, а также разности элементов побочной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными побочной диагонали.
Схематично это правило изображается так (правило треугольника):
Например,
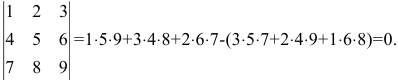
Отметим некоторые свойства определителя.
- Определитель треугольной матрицы равен произведению элементов главной диагонали.
- При транспонировании матрицы ее определитель не изменяется.
- От перестановки двух рядов (строк или столбцов) определитель меняет знак.
- Общий множитель всех элементов некоторого ряда определителя можно выносить за знак определителя.
- Если все элементы какого-нибудь ряда матрицы равны нулю, то определитель равен нулю.
- Определитель, содержащий два пропорциональных ряда, равен нулю.
- Определитель не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы другого ряда, умноженные на одно и то же число.
- Определитель произведения двух матриц одинакового порядка равен произведению определителей этих матриц.
Минором элемента 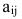
Алгебраическим дополнением элемента 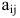
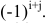
Теорема разложения.
Определитель матрицы равен сумме произведений элементов любого ряда на их алгебраические дополнения.
Пример №2
Вычислить определитель, разлагая его по элементам первой строки:
Решение:
По теореме разложения
Найдем алгебраические дополнения элементов матрицы А:
Следовательно,
Для вычисления определителя порядка выше третьего удобно пользоваться теоремой разложения (метод понижения порядка) или методом приведения определителя к треугольному виду.
Пример №3
Вычислить определитель, приведя его к треугольному виду:
Решение:
Применяя свойство 6 определителей, преобразуем последовательно второй, третий, четвертый столбцы матрицы.
- прибавили ко второму столбцу первый, умноженный на -2;
- прибавили к третьему столбцу первый, умноженный на -3;
- прибавили к четвертому столбцу первый, умноженный на -4;
- применили свойство 1 определителей.
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
- Плоскость и прямая в пространстве







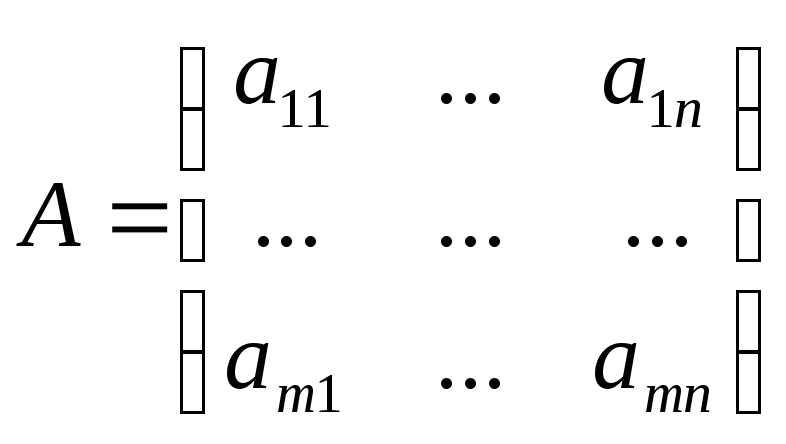
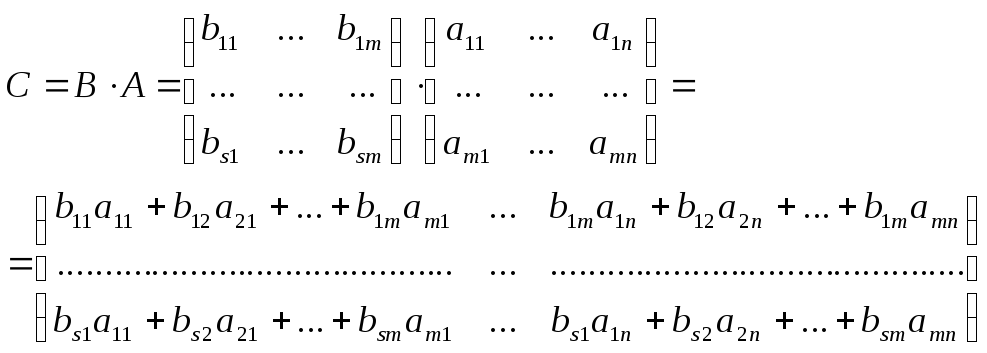














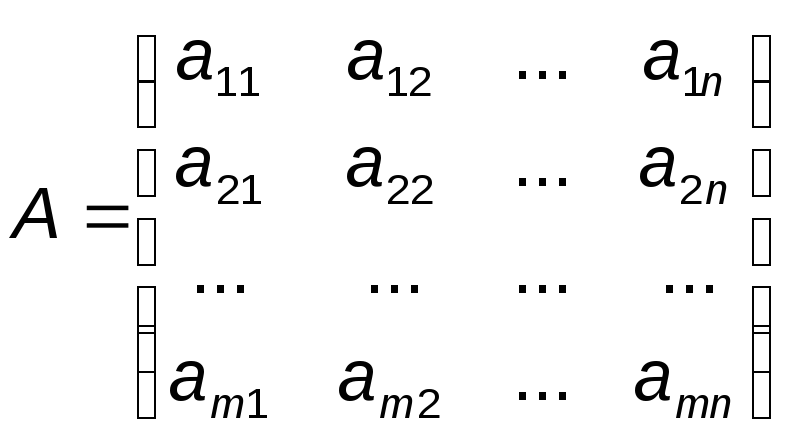






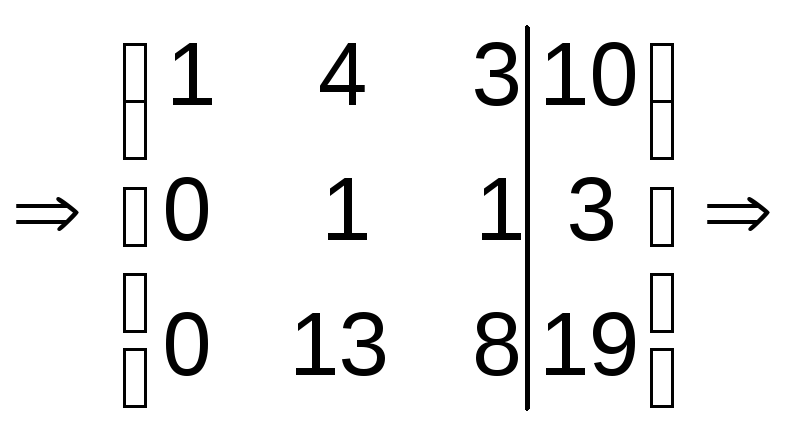



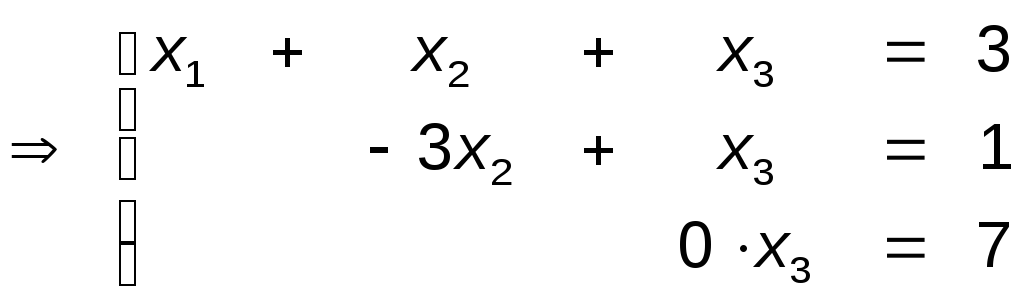



















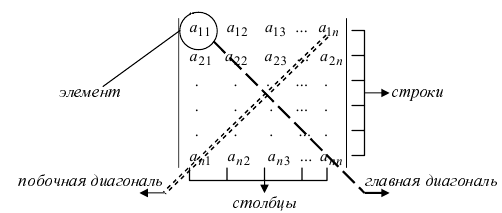
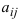
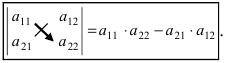
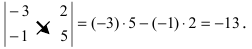
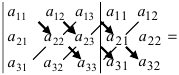
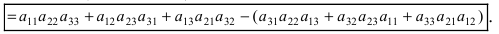
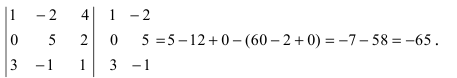
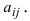
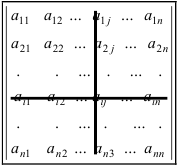
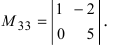
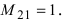
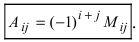

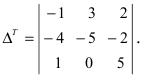
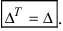
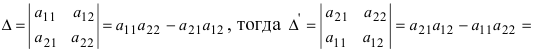
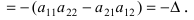
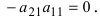
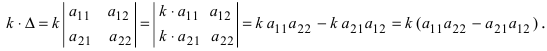
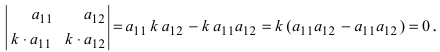
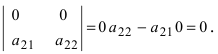
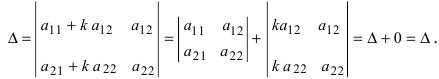
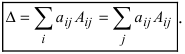
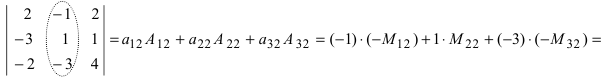
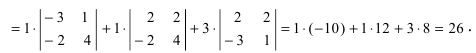
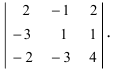
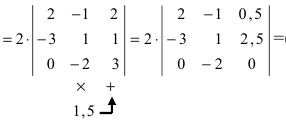
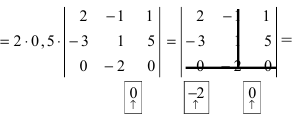
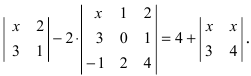
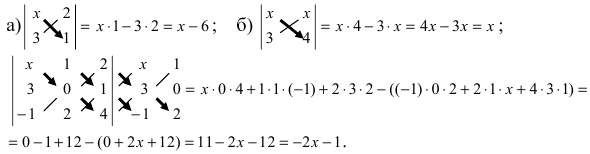
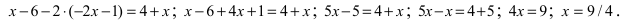

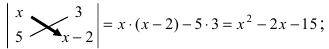
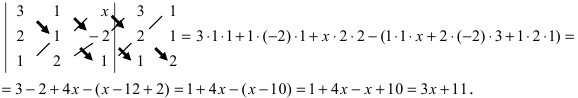
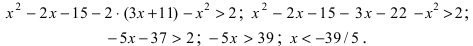

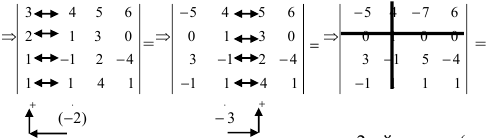
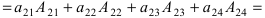
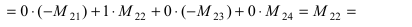
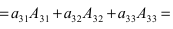
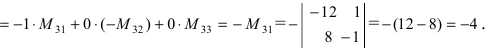
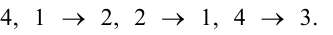


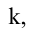 то сам определитель умножится на
то сам определитель умножится на 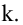
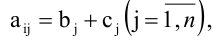 то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов
то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов 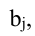 в другом — из элементов
в другом — из элементов