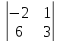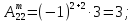С помощью метода Саррюса находится определитель матрицы третьего порядка.
Матрица третьего порядка — это матрица 3х3. Что бы найти ее определитель, нужно воспользоваться формулой:
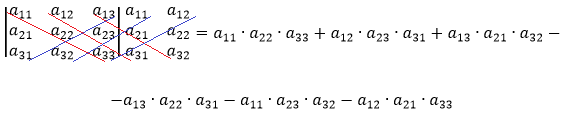
К определителю матрицы справа добавляется первых два столбца определителя. Складываем умноженные элементы на главной диагонали с умноженными элементами диагоналей параллельные главной. От полученного значения отнимаем умноженные элементы побочной диагонали с умноженными элементами диагоналей параллельные побочной.
Пример
Найдем определитель матрицы третьего порядка методом Саррюса.
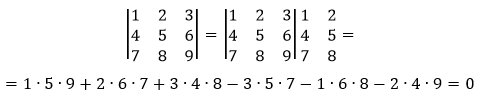
Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
Перед тем как находить и считать определитель, дадим определение определителю матрицы.
Что такое определитель матрицы или детерминант матрицы? Определитель матрицы — это некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.
|А|, ∆, det A — символы, которыми обозначают определитель матрицы.
Как найти определитель матрицы? Вычислить определитель или найти определитель можно с помощью разных способов (в том числе онлайн и при помощи калькулятора). Конкретный способ поиска и того, как решать, выбирают в зависимости от порядка матрицы.
Определитель матрицы второго порядка можно вычислять по формуле:
А=1-231.
Решение матрицы:
det A=1-231=1×1-3×(-2)=1+6=7
Определитель матрицы 3-го порядка: правило треугольника
Нахождение определителя матрицы 3-го порядка осуществляется по одному из правил:
- он может считаться по правилу треугольника;
- расчет также проводится по правилу Саррюса.
Как найти определитель матрицы третьего порядка по методу треугольника (определитель матрицы 3×3)?
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
А=13402115-1
Решение:
det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицы четвертого порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.
Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение матрицы по элементам строки:
det A=ai1×Ai1+ai2×Ai2+…+аin×Аin
Разложение матрицы по элементам столбца:
det A=а1i×А1i+а2i×А2i+…+аni×Аni
Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
А=01-132100-24513210
Решение:
- раскладываем по 2-ой строке:
А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310
- раскладываем по 4-му столбцу:
А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321
Свойства определителя
Свойства определителя:
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
В рамках темы советуем обратиться к модулю определителя.
А=134021005
Решение:
det А=134021005=1×5×2=10
Матричныый определитель, который содержит нулевой столбец, равный нулю (представляет собой минор).
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
Правило Саррюса (правило треугольника).
Пример
1:

–
2×1×
(–5)
+ 5×4×(–
4)
+ 3×2×(–
3)
–
(–
3)
×1× (–
4)
–
4×2×
(–
2)
–
5×3 × (–
5)
= 10 –
80
–18
–12
+16 +75 = –
9.
Пример
2:

45 + 8 ‒ 24 ‒ 60 + 6 ‒ 24 = ‒ 49.
Минором
Mij
элемента aijквадратной
матрицы n
‒ го порядка называется определитель
(n
‒ 1) ‒ го порядка, полученный из данной
матрицы вычеркиванием i
‒ й
строки и j
‒ го
столбца, на пересечении которых стоит
данный элемент.
Пример:

M11
=
= 15 + 2 = 17;
M12
=
= –
6
–
6
= –12;
и т. д. всего 9 миноров.
Алгебраическим
дополнением Aijэлемента
aij
квадратной матрицы называется его
минор,
взятый со знаком (‒1)i+j.
Пример:
А
11 =
(–1)1+1
×
M11
=
17.
А
12 =
(–1)1+2
×
M12
=
‒ 1×M12
= 12.
А
13 =
(–1)1+3
×

4 ‒ 30= – 26; и т.д.
Теорема Лапласа
Определитель
квадратной матрицы равен сумме
произведений элементов любой строки
(столбца) на их алгебраические дополнения.

I
стр. =

(–1)
1+2
×


1+2
×
×


1+2×

Пример:

II
стр. = ‒ 2×(–1)2+1
×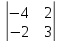
×
×(–1)
2+3×
2×(–12+4)+5×(9–12)–1×(–6+24) = 16–15–18= – 49.
Свойства определителей.
1.
Определитель равен нулю, если содержит:
—
нулевую строку или нулевой столбец;
—
две одинаковые строки (столбца);
—
две пропорциональных строки (столбца).
Пример:

0;


= I
× (-3).
2.
Общий множитель элементов любой строки
(столбца) можно выносить за знак
определителя.
Пример:

2×
3.
Определитель не изменится, если к
элементам любой строки (столбца) прибавить
элементы другой строки (столбца)
умноженные на одно число.
Пример:

× 5 + II; I × (‒2) + III; I × (‒ 4) + IV;
=


Вырожденные и невырожденные матрицы, обратная матрица.
Матрица
А-1называется
обратной к матрице A,
если при умножении ее на матрицу A,
как справа, так и слева, получится
единичная матрица.
А-1×A=A×
А-1=E
Матрица
называется невырожденной,
если ее определитель не равен 0, и
называется вырожденной,
если ее определитель равен 0.
Теорема.
Обратная
матрица А-1существует
только тогда, когда матрица невырожденная,
т.е. |A|
≠ 0.
Алгоритм
нахождения.
1.
Найти определитель матрицы А.
Если
│A│=
0, то обратная матрица не существует,
если │A│≠
0, то перейти ко второму шагу.
2.
Найти матрицу AT,
транспонированную к матрице А.
3.
Найти алгебраические дополнения
элементов матрицы AT
и составить из них матрицу Ã,
которая называется присоединенной.
Ã
=
4.
Обратную матрицу найти по формуле:
5.
Сделать проверку А—1
×
A
= E
Решение матричных уравнений.
Матричное
уравнение имеет вид:
A
× Х= B
Умножим
обе части уравнения на матрицу А—1
слева:
А-1×
A
×Х = А-1
×
В.
Так
как
А-1×А=Е,
то
Е×Х = А-1×В.
Так
какЕ
× Х=X,
то
Х= А-1×В
Пример:
Дано:
А
=

В
=

Найти:
X
‒?
Решение:
1)
│А│=
2)
AT=

3)
Ã=

4)
А-1
=



Х=
А-1×
B
=
Ответ:
Ранг матрицы, нахождение ранга матрицы.
Рангом
матрицы называется наивысший порядок
не равных нулю миноров этой матрицы.
Обозначается
rang
(A)
или r
(A).
Теорема
1.
Ранг матрицы не превосходит наименьшего
из ее размеров.
r(A)
≤ min (m; n)
Пример:
А2×3
=

r
(A)
≤ min
(2; 3) = 2, т. е. согласно теореме r
(A)
≤ 2.

3 + 24 = 27
0; r
(A)
= 2 (порядок ненулевого минора).
Теорема
2.
Ранг квадратной матрицы n-го
порядка равен ее порядку, если она не
вырожденная.
Примеры:
1)А3×3
=
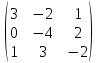
r
(A)
≤ 3.
│А│=
= 24 + 0 – 4 + 4 – 18 – 0 = 6
0


(A)
= 3.
2)А3×3
=
│А│=
0, т.к.
III = I × (– 3)

(A)
< 3.
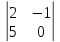
0 + 5 = 5
0

(A)
= 2 (порядок ненулевого минора).
Теорема
3.
Ранг матрицы не изменяется при элементарных
преобразованиях матрицы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Существует несколько способов нахождения определителей матриц третьего порядка. Рассмотрим их подробнее.
Перечислим основные способы, используемые для этого:
- Правило Саррюса;
- Правило треугольников;
- Использование специальной формулы для вычисления;
- Использование метода Гаусса или иначе метода перестановок.
Правило Саррюса
Правило Саррюса для вычисления матриц 3-ьего порядка применяется просто: достаточно соответственно рисунку переписать 2 первых столбика справа рядом с матричной таблицей, а затем записать произведения, стоящие по диагоналям со знаками.
Замечание 1
Если диагональ идёт сверху слева вниз направо — то произведение записывается со знаком «+», а если диагональ идёт из правого верхнего угла в нижний левый — то со знаком «-».
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рисунок 1. Формула третьего порядка. Автор24 — интернет-биржа студенческих работ
Пример 1
Дана матричная таблица $A$. Вычислите детерминант с помощью правила Саррюса.
$A = begin{pmatrix} 0 & 3 & -1 \ 1 & 4 & 2 \ 2 & 5 & 3 \ end{pmatrix}$
Решение:
Рисунок 2. Вычисление определителя 3 порядка. Автор24 — интернет-биржа студенческих работ
$Δ = 0 cdot 4 cdot 3 + 3 cdot 2 cdot 2 – 1 cdot 1 cdot 5 – 3 cdot 1 cdot 3 – 0 cdot 2 cdot 5 + 1 cdot 4 cdot 2 = 0 + 12 – 5 — 9 – 0 + 8 = 6$
Правило треугольников
Это правило немного похоже на предыдущее. Суть его в том, что произведения элементов с главной диагонали и двух треугольников, задействующих все остальные элементы как показано на рисунке, записываются со знаком плюс, а произведения элементов с побочной диагонали и двух синих треугольников — с противоположным.
«Найти определитель матрицы третьего порядка» 👇
Рисунок 3. Треугольники. Автор24 — интернет-биржа студенческих работ
Пример 2
Найдите определитель из прошлого задания, используя метод треугольников.
Решение:
Рисунок 4. Наглядный пример как пользоваться. Автор24 — интернет-биржа студенческих работ
$Δ= 0 cdot 4 3 + 3 cdot 2 cdot 2 – 1 cdot 5 cdot 1 + 1 cdot 4 cdot 2 – 1 cdot 3 cdot 3 – 2 cdot 5 cdot 0 = 0 + 12 – 5 + 8 – 9 – 0 = 6$
Использование формулы разложения по строчке
$A = begin{pmatrix} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ end{pmatrix}$
Для матрицы 3 на 3, приведённой выше, определитель можно сосчитать по формуле:
$Δ =begin{array}{|ccc|} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ end{array}=a_{11} cdot begin{array}{|cc|} a_{22} & a_{23} \ a_{32} & a_{33} \ end{array} – a_{12} cdot begin{array}{|cc|} a_{11} & a_{13} \ a_{21} & a_{23} \ a_{31} & a_{33} \ end{array} + a_{13} cdot begin{array}{|cc|} a_{11} & a_{12} \ a_{21} & a_{22} \ a_{31} & a_{32} \ end{array}= a_{11} cdot a_{22} cdot a_{33} – a_{12} cdot a_{23} cdot a_{31} + a_{13} cdot a_{21} cdot a_{32} — a_{13} cdot a_{22} cdot a_{31}$.
Пример 3
Разложите определитель матрицы из предыдущих примеров по 1-ой строчке и найдите его.
Решение:
$Δ = 0 cdot begin{array}{|cc|} 4 & 2 \ 5 & 3 \ end{array} – 3 cdot begin{array} {|cc|} 1 & 2 \ 2 & 3 \ end{array} + (-1) cdot begin{array}{|cc|} 1 & 4 \ 2 & 5 \ end{array} = 0 – 3 cdot (1 cdot 3 – 2 cdot 2) + (-1) cdot (5 – 
Метод Гаусса
Чтобы вычислить детерминант этим методом, нужно используя разрешённые преобразования получить треугольную матрицу.
Разрешёнными преобразованиями являются сложение и вычитание строчек и столбцов, в то время как при перестановке строчек и столбцов между собой необходимо помнить о смене знака определителя в конце.
После этого нужно перемножить элементы, стоящие на главной диагонали, их произведение и будет определителем.
Пример 4
Примените метод Гаусса для получения детерминанта матрицы из предыдущих примеров.
Решение:
$A = begin{pmatrix} 0 & 3 & -1 \ 1 & 4 & 2 \ 2 & 5 & 3 \ end{pmatrix}$
Переставим первую строчку со второй, при этом запомним, что знак детерминанта в конце поменяется:
$begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 2 & 5 & 3 \ end{pmatrix}$;
Вычтем из третьей строчки 1-ую, умноженную на 2:
$begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 0 & -3 & -1 \ end{pmatrix}$;
Сложим между собой третью строчку со второй:
$begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 0 & 0 & -2 \ end{pmatrix}$;
Получили искомый вид матрицы. Теперь можно сосчитать определитель, минус появляется из-за перемены строчек местами:
$Δ=-begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 0 & 0 & -2 \ end{pmatrix}= -(1 cdot 3 cdot ( — 2) ) = 6 $
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме