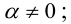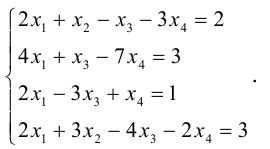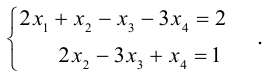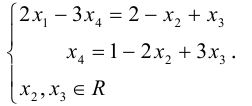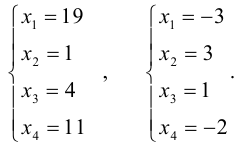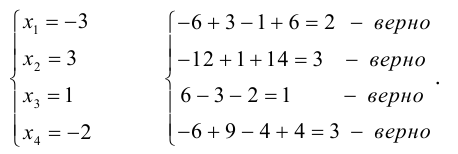1.1. Определители и матрицы
1.1.1. Понятие числовой матрицы
1.1.2. Определители второго порядка
1.1.3. Подматрица, минор, алгебраическое дополнение
1.1.4. Определители третьего порядка
1.1.5. Свойства определителей
1.1.6. Определители порядка n
1.2. Решение систем линейных уравнений методом Крамера
1.2.1. Понятие системы линейных уравнений
1.2.2. Формулы Крамера
1.3. Матрицы. Операции над матрицами
1.3.1. Умножение матрицы на число
1.3.2. Сложение матриц
1.3.3. Произведение матриц
1.3.4. Транспонирование матриц
1.3.5. Понятие обратной матрицы
1.3.6. Нахождение обратной матрицы методом Крамера
1.3.7. Алгоритм нахождения обратной матрицы методом Крамера
1.3.8. Элементарные преобразования матриц
1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований
1.4. Решение системы линейных уравнений
1.4.1. Системы линейных уравнений. Основные понятия
1.4.2. Метод Гаусса
1.5. Исследование систем линейных уравнений
1.5.1. Теоремы о ранге матриц
1.5.2. Исследование систем линейных уравнений
1.5.3. Теорема Кронекера-Капелли
1.5.4. Однородные системы линейных уравнений
1.5.5. Свойства решений линейной однородной системы уравнений
1.1. Определители и матрицы
1.1.1. Понятие числовой матрицы
Числовая матрица – прямоугольная таблица чисел, состоящая из строк и столбцов. Размеры матрицы обозначаются M * N, где M-число строк, N-число столбцов.
Пример:
A= 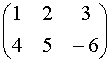
Общее обозначение:
A= или A=
, где
— элемент матрицы, находящийся на пересечении i-ой строки и j-ого столбца:
Если M=N, то матрица называется квадратной. В этом случае N – ее порядок. В квадратной матрице выделяются две диагонали – главная и побочная:
. . .
.
. . главная
. . .
побочная
. .
. .
Пример:
A = 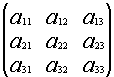
, а побочную
1.1.2. Определители второго порядка
Пусть дана матрица второго порядка
A= 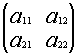
Определителем второго порядка называется число, вычисляемое по правилу:
Определитель второго порядка равен произведению элементов Главной диагонали минус произведение элементов Побочной диагонали.
=
1*(-4)-6 = -10
1.1.3. Подматрица, минор, алгебраическое дополнение
Пусть дана какая-либо матрица (например, порядка 3):
А=
Подматрицей матрицы А называется часть этой матрицы, полученная вычеркиванием какого-либо количества строк, и(или) какого-либо количества столбцов.
Например, если вычеркнуть первую строку и второй столбец, то получим подматрицу данной матрицы:
Минором элемента
определителя
называется определитель, полученный вычеркиванием i-ой строки и j-ого столбца.
Алгебраическим дополнением элемента называется минор, взятый со знаком “+” или “- ” в зависимости от места этого элемента в определителе.
Обозначение: =
Если i+j — четное число , то знак алгебраического дополнения и минора одинаковы, если нечетное , то их знаки противоположны.
Символически покажем положительные и отрицательные места в определителе:
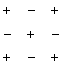
1.1.4. Определители третьего порядка
Определителем третьего порядка называется число, вычисляемое по правилу:
=
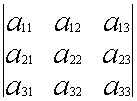
Определитель третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения.
Заменим алгебраические дополнения на миноры:
=
=
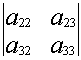
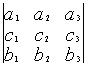
Вычисляя миноры, получим:
=
1.1.5. Свойства определителей
Свойство 1. При замене строк на столбцы определитель не меняется.
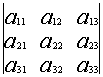
(такая операция называется транспонированием).
Следствие: строки и столбцы равноправны, т.е любые свойства или утверждения относительно строк справедливы и для столбцов и наоборот.
Свойство 2. При перестановке двух строк определитель меняет знак на противоположный.
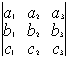
Следствие: любую строку (столбец) можно поставить первой (первым)
Свойство 3. Определитель с двумя равными строками равен нулю.

Свойство 4. Общий множитель элементов строки можно выносить за знак определителя.
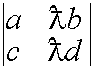
Следствие: Постоянный множитель можно внести в какую-нибудь строку
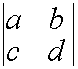
Свойство 5. Если элементы какой–либо строки состоят из двух слагаемых, то определитель можно представить в виде суммы двух определителей.
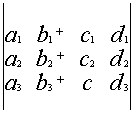
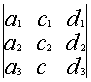
Свойство 6. Определитель не меняется, если любую строку умножить на любое число и прибавить к любой другой строке.
Случаи, когда определитель равен нулю:
- Все элементы какой-либо строки равны нулю
- Две строки одинаковы
- Элементы двух строк пропорциональны
1.1.6. Определители порядка n
Вычисление определителей порядка n.
Для вычисления порядка n используется метод разложения по cтроке.
Алгебраическое дополнение получается вычеркиванием i-строки и j-столбца. Этот процесс мы будем продолжать до тех пор пока не получим определители порядка 2 или 3

Формулу (1) используют как правило при i=1
Пример:
1.2. Решение систем линейных уравнений методом Крамера
1.2.1. Понятие системы линейных уравнений
Система линейных уравнений порядка n имеет вид:
При этом числа — называются коэффициентами
при неизвестных
— свободные члены
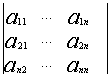
Числа 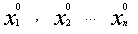
Система линейных уравнений называется совместной, если она имеет по крайней мере одно решение.
Если система линейных уравнений не имеет решений, то система называется несовместной.
1.2.2. Формулы Крамера
Рассмотрим систему уравнений (*). И пусть А — матрица системы
Если i – столбец заменим свободными членами, то соответствующую матрицу обозначим
Если система линейных уравнений (*) такова, что определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, которое находится по формуле:
1.3. Матрицы. Операции над матрицами
Две матрицы A и B называются равными, если они имеют один и тот же порядок и если элементы стоящие на соответствующих местах равны.
К линейным операциям относятся:
1.3.1. Умножение матрицы на число
Для того чтобы умножить матрицу на число нужно каждый элемент матрицы умножить на это число:
1.3.2. Сложение матриц
Складывать можно только матрицы одинаковых размеров:
Свойства линейных операций
Если матрица в качестве элементов имеет нули, то такая матрица называется нулевой.
1.3.3. Произведение матриц
Пример:
.
=
=
.
=
.
Если для матриц А и В выполняется равенство А*В=В*А, то матрицы называются перестановочными.
Если для матриц А, В, С имеет смысл операция произведения, то выполняются равенства
A(B*C)=(A*B)*C
A(B+C)=AB+AC
(B+C)A=BA+CA
1.3.4. Транспонирование матриц
Рассмотрим матрицы

AT называется транспонированной по отношению к A
Если AT получена из матрицы А заменой строк на столбцы то
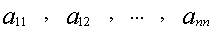
Очевидно:
Если для квадратной матрицы выполняется условие
то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.
1.3.5. Понятие обратной матрицы
Обратные матрицы существуют только для квадратных матриц. Квадратная матрица, у которой на главной диагонали стоят единицы, а
вне главной диагонали — нули, называется единичной матрицей.
Например, единичная матрица второго порядка:
Теорема.
Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:
Определение обратной матрицы:
Матрица В называется обратной для матрицы А, если А и В перестановочны и А*В=В*А=Е
Обозначение обратной матрицы:
Теорема.
Если матрица А имеет обратную, то ее определитель отличен от нуля.
Доказательство.
Так как А имеет обратную матрицу, то
Воспользуемся теоремой о том, что определитель произведения равен произведению определителей.
что и требовалось доказать.
1.3.6. Нахождение обратной матрицы методом Крамера
Теорема.
Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.
Доказательство.
Пусть матрица А такова, что её определитель отличен от нуля.
Докажем, что существует матрица В, такая что:
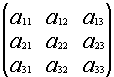
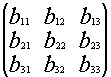
Отсюда, в частности, следует:
Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля, то эту систему можно решить методом Крамера причем решение (3) — единственно.
Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.
1.3.7. Алгоритм нахождения обратной матрицы методом Крамера
Первоначально находим определитель матрицы А и если он равен нулю, то обратной матрицы не существует.
Если определитель отличен от нуля, то находим союзную
матрицу
состоящую из алгебраических дополнений элементов матрицы А.
1.3.8. Элементарные преобразования матриц
Эквивалентные матрицы.
К элементарным преобразованиям относятся:
-
- умножение любой строки матрицы на число, отличное от нуля;
пример
=
- к любой строке можно добавить любую другую строку, умноженную на любое число;
- перестановка двух строк.
Матрицы, полученные с помощью элементарных преобразований называются эквивалентными
А~
В, В~
С, А~
С
1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований
Рассмотрим квадратную матрицу А и предположим, что
тогда используя элементарные преобразования эту матрицу можно привести к единичной матрице. Таким образом единичная матрица эквивалентна любой невырожденной матрице того же порядка.
Теорема
Если элементарные преобразования:
переводят невырожденную матрицу А в единичную, то те же самые преобразования, взятые в том же порядке, переводят единичную матрицу в обратную для A.
Доказательство:
отсюда
1.4. Решение системы линейных уравнений
1.4.1. Системы линейных уравнений. Основные понятия
Система уравнений вида:
называется линейной системой из n уравнений с m неизвестными.
(aij) коэффициенты при неизвестных x1, x2,…,xm
b1,b2,…,bn — свободные члены
Матрица А системы (*) состоит из коэффициентов aij, размера n*m .
Если неизвестные и свободные члены представим в виде:
,
то систему уравнений (*) мы можем переписать в виде: (3)
Запись системы в виде (3) называют матричной формой записи системы линейных уравнений (*). Следует особо обратить внимание на то, что m может быть неравно n. Если m=n и матрица А является невырожденной , то из соотношения (3) вытекает: (4)
Равенство (4) получается умножением (3) слева на А-1. Система (*) называется совместной, если она имеет по крайней мере одно решение. В противном случае система называется несовместной.
Решить систему — означает найти все её решения.
1.4.2. Метод Гаусса
Рассмотрим систему (*):
Припишем к матрице А
матрицу-столбец В
Припишем к матрице А матрицу-столбец
В:
Матрица H называется расширенной матрицей системы. Матрица, у которой ниже главной диагонали стоят нули называется треугольной. Метод Гаусса (метод исключения неизвестных) состоит в том, что расширенную матрицу системы с помощью элементарных преобразований мы приводим к треугольному виду. Если у нас при этом получается матрица вида: 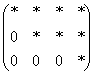
Если треугольная матрица получается вида: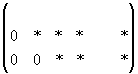
объявляются свободными, а остальные неизвестные могут быть выражены через них. Свободные неизвестные могут принимать любые значения. Если матрица примет вид: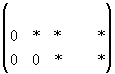
Пример:
Элементарные преобразования расширенной матрицы системы, приводящие её к треугольному виду, могут быть такими:
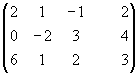
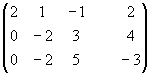
В итоге получим систему:
Откуда получим значения неизвестных: y = -7,25 x = 2,875
Пример:
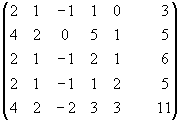
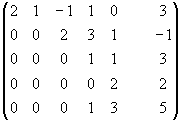
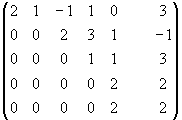
1.5. Исследование систем линейных уравнений
Рассмотрим систему линейных уравнений.
Задача: определить:
- Совместна или нет данная система
- Если совместна, то сколько имеет решений а) единственное б) бесконечное множество
Понятие ранга матрицы
А=() i=
j=
Возьмем в матрице К строк и К столбцов, тогда элементы матрицы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка К. Определитель этой квадратной матрицы называется минором порядка К для матрицы А.
Опр.1. Наибольший порядок минора матрицы, отличный от нуля называется рангом матрицы.
Опр.2. Число r(A)=k называется рангом матрицы А, если среди миноров порядка k есть по крайней мере один, отличный от нуля, а все миноры большего порядка равны нулю.
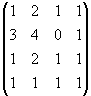
=0 М=
=-2
0 М=
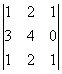
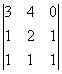
Совершенно очевидно, что нулевой ранг имеет только нулевая матрица. Если матрица не нулевая то её ранг1.
С другой стороны если матрица имеет порядок MxN, то r(A)min(M,N).
1.5.1. Теоремы о ранге матриц
Теорема 1
Если матрица А эквивалентна матрице B, то ранг матрицы А равен рангу матрицы B (элементарные преобразования не изменяют ранга матрицы).
Доказательство
Для доказательства достаточно доказать, что каждое из преобразований не может изменить ранга матрицы.
1) А~B B получена умножением строки(столбца) на отличное от нуля число.
А=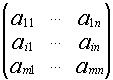
Если i-я строка не входит в выделенный минор то миноры матриц А и B совпадают. Если i-я строка входит в выделенный минор В=
А (по св-ву определителей). Если минор
А был отличен от нуля, то
В будет отличен от нуля. Таким образом умножение на отличное от нуля число не изменяет ранг матрицы.
2) A~B B получена прибавлением строк
А=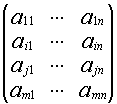
Если выбранные строки не содержат i-й строки, то соответствующие миноры матриц А и В полностью совпадают. Если минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А0, то и минор матрицы В
0.
Если выбранные миноры содержат i-ю и j-ю строки, тогда
М(А)=А=
В=
минор В получен из
А путем прибавления строки.
Элементарные преобразования получаются с помощью конечного числа преобразований 1 и 2 типа и по уже доказанному на каждом из шагов ранг матрицы не меняется. Следовательно, он не изменится и за конечное число шагов. Ранг матрицы не меняется, если произведено конечное число элементарных преобразований.
Теорема 2
Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Вычисление ранга матрицы
Используя утверждение доказанной теоремы, легко вычислить ранг матрицы
- с помощью элементарных преобразований матрица приводится к ступенчатому виду.
- считается число ненулевых строк ступенчатой матрицы
Ясно, что если матрица является квадратной и невырожденной, то её ранг равен порядку этой матрицы.
ПРИМЕР
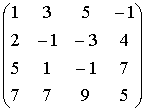
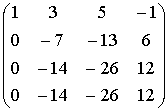
Ответ: r(A)=2
1.5.2. Исследование систем линейных уравнений
Рассмотрим систему линейных уравнений
(*)
А=()
H=
1.5.3. Теорема Кронекера-Капелли
Система ур-ний (*) совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы r(A)=r(H)
Если система совместна, то она имеет единственное решение, если r(A)=r(H)=n и его можно найти методами Крамера или Гаусса.
Если r(A)=r(H)=k<n, то система имеет бесконечно много решений. В этом случае n-k неизвестных объявляются свободными неизвестными (принимают любые значения), оставшиеся k неизвестных выражаются через эти свободные неизвестные.
1.5.4. Однородные системы линейных уравнений
Если в системе (*) все свободные члены равны нулю, то такая система является однородной.
Однородные системы всегда совместны т.к. =
=
=
=0 всегда является решением. Такое решение называется тривиальным.
1)
то
2) Если ранг матрицы А меньше числа неизвестных,то система имеет бесконечно много решений
1.5.5. Свойства решений линейной однородной системы уравнений
1) Если 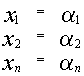
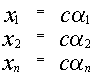
Доказательство.
2) Если 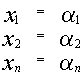
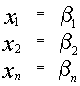
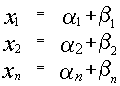
Доказательство.
+
откуда получим
3) Если 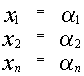
два различных решения системы, то их линейная комбинация, равная
также является решением системы.
Доказательство.
+
откуда получим
Каждое из решений системы можно записать в виде строки матрицы, тогда на основании свойств можно утверждать, что матрицы
есть решения, то
также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.
Пример.
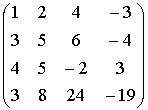
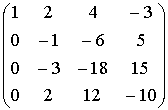
{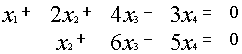
{
Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 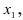
Второй столбец умножим на 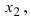

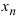
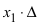
Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 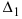
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 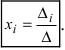
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 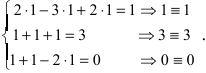
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 
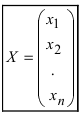
Тогда СЛАУ можно записать в матричном виде 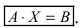
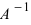
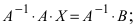
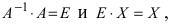
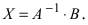
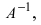
Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 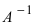
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 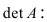
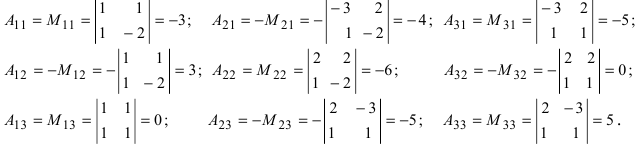
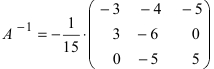
Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 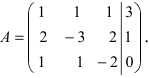
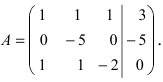
Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 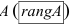
Если 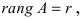
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 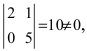
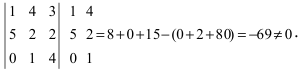
Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Основной определитель системы линейных уравнений
Дадим ряд необходимых определений.
Система линейных уравнений называется неоднородной, если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее свободные члены равны нулю.
Решением системы уравнений называется упорядоченный набор чисел, который, будучи подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Рассмотрим неоднородную систему линейных алгебраических уравнений, имеющую при n = m следующий общий вид:
Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:
Определитель главной матрицы системы называется главным определителем и обозначается ∆.
Вспомогательный определитель ∆ i получается из главного определителя путем замены i -го столбца на столбец свободных членов 
Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:
Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей). 
В свете приведенных выше определений , теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом 
После этого следует провести проверку полученного решения.
Пример 1.4. Решить систему методом Крамера
Решение. Так как главный определитель системы
отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители
Воспользуемся формулами Крамера (1.6): 
Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.
Определить стоимость 1 единицы продукции молокоцеха каждого вида.
Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:
Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):
Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):
По формулам Крамера (1.6) имеем:
Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей
Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.
В MathCAD для нахождения определителя пользуются палитрой оператора Matrix
Основной определитель системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений. Например,
. Решением этой системы является любая пара чисел, отличающихся знаком.
- И третий случай, когда система вообще не имеет решения. Например,
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Рассмотрим способы нахождения решений системы.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы 
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: 
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.
Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

Таким образом, x = 3, y = – 1.
Решите матричное уравнение: XA+B=C, где
Выразим искомую матрицу X из заданного уравнения.
Найдем матрицу А -1 .
Решите матричное уравнение AX+B=C, где
Из уравнения получаем 
Следовательно,
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и 
Наконец несложно заметить, что
Таким образом, получаем равенство: 
Следовательно, 
Аналогично выводятся равенства 

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:
Система имеет единственное решение, если Δ ≠ 0.


- При
- При p = 30 получаем систему уравнений
которая не имеет решений.
- При p = –30 система принимает вид
и, следовательно, имеет бесконечное множество решений x=y,y Î R.
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на 

Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
- перестановка строк или столбцов;
- умножение строки на число, отличное от нуля;
- прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
Вернемся к системе уравнений.
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
Таким образом, система имеет бесконечное множество решений.
http://www.sites.google.com/site/vyssaamatem/kupit-sklad/i-3-metod-kramera-resenia-sistem-linejnyh-algebraiceskih-uravnenij
http://toehelp.ru/theory/math/lecture14/lecture14.html
-
Определители и системы линейных уравнений
1.1.
Системы двух линейных уравнений и
определители второго порядка
Рассмотрим
систему двух линейных уравнений с двумя
неизвестными:
Коэффициенты
при неизвестных
и
имеют два индекса: первый указывает
номер уравнения, второй – номер
переменной.
|
Главным |
|
Вспомогательным |
|
Главнаядиагональ определителя – это диагональ, |
|
Определитель |
Правило
Крамера: Решение системы находят
путем деления вспомогательных
определителей на главный определитель
системы
,
Замечание
1.Использование правила Крамера
возможно, если определитель системы
не равен нулю.
Замечание
2.Формулы Крамера обобщаются и на
системы большего порядка.
Пример
1. Решить систему:
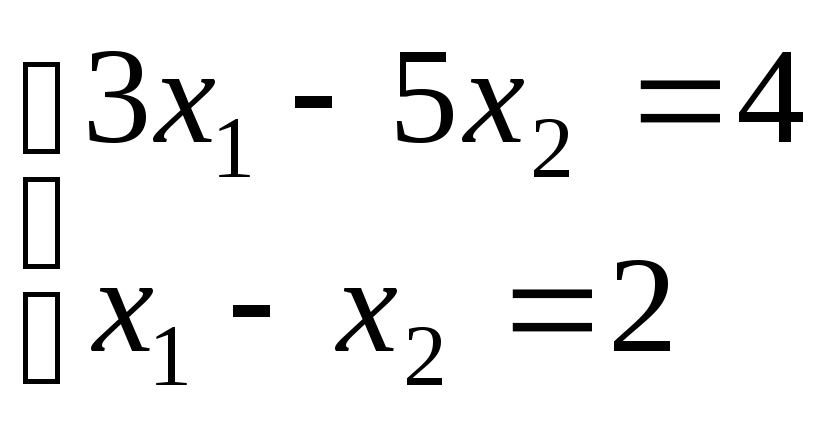
Решение.
;
;
;
Проверка:
Вывод:
Система решена верно:
.
1.2. Системы трех линейных уравнений и определители третьего порядка
Рассмотрим
систему трех линейных уравнений с тремя
неизвестными:
Определитель,
составленный из коэффициентов при
неизвестных, называется определителем
системы или главным определителем:
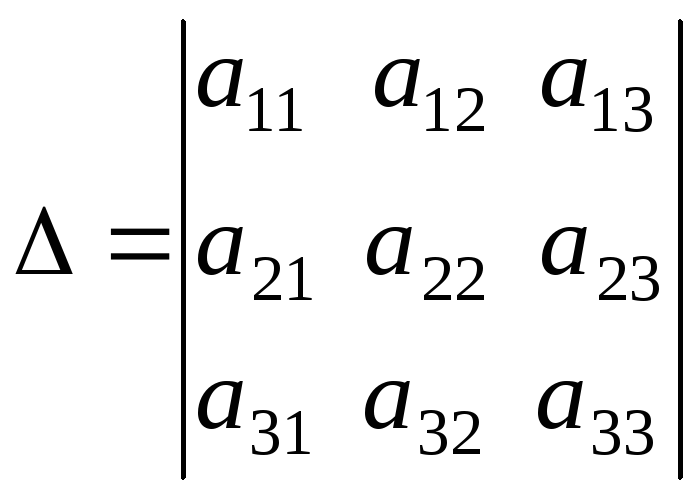
Если
то система имеет единственное решение,
которое определяется по формулам
Крамера:
где
где
определители
– называются вспомогательными и
получаются из определителя
путем замены его первого, второго или
третьего столбца столбцом свободных
членов системы.
Пример
2.Решить систему

Сформируем
главный и вспомогательные определители:
Осталось
рассмотреть правила вычисления
определителей третьего порядка. Их три:
правило дописывания столбцов, правило
Саррюса, правило разложения.
а)
Правило дописывания первых двух столбцов
к основному определителю:
.
Вычисление
проводятся следующим образом: со своим
знаком идут произведения элементов
главной диагонали и по параллелям к
ней, с обратным знаком берут произведения
элементов побочной диагонали и по
параллелям к ней.
б)
Правило Саррюса:
Со
своим знаком берут произведения элементов
главной диагонали и по параллелям к
ней, причем недостающий третий элемент
берут из противоположного угла. С
обратным знаком берут произведения
элементов побочной диагонали и по
параллелям к ней, третий элемент берут
из противоположного угла.
в)
Правило разложения по элементам строки
или столбца:
|
Определитель |
Если
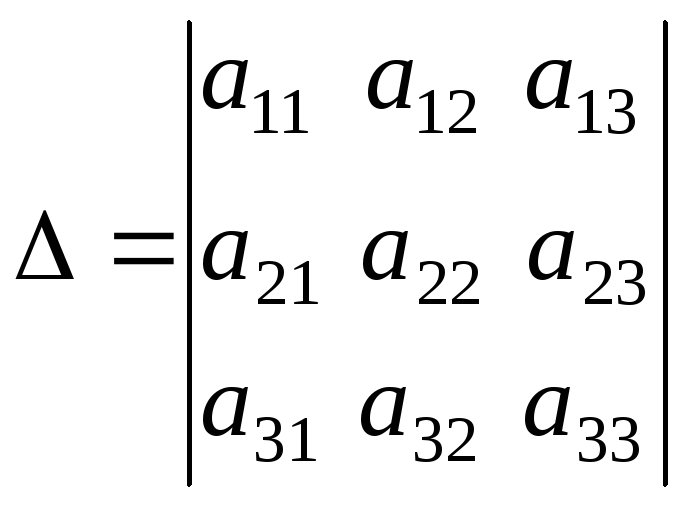
тогда
.
Алгебраическое
дополнение– это определитель более
низкого порядка, получаемый путем
вычеркивания соответствующей строки
и столбца и учитывающий знак
,
где– номер строки,
– номер столбца.
Например,
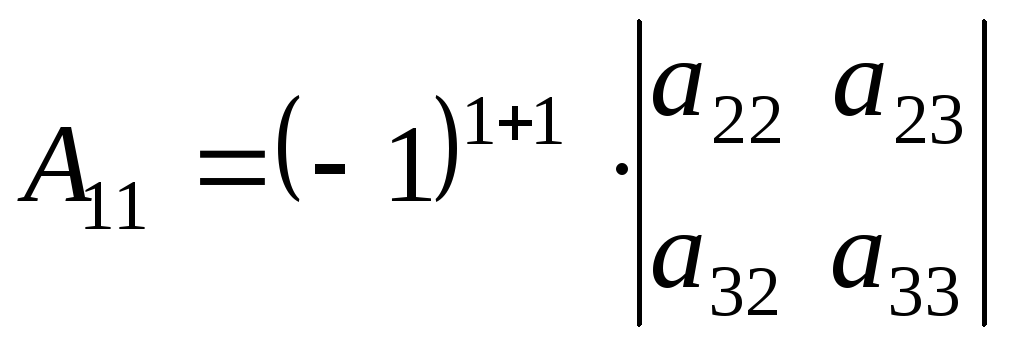
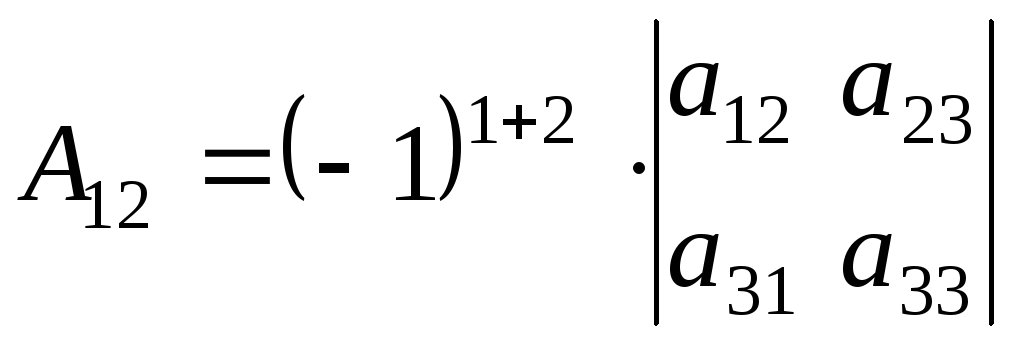
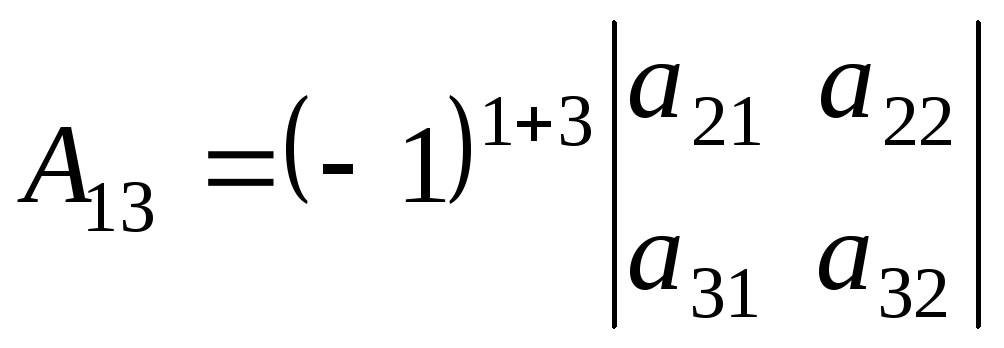
Вычислим
по этому правилу вспомогательные
определители
и
,
раскрывая их по элементам первой строки.
Вычислив
все определители, по правилу Крамера
найдем переменные:
Проверка:
Вывод:
система решена верно:
.
-
Основные
свойства определителей
Необходимо
помнить, что определитель – это число,
найденное по некоторым правилам. Его
вычисление может быть упрощено, если
пользоваться основными свойствами,
справедливыми для определителей любого
порядка.
Свойство
1.Значение определителя не изменится
от замены всех его строк соответствующими
по номеру столбцами и наоборот.
Операция
замены строк столбцами называется
транспонированием. Из этого свойства
вытекает, что всякое утверждение,
справедливое для строк определителя,
будет справедливым и для его столбцов.
Свойство
2.Если в определителе поменять
местами две строки (столбца), то знак
определителя поменяется на противоположный.
Свойство
3.Если все элементы какой-нибудь
строки определителя равны 0, то определитель
равен 0.
Свойство
4.Если элементы строки определителя
умножить (разделить) на какое-нибудь
число
,
то и значение определителя увеличится
(уменьшится) в
раз.
Если
элементы какой-нибудь строки, имеют
общий множитель, то его можно вынести
за знак определителя.
Свойство
5. Если определитель имеет две
одинаковые или пропорциональные строки,
то такой определитель равен 0.
Свойство
6. Если элементы какой-нибудь строки
определителя представляют собой сумму
двух слагаемых, то определитель равен
сумме двух определителей.
Свойство
7. Значение определителя не изменится,
если к элементам какой-нибудь строки
добавить элементы другой строки,
умноженной на одно и то же число.
В
этом определителе вначале ко второй
строке прибавили третью, умноженную на
2, затем из третьего столбца вычли второй,
после чего вторую строку прибавили к
первой и третьей, в результате получили
много нулей и упростили подсчет.
Элементарными
преобразованиями определителя
называются упрощения его благодаря
использованию указанных свойств.
Пример
1.Вычислить определитель
Непосредственный
подсчет по одному из рассмотренных выше
правил приводит к громоздким вычислениям.
Поэтому целесообразно воспользоваться
свойствами:
а)
из І строки вычтем вторую, умноженную
на 2;
б)
из ІІ строки вычтем третью, умноженную
на 3.
В
результате получаем:
Разложим
этот определитель по элементам первого
столбца, содержащего лишь один ненулевой
элемент.
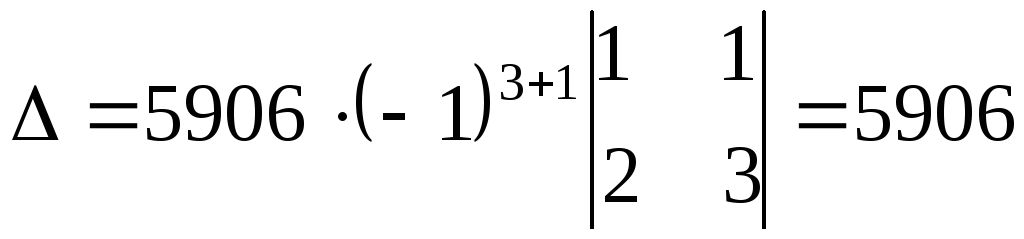
-
Системы
и определители высших порядков
Систему
линейных уравнений с
неизвестными можно записать в таком
виде:
Для
этого случая также можно составить
главный и вспомогательные определители,
а неизвестные определять по правилу
Крамера. Проблема состоит в том, что
определители более высокого порядка
могут быть вычислены только путем
понижения порядка и сведения их к
определителям третьего порядка. Это
может быть осуществлено способом прямого
разложения по элементам строк или
столбцов, а также с помощью предварительных
элементарных преобразований и дальнейшего
разложения.
Пример
4. Вычислить определитель четвертого
порядка
Решение
найдем двумя способами:
а)
путем прямого разложения по элементам
первой строки:
б)
путем предварительных преобразований
и дальнейшего разложения
|
|
а) |
|
|
б) |
|
а) |
|
|
б) |
|
|
в) |
Пример
5.Вычислить определитель пятого
порядка, получая нули в третьей строке
с помощью четвертого столбца
|
|
из |
из
второго столбца вычтем третий:
из
второй строки вычтем третью:
Пример
6.Решить систему:
Решение.Составим определитель системы и, применив
свойства определителей, вычислим его:
(из
первой строки вычтем третью, а затем в
полученном определителе третьего
порядка из третьего столбца вычитаем
первый, умноженный на 2). Определитель
,
следовательно, формулы Крамера применимы.
Вычислим
остальные определители:
Четвертый
столбец умножили на 2 и вычли из остальных
Четвертый
столбец вычли из первого, а затем, умножив
на 2, вычли из второго и третьего столбцов.
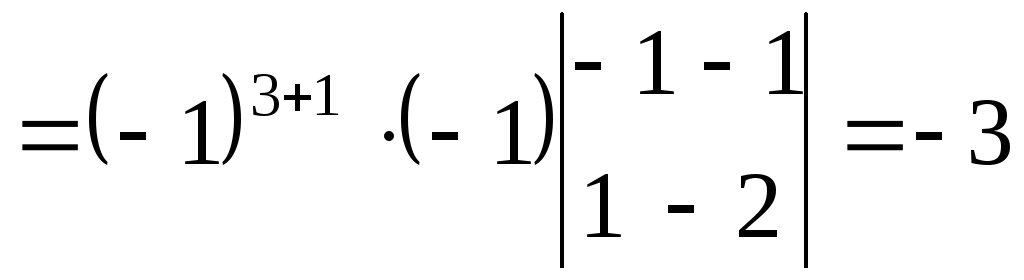
Здесь
выполнили те же преобразования, что и
для
.
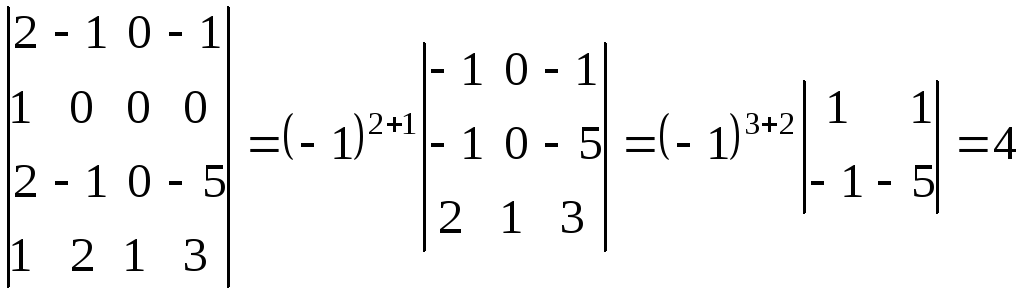
При
нахождении
первый столбец умножили на 2 и вычли из
остальных.
По
правилу Крамера имеем:
.
После
подстановки в уравнения найденных
значений убеждаемся в правильности
решения системы.
2.
МАТРИЦЫ и
ИХ
ИСПОЛЬЗОВАНИЕ
В
РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Линейная алгебра
Линейная алгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения, системы линейных уравнений, среди основных инструментов, используемых в линейной алгебре — определители, матрицы, сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры.
Матрицы и операции над ними
Основные определения:
В математике и ее приложениях наряду с числами часто бывает удобным использовать числовые таблицы, которые называются матрицами. Аппарат теории матриц эффективно применяется, например, при решении систем линейных уравнений, как мы скоро в этом убедимся. Перейдем к точным определениям.
Определение: Матрицей размерности m х n называется прямоугольная таблица действительных чисел, состоящая из m строк и n столбцов.
Числа, составляющие матрицу, называются ее элементами. Для доступа к элементам матрицы используются два индекса: первый указывает на номер строки, второй — на номер столбца, на пересечении которых расположен данный элемент.
Обозначаются матрицы, как правило, прописными латинскими буквами A, B, C,иногда указывается размерность, например, Amxn. В развернутой форме матрица записывается как таблица:
Более компактно с указанием элементов матрица записывается в виде:
Матрицы А и В одинаковой размерности считаются равными, если все элементы одной матрицы равны соответвующим элементам другой матрицы.
Рассмотрим некоторые специальные виды матриц.
Матрица, у которой все элементы равны нулю, называется нуль-матрицей и обозначается через O.
Матрица, у которой число строк равно числу столбцов, называется квадратной. Размерность квадратной матрицы часто называют ее порядком.
Числа 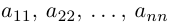
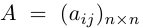
Квадратная матрица, диагональные элементы которой равны единице, а все остальные — нулю, называется единичной матрицей и обозначается через 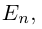
Таким образом,
Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (выше) главной диагонали, равны нулю. Например, треугольной является матрица
Матрица называется трапециевидной, если она представляет собой следующую таблицу:
Операции над матрицами
Введем сначала линейные операции над матрицами.
Произведением действительного числа 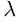
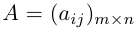
Суммой двух матриц 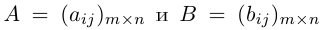
Таким образом, элементы суммы матриц равны суммам соответствующих элементов данных матриц.
Разность матриц А и B можно определить как А — В = А + (-1)В.
Свойства линейных операций над матрицами аналогичны соответствующим свойствам действительных чисел.
Пример №1
Даны матрицы
Найти матрицу -2А +3В.
Решение.
Тогда
Определим теперь операцию умножения матриц. Рассмотрим сначала матрицу-строку и матрицу-столбец с одинаковым числом элементов, т.е.
Произведением этих строки и столбца называется число1
Рассмотрим так называемые согласованные матрицы 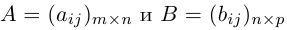
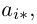
Произведением данных согласованных матриц А и B называется матрица
Часто для суммы n чисел 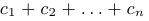
размерности m х p, элементы которой равны произведениям строк матрицы A на столбцы B.
Пример №2
Найти произведение согласованных матриц
Решение. Найдем произведение строк матрицы А на столбцы матрицы В.
Осталось записать искомое произведение матриц:
Отметим некоторые свойства произведения матриц1.
Первые три сразу следуют из определения произведения матриц. Докажем последнее свойство. Пусть заданы три матрицы 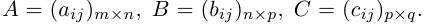
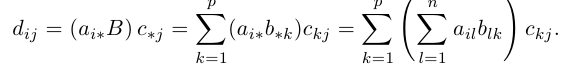
что представляет собой произведение Тем строки с номером i матрицы A на столбец с номером j матрицы ВС. Тем самым свойство 4 доказано.
Заметим, что в отличие от чисел матрицы, вообще говоря, не коммутируют (не перестановочны). Приведем соответствующий
Контрпример. Доказать, что матрицы
не коммутируют.
Действительно,
Таким образом, для этих матриц
Замечание. Пользуясь случаем, введем здесь определение n-мерного векторного пространства Rn, как множество упорядоченных совокупностей n действительных чисел. Каждую такую совокупность мы будем обозначать через и называть n-мерным вектором.
Мы предполагаем, что все матрицы в свойствах согласованы.
Очевидно, каждый вектор мы можем отождествить с соответствующей матрицей-строкой или матрицей-столбцом, поэтому на векторы автоматически переносятся линейные операции, которые мы определили выше для матриц.
Определитель матрицы и его свойства
Познакомимся теперь с такой важнейшей характеристикой матрицы, как определитель. Введем предварительно понятие перестановки и изучим некоторые ее свойства.
Перестановки
Перестановкой n натуральных чисел 1, 2, ….., n называется строка
содержащая все эти числа.
Первым элементом перестановки может быть любое из чисел 1, 2, …., n, вторым — любое из оставшихся n — 1 чисел и так далее, следовательно, число различных перестановок данных чисел равно 
Два числа в перестановке находятся в инверсии, если большее из них имеет меньший номер. Число всех инверсий в перестановке (1) мы обозначим через
В связи с этим перестановка (1) называется четной, если в ней число 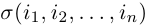
Отметим два свойства перестановок, которые мы будем использовать ниже.
Лемма 1. Характер четности перестановки изменится на противоположный, если в ней поменять местами какие-нибудь два элемента.
Доказательство. Предположим сначала, что меняются местами рядом стоящие элементы к и l перестановки. В этом случае число инверсий в новой перестановке изменится на единицу, а именно, увеличится на единицу, если к и l не находились в инверсии, или настолько же уменьшится, если они находились в инверсии. Таким образом, характер четности перестановки изменится на противоположный. Рассмотрим теперь случай, когда числа к и l разделяют s других элементов перестановки. Тогда поменять местами данные элементы мы можем последовательно переставляя число к с s промежуточными элементами, а затем переставляя число l в обратном порядке с элементом к и всеми s промежуточными. В результате мы выполним 2s + 1 обменов рядом стоящих элементов и, таким образом, характер четности исходной перестановки изменится нечетное число раз и, следовательно, он изменится на противоположный. Лемма доказана.
Из этой леммы сразу же следует, что количество четных перестановок равно количеству нечетных. В самом деле, поменяв местами любые два элемента в каждой из p четных перестановок, мы получим p нечетных и, следовательно, 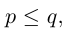
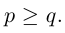
Лемма 2. Пусть
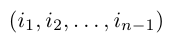
— перестановка чисел 1, 2, …, n — 1. Зафиксируем число j из множества {1, 2, … , n} и оставим его перестановку (2) на место с номером i, сдвинув вправо на одну позицию все ее элементы с номерами i, i + 1, … , n — 1 и увеличив на единицу все не меньшие, чем j элементы этой перестановки. В результате получим перестановку
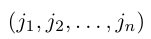
чисел 1, 2, …. , n. Четности перестановок (2) и (3) связаны равенством
Действительно, предположим сначало, что элемент j в перестановке (3) стоит на первом месте. Тогда, очевидно, количество инверсий в этой перестановке равно 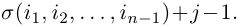
Определитель и его вычисление для матриц второго и третьего порядков
Рассмотрим квадратную матрицу порядка n :
Составим произведение элементов данной матрицы, взятых по одному из каждой строки и каждого столбца. Упорядочив элементы этого произведения по возрастанию номеров строк, мы можем записать его в виде:
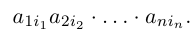
Номера столбцов в записанном произведении образуют перестановку чисел 1, 2, … , n.
Определение: Число, равное сумме всех n! произведений
называется определителем данной квадратной матрицы А (определителем n-го порядка) и обозначается через |А| или det А. В развернутой форме определитель записывается как
Найдем пользуясь этим определением выражение для определителей второго и третьего порядков.
Так как 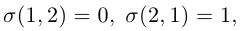
Аналогично, для вычисления определителя третьего порядка найдем число инверсий в каждой из перестановок чисел 1, 2, 3 :
Тогда
Для упрощения вычисления определителя третьего порядка можно использовать правило треугольников, согласно которому со знаком » + » следует брать произведения по схеме
а со знаком » — » — по схеме
Пример №3
Вычислить определитель
Решение. Воспользуемся правилом треугольников: 
Свойства определителя
1) Если какая-либо строка (столбец) определителя состоит из нулей, то и определитель равен нулю.
2) Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя.
3) Если все элементы какой-нибудь строки (столбца) определителя равны суммам двух слагаемых, то данный определитель равен сумме двух определителей, в которых в указанной строке (столбце) стоят, соответственно, первые и вторые слагаемые, а остальные элементы обоих определителей такие же, как и в исходном определителе.
Эти свойства напрямую следуют из определения определителя.
4) Если переставить две какие-нибудь строки (столбца) определителя, то он поменяет знак на противоположный.
Действительно, переставим, например, две строки определителя. В результате получим определитель, каждое слагаемое которого отличается знаком от соответствующего слагаемого исходного определителя, так как по доказанной в пункте 1 лемме 1 четность соответствующей перестановки вторых индексов изменится па противоположную.
5) Если в определителе совпадают (пропорциональны) две какие-нибудь строки (столбцы), то этот определитель равен нулю.
В самом деле, если в определителе совпадают две каие-нибудь строки (столбцы), то, с одной стороны, определитель при этом не изменится, а, с другой стороны, по предыдущему свойству его знак поменяется на противоположный. Таким образом |A| = — |A| и, стало быть, |A| = 0. Если же в определителе имеются две пропорциональные строки (столбца), то после вынесения за его знак по свойству 2) общего множителя элементов строки (столбца), мы получим определитель с двумя одинаковыми строками (столбцами), который равен нулю.
6) Определитель не изменится, если к элементам какой-нибудь строки (столбца) добавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.
Это следует из свойств 3) и 5), так как в этом случае полученный определитель можно представить в виде суммы двух определителей, один из которых равен исходному, а в другом имеются пропорциональные строки (столбцы), и поэтому он равен пулю.
Прежде чем сформулировать очередное свойство, введем понятие алгебраического дополнения к элементу матрицы.
Алгеброическим дополнением элемента aij квадратной матрицы A = (aij)nxn мы будем называть число
где 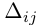
7) Разложение определителя по элементам строки (столбца).
Определитель матрицы равен сумме произведений элементов какой-нибудь строки (столбца) на соответствующие алгебраические дополнения. Таким образом,
или
Докажем, например, первую из этих формул. Убедимся в том, что правая часть данной формулы содержит все слагаемые определителя матрицы А. Выражение
содержит n(n — 1)! = n! различных произведений элементов определи теля матрицы A, взятых по одному из каждой строки и каждого столбца. Осталось проверить соответствие знаков.
Рассмотрим произвольное произведение
Каждое слагаемое определителя 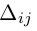
чисел 1, 2, … , n — 1. Умножив данное произведение на число 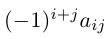
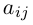
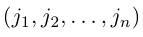
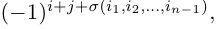
Таким образом, вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка.
Пример №4
Вычислить определитель.
Решение. Разложим этот определитель по элементам второй строки:
Пример №5
Вычислить определитель треугольной матрицы
Разлагая этот и следующие определители по первому столбцу, получим:
таким образом, определитель треугольной матрицы равен произведению диагональных элементов.

Это свойство является прямым следствием предыдущего.
9) Сумма произведений элементов какой-нибудь строки (столбца) на алгебраические дополнения к элементам какой-нибудь другой строки (столбца) определителя равна нулю.
Действительно, по предыдущему свойству эта сумма произведений равна определителю с двумя совпадающими строками (столбцами), а такой определитель по свойству 5) равен нулю.
10) Определитель произведения матриц равен произведению определителей этих матриц, т. е.
Достаточно громоздкое доказательство этого свойства мы приводить не будем.
Обратная матрица
Определение: Обратной к квадратной матрице 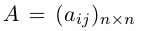
Из этого определения следует, что матрица А-1 также является квадратной той же размерности, что и матрица А.
Отметим некоторые свойства обратной матрицы, следующие из ее определения.
а) У матрицы не может существовать больше одной обратной.
Действительно, пусть для матрицы А имеются две обратные 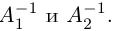
Умножив обе части первого равенства слева на матрицу 
b) (A-1)-1 = A.
c) Если для квадратных матриц А и В одного порядка существуют обратные, то и у матрицы АВ также существует обратная , причем
Выясним условия, при которых обратная матрица существует.
Теорема (критерий существования обратной матрицы). Для того, чтобы существовала матрица, обратная данной, необходимо и достаточно, чтобы данная матрица была невырожденной, то есть чтобы ее определитель был не равен нулю.
Доказательство. Докажем сначала необходимость условия теоремы. Пусть для матрицы А существует обратная матрица. Тогда из равенства АА-1 = E, воспользовавшись свойством 10) определителя произведения матриц, получаем: det(AA-1) = det А 
Убедимся теперь в том, что условие теоремы является и достаточным. Предположим, что матрица А является невырожденной. Проверим, что обратной к данной является матрица со следующей структурой 1:
Действительно, если
откуда, воспользовавшись свойствами 7) и 9) определителя (§2, пункт 3), заключаем:
т. е. АА-1 = Е. Аналогично убеждаем, что А-1А = Е. Теорема доказана.
В строках указанной ниже матрицы записаны алгебраические дополнения к элементам соответствующих столбцов.
Пример №6
Найти обратную к матрице
Решение. Найдем сначала определитель матрицы: 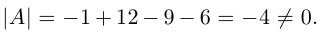
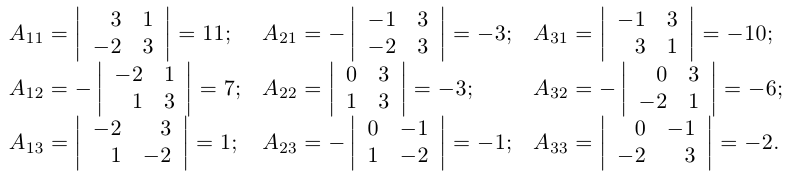
Обратную матрицу можно использовать при решении линейных матричных уравнений. Пусть, например, требуется решить матричное уравнение
AX = B
с известными матрицами А и B, причем матрица A является невырожденной. Умножая обе части данного матричного уравнения слева на обратную матрицу A-1, получим:
Аналогично, решением матричного уравнения XA = B является матрица X = BA-1, а решением матричного уравнения AXB = С с невырожденными матрицами A и B является матрица X = A-1CB-1.
Ранг матрицы и его вычисление
Рассмотрим произвольную матрицу
Минором порядка k матрицы A называется определитель, стоящий на пересечении выбранных k строк и k столбцов данной матрицы.
Определение: Рангом матрицы А называется максимальный из порядков ненулевых миноров этой матрицы. Обозначается ранг через rang A.
Естественно считать, что rang O = 0. Очевидно также, что
Пример №7
Найти ранг матрицы
Решение. Вычислим минор, находящийся на пересечении первых двух строк и первого и четвертого столбцов:
Все же миноры третьего порядка этой матрицы равны нулю, так как третья строка равна разности второй и первой строк. Следовательно, rang A = 2.
Как видно из определения, вычисление ранга матрицы через миноры является весьма трудоемкой задачей, особенно для матриц большой размерности. Значительно сократить объем вычислений позволяет другой метод, основанный на элементарных преобразованиях матрицы.
Элементарными преобразованиями матрицы называются следующие операции над ее строками или столбцами:
- перестановка двух строк (столбцов) матрицы;
- умножение строки (столбца) на ненулевое действительное число;
- добавление к строке (столбцу) другой строки (столбца), умноженной на действительное число.
Тот факт, что матрица В получена из матрицы А с помощью одного или нескольких последовательно выполненных элементарных преобразований, мы будем обе тачать как
Теорема. Ранг матрицы не меняется при ее элементарных преобразованиях.
Доказательство этого утверждения для первого и второго элементарных преобразований следует из того, что по свойствам 2) и 4) определителя (§2, пункт 3) миноры исходной матрицы могут отличаться от миноров преобразованной разве лишь знаком или ненулевым множителем, что. естественно, не отражается на ранге матрицы. Пусть теперь матрица А’ получена из матрицы А с помощью третьего элементарного преобразования, для определенности будем считать, что к строке с номером i добавлена строка с номером j, умноженная на действительное число 
Из этой теоремы следует, что для вычисления ранга матрицы достаточно привести ее с помощью элементарных преобразований к более простой — трапециевидной, ранг которой легко находится. Изложим соответствующий алгоритм, который мы будем использовать ниже при решении систем линейных алгебраических уравнений.
Итак, рассмотрим матрицу
Если А = О, то rang A = 0. Пусть теперь 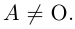
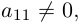
Повторяя теперь все рассуждения из предыдущего абзаца применительно к полученной матрице с вычеркнутыми из нее первой строкой и первым столбцом и всем последующим матрицам, после конечного числа шагов, не превышающего m — 1, мы придем к трапециевидной матрице
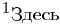
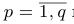
с r ненулевыми диагональными элементами a11, b22, . . . , crr. Ранг матрицы 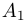
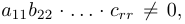
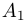
элементарных преобразований, то
Замечание. При практическом использовании приведенного алгоритма матрицу бывает
иногда удобно приводить к форме, которая отличается от трапециевидной порядком следования столбцов.
Пример №8
Найти ранг матрицы
Решение.
Приведем матрицу к трапециевидной с помощью элементарных преобразований:
Здесь вторая матрица получена из исходной вычитанием в ней из второй и третьей строк первой, умноженной на 4 и 3 соответственно, а затем вторая матрица преобразована в третью вычитанием из последней строки, умноженной на 5, второй строки. Перегнав в последней матрице четвертый столбец на первое место, получим трапециевидную матрицу с тремя ненулевыми элементами на диагонали. Следовательно, rang
Системы линейных алгебраических уравнений
Основные определения:
Определение: Системой m линейных алгебраических уравнений с n неизвестными (или, короче, линейной системой) называется система вида
где действительные числа 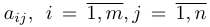
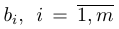
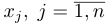
Числа 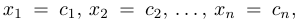
Для этого введем следующие обозначения:

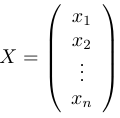
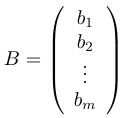
В этих обозначениях данная линейная система принимает вид:
AX = B.
Линейная система с нулевыми правыми частями, т.е. система АХ = О, называется однородной.
Решение невырожденных линейных систем
Рассмотрим линейную систему n уравнений с n неизвестными и невырожденной основной матрицей. Такая система называется невырожденной.
Рассмотрим два метода решения невырожденных систем.
Метод обратной матрицы
Так как определитель основной матрицы невырожденной системы линейных уравнений отличен от Iгуля. то решение этой системы мы можем найти как решение матричного линейного уравнения (§3)
по формуле
Полученное таким образом решение является единственным. Действительно, пусть 
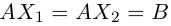
Пример №9
Решить систему линейных уравнений:
Решение.
Здесь
В §3 был вычислен определитель матрицы данной системы 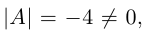
Тогда
Таким образом, 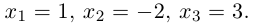
Формулы Крамера
Воспользовавшись представлением обратной матрицы через алгебраические дополнения, получим:
следовательно,
По свойству 
т. е. определителю, который может быть получен из определителя 
Пример №10
Решить систему линейных уравнений:
Решение. Для этой системы 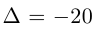
Тогда по формулам Крамера
Решение произвольных систем линейных уравнений. Метод исключения неизвестных (метод Гаусса)
Рассмотрим линейную систему общего вида:
Определим, как и для матриц, элементарные преобразования над уравнениями линейной системы. Таковыми являются:
- перестановка двух уравнений системы;
- умножение обеих частей уравнения на отличное от. нуля действительное число:
- добавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на действительное число.
Все эти преобразования, очевидно, обратимы и поэтому их результатом является система, эквивалентная исходной, т. е. система, множество решений которой, совпадает с множеством решений данной системы.
Упростим теперь систему, последовательно исключая неизвестные из ее уравнений с помощью элементарных преобразований. Для этого, расширенную матрицу системы
с помощью элементарных преобразований над ее строками приведем к трапециевидной форме с помощью алгоритма, изложенного в §4. В результате получим матрицу
где диагональные элементы 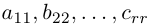
Очевидно, последняя система получена из исходной с помощью тех же элементарных преобразований, какими матрица 
Рассмотрим два случая, которые здесь возможны.
a) 
b)
Здесь, в свою очередь, представляются две возможности.
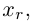
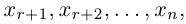
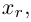
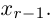
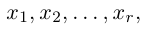
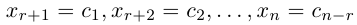
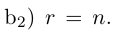
Приведенный алгоритм метода исключения неизвестных позволяет сформулировать критерий совместности линейной системы.
Теорема Кронекера. Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу ее расширенной матрицы.
Доказательство немедленно следует из вида матрицы 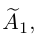
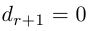
Из теоремы Кронекера следует, что если 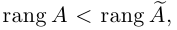
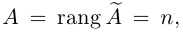
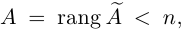
Пример №11
Решить систему линейных уравнений:
Решение. Приведем расширенную матрицу этой системы к трапециевидной с помощью элементарных преобразований над ее строками:
Вторая матрица получена из первой вычитанием из третьей строки второй и добавлением ко второй строке, умноженной на 2, первой строки. С точностью до перестановки столбцов, мы получили трапециевидную матрицу. Здесь, очевидно, rang 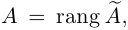
Придавая свободным неизвестным 
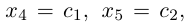
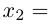
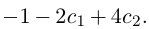
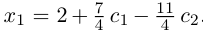
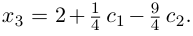
где 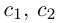
Замечание. Однородная система линейных уравнений всегда совместна, так как она имеет нулевое решение. Если rang A = n, то однородная система имеет единственное (нулевое) решение. а если 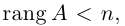
Обращение невырожденной матрицы с помощью элементарных преобразований
Рассмотрим невырожденную квадратную матрицу 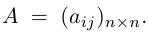
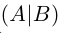
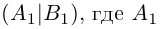
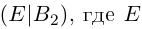
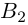
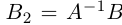
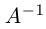
Таким образом, для того, чтобы найти матрицу, обратную к данной невырожденной матрице А, достаточно в расширенной матрице 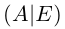
Пример №12
Найти обратную к матрице
Решение. Воспользуемся изложенным выше алгоритмом.
Следовательно,
Изложенный выше алгоритм нахождения обратной матрицы является более экономичным по сравнению с изложенным в §3, так как он требует гораздо меньшего объема вычислений. Заметим также, что программирование этого метода также не представляет трудностей.
Справочный материал по линейной алгебра
Этот раздел математики возник в связи с необходимостью решать системы линейных уравнений.
Рассмотрим систему линейных уравнений:
Чтобы решить ее, можно, например, выразить одну из переменных из первого уравнения, подставить во второе, после чего найти неизвестные x и y .
Однако можно найти решение быстрее: легко убедиться, что
Способ получения этого результата станет ясным, если рассмотреть таблицы, составленные из коэффициентов системы:
Такие таблицы называются матрицами второго порядка (так как в них две строки и два столбца), а соответствующие числа — определителями. Матрицы и определители играют важную роль при решении более сложных систем линейных уравнений, поэтому начнем изучение линейной алгебры с матриц.
Матрицы и действия над ними
Определение: Числовой матрицей размера 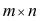
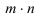
столбцов.
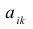
Определение: Если 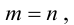
Элементы 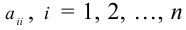
Матрица размера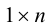
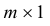
Пример №13
Определение: Две матрицы называются равными, если они имеют
одинаковый размер и равны их элементы, стоящие на одинаковых местах.
Пример №14
Определение: Квадратная матрица называется диагональной, если равны нулю все ее элементы, расположенные вне главной диагонали, то есть
На главной диагонали могут быть любые числа. Если все они равны 1, то диагональная матрица называется единичной и обозначается буквой E .
Пример №15
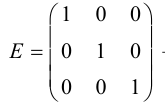
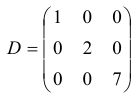
Определение: Квадратная матрица называется треугольной, если все ее элементы снизу (сверху) от главной диагонали равны нулю.
Пример №16
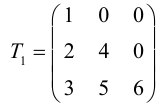
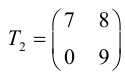
Линейные операции над матрицами
К числу линейных относятся операции сложения и умножения на число.
Определение: Пусть 
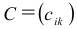
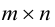
Пример №17
Определение: Произведением матрицы 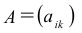
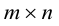
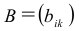
Пример №18
Определение: Нулевой матрицей O называется матрица, все элементы которой равны нулю.
Определение: Матрица (-1) * A называется противоположной для A и обозначается -A.
Очевидно, что 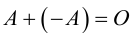
Определение: Разностью матриц A и B одного размера называется сумма 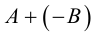
Определение: Результат конечного числа линейных операций над матрицами называется их линейной комбинацией.
Пример №19
Пусть
Матрица 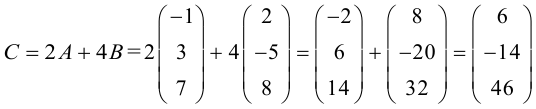
Свойства линейных операций
Если A , B , и C – матрицы одного размера, 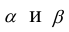
1. 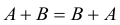
2. 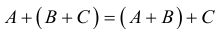
3. 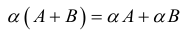
4. 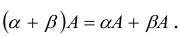
5.
Транспонирование и умножение матриц
Эти операции над матрицами не относятся к числу линейных.
Определение: Транспонированной матрицей 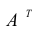
То есть, если
Пример №20
Определение: Если 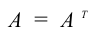
Все диагональные матрицы симметрические, так как равны их элементы,
симметричные относительно главной диагонали.
Очевидно, справедливы следующие свойства операции транспонирования:
Определение: Пусть 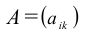
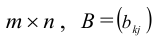
матрица размера 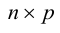
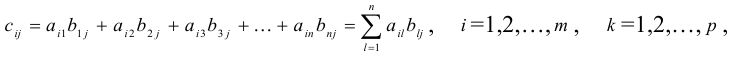
Пример №21
Произведение 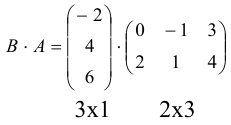
Свойства операции умножения матриц
1. 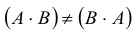
Пример №22
Определение: Матрицы A и B называются перестановочными, если 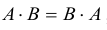
Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.
Пример №23
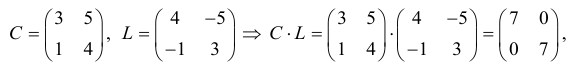
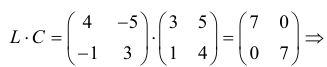
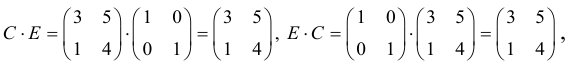
Вообще единичная матрица перестановочная с любой квадратной матрицей того же порядка, и для любой матрицы 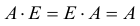
чисел таким свойством обладает число 1.
Если соответствующие произведения определены, то:
Пример №24
ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.
Пример №25
Определители и их свойства
Каждой квадратной матрице можно по определенным правилам поста-
вить в соответствие некоторое число, которое называется ее определителем.
Рассмотрим квадратную матрицу второго порядка:
Её определителем называется число, которое записывается и вычисляется так:
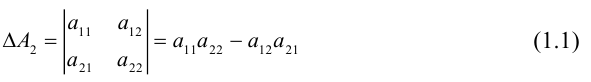
Такой определитель называется определителем второго порядка и может
обозначаться по-другому:
Определителем третьего порядка называется число, соответствующее квадратной матрице 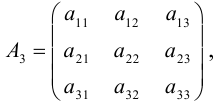
Это правило вычисления определителя третьего порядка называется правилом треугольников и схематически его можно представить так:

Пример №26
Если справа от определителя приписать первый, а затем второй столбец, то правило треугольников можно модифицировать:
Сначала умножаются числа на главной диагонали и двух ей параллельных диагоналях, затем – числа на другой (побочной) диагонали и ей параллельных. Из суммы первых трех произведений вычитается сумма остальных.
Группируя слагаемые в (1.2) и используя (1.1), заметим, что
То есть при вычислении определителя третьего порядка используются
определители второго порядка, причем 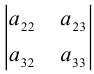
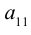
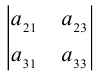
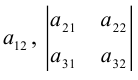
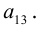
Определение: Дополнительным минором 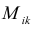
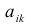
Пример №27
и так далее: матрица третьего порядка имеет 9 дополнительных миноров.
Определение: Алгебраическим дополнением элемента aik квадратной
матрицы A называется число
Пример №28
Для матрицы A2 :
Для матрицы A3: 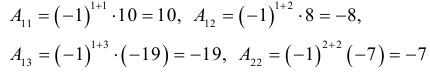
Итак, с учетом сформулированных определений (1.3) можно переписать в
виде: 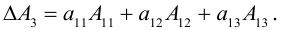
Перейдем теперь к общему случаю.
Определение: Определителем квадратной матрицы 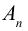
Равенство (1.4) называется разложением определителя по элементам первой строки. В этой формуле алгебраические дополнения вычисляются как определители 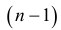
Пример №29
Рассмотрим (без доказательства) свойства определителей:
1. Определитель можно разложить по элементам первого столбца:
Пример №30
ЗАМЕЧАНИЕ. Рассмотренные примеры позволяют сделать вывод: определитель треугольной матрицы равен произведению элементов главной диагонали.
2. При транспонировании матрицы величина ее определителя не меняется:
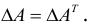
Отсюда следует, что строки и столбцы определителя равноправны.
3. Если в определителе поменять местами две строки (два столбца), то
определитель изменит свой знак, не изменившись по абсолютной вели-
чине.
4. Определитель, имеющий две равные строки (столбца), равен нулю.
5. Если все элементы некоторой строки (столбца) определителя умножить на число 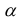
Отсюда, в частности, следует, что общий множитель любой строки (столбца) можно выносить за знак определителя. Кроме того, определитель, имеющий нулевую строку или нулевой столбец, равен нулю.
6. Определитель, имеющий пропорциональные строки (столбцы), равен нулю.
7. Определитель можно разложить по элементам любой строки (любого
столбца):
или
Равенство (1.6) называется разложением определителя по элементам i -й строки.
Равенство (1.7) называется разложением определителя по элементам k -го столбца.
8. Сумма произведений всех элементов некоторой строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю, то есть при
9. Определитель не изменится от прибавления ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца),умноженных на одно и то же число.
10. Определитель произведения двух матриц одного порядка равен произведению определителей этих матриц: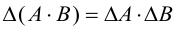
Пример №31
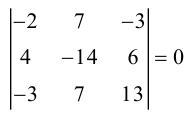
Особенно часто при вычислении определителей используется свойство 9, так как оно позволяет в любом определителе получать строку или столбец, где все элементы, кроме одного, равны нулю.
Пример №32
Определение обратной матрицы
Определение: Матрица 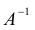
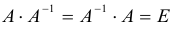
Из определения следует, что A и 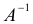
Определение: Квадратная матрица A называется невырожденной, если 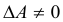
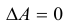
Пример №33
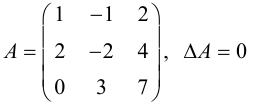
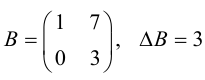
Теорема: Всякая невырожденная матрица имеет обратную, причем одну.
Доказательство: Рассмотрим для определенности квадратную матрицу A третьего порядка:
Покажем, что матрица вида 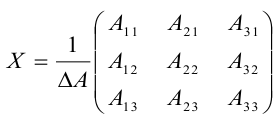
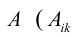
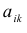
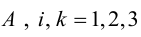
По условию A – невырожденная, т.е. 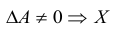
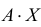
Аналогично доказывается, что 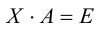
Следовательно, по определению матрица X является обратной для A .
Докажем единственность обратной матрицы.
Пусть невырожденная матрица A имеет две обратные: 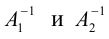
Умножим (1.8) слева на
Используя свойство 2 умножения матриц и равенство (1.9), получим:
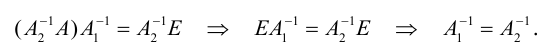
Таким образом, обратная матрица единственна, что и требовалось доказать.
Обратная матрица для матрицы A n — го порядка имеет вид:
Пример №34
Найти матрицу, обратную для
Проверка:
Пример №35
Найти матрицу, обратную для 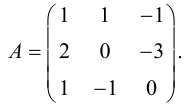
существует.
Проверка:
Аналогично проверяется, что
Крамеровские системы уравнений
Рассмотрим систему n линейных уравнений с n неизвестными:
Матрица, составленная из коэффициентов системы (1.10)
называется основной матрицей системы (1.10), 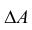
Определение: Система линейных уравнений называется Крамеровской, если
1) число уравнений равно числу неизвестных;
2) основной определитель не равен нулю.
Рассмотрим матрицы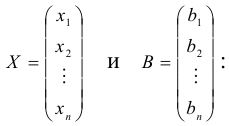
В – столбец правых частей. Очевидно, что система (1.10) может быть записана
в виде матричного уравнения
Определение: Совокупность n чисел 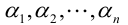
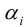
Теорема: Всякая Крамеровская система имеет решение, причем одно.
Доказательство: По условию 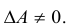
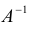
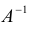
По формуле (1.12) определяется каждое из неизвестных 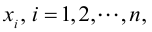
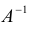
ЗАМЕЧАНИЕ. Способ решения системы (1.10) по формуле (1.12) называется матричным способом решения системы линейных уравнений.
Пример №36
Решить систему уравнений матричным способом:
В предыдущем примере было показано, что 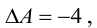
Таким образом, 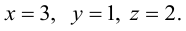
ЗАМЕЧАНИЕ. Матричный способ удобен, когда надо решить несколько Крамеровских систем, которые отличаются только правыми частями.
Вернемся к равенству (1.12). Из него следует, что
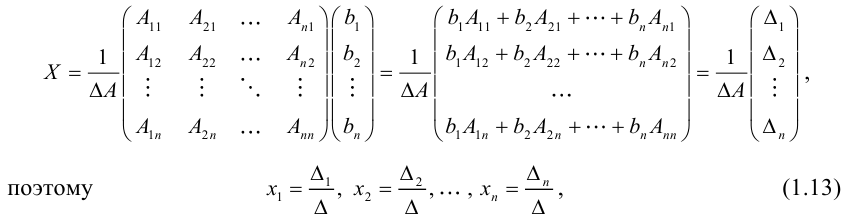
где 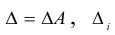
Ранг матрицы и элементарные преобразования
Определение: Минором порядка k матрицы А называется определитель k -го порядка, составленный из элементов матрицы А, стоящих на пересечении произвольно выбранных k строк и k столбцов без изменения порядка их следования.
Пример №37
Рассмотрим матрицу
Миноры первого порядка – каждый элемент матрицы A .
Миноры второго порядка: 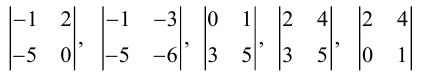
Матрица A имеет всего 18 миноров второго порядка.
Миноры третьего порядка:
Миноров четвертого порядка у этой матрицы нет.
Теорема: Если все миноры k -го порядка матрица А равны нулю, то равны нулю и все миноры старших порядков, если они существуют.
Доказательство: Рассмотрим минор порядка (k+1) . Это определитель (k-1) -го порядка, который ( по свойству 7 ) можно разложить по элементам некоторой строки (столбца ). В разложении будут алгебраические дополнения, которые с точностью до знака совпадают с минорами k — го порядка и по условию равны нулю. Поэтому равен нулю и рассматриваемый минор порядка k( 1 ). Аналогично равны нулю и миноры старших порядков 
Определение:. Рангом матрицы А называется такое целое число r ,
что среди ее миноров r -го порядка есть хотя бы один ненулевой, а все миноры
порядка (r+1) равны нулю.
Из доказанной теоремы следует, что, другими словами, ранг матрицы – это наивысший порядок отличного от нуля минора.
Будем обозначать 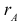
Ранг матрицы равен нулю тогда и только тогда, когда ее миноры равны
нулю, то есть если матрица нулевая.
Пример №38
Матрица F , очевидно, имеет ненулевой минор второго порядка, например,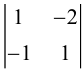
поэтому 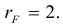
Определение: Элементарными преобразованиями матрицы называются следующие действия:
- умножение любой строки на число
;
- перемена местами двух строк;
- прибавление ко всем элементам строки соответствующих элементов другой строки, умноженных на одно и то же число
;
- отбрасывание нулевой строки;
- отбрасывание одной из двух пропорциональных строк;
- те же преобразования со столбцами.
Теорема: Элементарные преобразования не изменяют ранга матрицы.
С их помощью всякую матрицу можно привести к диагональному виду, и ее ранг равен количеству ненулевых элементов на главной диагонали (без доказательства).
Покажем теперь, что ранг матрицы F из последнего примера равен 2.
При переходе от F к 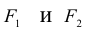
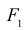
Вычислить 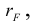
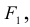
Исследование произвольных систем линейных уравнений
Рассмотрим систему m линейных уравнений с n неизвестными.
Матрица 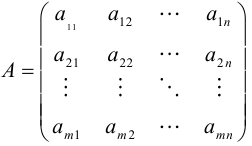
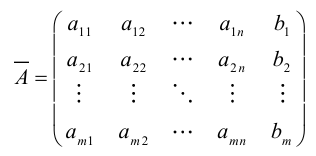
Определение: Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.
Определение: Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений у нее более одного.
Пример №39
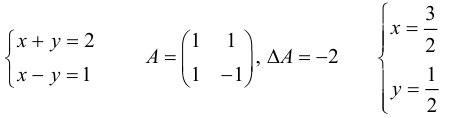
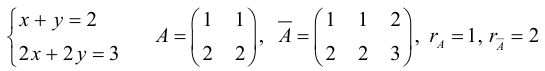
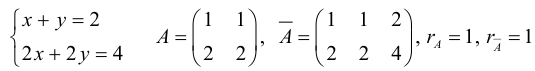
Теорема: (Кронекера-Капелли, критерий совместности системы линейных уравнений) Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной (без доказательства).
Теорема: (о числе решений). Пусть выполнены условия совместности системы линейных уравнений. Тогда, если 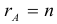
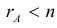
Однородные системы линейных уравнений
Система линейных уравнений вида
называется однородной.
Однородная система всегда совместна, так как 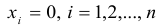
Теорема: Для того чтобы система линейных однородных уравнений (1.15) имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы r был меньше числа неизвестных n .
Доказательство:
- Достаточность:
(1.15) имеет нетривиальное решение. По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные.
- Необходимость: (1.15) имеет нетривиальное решение
Пусть r = n, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и r > n.
Следствие: Для того чтобы однородная система n уравнений с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее основной определитель был равен нулю.
Доказательство:
- Достаточность:
система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r < n, значит, нетривиальное решение существует.
- Необходимость: система имеет нетривиальное решение
Если
то не равен нулю минор n -го порядка основной матрицы, значит, r = n и решение единственно, что противоречит условию.
Метод Гаусса
Этим методом можно решить любую систему линейных уравнений (1.14) или доказать, что она несовместна. Он состоит в последовательном исключении неизвестных системы (1.14) по следующей схеме: выписывается расширенная матрица системы 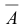
- перемена местами двух строк (уравнений);
- умножение любой строки (уравнения) на число
- отбрасывание одной из двух равных или пропорциональных строк (уравнений) ;
- прибавление к любой строке (уравнению) другой строки (уравнения), умноженной на число
После выполнения преобразований возможны три случая:
а)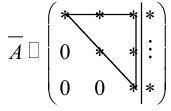
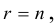
б) 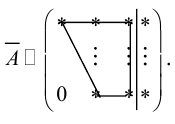
в) 
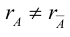
Пример №40
Решить систему линейных уравнений:
Выпишем расширенную матрицу и системы и упростим ее с помощью элементарных преобразований над строками:
Очевидно, что 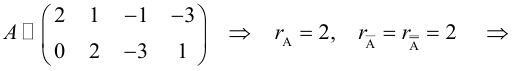
Кронекера-Капелли система совместна.
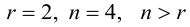
Выпишем систему, соответствующую матрице 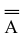
Перенесем в правую часть переменные 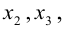
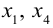
Теперь подставим 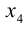
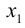
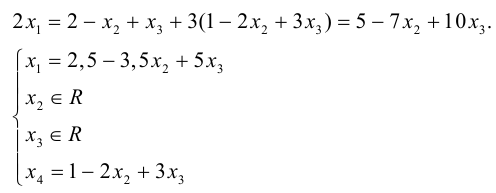
Определение: Общим решением системы (1.14) называется решение, содержащее информацию обо всех неизвестных, в котором зависимые переменные выражаются как функции свободных.
Решение, полученное из общего при конкретных значениях свободных переменных, называется частным решением.
Например, частными решениями этой системы являются:
Сделаем проверку частного решения (для всех уравнений исходной системы!):
Лекции по предметам:
- Математика
- Алгебра
- Векторная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
(схема 16)
Дадим ряд необходимых определений.
Система линейных уравнений называется неоднородной,
если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее
свободные члены равны нулю.
Решением системы уравнений называется упорядоченный набор чисел, который, будучи
подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.
Система уравнений называется совместной, если она
имеет хотя бы одно решение, и несовместной, если она решений не
имеет.
Совместная система уравнений называется определенной,
если она имеет единственное решение, и неопределенной, если она имеет более
одного решения.
Рассмотрим неоднородную систему линейных
алгебраических уравнений, имеющую при n=m следующий
общий вид:

Главной матрицей A системы
линейных алгебраических уравнений называется матрица, составленная из
коэффициентов, стоящих при неизвестных:

Определитель главной матрицы системы называется главным
определителем и обозначается ∆.
Вспомогательный определитель ∆i получается
из главного определителя путем замены i-го
столбца на столбец свободных членов
Теорема 1.1
(теорема Крамера). Если главный
определитель системы линейных алгебраических уравнений отличен от нуля, то
система имеет единственное решение, вычисляемое по формулам:

Если
главный определитель ∆=0, то система либо
имеет бесконечное множество решений (при всех нулевых вспомогательных
определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного
из вспомогательных определителей).
В свете приведенных выше определений, теорема Крамера может быть сформулирована иначе: если
главный определитель системы линейных алгебраических уравнений отличен от нуля,
то система является совместной определенной и при этом 
либо совместной неопределенной (при всех ∆i=0),
либо несовместной (при отличии хотя бы одного из ∆i от нуля).
После этого следует провести проверку полученного
решения.
Пример 1.4. Решить
систему методом Крамера
Решение. Так
как главный определитель системы
отличен от нуля, то система имеет единственное
решение. Вычислим вспомогательные определители
Воспользуемся
формулами Крамера (1.6):
Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла
и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.
Таблица 1.4
Определить стоимость 1 единицы продукции молокоцеха
каждого вида.
Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z –
1 кг
творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из
трех дней реализации можно отобразить следующей системой:

Решим систему методом Крамера. Найдем главный
определитель системы по формуле (1.2):
Так
как он отличен от нуля, то система имеет единственное решение. Вычислим
вспомогательные определители с помощью формулы (1.2):
По формулам Крамера (1.6) имеем:
Вернувшись к обозначениям, видим, что стоимость 1
литра молока равна 44 рубля, 1
кг масла – 540 рублей, 1 кг творога – 176 рублей
Примечание. Как видно, процесс вычисления определителей вручную с
помощью калькулятора трудоемок, поэтому на практике используют персональный
компьютер. Так, для решения систем линейных алгебраических уравнений методом
Крамера в MS Excel высчитывают ее главный и вспомогательные определители
с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек
и элементы матрицы, определитель которой находится.
В MathCAD для
нахождения определителя пользуются палитрой оператора Matrix
Вопросы для
самопроверки

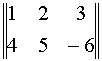
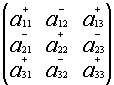
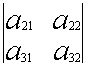
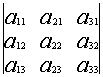
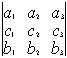
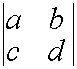
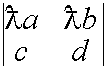
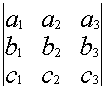
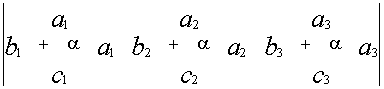
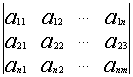

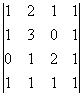
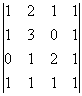
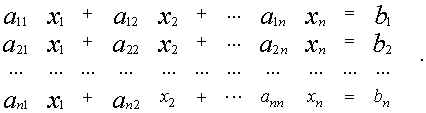
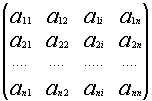
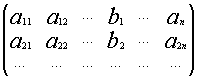
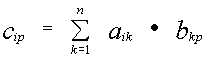
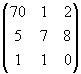

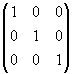
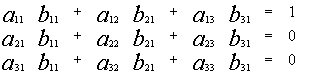
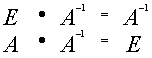
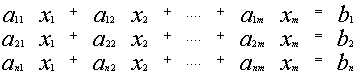

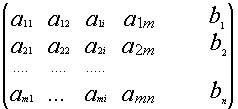
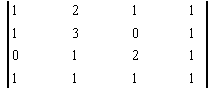
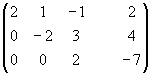
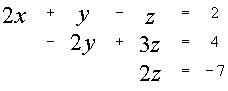
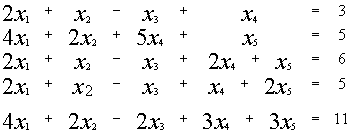
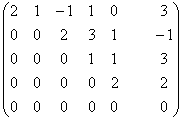
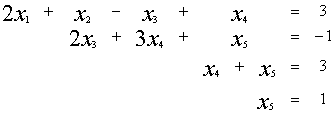
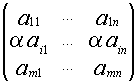
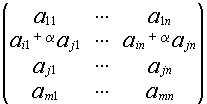
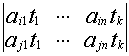
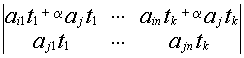
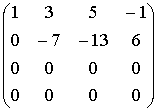
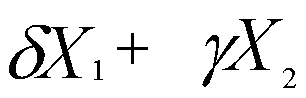
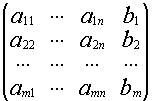
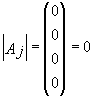
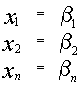
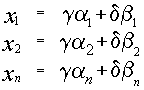
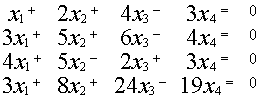
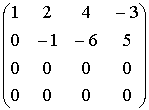
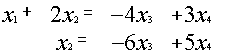
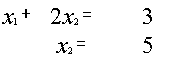
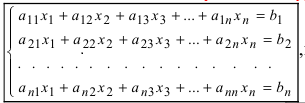

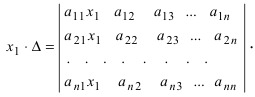
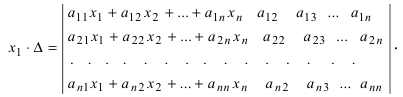
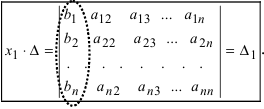

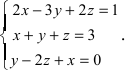
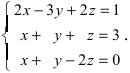
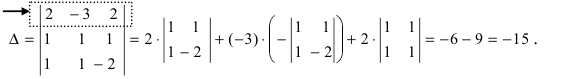
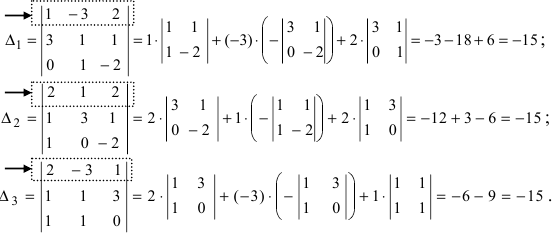
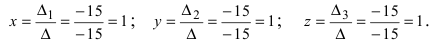

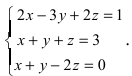
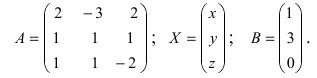
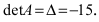
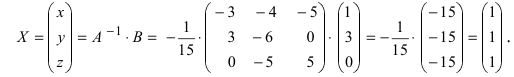
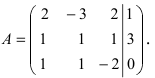
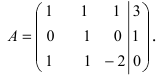
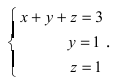
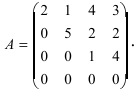








 . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком. , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.





















 которая не имеет решений.
которая не имеет решений. и, следовательно, имеет бесконечное множество решений x=y,y Î R.
и, следовательно, имеет бесконечное множество решений x=y,y Î R.









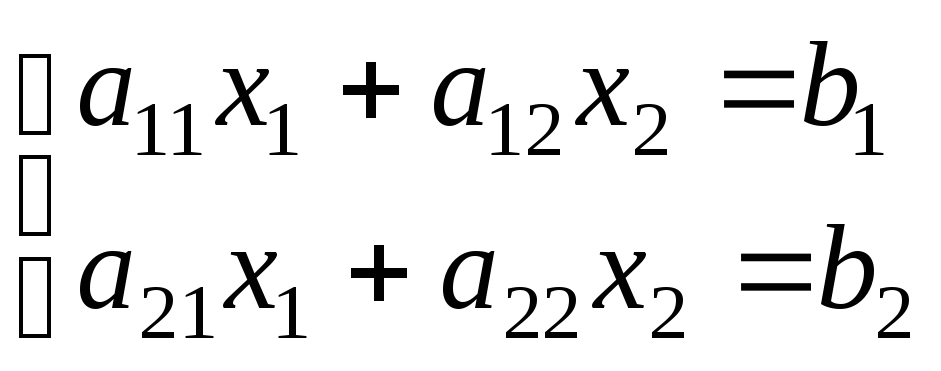
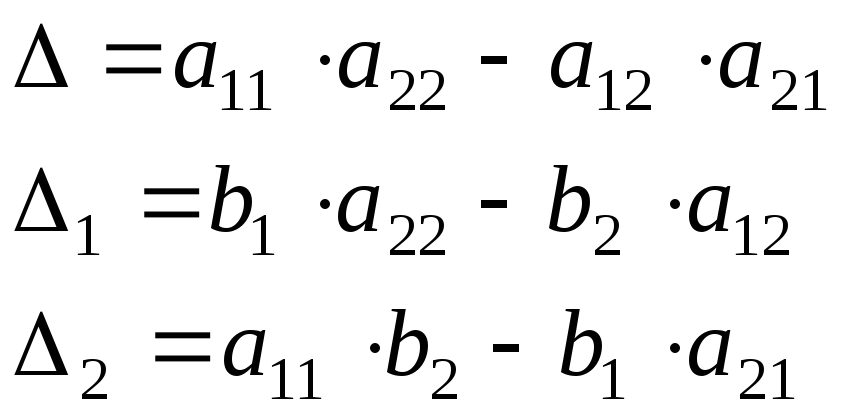

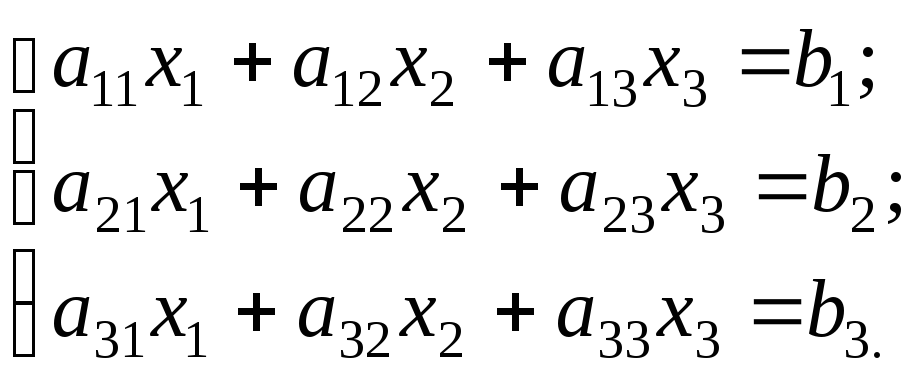
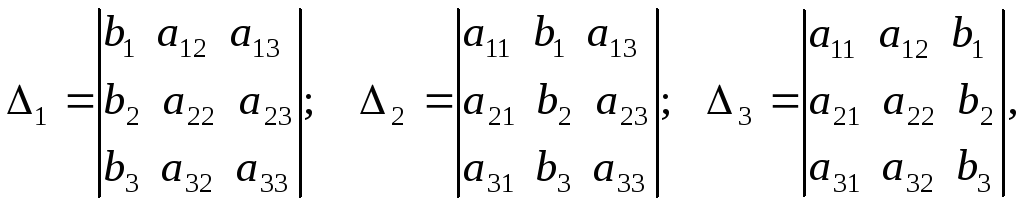
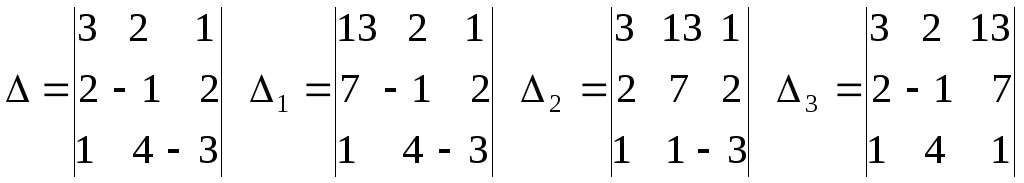
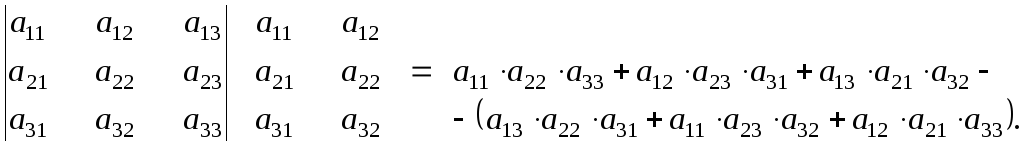

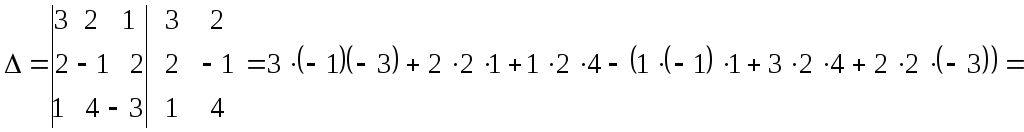
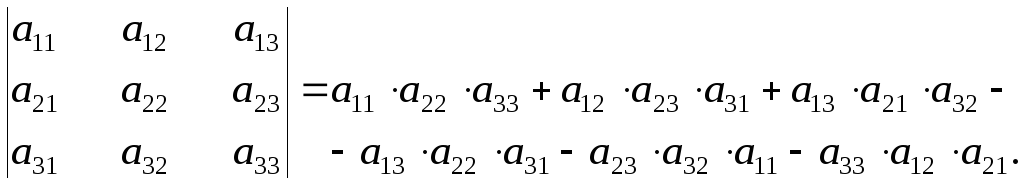
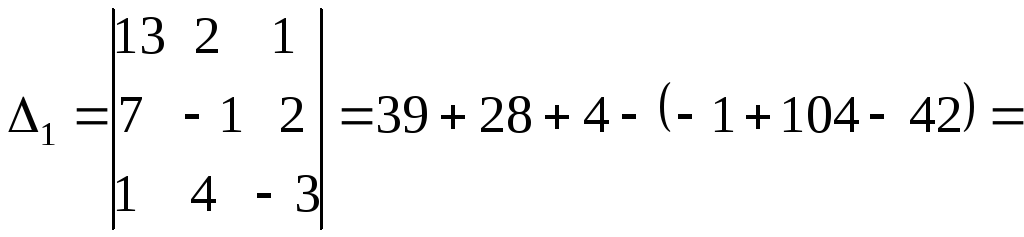
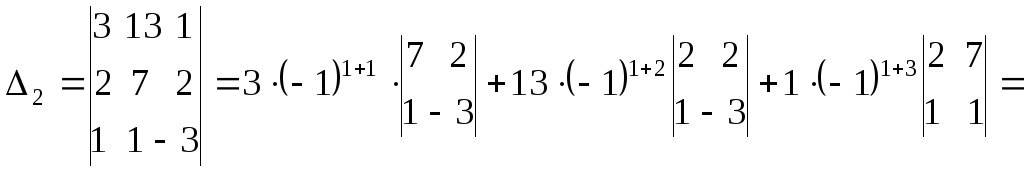
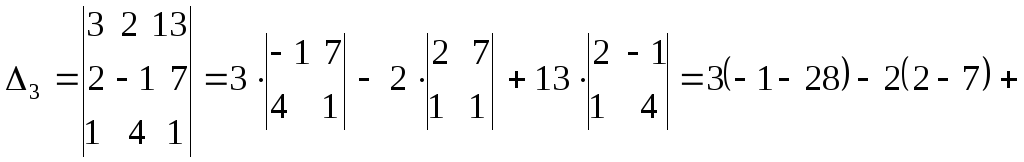
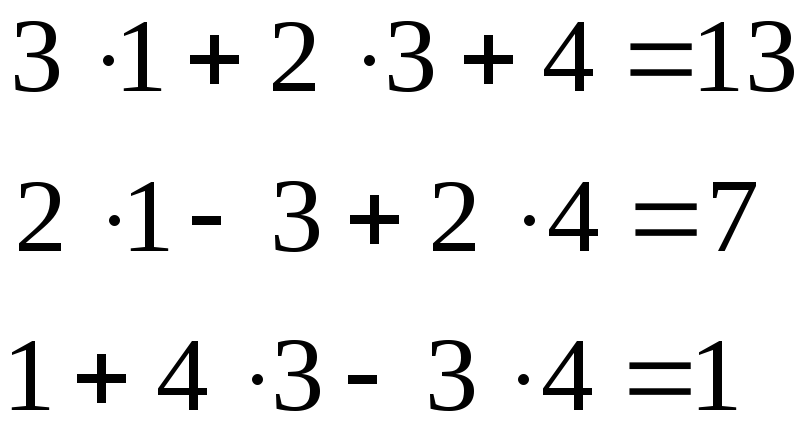
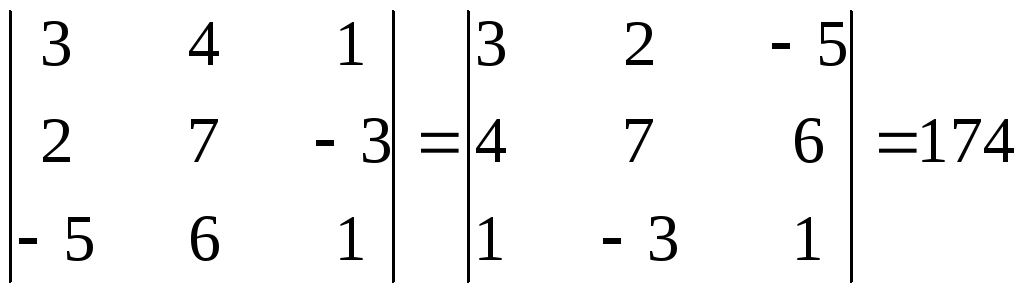
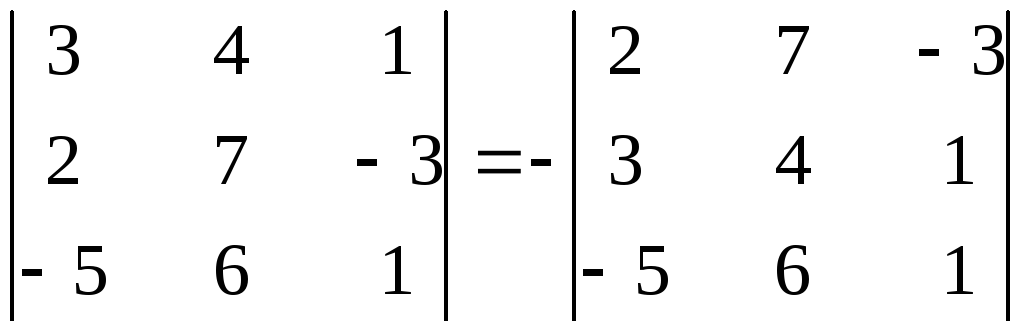
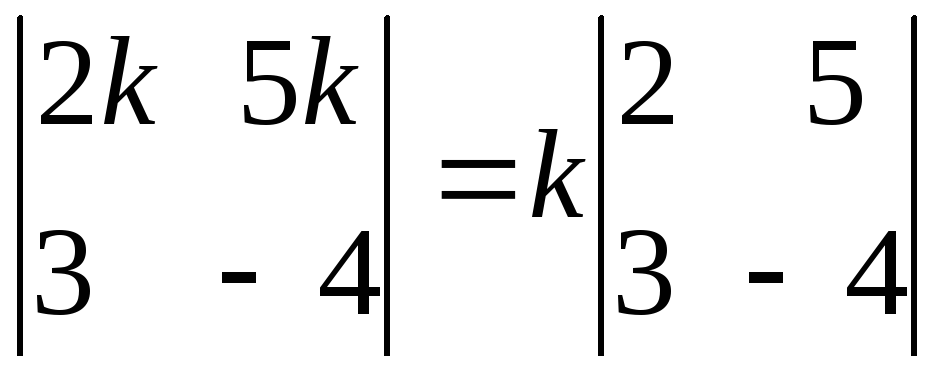
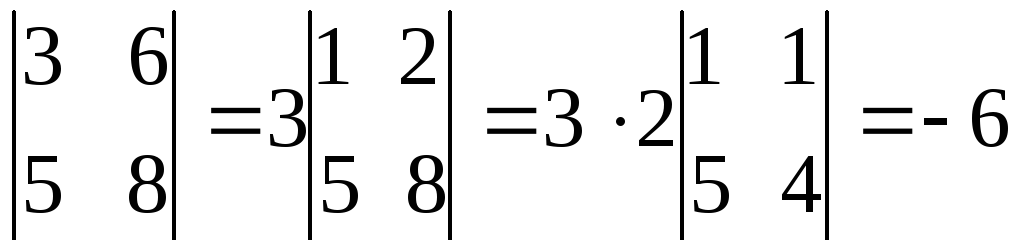
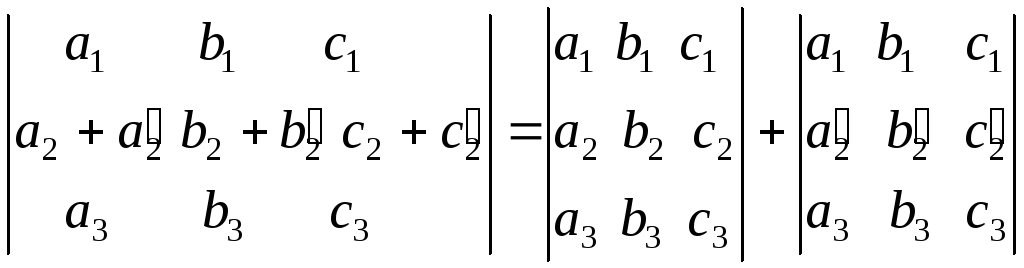
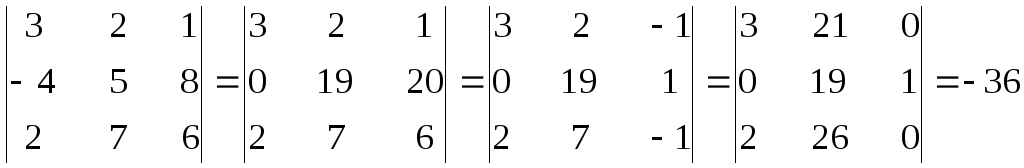



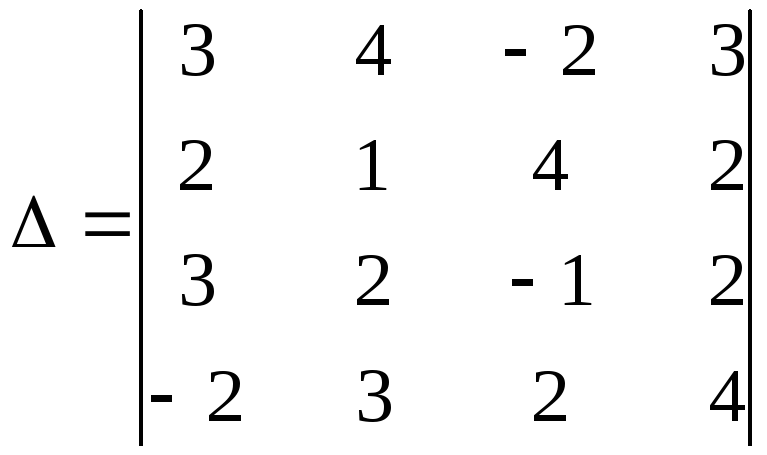
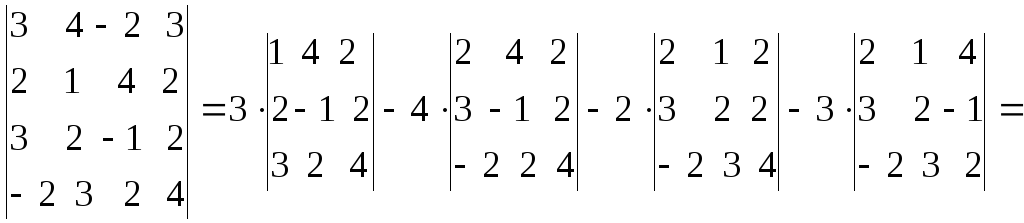
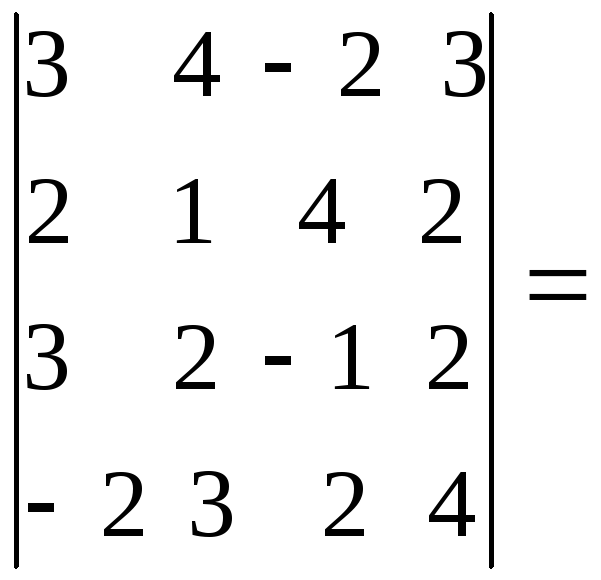
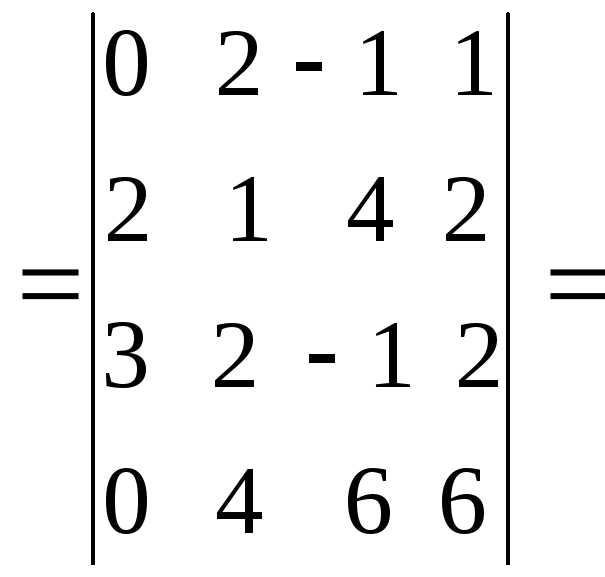
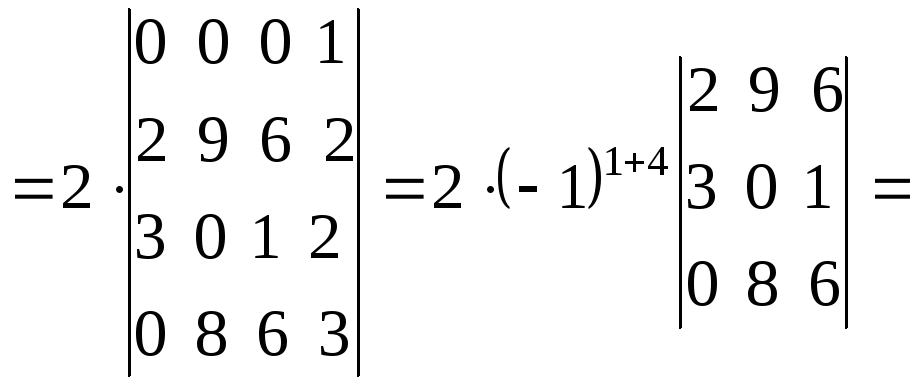
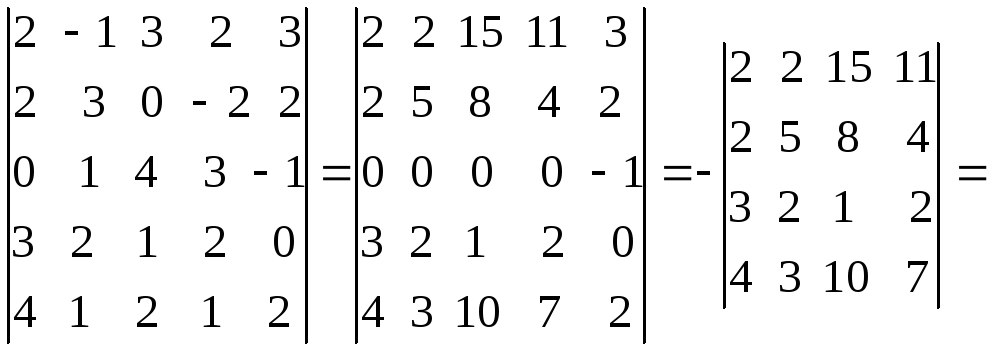
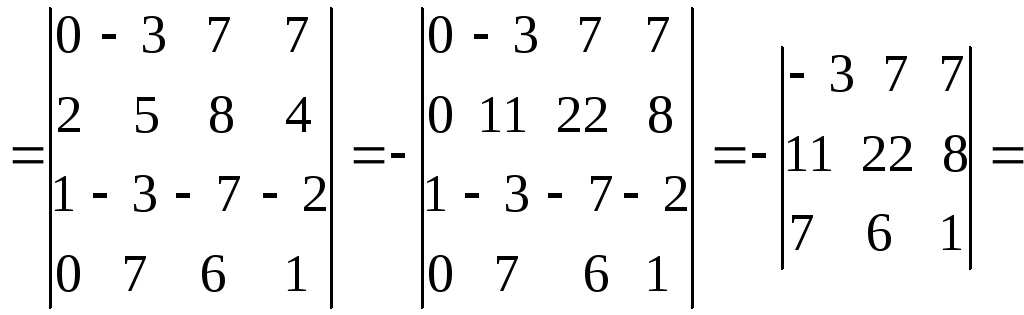
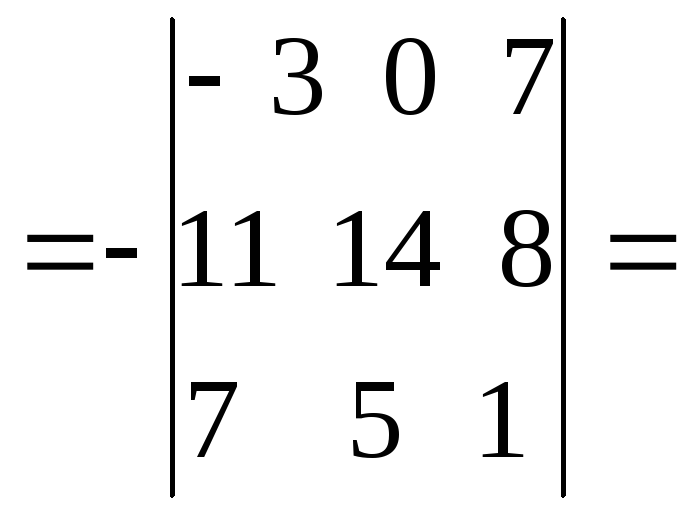
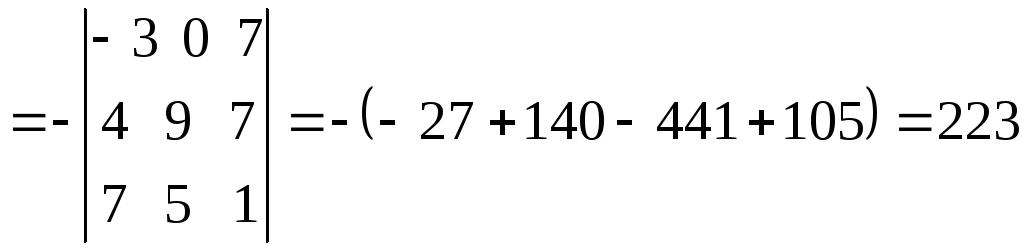
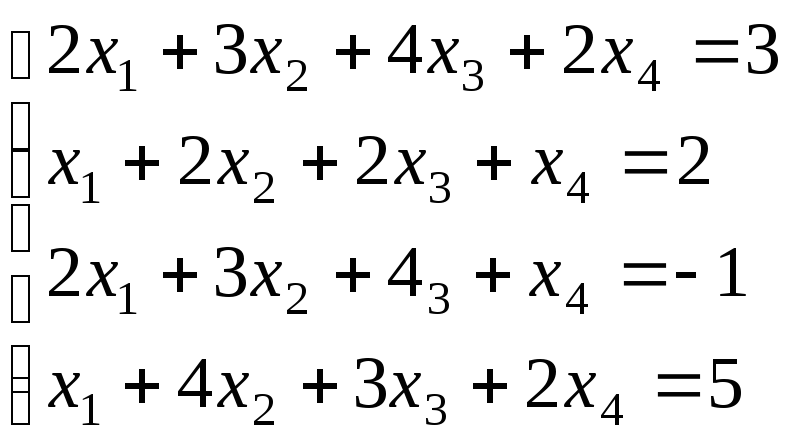
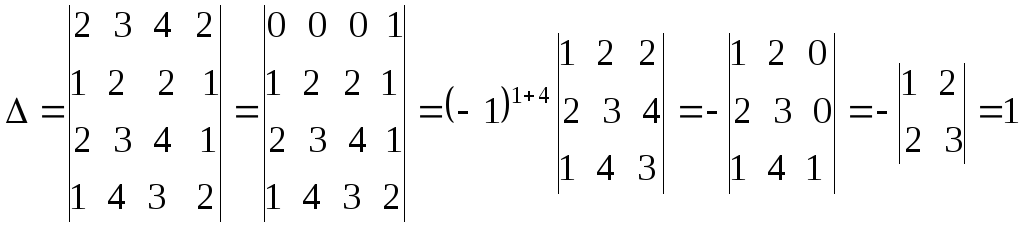
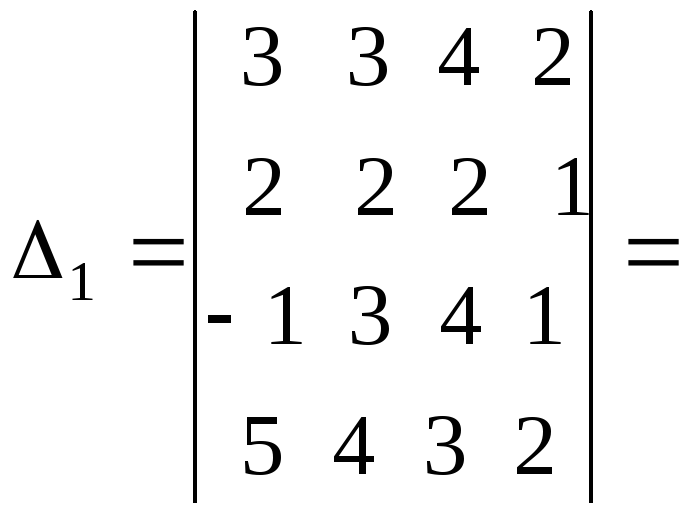
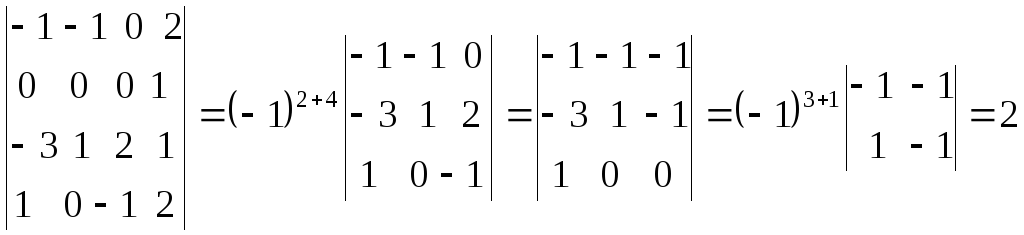
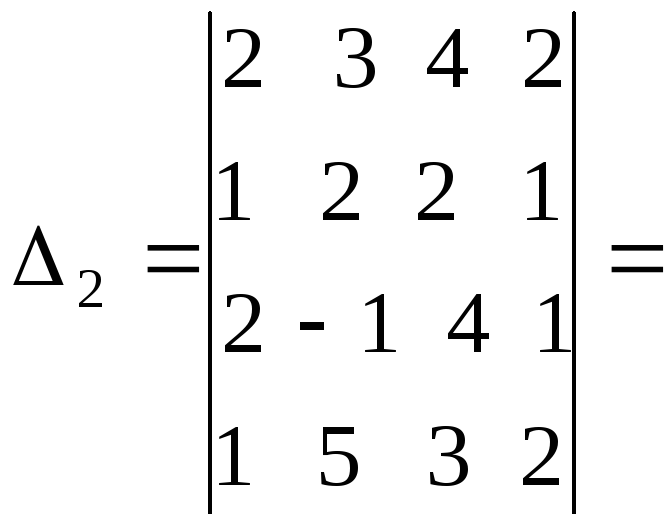

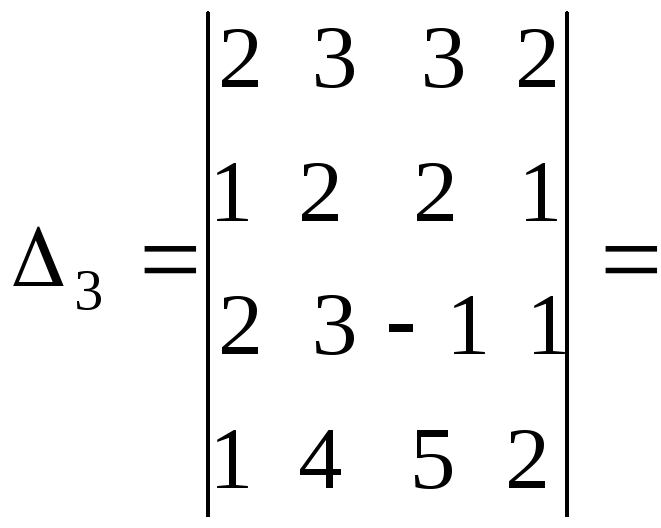

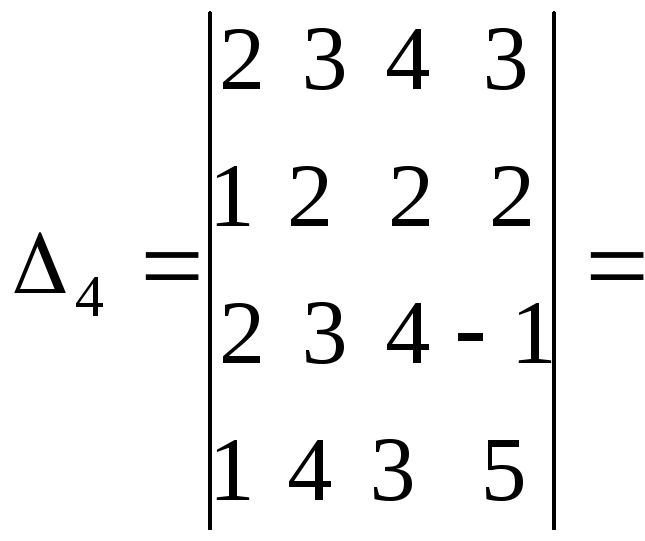

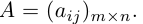
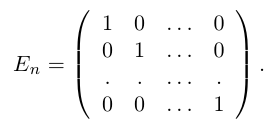

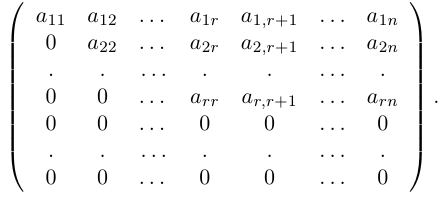
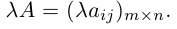
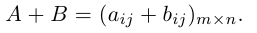
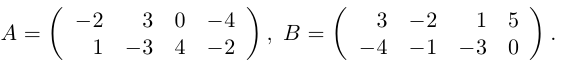
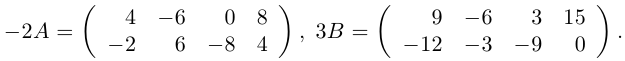
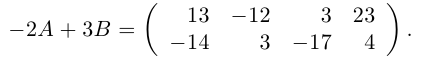
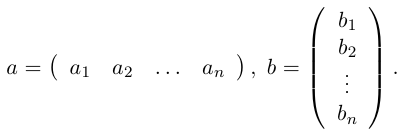
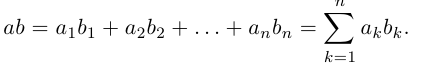
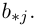
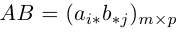
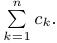
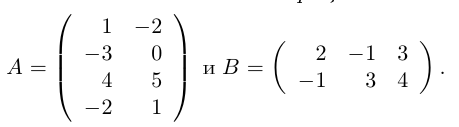
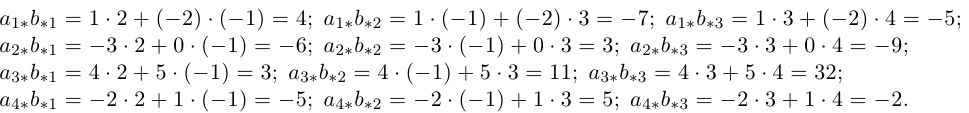
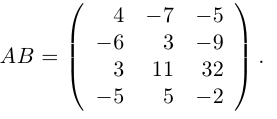
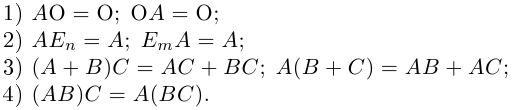
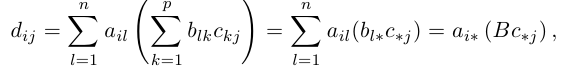
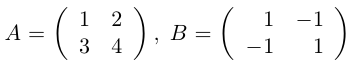
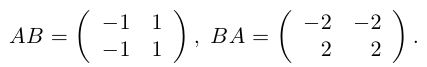
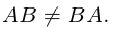
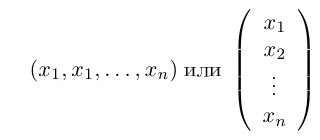
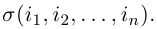

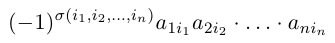

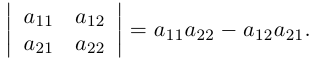
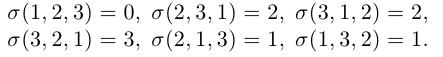
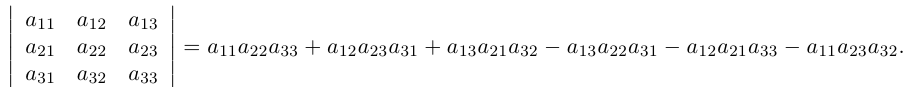
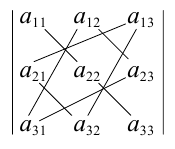
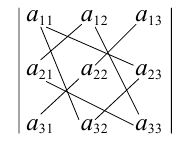

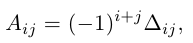
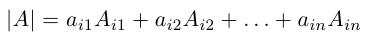
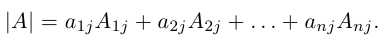
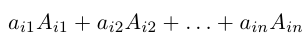
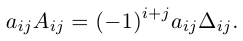

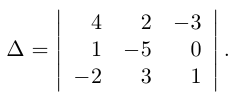
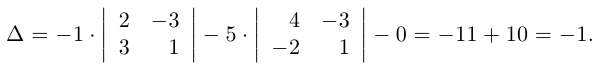

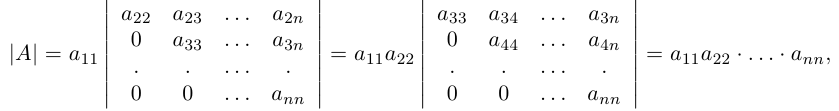
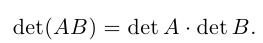
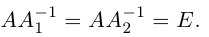
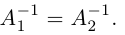
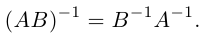
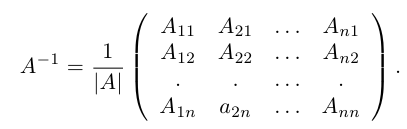
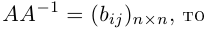
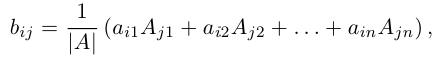
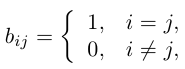
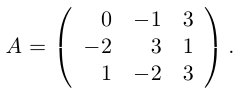
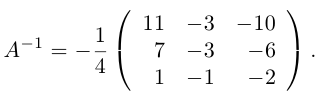
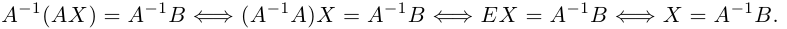
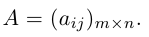
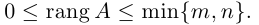
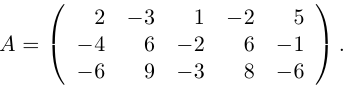
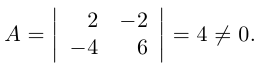

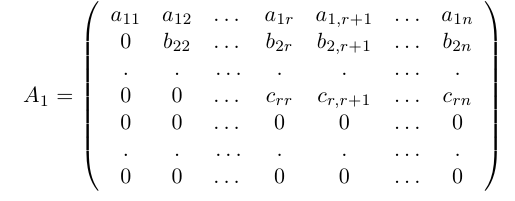
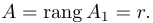
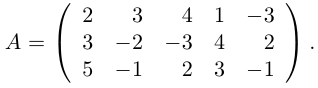
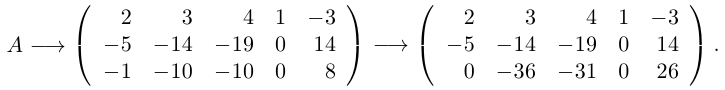
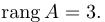
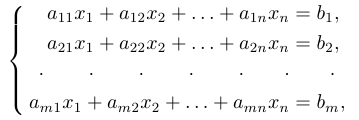
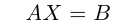
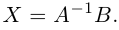
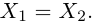
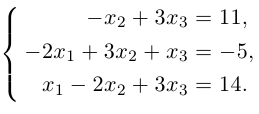
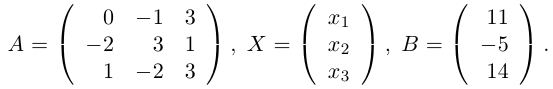
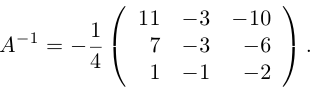
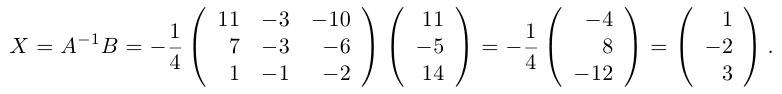

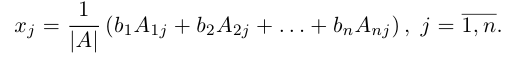
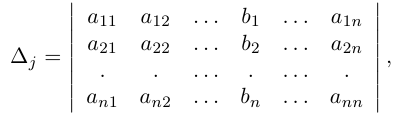
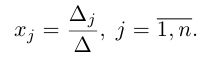
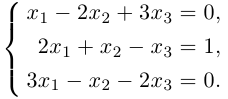
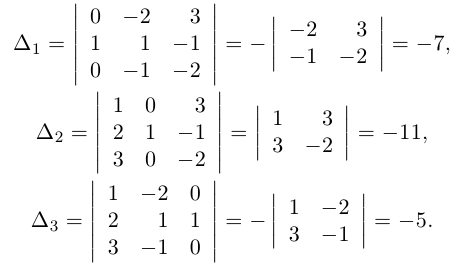
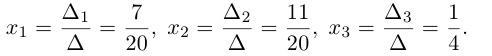
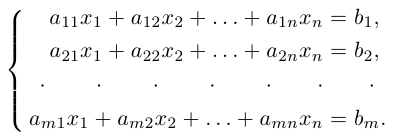
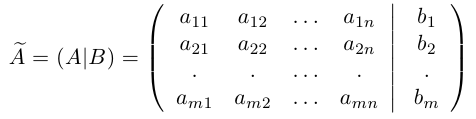
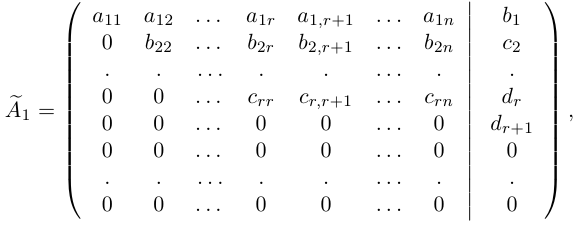
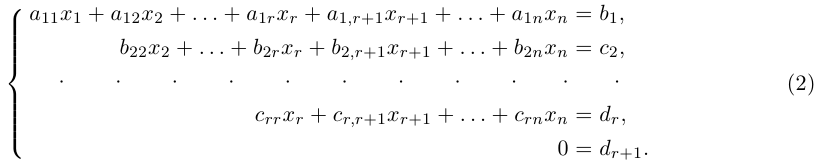
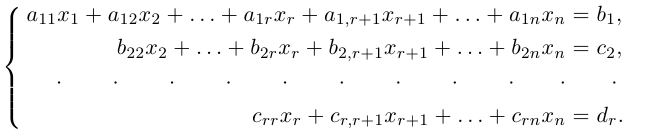
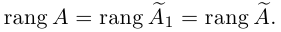
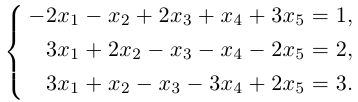

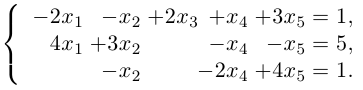
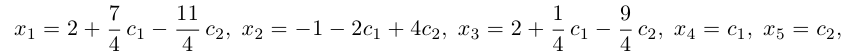
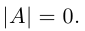
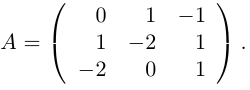

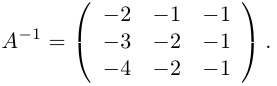
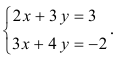
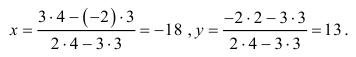
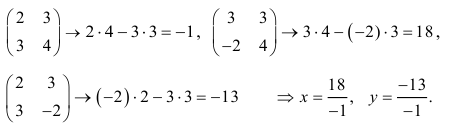
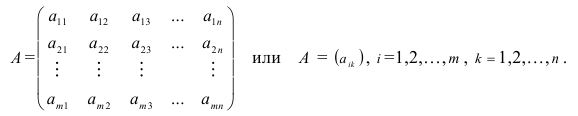
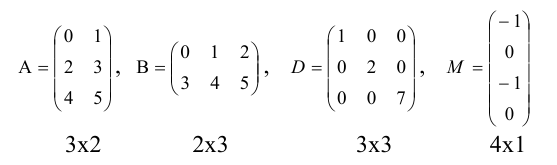
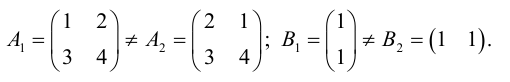
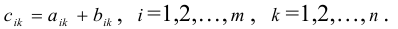
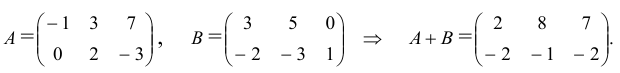

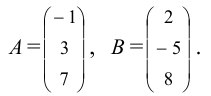
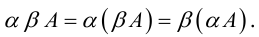
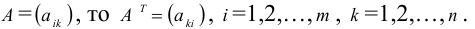
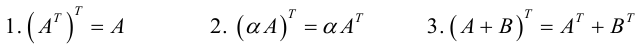
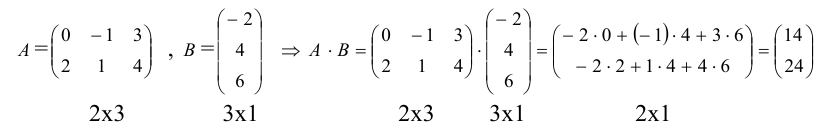
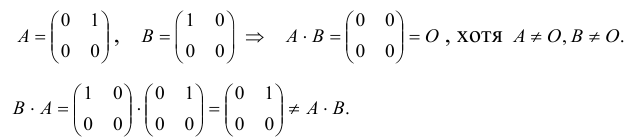
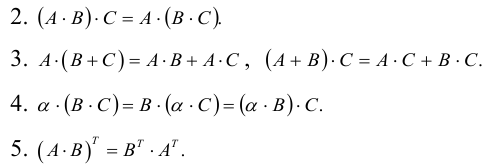
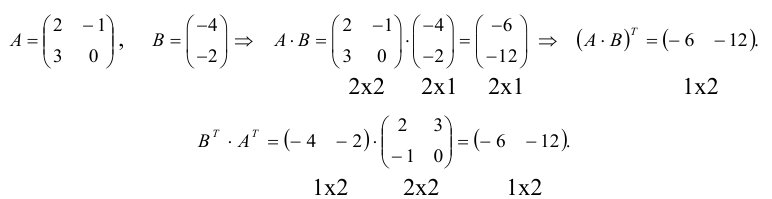
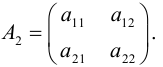
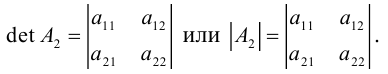
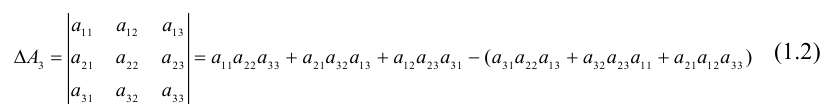
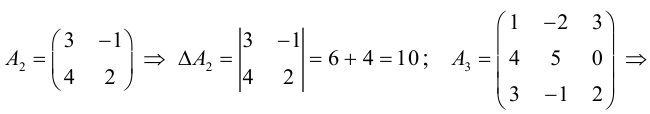
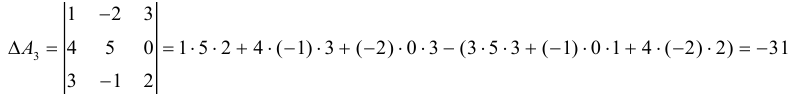
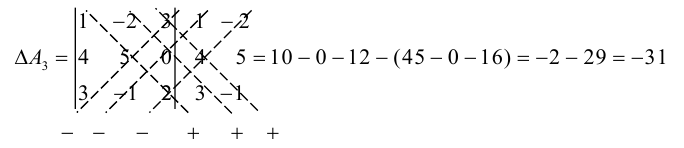
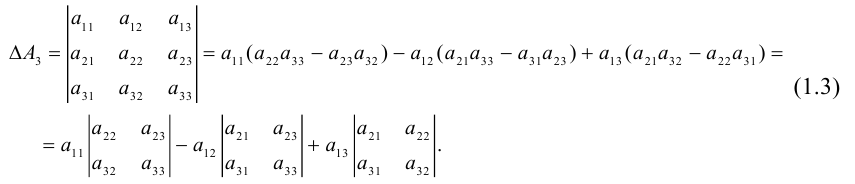
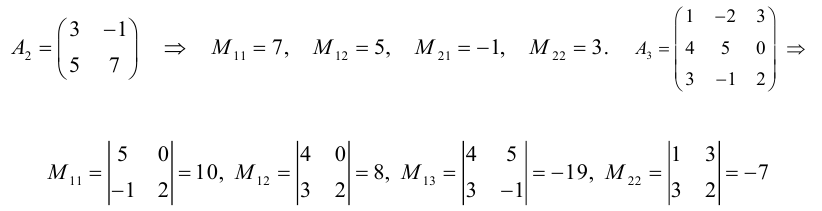
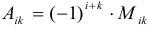
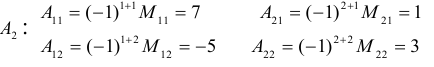
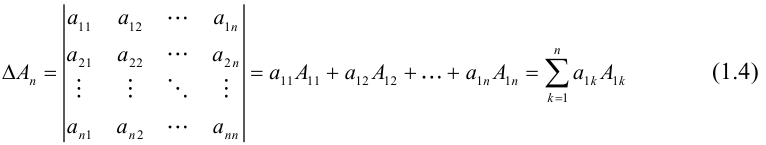
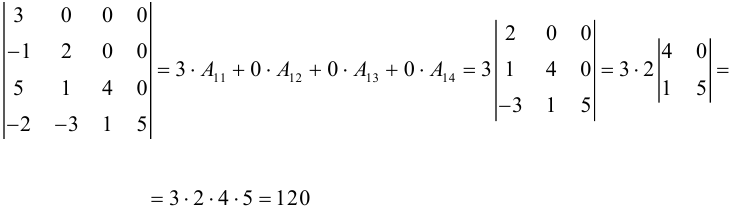
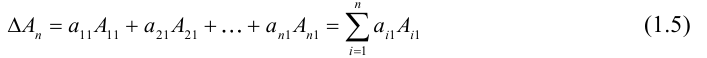
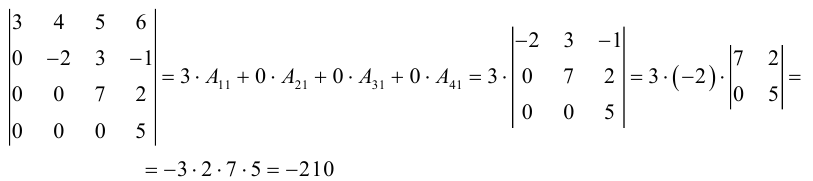
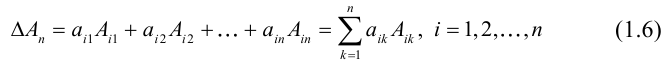
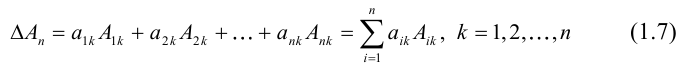
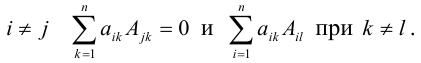

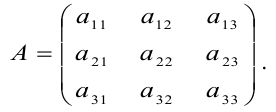
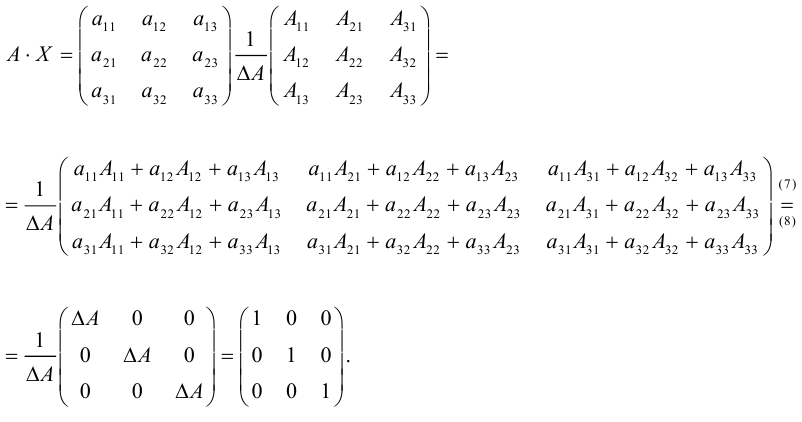

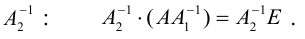

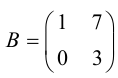
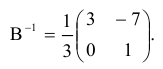
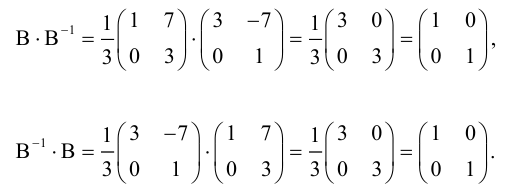
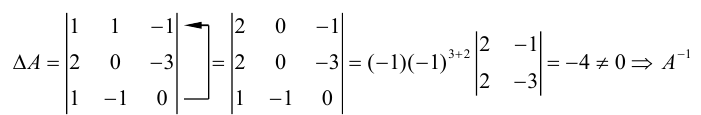
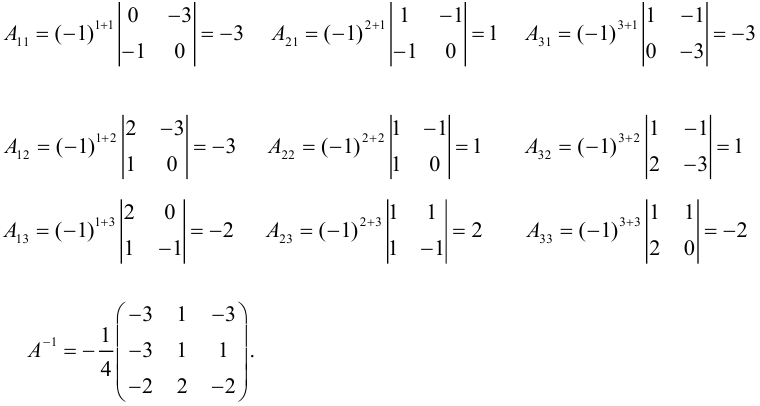
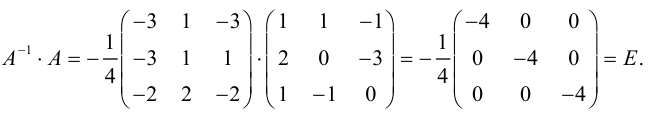
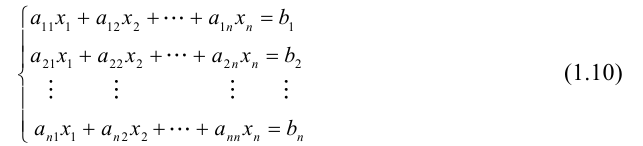
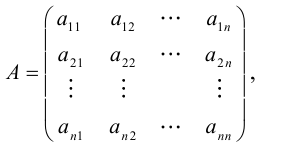

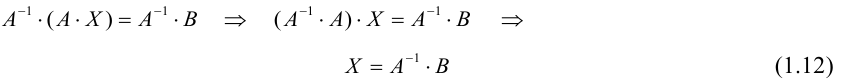
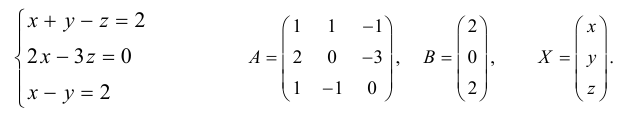
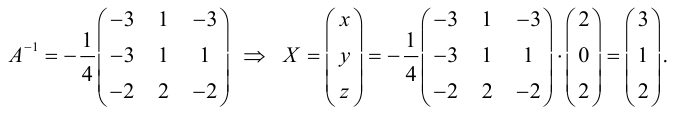
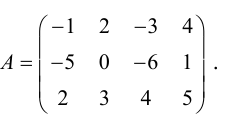
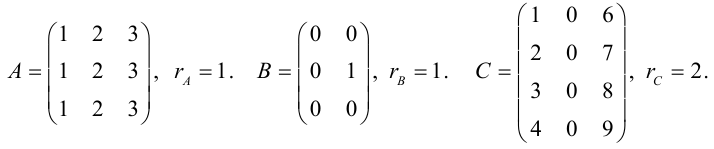
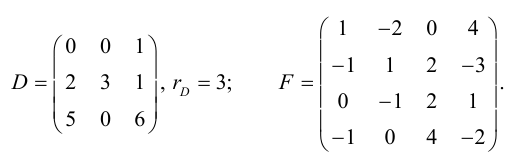
 ;
;  ;
; 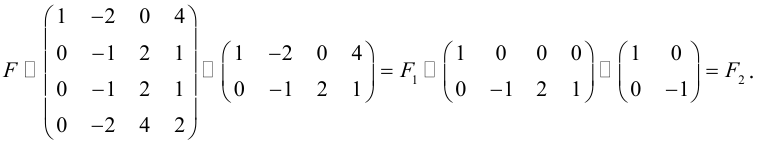
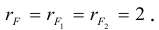
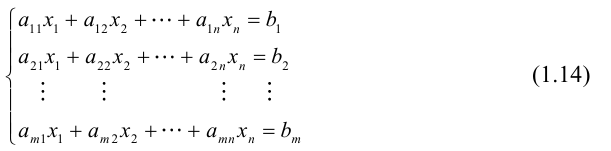
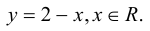
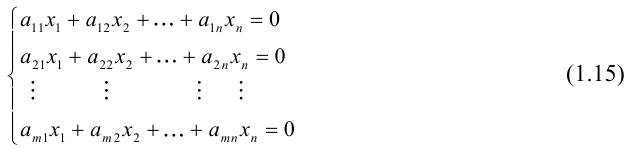
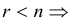 (1.15) имеет нетривиальное решение. По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные.
(1.15) имеет нетривиальное решение. По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные. 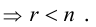 Пусть r = n, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и r > n.
Пусть r = n, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и r > n.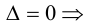 система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r < n, значит, нетривиальное решение существует.
система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r < n, значит, нетривиальное решение существует. 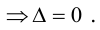 Если
Если 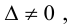 то не равен нулю минор n -го порядка основной матрицы, значит, r = n и решение единственно, что противоречит условию.
то не равен нулю минор n -го порядка основной матрицы, значит, r = n и решение единственно, что противоречит условию.