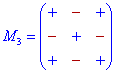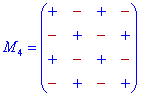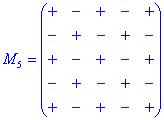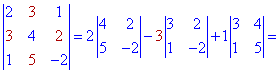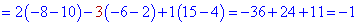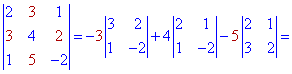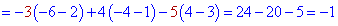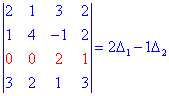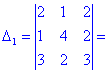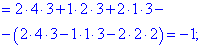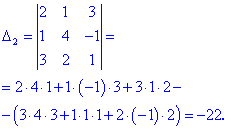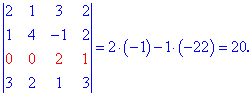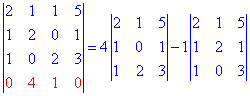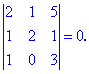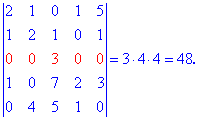Найти определитель матрицы
Этот калькулятор поможет Вам вычислить определитель, разложив его по строке или столбцу, либо предварительно получив нули в строке или столбце. Детерминант будет вычислен с выводом промежуточных результатов.
- Оставляйте лишние ячейки пустыми для ввода неквадратных матриц.
-
Элементы матриц — десятичные (конечные и периодические) дроби:
1/3,3,14,-1,3(56)или1,2e-4; либо арифметические выражения:2/3+3*(10-4),(1+x)/y^2,2^0,5 (=2),2^(1/3),2^n,sin(phi),cos(3,142rad),a_1или(root of x^5-x-1 near 1,2).-
decimal (finite and periodic) fractions:
1/3,3,14,-1,3(56)или1,2e-4 -
2/3+3*(10-4),(1+x)/y^2,2^0,5 (=2),2^(1/3),2^n,sin(phi),cos(3,142rad),a_1или(root of x^5-x-1 near 1,2) -
matrix literals:
{{1,3},{4,5}} -
operators:
+,-,*,/,,!,^,^{*},,,;,≠,=,⩾,⩽,>и< -
functions:
sqrt,cbrt,exp,log,abs,conjugate,min,max,gcd,rank,adjugate,inverse,determinant,transpose,pseudoinverse,cos,sin,tan,cot,cosh,sinh,tanh,coth,arccos,arcsin,arctan,arccot,arcosh,arsinh,artanhиarcoth -
units:
rad,deg -
special symbols:
pi,e,i— mathematical constantsk,n— integersIorE— identity matrixX,Y— matrix symbols
-
- Используйте ↵ Ввод, Пробел, ←↑↓→, Backspace и Delete для перемещения по ячейкам, Ctrl⌘ Cmd+C/Ctrl⌘ Cmd+V — для копирования матриц.
- Перетаскивайте матрицы из результата (drag-and-drop), или даже из текстового редактора.
- За теорией о матрицах и операциях над ними обращайтесь к страничке на Википедии.
Понижение порядка определителя. Разложение определителя по строке (столбцу).
Для определителя четвёртого и более высоких порядков обычно применяются иные методы вычисления, нежели использование готовых формул как для вычисления определителей второго и третьего порядков. Один из методов вычисления определителей высших порядков – использование следствия из теоремы Лапласа (саму теорему можно посмотреть, например, в книге А.Г. Куроша «Курс высшей алгебры»). Это следствие позволяет разложить определитель по элементам некоторой строки или столбца. При этом вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка. Именно поэтому такое преобразование именуют понижением порядка определителя. Например, вычисление определителя четвёртого порядка сводится к нахождению четырёх определителей третьего порядка.
Допустим, нам задана квадратная матрица n-го порядка, т.е. $A=left( begin{array} {cccc} a_{11} & a_{12} & ldots & a_{1n} \
a_{21} & a_{22} & ldots & a_{2n} \
ldots & ldots & ldots & ldots \
a_{n1} & a_{n2} & ldots & a_{nn} \
end{array} right)$. Вычислить определитель этой матрицы можно, разложив его по строке или по столбцу.
Зафиксируем некоторую строку, номер которой равен $i$. Тогда определитель матрицы $A_{ntimes n}$ можно разложить по выбранной i-й строке, используя следующую формулу:
$$
begin{equation}
Delta A=sumlimits_{j=1}^{n}a_{ij}A_{ij}=a_{i1}A_{i1}+a_{i2}A_{i2}+ldots+a_{in}A_{in}
end{equation}
$$
Что такое $A_{ij}$ и $a_{ij}$? показатьскрыть
Что обозначает знак $sum$? показатьскрыть
Аналог формулы (1) существует и для столбцов. Формула для разложения определителя по j-му столбцу выглядит следующим образом:
$$
begin{equation}
Delta A=sumlimits_{i=1}^{n}a_{ij}A_{ij}=a_{1j}A_{1j}+a_{2j}A_{2j}+ldots+a_{nj}A_{nj}
end{equation}
$$
Правила, выраженные формулами (1) и (2), можно сформулировать так: определитель равен сумме произведений элементов некоей строки или столбца на алгебраические дополнения этих элементов. Для наглядности рассмотрим определитель четвёртого порядка, записанный в общем виде. Для примера разложим его по элементам четвёртого столбца (элементы этого столбца выделены зелёным цветом):
$$Delta=left| begin{array} {cccc}
a_{11} & a_{12} & a_{13} & normgreen{a_{14}} \
a_{21} & a_{22} & a_{23} & normgreen{a_{24}} \
a_{31} & a_{32} & a_{33} & normgreen{a_{34}} \
a_{41} & a_{42} & a_{43} & normgreen{a_{44}} \
end{array} right|$$
$$
Delta
=normgreen{a_{14}}cdot{A_{14}}+normgreen{a_{24}}cdot{A_{24}}+normgreen{a_{34}}cdot{A_{34}}+normgreen{a_{44}}cdot{A_{44}}
$$
Аналогично, раскладывая, к примеру, по третьей строке, получим такую формулу для вычисления определителя:
$$
Delta
=a_{31}cdot{A_{31}}+a_{32}cdot{A_{32}}+a_{33}cdot{A_{33}}+a_{34}cdot{A_{34}}
$$
Пример №1
Вычислить определитель матрицы $A=left( begin{array} {ccc} 5 & -4 & 3 \ 7 & 2 & -1 \ 9 & 0 & 4 end{array} right)$, используя разложение по первой строке и второму столбцу.
Решение
Нам нужно вычислить определитель третьего порядка $Delta A=left| begin{array} {ccc} 5 & -4 & 3 \ 7 & 2 & -1 \ 9 & 0 & 4 end{array} right|$. Чтобы разложить его по первой строке нужно использовать формулу (1). Запишем это разложение в общем виде:
$$
Delta A= a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}.
$$
Для нашей матрицы $a_{11}=5$, $a_{12}=-4$, $a_{13}=3$. Для вычисления алгебраических дополнений $A_{11}$, $A_{12}$, $A_{13}$ станем использовать формулу №1 из темы, посвящённой определителям второго и третьего порядков. Итак, искомые алгебраические дополнения таковы:
begin{aligned}
& A_{11}=(-1)^2cdot left| begin{array} {cc} 2 & -1 \ 0 & 4 end{array} right|=2cdot 4-(-1)cdot 0=8;\
& A_{12}=(-1)^3cdot left| begin{array} {cc} 7 & -1 \ 9 & 4 end{array} right|=-(7cdot 4-(-1)cdot 9)=-37;\
& A_{13}=(-1)^4cdot left| begin{array} {cc} 7 & 2 \ 9 & 0 end{array} right|=7cdot 0-2cdot 9=-18.
end{aligned}
Как мы нашли алгебраические дополнения? показатьскрыть
Подставляя все найденные значения в записанную выше формулу, получим:
$$
Delta A= a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}=5cdot{8}+(-4)cdot(-37)+3cdot(-18)=134.
$$
Как видите, процесс нахождения определителя третьего порядка мы свели к вычислению значений трёх определителей второго порядка. Иными словами, мы понизили порядок исходного определителя.
Обычно в таких простых случаях не расписывают решение подробно, отдельно находя алгебраические дополнения, а уж затем подставляя их в формулу для вычисления определителя. Чаще всего просто продолжают запись общей формулы, – до тех пор, пока не будет получен ответ. Именно так мы станем раскладывать определитель по второму столбцу.
Итак, приступим к разложению определителя по второму столбцу. Вспомогательных вычислений производить не будем, – просто продолжим формулу до получения ответа. Обратите внимание, что во втором столбце один элемент равен нулю, т.е. $a_{32}=0$. Это говорит о том, что слагаемое $a_{32}cdot A_{32}=0cdot A_{23}=0$. Используя формулу (2) для разложения по второму столбцу, получим:
$$
Delta A= a_{12}cdot A_{12}+a_{22}cdot A_{22}+a_{32}cdot A_{32}=-4cdot (-1)cdot left| begin{array} {cc} 7 & -1 \ 9 & 4 end{array} right|+2cdot left| begin{array} {cc} 5 & 3 \ 9 & 4 end{array} right|=4cdot 37+2cdot (-7)=134.
$$
Ответ получен. Естественно, что результат разложения по второму столбцу совпал с результатом разложения по первой строке, ибо мы раскладывали один и тот же определитель. Заметьте, что при разложении по второму столбцу мы делали меньше вычислений, так как один элемент второго столбца был равен нулю. Именно исходя из таких соображений для разложения стараются выбирать тот столбец или строку, которые содержат побольше нулей.
Ответ: $Delta A=134$.
Пример №2
Вычислить определитель матрицы $A=left( begin{array} {cccc}
-1 & 3 & 2 & -3\
4 & -2 & 5 & 1\
-5 & 0 & -4 & 0\
9 & 7 & 8 & -7 end{array} right)$, используя разложение по выбранной строке или столбцу.
Решение
Для разложения выгоднее всего выбирать ту строку или столбец, которые содержат более всего нулей. Естественно, что в данном случае имеет смысл раскладывать по третьей строке, так как она содержит два элемента, равных нулю. Используя формулу (1), запишем разложение определителя по третьей строке:
$$
Delta A= a_{31}cdot A_{31}+a_{32}cdot A_{32}+a_{33}cdot A_{33}+a_{34}cdot A_{34}.
$$
Так как $a_{31}=-5$, $a_{32}=0$, $a_{33}=-4$, $a_{34}=0$, то записанная выше формула станет такой:
$$
Delta A= -5 cdot A_{31}-4cdot A_{33}.
$$
Обратимся к алгебраическим дополнениям $A_{31}$ и $A_{33}$. Для их вычисления будем использовать формулу №2 из темы, посвящённой определителям второго и третьего порядков (в этом же разделе есть подробные примеры применения данной формулы).
begin{aligned}
& A_{31}=(-1)^4cdot left| begin{array} {ccc} 3 & 2 & -3 \ -2 & 5 & 1 \ 7 & 8 & -7 end{array} right|=10;\
& A_{33}=(-1)^6cdot left| begin{array} {ccc} -1 & 3 & -3 \ 4 & -2 & 1 \ 9 & 7 & -7 end{array} right|=-34.
end{aligned}
Подставляя полученные данные в формулу для определителя, будем иметь:
$$
Delta A= -5 cdot A_{31}-4cdot A_{33}=-5cdot 10-4cdot (-34)=86.
$$
В принципе, всё решение можно записать в одну строку. Если пропустить все пояснения и промежуточные вычисления, то запись решения будет такова:
$$
Delta A= a_{31}cdot A_{31}+a_{32}cdot A_{32}+a_{33}cdot A_{33}+a_{34}cdot A_{34}=\=
-5 cdot (-1)^4cdot left| begin{array} {ccc} 3 & 2 & -3 \ -2 & 5 & 1 \ 7 & 8 & -7 end{array} right|-4cdot (-1)^6cdot left| begin{array} {ccc} -1 & 3 & -3 \ 4 & -2 & 1 \ 9 & 7 & -7 end{array} right|=-5cdot 10-4cdot (-34)=86.
$$
Ответ: $Delta A=86$.
Если вы приступили к изучению данной темы, то вы уже знакомы с понятием определителя матрицы и умеете находить определители первого, второго и третьего порядка.
Прежде чем начать рассмотрение новой темы, рекомендуется повторить правило вычисления определителя по строке и столбцу, рассматривающееся в теме «Как вычислить определитель матрицы третьего порядка», свойства определителей, а также нахождение миноров и алгебраических дополнений.
Разложение определителей по строкам или столбцам
Для вычисления определителей высших порядков применяется способ разложения определителя по строке или столбцу. Это позволяет представить детерминант в виде суммы произведений элементов какой-либо его строки или столбца на соответствующие этим элементам алгебраические дополнения. В таком случае вычисление определителя nn-го порядка сводится к вычислению определителей n−1n-1-го порядка.
Пример 1
Найти определитель ∣32454−32−45−2−3−7−3429∣begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix} двумя способами:
- по 2-й строке;
- по 3-у столбцу.
1 способ. Разложим определитель 4-го порядка по строке №2 и вычислим его:
∣32454−32−45−2−3−7−3429∣=4(−1)2+1∣245−2−3−7429∣+(−3)(−1)2+2∣3455−3−7−329∣+2(−1)2+3∣3255−2−7−349∣+(−4)(−1)2+4∣3245−2−3−342∣=begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix}=4(-1)^{2+1}begin{vmatrix}2&4&5\-2&-3&-7\4&2&9end{vmatrix}+(-3)(-1)^{2+2}begin{vmatrix}3&4&5\5&-3&-7\-3&2&9end{vmatrix}+2(-1)^{2+3}begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}+(-4)(-1)^{2+4}begin{vmatrix}3&2&4\5&-2&-3\-3&4&2end{vmatrix}=
=−4∣245−2−3−7429∣−3∣3455−3−7−329∣−2∣3255−2−7−349∣−4∣3245−2−3−342∣=−4(−54−20−112+60+28+72)−3(−81+50+84−45+42−180)−2(−54+100+42−30+84−90)−4(−12+80+18−24+36−20)=−4(−26)−3(−130)−2⋅52−4⋅78=104+390−104−312=78=-4begin{vmatrix}2&4&5\-2&-3&-7\4&2&9end{vmatrix}-3begin{vmatrix}3&4&5\5&-3&-7\-3&2&9end{vmatrix}-2begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}-4begin{vmatrix}3&2&4\5&-2&-3\-3&4&2end{vmatrix}=-4(-54-20-112+60+28+72)-3(-81+50+84-45+42-180)-2(-54+100+42-30+84-90)-4(-12+80+18-24+36-20)=-4(-26)-3(-130)-2cdot52-4cdot78=104+390-104-312=78.
2 способ. Разложим определитель 4-го порядка по 3 столбцу и вычислим его:
∣32454−32−45−2−3−7−3429∣=4(−1)1+3∣4−3−45−2−7−349∣+2(−1)2+3∣3255−2−7−349∣+(−3)(−1)3+3∣3254−3−4−349∣+2(−1)4+3∣3254−3−45−2−7∣=begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix}=4(-1)^{1+3}begin{vmatrix}4&-3&-4\5&-2&-7\-3&4&9end{vmatrix}+2(-1)^{2+3}begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}+(-3)(-1)^{3+3}begin{vmatrix}3&2&5\4&-3&-4\-3&4&9end{vmatrix}+2(-1)^{4+3}begin{vmatrix}3&2&5\4&-3&-4\5&-2&-7end{vmatrix}=
=4∣4−3−45−2−7−349∣−2∣3255−2−7−349∣−3∣3254−3−4−349∣−2∣3254−3−45−2−7∣=4(−72−80−63+24+112+135)−2(−54+100+42−30+84−90)−3(−81+80+24−45+48−72)−2(63−40−40+75−24+56)=4⋅56−2⋅52−3⋅(−45)−2⋅90=224−104+138−180=78=4begin{vmatrix}4&-3&-4\5&-2&-7\-3&4&9end{vmatrix}-2begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}-3begin{vmatrix}3&2&5\4&-3&-4\-3&4&9end{vmatrix}-2begin{vmatrix}3&2&5\4&-3&-4\5&-2&-7end{vmatrix}=4(-72-80-63+24+112+135)-2(-54+100+42-30+84-90)-3(-81+80+24-45+48-72)-2(63-40-40+75-24+56)=4cdot56-2cdot52-3cdot(-45)-2cdot90=224-104+138-180=78.
Метод понижения порядка
Для упрощения расчетов при вычислении определителей рекомендуется применять их свойства. Рассмотрим примеры вычисления определителей с применением их свойств.
Пример 1
Вычислить определитель
∣638−45642034241−46∣begin{vmatrix}6&3&8&-4\5&6&4&2\0&3&4&2\4&1&-4&6end{vmatrix}.
Вынесем из столбца №3 множитель 4:
∣638−45642034241−46∣=4⋅∣632−45612031241−16∣begin{vmatrix}6&3&8&-4\5&6&4&2\0&3&4&2\4&1&-4&6end{vmatrix}=4cdotbegin{vmatrix}6&3&2&-4\5&6&1&2\0&3&1&2\4&1&-1&6end{vmatrix}.
Вынесем из столбца №4 множитель 2:
4⋅∣632−45612031241−16∣=4⋅2⋅∣632−25611031141−13∣=8⋅∣632−25611031141−13∣4cdotbegin{vmatrix}6&3&2&-4\5&6&1&2\0&3&1&2\4&1&-1&6end{vmatrix}=4cdot2cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}.
Прибавим к строке №1 строку №2, умноженную на -2:
8⋅∣632−25611031141−13∣=8⋅∣−4−90−45611031141−13∣8cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}.
Прибавим к строке №3 строку №2, умноженную на -1:
8⋅∣−4−90−45611031141−13∣=8⋅∣−4−90−45611−5−30041−13∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\4&1&-1&3end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на 1:
8⋅∣−4−90−45611−5−30041−13∣=8⋅∣−4−90−45611−5−3009704∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\9&7&0&4end{vmatrix}.
Разложим определитель по столбцу №3:
8⋅∣−4−90−45611−5−3009704∣=8⋅1⋅(−1)2+3∣−4−9−4−5−30974∣=8⋅(−1)5∣−4−9−4−5−30974∣=−8∣−4−9−4−5−30974∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\9&7&0&4end{vmatrix}=8cdot1cdot(-1)^{2+3}begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=8cdot(-1)^{5}begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=-8begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}.
Прибавим к строке №1 строку №3, умноженную на 1:
−8∣−4−9−4−5−30974∣=−8∣5−20−5−30974∣-8begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=-8begin{vmatrix}5&-2&0\-5&-3&0\9&7&4end{vmatrix}.
Разложим определитель по столбцу №3 и вычислим его:
−8∣5−20−5−30974∣=−8⋅4⋅(−1)3+3∣5−2−5−3∣=−32⋅(−1)6∣5−2−5−3∣=−32∣5−2−5−3∣-8begin{vmatrix}5&-2&0\-5&-3&0\9&7&4end{vmatrix}=-8cdot4cdot(-1)^{3+3}begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32cdot(-1)^{6}begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32begin{vmatrix}5&-2\-5&-3end{vmatrix}.
Прибавим к строке №2 строку №1, умноженную на 1:
−32∣5−2−5−3∣=−32∣5−20−5∣-32begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32begin{vmatrix}5&-2\0&-5end{vmatrix}.
Разложим определитель по столбцу №1 и заменим определитель 1-го порядка единственным его элементом:
−32∣5−20−5∣=−32⋅5⋅(−1)1+1⋅(−5)=−32⋅5⋅1⋅(−5)=800-32begin{vmatrix}5&-2\0&-5end{vmatrix}=-32cdot5cdot(-1)^{1+1}cdot(-5)=-32cdot5cdot1cdot(-5)=800.
Пример 2
Вычислить определитель
∣44−10−18237523325732122112176657211221∣begin{vmatrix}4&4&-1&0&-1&8\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №1 строку №4, умноженную на -4:
∣44−10−18237523325732122112176657211221∣=∣0−4−9−4−50237523325732122112176657211221∣begin{vmatrix}4&4&-1&0&-1&8\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №2 строку №4, умноженную на -2:
∣0−4−9−4−50237523325732122112176657211221∣=∣0−4−9−4−500−1330−1325732122112176657211221∣begin{vmatrix}0&-4&-9&-4&-5&0\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №3 строку №4, умноженную на -3:
∣0−4−9−4−500−1330−1325732122112176657211221∣=∣0−4−9−4−500−1330−10−4−140−4122112176657211221∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №5 строку №4, умноженную на -1:
∣0−4−9−4−500−1330−10−4−140−4122112176657211221∣=∣0−4−9−4−500−1330−10−4−140−4122112054545211221∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\2&1&1&2&2&1end{vmatrix}.
Прибавим к строке №6 строку №4, умноженную на -2:
∣0−4−9−4−500−1330−10−4−140−4122112054545211221∣=∣0−4−9−4−500−1330−10−4−140−41221120545450−3−300−3∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\0&-3&-3&0&0&-3end{vmatrix}.
Разложим определитель по 1 столбцу:
∣0−4−9−4−500−1330−10−4−140−41221120545450−3−300−3∣=1⋅(−1)4+1∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣=−∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\0&-3&-3&0&0&-3end{vmatrix}=1cdot(-1)^{4+1}begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.
Прибавим к строке №1 строку №3, умноженную на -1:
−∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣=−∣0−8−8−54−1330−1−4−140−454545−3−300−3∣-begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.
Прибавим к строке №3 строку №2, умноженную на -4:
−∣0−8−8−54−1330−1−4−140−454545−3−300−3∣=−∣0−8−8−54−1330−10−13−80054545−3−300−3∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на 5:
−∣0−8−8−54−1330−10−13−80054545−3−300−3∣=−∣0−8−8−54−1330−10−13−8000192040−3−300−3∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\-3&-3&0&0&-3end{vmatrix}.
Прибавим у строке №5 строку №2, умноженную на -3:
−∣0−8−8−54−1330−10−13−8000192040−3−300−3∣=−∣0−8−8−54−1330−10−13−80001920400−12−900∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\0&-12&-9&0&0end{vmatrix}.
Разложим определитель по 1 столбцу:
−∣0−8−8−54−1330−10−13−80001920400−12−900∣=−(−1)⋅(−1)2+1∣−8−8−54−13−800192040−12−900∣=(−1)3∣−8−8−54−13−800192040−12−900∣=−∣−8−8−54−13−800192040−12−900∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\0&-12&-9&0&0end{vmatrix}=-(-1)cdot(-1)^{2+1}begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=(-1)^{3}begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=-begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}.
Вынесем множитель -3 из строки №4:
−∣−8−8−54−13−800192040−12−900∣=−(−3)∣−8−8−54−13−8001920404300∣=3∣−8−8−54−13−8001920404300∣-begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=-(-3)begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}=3begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}.
Разложим определитель по 4 столбцу:
3∣−8−8−54−13−8001920404300∣=3⋅4⋅(−1)1+4∣−13−8019204430∣=12⋅(−1)5∣−13−8019204430∣=−12∣−13−8019204430∣3begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}=3cdot4cdot(-1)^{1+4}begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=12cdot(-1)^{5}begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=-12begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}.
Разложим определитель по столбцу №3 и вычислим его:
−12∣−13−8019204430∣=−12⋅4⋅(−1)2+3∣−13−843∣=−48⋅(−1)5∣−13−843∣=48∣−13−843∣-12begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=-12cdot4cdot(-1)^{2+3}begin{vmatrix}-13&-8\4&3end{vmatrix}=-48cdot(-1)^{5}begin{vmatrix}-13&-8\4&3end{vmatrix}=48begin{vmatrix}-13&-8\4&3end{vmatrix}.
Прибавим к строке №1 строку №2, умноженную на 3:
48∣−13−843∣=48∣−1143∣48begin{vmatrix}-13&-8\4&3end{vmatrix}=48begin{vmatrix}-1&1\4&3end{vmatrix}.
Прибавим к строке №2 строку №1, умноженную на 4:
48∣−1143∣=48∣−1107∣48begin{vmatrix}-1&1\4&3end{vmatrix}=48begin{vmatrix}-1&1\0&7end{vmatrix}.
Разложим определитель по столбцу №1 и заменим определитель 1-го порядка единственным его элементом:
48∣−1107∣=48⋅(−1)⋅(−1)1+1⋅7=48⋅(−1)⋅1⋅7=−33648begin{vmatrix}-1&1\0&7end{vmatrix}=48cdot(-1)cdot(-1)^{1+1}cdot7=48cdot(-1)cdot1cdot7=-336
.
Приведение к треугольному виду
Данный метод состоит в том, чтобы привести определитель к треугольному виду, а затем вычислить произведение элементов, стоящих на главной диагонали.
Пример 1
Вычислить определитель ∣4−20532−21−213−123−6−3∣begin{vmatrix}4&-2&0&5\3&2&-2&1\-2&1&3&-1\2&3&-6&-3end{vmatrix}.
Поменяем местами строки №1 и №3:
∣4−20532−21−213−123−6−3∣=−∣−213−132−214−20523−6−3∣begin{vmatrix}4&-2&0&5\3&2&-2&1\-2&1&3&-1\2&3&-6&-3end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\2&3&-6&-3end{vmatrix}.
Прибавим к строке №4 строку №1, умноженную на 1:
−∣−213−132−214−20523−6−3∣=−∣−213−132−214−20504−3−4∣-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\2&3&-6&-3end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\0&4&-3&-4end{vmatrix}.
Прибавим к строке №3 строку №1, умноженную на 2:
−∣−213−132−214−20504−3−4∣=−∣−213−132−21006304−3−4∣-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\0&4&-3&-4end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\0&0&6&3\0&4&-3&-4end{vmatrix}.
Умножим строку №2 на 2:
∣−213−132−21006304−3−4∣=−12∣−213−164−42006304−3−4∣begin{vmatrix}-2&1&3&-1\3&2&-2&1\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}begin{vmatrix}-2&1&3&-1\6&4&-4&2\0&0&6&3\0&4&-3&-4end{vmatrix}.
Прибавим к строке №2 строку №1, умноженную на 3:
−12∣−213−164−42006304−3−4∣=−12∣−213−1075−1006304−3−4∣-frac{1}{2}begin{vmatrix}-2&1&3&-1\6&4&-4&2\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&4&-3&-4end{vmatrix}.
Умножим строку №4 на 7:
−12∣−213−1075−1006304−3−4∣=−12⋅17∣−213−1075−10063028−21−28∣-frac{1}{2}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&28&-21&-28end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на -4:
−12⋅17∣−213−1075−10063028−21−28∣=−12⋅17∣−213−1075−1006300−41−24∣-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&28&-21&-28end{vmatrix}=-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&0&-41&-24end{vmatrix}.
Поменяем местами столбцы №3 и №4:
−12⋅17∣−213−1075−1006300−41−24∣=12⋅17∣−21−1307−15003600−24−41∣-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&0&-41&-24end{vmatrix}=frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&-24&-41end{vmatrix}.
Прибавим к строке №4 строку №3, умноженную на 8 и вычислим определитель:
12⋅17∣−21−1307−15003600−24−41∣=12⋅17∣−21−1307−1500360007∣=12⋅17⋅(−2)⋅7⋅3⋅7=−21frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&-24&-41end{vmatrix}=frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&0&7end{vmatrix}=frac{1}{2}cdotfrac{1}{7}cdot(-2)cdot7cdot3cdot7=-21.
Пример 2
Вычислить определитель
∣7694−410−266789−1−61−1−245−70−92−2∣begin{vmatrix}7&6&9&4&-4\1&0&-2&6&6\7&8&9&-1&-6\1&-1&-2&4&5\-7&0&-9&2&-2end{vmatrix}.
Поменяем местами строки №1 и №4:
∣7694−410−266789−1−61−1−245−70−92−2∣=−∣1−1−24510−266789−1−67694−4−70−92−2∣begin{vmatrix}7&6&9&4&-4\1&0&-2&6&6\7&8&9&-1&-6\1&-1&-2&4&5\-7&0&-9&2&-2end{vmatrix}=-begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\7&8&9&-1&-6\7&6&9&4&-4\-7&0&-9&2&-2end{vmatrix}.
Поменяем местами строки №3 и №5:
−∣1−1−24510−266789−1−67694−4−70−92−2∣=∣1−1−24510−266−70−92−27694−4789−1−6∣-begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\7&8&9&-1&-6\7&6&9&4&-4\-7&0&-9&2&-2end{vmatrix}=begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\-7&0&-9&2&-2\7&6&9&4&-4\7&8&9&-1&-6end{vmatrix}.
Поменяем местами столбцы №4 и №5:
∣1−1−24510−266−70−92−27694−4789−1−6∣=−∣1−1−25410−266−70−9−22769−44789−6−1∣begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\-7&0&-9&2&-2\7&6&9&4&-4\7&8&9&-1&-6end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\1&0&-2&6&6\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}.
Прибавим к строке №2 строку №1, умноженную на -1:
−∣1−1−25410−266−70−9−22769−44789−6−1∣=−∣1−1−25401012−70−9−22769−44789−6−1∣-begin{vmatrix}1&-1&-2&5&4\1&0&-2&6&6\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}.
Прибавим к строке №4 строку №3, умноженную на 1:
−∣1−1−25401012−70−9−22769−44789−6−1∣=−∣1−1−25401012−70−9−22060−66789−6−1∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\7&8&9&-6&-1end{vmatrix}.
Прибавим к строке №5 строку №3, умноженную на 1:
−∣1−1−25401012−70−9−22060−66789−6−1∣=−∣1−1−25401012−70−9−22060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.
Прибавим к строке №3 строку №1, умноженную на 7:
−∣1−1−25401012−70−9−22060−66080−81∣=−∣1−1−254010120−7−233330060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&-7&-23&33&30\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.
Прибавим к строке №3 строку №2, умноженную на 7:
−∣1−1−254010120−7−233330060−66080−81∣=−∣1−1−2540101200−234044060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&-7&-23&33&30\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.
Вынесем из строки №4 множитель 6:
−∣1−1−2540101200−234044060−66080−81∣=−6∣1−1−2540101200−234044010−11080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&8&0&-8&1end{vmatrix}.
Прибавим к строке №5 строку №4, умноженную на -8:
−6∣1−1−2540101200−234044010−11080−81∣=−6∣1−1−2540101200−234044010−110000−7∣-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&8&0&-8&1end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&0&0&0&-7end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на -1 и вычислим определитель:
−6∣1−1−2540101200−234044010−110000−7∣=−6∣1−1−2540101200−234044000−2−10000−7∣=−6⋅1⋅1⋅(−23)⋅(−2)⋅(−7)=1932-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&0&0&0&-7end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&0&0&-2&-1\0&0&0&0&-7end{vmatrix}=-6cdot1cdot1cdot(-23)cdot(-2)cdot(-7)=1932.
Мы рассмотрели наиболее распространенные методы вычисления определителей высших порядков. Каждый из них может применяться для их нахождения.
Онлайн-помощь с решением контрольных работ на бирже Студворк!
Тест по теме «Как вычислить определитель матрицы высших порядков»
При нахождении определителей второго, третьего порядка можно пользоваться стандартными формулами (2 — разница произведения диагональных элементов, 3 — правило треугольника). Однако для вычисления определителя четвертого, пятого порядка и старших гораздо быстрее разложить их по элементам строки или столбца, содержащего больше всего нулей и свести к расчету нескольких определителей на единицу меньшего порядка.
Схемы знаков при минорах для детерминантов 3-го — 5-го порядка приведены ниже.
Их не трудно запомнить, если знать следующие правила:
Дополнение к элементам главной диагонали идут со знаком «+», а на параллельных диагоналям чередуются «-», «+», «-», …
Дополнение к элементам нечетных столбцов и строк начинаются с знака «+», а дальше чередуются «-», «+», для парных начинаются со знака «-», а дальше поочередно меняются «+», «-»,…
Вторым правилом пользуется большинство студентов, поскольку оно привязано к столбца или строки по которому осуществляется расписание определителя.
Перейдем к рассмотрению примеров разложения определителя и изучению особенностей этого метода.
Пример 1.
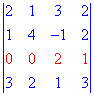
Разложить определитель третьего порядка по элементам первой строки и второго столбца
Решение.
Проводим разложение определителя по элементам первой строки
Подобным образом выполняем вычисления разложения по элементам второго столбца
Оба значения одинаковы, а значит расчеты проведены правильно. Если у Вас получится что определители полученные расписанием по строке и столбцу не совпадают — значит где-то допущена ошибка при вычислениях и нужно перечислить или найти ее.
Пример 2.
Найти определитель четвертого порядка методом разложения
Решение.
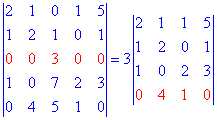
Проводим разложение по элементам третьей строки (выделена красным) так как в ней больше всего нулевых элементов.
Определители, входящие в расписание находим по правилу треугольников
Найденные значения подставляем и посчитываем
На этом примере метод разложения показал свою эффективность и простоту. Стандартные правила оказались бы слишком громоздкими в вычислениях.
Пример 3.
Найти определитель пятого порядка методом разложения
Решение.
Как и в предыдущем задании ищем строку или столбец содержащие максимальное количество нулевых элементов. Проводим расписание определителя
Полученный определитель разложим по четвертой строке
и вычисляем значение
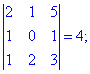
Подставляем в выходной определитель и находим его
Метод разложения определителя по элементам строк или столбцов является самым быстрым при исчислении определителей больших размеров. Вместо громоздких и сложных вычислений он сводит отыскания определителя к большому количеству простых операций, которые под силу каждому.
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
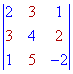
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.