Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 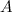
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
Определитель матрицы и его свойства
8 февраля 2018
В этом уроке мы детально рассмотрим несколько ключевые вопросов и определений, благодаря чему вы раз и навсегда разберётесь и с матрицами, и с определителями, и со всеми их свойствами.
Определители — центральное понятие в алгебре матриц. Подобно формулам сокращённого умножения, они будут преследовать вас на протяжении всего курса высшей математики. Поэтому читаем, смотрим и разбираемся досконально.:)
И начнём мы с самого сокровенного — а что такое матрица? И как правильно с ней работать.
Правильная расстановка индексов в матрице
Матрица — это просто таблица, заполненная числами. Нео тут ни при чём.
Одна из ключевых характеристик матрицы — это её размерность, т.е. количество строк и столбцов, из которых она состоит. Обычно говорят, что некая матрица $A$ имеет размер $left[ mtimes n right]$, если в ней имеется $m$ строк и $n$ столбцов. Записывают это так:
[A=left[ mtimes n right]]
Или вот так:
[A=left( {{a}_{ij}} right),quad 1le ile m;quad 1le jle n.]
Бывают и другие обозначения — тут всё зависит от предпочтений лектора/ семинариста/ автора учебника. Но в любом случае со всеми этими $left[ mtimes n right]$ и ${{a}_{ij}}$ возникает одна и та же проблема:
Какой индекс за что отвечает? Сначала идёт номер строки, затем — столбца? Или наоборот?
При чтении лекций и учебников ответ будет казаться очевидным. Но когда на экзамене перед вами — только листик с задачей, можно переволноваться и внезапно запутаться.
Поэтому давайте разберёмся с этим вопросом раз и навсегда. Для начала вспомним обычную систему координат из школьного курса математики:
Помните её? У неё есть начало координат (точка $O=left( 0;0 right)$) оси $x$и $y$, а каждая точка на плоскости однозначно определяется по координатам: $A=left( 1;2 right)$, $B=left( 3;1 right)$ и т.д.
А теперь давайте возьмём эту конструкцию и поставим её рядом с матрицей так, чтобы начало координат находилось в левом верхнем углу. Почему именно там? Да потому что открывая книгу, мы начинаем читать именно с левого верхнего угла страницы — запомнить это легче лёгкого.
Но куда направить оси? Мы направим их так, чтобы вся наша виртуальная «страница» была охвачена этими осями. Правда, для этого придётся повернуть нашу систему координат. Единственно возможный вариант такого расположения:
Теперь всякая клетка матрицы имеет однозначные координаты $x$ и $y$. Например запись ${{a}_{24}}$ означает, что мы обращаемся к элементу с координатами $x=2$ и $y=4$. Размеры матрицы тоже однозначно задаются парой чисел:
Просто всмотритесь в эту картинку внимательно. Поиграйтесь с координатами (особенно когда будете работать с настоящими матрицами и определителями) — и очень скоро поймёте, что даже в самых сложных теоремах и определениях вы прекрасно понимаете, о чём идёт речь.
Разобрались? Что ж, переходим к первому шагу просветления — геометрическому определению определителя.:)
Геометрическое определение
Прежде всего хотел бы отметить, что определитель существует только для квадратных матриц вида $left[ ntimes n right]$. Определитель — это число, которое cчитается по определённым правилам и является одной из характеристик этой матрицы (есть другие характеристики: ранг, собственные вектора, но об этом в других уроках).
Ну и что это за характеристика? Что он означает? Всё просто:
Определитель квадратной матрицы $A=left[ ntimes n right]$ — это объём $n$-мерного параллелепипеда, который образуется, если рассмотреть строки матрицы в качестве векторов, образующих рёбра этого параллелепипеда.
Например, определитель матрицы размера 2×2 — это просто площадь параллелограмма, а для матрицы 3×3 это уже объём 3-мерного параллелепипеда — того самого, который так бесит всех старшеклассников на уроках стереометрии.
На первый взгляд это определение может показаться совершенно неадекватным. Но давайте не будем спешить с выводами — глянем на примеры. На самом деле всё элементарно, Ватсон:
Задача. Найдите определители матриц:
[left| begin{matrix} 1 & 0 \ 0 & 3 \end{matrix} right|quad left| begin{matrix} 1 & -1 \ 2 & 2 \end{matrix} right|quad left| begin{matrix}2 & 0 & 0 \ 1 & 3 & 0 \ 1 & 1 & 4 \end{matrix} right|]
Решение. Первые два определителя имеют размер 2×2. Значит, это просто площади параллелограммов. Начертим их и посчитаем площадь.
Первый параллелограмм построен на векторах ${{v}_{1}}=left( 1;0 right)$ и ${{v}_{2}}=left( 0;3 right)$:
Определитель 2×2 — это площадь параллелограмма Очевидно, это не просто параллелограмм, а вполне себе прямоугольник. Его площадь равна
[S=1cdot 3=3]
Второй параллелограмм построен на векторах ${{v}_{1}}=left( 1;-1 right)$ и ${{v}_{2}}=left( 2;2 right)$. Ну и что с того? Это тоже прямоугольник:
Ещё один определитель 2×2 Стороны этого прямоугольника (по сути — длины векторов) легко считаются по теореме Пифагора:
[begin{align} & left| {{v}_{1}} right|=sqrt{{{1}^{2}}+{{left( -1 right)}^{2}}}=sqrt{2}; \ & left| {{v}_{2}} right|=sqrt{{{2}^{2}}+{{2}^{2}}}=sqrt{8}=2sqrt{2}; \ & S=left| {{v}_{1}} right|cdot left| {{v}_{2}} right|=sqrt{2}cdot 2sqrt{2}=4. \end{align}]
Осталось разобраться с последним определителем — там уже матрица 3×3. Придётся вспоминать стереометрию:
Определитель 3×3 — это объём параллелепипеда Выглядит мозговыносяще, но по факту достаточно вспомнить формулу объёма параллелепипеда:
[V=Scdot h]
где $S$ — площадь основания (в нашем случае это площадь параллелограмма на плоскости $OXY$), $h$ — высота, проведённая к этому основанию (по сути, $z$-координата вектора ${{v}_{3}}$).
Площадь параллелограмма (мы начертили его отдельно) тоже считается легко:
[begin{align} & S=2cdot 3=6; \ & V=Scdot h=6cdot 4=24. \end{align}]
Вот и всё! Записываем ответы.
Ответ: 3; 4; 24.
Небольшое замечание по поводу системы обозначений. Кому-то наверняка не понравится, что я игнорирую «стрелочки» над векторами. Якобы так можно спутать вектор с точкой или ещё с чем.
Но давайте серьёзно: мы с вами уже взрослые мальчики и девочки, поэтому из контекста прекрасно понимаем, когда речь идёт о векторе, а когда — о точке. Стрелки лишь засоряют повествование, и без того под завязку напичканное математическими формулами.
И ещё. В принципе, ничто не мешает рассмотреть и определитель матрицы 1×1 — такая матрица представляет собой просто одну клетку, а число, записанное в этой клетке, и будет определителем. Но тут есть важное замечание:
В отличие от классического объёма, определитель даст нам так называемый «ориентированный объём», т.е. объём с учётом последовательности рассмотрения векторов-строк.
И если вы хотите получить объём в классическом смысле этого слова, придётся взять модуль определителя, но сейчас не стоит париться об этом — всё равно через несколько секунд мы научимся считать любой определитель с любыми знаками, размерами и т.д.:)
Алгебраическое определение
При всей красоте и наглядности геометрического подхода у него есть серьёзный недостаток: он ничего не говорит нам о том, как этот самый определитель считать.
Поэтому сейчас мы разберём альтернативное определение — алгебраическое. Для этого нам потребуется краткая теоретическая подготовка, зато на выходе мы получим инструмент, позволяющий считать в матрицах что и как угодно.
Правда, там появится новая проблема… но обо всём по порядку.
Перестановки и инверсии
Давайте выпишем в строчку числа от 1 до $n$. Получится что-то типа этого:
[1;2;3;4;5;…;n-1;n]
Теперь (чисто по приколу) поменяем парочку чисел местами. Можно поменять соседние:
[1;3;2;4;5;…;n-1;n]
А можно — не особо соседние:
[n;2;3;4;5;…;n-1;1]
И знаете, что? А ничего! В алгебре эта хрень называется перестановкой. И у неё есть куча свойств.
Определение. Перестановка длины $n$ — строка из $n$ различных чисел, записанных в любой последовательности. Обычно рассматриваются первые $n$ натуральных чисел (т.е. как раз числа 1, 2, …, $n$), а затем их перемешивают для получения нужной перестановки.
Обозначаются перестановки так же, как и векторы — просто буквой и последовательным перечислением своих элементов в скобках. Например: $p=left( 1;3;2 right)$ или $p=left( 2;5;1;4;3 right)$. Буква может быть любой, но пусть будет $p$.:)
Далее для простоты изложения будем работать с перестановками длины 5 — они уже достаточно серьёзны для наблюдения всяких подозрительных эффектов, но ещё не настолько суровы для неокрепшего мозга, как перестановки длины 6 и более. Вот примеры таких перестановок:
[begin{align} & {{p}_{1}}=left( 1;2;3;4;5 right) \ & {{p}_{2}}=left( 1;3;2;5;4 right) \ & {{p}_{3}}=left( 5;4;3;2;1 right) \end{align}]
Естественно, перестановку длины $n$ можно рассматривать как функцию, которая определена на множестве $left{ 1;2;…;n right}$ и биективно отображает это множество на себя же. Возвращаясь к только что записанным перестановкам ${{p}_{1}}$, ${{p}_{2}}$ и ${{p}_{3}}$, мы вполне законно можем написать:
[{{p}_{1}}left( 1 right)=1;{{p}_{2}}left( 3 right)=2;{{p}_{3}}left( 2 right)=4;]
Количество различных перестановок длины $n$ всегда ограничено и равно $n!$ — это легко доказуемый факт из комбинаторики. Например, если мы захотим выписать все перестановки длины 5, то мы весьма заколебёмся, поскольку таких перестановок будет
[n!=5!=1cdot 2cdot 3cdot 4cdot 5=120]
Одной из ключевых характеристик всякой перестановки является количество инверсий в ней.
Определение. Инверсия в перестановке $p=left( {{a}_{1}};{{a}_{2}};…;{{a}_{n}} right)$ — всякая пара $left( {{a}_{i}};{{a}_{j}} right)$ такая, что $i lt j$, но ${{a}_{i}} gt {{a}_{j}}$. Проще говоря, инверсия — это когда большее число стоит левее меньшего (не обязательно соседнего).
Мы будем обозначать через $Nleft( p right)$ количество инверсий в перестановке $p$, но будьте готовы встретиться и с другими обозначениями в разных учебниках и у разных авторов — единых стандартов тут нет. Тема инверсий весьма обширна, и ей будет посвящён отдельный урок. Сейчас же наша задача — просто научиться считать их в реальных задачах.
Например, посчитаем количество инверсий в перестановке $p=left( 1;4;5;3;2 right)$:
[left( 4;3 right);left( 4;2 right);left( 5;3 right);left( 5;2 right);left( 3;2 right).]
Таким образом, $Nleft( p right)=5$. Как видите, ничего страшного в этом нет. Сразу скажу: дальше нас будет интересовать не столько само число $Nleft( p right)$, сколько его чётность/ нечётность. И тут мы плавно переходим к ключевому термину сегодняшнего урока.
Что такое определитель
Пусть дана квадратная матрица $A=left[ ntimes n right]$. Тогда:
Определение. Определитель матрицы $A=left[ ntimes n right]$ — это алгебраическая сумма $n!$ слагаемых, составленных следующим образом. Каждое слагаемое — это произведение $n$ элементов матрицы, взятых по одному из каждой строки и каждого столбца, умноженное на (−1) в степени количество инверсий:
[left| A right|=sumlimits_{n!}{{{left( -1 right)}^{Nleft( p right)}}cdot {{a}_{1;pleft( 1 right)}}cdot {{a}_{2;pleft( 2 right)}}cdot …cdot {{a}_{n;pleft( n right)}}}]
Принципиальным моментом при выборе множителей для каждого слагаемого в определителе является тот факт, что никакие два множителя не стоят в одной строчке или в одном столбце.
Благодаря этому можно без ограничения общности считать, что индексы $i$ множителей ${{a}_{i;j}}$ «пробегают» значения 1, …, $n$, а индексы $j$ являются некоторой перестановкой от первых:
[j=pleft( i right),quad i=1,2,…,n]
А когда есть перестановка $p$, мы легко посчитаем инверсии $Nleft( p right)$ — и очередное слагаемое определителя готово.
Естественно, никто не запрещает поменять местами множители в каком-либо слагаемом (или во всех сразу — чего мелочиться-то?), и тогда первые индексы тоже будут представлять собой некоторую перестановку. Но в итоге ничего не поменяется: суммарное количество инверсий в индексах $i$ и $j$ сохраняет чётность при подобных извращениях, что вполне соответствует старому-доброму правилу:
От перестановки множителей произведение чисел не меняется.
Вот только не надо приплетать это правило к умножению матриц — в отличие от умножения чисел, оно не коммутативно. Но это я отвлёкся.:)
Матрица 2×2
Вообще-то можно рассмотреть и матрицу 1×1 — это будет одна клетка, и её определитель, как нетрудно догадаться, равен числу, записанному в этой клетке. Ничего интересного.
Поэтому давайте рассмотрим квадратную матрицу размером 2×2:
[left[ begin{matrix} {{a}_{11}} & {{a}_{12}} \ {{a}_{21}} & {{a}_{22}} \end{matrix} right]]
Поскольку количество строк в ней $n=2$, то определитель будет содержать $n!=2!=1cdot 2=2$ слагаемых. Выпишем их:
[begin{align} & {{left( -1 right)}^{Nleft( 1;2 right)}}cdot {{a}_{11}}cdot {{a}_{22}}={{left( -1 right)}^{0}}cdot {{a}_{11}}cdot {{a}_{22}}={{a}_{11}}{{a}_{22}}; \ & {{left( -1 right)}^{Nleft( 2;1 right)}}cdot {{a}_{12}}cdot {{a}_{21}}={{left( -1 right)}^{1}}cdot {{a}_{12}}cdot {{a}_{21}}={{a}_{12}}{{a}_{21}}. \end{align}]
Очевидно, что в перестановке $left( 1;2 right)$, состоящей из двух элементов, нет инверсий, поэтому $Nleft( 1;2 right)=0$. А вот в перестановке $left( 2;1 right)$ одна инверсия имеется (собственно, 2 < 1), поэтому $Nleft( 2;1 right)=1.$
Итого универсальная формула вычисления определителя для матрицы 2×2 выглядит так:
[left| begin{matrix} {{a}_{11}} & {{a}_{12}} \ {{a}_{21}} & {{a}_{22}} \end{matrix} right|={{a}_{11}}{{a}_{22}}-{{a}_{12}}{{a}_{21}}]
Графически это можно представить как произведение элементов, стоящих на главной диагонали, минус произведение элементов на побочной:
Рассмотрим пару примеров:
Задача. Вычислите определитель:
[left| begin{matrix} 5 & 6 \ 8 & 9 \end{matrix} right|;quad left| begin{matrix} 7 & 12 \ 14 & 1 \end{matrix} right|.]
Решение. Всё считается в одну строчку. Первая матрица:
[5cdot 9-8cdot 6=45-48=-3]
И вторая:
[7cdot 1-14cdot 12=7-168=-161]
Ответ: −3; −161.
Впрочем, это было слишком просто. Давайте рассмотрим матрицы 3×3 — там уже интересно.
Матрица 3×3
Теперь рассмотрим квадратную матрицу размера 3×3:
[left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \end{matrix} right]]
При вычислении её определителя мы получим $3!=1cdot 2cdot 3=6$ слагаемых — ещё не слишком много для паники, но уже достаточно, чтобы начать искать какие-то закономерности. Для начала выпишем все перестановки из трёх элементов и посчитаем инверсии в каждой из них:
[begin{align} & {{p}_{1}}=left( 1;2;3 right)Rightarrow Nleft( {{p}_{1}} right)=Nleft( 1;2;3 right)=0; \ & {{p}_{2}}=left( 1;3;2 right)Rightarrow Nleft( {{p}_{2}} right)=Nleft( 1;3;2 right)=1; \ & {{p}_{3}}=left( 2;1;3 right)Rightarrow Nleft( {{p}_{3}} right)=Nleft( 2;1;3 right)=1; \ & {{p}_{4}}=left( 2;3;1 right)Rightarrow Nleft( {{p}_{4}} right)=Nleft( 2;3;1 right)=2; \ & {{p}_{5}}=left( 3;1;2 right)Rightarrow Nleft( {{p}_{5}} right)=Nleft( 3;1;2 right)=2; \ & {{p}_{6}}=left( 3;2;1 right)Rightarrow Nleft( {{p}_{6}} right)=Nleft( 3;2;1 right)=3. \end{align}]
Как и предполагалось, всего выписано 6 перестановок ${{p}_{1}}$, … ${{p}_{6}}$ (естественно, можно было бы выписать их в другой последовательности — суть от этого не изменится), а количество инверсий в них меняется от 0 до 3.
В общем, у нас будет три слагаемых с «плюсом» (там, где $Nleft( p right)$ — чётное) и ещё три с «минусом». А в целом определитель будет считаться по формуле:
[left| begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \end{matrix} right|=begin{matrix} {{a}_{11}}{{a}_{22}}{{a}_{33}}+{{a}_{12}}{{a}_{23}}{{a}_{31}}+{{a}_{13}}{{a}_{21}}{{a}_{32}}- \ -{{a}_{13}}{{a}_{22}}{{a}_{31}}-{{a}_{12}}{{a}_{21}}{{a}_{33}}-{{a}_{11}}{{a}_{23}}{{a}_{32}} \end{matrix}]
Вот только не надо сейчас садиться и яростно зубрить все эти индексы! Вместо непонятных цифр лучше запомните следующее мнемоническое правило:
Правило треугольника. Для нахождения определителя матрицы 3×3 нужно сложить три произведения элементов, стоящих на главной диагонали и в вершинах равнобедренных треугольников со стороной, параллельной этой диагонали, а затем вычесть такие же три произведения, но на побочной диагонали. Схематически это выглядит так:
Определитель матрицы 3×3: правило треугольников
Именно эти треугольники (или пентаграммы — кому как больше нравится) любят рисовать во всяких учебниках и методичках по алгебре. Впрочем, не будем о грустном. Давайте лучше посчитаем один такой определитель — для разминки перед настоящей жестью.:)
Задача. Вычислите определитель:
[left| begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 1 \end{matrix} right|]
Решение. Работаем по правилу треугольников. Сначала посчитаем три слагаемых, составленных из элементов на главной диагонали и параллельно ей:
[begin{align} & 1cdot 5cdot 1+2cdot 6cdot 7+3cdot 4cdot 8= \ & =5+84+96=185 \end{align}]
Теперь разбираемся с побочной диагональю:
[begin{align} & 3cdot 5cdot 7+2cdot 4cdot 1+1cdot 6cdot 8= \ & =105+8+48=161 \end{align}]
Осталось лишь вычесть из первого числа второе — и мы получим ответ:
[185-161=24]
Вот и всё!
Ответ: 24.
Тем не менее, определители матриц 3×3 — это ещё не вершина мастерства. Самое интересное ждёт нас дальше.:)
Общая схема вычисления определителей
Как мы знаем, с ростом размерности матрицы $n$ количество слагаемых в определителе составляет $n!$ и быстро растёт. Всё-таки факториал — это вам не хрен собачий довольно быстро растущая функция.
Уже для матриц 4×4 считать определители напролом (т.е. через перестановки) становится как-то не оч. Про 5×5 и более вообще молчу. Поэтому к делу подключаются некоторые свойства определителя, но для их понимания нужна небольшая теоретическая подготовка.
Готовы? Поехали!
Что такое минор матрицы
Пусть дана произвольная матрица $A=left[ mtimes n right]$. Заметьте: не обязательно квадратная. В отличие от определителей, миноры — это такие няшки, которые существуют не только в суровых квадратных матрицах. Выберем в этой матрице несколько (например, $k$) строк и столбцов, причём $1le kle m$ и $1le kle n$. Тогда:
Определение. Минор порядка $k$ — определитель квадратной матрицы, возникающей на пересечении выбранных $k$ столбцов и строк. Также минором мы будем называть и саму эту новую матрицу.
Обозначается такой минор ${{M}_{k}}$. Естественно, у одной матрицы может быть целая куча миноров порядка $k$. Вот пример минора порядка 2 для матрицы $left[ 5times 6 right]$:
Выбор $k = 2$ столбцов и строк для формирования минора
Совершенно необязательно, чтобы выбранные строки и столбцы стояли рядом, как в рассмотренном примере. Главное, чтобы количество выбранных строк и столбцов было одинаковым (это и есть число $k$).
Есть и другое определение. Возможно, кому-то оно больше придётся по душе:
Определение. Пусть дана прямоугольная матрица $A=left[ mtimes n right]$. Если после вычеркивания в ней одного или нескольких столбцов и одной или нескольких строк образуется квадратная матрица размера $left[ ktimes k right]$, то её определитель — это и есть минор ${{M}_{k}}$. Саму матрицу мы тоже иногда будем называть минором — это будет ясно из контекста.
Как говорил мой кот, иногда лучше один раз навернуться с 11-го этажа есть корм, чем мяукать, сидя на балконе.
Пример. Пусть дана матрица
[A=left[ begin{matrix} begin{matrix} 1 \ 2 \ 3 \end{matrix} & begin{matrix} 7 \ 4 \ 0 \end{matrix} & begin{matrix} 9 \ 5 \ 6 \end{matrix} & begin{matrix} 0 \ 3 \ 1 \end{matrix} \end{matrix} right]]
Выбирая строку 1 и столбец 2, получаем минор первого порядка:
[{{M}_{1}}=left| 7 right|=7]
Выбирая строки 2, 3 и столбцы 3, 4, получаем минор второго порядка:
[{{M}_{2}}=left| begin{matrix} 5 & 3 \ 6 & 1 \end{matrix} right|=5-18=-13]
А если выбрать все три строки, а также столбцы 1, 2, 4, будет минор третьего порядка:
[{{M}_{3}}=left| begin{matrix} 1 & 7 & 0 \ 2 & 4 & 3 \ 3 & 0 & 1 \end{matrix} right|]
Считать этот определитель мне уже в лом. Но он равен 53.:)
Читателю не составит труда найти и другие миноры порядков 1, 2 или 3. Поэтому идём дальше.
Алгебраические дополнения
«Ну ok, и что дают нам эти миньоны миноры?» — наверняка спросите вы. Сами по себе — ничего. Но в квадратных матрицах у каждого минора появляется «компаньон» — дополнительный минор, а также алгебраическое дополнение. И вместе эти два ушлёпка позволят нам щёлкать определители как орешки.
Определение. Пусть дана квадратная матрица $A=left[ ntimes n right]$, в которой выбран минор ${{M}_{k}}$. Тогда дополнительный минор для минора ${{M}_{k}}$ — это кусок исходной матрицы $A$, который останется при вычёркивании всех строк и столбцов, задействованных при составлении минора ${{M}_{k}}$:
Дополнительный минор к минору ${{M}_{2}}$ Уточним один момент: дополнительный минор — это не просто «кусок матрицы», а определитель этого куска.
Обозначаются дополнительные миноры с помощью «звёздочки»: $M_{k}^{*}$:
[M_{k}^{*}=left| Anabla {{M}_{k}} right|]
где операция $Anabla {{M}_{k}}$ буквально означает «вычеркнуть из $A$ строки и столбцы, входящие в ${{M}_{k}}$». Эта операция не является общепринятой в математике — я её сам только что придумал для красоты повествования.:)
Дополнительные миноры редко используются сами по себе. Они являются частью более сложной конструкции — алгебраического дополнения.
Определение. Алгебраическое дополнение минора ${{M}_{k}}$ — это дополнительный минор $M_{k}^{*}$, умноженный на величину ${{left( -1 right)}^{S}}$, где $S$ — сумма номеров всех строк и столбцов, задействованных в исходном миноре ${{M}_{k}}$.
Как правило, алгебраическое дополнение минора ${{M}_{k}}$ обозначается через ${{A}_{k}}$. Поэтому:
[{{A}_{k}}={{left( -1 right)}^{S}}cdot M_{k}^{*}]
Сложно? На первый взгляд — да. Но это не точно. Потому что на самом деле всё легко. Рассмотрим пример:
Пример. Дана матрица 4×4:
[A=left[ begin{matrix} 1 & 2 & 3 & 4 \ 5 & 6 & 7 & 8 \ 9 & 10 & 11 & 12 \ 13 & 14 & 15 & 16 \end{matrix} right]]
Выберем минор второго порядка
[{{M}_{2}}=left| begin{matrix} 3 & 4 \ 15 & 16 \end{matrix} right|]
Капитан Очевидность как бы намекает нам, что при составлении этого минора были задействованы строки 1 и 4, а также столбцы 3 и 4. Вычёркиваем их — получим дополнительный минор:
[M_{2}^{*}=left| begin{matrix} 5 & 6 \ 9 & 10 \end{matrix} right|=50-54=-4]
Осталось найти число $S$ и получить алгебраическое дополнение. Поскольку мы знаем номера задействованных строк (1 и 4) и столбцов (3 и 4), всё просто:
[begin{align} & S=1+4+3+4=12; \ & {{A}_{2}}={{left( -1 right)}^{S}}cdot M_{2}^{*}={{left( -1 right)}^{12}}cdot left( -4 right)=-4end{align}]
Ответ: ${{A}_{2}}=-4$
Вот и всё! По сути, всё различие между дополнительным минором и алгебраическим дополнением — только в минусе спереди, да и то не всегда.
Наша задача сейчас — научиться быстро считать алгебраические дополнения, потому что они являются составной частью «Теоремы, Которую Нельзя Называть». Но мы всё же назовём. Встречайте:
Теорема Лапласа
И вот мы пришли к тому, зачем, собственно, все эти миноры и алгебраические дополнения были нужны.
Теорема Лапласа о разложении определителя. Пусть в матрице размера $left[ ntimes n right]$ выбрано $k$ строк (столбцов), причём $1le kle n-1$. Тогда определитель этой матрицы равен сумме всех произведений миноров порядка $k$, содержащихся в выбранных строках (столбцах), на их алгебраические дополнения:
[left| A right|=sum{{{M}_{k}}cdot {{A}_{k}}}]
Причём таких слагаемых будет ровно $C_{n}^{k}$.
Ладно, ладно: про $C_{n}^{k}$ — это я уже понтуюсь, в оригинальной теореме Лапласа ничего такого не было. Но комбинаторику никто не отменял, и буквально беглый взгляд на условие позволит вам самостоятельно убедиться, что слагаемых будет именно столько.:)
Мы не будем её доказывать, хоть это и не представляет особой трудности — все выкладки сводятся к старым-добрым перестановкам и чётности/ нечётности инверсий. Тем не менее, доказательство будет представлено в отдельном параграфе, а сегодня у нас сугубо практический урок.
Поэтому переходим к частному случаю этой теоремы, когда миноры представляют собой отдельные клетки матрицы.
Разложение определителя по строке и столбцу
То, о чём сейчас пойдёт речь — как раз и есть основной инструмент работы с определителями, ради которого затевались вся эта дичь с перестановками, минорами и алгебраическими дополнениями.
Читайте и наслаждайтесь:
Следствие из Теоремы Лапласа (разложение определителя по строке/столбцу). Пусть в матрице размера $left[ ntimes n right]$ выбрана одна строка. Минорами в этой строке будут $n$ отдельных клеток:
[{{M}_{1}}={{a}_{ij}},quad j=1,…,n]
Дополнительные миноры тоже легко считаются: просто берём исходную матрицу и вычёркиваем строку и столбец, содержащие ${{a}_{ij}}$. Назовём такие миноры $M_{ij}^{*}$.
Для алгебраического дополнения ещё нужно число $S$, но в случае с минором порядка 1 это просто сумма «координат» клетки ${{a}_{ij}}$:
[S=i+j]
И тогда исходный определитель можно расписать через ${{a}_{ij}}$ и $M_{ij}^{*}$ согласно теореме Лапласа:
[left| A right|=sumlimits_{j=1}^{n}{{{a}_{ij}}cdot {{left( -1 right)}^{i+j}}cdot {{M}_{ij}}}]
Это и есть формула разложения определителя по строке. Но то же верно и для столбцов.
Из этого следствия можно сразу сформулировать несколько выводов:
- Эта схема одинаково хорошо работает как для строк, так и для столбцов. На самом деле чаще всего разложение будет идти именно по столбцам, нежели по строкам.
- Количество слагаемых в разложении всегда ровно $n$. Это существенно меньше $C_{n}^{k}$ и уж тем более $n!$.
- Вместо одного определителя $left[ ntimes n right]$ придётся считать несколько определителей размера на единицу меньше: $left[ left( n-1 right)times left( n-1 right) right]$.
Последний факт особенно важен. Например, вместо зверского определителя 4×4 теперь достаточно будет посчитать несколько определителей 3×3 — с ними мы уж как-нибудь справимся.:)
Что ж, попробуем посчитать одну такую задачку?
Задача. Найдите определитель:
[left| begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ 7 & 8 & 9 \end{matrix} right|]
Решение. Разложим этот определитель по первой строке:
[begin{align} left| A right|=1cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} 5 & 6 \ 8 & 9 \end{matrix} right|+ & \ 2cdot {{left( -1 right)}^{1+2}}cdot left| begin{matrix} 4 & 6 \ 7 & 9 \end{matrix} right|+ & \ 3cdot {{left( -1 right)}^{1+3}}cdot left| begin{matrix} 4 & 5 \ 7 & 8 \end{matrix} right|= & \end{align}]
[begin{align} & =1cdot left( 45-48 right)-2cdot left( 36-42 right)+3cdot left( 32-35 right)= \ & =1cdot left( -3 right)-2cdot left( -6 right)+3cdot left( -3 right)=0. \end{align}]
Ответ: 0.
Задача. Найдите определитель:
[left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|]
Решение. Для разнообразия давайте в этот раз работать со столбцами. Например, в последнем столбце присутствуют сразу два нуля — очевидно, это значительно сократит вычисления. Сейчас увидите почему.
Итак, раскладываем определитель по четвёртому столбцу:
[begin{align} left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|=0cdot {{left( -1 right)}^{1+4}}cdot left| begin{matrix} 1 & 0 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|+ & \ +1cdot {{left( -1 right)}^{2+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|+ & \ +1cdot {{left( -1 right)}^{3+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 1 \end{matrix} right|+ & \ +0cdot {{left( -1 right)}^{4+4}}cdot left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end{matrix} right| & \end{align}]
И тут — о, чудо! — два слагаемых сразу улетают коту под хвост, поскольку в них есть множитель «0». Остаётся ещё два определителя 3×3, с которыми мы легко разберёмся:
[begin{align} & left| begin{matrix} 0 & 1 & 1 \ 1 & 1 & 0 \ 1 & 1 & 1 \end{matrix} right|=0+0+1-1-1-0=-1; \ & left| begin{matrix} 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 1 \end{matrix} right|=0+1+1-0-0-1=1. \end{align}]
Возвращаемся к исходнику и находим ответ:
[left| begin{matrix} 0 & 1 & 1 & 0 \ 1 & 0 & 1 & 1 \ 1 & 1 & 0 & 1 \ 1 & 1 & 1 & 0 \end{matrix} right|=1cdot left( -1 right)+left( -1 right)cdot 1=-2]
Ну вот и всё. И никаких 4! = 24 слагаемых считать не пришлось.:)
Ответ: −2
Основные свойства определителя
В последней задаче мы видели, как наличие нулей в строках (столбцах) матрицы резко упрощает разложение определителя и вообще все вычисления. Возникает естественный вопрос: а нельзя ли сделать так, чтобы эти нули появились даже в той матрице, где их изначально не было?
Ответ однозначен: можно. И здесь нам на помощь приходят свойства определителя:
- Если поменять две строчки (столбца) местами, определитель поменяет знак;
- Если одну строку (столбец) умножить на число $k$, то весь определитель тоже умножится на число $k$;
- Если взять одну строку и прибавить (вычесть) её сколько угодно раз из другой, определитель не изменится;
- Если две строки определителя одинаковы, либо пропорциональны, либо одна из строк заполнена нулями, то весь определитель равен нулю;
- Все указанные выше свойства верны и для столбцов.
- При транспонировании матрицы определитель не меняется;
- Определитель произведения матриц равен произведению определителей.
Особую ценность представляет третье свойство: мы можем вычитать из одной строки (столбца) другую до тех пор, пока в нужных местах не появятся нули.
Чаще всего расчёты сводится к тому, чтобы «обнулить» весь столбец везде, кроме одного элемента, а затем разложить определитель по этому столбцу, получив матрицу размером на 1 меньше.
Давайте посмотрим, как это работает на практике:
Задача. Найдите определитель:
[left| begin{matrix} 1 & 2 & 3 & 4 \ 4 & 1 & 2 & 3 \ 3 & 4 & 1 & 2 \ 2 & 3 & 4 & 1 \end{matrix} right|]
Решение. Нулей тут как бы вообще не наблюдается, поэтому можно «долбить» по любой строке или столбцу — объём вычислений будет примерно одинаковым. Давайте не будем мелочиться и «обнулим» первый столбец: в нём уже есть клетка с единицей, поэтому просто возьмём первую строчку и вычтем её 4 раза из второй, 3 раза из третьей и 2 раза из последней.
В результате мы получим новую матрицу, но её определитель будет тем же:
[begin{matrix} left| begin{matrix} 1 & 2 & 3 & 4 \ 4 & 1 & 2 & 3 \ 3 & 4 & 1 & 2 \ 2 & 3 & 4 & 1 \end{matrix} right|begin{matrix} downarrow \ -4 \ -3 \ -2 \end{matrix}= \ =left| begin{matrix} 1 & 2 & 3 & 4 \ 4-4cdot 1 & 1-4cdot 2 & 2-4cdot 3 & 3-4cdot 4 \ 3-3cdot 1 & 4-3cdot 2 & 1-3cdot 3 & 2-3cdot 4 \ 2-2cdot 1 & 3-2cdot 2 & 4-2cdot 3 & 1-2cdot 4 \end{matrix} right|= \ =left| begin{matrix} 1 & 2 & 3 & 4 \ 0 & -7 & -10 & -13 \ 0 & -2 & -8 & -10 \ 0 & -1 & -2 & -7 \end{matrix} right| \end{matrix}]
Теперь с невозмутимостью Пятачка раскладываем этот определитель по первому столбцу:
[begin{matrix} 1cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} -7 & -10 & -13 \ -2 & -8 & -10 \ -1 & -2 & -7 \end{matrix} right|+0cdot {{left( -1 right)}^{2+1}}cdot left| … right|+ \ +0cdot {{left( -1 right)}^{3+1}}cdot left| … right|+0cdot {{left( -1 right)}^{4+1}}cdot left| … right| \end{matrix}]
Понятно, что «выживет» только первое слагаемое — в остальных я даже определители не выписывал, поскольку они всё равно умножаются на ноль. Коэффициент перед определителем равен единице, т.е. его можно не записывать.
Зато можно вынести «минусы» из всех трёх строк определителя. По сути, мы трижды вынесли множитель (−1):
[left| begin{matrix} -7 & -10 & -13 \ -2 & -8 & -10 \ -1 & -2 & -7 \end{matrix} right|=cdot left| begin{matrix} 7 & 10 & 13 \ 2 & 8 & 10 \ 1 & 2 & 7 \end{matrix} right|]
Получили мелкий определитель 3×3, который уже можно посчитать по правилу треугольников. Но мы попробуем разложить и его по первому столбцу — благо в последней строчке гордо стоит единица:
[begin{align} & left( -1 right)cdot left| begin{matrix} 7 & 10 & 13 \ 2 & 8 & 10 \ 1 & 2 & 7 \end{matrix} right|begin{matrix} -7 \ -2 \ uparrow \end{matrix}=left( -1 right)cdot left| begin{matrix} 0 & -4 & -36 \ 0 & 4 & -4 \ 1 & 2 & 7 \end{matrix} right|= \ & =cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right|=left( -1 right)cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right| \end{align}]
Можно, конечно, ещё поприкалываться и разложить матрицу 2×2 по строке (столбцу), но мы же с вами адекватны, поэтому просто посчитаем ответ:
[left( -1 right)cdot left| begin{matrix} -4 & -36 \ 4 & -4 \end{matrix} right|=left( -1 right)cdot left( 16+144 right)=-160]
Вот так и разбиваются мечты. Всего-то −160 в ответе.:)
Ответ: −160.
Парочка замечаний перед тем, как мы перейдём к последней задаче:
- Исходная матрица была симметрична относительно побочной диагонали. Все миноры в разложении тоже симметричны относительно той же побочной диагонали.
- Строго говоря, мы могли вообще ничего не раскладывать, а просто привести матрицу к верхнетреугольному виду, когда под главной диагональю стоят сплошные нули. Тогда (в точном соответствии с геометрической интерпретацией, кстати) определитель равен произведению ${{a}_{ii}}$ — чисел на главной диагонали.
Идём дальше. Последняя задача в сегодняшнем уроке.
Задача. Найдите определитель:
[left| begin{matrix} 1 & 1 & 1 & 1 \ 2 & 4 & 8 & 16 \ 3 & 9 & 27 & 81 \ 5 & 25 & 125 & 625 \end{matrix} right|]
Решение. Ну, тут первая строка прямо-таки напрашивается на «обнуление». Берём первый столбец и вычитаем ровно один раз из всех остальных:
[begin{align} & left| begin{matrix} 1 & 1 & 1 & 1 \ 2 & 4 & 8 & 16 \ 3 & 9 & 27 & 81 \ 5 & 25 & 125 & 625 \end{matrix} right|= \ & =left| begin{matrix} 1 & 1-1 & 1-1 & 1-1 \ 2 & 4-2 & 8-2 & 16-2 \ 3 & 9-3 & 27-3 & 81-3 \ 5 & 25-5 & 125-5 & 625-5 \end{matrix} right|= \ & =left| begin{matrix} 1 & 0 & 0 & 0 \ 2 & 2 & 6 & 14 \ 3 & 6 & 24 & 78 \ 5 & 20 & 120 & 620 \end{matrix} right| \end{align}]
Раскладываем по первой строке, а затем выносим общие множители из оставшихся строк:
[cdot left| begin{matrix} 2 & 6 & 14 \ 6 & 24 & 78 \ 20 & 120 & 620 \end{matrix} right|=cdot left| begin{matrix} 1 & 3 & 7 \ 1 & 4 & 13 \ 1 & 6 & 31 \end{matrix} right|]
Снова наблюдаем «красивые» числа, но уже в первом столбце — раскладываем определитель по нему:
[begin{align} & 240cdot left| begin{matrix} 1 & 3 & 7 \ 1 & 4 & 13 \ 1 & 6 & 31 \end{matrix} right|begin{matrix} downarrow \ -1 \ -1 \end{matrix}=240cdot left| begin{matrix} 1 & 3 & 7 \ 0 & 1 & 6 \ 0 & 3 & 24 \end{matrix} right|= \ & =240cdot {{left( -1 right)}^{1+1}}cdot left| begin{matrix} 1 & 6 \ 3 & 24 \end{matrix} right|= \ & =240cdot 1cdot left( 24-18 right)=1440 \end{align}]
Порядок. Задача решена.
Ответ: 1440
Всё. Хорош читать этот бред.:)
Смотрите также:
- Обратная матрица
- Умножение матриц
- Геометрическая вероятность
- Решение задач B12: №448—455
- Задачи на проценты: формула, упрощающая вычисления
- Задача B4 про три дороги — стандартная задача на движение
Мы уже знакомы с понятием определителя матрицы. Также мы рассмотрели правила вычисления детерминантов (определителей) первого и второго порядка. Познакомимся с различными вариантами нахождения определителей третьего порядка.
Вычисление определителей по правилу треугольника
Схематически раскрытие определителя по этому правилу выглядит так:
Согласно рисункам №1 и №2 мы перемножаем элементы, соединенные прямыми. Произведения элементов будут иметь определенные знаки: для рисунка 1 — «+», для рисунка 2 — «-».
| Произведения, которые берутся со знаком «+» | Произведения, которые берутся со знаком «-» |
|---|---|
| a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33} | a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31} |
| a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31} | a12⋅a33⋅a21a_{12}cdot a_{33}cdot a_{21} |
| a13⋅a32⋅a21a_{13} cdot a_{32} cdot a_{21} | a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32} |
На рисунке 1 мы видим равнобедренные треугольники с основаниями, параллельными главной диагонали; на рисунке 2 — равнобедренные треугольники с основаниями, параллельными второй (побочной) диагонали. Поэтому данное правило имеет такое название.
Определитель может быть вычислен по формуле:
∣a11a12a13a21a22a23a31a32a33∣=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=
=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a32⋅a21−a13⋅a22⋅a31−a12⋅a33⋅a21−a11⋅a23⋅a32=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{32}cdot a_{21}-a_{13}cdot a_{22}cdot a_{31}-a_{12}cdot a_{33}cdot a_{21}-a_{11}cdot a_{23}cdot a_{32}.
Примеры
Рассмотрим примеры нахождения определителя по правилу треугольника.
Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу треугольника.
По правилу треугольника определитель третьего порядка равен:
∣925148637∣=9⋅4⋅7+2⋅8⋅6+5⋅3⋅1−5⋅4⋅6−2⋅7⋅1−9⋅8⋅3=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=9cdot4cdot7+2cdot8cdot6+5cdot3cdot1-5cdot4cdot6-2cdot7cdot1-9cdot8cdot3=
=252+96+15−120−14−216=13=252+96+15-120-14-216=13.
Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу треугольника.
Искомый определитель третьего порядка равен:
∣21−46−3510−1∣=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=
=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅0⋅6−(−4)⋅(−3)⋅1−1⋅(−1)⋅6−2⋅5⋅0=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot0cdot6-(-4)cdot(-3)cdot1-1cdot(-1)cdot6-2cdot5cdot0=6+5-12+6=5.
При вычислении определителей таким способом можно легко совершить ошибку из-за невнимательности. Чтобы избежать таких ошибок существует второй способ, называемый правилом Саррюса, или способом «параллельных полосок».
Вычисление определителей по правилу Саррюса
Правило Саррюса также именуют способом присоединения двух строк/столбцов или правилом параллельных полосок.
Основная идея этого правила состоит в приписывании первого и второго столбца справа от определителя.
Вычисления будем производить по следующей схеме:
Перемножаем элементы, соединенные прямыми. Данные произведения берем со знаком «+», если диагональ, на которой они стоят, является главной или параллельной ей; со знаком «-», если она является второй (побочной) или параллельной ей.
| Произведения, которые берутся со знаком «+» | Произведения, которые берутся со знаком «-» |
|---|---|
| a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33} | a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31} |
| a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31} | a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32} |
| a13⋅a21⋅a32a_{13} cdot a_{21} cdot a_{32} | a12⋅a21⋅a33a_{12}cdot a_{21}cdot a_{33} |
В общем виде вычисление по правилу Саррюса можно записать следующим образом:
∣a11a12a13a21a22a23a31a32a33∣=∣a11a12a13a21a22a23a31a32a33∣a11a12a21a22a31a32=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}begin{matrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}end{matrix}=
=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a21⋅a32−a13⋅a22⋅a31−a11⋅a23⋅a32−a12⋅a21⋅a33=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{21}cdot a_{32}-a_{13}cdot a_{22}cdot a_{31}-a_{11}cdot a_{23}cdot a_{32}-a_{12}cdot a_{21}cdot a_{33}.
Сравнивая эти два способа вычисления определителей, видим одинаковые множители, которые во втором случае немного переставлены местами.
Возможность допустить ошибку, вычисляя определитель по правилу Саррюса, намного меньше.
Примеры
Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу Саррюса.
Приписываем два первых столбца справа от определителя и вычисляем его:
∣925148637∣921463=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}begin{matrix}9&2\1&4\6&3end{matrix}=
=9⋅4⋅7+2⋅8⋅6+5⋅1⋅3−5⋅4⋅6−9⋅8⋅3−2⋅1⋅7=252+96+15−120−216−14=13=9cdot4cdot7+2cdot8cdot6+5cdot1cdot3-5cdot4cdot6-9cdot8cdot3-2cdot1cdot7=252+96+15-120-216-14=13.
Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу Саррюса.
Приписываем два первых столбца справа от определителя и вычисляем его:
∣21−46−3510−1∣216−310=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}begin{matrix}2&1\6&-3\1&0end{matrix}=
=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅6⋅0−(−4)⋅(−3)⋅1−2⋅5⋅0−1⋅6⋅(−1)=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot6cdot0-(-4)cdot(-3)cdot1-2cdot5cdot0-1cdot6cdot(-1)=6+5-12+6=5.
Существует еще одна вариация правила Саррюса. Она состоит в приписывании первой и второй строки снизу от определителя. Вычисления производятся аналогично.
Минор и алгебраическое дополнение
Прежде чем перейти к рассмотрению еще одного способа вычисления определителей 3-го порядка разберем 2 понятия: минор, алгебраическое дополнение.
Минор
Минором MijM_{ij} к элементу aija_{ij} определителя n-го порядка называется определитель (n−1)(n-1)-го порядка, который получается из исходного определителя вычеркиванием ii-той строки и jj-того столбца.
Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M11M_{11} получается вычеркиванием 1-й строки и 1-го столбца, M23M_{23} — вычеркиванием 2-й строки и 3-го столбца.
Алгоритм нахождения миноров:
- вычеркиваем ii-ю строку;
- вычеркиваем jj-й столбец;
- записываем определитель, который получили в результате действий 1 и 2.
Примеры
Найти миноры матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.
M11=∣925148637∣=∣4837∣=4⋅7−3⋅8=28−24=4M_{11}=begin{vmatrix}color{green}9&color{green}2&color{green}5\color{green}1&4&8\color{green}6&3&7end{vmatrix}=begin{vmatrix}4&8\3&7end{vmatrix}=4cdot7-3cdot8=28-24=4,
M12=∣925148637∣=∣1867∣=1⋅7−6⋅8=7−48=−41M_{12}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&color{green}4&8\6&color{green}3&7end{vmatrix}=begin{vmatrix}1&8\6&7end{vmatrix}=1cdot7-6cdot8=7-48=-41,
M13=∣925148637∣=∣1463∣=1⋅3−6⋅4=3−24=−21M_{13}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}1&4\6&3end{vmatrix}=1cdot3-6cdot4=3-24=-21,
M21=∣925148637∣=∣2537∣=2⋅7−3⋅5=14−15=−1M_{21}=begin{vmatrix}color{green}9&2&5\color{green}1&color{green}4&color{green}8\color{green}6&3&7end{vmatrix}=begin{vmatrix}2&5\3&7end{vmatrix}=2cdot7-3cdot5=14-15=-1,
M22=∣925148637∣=∣9567∣=9⋅7−6⋅5=63−30=33M_{22}=begin{vmatrix}9&color{green}2&5\color{green}1&color{green}4&color{green}8\6&color{green}3&7end{vmatrix}=begin{vmatrix}9&5\6&7end{vmatrix}=9cdot7-6cdot5=63-30=33,
M23=∣925148637∣=∣9263∣=9⋅3−6⋅2=27−12=15M_{23}=begin{vmatrix}9&2&color{green}5\color{green}1&color{green}4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}9&2\6&3end{vmatrix}=9cdot3-6cdot2=27-12=15,
M31=∣925148637∣=∣2548∣=2⋅8−4⋅5=16−20=−4M_{31}=begin{vmatrix}color{green}9&2&5\color{green}1&4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}2&5\4&8end{vmatrix}=2cdot8-4cdot5=16-20=-4,
M32=∣925148637∣=∣9518∣=9⋅8−1⋅5=72−5=67M_{32}=begin{vmatrix}9&color{green}2&5\1&color{green}4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&5\1&8end{vmatrix}=9cdot8-1cdot5=72-5=67,
M33=∣925148637∣=∣9214∣=9⋅4−1⋅2=36−2=34M_{33}=begin{vmatrix}9&2&color{green}5\1&4&color{green}8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&2\1&4end{vmatrix}=9cdot4-1cdot2=36-2=34.
Найти миноры матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.
M11=∣21−46−3510−1∣=∣−350−1∣=(−3)⋅(−1)−0⋅5=3−0=3M_{11}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\color{green}6&-3&5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}-3&5\0&-1end{vmatrix}=(-3)cdot(-1)-0cdot5=3-0=3,
M12=∣21−46−3510−1∣=∣651−1∣=6⋅(−1)−1⋅5=−6−5=−11M_{12}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&color{green}-3&5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}6&5\1&-1end{vmatrix}=6cdot(-1)-1cdot5=-6-5=-11,
M13=∣21−46−3510−1∣=∣6−310∣=6⋅0−1⋅(−3)=0+3=3M_{13}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}6&-3\1&0end{vmatrix}=6cdot0-1cdot(-3)=0+3=3,
M21=∣21−46−3510−1∣=∣1−40−1∣=1⋅(−1)−0⋅(−4)=−1−0=−1M_{21}=begin{vmatrix}color{green}2&1&-4\color{green}6&color{green}-3&color{green}5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}1&-4\0&-1end{vmatrix}=1cdot(-1)-0cdot(-4)=-1-0=-1,
M22=∣21−46−3510−1∣=∣2−41−1∣=2⋅(−1)−1⋅(−4)=−2+4=2M_{22}=begin{vmatrix}2&color{green}1&-4\color{green}6&color{green}-3&color{green}5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}2&-4\1&-1end{vmatrix}=2cdot(-1)-1cdot(-4)=-2+4=2,
M23=∣21−46−3510−1∣=∣2110∣=2⋅0−1⋅1=0−1=−1M_{23}=begin{vmatrix}2&1&color{green}-4\color{green}6&color{green}-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\1&0end{vmatrix}=2cdot0-1cdot1=0-1=-1,
M31=∣21−46−3510−1∣=∣1−4−35∣=1⋅5−(−3)⋅(−4)=5−12=−7M_{31}=begin{vmatrix}color{green}2&1&-4\color{green}6&-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}
1&-4\-3&5end{vmatrix}=1cdot5-(-3)cdot(-4)=5-12=-7,
M32=∣21−46−3510−1∣=∣2−465∣=2⋅5−6⋅(−4)=10+24=34M_{32}=begin{vmatrix}2&color{green}1&-4\6&color{green}-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&-4\6&5end{vmatrix}=2cdot5-6cdot(-4)=10+24=34,
M33=∣21−46−3510−1∣=∣216−3∣=2⋅(−3)−6⋅1=−6−6=−12M_{33}=begin{vmatrix}2&1&color{green}-4\6&-3&color{green}5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\6&-3end{vmatrix}=2cdot(-3)-6cdot1=-6-6=-12.
Алгебраическое дополнение
Алгебраическим дополнением AijA_{ij} к элементу aija_{ij} определителя nn-го порядка называется число Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij},
где ii, jj — соответствующие строка и столбец,
MijM_{ij} — минор к элементу aija_{ij}.
Алгоритм нахождения алгебраических дополнений:
- найти сумму номеров строки (i)(i) и столбца (j)(j);
- найти минор MijM_{ij} по алгоритму нахождения миноров, который представлен выше;
- подставить значения, полученные на шагах 1 и 2, в формулу Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}.
Примеры
Найти алгебраические дополнения матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.
A11=(−1)1+1⋅M11=(−1)2⋅∣4837∣=4A_{11}=(-1)^{1+1}cdot M_{11}= (-1)^{2}cdotbegin{vmatrix}4&8\3&7end{vmatrix}=4,
A12=(−1)1+2⋅M12=(−1)3⋅∣1867∣=41A_{12}=(-1)^{1+2}cdot M_{12}= (-1)^{3}cdotbegin{vmatrix}1&8\6&7end{vmatrix}=41,
A13=(−1)1+3⋅M13=(−1)4⋅∣1463∣=−21A_{13}=(-1)^{1+3}cdot M_{13}= (-1)^{4}cdotbegin{vmatrix}1&4\6&3end{vmatrix}=-21,
A21=(−1)2+1⋅M21=(−1)3⋅∣2537∣=1A_{21}=(-1)^{2+1}cdot M_{21}= (-1)^{3}cdotbegin{vmatrix}2&5\3&7end{vmatrix}=1,
A22=(−1)2+2⋅M22=(−1)4⋅∣9567∣=33A_{22}=(-1)^{2+2}cdot M_{22}= (-1)^{4}cdotbegin{vmatrix}9&5\6&7end{vmatrix}=33,
A23=(−1)2+3⋅M23=(−1)5⋅∣9263∣=−15A_{23}=(-1)^{2+3}cdot M_{23}= (-1)^{5}cdotbegin{vmatrix}9&2\6&3end{vmatrix}=-15,
A31=(−1)3+1⋅M31=(−1)4⋅∣2548∣=−4A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}2&5\4&8end{vmatrix}=-4,
A32=(−1)3+2⋅M32=(−1)5⋅∣9518∣=−67A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}9&5\1&8end{vmatrix}=-67,
A33=(−1)3+3⋅M33=(−1)6⋅∣9214∣=34A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}9&2\1&4end{vmatrix}=34.
Найти алгебраические дополнения матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.
A11=(−1)1+1⋅M11=(−1)2⋅∣−350−1∣=3A_{11}=(-1)^{1+1}cdot M_{11}=(-1)^{2}cdotbegin{vmatrix}-3&5\0&-1end{vmatrix}=3,
A12=(−1)1+2⋅M12=(−1)3⋅∣651−1∣=11A_{12}=(-1)^{1+2}cdot M_{12}=(-1)^{3}cdotbegin{vmatrix}6&5\1&-1end{vmatrix}=11,
A13=(−1)1+3⋅M13=(−1)4⋅∣6−310∣=3A_{13}=(-1)^{1+3}cdot M_{13}=(-1)^{4}cdotbegin{vmatrix}6&-3\1&0end{vmatrix}=3,
A21=(−1)2+1⋅M21=(−1)3⋅∣1−40−1∣=1A_{21}=(-1)^{2+1}cdot M_{21}=(-1)^{3}cdotbegin{vmatrix}1&-4\0&-1end{vmatrix}=1,
A22=(−1)2+2⋅M22=(−1)4⋅∣2−41−1∣=2A_{22}=(-1)^{2+2}cdot M_{22}=(-1)^{4}cdotbegin{vmatrix}2&-4\1&-1end{vmatrix}=2,
A23=(−1)2+3⋅M23=(−1)5⋅∣2110∣=1A_{23}=(-1)^{2+3}cdot M_{23}=(-1)^{5}cdotbegin{vmatrix}2&1\1&0end{vmatrix}=1,
A31=(−1)3+1⋅M31=(−1)4⋅∣1−4−35∣=−7A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}1&-4\-3&5end{vmatrix}=-7,
A32=(−1)3+2⋅M32=(−1)5⋅∣2−465∣=−34A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}2&-4\6&5end{vmatrix}=-34,
A33=(−1)3+3⋅M33=(−1)6⋅∣216−3∣=−12A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}2&1\6&-3end{vmatrix}=-12.
Зная, что такое миноры и алгебраические дополнения, рассмотрим вычисление определителя по строке и столбцу.
Вычисление определителя по строке или столбцу
Определитель матрицы равен сумме произведений элементов строки (столбца) на их алгебраические дополнения.
Алгоритм вычисления определителя по строке или столбцу:
- находим алгебраические дополнения элементов строки или столбца;
- находим произведения элементов на их алгебраические дополнения;
- находим сумму, полученных на шаге 2, произведений.
Примеры
Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по 2 столбцу.
∣925148637∣=2⋅A12+4⋅A22+3⋅begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=2cdot A_{12}+4cdot A_{22}+3cdot
A32=2(−1)3M12+4(−1)4M22+3(−1)5M32=2(−1)3∣1867∣+4(−1)4∣9567∣+3(−1)5∣9518∣=A_{32}=2(-1)^{3}M_{12}+4(-1)^{4}M_{22}+3(-1)^{5}M_{32}=2(-1)^{3}begin{vmatrix}1&8\6&7end{vmatrix}+4(-1)^{4}begin{vmatrix}9&5\6&7end{vmatrix}+3(-1)^{5}begin{vmatrix}9&5\1&8end{vmatrix}=
=−2⋅(−41)+4⋅33−3⋅67=82+132−201=13=-2cdot(-41)+4cdot33-3cdot67=82+132-201=13.
Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по 3 строке.
∣21−46−3510−1∣=1⋅A31+0⋅A32−1⋅A33=1(−1)4M31+0(−1)5M32−1(−1)6M33=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=1cdot A_{31}+0cdot A_{32}-1cdot A_{33}=1(-1)^{4}M_{31}+0(-1)^{5}M_{32}-1(-1)^{6}M_{33}=
=1(−1)4∣1−4−35∣+0(−1)5∣2−465∣−1(−1)6∣216−3∣=−7+0+12=5=1(-1)^{4}begin{vmatrix}1&-4\-3&5end{vmatrix}+0(-1)^{5}begin{vmatrix}2&-4\6&5end{vmatrix}-1(-1)^{6}begin{vmatrix}2&1\6&-3end{vmatrix}=-7+0+12=5.
Любой из рассмотренных способов можно применять при нахождении определителей третьего порядка. В следующий раз мы разберем вычисление определителей матриц высших порядков.
Оформите решение задачи на заказ онлайн, если возникают трудности с выполнением!
Тест по теме «Как вычислить определитель матрицы третьего порядка»
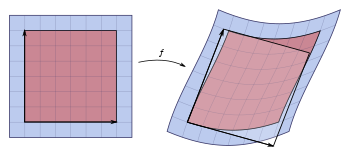
This article is about mathematics. For determinants in epidemiology, see Risk factor. For determinants in immunology, see Epitope.
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants (the preceding property is a corollary of this one).
The determinant of a matrix A is denoted det(A), det A, or |A|.
The determinant of a 2 × 2 matrix is
and the determinant of a 3 × 3 matrix is
The determinant of an n × n matrix can be defined in several equivalent ways. The Leibniz formula expresses the determinant as a sum of signed products of matrix entries such that each summand is the product of n different entries, and the number of these summands is 

Determinants can also be defined by some of their properties: the determinant is the unique function defined on the n × n matrices that has the four following properties. The determinant of the identity matrix is 1; the exchange of two rows (or of two columns) multiplies the determinant by −1; multiplying a row (or a column) by a number multiplies the determinant by this number; and adding to a row (or a column) a multiple of another row (or column) does not change the determinant.
Determinants occur throughout mathematics. For example, a matrix is often used to represent the coefficients in a system of linear equations, and determinants can be used to solve these equations (Cramer’s rule), although other methods of solution are computationally much more efficient. Determinants are used for defining the characteristic polynomial of a matrix, whose roots are the eigenvalues. In geometry, the signed n-dimensional volume of a n-dimensional parallelepiped is expressed by a determinant. This is used in calculus with exterior differential forms and the Jacobian determinant, in particular for changes of variables in multiple integrals.
Two by two matrices[edit]
The determinant of a 2 × 2 matrix 
For example,
First properties[edit]
The determinant has several key properties that can be proved by direct evaluation of the definition for 

Second, the determinant is zero if two rows are the same:
This holds similarly if the two columns are the same. Moreover,
Finally, if any column is multiplied by some number 
Geometric meaning[edit]
The area of the parallelogram is the absolute value of the determinant of the matrix formed by the vectors representing the parallelogram’s sides.
If the matrix entries are real numbers, the matrix A can be used to represent two linear maps: one that maps the standard basis vectors to the rows of A, and one that maps them to the columns of A. In either case, the images of the basis vectors form a parallelogram that represents the image of the unit square under the mapping. The parallelogram defined by the rows of the above matrix is the one with vertices at (0, 0), (a, b), (a + c, b + d), and (c, d), as shown in the accompanying diagram.
The absolute value of ad − bc is the area of the parallelogram, and thus represents the scale factor by which areas are transformed by A. (The parallelogram formed by the columns of A is in general a different parallelogram, but since the determinant is symmetric with respect to rows and columns, the area will be the same.)
The absolute value of the determinant together with the sign becomes the oriented area of the parallelogram. The oriented area is the same as the usual area, except that it is negative when the angle from the first to the second vector defining the parallelogram turns in a clockwise direction (which is opposite to the direction one would get for the identity matrix).
To show that ad − bc is the signed area, one may consider a matrix containing two vectors u ≡ (a, b) and v ≡ (c, d) representing the parallelogram’s sides. The signed area can be expressed as |u| |v| sin θ for the angle θ between the vectors, which is simply base times height, the length of one vector times the perpendicular component of the other. Due to the sine this already is the signed area, yet it may be expressed more conveniently using the cosine of the complementary angle to a perpendicular vector, e.g. u⊥ = (−b, a), so that |u⊥| |v| cos θ′, which can be determined by the pattern of the scalar product to be equal to ad − bc:
The volume of this parallelepiped is the absolute value of the determinant of the matrix formed by the columns constructed from the vectors r1, r2, and r3.
Thus the determinant gives the scaling factor and the orientation induced by the mapping represented by A. When the determinant is equal to one, the linear mapping defined by the matrix is equi-areal and orientation-preserving.
The object known as the bivector is related to these ideas. In 2D, it can be interpreted as an oriented plane segment formed by imagining two vectors each with origin (0, 0), and coordinates (a, b) and (c, d). The bivector magnitude (denoted by (a, b) ∧ (c, d)) is the signed area, which is also the determinant ad − bc.[2]
If an n × n real matrix A is written in terms of its column vectors ![{displaystyle A=left[{begin{array}{c|c|c|c}mathbf {a} _{1}&mathbf {a} _{2}&cdots &mathbf {a} _{n}end{array}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1d60337c4cde7b2d5fc3e0365bc8ec5e699ea1a)
This means that 


The determinant gives the signed n-dimensional volume of this parallelotope, 
Definition[edit]
Let A be a square matrix with n rows and n columns, so that it can be written as
The entries 
The determinant of A is denoted by det(A), or it can be denoted directly in terms of the matrix entries by writing enclosing bars instead of brackets:
There are various equivalent ways to define the determinant of a square matrix A, i.e. one with the same number of rows and columns: the determinant can be defined via the Leibniz formula, an explicit formula involving sums of products of certain entries of the matrix. The determinant can also be characterized as the unique function depending on the entries of the matrix satisfying certain properties. This approach can also be used to compute determinants by simplifying the matrices in question.
Leibniz formula[edit]
3 × 3 matrices[edit]
The Leibniz formula for the determinant of a 3 × 3 matrix is the following:
The rule of Sarrus is a mnemonic for the expanded form of this determinant: the sum of the products of three diagonal north-west to south-east lines of matrix elements, minus the sum of the products of three diagonal south-west to north-east lines of elements, when the copies of the first two columns of the matrix are written beside it as in the illustration. This scheme for calculating the determinant of a 3 × 3 matrix does not carry over into higher dimensions.
n × n matrices[edit]
In higher dimension, the Leibniz formula expresses the determinant of an 










Given a matrix
the Leibniz formula for its determinant is, using sigma notation,
Using pi notation, this can be shortened into
.
The Levi-Civita symbol 

where the sum is taken over all n-tuples of integers in
[4][5]
Properties of the determinant[edit]
Characterization of the determinant[edit]
The determinant can be characterized by the following three key properties. To state these, it is convenient to regard an 

where the column vector 
-
, where
is an identity matrix.
- The determinant is multilinear: if the jth column of a matrix
is written as a linear combination
of two column vectors v and w and a number r, then the determinant of A is expressible as a similar linear combination:
- The determinant is alternating: whenever two columns of a matrix are identical, its determinant is 0:
If the determinant is defined using the Leibniz formula as above, these three properties can be proved by direct inspection of that formula. Some authors also approach the determinant directly using these three properties: it can be shown that there is exactly one function that assigns to any 
To see this it suffices to expand the determinant by multi-linearity in the columns into a (huge) linear combination of determinants of matrices in which each column is a standard basis vector. These determinants are either 0 (by property 9) or else ±1 (by properties 1 and 12 below), so the linear combination gives the expression above in terms of the Levi-Civita symbol. While less technical in appearance, this characterization cannot entirely replace the Leibniz formula in defining the determinant, since without it the existence of an appropriate function is not clear.[citation needed]
Immediate consequences[edit]
These rules have several further consequences:
- The determinant is a homogeneous function, i.e.,
(for an
matrix
).
- Interchanging any pair of columns of a matrix multiplies its determinant by −1. This follows from the determinant being multilinear and alternating (properties 2 and 3 above):
This formula can be applied iteratively when several columns are swapped. For example
Yet more generally, any permutation of the columns multiplies the determinant by the sign of the permutation.
- If some column can be expressed as a linear combination of the other columns (i.e. the columns of the matrix form a linearly dependent set), the determinant is 0. As a special case, this includes: if some column is such that all its entries are zero, then the determinant of that matrix is 0.
- Adding a scalar multiple of one column to another column does not change the value of the determinant. This is a consequence of multilinearity and being alternative: by multilinearity the determinant changes by a multiple of the determinant of a matrix with two equal columns, which determinant is 0, since the determinant is alternating.
- If
is a triangular matrix, i.e.
, whenever
or, alternatively, whenever
, then its determinant equals the product of the diagonal entries:
Indeed, such a matrix can be reduced, by appropriately adding multiples of the columns with fewer nonzero entries to those with more entries, to a diagonal matrix (without changing the determinant). For such a matrix, using the linearity in each column reduces to the identity matrix, in which case the stated formula holds by the very first characterizing property of determinants. Alternatively, this formula can also be deduced from the Leibniz formula, since the only permutation
which gives a non-zero contribution is the identity permutation.
Example[edit]
These characterizing properties and their consequences listed above are both theoretically significant, but can also be used to compute determinants for concrete matrices. In fact, Gaussian elimination can be applied to bring any matrix into upper triangular form, and the steps in this algorithm affect the determinant in a controlled way. The following concrete example illustrates the computation of the determinant of the matrix 
| Matrix |  |
|
|
|
| Obtained by |
add the second column to the first |
add 3 times the third column to the second |
swap the first two columns |
add |
| Determinant |  |
|
|
|
Combining these equalities gives 
Transpose[edit]
The determinant of the transpose of 
.
This can be proven by inspecting the Leibniz formula.[7] This implies that in all the properties mentioned above, the word «column» can be replaced by «row» throughout. For example, viewing an n × n matrix as being composed of n rows, the determinant is an n-linear function.
Multiplicativity and matrix groups[edit]
The determinant is a multiplicative map, i.e., for square matrices 

This key fact can be proven by observing that, for a fixed matrix 



A matrix 
.
In particular, products and inverses of matrices with non-zero determinant (respectively, determinant one) still have this property. Thus, the set of such matrices (of fixed size 



Because the determinant respects multiplication and inverses, it is in fact a group homomorphism from 







The Cauchy–Binet formula is a generalization of that product formula for rectangular matrices. This formula can also be recast as a multiplicative formula for compound matrices whose entries are the determinants of all quadratic submatrices of a given matrix.[9][10]
Laplace expansion[edit]
Laplace expansion expresses the determinant of a matrix 







which is called the Laplace expansion along the ith row. For example, the Laplace expansion along the first row (
Unwinding the determinants of these 

Laplace expansion can be used iteratively for computing determinants, but this approach is inefficient for large matrices. However, it is useful for computing the determinants of highly symmetric matrix such as the Vandermonde matrix
This determinant has been applied, for example, in the proof of Baker’s theorem in the theory of transcendental numbers.
Adjugate matrix[edit]
The adjugate matrix 
For every matrix, one has[11]
Thus the adjugate matrix can be used for expressing the inverse of a nonsingular matrix:
Block matrices[edit]
The formula for the determinant of a 





If 

If 


If the blocks are square matrices of the same size further formulas hold. For example, if 


This formula has been generalized to matrices composed of more than 
For 



Sylvester’s determinant theorem[edit]
Sylvester’s determinant theorem states that for A, an m × n matrix, and B, an n × m matrix (so that A and B have dimensions allowing them to be multiplied in either order forming a square matrix):
where Im and In are the m × m and n × n identity matrices, respectively.
From this general result several consequences follow.
Sum[edit]
The determinant of the sum 



with the corollary[16][17]
Conversely, if 



by homogeneity.
Sum identity for 2×2 matrices[edit]
For the special case of 
Proof of identity
This can be shown by writing out each term in components 
Expanding gives
The terms which are quadratic in 


We can then write the cross-terms as
which can be recognized as
which completes the proof.
This has an application to 
with 




This result followed just from 

Properties of the determinant in relation to other notions[edit]
Eigenvalues and characteristic polynomial[edit]
The determinant is closely related to two other central concepts in linear algebra, the eigenvalues and the characteristic polynomial of a matrix. Let 



The product of all non-zero eigenvalues is referred to as pseudo-determinant.
From this, one immediately sees that the determinant of a matrix 





The characteristic polynomial is defined as[19]
Here, 




A Hermitian matrix is positive definite if all its eigenvalues are positive. Sylvester’s criterion asserts that this is equivalent to the determinants of the submatrices
being positive, for all 


Trace[edit]
The trace tr(A) is by definition the sum of the diagonal entries of A and also equals the sum of the eigenvalues. Thus, for complex matrices A,
or, for real matrices A,
Here exp(A) denotes the matrix exponential of A, because every eigenvalue λ of A corresponds to the eigenvalue exp(λ) of exp(A). In particular, given any logarithm of A, that is, any matrix L satisfying
the determinant of A is given by
For example, for n = 2, n = 3, and n = 4, respectively,
cf. Cayley-Hamilton theorem. Such expressions are deducible from combinatorial arguments, Newton’s identities, or the Faddeev–LeVerrier algorithm. That is, for generic n, detA = (−1)nc0 the signed constant term of the characteristic polynomial, determined recursively from
In the general case, this may also be obtained from[21]
where the sum is taken over the set of all integers kl ≥ 0 satisfying the equation
The formula can be expressed in terms of the complete exponential Bell polynomial of n arguments sl = −(l – 1)! tr(Al) as
This formula can also be used to find the determinant of a matrix AIJ with multidimensional indices I = (i1, i2, …, ir) and J = (j1, j2, …, jr). The product and trace of such matrices are defined in a natural way as
An important arbitrary dimension n identity can be obtained from the Mercator series expansion of the logarithm when the expansion converges. If every eigenvalue of A is less than 1 in absolute value,
where I is the identity matrix. More generally, if
is expanded as a formal power series in s then all coefficients of sm for m > n are zero and the remaining polynomial is det(I + sA).
Upper and lower bounds[edit]
For a positive definite matrix A, the trace operator gives the following tight lower and upper bounds on the log determinant
with equality if and only if A = I. This relationship can be derived via the formula for the Kullback-Leibler divergence between two multivariate normal distributions.
Also,
These inequalities can be proved by expressing the traces and the determinant in terms of the eigenvalues. As such, they represent the well-known fact that the harmonic mean is less than the geometric mean, which is less than the arithmetic mean, which is, in turn, less than the root mean square.
Derivative[edit]
The Leibniz formula shows that the determinant of real (or analogously for complex) square matrices is a polynomial function from 

where 


Expressed in terms of the entries of 
Yet another equivalent formulation is
,
using big O notation. The special case where 
This identity is used in describing Lie algebras associated to certain matrix Lie groups. For example, the special linear group 


Writing a 


History[edit]
Historically, determinants were used long before matrices: A determinant was originally defined as a property of a system of linear equations.
The determinant «determines» whether the system has a unique solution (which occurs precisely if the determinant is non-zero).
In this sense, determinants were first used in the Chinese mathematics textbook The Nine Chapters on the Mathematical Art (九章算術, Chinese scholars, around the 3rd century BCE). In Europe, solutions of linear systems of two equations were expressed by Cardano in 1545 by a determinant-like entity.[23]
Determinants proper originated from the work of Seki Takakazu in 1683 in Japan and parallelly of Leibniz in 1693.[24][25][26][27] Cramer (1750) stated, without proof, Cramer’s rule.[28] Both Cramer and also Bezout (1779) were led to determinants by the question of plane curves passing through a given set of points.[29]
Vandermonde (1771) first recognized determinants as independent functions.[25] Laplace (1772) gave the general method of expanding a determinant in terms of its complementary minors: Vandermonde had already given a special case.[30] Immediately following, Lagrange (1773) treated determinants of the second and third order and applied it to questions of elimination theory; he proved many special cases of general identities.
Gauss (1801) made the next advance. Like Lagrange, he made much use of determinants in the theory of numbers. He introduced the word «determinant» (Laplace had used «resultant»), though not in the present signification, but rather as applied to the discriminant of a quantic.[31] Gauss also arrived at the notion of reciprocal (inverse) determinants, and came very near the multiplication theorem.
The next contributor of importance is Binet (1811, 1812), who formally stated the theorem relating to the product of two matrices of m columns and n rows, which for the special case of m = n reduces to the multiplication theorem. On the same day (November 30, 1812) that Binet presented his paper to the Academy, Cauchy also presented one on the subject. (See Cauchy–Binet formula.) In this he used the word «determinant» in its present sense,[32][33] summarized and simplified what was then known on the subject, improved the notation, and gave the multiplication theorem with a proof more satisfactory than Binet’s.[25][34] With him begins the theory in its generality.
(Jacobi 1841) used the functional determinant which Sylvester later called the Jacobian.[35] In his memoirs in Crelle’s Journal for 1841 he specially treats this subject, as well as the class of alternating functions which Sylvester has called alternants. About the time of Jacobi’s last memoirs, Sylvester (1839) and Cayley began their work. Cayley 1841 introduced the modern notation for the determinant using vertical bars.[36][37]
The study of special forms of determinants has been the natural result of the completion of the general theory. Axisymmetric determinants have been studied by Lebesgue, Hesse, and Sylvester; persymmetric determinants by Sylvester and Hankel; circulants by Catalan, Spottiswoode, Glaisher, and Scott; skew determinants and Pfaffians, in connection with the theory of orthogonal transformation, by Cayley; continuants by Sylvester; Wronskians (so called by Muir) by Christoffel and Frobenius; compound determinants by Sylvester, Reiss, and Picquet; Jacobians and Hessians by Sylvester; and symmetric gauche determinants by Trudi. Of the textbooks on the subject Spottiswoode’s was the first. In America, Hanus (1886), Weld (1893), and Muir/Metzler (1933) published treatises.
Applications[edit]
Cramer’s rule[edit]
Determinants can be used to describe the solutions of a linear system of equations, written in matrix form as 


where 



where the vectors 
Cramer’s rule can be implemented in 
Linear independence[edit]
Determinants can be used to characterize linearly dependent vectors: 






It is non-zero (for some 

Orientation of a basis[edit]
The determinant can be thought of as assigning a number to every sequence of n vectors in Rn, by using the square matrix whose columns are the given vectors. The determinant will be nonzero iff the sequence of vectors is a basis for Rn. In that case, the sign of the determinant determines whether the orientation of the basis is consistent with or opposite to the orientation of the standard basis. In the case of an orthogonal basis, the magnitude of the determinant is equal to the product of the lengths of the basis vectors. For instance, an orthogonal matrix with entries in Rn represents an orthonormal basis in Euclidean space, and hence has determinant of ±1 (since all the vectors have length 1). The determinant is +1 iff the basis has the same orientation. It is −1 iff the basis has the opposite orientation.
More generally, if the determinant of A is positive, A represents an orientation-preserving linear transformation (if A is an orthogonal 2 × 2 or 3 × 3 matrix, this is a rotation), while if it is negative, A switches the orientation of the basis.
Volume and Jacobian determinant[edit]
As pointed out above, the absolute value of the determinant of real vectors is equal to the volume of the parallelepiped spanned by those vectors. As a consequence, if 










By calculating the volume of the tetrahedron bounded by four points, they can be used to identify skew lines. The volume of any tetrahedron, given its vertices 

A nonlinear map 
For a general differentiable function, much of the above carries over by considering the Jacobian matrix of f. For
the Jacobian matrix is the n × n matrix whose entries are given by the partial derivatives
Its determinant, the Jacobian determinant, appears in the higher-dimensional version of integration by substitution: for suitable functions f and an open subset U of Rn (the domain of f), the integral over f(U) of some other function φ : Rn → Rm is given by
The Jacobian also occurs in the inverse function theorem.
When applied to the field of Cartography, the determinant can be used to measure the rate of expansion of a map near the poles. [42]
Abstract algebraic aspects [edit]
Determinant of an endomorphism[edit]
The above identities concerning the determinant of products and inverses of matrices imply that similar matrices have the same determinant: two matrices A and B are similar, if there exists an invertible matrix X such that A = X−1BX. Indeed, repeatedly applying the above identities yields
The determinant is therefore also called a similarity invariant. The determinant of a linear transformation
for some finite-dimensional vector space V is defined to be the determinant of the matrix describing it, with respect to an arbitrary choice of basis in V. By the similarity invariance, this determinant is independent of the choice of the basis for V and therefore only depends on the endomorphism T.
Square matrices over commutative rings[edit]
The above definition of the determinant using the Leibniz rule holds works more generally when the entries of the matrix are elements of a commutative ring 


A matrix 



The determinant being multiplicative, it defines a group homomorphism
between the general linear group (the group of invertible 


The determinant is a natural transformation.
Given a ring homomorphism 



holds. In other words, the displayed commutative diagram commutes.
For example, the determinant of the complex conjugate of a complex matrix (which is also the determinant of its conjugate transpose) is the complex conjugate of its determinant, and for integer matrices: the reduction modulo 



Exterior algebra[edit]
The determinant of a linear transformation 








As 




This definition agrees with the more concrete coordinate-dependent definition. This can be shown using the uniqueness of a multilinear alternating form on 

For this reason, the highest non-zero exterior power 



Generalizations and related notions[edit]
Determinants as treated above admit several variants: the permanent of a matrix is defined as the determinant, except that the factors 

Determinants for finite-dimensional algebras[edit]
For any associative algebra 

[48]
This definition proceeds by establishing the characteristic polynomial independently of the determinant, and defining the determinant as the lowest order term of this polynomial. This general definition recovers the determinant for the matrix algebra 
,
the norm 
Infinite matrices[edit]
For matrices with an infinite number of rows and columns, the above definitions of the determinant do not carry over directly. For example, in the Leibniz formula, an infinite sum (all of whose terms are infinite products) would have to be calculated. Functional analysis provides different extensions of the determinant for such infinite-dimensional situations, which however only work for particular kinds of operators.
The Fredholm determinant defines the determinant for operators known as trace class operators by an appropriate generalization of the formula
Another infinite-dimensional notion of determinant is the functional determinant.
Operators in von Neumann algebras[edit]
For operators in a finite factor, one may define a positive real-valued determinant called the Fuglede−Kadison determinant using the canonical trace. In fact, corresponding to every tracial state on a von Neumann algebra there is a notion of Fuglede−Kadison determinant.
[edit]
For matrices over non-commutative rings, multilinearity and alternating properties are incompatible for n ≥ 2,[49] so there is no good definition of the determinant in this setting.
For square matrices with entries in a non-commutative ring, there are various difficulties in defining determinants analogously to that for commutative rings. A meaning can be given to the Leibniz formula provided that the order for the product is specified, and similarly for other definitions of the determinant, but non-commutativity then leads to the loss of many fundamental properties of the determinant, such as the multiplicative property or that the determinant is unchanged under transposition of the matrix. Over non-commutative rings, there is no reasonable notion of a multilinear form (existence of a nonzero bilinear form[clarify] with a regular element of R as value on some pair of arguments implies that R is commutative). Nevertheless, various notions of non-commutative determinant have been formulated that preserve some of the properties of determinants, notably quasideterminants and the Dieudonné determinant. For some classes of matrices with non-commutative elements, one can define the determinant and prove linear algebra theorems that are very similar to their commutative analogs. Examples include the q-determinant on quantum groups, the Capelli determinant on Capelli matrices, and the Berezinian on supermatrices (i.e., matrices whose entries are elements of 
Calculation[edit]
Determinants are mainly used as a theoretical tool. They are rarely calculated explicitly in numerical linear algebra, where for applications such as checking invertibility and finding eigenvalues the determinant has largely been supplanted by other techniques.[51] Computational geometry, however, does frequently use calculations related to determinants.[52]
While the determinant can be computed directly using the Leibniz rule this approach is extremely inefficient for large matrices, since that formula requires calculating 



Decomposition methods[edit]
Some methods compute 


For example, LU decomposition expresses 
of a permutation matrix 



The determinants of the two triangular matrices 






Further methods[edit]
The order 






In addition to the complexity of the algorithm, further criteria can be used to compare algorithms.
Especially for applications concerning matrices over rings, algorithms that compute the determinant without any divisions exist. (By contrast, Gauss elimination requires divisions.) One such algorithm, having complexity 


If the determinant of A and the inverse of A have already been computed, the matrix determinant lemma allows rapid calculation of the determinant of A + uvT, where u and v are column vectors.
Charles Dodgson (i.e. Lewis Carroll of Alice’s Adventures in Wonderland fame) invented a method for computing determinants called Dodgson condensation. Unfortunately this interesting method does not always work in its original form.[59]
See also[edit]
- Cauchy determinant
- Cayley–Menger determinant
- Dieudonné determinant
- Slater determinant
- Determinantal conjecture
Notes[edit]
- ^ Lang 1985, §VII.1
- ^ Wildberger, Norman J. (2010). Episode 4 (video lecture). WildLinAlg. Sydney, Australia: University of New South Wales. Archived from the original on 2021-12-11 – via YouTube.
- ^ «Determinants and Volumes». textbooks.math.gatech.edu. Retrieved 16 March 2018.
- ^ McConnell (1957). Applications of Tensor Analysis. Dover Publications. pp. 10–17.
- ^ Harris 2014, §4.7
- ^ Serge Lang, Linear Algebra, 2nd Edition, Addison-Wesley, 1971, pp 173, 191.
- ^ Lang 1987, §VI.7, Theorem 7.5
- ^ Alternatively, Bourbaki 1998, §III.8, Proposition 1 proves this result using the functoriality of the exterior power.
- ^ Horn & Johnson 2018, §0.8.7
- ^ Kung, Rota & Yan 2009, p. 306
- ^ Horn & Johnson 2018, §0.8.2.
- ^
- ^ Silvester, J. R. (2000). «Determinants of Block Matrices». Math. Gazette. 84 (501): 460–467. doi:10.2307/3620776. JSTOR 3620776. S2CID 41879675.
- ^ Sothanaphan, Nat (January 2017). «Determinants of block matrices with noncommuting blocks». Linear Algebra and Its Applications. 512: 202–218. arXiv:1805.06027. doi:10.1016/j.laa.2016.10.004. S2CID 119272194.
- ^ Proofs can be found in http://www.ee.ic.ac.uk/hp/staff/dmb/matrix/proof003.html
- ^ Lin, Minghua; Sra, Suvrit (2014). «Completely strong superadditivity of generalized matrix functions». arXiv:1410.1958 [math.FA].
- ^ Paksoy; Turkmen; Zhang (2014). «Inequalities of Generalized Matrix Functions via Tensor Products». Electronic Journal of Linear Algebra. 27: 332–341. doi:10.13001/1081-3810.1622.
- ^ Serre, Denis (Oct 18, 2010). «Concavity of det1⁄n over HPDn«. MathOverflow.
- ^ Lang 1985, §VIII.2, Horn & Johnson 2018, Def. 1.2.3
- ^ Horn & Johnson 2018, Observation 7.1.2, Theorem 7.2.5
- ^ A proof can be found in the Appendix B of Kondratyuk, L. A.; Krivoruchenko, M. I. (1992). «Superconducting quark matter in SU(2) color group». Zeitschrift für Physik A. 344 (1): 99–115. Bibcode:1992ZPhyA.344…99K. doi:10.1007/BF01291027. S2CID 120467300.
- ^ Horn & Johnson 2018, § 0.8.10
- ^ Grattan-Guinness 2003, §6.6
- ^ Cajori, F. A History of Mathematics p. 80
- ^ a b c Campbell, H: «Linear Algebra With Applications», pages 111–112. Appleton Century Crofts, 1971
- ^ Eves 1990, p. 405
- ^ A Brief History of Linear Algebra and Matrix Theory at: «A Brief History of Linear Algebra and Matrix Theory». Archived from the original on 10 September 2012. Retrieved 24 January 2012.
- ^ Kleiner 2007, p. 80
- ^ Bourbaki (1994, p. 59)
- ^ Muir, Sir Thomas, The Theory of Determinants in the historical Order of Development [London, England: Macmillan and Co., Ltd., 1906]. JFM 37.0181.02
- ^ Kleiner 2007, §5.2
- ^ The first use of the word «determinant» in the modern sense appeared in: Cauchy, Augustin-Louis «Memoire sur les fonctions qui ne peuvent obtenir que deux valeurs égales et des signes contraires par suite des transpositions operées entre les variables qu’elles renferment,» which was first read at the Institute de France in Paris on November 30, 1812, and which was subsequently published in the Journal de l’Ecole Polytechnique, Cahier 17, Tome 10, pages 29–112 (1815).
- ^ Origins of mathematical terms: http://jeff560.tripod.com/d.html
- ^ History of matrices and determinants: http://www-history.mcs.st-and.ac.uk/history/HistTopics/Matrices_and_determinants.html
- ^ Eves 1990, p. 494
- ^ Cajori 1993, Vol. II, p. 92, no. 462
- ^ History of matrix notation: http://jeff560.tripod.com/matrices.html
- ^ Habgood & Arel 2012
- ^ Lang 1985, §VII.3
- ^ Lang 2002, §IV.8
- ^ Lang 1985, §VII.6, Theorem 6.10
- ^ Lay, David (2021). Linear Algebra and It’s Applications 6th Edition. Pearson. p. 172.
- ^ Dummit & Foote 2004, §11.4
- ^ Dummit & Foote 2004, §11.4, Theorem 30
- ^ Mac Lane 1998, §I.4. See also Natural transformation § Determinant.
- ^ Bourbaki 1998, §III.8
- ^ Lombardi & Quitté 2015, §5.2, Bourbaki 1998, §III.5
- ^ Garibaldi 2004
- ^ In a non-commutative setting left-linearity (compatibility with left-multiplication by scalars) should be distinguished from right-linearity. Assuming linearity in the columns is taken to be left-linearity, one would have, for non-commuting scalars a, b:
a contradiction. There is no useful notion of multi-linear functions over a non-commutative ring.
- ^ Varadarajan, V. S (2004), Supersymmetry for mathematicians: An introduction, ISBN 978-0-8218-3574-6.
- ^ «… we mention that the determinant, though a convenient notion theoretically, rarely finds a useful role in numerical algorithms.», see Trefethen & Bau III 1997, Lecture 1.
- ^ Fisikopoulos & Peñaranda 2016, §1.1, §4.3
- ^ Camarero, Cristóbal (2018-12-05). «Simple, Fast and Practicable Algorithms for Cholesky, LU and QR Decomposition Using Fast Rectangular Matrix Multiplication». arXiv:1812.02056 [cs.NA].
- ^ Bunch & Hopcroft 1974
- ^ Fisikopoulos & Peñaranda 2016, §1.1
- ^ Rote 2001
- ^ Fang, Xin Gui; Havas, George (1997). «On the worst-case complexity of integer Gaussian elimination» (PDF). Proceedings of the 1997 international symposium on Symbolic and algebraic computation. ISSAC ’97. Kihei, Maui, Hawaii, United States: ACM. pp. 28–31. doi:10.1145/258726.258740. ISBN 0-89791-875-4. Archived from the original (PDF) on 2011-08-07. Retrieved 2011-01-22.
- ^ Fisikopoulos & Peñaranda 2016, §1.1, Bareiss 1968
- ^ Abeles, Francine F. (2008). «Dodgson condensation: The historical and mathematical development of an experimental method». Linear Algebra and Its Applications. 429 (2–3): 429–438. doi:10.1016/j.laa.2007.11.022.
References[edit]
- Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
- Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
- Bareiss, Erwin (1968), «Sylvester’s Identity and Multistep Integer-Preserving Gaussian Elimination» (PDF), Mathematics of Computation, 22 (102): 565–578, doi:10.2307/2004533, JSTOR 2004533, archived (PDF) from the original on 2012-10-25
- de Boor, Carl (1990), «An empty exercise» (PDF), ACM SIGNUM Newsletter, 25 (2): 3–7, doi:10.1145/122272.122273, S2CID 62780452, archived (PDF) from the original on 2006-09-01
- Bourbaki, Nicolas (1998), Algebra I, Chapters 1-3, Springer, ISBN 9783540642435
- Bunch, J. R.; Hopcroft, J. E. (1974). «Triangular Factorization and Inversion by Fast Matrix Multiplication». Mathematics of Computation. 28 (125): 231–236. doi:10.1090/S0025-5718-1974-0331751-8.
- Dummit, David S.; Foote, Richard M. (2004), Abstract algebra (3rd ed.), Hoboken, NJ: Wiley, ISBN 9780471452348, OCLC 248917264
- Fisikopoulos, Vissarion; Peñaranda, Luis (2016), «Faster geometric algorithms via dynamic determinant computation», Computational Geometry, 54: 1–16, doi:10.1016/j.comgeo.2015.12.001
- Garibaldi, Skip (2004), «The characteristic polynomial and determinant are not ad hoc constructions», American Mathematical Monthly, 111 (9): 761–778, arXiv:math/0203276, doi:10.2307/4145188, JSTOR 4145188, MR 2104048
- Habgood, Ken; Arel, Itamar (2012). «A condensation-based application of Cramer’s rule for solving large-scale linear systems» (PDF). Journal of Discrete Algorithms. 10: 98–109. doi:10.1016/j.jda.2011.06.007. Archived (PDF) from the original on 2019-05-05.
- Harris, Frank E. (2014), Mathematics for Physical Science and Engineering, Elsevier, ISBN 9780128010495
- Kleiner, Israel (2007), Kleiner, Israel (ed.), A history of abstract algebra, Birkhäuser, doi:10.1007/978-0-8176-4685-1, ISBN 978-0-8176-4684-4, MR 2347309
- Kung, Joseph P.S.; Rota, Gian-Carlo; Yan, Catherine (2009), Combinatorics: The Rota Way, Cambridge University Press, ISBN 9780521883894
- Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7
- Lombardi, Henri; Quitté, Claude (2015), Commutative Algebra: Constructive Methods, Springer, ISBN 9789401799447
- Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics 5 (2nd ed.), Springer-Verlag, ISBN 0-387-98403-8
- Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8, archived from the original on 2009-10-31
- Muir, Thomas (1960) [1933], A treatise on the theory of determinants, Revised and enlarged by William H. Metzler, New York, NY: Dover
- Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3
- G. Baley Price (1947) «Some identities in the theory of determinants», American Mathematical Monthly 54:75–90 MR0019078
- Horn, Roger Alan; Johnson, Charles Royal (2018) [1985]. Matrix Analysis (2nd ed.). Cambridge University Press. ISBN 978-0-521-54823-6.
- Lang, Serge (1985), Introduction to Linear Algebra, Undergraduate Texts in Mathematics (2 ed.), Springer, ISBN 9780387962054
- Lang, Serge (1987), Linear Algebra, Undergraduate Texts in Mathematics (3 ed.), Springer, ISBN 9780387964126
- Lang, Serge (2002). Algebra. Graduate Texts in Mathematics. New York, NY: Springer. ISBN 978-0-387-95385-4.
- Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall
- Rote, Günter (2001), «Division-free algorithms for the determinant and the Pfaffian: algebraic and combinatorial approaches» (PDF), Computational discrete mathematics, Lecture Notes in Comput. Sci., vol. 2122, Springer, pp. 119–135, doi:10.1007/3-540-45506-X_9, ISBN 978-3-540-42775-9, MR 1911585, archived from the original (PDF) on 2007-02-01, retrieved 2020-06-04
- Trefethen, Lloyd; Bau III, David (1997), Numerical Linear Algebra (1st ed.), Philadelphia: SIAM, ISBN 978-0-89871-361-9
Historical references[edit]
- Bourbaki, Nicolas (1994), Elements of the history of mathematics, translated by Meldrum, John, Springer, doi:10.1007/978-3-642-61693-8, ISBN 3-540-19376-6
- Cajori, Florian (1993), A history of mathematical notations: Including Vol. I. Notations in elementary mathematics; Vol. II. Notations mainly in higher mathematics, Reprint of the 1928 and 1929 originals, Dover, ISBN 0-486-67766-4, MR 3363427
- Bezout, Étienne (1779), Théorie générale des equations algébriques, Paris
- Cayley, Arthur (1841), «On a theorem in the geometry of position», Cambridge Mathematical Journal, 2: 267–271
- Cramer, Gabriel (1750), Introduction à l’analyse des lignes courbes algébriques, Genève: Frères Cramer & Cl. Philibert, doi:10.3931/e-rara-4048
- Eves, Howard (1990), An introduction to the history of mathematics (6 ed.), Saunders College Publishing, ISBN 0-03-029558-0, MR 1104435
- Grattan-Guinness, I., ed. (2003), Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences, vol. 1, Johns Hopkins University Press, ISBN 9780801873966
- Jacobi, Carl Gustav Jakob (1841), «De Determinantibus functionalibus», Journal für die reine und angewandte Mathematik, 1841 (22): 320–359, doi:10.1515/crll.1841.22.319, S2CID 123637858
- Laplace, Pierre-Simon, de (1772), «Recherches sur le calcul intégral et sur le systéme du monde», Histoire de l’Académie Royale des Sciences, Paris (seconde partie): 267–376
External links[edit]
- Suprunenko, D.A. (2001) [1994], «Determinant», Encyclopedia of Mathematics, EMS Press
- Weisstein, Eric W. «Determinant». MathWorld.
- O’Connor, John J.; Robertson, Edmund F., «Matrices and determinants», MacTutor History of Mathematics archive, University of St Andrews
- Determinant Interactive Program and Tutorial
- Linear algebra: determinants. Archived 2008-12-04 at the Wayback Machine Compute determinants of matrices up to order 6 using Laplace expansion you choose.
- Determinant Calculator Calculator for matrix determinants, up to the 8th order.
- Matrices and Linear Algebra on the Earliest Uses Pages
- Determinants explained in an easy fashion in the 4th chapter as a part of a Linear Algebra course.
Оглавление:
- Основные теоретические сведения
- Матрицы
- Обратная матрица
- Матрицы. Вся теория и задачи с решениями или ответами
Основные теоретические сведения
Матрицы
К оглавлению…
Матрицей называют прямоугольную таблицу, заполненную числами. Важнейшие характеристики матрицы – число строк и число столбцов. Если у матрицы одинаковое число строк и столбцов, ее называют квадратной. Обозначают матрицы большими латинскими буквами.
Сами числа называют элементами матрицы и характеризуют их положением в матрице, задавая номер строки и номер столбца и записывая их в виде двойного индекса, причем вначале записывают номер строки, а затем столбца. Например, a14 есть элемент матрицы, стоящий в первой строке и четвертом столбце, a32 стоит в третьей строке и втором столбце.
Главной диагональю квадратной матрицы называют элементы, имеющие одинаковые индексы, то есть те элементы, у которых номер строки совпадает с номером столбца. Побочная диагональ идет «перпендикулярно» главной диагонали.
Особую важность представляют собой так называемые единичные матрицы. Это квадратные матрицы, у которых на главной диагонали стоят 1, а все остальные числа равны 0. Обозначают единичные матрицы E. Матрицы называют равными, если у них равны число строк, число столбцов, и все элементы, имеющие одинаковые индексы, равны. Матрица называется нулевой, если все ее элементы равны 0. Обозначается нулевая матрица О.
Простейшие действия с матрицами
1. Умножение матрицы на число. Для этого необходимо умножить каждый элемент матрицы на данное число.
2. Сложение матриц. Складывать можно только матрицы одинакового размера, то есть имеющие одинаковое число строк и одинаковое число столбцов. При сложении матриц соответствующие их элементы складываются.
3. Транспонирование матрицы. При транспонировании у матрицы строки становятся столбцами и наоборот. Полученная матрица называется транспонированной и обозначается AT. Для транспонирования матриц справедливы следующие свойства:
4. Умножение матриц. Для произведения матриц существуют следующие свойства:
- Умножать можно матрицы, если число столбцов первой матрицы равно числу строк второй матрицы.
- В результате получится матрица, число строк которой равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.
- Умножение матриц некоммутативно. Это значит, что от перестановки местами матриц в произведении результат меняется. Более того, если можно посчитать произведение A∙B, это совсем не означает, что можно посчитать произведение B∙A.
- Пусть C = A∙B. Для определения элемента матрицы С, стоящего в i-той строке и k-том столбце необходимо взять i-тую строку первой умножаемой матрицы и k-тый столбец второй. Далее поочередно брать элементы этих строки и столбца и умножать их. Берем первый элемент из строки первой матрицы и умножаем на первый элемент столбца второй матрицы. Далее берем второй элемент строки первой матрицы и умножаем на второй элемент столбца второй матрицы и так далее. А потом все эти произведения надо сложить.
Свойства произведения матриц:
Определитель матрицы
Определителем (детерминантом) квадратной матрицы А называется число, которое обозначается detA, реже |A| или просто Δ, и вычисляется определённым образом. Для матрицы размера 1х1 определителем является сам единственный элемент матрицы. Для матрицы размера 2х2 определитель находят по следующей формуле:
Миноры и алгебраические дополнения
Рассмотрим матрицу А. Выберем в ней s строк и s столбцов. Составим квадратную матрицу из элементов, стоящих на пересечении полученных строк и столбцов. Минором матрицы А порядка s называют определитель полученной матрицы.
Рассмотрим квадратную матрицу А. Выберем в ней s строк и s столбцов. Дополнительным минором к минору порядка s называют определитель, составленный из элементов, оставшихся после вычеркивания данных строк и столбцов.
Алгебраическим дополнением к элементу aik квадратной матрицы А называют дополнительный минор к этому элементу, умноженный на (–1)i+k, где i+k есть сумма номеров строки и столбца элемента aik. Обозначают алгебраическое дополнение Aik.
Вычисление определителя матрицы через алгебраические дополнения
Рассмотрим квадратную матрицу А. Для вычисления ее определителя необходимо выбрать любую ее строку или столбец и найти произведения каждого элемента этой строки или столбца на алгебраическое дополнение к нему. А дальше надо просуммировать все эти произведения.
Когда будете считать алгебраические дополнения, не забывайте про множитель (–1)i+k. Чтобы счет был более простым, выбирайте ту строку или столбец матрицы, который содержит наибольшее число нулей.
Расчет алгебраического дополнения может сводиться к расчету определителя размером более чем 2х2. В этом случае такой расчет также нужно проводить через алгебраические дополнения, и так далее до тех пор, пока алгебраические дополнения, которые нужно будет считать, не станут размером 2х2, после чего воспользоваться формулой выше.
Обратная матрица
К оглавлению…
Рассмотрим квадратную матрицу А. Матрица A–1 называется обратной к матрице А, если их произведения равны единичной матрице. Обратная матрица существует только для квадратных матриц. Обратная матрица существует, только если матрица А невырождена, то есть ее определитель не равен нулю. В противном случае обратную матрицу посчитать невозможно. Для построения обратной матрицы необходимо:
- Найти определитель матрицы.
- Найти алгебраическое дополнение для каждого элемента матрицы.
- Построить матрицу из алгебраических дополнений и обязательно транспонировать ее. Часто про транспонирование забывают.
- Разделить полученную матрицу на определитель исходной матрицы.
Таким образом, в случае, если матрица А имеет размер 3х3, обратная к ней матрица имеет вид:
Матрицы. Вся теория и задачи с решениями или ответами
К оглавлению…

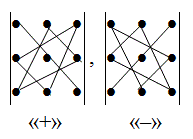
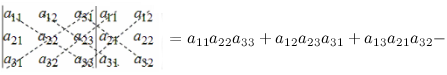
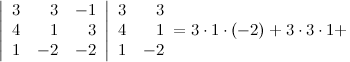
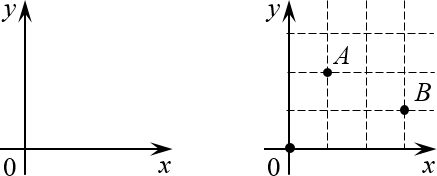
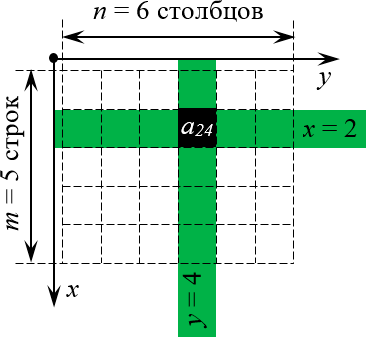
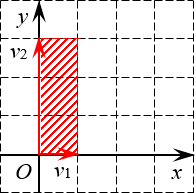
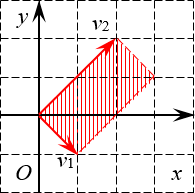
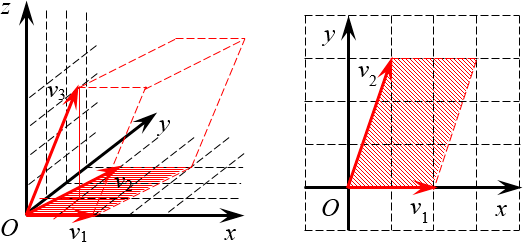
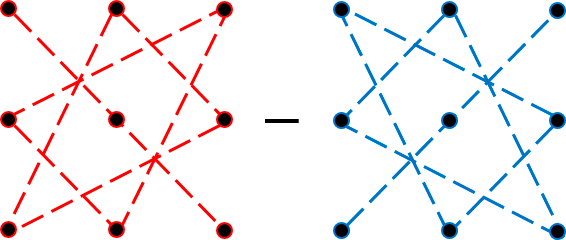
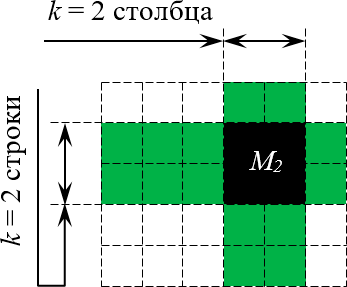

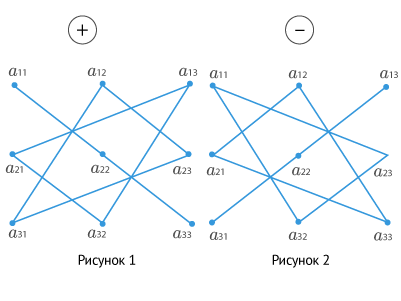
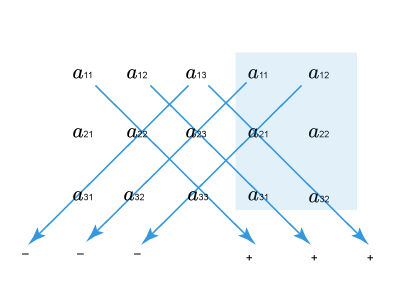














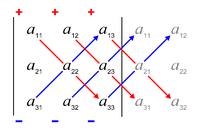



























![{displaystyle det left(A^{-1}right)={frac {1}{det(A)}}=[det(A)]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4f6798a0a88679c1b82126428cf67aae28244fc)














![{displaystyle {sqrt[{n}]{det {!(A+B)}}}geq {sqrt[{n}]{det {!(A)}}}+{sqrt[{n}]{det {!(B)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e77020a4af805fa2f6e3d5b1a1eaab10c936bcb)