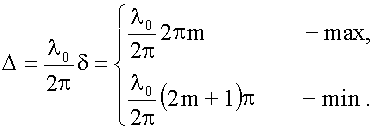Как найти оптическую разность хода интерферирующих лучей - Исправление недочетов и поиск решений вместе с Examum.ru

Оптическая разность хода.

Вместо разности фаз

интерферирующих волн удобно ввести в
рассмотрение пропорциональную ей
величину

— оптическую разность хода, которая
отличается множителем

,
где

— длина световой волны.

Изменению
разности фаз на

соответствует изменение разности хода
на

В
вакууме оптическая разность хода в
отличие от разности фаз имеет наглядную
и
нтерпретацию.
Если две интерферирующие волны испускаются
одним источником света, то разность
хода — это геометрическая разность длин
путей, по которым два интерферирующих
луча от одной точки источника достигли
одной точки экрана.

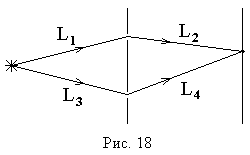
Например,
в оптической схеме опыта Юнга, изображенной
на рис. 18, разность хода для точки P на
экране находится по формуле:

В
изотропной среде скорость света в n
раз меньше, чем в вакууме, здесь n
— показатель преломления среды. Частота
света в среде и в вакууме одинакова,
поэтому длина волны в среде в n
раз меньше. В соответствии с соотношением

вместо реального уменьшения длины волны

можно рассматривать неизменную

и соответствующее увеличение длины
пути луча. С этой целью вводится понятие
оптической длины пути, которая в n
раз больше геометрической длины. Далее,
употребляя термин «разность хода»,
всегда будем иметь в виду оптическую
разность хода.

Заменяя
разность фаз интерферирующих волн
оптической разностью хода, получаем
следующее выражение для интенсивности
интерференционной картины:

Приемники
света в оптическом диапазоне реагируют
на интенсивность света, а не на
напряженность электрического или
магнитного полей. Поэтому измеряемые
в опыте величины, ширина полос и видность,
также могут быть выражены через
интенсивность, а значит и через оптическую
разность хода. Следовательно, понятие
оптической разности хода позволяет
свести оптическую задачу по интерференции
к геометрической задаче отыскания
разности хода.

Отметим,
что разность хода лучей можно отсчитывать
не только как разность длин путей от
источника до точки наблюдения, но и как
разность длин путей от двух точек любой
поверхности равной фазы волны до точки
наблюдения. При этом, конечно, две точки
на поверхности равной фазы — не произвольные
точки, а должны быть точками, через
которые реально проходят лучи, попадающие
в точку наблюдения. Так на рис. 18

,
поэтому две щели находятся на поверхности
равной фазы, и, следовательно, разность
хода можно найти по упрощенной формуле

.
Этот прием часто используется при
решении задач.

18.1.2.1. Условия максимума и минимума на разность фаз δ

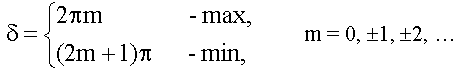
18.1.2.2. Оптическая разность хода

Пусть
для простоты, начальные фазы α₁
и α₂
интерферирующих волн равны нулю, тогда:

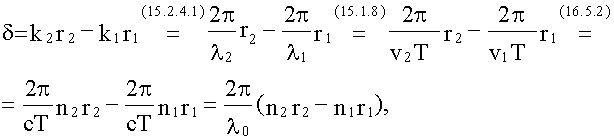
здесь
λ₀ = cT
— длина световой волны в вакууме.

Оптической
разностью хода называют величину:

Тогда:

18.1.2.3. Условия максимума и минимума на оптическую разность хода

Из
(18.1.2.1.)
и (18.1.2.2.):

П
осле
сокращения получим условия на Δ:

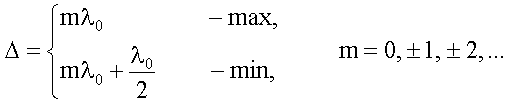
30. Интерференция при отражении от тонких пленок. Пример расчета интерференционной картины для плоскопараллельной пластинки.

Интерференция
— физическое явление, наблюдаемое при
сложении волн (световых, звуковых и т.
п.), усиление волн в одних точках
пространства и ослабление в других (или
сложение двух или более
волн, при котором амплитуда результирующей
волны зависит от разности фаз исходных
волн в данной точке пространства)

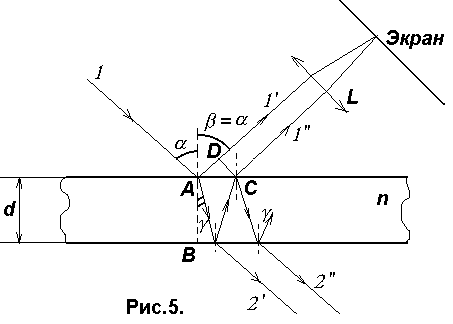
Пусть
на плоскопараллельную прозрачную пленку
(пластинку) с показателем преломления
n и толщиной d под углом 
падает плоская монохроматическая волна
(для простоты рассмотрим один луч).

На
поверхности пленки в точке А волна
частично отражается (луч 1- ) и частично
преломляется (луч АВ). В точке В волна
также частично отражается (луч ВС) и
частично преломляется (луч 2- ). То же
самое происходит в точке С.

Причем
преломленная волна (луч 1″ ) накладывается
на волну непосредственно отраженную
от верхней поверхности (луч 1- ). Эти две
волны когерентны, если оптическая
разность хода

меньше
длины когерентности l_ког, и в этом
случае они интерферируют.

Оптическая
разность хода двух волн =(AB+BC)n-(AD-/2),

где
/2 — потеря полуволны
при отражении луча 1- в точке А. Используя
закон преломления n₁sin
= n₂sin и учитывая,
что в рассматриваемом случае n₁=1,
n₂=n, можно показать, что

.(17)

В
точке наблюдения на экране будет
максимум, если m
и минимум, если (2m+1)/2[см.(15),(16)].

Возможность
уменьшения вредного отражения света
вследствие интерференции в тонких
пленках широко используется в современных
оптических приборах. Для этого на
передние поверхности линз, призм наносят
тонкие пленки с показателем преломления
n=

и толщиной d, которая определяется из
условия минимума при интерференции
волн, отраженных от границ раздела сред
с n₁ и n и n и n₂


2dn=(2m+1)/2,
m=0,1,2-(18)

Минимальная
толщина пленки соответствует m=0

d=/(4n)

Такая
оптика получила название просветленной
оптики.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Интерференция света

Явление интерференции свидетельствует о том, что свет — это волна.

Интерференцией световых волн называется сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.

Условия интерференции

Волны должны быть когерентны. Когерентность – согласованность. В простейшем случае когерентными являются волны одинаковой длины, между которыми существует постоянная разность фаз.

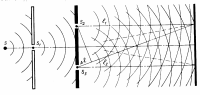
Все источники света, кроме лазера, некогерентны, однако Т. Юнг впервые пронаблюдал (1802) явление интерференции, разделив волну на две с помощью двойной щели.
Свет от точечного монохроматического источника S падал на два небольших отверстия на экране. Эти отверстия действуют как два когерентных источника света S₁ и S₂.
Волны от них интерферируют в области перекрытия, проходя разные пути: ℓ₁ и ℓ_2.
На экране наблюдается чередование светлых и темных полос.

Условие максимума.

Пусть разность хода между двумя точками ,

тогда условие максимума:
т. е. на разности хода волн укладывается четное число полуволн (k= 1, 2, 3, …).

или

Условие минимума

Пусть разность хода между двумя точками ,

тогда условие минимума: ,

т. е. на разности хода волн укладывается нечетное число полуволн (k= 1, 2, 3, …).

Интерференция света в тонких пленках

Различные цвета тонких пленок — результат интерференции двух волн, отражающихся от нижней и верхней поверхностей пленки. При отражении от верхней поверхности пленки происходит потеря полуволны. Следовательно, оптическая разность хода .

Тогда условие максимального усиления интерферирующих лучей в отраженном свете следующее: .

Если потерю полуволны не учитывать, то .

Кольца Ньютона

Интерференционная картина в тонкой прослойке воздуха между стеклянными пластинами — кольца Ньютона.

Волна 1 — результат отражения ее от точки А (граница стекло —воздух). Волна 2 — отражение от плоской пластины (точка В, граница воздух — стекло). Волны когерентны: возникает интерференционная картина в прослойке воздуха между точками А и В в виде-концентрических колец. Зная радиусы колец, можно вычислить длину волны, используя формулу , где r — радиус кольца, R — радиус кривизны выпуклой поверхности линзы.

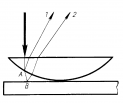
Использование интерференции в технике

Проверка качества обработки поверхности до одной десятой длины волны. Несовершенство обработки определяют но искривлению интерференционных полос, образующихся при отражении света от проверяемой поверхности. Интерферометры служат для точного измерения показателя преломления газов и других веществ, длин световых волн.

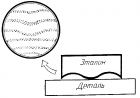
Просветление оптики. Объективы фотоаппаратов и кинопроекторов, перископы подводных лодок и другие оптические устройства состоят из большого числа оптических стекол, линз, призм. Каждая отполированная поверхность стекла отражает около 5% падающего на нее света. Чтобы уменьшить долю отражаемой энергии, используется явление интерференции света.

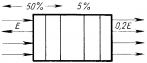
На поверхность оптического стекла наносят тонкую пленку. Для того чтобы волны 1 и 2 ослабляли друг друга, должно выполняться условие минимума. В отраженном свете разность хода волн равна: . Потеря полуволны происходит при отражении как от пленки, так и от стекла (показатель преломления стекла больше, чем пленки), поэтому, эту потерю можно не учитывать. Следовательно, , где n — показатель преломления пленки; h — толщина пленки. Минимальная толщина пленки будет при k=0. Поэтому . При равенстве амплитуд гашение света будет полным. Толщину пленки подбирают так, чтобы полное гашение при нормальном падении имело место для длин волн средней части спектра (для зеленого цвета):

Чтобы рассчитать толщину пленки в этой формуле необходимо взять длину волны и показатель преломления зеленого света.

Лучи красного и фиолетового цвета ослабляются незначительно.поэтому объективы оптических приборов в отраженном свете имеют сиреневые оттенки

Источник

Интерференция света – явление ослабления или усиления интенсивности света в зависимости от соотношения фаз складываемых световых когерентных волн, линейно поляризованных в одной плоскости. Для уровня школьной физики данное определение является излишним. По умолчанию, световые волны являются когерентными и линейно поляризованными.

Таким образом, для нас в задачах на интерференцию важно наличие нескольких (чаще всего двух) волн и разности фаз (разности хода) между ними.

В школьных задачах на интерференцию основным вопросом является результат интерференции в наблюдаемой точке (усиление или ослабление света).

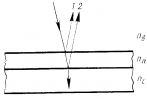
Для математического описания явления интерференции вводят оптическую длину пути ( displaystyle nr ) — произведение показателя преломления среды, по которой проходит свет, на геометрическую длину пути, которую прошёл луч. Тогда для двух лучей (рис. 1):

$displaystyle delta ={{n}_{1}}{{r}_{1}}-{{n}_{2}}{{r}_{2}}$ (1)

где

Рис. 1. Интерференция

Пусть от точечного источника системой зеркал два луча развели по двум областям с различными показателями преломления ( $displaystyle {{n}_{2}}$ и $displaystyle {{r}_{1}}$ ). Пути лучей в этих системах $displaystyle {{r}_{2}}$ и соответственно. Затем, вышедшие из областей, лучи обратно свели в точку displaystyle S' . За счёт того, что в средах с различным показателем преломления луч от одного и того же источника движется с разной скоростью, к одной и той же точке они приходят с ненулевой разностью хода (1).

Тогда результат интерференции (усиление или ослабление света) диктуется соотношениями:

максимум интерференции (максимальное усиление):

displaystyle delta =mlambda (2)

где
минимум интерференции (максимальное ослабление):

$displaystyle delta =(2m-1)frac{lambda }{2}$ (3)

где

Тогда для ответа на вопрос об усилении и ослаблении света можно анализировать приведённое уравнение (2):

$displaystyle m=frac{delta }{lambda }$ (4)

Тогда, если полученное целое или ближе к целому, то в точке наблюдается усиление света, в случае, если полуцелое или близко к полуцелому, в точке displaystyle S' — темнота.

Вывод: фактически задачи на интерференцию сводятся к анализу уравнения (4) и поиску оптической длины пути для (1).

Пример: Оптическая разность хода волн от двух когерентных источников в некоторой точке пространства $displaystyle {{lambda }_{1}}=671,$ мкм. Каков будет результат интерференции в этой точке, если длина волны будет: $displaystyle {{lambda }_{2}}=406,$ нм, $displaystyle {{lambda }_{2}}=406,$ нм.

Исходя из аналитической формулы (4):

$displaystyle {{m}_{1}}=frac{delta }{{{lambda }_{1}}}=frac{8,723*{{10}^{-6}}}{671*{{10}^{-9}}}=13,00$ (5)

$displaystyle {{m}_{2}}=frac{delta }{{{lambda }_{2}}}=frac{8,723*{{10}^{-6}}}{405*{{10}^{-9}}}approx 21,54$ (6)

Таким образом, получившийся параметр $displaystyle {{m}_{2}}$ получился целым числом, это говорит о том, что при данных параметрах в точке соединения лучей будет наблюдаться усиление света. Параметр $displaystyle {{m}_{2}}$ оказался ближе к полуцелому, таким образом, в исследуемой точке будет наблюдаться ослабление света.

Источник