For the orbit of an object around the Moon, see Lunar orbit.
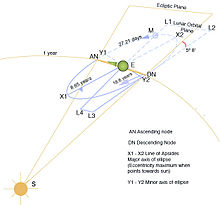
Diagram of the Moon’s orbit with respect to the Earth. While angles and relative sizes are to scale, distances are not. |
|
| Semi-major axis[a] | 384,748 km (239,071 mi)[1] |
|---|---|
| Mean distance[b] | 385,000 km (239,000 mi)[2] |
| Inverse sine parallax[c] | 384,400 km (238,900 mi) |
| Perigee | 363,228.9 km (225,700.0 mi), avg. (356400–370400 km) |
| Apogee | 405,400 km (251,900 mi), avg. (404000–406700 km) |
| Mean eccentricity | 0.0549006 (0.026–0.077)[3] |
| Mean obliquity | 6.687°[5] |
| Mean inclination | |
| of orbit to ecliptic | 5.15° (4.99–5.30)[3] |
| of lunar equator to ecliptic | 1.543° |
| Period of | |
| orbit around Earth (sidereal) | 27.322 days |
| orbit around Earth (synodic) | 29.530 days |
| precession of nodes | 18.5996 years |
| precession of line of apsides | 8.8504 years |
The Moon orbits Earth in the prograde direction and completes one revolution relative to the Vernal Equinox and the stars in about 27.32 days (a tropical month and sidereal month) and one revolution relative to the Sun in about 29.53 days (a synodic month). Earth and the Moon orbit about their barycentre (common centre of mass), which lies about 4,670 km (2,900 mi) from Earth’s centre (about 73% of its radius), forming a satellite system called the Earth–Moon system. On average, the distance to the Moon is about 385,000 km (239,000 mi) from Earth’s centre, which corresponds to about 60 Earth radii or 1.282 light-seconds.
With a mean orbital velocity of 1.022 km/s (0.635 miles/s, 2,286 miles/h),[6] the Moon covers a distance approximately its diameter, or about half a degree on the celestial sphere, each hour. The Moon differs from most satellites of other planets in that its orbit is close to the ecliptic plane instead of to its primary’s (in this case, Earth’s) equatorial plane. The Moon’s orbital plane is inclined by about 5.1° with respect to the ecliptic plane, whereas the Moon’s equatorial plane is tilted by only 1.5°.
Properties[edit]
The properties of the orbit described in this section are approximations. The Moon’s orbit around Earth has many variations (perturbations) due to the gravitational attraction of the Sun and planets, the study of which (lunar theory) has a long history.[7]
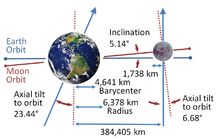
Moon’s orbit and sizes of Earth and Moon to scale.
Elliptic shape[edit]
The orbit of the Moon is a nearly circular ellipse about the Earth (the semimajor and semiminor axes are 384,400 km and 383,800 km, respectively: a difference of only 0.16%). The equation of the ellipse yields an eccentricity of 0.0549 and perigee and apogee distances of 362,600 km and 405,400 km respectively (a difference of 12%).
Since nearer objects appear larger, the Moon’s apparent size changes as it moves toward and away from an observer on Earth. An event referred to as a «supermoon» occurs when the full Moon is at its closest to Earth (perigee). The largest possible apparent diameter of the Moon is the same 12% larger (as perigee versus apogee distances) than the smallest; the apparent area is 25% more and so is the amount of light it reflects toward Earth.
The variance in the Moon’s orbital distance corresponds with changes in its tangential and angular speeds, as stated in Kepler’s second law. The mean angular movement relative to an imaginary observer at the Earth–Moon barycentre is 13.176° per day to the east (J2000.0 epoch).
Minimum, mean and maximum distances of the Moon from Earth with its angular diameter as seen from Earth’s surface, to scale. Scroll to right to see moon.
Elongation[edit]
The Moon’s elongation is its angular distance east of the Sun at any time. At new moon, it is zero and the Moon is said to be in conjunction. At full moon, the elongation is 180° and it is said to be in opposition. In both cases, the Moon is in syzygy, that is, the Sun, Moon and Earth are nearly aligned. When elongation is either 90° or 270°, the Moon is said to be in quadrature.
Precession[edit]
Apsidal precession—The major axis of Moon’s elliptical orbit rotates by one complete revolution once every 8.85 years in the same direction as the Moon’s rotation itself. This image looks upwards depicting Earth’s geographic south pole and the elliptical shape of the Moon’s orbit (vastly exaggerated from its almost circular shape to make the precession evident) is rotating from white to greyer orbits.
Animation of Moon orbit around Earth
Moon ·
Earth
Top: polar view; bottom: equatorial view
Earth’s lunar orbit perturbations
The orientation of the orbit is not fixed in space but rotates over time. This orbital precession is called apsidal precession and is the rotation of the Moon’s orbit within the orbital plane, i.e. the axes of the ellipse change direction. The lunar orbit’s major axis – the longest diameter of the orbit, joining its nearest and farthest points, the perigee and apogee, respectively – makes one complete revolution every 8.85 Earth years, or 3,232.6054 days, as it rotates slowly in the same direction as the Moon itself (direct motion) – meaning precesses eastward by 360°. The Moon’s apsidal precession is distinct from the nodal precession of its orbital plane and axial precession of the moon itself.
Inclination[edit]
Orbital inclination—the Moon’s orbit is inclined by 5.14° to the ecliptic. This shows the specific configuration at major northern lunistice. At such times, the earth’s north pole is toward the moon and the moon is north of the ecliptic.
The mean inclination of the lunar orbit to the ecliptic plane is 5.145°. Theoretical considerations show that the present inclination relative to the ecliptic plane arose by tidal evolution from an earlier near-Earth orbit with a fairly constant inclination relative to Earth’s equator.[8] It would require an inclination of this earlier orbit of about 10° to the equator to produce a present inclination of 5° to the ecliptic. It is thought that originally the inclination to the equator was near zero, but it could have been increased to 10° through the influence of planetesimals passing near the Moon while falling to the Earth.[9] If this had not happened, the Moon would now lie much closer to the ecliptic and eclipses would be much more frequent.[10]
The rotational axis of the Moon is not perpendicular to its orbital plane, so the lunar equator is not in the plane of its orbit, but is inclined to it by a constant value of 6.688° (this is the obliquity). As was discovered by Jacques Cassini in 1722, the rotational axis of the Moon precesses with the same rate as its orbital plane, but is 180° out of phase (see Cassini’s Laws). Therefore, the angle between the ecliptic and the lunar equator is always 1.543°, even though the rotational axis of the Moon is not fixed with respect to the stars.[11] It also means that when the moon is farthest north of the ecliptic, the centre of the part we see is about 6.7° south of the lunar equator and the south pole is visible, whereas when the moon is farthest south of the ecliptic the centre of the visible part is 6.7° north of the equator and the north pole is visible. This is called libration in latitude.
Nodes[edit]
The nodes are points at which the Moon’s orbit crosses the ecliptic. The Moon crosses the same node every 27.2122 days, an interval called the draconic month or draconitic month. The line of nodes, the intersection between the two respective planes, has a retrograde motion: for an observer on Earth, it rotates westward along the ecliptic with a period of 18.6 years or 19.3549° per year. When viewed from the celestial north, the nodes move clockwise around Earth, opposite to Earth’s own spin and its revolution around the Sun. An Eclipse of the Moon or Sun can occur when the nodes align with the Sun, roughly every 173.3 days. Lunar orbit inclination also determines eclipses; shadows cross when nodes coincide with full and new moon when the Sun, Earth, and Moon align in three dimensions.
In effect, this means that the «tropical year» on the Moon is only 347 days long. This is called the draconic year or eclipse year. The «seasons» on the Moon fit into this period. For about half of this draconic year, the Sun is north of the lunar equator (but at most 1.543°), and for the other half, it is south of the lunar equator. Obviously, the effect of these seasons is minor compared to the difference between lunar night and lunar day. At the lunar poles, instead of usual lunar days and nights of about 15 Earth days, the Sun will be «up» for 173 days as it will be «down»; polar sunrise and sunset takes 18 days each year. «Up» here means that the centre of the Sun is above the horizon.[12] Lunar polar sunrises and sunsets occur around the time of eclipses (solar or lunar). For example, at the Solar eclipse of March 9, 2016, the Moon was near its descending node, and the Sun was near the point in the sky where the equator of the Moon crosses the ecliptic. When the Sun reaches that point, the centre of the Sun sets at the lunar north pole and rises at the lunar south pole.
The solar eclipse of September 1 of the same year, the Moon was near its ascending node, and the Sun was near the point in the sky where the equator of the Moon crosses the ecliptic. When the Sun reaches that point, the centre of the Sun rises at the lunar north pole and sets at the lunar south pole.
Inclination to the equator and lunar standstill[edit]
Every 18.6 years, the angle between the Moon’s orbit and Earth’s equator reaches a maximum of 28°36′, the sum of Earth’s equatorial tilt (23°27′) and the Moon’s orbital inclination (5°09′) to the ecliptic. This is called major lunar standstill. Around this time, the Moon’s declination will vary from −28°36′ to +28°36′. Conversely, 9.3 years later, the angle between the Moon’s orbit and Earth’s equator reaches its minimum of 18°20′. This is called a minor lunar standstill. The last lunar standstill was a minor standstill in October 2015. At that time the descending node was lined up with the equinox (the point in the sky having right ascension zero and declination zero). The nodes are moving west by about 19° per year. The Sun crosses a given node about 20 days earlier each year.
When the inclination of the Moon’s orbit to the Earth’s equator is at its minimum of 18°20′, the centre of the Moon’s disk will be above the horizon every day from latitudes less than 70°43′ (90° − 18°20′ – 57′ parallax) north or south. When the inclination is at its maximum of 28°36′, the centre of the Moon’s disk will be above the horizon every day only from latitudes less than 60°27′ (90° − 28°36′ – 57′ parallax) north or south.
At higher latitudes, there will be a period of at least one day each month when the Moon does not rise, but there will also be a period of at least one day each month when the Moon does not set. This is similar to the seasonal behaviour of the Sun, but with a period of 27.2 days instead of 365 days. Note that a point on the Moon can actually be visible when it is about 34 arc minutes below the horizon, due to atmospheric refraction.
Because of the inclination of the Moon’s orbit with respect to the Earth’s equator, the Moon is above the horizon at the North and South Pole for almost two weeks every month, even though the Sun is below the horizon for six months at a time. The period from moonrise to moonrise at the poles is a tropical month, about 27.3 days, quite close to the sidereal period. When the Sun is the furthest below the horizon (winter solstice), the Moon will be full when it is at its highest point. When the Moon is in Gemini it will be above the horizon at the North Pole, and when it is in Sagittarius it will be up at the South Pole.
The Moon’s light is used by zooplankton in the Arctic when the Sun is below the horizon for months[13] and must have been helpful to the animals that lived in Arctic and Antarctic regions when the climate was warmer.
Scale model[edit]
Scale model of the Earth–Moon system: Sizes and distances are to scale. It represents the mean distance of the orbit and the mean radii of both bodies. Scroll to right to find Moon.
History of observations and measurements[edit]
The apparent trajectory of the Moon in the sky seen from Earth each night is like a wide ellipse, although the path depends on the time of the year and latitude.
About 1000 BC, the Babylonians were the first human civilization known to have kept a consistent record of lunar observations. Clay tablets from that period, which have been found over the territory of present-day Iraq, are inscribed with cuneiform writing recording the times and dates of moonrises and moonsets, the stars that the Moon passed close by, and the time differences between rising and setting of both the Sun and the Moon around the time of the full moon. Babylonian astronomy discovered the three main periods of the Moon’s motion and used data analysis to build lunar calendars that extended well into the future.[7] This use of detailed, systematic observations to make predictions based on experimental data may be classified as the first scientific study in human history. However, the Babylonians seem to have lacked any geometrical or physical interpretation of their data, and they could not predict future lunar eclipses (although «warnings» were issued before likely eclipse times).
Ancient Greek astronomers were the first to introduce and analyze mathematical models of the motion of objects in the sky. Ptolemy described lunar motion by using a well-defined geometric model of epicycles and evection.[7]
Sir Isaac Newton was the first to develop a complete theory of motion, mechanics. The observations of the lunar motion were the main test of his theory.[7]
Lunar periods[edit]
| Name | Value (days) | Definition |
|---|---|---|
| Sidereal month | 27.321662 | with respect to the distant stars (13.36874634 passes per solar orbit) |
| Synodic month | 29.530589 | with respect to the Sun (phases of the Moon, 12.36874634 passes per solar orbit) |
| Tropical month | 27.321582 | with respect to the vernal point (precesses in ~26,000 years) |
| Anomalistic month | 27.554550 | with respect to the perigee (precesses in 3232.6054 days = 8.850578 years) |
| Draconic month | 27.212221 | with respect to the ascending node (precesses in 6793.4765 days = 18.5996 years)[citation needed] |
There are several different periods associated with the lunar orbit.[14] The sidereal month is the time it takes to make one complete orbit around Earth with respect to the fixed stars. It is about 27.32 days. The synodic month is the time it takes the Moon to reach the same visual phase. This varies notably throughout the year,[15] but averages around 29.53 days. The synodic period is longer than the sidereal period because the Earth–Moon system moves in its orbit around the Sun during each sidereal month, hence a longer period is required to achieve a similar alignment of Earth, the Sun, and the Moon. The anomalistic month is the time between perigees and is about 27.55 days. The Earth–Moon separation determines the strength of the lunar tide raising force.
The draconic month is the time from ascending node to ascending node. The time between two successive passes of the same ecliptic longitude is called the tropical month. The latter periods are slightly different from the sidereal month.
The average length of a calendar month (a twelfth of a year) is about 30.4 days. This is not a lunar period, though the calendar month is historically related to the visible lunar phase.
Tidal evolution[edit]
The gravitational attraction that the Moon exerts on Earth is the cause of tides in both the ocean and the solid Earth; the Sun has a smaller tidal influence. The solid Earth responds quickly to any change in the tidal forcing, the distortion taking the form of an ellipsoid with the high points roughly beneath the Moon and on the opposite side of Earth. This is a result of the high speed of seismic waves within the solid Earth.
However the speed of seismic waves is not infinite and, together with the effect of energy loss within the Earth, this causes a slight delay between the passage of the maximum forcing due to the Moon across and the maximum Earth tide. As the Earth rotates faster than the Moon travels around its orbit, this small angle produces a gravitational torque which slows the Earth and accelerates the Moon in its orbit.
In the case of the ocean tides, the speed of tidal waves in the ocean[16] is far slower than the speed of the Moon’s tidal forcing. As a result, the ocean is never in near equilibrium with the tidal forcing. Instead, the forcing generates the long ocean waves which propagate around the ocean basins until eventually losing their energy through turbulence, either in the deep ocean or on shallow continental shelves.
Although the ocean’s response is the more complex of the two, it is possible to split the ocean tides into a small ellipsoid term which affects the Moon plus a second term which has no effect. The ocean’s ellipsoid term also slows the Earth and accelerates the Moon, but because the ocean dissipates so much tidal energy, the present ocean tides have an order of magnitude greater effect than the solid Earth tides.
Because of the tidal torque, caused by the ellipsoids, some of Earth’s angular (or rotational) momentum is gradually being transferred to the rotation of the Earth–Moon pair around their mutual centre of mass, called the barycentre. See tidal acceleration for a more detailed description.
This slightly greater orbital angular momentum causes the Earth–Moon distance to increase at approximately 38 millimetres per year.[17] Conservation of angular momentum means that Earth’s axial rotation is gradually slowing, and because of this its day lengthens by approximately 24 microseconds every year (excluding glacial rebound). Both figures are valid only for the current configuration of the continents. Tidal rhythmites from 620 million years ago show that, over hundreds of millions of years, the Moon receded at an average rate of 22 mm (0.87 in) per year (2200 km or 0.56% or the Earth-moon distance per hundred million years) and the day lengthened at an average rate of 12 microseconds per year (or 20 minutes per hundred million years), both about half of their current values.
The present high rate may be due to near resonance between natural ocean frequencies and tidal frequencies.[18] Another explanation is that in the past the Earth rotated much faster, a day possibly lasting only 9 hours on the early Earth. The resulting tidal waves in the ocean would have then been much shorter and it would have been more difficult for the long wavelength tidal forcing to excite the short wavelength tides.[19]
The Moon is gradually receding from Earth into a higher orbit, and calculations suggest that this would continue for about 50 billion years.[20][21] By that time, Earth and the Moon would be in a mutual spin–orbit resonance or tidal locking, in which the Moon will orbit Earth in about 47 days (currently 27 days), and both the Moon and Earth would rotate around their axes in the same time, always facing each other with the same side. This has already happened to the Moon—the same side always faces Earth—and is also slowly happening to the Earth. However, the slowdown of Earth’s rotation is not occurring fast enough for the rotation to lengthen to a month before other effects change the situation: approximately 2.3 billion years from now, the increase of the Sun’s radiation will have caused Earth’s oceans to evaporate,[22] removing the bulk of the tidal friction and acceleration.
Libration[edit]
Animation of the Moon as it cycles through its phases. The apparent wobbling of the Moon is known as libration.
The Moon is in synchronous rotation, meaning that it keeps the same face toward Earth at all times. This synchronous rotation is only true on average because the Moon’s orbit has a definite eccentricity. As a result, the angular velocity of the Moon varies as it orbits Earth and hence is not always equal to the Moon’s rotational velocity which is more constant. When the Moon is at its perigee, its orbital motion is faster than its rotation. At that time the Moon is a bit ahead in its orbit with respect to its rotation about its axis, and this creates a perspective effect which allows us to see up to eight degrees of longitude of its eastern (right) far side. Conversely, when the Moon reaches its apogee, its orbital motion is slower than its rotation, revealing eight degrees of longitude of its western (left) far side. This is referred to as optical libration in longitude.
The Moon’s axis of rotation is inclined by in total 6.7° relative to the normal to the plane of the ecliptic. This leads to a similar perspective effect in the north–south direction that is referred to as optical libration in latitude, which allows one to see almost 7° of latitude beyond the pole on the far side. Finally, because the Moon is only about 60 Earth radii away from Earth’s centre of mass, an observer at the equator who observes the Moon throughout the night moves laterally by one Earth diameter. This gives rise to a diurnal libration, which allows one to view an additional one degree’s worth of lunar longitude. For the same reason, observers at both of Earth’s geographical poles would be able to see one additional degree’s worth of libration in latitude.
Besides these «optical librations» caused by the change in perspective for an observer on Earth, there are also «physical librations» which are actual nutations of the direction of the pole of rotation of the Moon in space: but these are very small.
Path of Earth and Moon around Sun[edit]
Section of Earth’s and Moon’s trajectories around the Sun[23]
When viewed from the north celestial pole (i.e., from the approximate direction of the star Polaris) the Moon orbits Earth anticlockwise and Earth orbits the Sun anticlockwise, and the Moon and Earth rotate on their own axes anticlockwise.
The right-hand rule can be used to indicate the direction of the angular velocity. If the thumb of the right hand points to the north celestial pole, its fingers curl in the direction that the Moon orbits Earth, Earth orbits the Sun, and the Moon and Earth rotate on their own axes.
In representations of the Solar System, it is common to draw the trajectory of Earth from the point of view of the Sun, and the trajectory of the Moon from the point of view of Earth. This could give the impression that the Moon orbits Earth in such a way that sometimes it goes backwards when viewed from the Sun’s perspective. However, because the orbital velocity of the Moon around Earth (1 km/s) is small compared to the orbital velocity of Earth about the Sun (30 km/s), this never happens. There are no rearward loops in the Moon’s solar orbit.
Considering the Earth–Moon system as a binary planet, its centre of gravity is within Earth, about 4,671 km (2,902 mi)[24] or 73.3% of the Earth’s radius from the centre of the Earth. This centre of gravity remains on the line between the centres of the Earth and Moon as the Earth completes its diurnal rotation. The path of the Earth–Moon system in its solar orbit is defined as the movement of this mutual centre of gravity around the Sun. Consequently, Earth’s centre veers inside and outside the solar orbital path during each synodic month as the Moon moves in its orbit around the common centre of gravity.[25]
The Sun’s gravitational effect on the Moon is more than twice that of Earth’s on the Moon; consequently, the Moon’s trajectory is always convex[25][26] (as seen when looking Sunward at the entire Sun–Earth–Moon system from a great distance outside Earth–Moon solar orbit), and is nowhere concave (from the same perspective) or looped.[23][25] That is, the region enclosed by the Moon’s orbit of the Sun is a convex set.
See also[edit]
- Ernest William Brown
- Double planet
- List of orbits
- ELP2000
- Ephemeris
- Jet Propulsion Laboratory Development Ephemeris
- Lunar Laser Ranging experiment
- Milankovitch cycles
- Orbital elements
Notes[edit]
- ^ The geometric mean distance in the orbit (of ELP) which is the semimajor axis of the Moon’s elliptical orbit via Kepler’s laws.
- ^ The constant in the ELP expressions for the distance, which is the mean distance averaged over time.
- ^ The inverse sine parallax ɑ/sin π is traditionally the Moon’s mean distance from Earth (center to center), where ɑ is Earth’s equatorial radius, and π is the Moon’s parallax between the ends of ɑ.[3] Three of the IAU 1976 Astronomical Constants were «mean distance of Moon from Earth» 384,400 km, «equatorial horizontal parallax at mean distance» 3422.608″, and «equatorial radius for Earth» 6,378.14 km.[4]
References[edit]
- ^ M. Chapront-Touzé; J. Chapront (1983). «The lunar ephemeris ELP-2000». Astronomy & Astrophysics. 124: 54. Bibcode:1983A&A…124…50C.
- ^ M. Chapront-Touzé; J. Chapront (1988). «ELP2000-85: a semi-analytical lunar ephemeris adequate for historical times». Astronomy & Astrophysics. 190: 351. Bibcode:1988A&A…190..342C.
- ^ a b c Meeus, Jean (1997), Mathematical Astronomy Morsels, Richmond, VA: Willmann-Bell, pp. 11–12, 22–23, ISBN 0-943396-51-4
- ^ Seidelmann, P. Kenneth, ed. (1992), Explanatory Supplement to the Astronomical Almanac, University Science Books, pp. 696, 701, ISBN 0-935702-68-7
- ^
Lang, Kenneth R. (2011), The Cambridge Guide to the Solar System, 2nd ed., Cambridge University Press. - ^ «Moon Fact Sheet». NASA. Retrieved 2014-01-08.
- ^ a b c d Martin C. Gutzwiller (1998). «Moon-Earth-Sun: The oldest three-body problem». Reviews of Modern Physics. 70 (2): 589–639. Bibcode:1998RvMP…70..589G. doi:10.1103/RevModPhys.70.589.
- ^ Peter Goldreich (Nov 1966). «History of the Lunar Orbit». Reviews of Geophysics. 4 (4): 411. Bibcode:1966RvGSP…4..411G. doi:10.1029/RG004i004p00411. Jihad Touma & Jack Wisdom (Nov 1994). «Evolution of the Earth-Moon system». The Astronomical Journal. 108: 1943. Bibcode:1994AJ….108.1943T. doi:10.1086/117209.
- ^ Kaveh Pahlevan & Alessandro Morbidelli (Nov 26, 2015). «Collisionless encounters and the origin of the lunar inclination». Nature. 527 (7579): 492–494. arXiv:1603.06515. Bibcode:2015Natur.527..492P. doi:10.1038/nature16137. PMID 26607544. S2CID 4456736.
- ^ Jacob Aron (Nov 28, 2015). «Flying gold knocked the moon off course and ruined eclipses». New Scientist.
- ^ «View of the Moon». U. of Arkansas at Little Rock. Retrieved May 9, 2016.
- ^ Calculated from arcsin(0.25°/1.543°)/90° times 173 days, since the angular radius of the Sun is about 0.25°.
- ^ «Moonlight helps plankton escape predators during Arctic winters». New Scientist. Jan 16, 2016.
- ^ The periods are calculated from orbital elements, using the rate of change of quantities at the instant J2000. The J2000 rate of change equals the coefficient of the first-degree term of VSOP polynomials. In the original VSOP87 elements, the units are arcseconds(”) and Julian centuries. There are 1,296,000” in a circle, 36525 days in a Julian century. The sidereal month is the time of a revolution of longitude λ with respect to the fixed J2000 equinox. VSOP87 gives 1732559343.7306” or 1336.8513455 revolutions in 36525 days–27.321661547 days per revolution. The tropical month is similar, but the longitude for the equinox of date is used. For the anomalistic year, the mean anomaly (λ−ω) is used (equinox does not matter). For the draconic month, (λ−Ω) is used. For the synodic month, the sidereal period of the mean Sun (or Earth) and the Moon. The period would be 1/(1/m−1/e). VSOP elements from
Simon, J.L.; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (February 1994). «Numerical expressions for precession formulae and mean elements for the Moon and planets». Astronomy and Astrophysics. 282 (2): 669. Bibcode:1994A&A…282..663S. - ^ Jean Meeus, Astronomical Algorithms (Richmond, VA: Willmann-Bell, 1998) p 354. From 1900–2100, the shortest time from one new moon to the next is 29 days, 6 hours, and 35 min, and the longest 29 days, 19 hours, and 55 min.
- ^ J.B. Zirkir (2013). The Science of Ocean Waves. Johns Hopkins University Press. p. 264. ISBN 9781421410784.
- ^ Williams, James G.; Boggs, Dale H. (2016). «Secular tidal changes in lunar orbit and Earth rotation». Celestial Mechanics and Dynamical Astronomy. 126 (1): 89–129. Bibcode:2016CeMDA.126…89W. doi:10.1007/s10569-016-9702-3. ISSN 0923-2958. S2CID 124256137.
- ^ Williams, George E. (2000). «Geological constraints on the Precambrian history of Earth’s rotation and the Moon’s orbit». Reviews of Geophysics. 38 (1): 37–60. Bibcode:2000RvGeo..38…37W. doi:10.1029/1999RG900016. S2CID 51948507.
- ^ Webb, David J. (1982). «Tides and the evolution of the Earth-Moon system». Geophysical Journal of the Royal Astronomical Society. 70 (1): 261–271. Bibcode:1982GeoJ…70..261W. doi:10.1111/j.1365-246X.1982.tb06404.x.
- ^ C.D. Murray; S.F. Dermott (1999). Solar System Dynamics. Cambridge University Press. p. 184.
- ^ Dickinson, Terence (1993). From the Big Bang to Planet X. Camden East, Ontario: Camden House. pp. 79–81. ISBN 0-921820-71-2.
- ^ Caltech Scientists Predict Greater Longevity for Planets with Life Archived 2012-03-30 at the Wayback Machine
- ^ a b The reference by H. L. Vacher (2001) (details separately cited in this list) describes this as ‘convex outward’, whereas older references such as «The Moon’s Orbit Around the Sun, Turner, A. B. Journal of the Royal Astronomical Society of Canada, Vol. 6, p. 117, 1912JRASC…6..117T»; and «H Godfray, Elementary Treatise on the Lunar Theory» describe the same geometry by the words concave to the sun.
- ^ Seidelmann, P. Kenneth, ed. (1992), Explanatory Supplement to the Astronomical Almanac, University Science Books, p. 701, ISBN 0-935702-68-7
- ^ a b c «The Orbit of the Moon around the Sun is Convex!». Archived from the original on 31 March 2004. Retrieved 2022-04-14.
- ^ The Moon Always Veers Toward the Sun at MathPages
External links[edit]
- View of the Moon Good diagrams of Moon, Earth, tilts of orbits and axes, courtesy of U. of Arkansas
Светлой памяти моего учителя — первого декана физико-математического факультета Новочеркасского политехнического института, заведующего кафедрой «Теоретическая механика» Кабелькова Александра Николаевича
Введение
Август, лето подходит к концу. Народ яростно рванул на моря, да оно и неудивительно — самый сезон. А на Хабре, тем временем, буйным цветом распускается и пахнет лженаука. Если говорить о теме данного выпуска «Моделирования…», то в нем мы совместим приятное с полезным — продолжим обещанный цикл и совсем чуть-чуть поборемся с этой самой лженаукой за пытливые умы современной молодежи.
А вопрос ведь действительной не праздный — со школьных лет мы привыкли считать, что наш ближайший спутник в космическом пространстве — Луна движется вокруг Земли с периодом 29,5 суток, особенно не вдаваясь в сопутствующие подробности. На самом же деле наша соседка своеобразный и в какой-то степени уникальный астрономический объект, с движением которого вокруг Земли не всё так просто, как, возможно хотелось бы некоторым моим коллегам из ближайшего зарубежья.
Итак, оставив полемику в стороне, попытаемся с разных сторон, в меру своей компетенции, рассмотреть эту безусловно красивую, интересную и очень показательную задачу.
1. Закон всемирного тяготения и какие выводы мы можем из него сделать
Открытый ещё во второй половине 17 века, сэром Исааком Ньютоном, закон всемирного тяготения говорит о том, что Луна притягивается к Земле (и Земля к Луне!) с силой, направленной вдоль прямой, соединяющей центры рассматриваемых небесных тел, и равной по модулю
где m1, m2 — массы, соответственно Луны и Земли; G = 6,67e-11 м3/(кг * с2) — гравитационная постоянная; r1,2 — расстояние между центрами Луны и Земли. Если принимать во внимание только эту силу, то, решив задачу о движении Луны как спутника Земли и научившись рассчитывать положение Луны на небе на фоне звезд, мы довольно скоро убедимся, путем прямых измерений экваториальных координат Луны, что в нашей консерватории не всё так гладко как хотелось бы. И дело здесь не в законе всемирного тяготения (а на ранних этапах развития небесной механики такие мысли высказывались весьма нередко), а в неучтенном возмущении движения Луны со стороны других тел. Каких? Смотрим на небо и наш взгляд сразу упирается в здоровенный, массой аж 1,99e30 килограмм плазменный шар прямо у нас под носом — Солнце. Луна притягивается к Солнцу? Ещё как, с силой, равной по модулю
где m3 — масса Солнца; r1,3 — расстояние от Луны до Солнца. Сравним эту силу с предыдущей
Возьмем положение тел, в котором притяжение Луны к Солнцу будет минимальным: все три тела на одной прямой и Земля располагается между Луной и Солнцем. В этом случае наша формула примет вид:
где
, м — среднее расстояние от Земли до Луны;
, м — среднее расстояние от Земли до Солнца. Подставим в эту формулу реальные параметры
Вот это номер! Получается Луна притягивается к Солнцу силой, более чем в два раза превышающей силу её притяжения к Земле.
Подобное возмущение уже нельзя не учитывать и оно определенно повлияет на конечную траекторию движения Луны. Пойдем дальше, принимая во внимание допущение о том, что орбита Земли круговая с радиусом a, найдем геометрическое место точек вокруг Земли, где сила притяжения любого объекта к Земле равна силе его притяжения к Солнцу. Это будет сфера, с радиусом
смещенная вдоль прямой, соединяющей Землю и Солнце в сторону противоположенную направлению на Солнце на расстояние
где
— отношение массы Земли к массе Солнца. Подставив численные значения параметров получим фактические размеры данной области: R = 259300 километров, и l = 450 километров. Эта сфера носит название сферы тяготения Земли относительно Солнца.
Известная нам орбита Луны лежит вне этой области. То есть в любой точке траектории Луна испытывает со стороны Солнца существенно большее притяжение, чем со стороны Земли.
2. Спутник или планета? Гравитационная сфера действия
Эта информация, часто порождает споры, о том, что Луна не спутник Земли, а самостоятельная планета Солнечной системы, орбита которой возмущена притяжением близкой Земли.
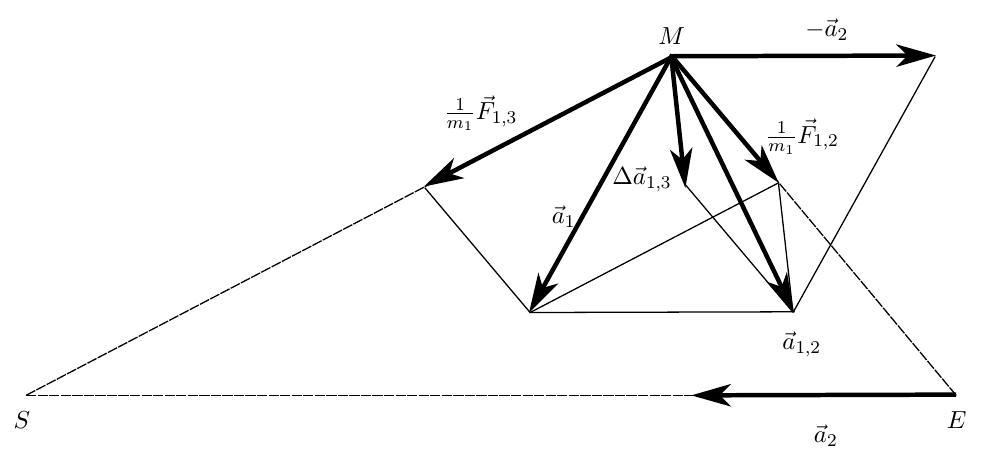
Оценим возмущение, вносимое Солнцем в траекторию Луны относительно Земли, а так же возмущение, вносимое Землей в траекторию Луны относительно Солнца, воспользовавшись критерием, предложенным П. Лапласом. Рассмотрим три тела: Солнце (S), Землю (E) и Луну (M).
Примем допущение, что орбиты Земли относительно Солнца и Луны относительно Земли являются круговыми.
Рассмотрим движение Луны в геоцентрической инерциальной системе отсчета. Абсолютное ускорение Луны в гелиоцентрической системе отсчета определяется действующими на неё силами тяготения и равно:
С другой стороны, в соответствии с теоремой Кориолиса, абсолютное ускорение Луны
где
— переносное ускорение, равное ускорению Земли относительно Солнца;
— ускорение Луны относительно Земли. Ускорения Кориолиса здесь не будет — выбранная нами система координат движется поступательно. Отсюда получаем ускорение Луны относительно Земли
Часть этого ускорения, равная
обусловлена притяжением Луны к Земле и характеризует её невозмущенное геоцентрическое движение. Оставшаяся часть
ускорение Луны, вызванное возмущением со стороны Солнца.
Если рассматривать движение Луны в гелиоцентрической инерциальной системе отсчета, то всё намного проще, ускорение
характеризует невозмущенное гелиоцентрическое движение Луны, а ускорение
— возмущение этого движения со стороны Земли.
При существующих в текущую эпоху параметрах орбит Земли и Луны, в каждой точке траектории Луны справедливо неравенство
что можно проверить и непосредственным вычислением, но я сошлюсь на источник, дабы излишне не загромождать статью.
Что означает неравенство (1)? Да то, что в относительном выражении эффект от возмущения Луны Солнцем (причем очень существенно) меньше эффекта от притяжения Луны к Земле. И наоборот, возмущение Землей геолиоцентрической траектории Луны оказывает решающее влияние на характер её движения. Влияние земной гравитации в данном случае более существенно, а значит Луна «принадлежит» Земле по праву и является её спутником.
Интересным является другое — превратив неравенство (1) в уравнение можно найти геометрическое место точек, где эффекты возмущения Луны (да и любого другого тела) Землей и Солнцем одинаковы. К сожалению это у же не так просто, как в случае со сферой тяготения. Расчеты показывают, что данная поверхность описывается уравнением сумасшедшего порядка, но близка к эллипсоиду вращения. Всё что мы может сделать без лишних заморочек, это оценить общие габариты этой поверхности относительно центра Земли. Решая численно уравнение
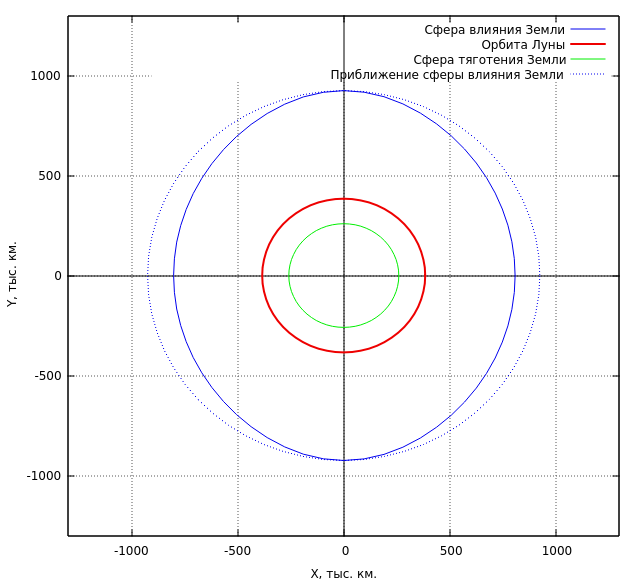
относительно расстояния от центра Земли до искомой поверхности на достаточном количестве точек, получаем сечение искомой поверхности плоскостью эклиптики
Для наглядности здесь показаны и геоцентрическая орбита Луны и, найденная нами выше сфера тяготения Земли относительно Солнца. Из рисунка видно, что сфера влияния, или сфера гравитационного действия Земли относительно Солнца есть поверхность вращения относительно оси X, сплющенная вдоль прямой, соединяющей Землю и Солнце (вдоль оси затмений). Орбита Луны находится глубоко внутри этой воображаемой поверхности.
Для практических расчетов данную поверхность удобно аппроксимировать сферой с центром в центра Земли и радиусом равным
где m — масса меньшего небесного тела; M — масса большего тела, в поле тяготения которого движется меньшее тело; a — расстояние между центрами тел. В нашем случае
Вот этот недоделанный миллион километров и есть тот теоретический предел, за который власть старушки Земли не распространяется — её влияние на траектории астрономических объектов настолько мало, что им можно пренебречь. А значит, запустить Луну по круговой орбите на расстоянии 38,4 млн. километров от Земли (как делают некоторые лингвисты) не получится, это физически невозможно.
Эта сфера, для сравнения, показана на рисунке синей пунктирной линией. При оценочных расчетах принято считать, что тело, находящееся внутри данной сферы будет испытывать тяготение исключительно со стороны Земли. Если тело находится снаружи данной сферы — считаем что тело движется в поле тяготения Солнца. В практической космонавтике известен метод сопряжения конических сечений, позволяющий приближенно рассчитать траекторию космического аппарата, используя решение задачи двух тел. При этом всё пространство, которое преодолевает аппарат разбивается на подобные сферы влияния.
Например, теперь понятно, для того чтобы иметь теоретическую возможность совершить маневры для выхода на окололунную орбиту, космический аппарат должен попасть внутрь сферы действия Луны относительно Земли. Её радиус легко рассчитать по формуле (3) и он равен 66 тысяч километров.
Таким образом, Луна справедливо может считаться спутником Земли. Однако, ввиду существенно влияния гравитационного поля Солнца она движется не в центральном гравитационном поле, а значит её траектория не является коническим сечением.
3. Задача трех тел в классической постановке
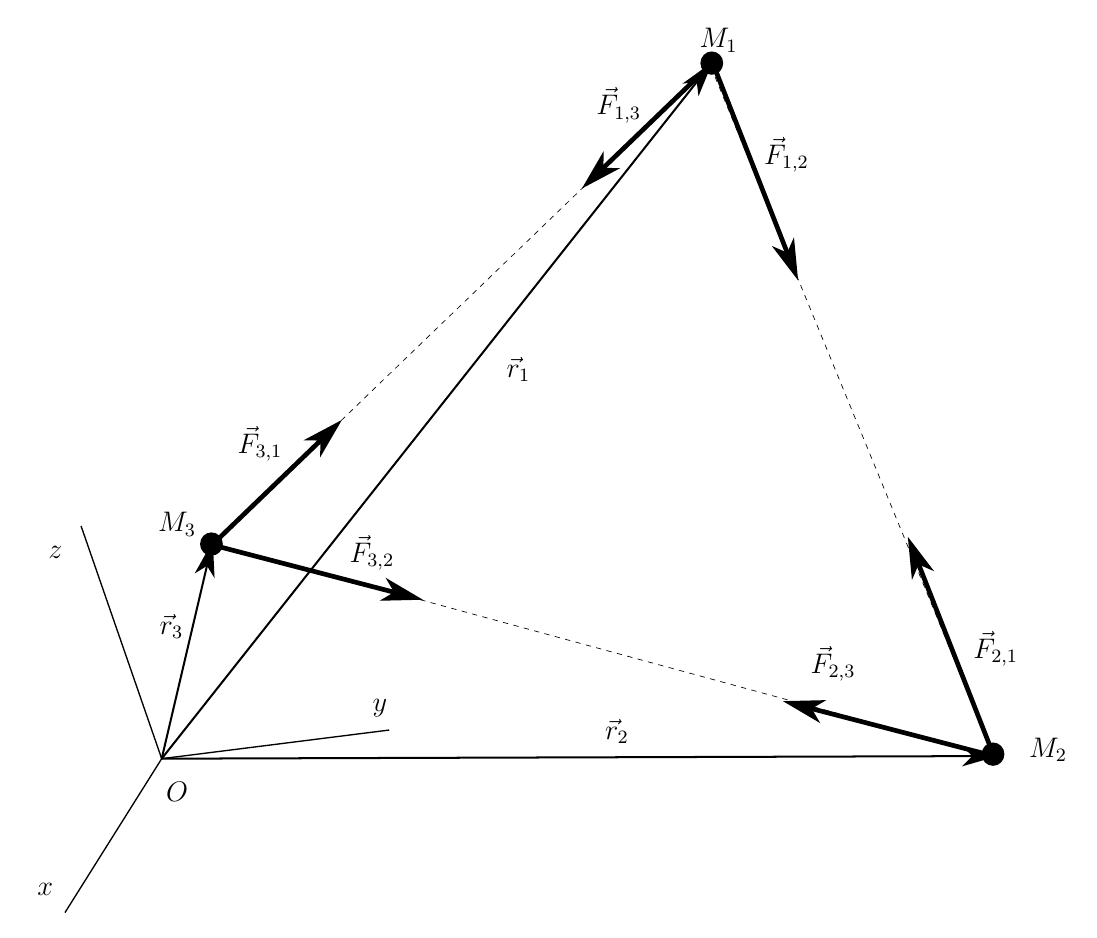
Итак, рассмотрим модельную задачу в общей постановке, известную в небесной механике как задача трех тел. Рассмотрим три тела произвольной массы, расположенных произвольным образом в пространстве и движущихся исключительно под действием сил взаимного гравитационного притяжения
Тела считаем материальными точками. Положение тел будем отсчитывать в произвольном базисе, с которым связана инерциальная система отсчета Oxyz. Положение каждого из тел задается радиус-вектором соответственно
,
и
. На каждое тело действует сила гравитационного притяжения со стороны двух других тел, причем в соответствии с третьей аксиомой динамики точки (3-й закон Ньютона)
Запишем дифференциальные уравнения движения каждой точки в векторной форме
или, с учетом (4)
В соответствии с законом всемирного тяготения, силы взаимодействия направлены вдоль векторов
Вдоль каждого из этих векторов выпустим соответствующий орт
тогда каждая из гравитационных сил рассчитывается по формуле
С учетом всего этого система уравнений движения принимает вид
Введем обозначение, принятое в небесной механике
— гравитационный параметр притягивающего центра. Тогда уравнения движения примут окончательный векторный вид
4. Нормирование уравнений к безразмерным переменным
Довольно популярным приемом при математическом моделировании является приведение дифференциальных уравнений и прочих соотношений, описывающих процесс, к безразмерным фазовым координатам и безразмерному времени. Нормируются так же и другие параметры. Это позволяет рассматривать, хоть и с применением численного моделирования, но в достаточно общем виде целый класс типовых задач. Вопрос о том, насколько это оправдано в каждой решаемой задаче оставляю открытым, но соглашусь, что в данном случае такой подход вполне справедлив.
Итак, введем некое абстрактное небесное тело с гравитационным параметром
, такое, что период обращения спутника по эллиптической орбите с большой полуосью
вокруг него равен
. Все эти величины, в силу законов механики, связаны соотношением
Введем замену параметров. Для положения точек нашей системы
где
— безразмерный радиус-вектор i-й точки;
для гравитационных параметров тел
где
— безразмерный гравитационный параметр i-й точки;
для времени
где
— безразмерное время.
Теперь пересчитаем ускорения точек системы через эти безразмерные параметры. Применим прямое двукратное дифференцирование по времени. Для скоростей
Для ускорений
При подстановке полученных соотношений в уравнения движения всё элегантно схлопывается в красивые уравнения:
Данная система уравнений до сих пор считается не интегрируемой в аналитических функциях. Почему считается а не является? Потому что успехи теории функции комплексного переменного привели к тому, что общее решение задачи трех тел таки появилось в 1912 году — Карлом Зундманом был найден алгоритм отыскания коэффициентов для бесконечных рядов относительно комплексного параметра, теоретически являющихся общим решением задачи трех тел. Но… для применения рядов Зундмана в практических расчетах с требуемой для них точностью требует получения такого числа членов этих рядов, что эта задача во много превосходит возможности вычислительных машин даже на сегодняшний день.
Поэтому численное интегрирование — единственный способ анализа решения уравнения (5)
5. Расчет начальных условий: добываем исходные данные
Как я уже писал ранее, прежде чем начинать численное интегрирование, следует озаботится расчетом начальных условий для решаемой задачи. В рассматриваемой задаче поиск начальных условий превращается в самостоятельную подзадачу, так как система (5) дает нам девять скалярных уравнений второго порядка, что при переходе к нормальной форме Коши повышает порядок системы ещё в 2 раза. То есть нам необходимо рассчитать целых 18 параметров — начальные положения и компоненты начальной скорости всех точек системы. Где мы возьмем данные о положении интересующих нас небесных тел? Мы живем в мире, где человек ходил по Луне — естественно человечество должно обладать информацией, как эта самая Луна движется и где она находится.
То есть, скажете вы, ты, чувак, предлагаешь нам взять с полок толстые астрономические справочники, сдуть с них пыль… Не угадали! Я предлагаю сходить за этими данными к тем, кто собственно ходил по Луне, к NASA, а именно в Лабораторию реактивного движения, Пасадена, штат Калифорния. Вот сюда — JPL Horizonts web interface.
Здесь, потратив немного времени на изучение интерфейса, мы добудем все необходимые нам данные. Выберем дату, например, да нам всё равно, но пусть это будет 27 июля 2018 года UT 20:21. Как раз в этот момент наблюдалась полная фаза лунного затмения. Программа выдаст нам огромную портянку
Полный вывод для эфемерид Луны на 27.07.2018 20:21 (начало координат в центре Земли)
*******************************************************************************
Revised: Jul 31, 2013 Moon / (Earth) 301
GEOPHYSICAL DATA (updated 2018-Aug-13):
Vol. Mean Radius, km = 1737.53+-0.03 Mass, x10^22 kg = 7.349
Radius (gravity), km = 1738.0 Surface emissivity = 0.92
Radius (IAU), km = 1737.4 GM, km^3/s^2 = 4902.800066
Density, g/cm^3 = 3.3437 GM 1-sigma, km^3/s^2 = +-0.0001
V(1,0) = +0.21 Surface accel., m/s^2 = 1.62
Earth/Moon mass ratio = 81.3005690769 Farside crust. thick. = ~80 - 90 km
Mean crustal density = 2.97+-.07 g/cm^3 Nearside crust. thick.= 58+-8 km
Heat flow, Apollo 15 = 3.1+-.6 mW/m^2 k2 = 0.024059
Heat flow, Apollo 17 = 2.2+-.5 mW/m^2 Rot. Rate, rad/s = 0.0000026617
Geometric Albedo = 0.12
Mean angular diameter = 31'05.2" Orbit period = 27.321582 d
Obliquity to orbit = 6.67 deg Eccentricity = 0.05490
Semi-major axis, a = 384400 km Inclination = 5.145 deg
Mean motion, rad/s = 2.6616995x10^-6 Nodal period = 6798.38 d
Apsidal period = 3231.50 d Mom. of inertia C/MR^2= 0.393142
beta (C-A/B), x10^-4 = 6.310213 gamma (B-A/C), x10^-4 = 2.277317
Perihelion Aphelion Mean
Solar Constant (W/m^2) 1414+-7 1323+-7 1368+-7
Maximum Planetary IR (W/m^2) 1314 1226 1268
Minimum Planetary IR (W/m^2) 5.2 5.2 5.2
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 20:45:05 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Moon (301) {source: DE431mx}
Center body name: Earth (399) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0.00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : 6378.1 x 6378.1 x 6356.8 km {Equator, meridian, pole}
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 1.537109094089627E-03 Y =-2.237488447258137E-03 Z = 5.112037386426180E-06
VX= 4.593816208618667E-04 VY= 3.187527302531735E-04 VZ=-5.183707711777675E-05
LT= 1.567825598846416E-05 RG= 2.714605874095336E-03 RR=-2.707898607099066E-06
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000.0
XY-plane: plane of the Earth's orbit at the reference epoch
Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76)
X-axis : out along ascending node of instantaneous plane of the Earth's
orbit and the Earth's mean equator at the reference epoch
Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense
of Earth's north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time
X X-component of position vector (au)
Y Y-component of position vector (au)
Z Z-component of position vector (au)
VX X-component of velocity vector (au/day)
VY Y-component of velocity vector (au/day)
VZ Z-component of velocity vector (au/day)
LT One-way down-leg Newtonian light-time (day)
RG Range; distance from coordinate center (au)
RR Range-rate; radial velocity wrt coord. center (au/day)
Geometric states/elements have no aberrations applied.
Computations by ...
Solar System Dynamics Group, Horizons On-Line Ephemeris System
4800 Oak Grove Drive, Jet Propulsion Laboratory
Pasadena, CA 91109 USA
Information: http://ssd.jpl.nasa.gov/
Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser)
http://ssd.jpl.nasa.gov/?horizons
telnet ssd.jpl.nasa.gov 6775 (via command-line)
Author : Jon.D.Giorgini@jpl.nasa.gov
*******************************************************************************
Бр-р-р, что это? Без паники, для того, кто хорошо учил в школе астрономию, механику и математику тут боятся нечего. Итак, самое главное конечное искомые координаты и компоненты скорости Луны.
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 1.537109094089627E-03 Y =-2.237488447258137E-03 Z = 5.112037386426180E-06
VX= 4.593816208618667E-04 VY= 3.187527302531735E-04 VZ=-5.183707711777675E-05
LT= 1.567825598846416E-05 RG= 2.714605874095336E-03 RR=-2.707898607099066E-06
$$EOE
Да-да-да, они декартовы! Если внимательно прочесть всю портянку, то мы узнаем, что начало этой системы координат совпадает с центром Земли. Плоскость XY лежит в плоскости земной орбиты (плоскости эклиптики) на эпоху J2000. Ось X направлена вдоль линии пересечения плоскости экватора Земли и эклиптики в точку весеннего равноденствия. Ось Z смотрит в направлении северного полюса Земли перпендикулярно плоскости эклиптики. Ну а ось Y дополняет всё это счастье до правой тройки векторов. По-умолчанию единицы измерения координат: астрономические единицы (умнички из NASA приводят и величину автрономической единицы в километрах). Единицы измерения скорости: астрономические единицы в день, день принимается равным 86400 секундам. Полный фарш!
Аналогичную информацию мы можем получить и для Земли
Полный вывод эфемерид Земли на 27.07.2018 20:21 (начало координат в центре масс Солнечной системы)
*******************************************************************************
Revised: Jul 31, 2013 Earth 399
GEOPHYSICAL PROPERTIES (revised Aug 13, 2018):
Vol. Mean Radius (km) = 6371.01+-0.02 Mass x10^24 (kg)= 5.97219+-0.0006
Equ. radius, km = 6378.137 Mass layers:
Polar axis, km = 6356.752 Atmos = 5.1 x 10^18 kg
Flattening = 1/298.257223563 oceans = 1.4 x 10^21 kg
Density, g/cm^3 = 5.51 crust = 2.6 x 10^22 kg
J2 (IERS 2010) = 0.00108262545 mantle = 4.043 x 10^24 kg
g_p, m/s^2 (polar) = 9.8321863685 outer core = 1.835 x 10^24 kg
g_e, m/s^2 (equatorial) = 9.7803267715 inner core = 9.675 x 10^22 kg
g_o, m/s^2 = 9.82022 Fluid core rad = 3480 km
GM, km^3/s^2 = 398600.435436 Inner core rad = 1215 km
GM 1-sigma, km^3/s^2 = 0.0014 Escape velocity = 11.186 km/s
Rot. Rate (rad/s) = 0.00007292115 Surface Area:
Mean sidereal day, hr = 23.9344695944 land = 1.48 x 10^8 km
Mean solar day 2000.0, s = 86400.002 sea = 3.62 x 10^8 km
Mean solar day 1820.0, s = 86400.0
Moment of inertia = 0.3308 Love no., k2 = 0.299
Mean Temperature, K = 270 Atm. pressure = 1.0 bar
Vis. mag. V(1,0) = -3.86 Volume, km^3 = 1.08321 x 10^12
Geometric Albedo = 0.367 Magnetic moment = 0.61 gauss Rp^3
Solar Constant (W/m^2) = 1367.6 (mean), 1414 (perihelion), 1322 (aphelion)
ORBIT CHARACTERISTICS:
Obliquity to orbit, deg = 23.4392911 Sidereal orb period = 1.0000174 y
Orbital speed, km/s = 29.79 Sidereal orb period = 365.25636 d
Mean daily motion, deg/d = 0.9856474 Hill's sphere radius = 234.9
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 21:16:21 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Earth (399) {source: DE431mx}
Center body name: Solar System Barycenter (0) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0.00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : (undefined)
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 5.755663665315949E-01 Y =-8.298818915224488E-01 Z =-5.366994499016168E-05
VX= 1.388633512282171E-02 VY= 9.678934168415631E-03 VZ= 3.429889230737491E-07
LT= 5.832932117417083E-03 RG= 1.009940888883960E+00 RR=-3.947237246302148E-05
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000.0
XY-plane: plane of the Earth's orbit at the reference epoch
Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76)
X-axis : out along ascending node of instantaneous plane of the Earth's
orbit and the Earth's mean equator at the reference epoch
Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense
of Earth's north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time
X X-component of position vector (au)
Y Y-component of position vector (au)
Z Z-component of position vector (au)
VX X-component of velocity vector (au/day)
VY Y-component of velocity vector (au/day)
VZ Z-component of velocity vector (au/day)
LT One-way down-leg Newtonian light-time (day)
RG Range; distance from coordinate center (au)
RR Range-rate; radial velocity wrt coord. center (au/day)
Geometric states/elements have no aberrations applied.
Computations by ...
Solar System Dynamics Group, Horizons On-Line Ephemeris System
4800 Oak Grove Drive, Jet Propulsion Laboratory
Pasadena, CA 91109 USA
Information: http://ssd.jpl.nasa.gov/
Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser)
http://ssd.jpl.nasa.gov/?horizons
telnet ssd.jpl.nasa.gov 6775 (via command-line)
Author : Jon.D.Giorgini@jpl.nasa.gov
*******************************************************************************
Здесь в качестве начала координат выбран барицентр (центр масс) Солнечной системы. Интересующие нас данные
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 5.755663665315949E-01 Y =-8.298818915224488E-01 Z =-5.366994499016168E-05
VX= 1.388633512282171E-02 VY= 9.678934168415631E-03 VZ= 3.429889230737491E-07
LT= 5.832932117417083E-03 RG= 1.009940888883960E+00 RR=-3.947237246302148E-05
$$EOE
Для Луны нам понадобятся координаты и скорость относительно барицентра Солнечной системы, мы можем их посчитать, а можем попросит NASA дать нам такие данные
Полный вывод эфемерид Луны на 27.07.2018 20:21 (начало координат в центре масс Солнечной системы)
*******************************************************************************
Revised: Jul 31, 2013 Moon / (Earth) 301
GEOPHYSICAL DATA (updated 2018-Aug-13):
Vol. Mean Radius, km = 1737.53+-0.03 Mass, x10^22 kg = 7.349
Radius (gravity), km = 1738.0 Surface emissivity = 0.92
Radius (IAU), km = 1737.4 GM, km^3/s^2 = 4902.800066
Density, g/cm^3 = 3.3437 GM 1-sigma, km^3/s^2 = +-0.0001
V(1,0) = +0.21 Surface accel., m/s^2 = 1.62
Earth/Moon mass ratio = 81.3005690769 Farside crust. thick. = ~80 - 90 km
Mean crustal density = 2.97+-.07 g/cm^3 Nearside crust. thick.= 58+-8 km
Heat flow, Apollo 15 = 3.1+-.6 mW/m^2 k2 = 0.024059
Heat flow, Apollo 17 = 2.2+-.5 mW/m^2 Rot. Rate, rad/s = 0.0000026617
Geometric Albedo = 0.12
Mean angular diameter = 31'05.2" Orbit period = 27.321582 d
Obliquity to orbit = 6.67 deg Eccentricity = 0.05490
Semi-major axis, a = 384400 km Inclination = 5.145 deg
Mean motion, rad/s = 2.6616995x10^-6 Nodal period = 6798.38 d
Apsidal period = 3231.50 d Mom. of inertia C/MR^2= 0.393142
beta (C-A/B), x10^-4 = 6.310213 gamma (B-A/C), x10^-4 = 2.277317
Perihelion Aphelion Mean
Solar Constant (W/m^2) 1414+-7 1323+-7 1368+-7
Maximum Planetary IR (W/m^2) 1314 1226 1268
Minimum Planetary IR (W/m^2) 5.2 5.2 5.2
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 21:19:24 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Moon (301) {source: DE431mx}
Center body name: Solar System Barycenter (0) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0.00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : (undefined)
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 5.771034756256845E-01 Y =-8.321193799697072E-01 Z =-4.855790760378579E-05
VX= 1.434571674368357E-02 VY= 9.997686898668805E-03 VZ=-5.149408819470315E-05
LT= 5.848610189172283E-03 RG= 1.012655462859054E+00 RR=-3.979984423450087E-05
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000.0
XY-plane: plane of the Earth's orbit at the reference epoch
Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76)
X-axis : out along ascending node of instantaneous plane of the Earth's
orbit and the Earth's mean equator at the reference epoch
Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense
of Earth's north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time
X X-component of position vector (au)
Y Y-component of position vector (au)
Z Z-component of position vector (au)
VX X-component of velocity vector (au/day)
VY Y-component of velocity vector (au/day)
VZ Z-component of velocity vector (au/day)
LT One-way down-leg Newtonian light-time (day)
RG Range; distance from coordinate center (au)
RR Range-rate; radial velocity wrt coord. center (au/day)
Geometric states/elements have no aberrations applied.
Computations by ...
Solar System Dynamics Group, Horizons On-Line Ephemeris System
4800 Oak Grove Drive, Jet Propulsion Laboratory
Pasadena, CA 91109 USA
Information: http://ssd.jpl.nasa.gov/
Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser)
http://ssd.jpl.nasa.gov/?horizons
telnet ssd.jpl.nasa.gov 6775 (via command-line)
Author : Jon.D.Giorgini@jpl.nasa.gov
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 5.771034756256845E-01 Y =-8.321193799697072E-01 Z =-4.855790760378579E-05
VX= 1.434571674368357E-02 VY= 9.997686898668805E-03 VZ=-5.149408819470315E-05
LT= 5.848610189172283E-03 RG= 1.012655462859054E+00 RR=-3.979984423450087E-05
$$EOE
Чудесно! Теперь необходимо слегка обработать полученные данные напильником.
6. 38 попугаев и одно попугайское крылышко
Для начала определимся с масштабом, ведь наши уравнения движения (5) записаны в безразмерной форме. Данные, предоставленные NASA сами подсказывают нам, что за масштаб координат стоит взять одну астрономическую единицу. Соответственно в качестве эталонного тела, к которому мы будем нормировать массы других тел мы возьмем Солнце, а в качестве масштаба времени — период обращения Земли вокруг Солнца.
Все это конечно очень хорошо, но мы не задали начальные условия для Солнца. «Зачем?» — спросил бы меня какой-нибудь лингвист. А я бы ответил, что Солнце отнюдь не неподвижно, а тоже вращается по своей орбите вокруг центра масс Солнечной системы. В этом можно убедится, взглянув на данные NASA для Солнца
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 6.520050993518213E+04 Y = 1.049687363172734E+06 Z =-1.304404963058507E+04
VX=-1.265326939350981E-02 VY= 5.853475278436883E-03 VZ= 3.136673455633667E-04
LT= 3.508397935601254E+00 RG= 1.051791240756026E+06 RR= 5.053500842402456E-03
$$EOE
Взглянув на параметр RG мы увидим, что Солнце вращается вокруг барицентра Солнечной системы, и на 27.07.2018 центр звезды находится от него на расстоянии в миллион километров. Радиус Солнца, для справки — 696 тысяч километров. То есть барицентр Солнечной системы лежит в полумиллионе километров от поверхности светила. Почему? Да потому что все остальные тела, взаимодействующие с Солнцем так же сообщают ему ускорение, главным образом, конечно тяжеленький Юпитер. Соответственно у Солнца тоже есть своя орбита.
Мы конечно можем выбрать эти данные в качестве начальных условий, но нет — мы же решаем модельную задачу трех тел, и Юпитер и прочие персонажи в неё не входят. Так что в ущерб реализму, зная положение и скорости Земли и Луны мы пересчитаем начальные условия для Солнца, так, чтобы центр масс системы Солнце — Земля — Луна находился в начале координат. Для центра масс нашей механической системы справедливо уравнение
Поместим центр масс в начало координат, то есть зададимся
, тогда
откуда
Перейдем к безразмерным координатам и параметрам, выбрав
Дифференцируя (6) по времени и переходя к безразмерному времени получаем и соотношение для скоростей
где
Теперь напишем программу, которая сформирует начальные условия в выбранных нами «попугаях». На чем будем писать? Конечно же на Питоне! Ведь, как известно, это самый лучший язык для математического моделирования.
Однако, если уйти от сарказма, то мы действительно попробуем для этой цели питон, а почему нет? Я обязательно приведу ссылку на весь код в моем профиле Github.
Расчет начальных условий для системы Луна — Земля — Солнце
#
# Исходные данные задачи
#
# Гравитационная постоянная
G = 6.67e-11
# Массы тел (Луна, Земля, Солнце)
m = [7.349e22, 5.792e24, 1.989e30]
# Расчитываем гравитационные параметры тел
mu = []
print("Гравитационные параметры тел")
for i, mass in enumerate(m):
mu.append(G * mass)
print("mu[" + str(i) + "] = " + str(mu[i]))
# Нормируем гравитационные параметры к Солнцу
kappa = []
print("Нормированные гравитационные параметры")
for i, gp in enumerate(mu):
kappa.append(gp / mu[2])
print("xi[" + str(i) + "] = " + str(kappa[i]))
print("n")
# Астрономическая единица
a = 1.495978707e11
import math
# Масштаб безразмерного времени, c
T = 2 * math.pi * a * math.sqrt(a / mu[2])
print("Масштаб времени T = " + str(T) + "n")
# Координаты NASA для Луны
xL = 5.771034756256845E-01
yL = -8.321193799697072E-01
zL = -4.855790760378579E-05
import numpy as np
xi_10 = np.array([xL, yL, zL])
print("Начальное положение Луны, а.е.: " + str(xi_10))
# Координаты NASA для Земли
xE = 5.755663665315949E-01
yE = -8.298818915224488E-01
zE = -5.366994499016168E-05
xi_20 = np.array([xE, yE, zE])
print("Начальное положение Земли, а.е.: " + str(xi_20))
# Расчитываем начальное положение Солнца, полагая что начало координат - в центре масс всей системы
xi_30 = - kappa[0] * xi_10 - kappa[1] * xi_20
print("Начальное положение Солнца, а.е.: " + str(xi_30))
# Вводим константы для вычисления безразмерных скоростей
Td = 86400.0
u = math.sqrt(mu[2] / a) / 2 / math.pi
print("n")
# Начальная скорость Луны
vxL = 1.434571674368357E-02
vyL = 9.997686898668805E-03
vzL = -5.149408819470315E-05
vL0 = np.array([vxL, vyL, vzL])
uL0 = np.array([0.0, 0.0, 0.0])
for i, v in enumerate(vL0):
vL0[i] = v * a / Td
uL0[i] = vL0[i] / u
print("Начальная скорость Луны, м/с: " + str(vL0))
print(" -//- безразмерная: " + str(uL0))
# Начальная скорость Земли
vxE = 1.388633512282171E-02
vyE = 9.678934168415631E-03
vzE = 3.429889230737491E-07
vE0 = np.array([vxE, vyE, vzE])
uE0 = np.array([0.0, 0.0, 0.0])
for i, v in enumerate(vE0):
vE0[i] = v * a / Td
uE0[i] = vE0[i] / u
print("Начальная скорость Земли, м/с: " + str(vE0))
print(" -//- безразмерная: " + str(uE0))
# Начальная скорость Солнца
vS0 = - kappa[0] * vL0 - kappa[1] * vE0
uS0 = - kappa[0] * uL0 - kappa[1] * uE0
print("Начальная скорость Солнца, м/с: " + str(vS0))
print(" -//- безразмерная: " + str(uS0))
Выхлоп программы
Гравитационные параметры тел
mu[0] = 4901783000000.0
mu[1] = 386326400000000.0
mu[2] = 1.326663e+20
Нормированные гравитационные параметры
xi[0] = 3.6948215183509304e-08
xi[1] = 2.912016088486677e-06
xi[2] = 1.0
Масштаб времени T = 31563683.35432583
Начальное положение Луны, а.е.: [ 5.77103476e-01 -8.32119380e-01 -4.85579076e-05]
Начальное положение Земли, а.е.: [ 5.75566367e-01 -8.29881892e-01 -5.36699450e-05]
Начальное положение Солнца, а.е.: [-1.69738146e-06 2.44737475e-06 1.58081871e-10]
Начальная скорость Луны, м/с: [24838.98933473 17310.56333294 -89.15979106]
-//- безразмерная: [ 5.24078311 3.65235907 -0.01881184]
Начальная скорость Земли, м/с: [2.40435899e+04 1.67586567e+04 5.93870516e-01]
-//- безразмерная: [5.07296163e+00 3.53591219e+00 1.25300854e-04]
Начальная скорость Солнца, м/с: [-7.09330769e-02 -4.94410725e-02 1.56493465e-06]
-//- безразмерная: [-1.49661835e-05 -1.04315813e-05 3.30185861e-10]
7. Интегрирование уравнений движения и анализ результатов
Собственно само интегрирование сводится к более-менее стандартной для SciPy процедуре подготовки системы уравнений: преобразованию системы ОДУ к форме Коши и вызову соответствующих функций-решателей. Для преобразования системы к форме Коши вспоминаем, что
Тогда введя вектор состояния системы
сводим (7) и (5) к одному векторному уравнению
Для интегрирования (8) с имеющимися начальными условиями напишем немного, совсем немного кода
Интегрирования уравнений движения в задаче трех тел
#
# Вычисление векторов обобщенных ускорений
#
def calcAccels(xi):
k = 4 * math.pi ** 2
xi12 = xi[1] - xi[0]
xi13 = xi[2] - xi[0]
xi23 = xi[2] - xi[1]
s12 = math.sqrt(np.dot(xi12, xi12))
s13 = math.sqrt(np.dot(xi13, xi13))
s23 = math.sqrt(np.dot(xi23, xi23))
a1 = (k * kappa[1] / s12 ** 3) * xi12 + (k * kappa[2] / s13 ** 3) * xi13
a2 = -(k * kappa[0] / s12 ** 3) * xi12 + (k * kappa[2] / s23 ** 3) * xi23
a3 = -(k * kappa[0] / s13 ** 3) * xi13 - (k * kappa[1] / s23 ** 3) * xi23
return [a1, a2, a3]
#
# Система уравнений в нормальной форме Коши
#
def f(t, y):
n = 9
dydt = np.zeros((2 * n))
for i in range(0, n):
dydt[i] = y[i + n]
xi1 = np.array(y[0:3])
xi2 = np.array(y[3:6])
xi3 = np.array(y[6:9])
accels = calcAccels([xi1, xi2, xi3])
i = n
for accel in accels:
for a in accel:
dydt[i] = a
i = i + 1
return dydt
# Начальные условия задачи Коши
y0 = [xi_10[0], xi_10[1], xi_10[2],
xi_20[0], xi_20[1], xi_20[2],
xi_30[0], xi_30[1], xi_30[2],
uL0[0], uL0[1], uL0[2],
uE0[0], uE0[1], uE0[2],
uS0[0], uS0[1], uS0[2]]
#
# Интегрируем уравнения движения
#
# Начальное время
t_begin = 0
# Конечное время
t_end = 30.7 * Td / T;
# Интересующее нас число точек траектории
N_plots = 1000
# Шаг времени между точкими
step = (t_end - t_begin) / N_plots
import scipy.integrate as spi
solver = spi.ode(f)
solver.set_integrator('vode', nsteps=50000, method='bdf', max_step=1e-6, rtol=1e-12)
solver.set_initial_value(y0, t_begin)
ts = []
ys = []
i = 0
while solver.successful() and solver.t <= t_end:
solver.integrate(solver.t + step)
ts.append(solver.t)
ys.append(solver.y)
print(ts[i], ys[i])
i = i + 1
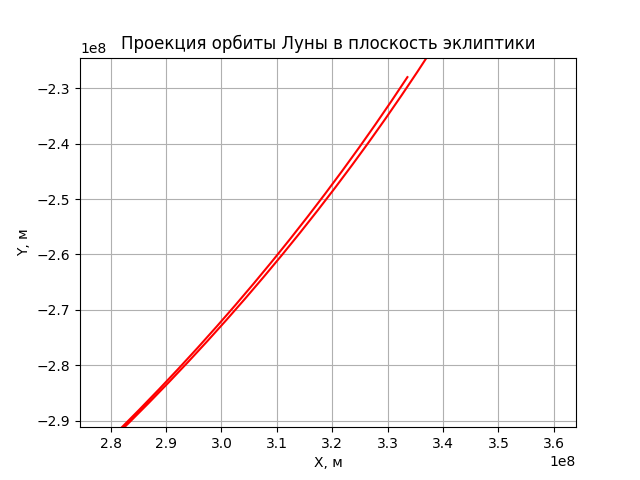
Посмотрим что у нас получилось. Получилась пространственная траектория Луны на первые 29 суток от выбранной нами начальной точки
а так же её проекция в плоскость эклиптики.
«Эй, дядя, что ты нам впариваешь?! Это же окружность!».
Во-первых, таки не окружность — заметно смещение проекции траектории от начала координат вправо и вниз. Во-вторых — ничего не замечаете? Не, ну правда?
Обещаю подготовить обоснование того (на основе анализа погрешностей счета и данных NASA), что полученное смещение траектории не есть следствие ошибок интегрирования. Пока предлагаю читателю поверить мне на слово — это смещение есть следствие солнечного возмущения лунной траектории. Крутанем-ка еще один оборот
Во как! Причем обратите внимание на то, что исходя из начальных данных задачи Солнце находится как раз в той стороне, куда смещается траектория Луны на каждом обороте. Да это наглое Солнце ворует у нас наш любимый спутник! Ох уж это Солнце!
Можно сделать вывод, что солнечная гравитация влияет на орбиту Луны достаточно существенно — старушка не ходит по небу дважды одним и тем же путём. Картинка за полгода движения позволяет (по крайней мере качественно) убедится в этом (картинка кликабельна)
Интересно? Ещё бы. Астрономия вообще наука занятная.
Постскриптум
В вузе, где я учился и работал без малого семь лет — Новочеркасском политехе — ежегодно проводилась зональная олимпиада студентов по теоретической механике вузов Северного Кавказа. Трижды мы принимали и Всероссийскую олимпиаду. На открытии, наш главный «олимпиец», профессор Кондратенко А.И., всегда говорил: «Академик Крылов называл механику поэзией точных наук».
Я люблю механику. Всё то хорошее, чего я добился в своей жизни и карьере произошло благодаря этой науке и моим замечательным учителям. Я уважаю механику.
Поэтому, я никогда не позволю издеваться над этой наукой и нагло эксплуатировать её в своих целях никому, будь он хоть трижды доктор наук и четырежды лингвист, и разработал хоть миллион учебных программ. Я искренне считаю, что написание статей на популярном публичном ресурсе должно предусматривать их тщательную вычитку, нормальное оформление (формулы LaTeX — это не блажь разработчиков ресурса!) и отсутствие ошибок, приводящих к результатам нарушающим законы природы. Последнее вообще «маст хэв».
Я часто говорю своим студентам: «компьютер освобождает ваши руки, но это не значит, что при этом нужно отключать и мозг».
Ценить и уважать механику я призываю и вас, мои уважаемые читатели. Охотно отвечу на любые вопросы, а исходный текст примера решения задачи трех тел на языке Python, как и обещал, выкладываю в своем профиле Github.
Спасибо за внимание!
Солнечная система > Система Земля-Луна > Спутник Луна > Орбита Луны
Люди всегда с восторгом смотрели на соседний спутник, кажущийся чем-то божественным из-за своей яркости. Луна вращается по орбите вокруг Земли с момента создания, поэтому за ней наблюдали и первые люди. Любопытство и эволюция привели к тому, что появились вычисления и мы начали отмечать шаблоны поведения.
Вращение Луны по орбите
К примеру, ось вращения Луны совпадает с орбитальным. По сути, спутник расположен в гравитационном блоке, то есть, мы всегда смотрим на одну сторону (так возникла идея о загадочной обратной стороне Луны). Из-за эллиптического пути небесное тело периодически кажется больше или меньше.
Орбитальные параметры Луны
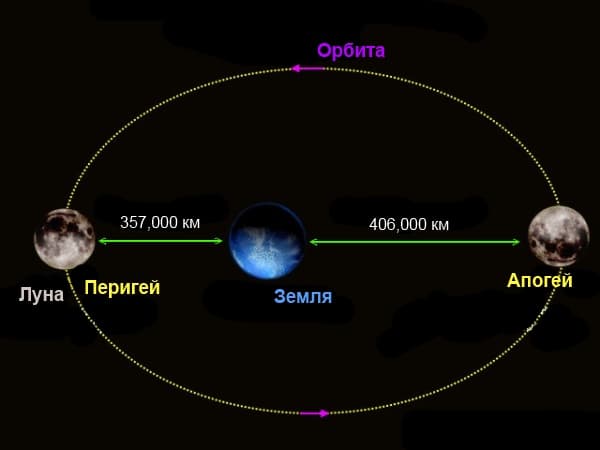
Средний лунный эксцентриситет составляет – 0.0549, а значит Луна не проходит вокруг Земли по идеальному кругу. Среднее расстояние от Луны до Земли – 384748 км. Но может меняться от 364397 км до 406748 км.
Сопоставление кажущегося лунного размера в перигее и апогее
Это приводит к перемене угловой скорости и наблюдаемого размера. В фазе полной Луны и на позиции перигелия (ближе всего) мы видим ее на 10% крупнее и на 30% ярче, чем в апогее (максимальная отдаленность).
Средний наклон орбиты по отношению к плоскости эклиптики – 5.155°. Совпадают сидерический период и осевой – 27.3 дней. Это именуют синхронным вращением. Именно поэтому появилась «темная сторона», которую мы просто не видим.
Земля также совершает обороты вокруг Солнца, а Луна вращается вокруг Земли за 29.53 дней. Это синодический период, который подвергается фазам.
Лунный цикл орбиты
Лунный цикл порождает фазы Луны — кажущаяся перемена внешнего вида небесного тела в небе из-за изменения количества освещенности. Когда звезда, планета и спутник выстраиваются в одну линию, то угол между Луной и Солнцем составляет 0 градусов.
Хотите получить индивидуальный расклад?
Опытный таролог ответит на вопросы:
Что ждёт Вас в будущем? Как сложатся отношения? Какое решение — верное?
В этом периоде лунная сторона, повернутая к Солнцу, получает максимум лучей, а обращенная к нам – темная. Далее идет проход и угол растет. После Новолуния объекты разделены на 90 градусов, и мы уже видим иную картину. На нижней схеме можно подробно изучить, как формируются лунные фазы.
Если они расположены в противоположных сторонах, то угол – 180 градусов. Лунный месяц длится 28 дней, во время которого спутник «растет» и «убывает».
При четверти Луна заполнена меньше чем наполовину и растет. Далее идет переход за половину, и она угасает. Мы встречаем последнюю четверть, где освещена уже другая сторона диска.
Будущее лунной орбиты
Мы уже знаем, что спутник постепенно отдаляется по орбите от планеты (1-2 см в год). И это влияет на то, что с каждым веком день у нас становится на 1/500 секунды длиннее. То есть, примерно 620 млн. лет назад Земля могла похвастаться лишь 21 часом.
Сейчас сутки охватывают 24 часа, но Луна не прекращает попыток сбежать. Мы привыкли к спутнику и грустно терять такого напарника. Но отношения между объектами меняются. Интересно лишь, как это отразится на нас.
Читайте также:
- Интересные факты о Луне;
- Что такое Луна?
- Как образовалась Луна;
- Как сформировалась Луна?
- Постройка лунной базы: часть 1
- Постройка лунной базы: часть 2
- Постройка лунной базы: часть 3
- Постройка лунной базы: часть 4
- Как можно уничтожить Луну?
- Как понять, что лунная посадка не была фальшивкой?
- Нужна ли нам Луна для выживания?
- Как заработать на Луне?
- Как в НАСА записали отправку астронавтов с Луны?
- Куда лучше направиться: на Марс или Луну?
- Не пришло ли время вернуться на Луну?
- Какое настоящее название Луны?
Положение и движение Луны
- Орбита Луны;
- Солнце и Луна
- Почему Солнце не поглотит Луну?
- Какие бывают фазы Луны
- Что такое выпуклая Луна?
- Почему Луна кажется такой большой?
- Почему Луна удаляется от нас?
- Почему мы видим Солнце и Луну одновременно?
- Как долго добираться до Луны?
- Расстояние от Земли до Луны;
- Вращение Луны;
- Обратная сторона Луны;
- Второй земной спутник покидает нас
Строение Луны
- Строение Луны
- Размеры Луны;
- Диаметр Луны;
- Масса Луны;
- Является ли Луна планетой?
Поверхность Луны
- Поверхность Луны;
- Вода на Луне
- Новые кратеры на Луне
- Создание Луны: практика формирования кратеров
- Лавовые трубы на Луне
- Первые люди на Луне
- Сколько людей было на Луне?
- Что находится на дальней стороне Луны?
- Старое оборудование НАСА можно рассмотреть на Луне
- Терраформирование Луны
- Токсичность Луны
- Атмосфера Луны;
- Гравитация на Луне;
- Возраст Луны;
- Температура на Луне;
- Почему Луна светит?
- Почему мы видим «человека на Луне»?
- Почему на дальней стороне Луны нет морей?
- Цвет Луны;
- Море Спокойствия;
План урока:
Сидерический и синодический месяцы
Смена лунных фаз
Что такое сарос
Время и календарь
Сидерический и синодический месяцы
Период, за который Луна вращается вокруг Земного шара относительно неподвижных звезд, называется сидерическим месяцем. Его продолжительность составляет 27.32 суток. За одни сутки небесное тело смещается на 13,20. Луна, Солнце по эклиптике движутся в одну и ту же сторону. За сидерический месяц Солнце переместится по эклиптике приблизительно на 270, а Луне потребуется еще 2.21 суток, чтобы возвратиться в исходное положение по отношению к Солнцу. Период, за который Луна вращается вокруг Земли относительно Светила, принято называть в астрономии синодическим месяцем. В отличие от сидерического, длительность синодического месяца немного больше и составляет 29,53 суток.
Внешний вид Луны напрямую зависит от взаимного расположения Солнца и Луны. Именно поэтому под понятием «месяц» подразумевают именно синодический месяц. За начало синодического месяца принимается расположение Лунного диска между Земным шаром и Солнцем, когда его сторона, обращенная к Земле, не видна. В этот момент освещается обратная сторона земного спутника.
Движение Луны по небесной сфере
Между временным отрезком вращения Луны вокруг своей оси и вокруг Земного шара можно поставить знак равенства. Это время одинаково и составляет примерно 28 суток. Это и стало причиной того, что, наблюдая за природным спутником, человек видит постоянно только одну его сторону. Луна сильно влияет на планету. Благодаря гравитационной силе на Луне происходит притягивание большого количества водных масс на Земном шаре, что создает эффект прилива. На максимально приближенной к спутнику стороне планеты наблюдаем приливы, а по обоим ее бокам отливы. Приливы также будут на противоположной стороне Земли, но они образуются уже в результате гравитации Солнца. В то время как Земной шар движется вокруг своей оси, приливные волны «следуют» за диском Луны и оказывают воздействие на него. В связи с тем, что расстояние между Землей и Луной постоянно меняется, приливообразующая сила Луны также может изменяться до 40% в течение месяца. Приливообразующая сила Солнца в течение года меняется всего лишь на 10%. Лунные приливы в 2,17 раз сильнее солнечных.
Источник
Движение большой массы воды, которая образуется во время приливов и отливов, приводит не только к замедлению движения Земного шара, но и к ускорению и «отталкиванию» Луны от Земли.Ежегодно расстояние, на которое ночное светило удаляется от планеты, составляет 38 мм. Именно из-за приливного ускорения лунная орбита напоминает собой спираль, которая медленно раскручивается.
Также будет интересно знать, что наблюдатели видят с поверхности Земли где-то 55%от всей площади Луны. Причиной этому является эллиптическая форма орбиты и небольшое наклонение оси вращения Луны по отношению к орбитальной плоскости.
Смена лунных фаз
Наблюдая за Луной, человек замечает, как ночное светило на протяжении определенного времени меняет свой внешний вид. Это явление называется сменой лунных фаз. С астрономической точки зрения лунная фаза — освещенная Солнцем часть Луны, которую человек может наблюдать с поверхности Земли в определенный момент. Луна сама по себе не светится. Ее свет представляет собой отражение солнечного света. От того как расположены в определенный момент Солнце, Земля и Луна по отношению друг к другу и будет зависеть внешний вид природного спутника. Традиционно выделяют четыре фазы Луны:
- Новолуние – лунный диск движется между Солнцем и Земным шаром. В этот период он обращен к планете стороной, на которую не попадают солнечные лучи. Поэтому его не видно на небосводе.
- Первая четверть – наблюдается лишь ½ часть диска, который освещен. В Северном полушарии это будет правая сторона Луны.
- Полнолуние – в это время вся сторона Луны, освещенная Солнцем, направлена к Земле, и наблюдатель видит полный диск.
- Последняя четверть – снова видна только ½ часть освещенного диска, только теперь это будет его левая сторон.
Источник
В течение так называемого синодического месяца происходит смена лунных фаз.Он имеет строгие временные рамки и составляет 29.53 суток. Период фаз включает время, за которое происходит смена всех лунных фаз. Каждая основная фаза длится около семи суток, это позволяет определять возраст Луны:
- 0 или 30-ый день – лунный диск не видно;
- 7 дней – первая четверть, наблюдать за спутником лучше всего вечером;
- 15 дней – полнолуние, лунный диск видно на протяжении всей ночи;
- 22 дня – последняя четверть, наблюдать за Луной лучше всего ближе к утру.
Со сменой возраста Луна меняет свое месторасположение на небе. Зная некоторые особенности, человек с легкостью может определить стороны света и ориентироваться на местности без дополнительных приборов.
В первую четверть около 19:00 Луна будет на южной стороне, а к часу ночи она переместиться на запад. Во время полнолуния в 19:00 она появится на востоке, к часу ночи достигнет южного направления, в 7 часов утра окажется на западе. В последнюю четверть в час ночи Луну можно увидеть на востоке, а уже в 7 часов утра она будет указывать на южное направление. Зная хотя бы одну сторону света, всегда можно определить остальные.
Источник
Солнечное затмение
Наблюдать солнечные затмения человечество может только во время новолуния, то есть лунный диск должен расположиться между Солнцем и планетой Земля.
Известно, что Земной шар за сутки совершает один оборот вокруг оси и параллельно движется вокруг Солнца. Чтобы сделать полный круг по орбите вокруг Светила необходим 1 год (примерно 365 суток). Луна в это время также не стоит на месте, она движется вокруг планеты, для полного оборота ей необходимо 29.5 суток.
Расположение небесных тел в системе Земля-Луна-Солнце по отношению друг к другу постоянно меняется. Во время движения Луна в определенные моменты проходит между Солнцем и Землей. Так как земной спутник является темным непрозрачным шаром, он может выполнять функции «большого щита» и закрывать собой Светило, что и приводит к затмению.
Солнце от Земли отдалено примерно на 150 000 000 км, Луна – на 384 000 км. Каждому известно, чем ближе расположен объект, тем большим он будет казаться. Если сравнивать Луну и Солнце, то спутник будет ближе к Земному шару в 400 раз. Кроме этого солнечный диаметр больше лунного также в 400 раз. Земной спутник способен собой целиком закрывать Солнце, потому что видимые размеры этих двух космических объектов практически не отличаются. Ученые-астрономы выделяют разные виды солнечного затмения: полное, частичное, кольцевое.
В связи с тем, что небесные тела вращаются по эллиптическим орбитам расстояние от Земного шара до Светила и Луны постоянно меняется. Соответственно видимые размеры объектов также будут меняться. Когда происходит максимальное отдаление земного спутника от планеты, он не может собой закрыть Солнце целиком. Данное явление получило название кольцеобразное (кольцевое) солнечное затмение.
За один год Луна 12 раз проходит фазу новолуния. Исходя из этого, затмения Солнца должны были бы повторяться каждый месяц. Но фактически такого не бывает. Если бы небесные тела перемещались в одной плоскости, то земной спутник во все новолуния находился бы на прямой между Землей и Солнцем. И тогда бы затмения люди видели регулярно. В Солнечной системе вращение Земного шара и Луны происходит в разных плоскостях, которые не совпадают между собой. В большинстве случаев в новолуние земной спутник находится либо выше, либо ниже Светила.
Видимый путь перемещения диска Луны по небосводу отличается от солнечного.В небесном пространстве существует две точки, в которых происходит пересечение лунной орбиты с эклиптикой. Это узлы лунной орбиты (южный и северный). В них пути небесных тел максимально приближаются друг к другу. Следовательно, если вблизи узлов Луна вступит в фазу новолуния, то земляне станут свидетелями затмения.
Источник
Если Светило и земной спутник окажутся практически в точке узла, то произойдет полное или кольцеобразное солнечное затмение. Если же небесные тела будут немного отдалены от этих точек, то наблюдатель увидит частное (частичное) солнечное затмение. Звезда всегда начинает закрываться с западной (правой) стороны, так как земной спутник движется по небосводу с запада на восток.
Источник
Лунное затмение
Это природное явление напрямую зависит от того, как земной спутник (Луна) движется вокруг планеты. Именно особенности этого движения приводят к полным или частичным лунным затмениям.
Увидеть их можно, когда ночное светило находится в фазе полнолуния. А система Луна-Земля-Солнце выстаивается водну линию. При этом планета находится посредине, а слева и справа размещаются Солнце и Луна.
Попадая в тень Земного шара, Луна полностью не исчезает. Ее всегда слабо, но видно. Лучи Солнца, которые проходят сквозь атмосферу Земли, преломляются, и проникают внутрь земной тени, а затем попадают на Луну. В атмосфере красные лучи спектра рассеиваются меньше всего. Следовательно, в момент затмения земной спутник может приобрести бурый или красноватый оттенок.
В большинстве случаев наблюдатель видит не полное, а частичное (полутеневое) затмение Луны. Неполное затмение лунного диска происходит вследствие того, что ночное светило попадает в тень Земли не полностью, а частично. Наблюдать такое явление можно на всем полушарии планеты, которое в этот момент обращено к Солнцу.
Так как небесные тела движутся в разных плоскостях и в одну линию выстраиваются только в определенные моменты, лунные, как и солнечные затмения происходят не каждый месяц.
Источник
Что такое сарос
Затмение Луны и Солнца повторяются через определенный промежуток времени — цикл. Это открытие сделал Э. Галлей, дав название этому явлению «сарос».
За один сарос, как правило, происходит 43 солнечных затмений:
- 15 частных;
- 15 кольцеобразных;
- 13 полных.
Лунных затмений бывает 28:
- 13 полных;
- 15 частных.
Ежегодно в среднем человечество может наблюдать по 4 затмения. Чаще всего лунное и солнечное совпадают друг с другом. Если во время новолуния было солнечное затмение, то через 2 недели (в полнолуние), возможно, будет и лунное.
Время и календарь
Жизнь каждого современного человека в той или иной степени связана со временем и регулируется постоянной сменой дня и ночи, лета, осени, зимы и весны. Считать время научились еще в древние времена. А с развитием человечества методы исчисления только совершенствовались.
Звездное и солнечное время
В современном мире человек живет по солнечному времени. Единицей его измерения принято считать солнечный сутки, в которых 24 часа. Именно столько времени необходимо Земному шару для одного полного оборота вокруг собственной оси. Точкой отсчета считается Солнце. Еще из курса географии известно, что планета и вокруг оси вращается, и вокруг Светила движется. За то время, как Земной шар совершит один полный оборот, он пройдет определенное расстояние по своей орбите. Следовательно, происходит его смещение относительно Солнца. Также стоит учитывать, что планета движется не по круглой орбите, а по эллиптической. Как результат, солнечные сутки – это величина не постоянная, в течение года она то уменьшается, то увеличивается. Поэтому 24 часа – это среднее значение, которое принято использовать в повседневной жизни.
Астрономы в своих расчетах не могут полагаться на средние величины, так как от них зависит, куда и как отправиться космическая ракета. Для этого было введено понятие «звездное время».
Определение звездного времени происходит относительно неподвижных звезд, а не Солнца. Продолжительность звездных суток составляет 23 часа 56 минут 4.1 секунды.
Звездный и тропический год
Период, за который Земной шар, проходит полный круг вокруг Солнца по отношению к звездам, называется звездный, либо же сидерический год Земли. Он составляет 365 дней 6 часов 9 минут. За это время на Земле меняются времена года (сезоны). Вот только полный период смены сезонов никак не совпадают со временем обращения Земли вокруг Светила.
Период смены времен года принято называть тропическим годом. Длится он 365 дней 5 часов 51 минуту. Измеряют его от одного весеннего равноденствия до другого. Разница в 20 минут между периодами тропического и звездного года объясняется прецессией земной оси.
Чтобы удобно было делать расчеты, принято за один год брать ровно 365 суток. Оставшиеся шесть с небольшим часов один раз в четыре города складываются в дополнительные сутки, отсюда появилось понятие «високосный год», а в календаре — 29 февраля.
Лунный и солнечный календарь
В лунном календаре сутки считаются относительно фаз Луны, соответственно, образуются синодические месяцы. Один лунный месяц насчитывает 29,5 суток. Чтобы не было путаницы с дробными частями, один месяц в календаре записывают 29 дней, в другой – 30. Полный год также состоит из 12 месяцев. В лунном календаре есть понятие как простого, так и високосного года.
Для отражения тропического года используют солнечный календарь. В его основе заложены времена года. Полный год имеет 365,2 суток. В нем также присутствует и простой, и високосный год.
Большинство древних народов создавало свои первые календари, учитывая смену фаз ночного светила. Человек стал замечать, что Луна, освещающая путь, каждый день принимала другую форму. С определенной периодичностью эти формы повторялись. На основе наблюдений, время начали определять между новолуниями, а данному временному промежутку присвоили название синодический месяц. С появлением лунного календаря началось первое летоисчисление.
Первый лунный календарь
С развитием сельского хозяйства лунный календарь перестал удовлетворять потребности человечества. Нужен был календарь, который бы отображал смену времен года. Это привело к созданию тропического календаря, в котором также стали использовать месяцы. Он помог систематизировать и улучшить земледельческие работы, а также наладить скотоводство. На сегодняшний день оба календарь важны в жизни каждого человека, они имеют и общие черты, и определенные различия:
- оба календаря состоят из 12 месяцев (циклов);
- продолжительность циклов отличается;
- у солнечного календаря год всегда начинается с одной и той же даты, а у лунного она постоянно сдвигается, так как лунный цикл короче;
- сутки солнечного календаря – это всегда 24 часа, у лунного – это значение меняется, но в определенный день цикла время всегда определенное.
Благодаря солнечному календарю человек точно знает, когда будет тепло, а когда холодно, когда наступит утро, а когда ночь. По лунному календарю высчитывают, когда лучше растут волосы и ногти, когда благоприятней делать операции, когда лучше сажать растения и т.д.
Юлианский и григорианский календарь
45 год до нашей эры ознаменован созданием юлианского календаря. Имя он получил от славноизвестного Юлия Цезаря, который стоял у власти как раз в это время. За основу взят солнечный календарь, а летоисчисление ориентировалось на время, за которое Солнце проходило все точки равноденствия. На тот момент данная система являлась самой точной. В году насчитывали 365 дней, появилось понятие високосный год, который предусматривал в календаре дополнительный день. Юлианский солнечный календарь активно применялся многими государствами на протяжении 1,5 тысяч лет.
В конце семнадцатого столетия Папой Григорием XIII была предложена другая система летоисчисления, которая получила название григорианский календарь. Количество дней полностью совпадало с юлианским календарем. Но все же вносились некоторые поправки касательно года високосного. По григорианскому календарю год, который заканчивается нулями и при этом не делится на 4, не может считаться високосным. Как пример возьмем 2000 год. Он был високосным, а вот 2100 будет обычным. Папа Григорий XIII утверждал, что праздник Пасхи всегда должен быть в воскресенье, а по юлианскому календарю он каждый год отмечался в разный день недели. Официально григорианский календарь был введен 24 февраля 1582 года.
На сегодняшний день оба календаря продолжают существовать вместе. Большая часть стран пользуется григорианским. В то время как юлианский используют для расчета христианских праздников. Россия по григорианскому календарю живет с 1917 года. После перехода летоисчисление сдвинулось на 14 дней. Именно поэтому в стране дважды отмечают Новый год: 1 января – по григорианскому календарю, а 14 января – по старому стилю, то есть по юлианскому календарю.
Луна вращается вокруг земли и один оборот занимает примерно 29 дней. При этом она вращается не по идеальному кругу, а по эллипсу. Та траектория по которой она вращается вокруг земли называется орбитой.
За счет того, что орбита Луны эллиптическая (см. рисунок) один раз в 29 дней Луна максимально приближается к земле (Перигей) и один раз удаляется (Апогей).
Ниже ответы на интересные вопросы, которые возникают когда мы задумываемся про то, как мы видим Луну на небе.
Почему мы всегда видим одну сторону Луны?
Если задуматься это довольно странно. Ведь например, если поставить на пол футбольный мяч и начать вокруг него двигать маленький теннисный, то по мере движения теннисного мячика он будет поворачиваться разными сторонами.
Однако мы видим всегда только одну сторону. Так происходит потому, что вращаясь вокруг земли Луна при этом сама вращается вокруг своей оси и один оборот вокруг оси занимает ровно время оборота вокруг земли. Это похоже на чудо. У ученых две версии почему такое стало возможным:
- приливы, которые Земля вызывает в лунной коре;
- разница в распределении массы в оболочке луны.
Эти явления могли синхронизировать вращение луны вокруг своей оси и вокруг земли.
Обратная сторона луны никогда не освещается солнцем?
Нет. Половину лунного месяца (примерно 14 суток) одна часть луны освещена, а другая темная. Потом наоборот. При этом температура освещенной поверхности достигает 107 градусов, а неосвещенной -150 градусов по Цельсию.
Как определить номер лунного дня?
Номер лунного дня не совпадает с номером дня месяца, так как в лунном месяце 29 дней (примерно, каждый раз по разному), а в календарном от 27 до 31. Поэтому, чтобы узнать номер лунного дня вы можете использовать:
- Страница луна сегодня — номер лунного дня сегодня и завтра.
- Лунный календарь — от 1 года нашей эры до 3000 с полной информацией на каждый день.
Синодический месяц
Синодический месяц, это классический лунный месяц, к которому мы привыкли. Он равен промежутку между новолуниями. Продолжительность непостоянна; среднее значение составляет 29,5 суток.
Сидерический (звёздный) месяц
Промежуток времени между двумя последовательными возвращениями Луны, при её видимом месячном движении, в одно и то же (относительно звёзд) место небесной сферы. Продолжительность составляет 27,3216610 суток (27 суток 7 часов 43 минуты 11,51 секунды).