Солнечная система > Система Марс > Планета Марс > Орбита Марса
Если сравнивать Марс и Землю, то сразу видно, что они совершенно отличаются по орбитам. Из-за этого марсианский год длится целых 686.98 дней. Все дело в расстоянии от Солнца до Марса.
Орбитальный период Марса
Средняя удаленность планеты от звезды – 227 939 200 км, что в 1.5 раз больше расстояния от Земли до Солнца. Но из-за эксцентриситета в 0.0934 отдаленность колеблется от 206.7 млн. км до 249.2 млн. км. При орбитальной скорости в 24.077 км/с у Марса создается такой длительный год.
Эксцентриситет марсианской орбиты
По эксцентриситету Марс стоит на втором месте после Меркурия (0.205). Но еще 1.35 млн. лет назад показатель у Красной планеты был лишь 0.002, из-за чего орбитальный проход был практически круглым. Но через 24000 лет он станет 0.105.
Влияние орбиты на земные и марсианские дни
Хотя год на Марсе длится дольше, но длительность дней практически совпадает с земным. У Марса – 24 часа, 37 минут и 22 секунды. Столько времени уходит на вращение оси. Но Солнце на проход по небу требует 24 часа, 39 минут и 35 секунд.
Ровер Opportunity отобразил солнечный проход за марсианский год (2006-2008 гг.)
Влияние орбиты Марса на сезонные перемены
Благодаря эксцентриситету и осевому наклону в 25.19° Марс обладает сменой сезонов (времена года). Средняя отметка температуры приближается к -46°C, но может опускаться до -143°C или прогреваться на 35°C.
Особенности орбиты приводят к тому, что планета замедляет свой ход на отдаленности и ускоряется в приближенности к звезде. Из-за этого весна длится 7 месяцев, лето – 6, осень – 5.3, а зима – 4.
На юге длительность времен года отличается. Марс пребывает в перигелии, когда на юге лето, а на севере – зима. В афелии все наоборот.
Хотите получить индивидуальный расклад?
Опытный таролог ответит на вопросы:
Что ждёт Вас в будущем? Как сложатся отношения? Какое решение — верное?
Влияние орбиты Марса на погоду
Марс располагает системой погодных условий. Это отмечается в виде опасных пылевых бурь, которые периодически охватывают всю поверхность. Способны простираться на тысячи километров и окружают планету густым слоем. Когда они разрастаются, то могут перекрыть обзор поверхности.
Видимые размеры Марса во время последних противостояний
Таким образом не повезло Маринеру-9 в 1971 году. Когда он послал свои первые снимки, марсианская поверхность полностью укрылась бурей. Она была настолько массивной, что отыскать можно было лишь наивысшую гору Олимп.
В 2001 году за пылевой бурей следил телескоп Хаббл на территории бассейна Эллады. Она стала крупнейшей за 25 лет. Причем за ней могли наблюдать даже астрономы-любители.
Бури появляются чаще всего, когда планета приближается к звезде. Почва высыхает и пыль легче поднять. Эти бури заставляют температуру подниматься, из-за чего формируется собственный парниковый эффект.
Если учесть все эти факторы, то можно ли создать марсианский календарь? Ну, это было бы сложно. Марсианский день, циклы и длительность года все же отличаются от привычных нам. Особенно необычно обстоят дела с годом в 668.5921 дней.
Читайте также:
- Интересные факты о Марсе;
- Колонизация Марса;
- Марс и Земля;
- Есть ли жизнь на Марсе;
- Терраформирование Марса
- Когда мы отправим людей на Марс?
- Сравнение Марса и Земли
- Как Земля выглядит с Марса?
- Что такое марсианское проклятие?
- Когда открыли Марс?
Положение и движение Марса
- Орбита Марса;
- Сезоны на Марсе
- Как далеко Марс от Солнца?
- Сближение Марса
- Как далеко находится Марс?
- Сколько лететь до Марса;
- День на Марсе;
- Год на Марсе;
Строение Марса
- Размеры Марса;
- Кольца Марса;
- Состав Марса;
- Атмосфера Марса;
- Воздух на Марсе;
- Масса Марса;
Поверхность Марса
- Поверхность Марса;
- Лед на Марсе
- Радиация на Марсе
- Вода на Марсе;
- Температура на Марсе;
- Гравитация на Марсе;
- Цвет Марса;
- Почему Марс красный;
- Насколько холодный Марс;
- Вулканы на Марсе;
- Вулкан Олимп;
- Долина Маринер;
- Лицо на Марсе;
- Пирамида на Марсе;
From Wikipedia, the free encyclopedia
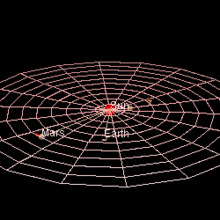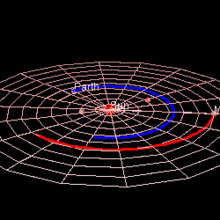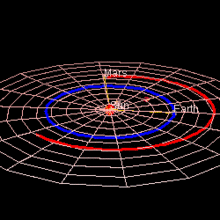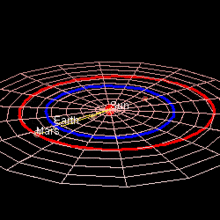
Orbit of Mars relative to the orbits of inner Solar system planets
Mars has an orbit with a semimajor axis of 1.524 astronomical units (228 million km), and an eccentricity of 0.0934.[1][2] The planet orbits the Sun in 687 days[3] and travels 9.55 AU in doing so,[4] making the average orbital speed 24 km/s.
The eccentricity is greater than that of every other planet except Mercury, and this causes a large difference between the aphelion and perihelion distances—they are 1.6660 and 1.3814 AU.[5][citation needed]
Changes in the orbit[edit]
Mars is in the midst of a long-term increase in eccentricity. It reached a minimum of 0.079 about 19 millennia ago, and will peak at about 0.105 after about 24 millennia from now (and with perihelion distances a mere 1.3621 astronomical units). The orbit is at times near circular: it was 0.002 1.35 million years ago, and will reach a similar minimum 1.05 million years into the future.[clarification needed] The maximum eccentricity between those two extreme minima is 0.12 in about 200 thousand years.[6]
Oppositions[edit]
Mars reaches opposition when there is a 180° difference between the geocentric longitudes of it and the Sun. At a time near opposition (within 8½ days) the Earth–Mars distance is as small as it will get during that 780-day synodic period.[7] Every opposition has some significance because Mars is visible from Earth all night, high and fully lit, but the ones of special interest happen when Mars is near perihelion, because this is when Mars is also nearest to Earth. One perihelic opposition is followed by another either 15 or 17 years later. In fact every opposition is followed by a similar one 7 or 8 synodic periods later, and by a very similar one 37 synodic periods (79 years) later.[8] In the so-called perihelic opposition Mars is closest to the Sun and is particularly close to Earth: Oppositions range from about 0.68 AU when Mars is near aphelion to only about 0.37 AU when Mars is near perihelion.[9]
Close approaches to Earth[edit]
Mars comes closer to Earth more than any other planet save Venus at its nearest—56 million km is the closest distance between Mars and Earth, whereas the closest Venus comes to Earth is 40 million km. Mars comes closest to Earth every other year, around the time of its opposition, when Earth is sweeping between the sun and Mars. Extra-close oppositions of Mars happen every 15 to 17 years, when we pass between Mars and the sun around the time of its perihelion (closest point to the sun in orbit). The minimum distance between Earth and Mars has been declining over the years, and in 2003 the minimum distance was 55.76 million km, nearer than any such encounter in almost 60,000 years (57,617 BC). The record minimum distance between Earth and Mars in 2729 will stand at 55.65 million km. In the year 3818, the record will stand at 55.44 million km, and the distances will continue to decrease for about 24,000 years.[10]
Historical importance[edit]
Until the work of Johannes Kepler (1571–1630), a German astronomer, the prevailing belief was that the sun and planets orbited the earth.
In 1543, Nicolaus Copernicus had proposed that all the planets orbited in circles around the sun, but his theory did not give very satisfactory predictions and was largely ignored. When Kepler studied his boss Tycho Brahe’s observations of Mars’s position in the sky on many nights, Kepler realized that Mars’s orbit could not be a circle. After years of analysis, Kepler discovered that Mars’s orbit was likely to be an ellipse, with the Sun at one of the ellipse’s focal points. This, in turn, led to Kepler’s discovery that all planets orbit the Sun in elliptical orbits, with the Sun at one of the two focal points. This became the first of Kepler’s three laws of planetary motion.[11][12]
Accuracy/predictability[edit]
From the perspective of all but the most demanding, the path of Mars is simple. An equation in Astronomical Algorithms that assumes an unperturbed elliptical orbit predicts the perihelion and aphelion times with an error of «a few hours».[13] Using orbital elements to calculate those distances agrees to actual averages to at least five significant figures. Formulas for computing position straight from orbital elements typically do not provide or need corrections for the effects of other planets.[14]
For a higher level of accuracy the perturbations of planets are required. These are well known, and are believed to be modeled well enough to achieve high accuracy. These are all of the bodies that need to be considered for even many demanding problems. When Aldo Vitagliano calculated the date of close Martian approaches in the distant past or future, he tested the potential effect caused by the uncertainties of the asteroid belt models by running the simulations both with and without the biggest three asteroids, and found the effects were negligible.
Observations are much better now, and space age technology has replaced the older techniques. E. Myles Standish wrote: «Classical ephemerides over the past centuries have been based entirely upon optical observations:almost exclusively, meridian circle transit timings. With the advent of planetary radar, spacecraft missions, VLBI, etc., the situation for the four inner planets has changed dramatically.» (8.5.1 page 10) For DE405, created in 1995, optical observations were dropped and as he wrote «initial conditions for the inner four planets were adjusted to ranging data primarily…»[15] The error in DE405 is known to be about 2 km and is now sub-kilometer.[16]
Although the perturbations on Mars by asteroids have caused problems, they have also been used to estimate the masses of certain asteroids.[17] But improving the model of the asteroid belt is of great concern to those requiring or attempting to provide the highest-accuracy ephemerides.[18]
Orbital parameters[edit]
No more than five significant figures are presented in the following table of Mars’s orbital elements. To this level of precision, the numbers match very well the VSOP87 elements and calculations derived from them, as well as Standish’s (of JPL) 250-year best fit, and calculations using the actual positions of Mars over time.
| Distances and eccentricity | (AU) | (million km) |
|---|---|---|
| Semimajor axis | 1.5237 | 227.9 |
| Perihelion | 1.3814 | 206.7 |
| Aphelion | 1.6660 | 249.2 |
| Average[19] | 1.5303 | 228.9 |
| Circumference | 9.553 | 1429 |
| Closest approach to Earth | 0.3727 | 55.76 |
| Farthest distance from Earth | 2.675 | 400.2 |
| Eccentricity | 0.0934 | |
| Angles | (°) | |
| Inclination | 1.850 | |
| Period | (days) | (years) |
| Orbital | 687.0 | 1.881 |
| Synodic | 779.9 | 2.135 |
| Speed | (km/s) | |
| Average | 24.1 | |
| Maximum | 26.5 | |
| Minimum | 22.0 |
References[edit]
- ^ Simon, J.L.; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (February 1994). «Numerical expressions for precession formulae and mean elements for the Moon and planets». Astronomy and Astrophysics. 282 (2): 663–683. Bibcode:1994A&A…282..663S.
- ^ Jean Meeus, Astronomical Formulæ for Calculators. (Richmond, VA: Willmann-Bell, 1988) 99. Elements by F. E. Ross
- ^ In ephemeris days of 86 400 seconds. The sidereal and anomalistic years are 686.980 days and 686.996 days long, respectively. (About a 20 minute difference). The sidereal year is the time taken to revolve around the Sun relative to a fixed reference frame. More precisely, the sidereal year is one way to express the rate of change of the mean longitude at one instant, with respect to a fixed equinox. The calculation shows how long it would take for the longitude to change 360 degrees at the given rate.
The anomalistic year is the time span between successive perihelion or aphelion passages. This may be calculated in the same manner as the sidereal year, but the mean anomaly is used. - ^ Jean Meeus, Astronomical Algorithms (Richmond, VA: Willmann-Bell, 1998) 238. The formula by Ramanujan is accurate enough.
- ^ The averages between 1850 and 2150. The extreme values in that range are 1.66635 and 1.38097 AU
- ^ «MarsDist». Archived from the original on 2007-09-07. Retrieved 2007-07-20. Mars distance and eccentricity, using SOLEX. By its creator, Aldo Vitagliano
- ^ The synodic period may be calculated as 1/(1/p-1/q), where p and q are the smaller and larger sidereal periods.
- ^ The synodic period of Mars is 92.9 days longer than its sidereal period of 687.0 days. It has then moved forward 92.9/687.0 times 360, or 48.7 degrees. After seven oppositions it has moved forward 341 degrees, and after eight it has advanced 390 degrees; in the first case its longitude is different from one revolution by 19°, and by 30° in the second. So the situations will then be similar. Similar calculations show that the longitude changes only 2° after 37 oppositions.
- ^ Sheehan, William (February 2, 1997). «Appendix 1: Oppositions of Mars, 1901–2035». The Planet Mars: A History of Observation and Discovery. University of Arizona Press. Archived from the original on June 25, 2010. Retrieved January 30, 2010.
- ^ Meeus, Jean (March 2003). «When Was Mars Last This Close?» (PDF). Planetarian: 13.
- ^ Carr, Michael H.; Malin, Michael C.; Belton, Michael J.S. (July 27, 2018). «Mars». Encyclopædia Britannica Online. p. 2.
- ^ William Sheehan, The Planet Mars: A History of Observation and Discovery (Tucson, AZ: The University of Arizona Press, 1996) Chapter 1
- ^ Meeus (1998) pp 269–270
- ^ see, for example, Simon et al. (1994) p. 681
- ^ Standish & Williams (2012). «CHAPTER 8: Orbital Ephemerides of the Sun, Moon, and Planets» (PDF). 2012 version of the Explanatory Supplement
- ^ As noted in a 2008 JPL Memorandum regarding DE421, «The error in the Earth and Mars orbits in DE405 is now known to be about 2 km, which was good accuracy in 1997 but much worse than the current sub-kilometer accuracy.»Folkner; et al. (2008). «The Planetary and Lunar Ephemeris DE421» (PDF). JPL Interoffice Memorandum IOM 343.R-08-003. p. 1
- ^ «asteroid.» Encyclopædia Britannica. Encyclopædia Britannica Online. Encyclopædia Britannica Inc., 2014. Web. 19 Aug. 2014. http://www.britannica.com/EBchecked/topic/39730/asteroid
- ^ «The uncertainty in the Mars orbit for a one-year prediction is about 300 m, as required for the Mars Science Laboratory mission, but grows rapidly for times before and
after the spacecraft observation time span due to the influence of asteroids with orbits near that of Mars. The predicted orbit and uncertainty depend greatly on the asteroid model used. «Folkner; et al. (2010). «Uncertainties in the JPL Planetary Ephemeris» (PDF). Proceedings of the Journées. p. 43. - ^ Average distance over times. Constant term in VSOP87. It corresponds to the average taken of many short, equal time intervals.
Важную роль в формировании представлений о строении Солнечной системы сыграли также законы движения планет, которые были открыты Иоганном Кеплером и стали первыми естественно-научными законами в их современном понимании. Работы Кеплера создали возможность для обобщения знаний по механике той эпохи в виде законов динамики и закона всемирного тяготения, сформулированных позднее Исааком Ньютоном. Многие учёные вплоть до начала XVII в. считали, что движение небесных тел должно быть равномерным и происходить по «самой совершенной» кривой — окружности. Лишь Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.
Иоганн Кеплер
В своих поисках Кеплер исходил из убеждения, что «в мире правит число», высказанного ещё Пифагором. Он искал соотношения между различными величинами, характеризующими движение планет, — размеры орбит, период обращения, скорость. Кеплер действовал фактически вслепую, чисто эмпирически. Он пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон описанных и вписанных в орбиты планет многоугольников и т. д.
Кеплеру необходимо было построить орбиты планет, перейти от экваториальной системы координат, указывающих положение планеты на небесной сфере, к системе координат, указывающих её положение в плоскости орбиты. Он воспользовался при этом собственными наблюдениями планеты Марс, а также многолетними определениями координат и конфигураций этой планеты, проведёнными его учителем Тихо Браге.
Рис. 3.5. Построение орбиты Марса Кеплером
Орбиту Земли Кеплер считал (в первом приближении) окружностью, что не противоречило наблюдениям. Чтобы построить орбиту Марса, он применил способ, который показан на рисунке 3.5.
Пусть нам известно угловое расстояние Марса от точки весеннего равноденствия во время одного из противостояний планеты — его прямое восхождение α1, которое выражается углом ♈T1M1, где T1 — положение Земли на орбите в этот момент, а M1 — положение Марса. Очевидно, что спустя 687 суток (таков звёздный период обращения Марса) планета придёт в ту же точку своей орбиты. Если определить прямое восхождение Марса на эту дату, то, как видно из рисунка 3.5, можно указать положение планеты в пространстве, точнее, в плоскости её орбиты. Земля в этот момент находится в точке T2, и, следовательно, угол ♈T2M1 есть не что иное, как прямое восхождение Марса — α2. Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил ещё целый ряд точек и, проведя по ним плавную кривую, построил орбиту этой планеты.
Изучив расположение полученных точек, он обнаружил, что скорость движения планеты по орбите меняется, но при этом
радиус-вектор планеты за равные промежутки времени описывает равные площади.

Рис. 3.6. Второй закон Кеплера
Впоследствии эта закономерность получила название второго закона Кеплера.
Этот закон, который часто называют законом площадей, иллюстрируется рисунком 3.6. Радиусом-вектором называют в данном случае переменный по своей величине отрезок, соединяющий Солнце и ту точку орбиты, в которой находится планета. AA1, BB1 и CC1 — дуги, которые проходит планета за равные промежутки времени. Площади заштрихованных фигур равны между собой.
Согласно закону сохранения энергии, полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остаётся неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной энергии. По мере приближения планеты к Солнцу возрастает её скорость — увеличивается кинетическая энергия, но вследствие уменьшения расстояния до Солнца уменьшается энергия потенциальная.
Установив закономерность изменения скорости движения планет, Кеплер задался целью определить, по какой кривой происходит их обращение вокруг Солнца. Он был поставлен перед необходимостью сделать выбор одного из двух возможных решений: 1) считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями (из-за ошибок наблюдений) на 8ʹ; 2) считать, что наблюдения таких ошибок не содержат, а орбита не является окружностью. Будучи уверенным в точности наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется эллипсом, при этом Солнце не располагается в центре эллипса. В результате был сформулирован закон, который называется первым законом Кеплера.
Каждая планета обращается вокруг Солнца по эллипсу, в одном из фоку- сов которого находится Солнце.

Рис. 3.7. Свойства эллипса
Как известно, эллипсом называется кривая, у которой сумма расстояний от любой точки P до его фокусов есть величина постоянная. На рисунках 3.6 и 3.7 обозначены: O — центр эллипса; S и S1 — фокусы эллипса; AB — его большая ось. Половина этой величины (a), которую обычно называют большой полуосью, характеризует размер орбиты планеты. Ближайшая к Солнцу точка A называется перигелий, а наиболее удалённая от него точка B — афелий. Отличие эллипса от окружности характеризуется величиной его эксцентриситета: e = OS/OA. В том случае, когда эксцентриситет равен 0, фокусы и центр сливаются в одну точку — эллипс превращается в окружность.
Примечательно, что книга, в которой в 1609 г. Кеплер опубликовал первые два открытых им закона, называлась «Новая астрономия, или Физика небес, изложенная в исследованиях движения планеты Марс…».
Оба этих закона, опубликованные в 1609 г., раскрывают характер движения каждой планеты в отдельности, что не удовлетворило Кеплера. Он продолжил поиски «гармонии» в движении всех планет, и спустя 10 лет ему удалось сформулировать третий закон Кеплера.
Квадраты звёздных периодов обращения планет относятся между собой как кубы больших полуосей их орбит.
Формула, выражающая третий закон Кеплера, такова:


где T1 и T2 — периоды обращения двух планет; a1 и a2 — большие полуоси их орбит.
Вот что писал Кеплер после открытия этого закона: «То, что 16 лет тому назад я решил искать, <…> наконец найдено, и это открытие превзошло все мои самые смелые ожидания…»
Действительно, третий закон заслуживает самой высокой оценки. Ведь он позволяет вычислить относительные расстояния планет от Солнца, используя при этом уже известные периоды их обращения вокруг Солнца. Не нужно определять расстояние от Солнца каждой из них, достаточно измерить расстояние от Солнца хотя бы одной планеты. Величина большой полуоси земной орбиты — астрономическая единица (а. е.) — стала основой для вычисления всех остальных расстояний в Солнечной системе.
Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
|
Дано: S = 2 г. T1 = 1 г. a1 = 1 а. е. |
Решение: Большую полуось орбиты планеты можно определить из третьего закона Кеплера:
|
|
a2 — ? |
Формула



используется для вычисления звёздного периода планеты:
T2 = 

Тогда a2 = 
Ответ: a2 = 1,59 а. е.

Вопросы 1. Сформулируйте законы Кеплера. 2. Как меняется скорость планеты при её перемещении от афелия к перигелию? 3. В какой точке орбиты планета обладает максимальной кинетической энергией; максимальной потенциальной энергией?

Упражнение 10 1. Марс в 1,5 раза дальше от Солнца, чем Земля. Какова продолжительность года на Марсе? Орбиты планет считать круговыми. 2. Синодический период внешней малой планеты 500 суток. Определите большую полуось её орбиты и звёздный период обращения.

Задание 11 Выполнение этого задания позволит узнать, как располагаются планеты на орбитах в настоящее время, и научиться самостоятельно отыскивать их на небе.
1) Нарисуйте в своей тетради орбиты четырёх ближайших к Солнцу планет: Меркурия, Венеры, Земли и Марса. Чтобы наибольшая из орбит — орбита Марса — уместилась на листе тетради, следует выбрать масштаб, при котором 1 см соответствует 30 млн км (1 : 3 000 000 000 000). Рассчитайте размеры орбит планет и с помощью циркуля проведите окружности соответствующего радиуса. Необходимые данные возьмите из приложения VI.
2) Используйте данные таблицы гелиоцентрических долгот Гелиоцентрической долготой называется угол при центре (Солнце) между направлениями на точку весеннего равноденствия и на планету. планет из «Школьного астрономического календаря» для ответа на следующие вопросы:
а) У какой планеты — Меркурия, Венеры, Земли или Марса — эксцентриситет орбиты наибольший?
б) На какие (примерно) даты приходятся прохождения Меркурия через перигелий; через афелий?
в) Найдите в таблице даты, на которые приходятся соединения планет с Солнцем, а также их противостояний.
3) Пользуясь таблицей гелиоцентрических долгот планет, на орбите каждой планеты отметьте её положения в сентябре — декабре текущего года. Для этого проведите из центра орбит в произвольном направлении луч, который будет указывать направление на точку весеннего равноденствия. От этого луча на каждой орбите в направлении, противоположном движению часовой стрелки, отложите дуги, соответствующие гелиоцентрической долготе данной планеты, и отметьте эти положения.
Для того чтобы узнать, где по отношению к Солнцу располагается на небе та или иная планета, ориентируйте нарисованный план так, чтобы линия, соединяющая на плане положение Земли на данные сутки и Солнца, была направлена в момент наблюдения на Солнце. Те планеты, которые согласно их положению на плане оказываются слева от направления на Солнце, заходят позже него. Планеты, которые находятся справа от этого направления, заходят раньше Солнца, но и восходят раньше него. Для того чтобы узнать, можно ли будет увидеть планеты, необходимо определить, как далеко от Солнца на небе они находятся. Если на плане угол между направлениями с Земли на Солнце и на планету менее 15°, то, скорее всего, планету нельзя будет наблюдать. Она либо зайдёт прежде, чем стемнеет, либо взойдёт уже после того, как станет светло. Если же планета удалена от Солнца более чем на 15°, то её следует поискать на небе на соответствующем угловом расстоянии от него.
Марс имеет орбиту с большой полуосью 1,524 астрономических единиц (228 миллионов км) и эксцентриситет 0,0934. Планета обращается вокруг Солнца за 687 дней и проходит при этом 9,55 а. Е., Делая среднюю орбитальную скорость 24 км / с.
Эксцентриситет больше, чем у любой другой планеты, кроме Меркурия, и это вызывает большую разницу между расстояниями афелия и перигелия — они составляют 1,6660 и 1,3814 а.е.
Содержание
- 1 Изменения орбиты
- 2 Оппозиции
- 3 Близкие подходы к Земле
- 4 Историческое значение
- 5 Точность / предсказуемость
- 6 Параметры орбиты
- 7 Источники
Изменения в орбита
Марс находится в процессе длительного увеличения эксцентриситета. Оно достигло минимума 0,079 около 19 тысячелетий назад и достигнет максимума около 0,105 примерно через 24 тысячелетия с настоящего момента (а расстояние до перигелия составляет всего 1,3621 астрономических единиц ). Орбита иногда близка к круговой: это было 0,002 1,35 миллиона лет назад и будет примерно 0,01 миллиона лет назад. Максимальный эксцентриситет между этими двумя минимумами составляет 0,12.
Оппозиции
Марс достигает оппозиции, когда существует разница в 180 ° между геоцентрическими долготами его и Солнца. Во время близкого противостояния (в пределах 8½ дней) расстояние Земля – Марс настолько мало, насколько оно будет в течение этого 780-дневного синодического периода. Каждое противодействие имеет какое-то значение, потому что Марс виден с Земли всю ночь, высоко и полностью освещен, но те, которые представляют особый интерес, случаются, когда Марс находится около перигелия, потому что именно тогда Марс находится ближе всего к Земле. За одним перигелическим противостоянием следует другое 15 или 17 лет спустя. Фактически, за каждой оппозицией следует подобное спустя 7 или 8 синодических периодов, а также очень похожее через 37 синодических периодов (79 лет) позже. В так называемой перигелической оппозиции Марс находится ближе всего к Солнцу и особенно близко к Земле: оппозиция колеблется от около 0,68 а.е., когда Марс находится около афелия, до всего около 0,37 а.е., когда Марс находится около перигелия.
Близкое приближение к Земле
Марс подходит к Земле ближе, чем любая другая планета, за исключением ближайшей Венеры — 56 против 40 миллионов км. С годами расстояния сокращались, и в 2003 году минимальное расстояние составляло 55,76 миллиона км, что ближе, чем любое подобное столкновение за почти 60 000 лет (57617 до н.э.). Этот современный рекорд будет побит в 2287 году, а рекорд до 3000 будет установлен в 2729 году на уровне 55,65. После, в 3818 году рекорд будет 55,44. Расстояния будут продолжать уменьшаться в течение примерно 24 000 лет.
Историческое значение
До работы Иоганна Кеплера (1571–1630), немецкого астронома, это было считали или предполагали, что планеты движутся по круговым орбитам вокруг Солнца. Когда Кеплер изучал тщательные наблюдения датского астронома Тихо Браге за положением Марса на небе в течение многих ночей, Кеплер понял, что орбита Марса не может быть круговой. После тщательного анализа Кеплер обнаружил, что орбита Марса представляет собой эллипс, причем Солнце занимает одну из двух фокальных точек эллиптической орбиты. Это, в свою очередь, привело к открытию Кеплера, что все планеты вращаются вокруг Солнца по эллиптическим орбитам, причем Солнце находится в одной из двух фокусных точек. Это стало первым из трех законов движения планет Кеплера..
Точность / предсказуемость
С точки зрения всех, кроме самых требовательных, путь Марса прост. Уравнение в астрономических алгоритмах, которое предполагает невозмущенную эллиптическую орбиту, предсказывает времена перигелия и афелия с погрешностью «несколько часов». Использование элементов орбиты для вычисления этих расстояний соответствует реальным средним значениям как минимум с пятью значащими цифрами. Формулы для вычисления положения прямо из орбитальных элементов обычно не обеспечивают и не требуют поправок на влияние других планет.
Для более высокого уровня точности требуются возмущения планет. Они хорошо известны и считаются достаточно хорошо смоделированными для достижения высокой точности. Это все органы, которые необходимо учитывать даже при решении многих сложных проблем. При вычислении даты близкого сближения Марса в далеком прошлом или будущем он проверил потенциальный эффект, вызванный неопределенностями моделей пояса астероидов, запустив моделирование как с тремя самыми большими астероидами, так и без них, и обнаружил, что эффекты незначительны.
Наблюдения стали намного лучше, и технологии космической эры заменили старые методы. Э. Майлс Стэндиш писал: «Классические эфемериды прошлых столетий полностью основывались на оптических наблюдениях: почти исключительно, времени прохождения меридионального круга. С появлением планетарных радаров, миссий космических кораблей, РСДБ и т. Д. Ситуация для четырех внутренних планеты сильно изменились ». (8.5.1 стр. 10) Для DE405, созданного в 1995 году, оптические наблюдения были прекращены, и, как он писал, «начальные условия для четырех внутренних планет были скорректированы в основном с учетом данных о дальности…» Известно, что ошибка в DE 405 составляет около 2 км и сейчас составляет менее километра.
Хотя возмущения на Марсе астероидами вызвали проблемы, они также использовались для оценки масс некоторых астероидов. Но улучшение модели пояса астероидов является серьезной проблемой для тех, кто требует или пытается предоставить эфемериды с высочайшей точностью.
Параметры орбиты
Не более пяти значащих цифр представлены в следующей таблице орбитальных элементов Марса. На этом уровне точности числа очень хорошо соответствуют элементам VSOP87 и вычислениям, полученным на их основе, а также наилучшему соответствию Стэндиша (JPL) за 250 лет и вычислениям с использованием фактических положений Марса во времени..
| Расстояния и эксцентриситет | (AU) | (млн км) |
|---|---|---|
| Большая полуось | 1,5237 | 227,9 |
| Перигелий | 1,3814 | 206,7 |
| Афелий | 1,6660 | 249,2 |
| Среднее | 1,5303 | 228,9 |
| Окружность | 9,553 | 1429 |
| Самый близкий подход к Земле | 0,3727 | 55,76 |
| Наибольшее расстояние от Земли | 2,675 | 400,2 |
| Эксцентриситет | 0,0934 | |
| Углы | (°) | |
| Наклон | 1,850 | |
| Период | (дни) | (годы) |
| Орбитальный | 687.0 | 1.881 |
| Синодический | 779.9 | 2,135 |
| Скорость | (км / с) | |
| Средняя | 24,1 | |
| Максимум | 26,5 | |
| Минимум | 22,0 |
Ссылки
Планета Марс на небе
Как найти ее невооруженным глазом и отличить от звёзд
Планета Марс — одна из самых загадочных и интересных планет Солнечной системы. Еще не так давно люди предполагали на Марсе наличие не просто жизни, а разумной цивилизации! Некогда шумевшие истории о марсианских каналах еще не выветрились из нашей памяти. Марс это не просто наиболее похожая на Землю планета, но и единственная планета Солнечной системы, у которой можно детально наблюдать в телескоп поверхность. А там есть, на что посмотреть! Это и рыжие пустыни, и темные пятна «морей», полярные шапки и даже облака, плавающие в разреженной атмосфере. Но, прежде чем наблюдать Марс в телескоп, нужно уметь его находить. Как выглядит планета Марс на небе? Как найти его невооруженным глазом? Об этом текущая статья.
Марс на звёздном небе
Марс — одна из внешних планет Солнечной системы. Это значит, что при движении на фоне звезд Марс проходит через несколько конфигураций.
- Соединение (с Солнцем). В это время планета не видна, так как находится на небе слишком близко к Солнцу.
- Восточная квадратура. Планета находится на угловом расстоянии 90° от Солнца и наблюдается на утреннем небе.
- Противостояние (или оппозиция). Марс располагается на противоположном участке неба от Солнца и наблюдается все темное время суток.
- Западная квадратура. Планета находится на угловом расстоянии 90° от Солнца и наблюдается на вечернем небе.
Основные конфигурации Марса и других внешних планет.
Цикл видимости Марса на небе длится около двух лет. В течение этого времени планета переходит с утреннего неба на ночное, а затем на вечернее. При этом яркость ее меняется весьма драматическим образом. В первых и последних фазах видимости Марс плохо заметен на небе, зато вблизи противостояний является одним из ярчайших небесных тел.
Марс на утреннем небе
Первое появление Марса на небе происходит примерно через месяц после соединения с Солнцем, когда планета появляется в лучах утренней зари на востоке. Увидеть Марс в это время непростая задача, так как он неярок и теряется на фоне светлеющего неба.
Постепенно Марс восходит все раньше и раньше, как бы отставая на небе от Солнца. Однако если внимательно наблюдать за планетой, то можно заметить, что она движется на фоне звезд в одном направлении с Солнцем — с запада на восток. Такое движение планет называется прямым.
Это видимое отставание объясняется разницей в угловых скоростях движения Земли и Марса вокруг Солнца. Если бы мы могли подняться над Солнечной системой и посмотреть на нее сверху, то увидели бы, что на самом деле не Марс отстает от Солнца, а Земля, двигаясь по орбите, догоняет Марс.
Процесс «погони» не быстрый и занимает на небе больше года. Первые 8 или 9 месяцев после появления на небе Марс мало заметен. Планета наблюдается только по утрам, а видимость (от восхода планеты до рассвета) составляет всего несколько часов. При этом Марс выглядит, как обычная звезда 2 величины. Его яркость сравнима с блеском звезд Большого ковша.
Марс в западной квадратуре
Через 10,5 месяцев после соединения Марс оказывается в западной квадратуре. Это значит, что угловое расстояние между Марсом и Солнцем на небе становится равным 90°.
Во время квадратуры встаньте лицом к Марсу и раскиньте руки в стороны. Если квадратура западная (утренняя), то левая рука укажет на Солнце, если восточная (вечерняя), то на Солнце укажет правая рука.
Находясь в квадратуре, Марс восходит около полуночи и наблюдается на небе вплоть до рассвета.
После западной квадратуры наступает благоприятное время для наблюдения Красной планеты — в том числе в телескоп. Однако лучшее время для наблюдения Марса начинается вблизи противостояния, примерно за месяц до события, и длится вплоть до достижения планеты восточной квадратуры.
Петля Марса на небе
Траектория движения Марса весьма замысловата. Через 11 месяцев после соединения планета останавливается на фоне звезд. Наступает стояние. Затем Марс начинает двигаться в обратном направлении — с востока на запад. Такое движение называется попятным или ретроградным.
Ретроградное движение Марса длится 2 месяца и 2 недели, после чего планета вновь сменяет движение на прямое. Если нарисовать траекторию движения Марса на фоне звезд в этот период, то мы увидим, что светило описывает на фоне звезд замысловатую кривую, часто похожую на петлю.
Петли Марса могут принимать самые разные формы — они могут быть замкнутыми, зигзагообразными (открытыми петлями) или их комбинацией. Точная форма зависит от того, где на небе в это время находится планета — выше эклиптики, ниже или пересекает ее. Замкнутые петли наиболее часты, а Z-образные наиболее редки.
Петлеобразное движение Марса связано с тем, что Земля, двигаясь по орбите вокруг Солнца, догоняет Красную планету. Так как Земля движется гораздо быстрее Марса, то в определенный момент мы видим, что Марс начинает двигаться попятно на фоне далеких звезд.
Представьте, что вы находитесь в быстро движущемся поезде и проезжаете мимо человека, идущего в том же направлении, что и поезд. Несмотря на то, что направления движения одинаковы, вам покажется, что человек движется в обратном направлении относительно далекого леса.
Петля на фоне звезд, которую совершает Марс в 2022 году. По форме траектория планеты является комбинацией замкнутой петли и Z-образной незамкнутой петли. Рисунок: Stellarium
Примерно в середине своего ретроградного движения наступает противостояние Марса.
Противостояния Марса
Противостояние Марса наступает через 14 месяцев после соединения. Это событие, когда Земля, двигаясь по орбите вокруг Солнца, наконец, догоняет Марс.
В этот момент Солнце, Земля и Марс располагаются на одной линии.
Как это отражается на положении Марса на небе? Угловая долгота Солнца и Марса во время противостояния составляет 180° — светила находятся на противоположных участках неба друг напротив друга.
Противостояния Марса — бесспорно лучшее время для наблюдения этой планеты. И вот почему:
- Во время противостояния Земля находится в ближайшей точке к планете в течение всего года. Это значит, что Марс достигает максимальной яркости на небе и имеет наибольшие угловые размеры при наблюдении в телескоп. Как следствие, наблюдатель может увидеть больше деталей на диске планеты.
- Во время и вблизи точки противостояния планета наблюдается на небе всю ночь: она восходит на закате Солнца, а заходит за горизонт на рассвете. Это позволяет выбирать удобное время для наблюдения.
- Наконец, к нам обращена полностью освещенная Солнцем сторона планеты, то есть ее фаза равна 1,0. Для Марса это имеет большое значение, так как во время квадратуры планета для нас выглядит не как диск, а как овал.
Ближайшее противостояние Марса наступит 1 декабря 2022 года в 2 часа 18 минут по Всемирному времени (5 часов 18 минут по московскому). Подробнее об этом событии можно прочитать здесь.
Марс и Млечный Путь вскоре после великого противостояния 2018 года. Фото: Tom Masterson
Противостояния Марса повторяются в среднем каждые каждые 2 года и 2 месяца. Следующее противостояние после 2022 года наступит зимой 2025 года. Противостояния Марса отличаются друг от друга. Некоторые считаются относительно неблагоприятными, другие благоприятными. Наконец, есть еще великие противостояния, когда Марс максимально сближается с Землей. Подробнее об этом читайте в статье Противостояния Марса.
Противостояние 2022 года считается относительно благоприятным. Интересно, что в день противостояния, 1 декабря, состоится редкое явление — покрытие Марса Луной!
Марс в восточной квадратуре
После противостояния Марс начинает постепенно удаляться от Земли. Яркость планеты начинает уменьшаться, как и видимые размеры при наблюдении в телескоп. Светило перемещается на вечернее небо.
Тем не менее планета остается достаточно яркой и заметной вплоть до восточной квадратуры, которая наступает через 3,5 месяца после противостояния. Но и в дальнейшем планета еще несколько месяцев проводит на вечернем небе. В это время ее можно увидеть после захода Солнца в течение нескольких часов на западе.
Через 7 месяцев после восточной квадратуры планета пропадает, теряясь в лучах вечерней зари. Цикл видимости Марса подходит к концу. Еще месяц спустя планета оказывается в соединении с Солнцем, окрывая новый цикл видимости.
Вблизи вечерней квадратуры удобнее всего наблюдать соединения Марса с другими планетами.
Яркость Марса
Яркость Марса сильно зависит от конфигурации планеты. Если в первые месяцы после своего появления на небе, планета выглядит как обычная звезда 1,5m, то вблизи квадратуры блеск Марса уже сравним с блеском ярчайших звезд.
Планета достигает максимальной яркости во время противостояния, когда находится на минимальном расстоянии от Земли. В это время Марс, как правило, намного ярче любой из звезд. А во время великих противостояний планета может быть даже немного ярче Юпитера! (Блеск планеты во время противостояний колеблется от -1,5m до -2,9m.)
Большие вариации яркости в течение периода видимости отличают Марс от других планет на небе.
Во время противостояний Марс — очень яркая планета, которая выделяется на небе благодаря своему красноватому цвету. Фото: Flickr.com/Maddin Seeger
Колебания яркости Марса в период с 2022 по 2050 годы. На графике по оси Х отложены годы, по оси Y — звездная величина планеты. Резкие пики — противостояния Марса, которые в среднем повторяются через каждые 2 года и 2 месяца. Источник: theskylive.com
Как выглядит Марс с Земли?
Марс на небе невооруженным глазом всегда выглядит как звездообразный объект. В сети Интернет уже больше 15 лет гуляет мем: «27 августа Марс приблизится к Земле и станет больше Луны». Это, конечно, обыкновенная утка. При наблюдении планет невооруженным глазом ни одна из них, включая Марс, не видна на небе в виде диска, как Луна или Солнце. Даже во время великих противостояний планета выглядит как очень яркий, но все же звездообразный объект. Чтобы увидеть диск Марса, вам понадобится телескоп.
Цвет Марса
Вблизи противостояний (перед 3-4 месяца перед ним и столько же после) бросается в глаза цвет Марса. Он может быть розовым, желтовато-красным, красноватым, медным… Конкретный цвет зависит от субъективного восприятия, но также от текущих условий на планете. В частности, влияние оказывают пылевые бури и сезонные изменения на поверхности Марса.
Марс привлекал внимание людей своим необычным поведением и цветом с древнейших времен. Колебания яркости выделяли эту планету из других, доступных для наблюдения невооруженным глазом. А красноватый цвет напоминал грекам и римлянам цвет крови. Греческий философ Аристотель назвал планету Аресом, в честь бога войны. Римляне имели аналогичного бога в своем пантеоне, Марса, имя которого стало общеупотребительным.
Как отличить Марс на небе от звезд?
Вблизи противостояний у Марса нет соперников на небе из числа обычных звезд. Только Венера и Юпитер ярче Красной планеты. В это время отличительная особенность Марса — спокойное ровное сияние. Планета не мерцает, ее свет не дрожит и не колеблется, как у звезд. Даже находясь низко над горизонтом, Марс похож больше на далекий прожектор, чем на настоящую звезду.
Совсем по-другому выглядит Марс в начале или в конце цикла видимости. Тогда планета выглядит настолько невзрачно, что без хорошего знания звездного неба ее не отличить от обычной звездочки. В этот период звездные карты и атласы вам в помощь!
Прекрасная Красная планета во время великого противостояния 2018 года. Фото: Sebastian Voltmer
Как найти Марс на небе?
Часто спрашивают, как увидеть Марс на небе невооруженным глазом? Легко ли найти планету?
Ответ на второй вопрос таков: смотря когда! Чтобы найти Марс на небе сегодня или в любой другой день, нужно знать: а) текущее положение Марса на небе и б) его текущую яркость.
Цикл видимости Марса длится 2 года и 2 месяца. Из них 2 месяца планета не видна невооруженным глазом вообще, так располагается на небе слишком близко к Солнцу. Большую часть остального времени планета пребывает либо на утреннем, либо на вечернем небе в виде звезды средней яркости.
Период, когда планета выделяется яркостью и пребывает на небе больше нескольких часов в сутки, длится около полугода в течение цикла.
Как узнать, где на небе находится Марс прямо сейчас?
Узнать положение Марса на небе на небе можно несколькими способами.
- Установите на ваш компьютер или телефон астрономическое приложение (Stellarium, Star Walk 2 или любое другое). Приложение или программа предоставит вам всю необходимую информацию.
- На сайте www.astronet.ru под редакцией Александра Козловского выходят еженедельные и ежемесячные обзоры астрономических явлений, где приводятся в том числе и положения всех планет. Также ежегодно на сайте выходит подробный астрономический календарь, где публикуются в том числе таблицы и карты видимости планет.
- Эфемериды Марса на 2022 — 2023 годы можно найти здесь.
- Воспользуйтесь помощью Луны! Практически ежемесячно наш спутник оказывается на небе возле Марса. Ниже указаны даты соединений Луны и Марса в 2022 — 2023 годах.
Марс рядом с Луной в конце 2022 и в 2023 году
В таблице указаны дата события, время (московское), угловое расстояние между Луной и Марсом на небе, фаза Луны и время суток, когда можно наблюдать светила.
| Дата | Время (МСК) | Угловое расстояние | Фаза Луны | Когда наблюдается | Примечание |
|---|---|---|---|---|---|
| 15 октября 2022 года | 7 ч 30 мин | 3°,6 | Убывающая | Ночь, утро | |
| 11 ноября 2022 года | 16 ч 45 мин | 2°,5 | Убывающая | Ночь, утро | |
| 8 декабря 2022 года | 7 ч 24 мин | 0°,5 | Полнолуние | Всю ночь | Покрытие Марса |
| 3 января 2023 года | 22 ч 36 мин | 0°,5 | Нарастающая | Вечер, ночь | Покрытие Марса |
| 31 января 2023 года | 7 ч 24 мин | 0°,1 | Нарастающая | Вечер, ночь | Покрытие Марса |
| 28 февраля 2023 года | 7 ч 31 мин | 1°,0 | Нарастающая | Вечер, ночь | Покрытие Марса |
| 28 марта 2023 года | 16 ч 15 мин | 2°,3 | Первая четверть | Вечер, ночь | |
| 26 апреля 2023 года | 5 ч 18 мин | 3°,2 | Растущий месяц | Вечер | |
| 24 мая 2023 года | 20 ч 31 мин | 3°,7 | Растущий месяц | Вечер | |
| 22 июня 2023 года | 13 ч 8 мин | 3°,8 | Растущий месяц | Вечер | |
| 21 июля 2023 года | 6 ч 59 мин | 3°,2 | Растущий месяц | Вечер | |
| 19 августа 2023 года | 2 ч 6 мин | 2°,2 | Растущий месяц | Вечер | Теряются в лучах зари |
| 16 сентября 2023 года | 22 ч 19 мин | 0°,6 | Растущий месяц | Вечер | Теряются в лучах зари |
На этом сайте вы также можете найти соответствующую информацию.


















