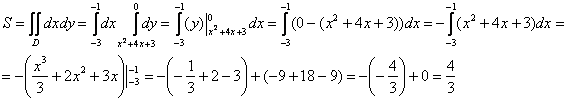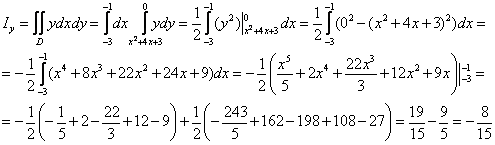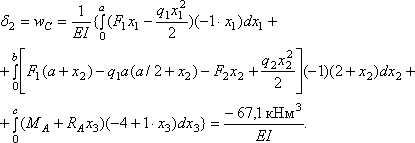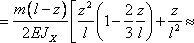Центр тяжести тела, теория и онлайн калькуляторы
Центр тяжести тела
Как известно, сила тяжести тела равна векторной сумме сил тяжести, которые действуют на все материальные точки, на которые можно разбить рассматриваемое тело. Точку, к которой приложена результирующая сила тяжести, называют центром тяжести. Если известно положение центра тяжести, то можно считать, что на тело действует только одна сила тяжести, приложенная к центру тяжести.
Следует учитывать, что силы тяжести, действующие на отдельные элементы тела, направлены к центру Земли и не являются строго параллельными. Но так как размеры большинства тел на Земле много меньше ее радиуса, поэтому эти силы считают параллельными.
Определение центра тяжести тела
Определение
Центром тяжести называют точку, через которую проходит равнодействующая всех сил тяжести, действующих на материальные точки, на которые разбито рассматриваемое тело, при любом положении тела в пространстве.
Центр тяжести — это точка, относительно которой суммарный момент сил тяжести равен нулю при любом положении тела.
От положения центра тяжести зависит устойчивость всех конструкций.
Как найти центр тяжести?
Для нахождения центра тяжести тела сложной формы необходимо мысленно разбить тело на части простой формы и определить место нахождения центров тяжести для них. У тел простой формы центр тяжести определяют, используя их симметрию. Так, центр тяжести однородных диска и шара расположен в их центре, однородного цилиндра в точке на середине его оси; однородного параллелепипеда на пересечении его диагоналей и т, д. У всех однородных тел центр тяжести совпадает с центром симметрии. Центр тяжести может находиться вне тела, например, у кольца.
Определив, где расположены центры тяжести отдельных частей тела, переходят к поиску места расположения центра тяжести тела в целом. Тело представляют в виде системы материальных точек. При этом каждая точка имеет массу своей части тела и располагается в ее центре тяжести.
Координаты центра тяжести тела
В трехмерном пространстве координаты центра тяжести для твердого тела нахояд как:
[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_c=frac{sumlimits_i{Delta m_iy_i}}{m};; \
z_c=frac{sumlimits_i{Delta m_iz_i}}{m} end{array}
right.left(1right),]
где $m$ — масса тела.$;;x_i$ — координата на оси X элементарной массы $Delta m_i$; $y_i$ — координата на оси Y элементарной массы $Delta m_i$; ; $z_i$ — координата на оси Z элементарной массы $Delta m_i$.
В векторной форме записи система уравнений (1) представляется как:
[{overline{r}}_c=frac{1}{m}sumlimits_i{m_i{overline{r}}_ileft(2right),}]
${overline{r}}_c$ — радиус — вектор, определяющий положение центра тяжести; ${overline{r}}_i$ — радиус-векторы, которые определяют положения элементарных масс.
Центр тяжести, центр масс и центр инерции тела
Считают, что центр тяжести тела совпадают с центром масс тела, если его размеры малы в сравнении с расстоянием до центра Земли. При этом формулы, которые определяют положение цента тяжести и центра масс тела совпадают с выражениями (1) и (2). В основной массе задач центр тяжести принимают совпадающим с центром масс тела.
Сила инерции в неинерциальных системах отсчета, движущихся поступательно, приложена к центру тяжести тела.
Но центробежная сила инерции (в общем случае) не приложена к центру тяжести, поскольку в неинерциальной системе отсчета на элементы тела действуют разные центробежные силы инерции (даже если массы элементов равны), так как расстояния до оси вращения разные.
Примеры задач с решением
Пример 1
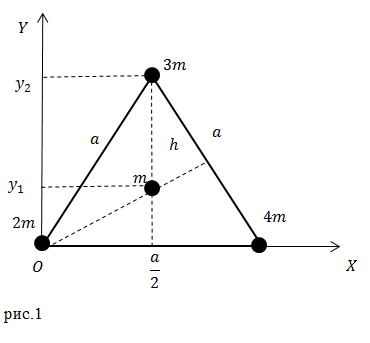
Задание: Каковы координаты центра тяжести системы из трех точечных масс, расположенных в вершинах и одной в центре равностороннего треугольника, со стороной равной $a (м)$ (рис.1)?
Решение: Определение для координат $x_c и y_c$ центра тяжести в нашем случае запишем в виде:
[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}(1.1);;]
[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}(1.2).]
Из рис.1 мы видим, что соответствующие абсциссы точек равны:
[left{ begin{array}{c}
m_1=2m, x_1=0;; \
{rm }m_2=3m, x_2=frac{a}{2};; \
m_3=m, x_3=frac{a}{2};; \
m_4=4m, x_4=a. end{array}
right.left(1.3right).]
Тогда абсцисса центра тяжести получается равной:
[x_c=frac{2mcdot 0+3mcdot frac{a}{2}+mcdot frac{a}{2}+4mcdot a}{2m+3m+m+4m}=frac{6ma}{10m}=0,6a (м);]
Найдем ординаты точек.
[ begin{array}{c}
m_1=2m, y_1=0;; \
{rm }m_2=3m, y_2=frac{asqrt{3}}{2};; \
m_3=m, y_3=frac{asqrt{3}}{6};; \
m_4=4m, y_4=0. end{array}
left(1.4right).]
Для того чтобы найти ординату $y_2$ найдем, высоту в равностороннем треугольнике:
[h=sqrt{a^2-frac{a^2}{4}}=frac{asqrt{3}}{2}=y_2left(1.5right).]
Ординату $y_3$ найдем, учитывая, что медианы в равностороннем треугольнике точкой пересечения делятся в отношении 2:1 от вершины, имеем:
[y_3=hcdot frac{1}{3}=frac{asqrt{3}}{6} left(1.6right).]
Вычислим ординату центра тяжести:
[y_c=frac{2mcdot 0+3mcdot frac{asqrt{3}}{2}+mcdot frac{asqrt{3}}{6}+4mcdot 0}{2m+3m+m+4m}=frac{10mfrac{asqrt{3}}{6}}{10m}=frac{asqrt{3} }{6}(м).]
Ответ: $x_c=0,6a {rm }{rm м}$; $y_c=frac{asqrt{3} }{6}$ м
Пример 2
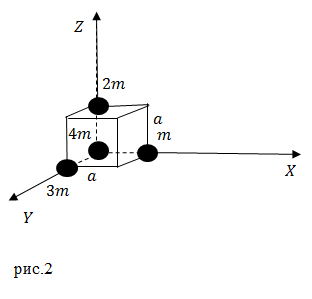
Задание: Каковы координаты центра тяжести системы из четырех элементарных масс, расположенных в вершинах куба со стороной равной $a$ (рис.2)?
Решение: Координату $x_c$ центра тяжести найдем как:
[x_c=frac{m_1x_1+m_2x_2+m_3x_3+m_4x_4}{m_1+m_2+m_3+m_4}=frac{mcdot a+2mcdot 0+3mcdot 0+4mcdot 0}{m+2m+3m+4m}=frac{am}{10m}=0,1 aleft(мright).]
Ординату центра тяжести вычислим как:
[y_c=frac{m_1y_1+m_2y_2+m_3y_3+m_4y_4}{m_1+m_2+m_3+m_4}=frac{mcdot 0+2mcdot 0+3mcdot a+4mcdot 0}{m+2m+3m+4m}=frac{acdot 3m}{10m}=0,3a left(мright).]
Для координаты $z_c$ получаем:
[z_c=frac{m_1z_1+m_2z_2+m_3z_3+m_4z_4}{m_1+m_2+m_3+m_4}=frac{mcdot 0+2mcdot a+3mcdot 0+4mcdot 0}{m+2m+3m+4m}=frac{acdot 2m}{10m}=0,2a left(мright).]
Ответ: ($x_{c, }y_c, z_c$)=($ 0,1 a$, $0,3a$, $0,2a$)(м)
Читать дальше: циклическая частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Содержание:
- Центр масс
- Центр параллельных сил
- Центр тяжести
- Центры тяжести некоторых плоских однородных фигур
- Центр тяжести дуги окружности
- Центр тяжести кругового сектора
- Центр тяжести кругового сегмента
- Центр тяжести треугольника
- Центр тяжести трапеции
- Примеры решения задач на тему: Центр масс
- Способы определения координат центра тяжести тела
- Метод симметрии
- Метод разбиения
- Метод дополнения
- Экспериментальные способы
- Центры тяжести некоторых однородных тел
- Центр тяжести дуги окружности
- Центр тяжести треугольника
- Центр тяжести сектора
Центр масс — это геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Центр масс
Центр масс — это некоторое положение, определяемое относительно объекта или системы объектов и это среднее положение всех частей системы, взвешенное в соответствии с их массами.
Центр параллельных сил
Если на тело действует система параллельных сил 




Координаты центра параллельных сил определяются по зависимостям:
где 

Центр параллельных сил имеет ту особенность, что через него обязательно будет проходить линия действия равнодействующей при вращении линий действия всех сил системы вокруг точек их приложения на один и тот же угол в одну и ту же сторону. Модули сил при вращении не должны меняться.
Центр тяжести
Если твердое тело находится возле поверхности Земли, то на каждую материальную часть этого тела действует сила тяжести 


Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил:
где 



Если тело однородное, то есть удельный вес не меняется по объему 
где 

Тогда формулы для определения координат центра тяжести твердого тела приобретут вид:
Положение центра тяжести однородного тела зависит только от формы объема, что занимает тело, и называется центром тяжести этого объема.
Если однородное тело имеет форму тонкой пластины, то его можно рассматривать как материальную плоскую фигуру. В этом случае положение центра тяжести плоской фигуры определяется двумя координатами 

где 

Центр тяжести однородной пластины называется центром тяжести плоской фигуры.
Если выбранный элементарный объем 
а) для однородного твердого тела:
где 
б) для однородной поверхности:
где 
в) для однородной плоской фигуры, лежащей в плоскости xy:
г) для однородной линии:
где 
Центры тяжести некоторых плоских однородных фигур
Для упрощения определения центра тяжести используются следующие вспомогательные правилами:
1. Если тело имеет плоскость симметрии, то центр тяжести лежит на этой плоскости.
2. Если тело симметрично относительно оси, то центр тяжести лежит на этой оси.
3. Если тело симметрично относительно точки, то центр тяжести лежит в центре симметрии.
4. Если тело состоит из нескольких частей, центры тяжести которых можно определить, то центр тяжести такого тела находят как центр тяжести нескольких материальных точек, а именно тех, в которых расположены весы каждой отдельной части тела.
Центр тяжести дуги окружности
Центр тяжести дуги окружности 

где 


Центр тяжести кругового сектора
Центр тяжести кругового сектора лежит на оси симметрии и имеет координаты:
где 

Центр тяжести кругового сегмента
Центр тяжести кругового сегмента лежит на оси симметрии сегмента и имеет координаты:
где 

Центр тяжести треугольника
Центр тяжести треугольника (рис. 9.6) лежит в точке пересечения его медиан — на расстоянии 1/3 каждой медианы от соответствующего основания треугольника.
Центр тяжести трапеции
Центр тяжести трапеции (рис.9.7) с основаниями 



Расстояния 


Наиболее распространенный способ определения положения центра тяжести однородного тела сложной формы заключается в том, что его разбивают на такие части, положение центров тяжести которых известно, или может быть легко определено.
Например, однородную плоскую фигуру (рис.9.8) разбивают на три части 1,2 и 3, положения центров тяжести которых, 
Координаты центра тяжести фигуры 
где 


Этим способом удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.9.9).
В этом случае площадь плоской фигуры можно записать в виде разницы площадей сплошной фигуры 1 (площадь положительная) и вырезанной части 2 (площадь отрицательная), то есть 
Координаты центра тяжести фигуры равны:
где 



Первый из этих методов имеет название «метод разбиения», второй — «метод дополнения», или «метод отрицательных масс». В общем случае формулы для определения центра тяжести плоской фигуры имеют вид:
где 
Примеры решения задач на тему: Центр масс
Задача № 1
Найти центр тяжести двутаврового профиля, размеры которого в сантиметрах указаны на рис.9.10.
Решение. Поскольку форма сечения имеет ось симметрии, ось 

В силу симметричности профиля относительно оси 
Линиями 

Запишем уравнение для определения абсциссы центра тяжести площади:
где 

Поскольку центры тяжести прямоугольников 

Площади этих прямоугольников соответственно равны:
Тогда:
Таким образом, центр тяжести фигуры лежит в точке 
Ответ:
Задача № 2
Найти координаты центра тяжести поперечного пересечения разностороннего угольника (рис.9.11), полки которого имеют ширину 
Решение. Разделим пересечение линией 


Запишем формулы для координат 

где 



С рис.9.11 видим, что
Тогда:
Ответ:
Задача № 3
Определить положение центра тяжести плоской фигуры (рис.9.12), ограниченной полуокружностью 



Решение. Данная площадь имеет ось симметрии, вдоль которой направим ось 

Разделим площадь 



Абсцисса центра тяжести площади 
где 





Для определения 
В случае половины круга
Площадь половины круга равна:
Центр тяжести треугольника лежит на пересечении его медиан (раздел 9.3.4). Поскольку треугольник 



Площадь треугольника 
Подставив найденные значения 




Ответ:
Задача № 4
Найти координаты центра тяжести квадратной пластины с вырезом в виде сегмента радиуса 
Решение. Осью симметрии рассматриваемой фигуры будет диагональ 
Поэтому направим ось 

Центр тяжести пластины будет лежать на оси 
Площадь фигуры 


Абсцисса центра тяжести фигуры будет равняться:
где 





Для квадрата 
Как следует из рис. 9.13, 
где 


Для кругового сектора (раздел 9.3.2) получим:
Поскольку 

Таким образом, абсцисса 
Площадь кругового сектора 
Подставив значение 




Ответ:
Задача № 5
Найти координаты центра тяжести площади, ограниченной (рис.9.14) правой веткой параболы 

Решение. На расстоянии 



Площадь выделенной элементарной площадки будет равняться:
Площадь фигуры, что ограничена заданными линиями:
Поскольку точка 


Отсюда:
Тогда:
Абсцисса центра тяжести
Для определения координаты 




Площадь выделенной площадки:
Ордината центра тяжести:
Тогда:
Ответ:
Способы определения координат центра тяжести тела
Существует несколько способов определения координат центра тяжести тел. среди них различают: метод симметрии, метод разбиения и дополнения, экспериментальные способы.
Рассмотрим последовательно эти способы.
Метод симметрии
Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, или на оси симметрии, или в центре симметрии.
Таким образом, центр тяжести однородных симметричных тел, таких как кольца,
прямоугольные пластины, прямоугольные параллелепипеды, шары и другие тела, которые
имеют центр симметрии, расположенный в геометрических центрах (центры симметрии) этих тел.
Метод разбиения
Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести нетрудно определяется, то координаты центра тяжести всего тела можно определить непосредственно по формулам выше. Причем количество слагаемых в числителе каждого из указанных выражений будет равно количеству частей, на которое разбивается тело.
Приведем пример определения центра тяжести тела методом разбиения его на отдельные тела, центры тяжести которых известны.
Пример:
Определить координаты центра тяжести однородной пластины. Размеры в
мм заданные на рис. 1.64
Решение.
Выберем оси координат x и y. Разбиваем пластину на отдельные прямоугольные части. Для каждого прямоугольника проводим диагонали, точки пересечения которых c1, c2 и c3 соответствуют центрам веса каждого прямоугольника. В принятой системе координат нетрудно получить значение координат этих точек. А именно: c1 (–1,1), c2 (1,5), c3 (5,9). Площади каждого тела соответственно равны: I — s1 = 4 см2; II — s2 = 20 см2; III — s3 = 12 см2. Площадь всей пластины равна: S = s1 + s2 + s3 = 36 см2.
Для определения координат центра тяжести заданной пластины используем выражение выше. Подставив значения всех известных величин в уравнения, получим
По вычисленным значениям координат центра тяжести пластины можно обозначить точку C на рисунке. Как видим, центр тяжести (геометрическая точка) пластины расположен за ее пределами.
Метод дополнения
Способ, о котором говорится далее, является некоторым случаем способа разбиения. Он может применяться к телам, которые имеют вырезы, полости, причем без учета выреза, или вырезанной части тела положение центра тяжести тела известно. Рассмотрим пример применения такого метода.
Пример. Определить положение центра тяжести круглой пластины радиусом R, имеет круговое отверстие радиуса r (рис. 1.65). Расстояние C1C2 = a.
Решение.
Как видно из рисунка, центр тяжести пластины находится на оси симметрии пластины x, то есть на прямой, проходящей через точки C1 и C2. Таким образом, для определения положения центра тяжести этой пластины необходимо вычислить только одну координату xC, поскольку вторая координата yC равна нулю. Покажем оси координат x, y. Примем, что пластина состоит из двух тел — с полного круга (без учета выреза) и тела,
образовано вырезом. В принятой системе координаты x для указанных тел будут равны: x1 = 0; x2 = C1C2 = a. Площади тел равны: 

заданной пластины используем первое уравнение выражения.
Подставив значения всех известных величин в это уравнение, получим
Таким образом, значение координаты xC отрицательное, а потому, поскольку вторая координата 0 yC = 0, то центр тяжести пластины C размещен на оси x слева от точки C1.
Экспериментальные способы
Эти способы нашли широкое применение при отыскании положения центра тяжести тел сложных форм и конфигураций, для которых другие способы почти непригодны вследствие громоздкости и сложности. К таким телам, в первую очередь, следует отнести комбайны, тракторы, сложные сельскохозяйственные машины и орудия. При применении экспериментальных способов отыскания положения
центра тяжести наиболее широко используют метод подвешивания и метод взвешивания тел.
При применении метода подвешивания тело на тросе подвешивают за различные его точки. Направление троса, будет давать каждый раз направление силы веса тела. Тогда точка пересечения этих направлений и дает положение центра тяжести тела.
Использование второго метода — взвешивание требует измерения веса всего тела, а также отдельных его частей. Рассмотрим пример применения этого метода.
Пример.
Определим продольную координату центра тяжести трактора, у которого продольная база составляет l (рис. 1.66).
Решение.
Сначала поставим на платформу весов задние колеса трактора, как это показано на рисунке. Итак, определяем силу давления задних колес на платформу, или реакцию 

Q = RA + RB.
Теперь составим алгебраическую сумму моментов всех сил относительно точки A. Она равна
Откуда определяем продольную координату центра тяжести:
xC = 
Для определения поперечной координаты центра тяжести трактора необходимо знать реакции левых колес (переднего и заднего) и правых, а также поперечную базу трактора. Дальше аналогичным выражением определяется эти координаты центра тяжести.
Центры тяжести некоторых однородных тел
Определим далее координаты центров тяжести некоторых простых однородных тел.
Центр тяжести дуги окружности
Рассмотрим дугу AB окружности радиусом R, в которой центральный угол OAB равен 2α (радиан) (рис. 1.67). Покажем оси координат x, y начало которых разместим в точке O. Вследствие того, что дуга имеет ось симметрии Ox, то центр ее тяжести будет расположен именно на этой оси (yC = 0). Остается только вычислить координату xC.
Используем для вычисления этой координаты первое уравнение выражения, а именно
Определим составляющие, которые необходимо подставить в это уравнение. Для этого выделим на дуге AB элемент M M1 длиной dl, равной:
dl = R · dφ.
Если φ — угол, определяющий положение элемента M M1 на дуге AB, то координата x элемента M M1 будет равна:
x = Rcosφ.
Общая длина дуги AB равна:
L = 2α · R.
Подставим эти значения в первое уравнение выражения. При этом считается, что интеграл в числителе данного выражения должен быть определенным по всей длине дуги. Будем иметь:
Таким образом, координата xC будет равняться
xC = 
Центр тяжести треугольника
Есть произвольный треугольник, вершины которого в принятой системе координат Oxy соответствуют точкам с координатами A1 (x1, y1), A2 (x2, y2), A3 (x3, y3) (рис. 1.68). Если провести прямые, которые будут параллельны основе A1A3 и провести их достаточное количество, то вся площадь треугольника будет состоять из полос бесконечно малой ширины, центры тяжести которых будут размещены посередине каждой полосы, а потому и центр тяжести треугольника будет расположенный на его медиане. А если провести линии, параллельные другой стороне треугольника, то и в этом случае центр тяжести будет размещен на соответствующей медиане. Таким образом, совершенно очевидно, что центр тяжести треугольника C будет расположен в точке пересечения его медиан.
Определим координаты этой точки. По курсу аналитической геометрии известно, что точка пересечения медиан треугольника в принятой системе координат определяется такими зависимостями
где x1, x2, …, y3 — координаты вершин треугольника.
Полезно также знать, что
Центр тяжести сектора
Рассмотрим круговой сектор OAB радиуса R, центральный угол которого равен 2α (радиан) (рис. 1.69). Центр тяжести сектора, вполне очевидно, лежит на оси его симметрии, то есть на биссектрисе угла AOB. Эту биссектрису примем за ось x и найдем на этой оси положение центра C. Разобьем площадь сектора на бесконечно большое число элементарных секторов с центральными углами ∆φ.
Будем рассматривать каждый сектор как треугольник с основанием R · ∆φ и высотой R. Центр тяжести каждого треугольника расположен на расстоянии 
Тогда учитывая, что
Будем иметь
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Предварительно изучите по учебнику Г. М. Фихтен-гольца главу XII, п° 206, 207. При решении задач рекомендуется помнить, что если кривая расположена симметрично относительно некоторой прямой, то центр тяжести кривой лежит на этой прямой.
592. Найти центр тяжести дуги цепной линии:
содержащейся между точками, для которых х = — а х = а.
Решение. Так как рассматриваемая дуга расположена симметрично относительно оси Oyt то центр тяжести дуги лежит на оси Oy и, следовательно,

Так как
и, следовательно,
593. Найти центр тяжести одной арки циклоиды:
Решение. Так как арка циклоиды расположена симметрично относительно прямой х = па, то центр тяжести дуги циклоиды лежит на этой прямой и, следовательно,
Ордината центра тяжести будет: ? ( ~ е [а I а
Ц — — Ie _L_£
1 a(e*~-)Ja 2 f
I = Jt а.
Найдем ординату центра тяжести по формуле:
Длина дуги одной арки циклоиды равна 8а (см. задачу
Найдем ординату центра тяжести:
594. Найти центр тяжести дуги кривой»
содержащейся между точками, для которых
(см. задачу 491).
Найдем абсциссу центра тяжести:
3 + 2 In 2
4
Найдем ординату центра тяжести:
2
595. Найти центр тяжести однородной треугольной пластинки.
ч
3 (3 + 2 In 2)
Решение. Разбиваем данную пластинку прямыми, параллельными одной из сторон, на бесконечно тонкие полоски. Центр тяжести каждой полоски находится в ее середине и лежит, таким образом, на медиане, а следовательно, и центр тяжести всей треугольной пластинки лежит на этой медиане. Так как это рассуждение применимо к любой стороне, то центр тяжести треугольника находится в точке пересечения его медиан.
Тот же результат получаем вычислением. Площадь полоски, отстоящей на расстояние х от данной стороны
Ь, равна dS = —(h—х) А я, где А —высота, опущенная h
на эту сторону, а Дл; — ширина полоски, следовательно, расстояние центра тяжести от этой стороны равно: н н
I*= — [ xdS — Г— (h—х) xdx =
SJ bh J h 9
A1 2 3 J I о 3 Таким образом, центр тяжести треугольника находится на расстоянии, равном — высоты от соответствующей
З
стороны, т. е. в точке пересечения его медиан, ибо это— е&инственная точка, обладающая таким свойством.
596. Найти центр тяжести площади, ограниченной осью Ox и одной полуволной синусоиды
Решение. Так как площадь одной полуволны синусоиды расположена симметрично относительно прямой
, то центр тяжести лежит на этой прямой и, сле
довательно, . Ордината центра тяжести находится
по формуле
Так как
то
Итак, центр тяжести данной площади находится в точке
597. Найти координаты центра тяжести площади, ограниченной параболами
Решение. Данные параболы, пересекающиеся в точках О (0, 0) и А (а; а), ограничивают площадь, расположенную симметрично относительно биссектрисы
Так как площадь ограничена двумя кривыми
и, то абсцисса центра тяжести площади на-
ходится по формуле:
найдем:
точке
598. Найти центр тяжести площади, ограниченной осью абсцисс и одной аркой циклоиды:
Таким образом, центр тяжести площади находится в
Решение. Данная площадь расположена симметрично относительно прямой
Найдем ц по формуле. Площадь S данной
фигуры была вычислена (см.
довательно,
Центр тяжести данной площади находится в точке
599. Пользуясь теоремой Гюльдена, вычислить поверхность тора, образованного вращением круга радиуса а вокруг оси, расположенной в его плоскости и отстоящей от центра его на расстояние
Решение. Так как длина данной окружности равна 

600. Пользуясь теоремой Гюльдена, вычислить объем и боковую поверхность прямого кругового конуса.
Решение. Боковая поверхность конуса с высотой




удален от оси вращения на
Площадь треугольника равна


601. На цилиндре, имеющем 6 см в диаметре, кругом вдоль поверхности вырезан канал, имеющий поперечным сечением равносторонний треугольник со стороной в 0,5 сж. Вычислить объем срезанного материала.
Решение. Искомый объем есть объем тела, получаемого при вращении равностороннего треугольника со стороной в 0,5 см вокруг оси, параллельной основанию и удаленной от него на 3 ел, причем вершина лежит между основанием и осью (рис. 26).
Высота треугольника равна
площадь его равна
Расстояние центра тяжести от оси ОС = OA — AC =

высоты). По второй теореме Гюльдена имеем:
602. Длина одной арки циклоиды



Решение. Пусть

Наибольшая ордината кривой соответствует
на 2а, причем касательная в этой точке параллельна оси Ох следовательно, расстояние центра тяжести от этой
касательной равно
Таким образом, искомая поверхность, образуемая’ вращением той же арки циклоиды вокруг касательной в верхней ее точке равна:
603. Найти центр тяжести дуги, составляющей четверть окружности радиуса
604. Найти центр тяжести расположенной в первом квандранте дуги гипоциклоиды x = acosst, у = a sin31.
605. Найти центр тяжести половины площади эллипса, опирающейся на большую ось.
606. Найти центр тяжести площади, заключенной
— L — L. L между параболой х2 — J — у2 = а 2 и осями координат.
607. Найти центр тяжести плоской фигуры, ограниченной кривой at/2 = Jc3 и прямой х = а {а > 0).
608. Найти центр тяжести площади, ограниченной кривыми
у = ах3, х = а, у = 0.
609. Найти центр тяжести площади, ограниченной эллипсом jc2 -)- 4у2 = 4 и окружностью х2— у2 = 4 и расположенной в первом квадранте.
610. Найти центр тяжести фигуры, ограниченной замкнутой кривой у2 = ах3 — х*.
| < Предыдущая | Следующая > |
|---|
1.6. Центр тяжести плоской фигуры
Это популярное физическое приложение двойного интеграла.
О центре тяжести плоской фигуры я рассказывал ещё в курсе аналитической геометрии, и сейчас мы на пальцах
повторим, что это такое. Вырежьте из тонкого куска картона произвольную фигуру, какую захотИте. …Есть? Поднимите указательный
палец строго вверх J. Теперь положите картонку на палец и добейтесь того, чтобы она не сваливалась. Эта точка картонной
фигуры – и есть её центр тяжести.
В студенческой практике для решения, как правило, предлагается простейший случай – плоская ограниченная однородная фигура,
то есть фигура постоянной физической плотности – стеклянная, деревянная, оловянная чугунные игрушки, тяжёлое детство и т.д.
Далее по умолчанию речь пойдёт только о таких фигурах.
Первое правило и простейший пример: если у плоской фигуры есть центр симметрии, то он является
центром тяжести данной фигуры. Например, центр круглой или квадратной однородной пластины. Логично и по-житейски
понятно – масса такой фигуры «справедливо распределена во все стороны» относительно центра.
Однако в суровых реалиях вам вряд ли подкинут такую халяву, и поэтому на помощь придётся привлечь серьёзный математический
аппарат:
Координаты центра тяжести
плоской однородной ограниченной фигуры
рассчитываются по
следующим формулам:
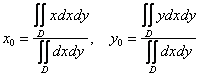
записать так:
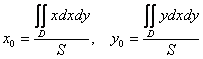
– площадь фигуры (области
).
И наиболее компактная запись:
, где
Интеграл будем
условно называть «иксовым» интегралом, а интеграл – «игрековым» интегралом.
Примечание-справка: для плоской ограниченной неоднородной фигуры, плотность которой задана функцией , формулы более
сложные:
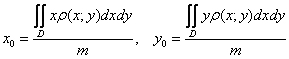
– масса фигуры;
в случае однородной плотности фигуры эти формулы упрощаются до вышеприведённых формул.
На формулах, собственно, вся новизна и заканчивается, остальное – это ваше умение решать двойные интегралы, кстати, сейчас предоставляется прекрасная возможность
потренироваться и усовершенствовать свою технику. А совершенству, как известно, нет предела: …или есть? 
Пример 29
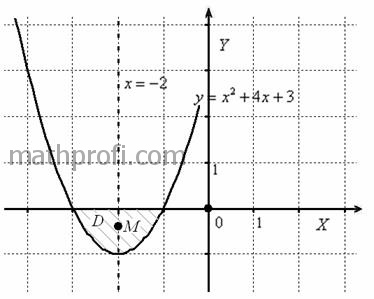
Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями .
Решение: линии здесь элементарны: задаёт ось абсцисс, а уравнение
– банальную параболу. Я выполню сразу весь чертёж с
готовой точкой центра тяжести фигуры:
Правило второе: если у фигуры существует ось симметрии, то центр тяжести данной фигуры
обязательно лежит на этой оси.
В нашем случае фигура симметрична относительно прямой (проведена пунктиром), то есть фактически мы уже знаем
«иксовую» координату точки «эм».
Также обратите внимание, что по вертикали центр тяжести смещён ближе к оси абсцисс, поскольку там фигура более массивна.
Полезная рекомендация: ещё до вычислений постарайтесь определить примерное расположение центра тяжести «на глазок» – это
поможет проверить полученные значения на предмет явных ошибок.
…Да, возможно, ещё не все до конца поняли, что такое центр тяжести: пожалуйста, поднимите вверх указательный палец и
мысленно поставьте на него заштрихованную «подошву» точкой . Теоретически фигура не должна упасть.
Координаты центра тяжести фигуры найдём по формулам , где
.
Порядок обхода области (фигуры) здесь очевиден:
Внимание! Определяемся с наиболее выгодным порядком обхода один раз – и используем его для всех двойных интегралов! А их тут будет три штуки:
1) Сначала вычислим площадь фигуры. Ввиду относительной простоты интеграла решение можно оформить «одной строкой», главное,
не запутаться в вычислениях:
Смотрим на чертёж и прикидываем по клеточкам площадь. Получилось около дела.
2) Иксовая координата центра тяжести уже найдена «графическим методом», поэтому можно
сослаться на симметрию и перейти к следующему пункту. Но делать так-таки не советую – велика вероятность, что вас заставят
решать по формуле.
В этой связи координату лучше рассчитать формально. Вычислим «иксовый» интеграл:
Таким образом: 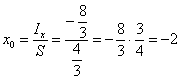
3) Найдём ординату центра тяжести. Вычислим «игрековый» интеграл, внутри
используем правило умножения
многочленов:
В результате: 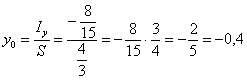
очень и очень похоже на правду. На заключительном этапе отмечаем на чертеже точку и записываем
Ответ:
Заметьте, что по условию не требовалось ничего чертить, но в большинстве задач мы волей-неволей вынуждены изобразить фигуру.
Зато есть безусловный плюс – визуальная и довольно эффективная проверка результата.
Следующие два примера для самостоятельного решения.
Попроще:
Пример 30
Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями
И посложнее:
Пример 31
Найти центр тяжести однородной плоской фигуры, ограниченной линиями . Фигуру и её центр тяжести изобразить на чертеже.
И это как раз тот случай, когда вроде бы выполнены предпосылки для перехода к полярной
системе координат, но в результате получаются настолько харкордные интегралы, что уж лучше решать в декартовых
координатах.
Примерные образцы решений в конце книги.
Но, разумеется, есть задачи, где решение в полярных координатах оправдано. Желающие могут в качестве тренировки найти
центр тяжести фигуры из Примера 23, тем более, там уже найдена площадь. Верный ответ . С подробным решением этого, а также более сложных
примеров можно ознакомиться в соответствующей статье
сайта.
Ну а сейчас пришло время немного отдохнуть и повысить ставки:


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Для
этого рассмотрим балку в состоянии под
действием только сосредоточенного
момента ,
приложенного в сечении 1 против часовой
стрелки (рис. ж).
Вычислим
опорные реакции, составив три уравнения
равновесия.
Проверка Реакции найдены верно
Эпюра показана на рис.
ж.
Далее
по формуле Мора
Сечение
1 поворачивается по часовой стрелке.
Пример
15.
Найдем
перемещения – прогиб сечения С и
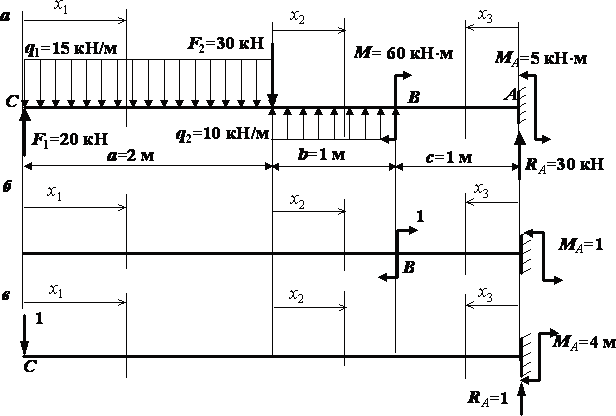
угол поворота сечения В в
балке, показанной на рис. 1, а,
методом Максвелла – Мора и сравним их
с теми же перемещениями, найденными
ранее аналитическим способом.
Решение.
В
соответствии с методом Максвелла –
Мора перемещения находим по формуле .
Рассмотрим два варианта использования
этой формулы:
—
аналитическое интегрирование формулы;
—
интегрирование с помощью правила
Верещагина.
Вариант
1. Аналитическое интегрирование формулы
Максвелла – Мора
Для
определения перемещений по формуле выпишем
выражения для изгибающих моментов в
балке от заданной нагрузки на каждом
участке балки. Начало координат х можно
выбирать произвольным образом, например,
так, как показано на рис. 1, а.
Рис.1
Тогда
выражения для изгибающих моментов на
трех участках будут такими:
участок
1: ;
;
участок
2: ;
;
участок
3: ;
.
Найдем
сначала угол
поворота сечения В балки.
Загрузим балку в сечении В единичной
обобщенной силой, соответствующей
искомому перемещению, то есть парой
сил, равной единице (рис. 1, б).
Запишем выражения для изгибающих
моментов на
каждом участке от единичной пары сил.
Начало отсчета координаты х должно
быть таким же, как при записи выражений
для изгибающих моментов от заданной
нагрузки (см. рис. 1, б).
Тогда:
участок
1: ;
;
участок
2: ;
;
участок
3: ;
.
Подставим
записанные выражения в интеграл Максвелла
– Мора и
проинтегрируем (на первых двух участках
интегралы в рассматриваемом примере
равны нулю):
.
Чтобы
найти прогиб сечения С ,
приложим в точке С новую
единичную обобщенную силу – сосредоточенную
силу, положив ее равной единице
(рис. 1, в).
Выражения для изгибающих моментов на
каждом участке от единичной сосредоточенной
силы будут такими:
участок
1: ;
;
участок
2: ;
;
участок
3: ;
.
После
подстановки функций и
в
интеграл и
интегрирования на каждом участке получим
Величины
найденных перемещений совпадают с
результатами, полученными ранее
аналитическим способом, а знак у угла
поворота другой. Это следствие разных
правил знаков в аналитическом методе
и методе Максвелла – Мора. Обсудим
полученные знаки перемещений. Положительный
знак угла поворота показывает, что
поворот происходит по направлению
обобщенной силы. Поскольку единичная
пара принята направленной по часовой
стрелке, то и сечение В поворачивается
по часовой стрелке. Отрицательный знак
прогиба означает, что сечение С перемещается
в сторону, противоположную принятому
направлению единичной силы, то есть
вверх. Таким образом, результаты решения
полностью совпадают с полученными ранее
аналитическим методом.
Вариант
2. Интегрирование формулы Максвелла –
Мора с помощью правила Верещагина
Как
отмечалось раньше, процесс интегрирования
формулы Максвелла – Мора с помощью
правила Верещагина (или Симпсона)
называется «перемножением эпюр».
Чтобы «перемножить эпюры», построим
их. Сначала построим эпюру изгибающих
моментов от заданной нагрузки (рис. 2, а).
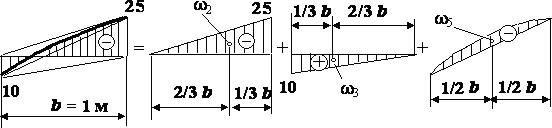
Разобьем эпюру М на 6 простых фигур: три
треугольника ,
и
,
два сегмента, ограниченных квадратной
параболой, и
и трапецию
.
Порядок разбивки эпюры моментов на
составляющие фигуры на втором участке
поясняет рис. 3 (эпюру М на втором
участке можно разбить и на две фигуры:
трапецию, у которой основания имеют
разные знаки (10 и –25) и сегмент .
В этом случае удобно воспользоваться
правилом перемножения трапеций ).
Найдем
площади этих фигур:
кНм2,
кНм2,
кНм2,
кНм2,
кНм2,
кНм2.
Рис.2
Рис.3
Для
определения площадей и
использована
формула .
Затем строим эпюры моментов от единичных
обобщенных сил, соответствующих искомым
перемещениям. Чтобы определить угол
поворота сечения В,
приложим в точке В балки
пару сил, равную единице, и построим
эпюру изгибающих моментов М1 от
этой пары сил (рис. 2, б).
Найдем ординату под центром тяжести
площади .
Независимо от положения центра тяжести
трапеции (а оно не определено) ордината
под центром тяжести равна единице, так
как изгибающий момент М1 на
участке перемножения является постоянной
величиной, всюду равной единице. То
есть .
Поскольку на всех остальных участках
изгибающий момент М1 =
0 и ,
то по формуле искомое
перемещение
.
Полученная
величина угла поворота совпадает с
найденной ранее аналитическим методом.
Положительный знак говорит о том, что
поворот сечения В происходит
по направлению обобщенной силы, то есть
в соответствии с принятым на
рис. 3, б направлением
единичной пары по часовой стрелке.
Теперь будем искать прогиб сечения С.
Загрузим балку новой обобщенной силой,
соответствующей прогибу в точке С.
Такой обобщенной силой будет сосредоточенная
сила, равная единице и приложенная в
точке С. Эпюра изгибающих моментов М2 от
этой единичной силы показана на рис. 3, в.
Согласно формуле искомый
прогиб
.
Найдем
ординаты на эпюре М2,
расположенные под центрами тяжести
шести фигур, на которые разбита эпюра М.
Положение центров тяжестей всех фигур,
кроме ,
показано на рис. 3, а.
Ординату на эпюре М2,
расположенную под центром тяжести
какой-то фигуры, можно найти либо из
подобия треугольников, либо как изгибающий
момент от единичной силы под центром
тяжести рассматриваемой фигуры.
Используем второй вариант вычисления
ординат. Изгибающий момент под центром
тяжести треугольника равен
значению силы (1), расположенной слева
от сечения, умноженной на плечо (4/3 м),
со знаком минус. То есть
м.
Аналогично
ордината под центром тяжести
треугольника равна
силе (1), умноженной на плечо (2 +2/3 = 8/3 м),
со знаком минус. И так же для остальных
фигур, положение центров тяжести которых
известно:
м,
м,
м,
м.
Поскольку
положение центра тяжести трапеции не
определено и невозможно в этом случае
найти ординату под центром тяжести,
воспользуемся на этом участке формулой
перемножения трапеций :
кНм3.
Искомое
перемещение – прогиб в точке С
.
Результат
совпадает с найденным ранее прогибом
в точке С аналитическим
способом. Отрицательный знак перемещения
показывает, что точка С перемещается
в сторону, противоположную выбранному
направлению единичной силы (см. рис. 3, в),
то есть вверх.
Пример
16.
Определим
угол поворота сечения А и
прогиб сечения D в
балке, показанной на рис. 1, а,
методом Максвелла – Мора с использованием
правила Верещагина (перемножением
эпюр). Ранее эти перемещения были найдены
аналитическим методом, сравним результаты,
полученные двумя способами.
Рис.1
Решение.
Построим
эпюры изгибающих моментов от заданной
нагрузки (рис. 2, а)
и от единичных обобщенных сил,
соответствующих искомым перемещениям
(рис. 2, б, в).
Рис.2
Разобьем
эпюру моментов от заданной нагрузки на
три треугольника и найдем их площади:
кНм2;
кНм2;
кНм2.
Для
определения угла
поворота сечения А перемножим
эпюры М и М1.
Для этого найдем
ординаты на эпюре М1,
расположенные под центрами тяжести
треугольников:
;
;
.
Тогда
угол поворота сечения А согласно
формуле
.
Положительный
знак угла поворота показывает, что
поворот сечения А происходит
по направлению обобщенной силы, то есть
в соответствии с показанной на
рис. 2, б единичной
парой сил по ходу часовой стрелки.
Результат совпадает с полученным ранее
аналитическим способом.
Чтобы
найти прогиб сечения D,
используем при перемножении эпюру М2.
Ординаты на эпюре М2 под
центрами тяжести треугольников будут
такими:
м;
м;
м.
Найдем
прогиб сечения D по
формуле :
.
Прогиб
сечения D получился
положительным. Это означает, что
точка D перемещается
по направлению единичной силы. Поскольку
единичная сила показана на
рис. 2, в направленной
вниз, то и перемещение точки D происходит
вниз. Полученный результат совпадает
с тем, который был получен ранее
аналитическим способом.
Пример
17.
Для
двутавровой балки № 12 определить
допускаемое значение момента из
условия жесткости, если мм (рис.1).
Рис.1
Решение.
Строим
эпюру грузовых моментов (рис.2)
и эпюру от
единичной силы, приложенной в произвольном
сечении (рис.3). Тогда прогиб в этом
сечении
Рис.2
Рис.3
где
Проверим
выполнение граничных условий. При и
.
Далее определяем величину максимального
прогиба .
Для этого необходимо решить
задачу определения экстремума
функции .
Вычисляя производную функции и приравнивая ее
нулю, получаем следующее уравнение
,
корни которого
равны .
Первый корень соответствует точке,
лежащей вне балки, а второй
или
.
Условие жесткости балки при этом
запишется:
Решая
это неравенство относительно m,
получаем
Таким
образом, допускаемый момент равен
Пример
18.
Исходные
данные.
,
,
,
,
жесткость балки EIx —
постоянная.
Требуется:
Определить
по правилу Верещагина вертикальное
перемещение точки «В»
Решение.
Определение
вертикального перемещения сечения «В»
выполняется в следующей последовательности:
—
Строим эпюру изгибающих моментов от
заданной нагрузки, то есть грузовую
эпюру (рис.1, б).
—
Рассматриваем единичное состояние системы:
к заданной конструкции в требуемом
направлении прикладываем единичную
безразмерную силу в том сечении, линейное
перемещение которого требуется определить
(рис.1, в).
—
Строим единичную эпюру, то есть эпюру
изгибающих моментов от единичной
нагрузки (рис.1, г).
—
Приводим в соответствие участки грузовой
и единичной эпюр: каждому участку
грузовой эпюры должен соответствовать
участок единичной эпюры, ограниченный
прямой (не ломаной) линией.
В
примере вдоль всей длины балки единичная
эпюра ограничена прямой, однако её
следует разбить на два участка, так как
грузовая эпюра состоит из двух участков,
площади которых и
(см.
рис.1, б).
—
Определяем площади отдельных участков
грузовой эпюры и соответствующие им
абсциссы центров тяжести.
Так
как участки грузовой эпюры представляют
собой фигуры, площади и центры тяжести
которых определить затруднительно,
разобьём их на более простые составляющие
с площадями ,
,
,
.
;
;
;
;
;
;
;
.
—
Определяем ординаты на единичной эпюре
под центрами тяжести простых составляющих
отдельных участков грузовой эпюры. Для
определения ординат используем подобие
треугольников, у которых отношения
катетов равны.
;
.
Аналогично:
,
.
—
Записываем формулу Верещагина для
рассматриваемой задачи. При этом
учитываем: если грузовая и единичная
эпюры на участке имеют одинаковый
знак, то произведение положительно,
если разный знак – отрицательно.
Если
общий вид формулы Верещагина: ,
то для рассматриваемой задачи она
принимает вид:
,
.
Положительное
значение указывает,
что перемещение конца консоли направлено
в сторону действия единичной нагрузки .
—
Можно воспользоваться иным подходом
для решения поставленной задачи. Ввиду
того, что грузовая эпюра изгибающих
моментов имеет сложные очертания, её
можно «расслоить», то есть построить
эпюру моментов от каждой нагрузки в
отдельности (рис.1, д).
Тогда
;
;
;
;
;
;
;
;
;
;
;
.
Полученный
результат отличается от предыдущего
на 0,8%, что лежит в пределах допустимой
погрешности. При решении можно
воспользоваться любым удобным для
студента подходом.
Пример
19.
Для
заданной стальной балки (рис.1)
требуется в сечении К определить прогиб Y и
угол поворота :
а)
методом начальных параметров;
б)
по интегралу Мора;
с)
способом Верещагина.
Исходные данные: q1 = q2 = 2
кН/м; F =
1 кН; М =
4 кНм; a =
4 м; b =
2 м; EJx = const.

Рис.1
Решение.
1.
Для определения перемещений методом
начальных параметров необходимо
знать все силы, приложенные к балке, в
том числе и силы реакции опор.
Определяем
опорные реакции:
;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #