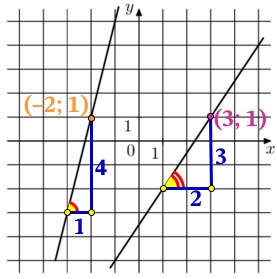
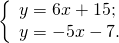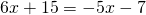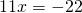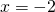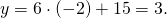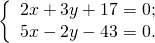Как найти ординату пересечения двух прямых - Исправление недочетов и поиск решений вместе с Examum.ru

Решение:

На рисунке изображены прямые, линейных функции их вид имеет вид:

y = kx + b

Найдём k и b функции справа.
k – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:

k=tg{color{Red}alpha}=frac{color{Blue} 3}{color{Blue} 2}=1,5

Подставим в общий вид функции значение k и координаты точки (3; 1) найдём b:

y = kx + b
1 = 1,5·3 + b
1 = 4,5 + b
1 – 4,5 = b
–3,5 = b

Функции справа имеет вид:

y = 1,5x – 3,5

Найдём k и b функции слева.

k=tg{color{Red}alpha}=frac{color{Blue} 4}{color{Blue} 1}=4

Подставим в общий вид функции значение k и координаты точки (–2; 1) найдём b:

y = kx + b
1 = 4·(–2) + b
1 = –8 + b
1 + 8 = b
9 = b

Функции слева имеет вид:

y = 4x + 9

В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:

1,5x – 3,5 = 4x + 9
1,5x – 4x = 9 + 3,5
–2,5x = 12,5
x=frac{12,5}{–2,5}=-5

Подставим значение х = –5, в любое уравнение и найдём ординату (y) точки пересечения прямых:

y = 4·(–5) + 9 = –20 + 9 = –11

Ответ: –11.

Источник

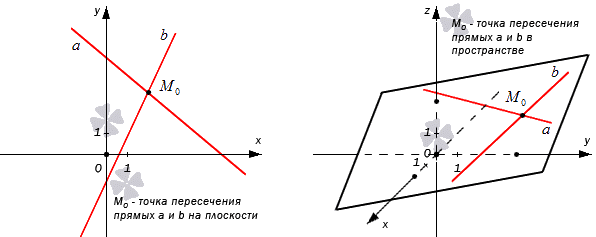
Координаты точки пересечения прямых

Две прямые на плоскости могут быть параллельными, пересекаться либо совпадать.

Чтобы найти координаты точки пересечения прямых, надо составить и решить систему уравнений, составленную из уравнений этих прямых.

Найти точку пересечения прямых заданных уравнениями:

2) 2x+3y+17=0; 5x-2y-43=0.

1) Составляем систему уравнений (здесь даны уравнения прямой с угловым коэффициентом):

Приравняем правые части уравнений:

Подставим x= -2 в уравнение первой прямой:

2) Составляем систему уравнений (здесь задано общее уравнение прямой):

Умножим 1-е уравнение системы на 2, а 2-е — на 3

Координаты точки пересечения двух прямых — примеры нахождения

Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.

Точка пересечения двух прямых – определение

Необходимо дать определение точкам пересечения двух прямых.

Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.

Определение точки пересечения прямых звучит так:

Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.

Рассмотрим на рисунке, приведенном ниже.

Нахождение координат точки пересечения двух прямых на плоскости

Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.

Если на плоскости имеется система координат О х у , то задаются две прямые a и b . Прямой a соответствует общее уравнение вида A 1 x + B 1 y + C 1 = 0 , для прямой b — A 2 x + B 2 y + C 2 = 0 . Тогда M 0 ( x 0 , y 0 ) является некоторой точкой плоскости необходимо выявить , будет ли точка М 0 являться точкой пересечения этих прямых.

Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M 0 ( x 0 , y 0 ) считается их точкой пересечения.

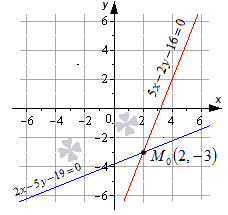
Даны две пересекающиеся прямые 5 x — 2 y — 16 = 0 и 2 x — 5 y — 19 = 0 . Будет ли точка М 0 с координатами ( 2 , — 3 ) являться точкой пересечения.

Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М 0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что

5 · 2 — 2 · ( — 3 ) — 16 = 0 ⇔ 0 = 0 2 · 2 — 5 · ( — 3 ) — 19 = 0 ⇔ 0 = 0

Оба равенства верные, значит М 0 ( 2 , — 3 ) является точкой пересечения заданных прямых.

Изобразим данное решение на координатной прямой рисунка, приведенного ниже.

Ответ: заданная точка с координатами ( 2 , — 3 ) будет являться точкой пересечения заданных прямых.

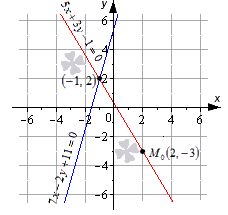
Пересекутся ли прямые 5 x + 3 y — 1 = 0 и 7 x — 2 y + 11 = 0 в точке M 0 ( 2 , — 3 ) ?

Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что

5 · 2 + 3 · ( — 3 ) — 1 = 0 ⇔ 0 = 0 7 · 2 — 2 · ( — 3 ) + 11 = 0 ⇔ 31 = 0

Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7 x — 2 y + 11 = 0 . Отсюда имеем, что точка М 0 не точка пересечения прямых.

Чертеж наглядно показывает, что М 0 — это не точка пересечения прямых. Они имеют общую точку с координатами ( — 1 , 2 ) .

Ответ: точка с координатами ( 2 , — 3 ) не является точкой пересечения заданных прямых.

Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.

Задаются две пересекающиеся прямые a и b уравнениями вида A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 , расположенных в О х у . При обозначении точки пересечения М 0 получим, что следует продолжить поиск координат по уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Из определения очевидно, что М 0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Иными словами это и есть решение полученной системы A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 .

Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.

Заданы две прямые x — 9 y + 14 = 0 и 5 x — 2 y — 16 = 0 на плоскости. необходимо найти их пересечение.

Данные по условию уравнения необходимо собрать в систему, после чего получим x — 9 y + 14 = 0 5 x — 2 y — 16 = 0 . Чтобы решить его, разрешается первое уравнение относительно x , подставляется выражение во второе:

x — 9 y + 14 = 0 5 x — 2 y — 16 = 0 ⇔ x = 9 y — 14 5 x — 2 y — 16 = 0 ⇔ ⇔ x = 9 y — 14 5 · 9 y — 14 — 2 y — 16 = 0 ⇔ x = 9 y — 14 43 y — 86 = 0 ⇔ ⇔ x = 9 y — 14 y = 2 ⇔ x = 9 · 2 — 14 y = 2 ⇔ x = 4 y = 2

Получившиеся числа являются координатами, которые необходимо было найти.

Ответ: M 0 ( 4 , 2 ) является точкой пересечения прямых x — 9 y + 14 = 0 и 5 x — 2 y — 16 = 0 .

Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.

Определить координаты точек пересечения прямых x — 5 = y — 4 — 3 и x = 4 + 9 · λ y = 2 + λ , λ ∈ R .

Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x = 4 + 9 · λ y = 2 + λ , λ ∈ R преобразуется таким образом:

x = 4 + 9 · λ y = 2 + λ ⇔ λ = x — 4 9 λ = y — 2 1 ⇔ x — 4 9 = y — 2 1 ⇔ ⇔ 1 · ( x — 4 ) = 9 · ( y — 2 ) ⇔ x — 9 y + 14 = 0

После чего беремся за уравнение канонического вида x — 5 = y — 4 — 3 и преобразуем. Получаем, что

x — 5 = y — 4 — 3 ⇔ — 3 · x = — 5 · y — 4 ⇔ 3 x — 5 y + 20 = 0

Отсюда имеем, что координаты – это точка пересечения

x — 9 y + 14 = 0 3 x — 5 y + 20 = 0 ⇔ x — 9 y = — 14 3 x — 5 y = — 20

Применим метод Крамера для нахождения координат:

∆ = 1 — 9 3 — 5 = 1 · ( — 5 ) — ( — 9 ) · 3 = 22 ∆ x = — 14 — 9 — 20 — 5 = — 14 · ( — 5 ) — ( — 9 ) · ( — 20 ) = — 110 ⇒ x = ∆ x ∆ = — 110 22 = — 5 ∆ y = 1 — 14 3 — 20 = 1 · ( — 20 ) — ( — 14 ) · 3 = 22 ⇒ y = ∆ y ∆ = 22 22 = 1

Ответ: M 0 ( — 5 , 1 ) .

Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x = x 1 + a x · λ y = y 1 + a y · λ , λ ∈ R . Тогда вместо значения x подставляется x = x 1 + a x · λ и y = y 1 + a y · λ , где получим λ = λ 0 , соответствующее точке пересечения, имеющей координаты x 1 + a x · λ 0 , y 1 + a y · λ 0 .

Определить координаты точки пересечения прямой x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x — 5 = y — 4 — 3 .

Необходимо выполнить подстановку в x — 5 = y — 4 — 3 выражением x = 4 + 9 · λ , y = 2 + λ , тогда получим:

4 + 9 · λ — 5 = 2 + λ — 4 — 3

При решении получаем, что λ = — 1 . Отсюда следует, что имеется точка пересечения между прямыми x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x — 5 = y — 4 — 3 . Для вычисления координат необходимо подставить выражение λ = — 1 в параметрическое уравнение. Тогда получаем, что x = 4 + 9 · ( — 1 ) y = 2 + ( — 1 ) ⇔ x = — 5 y = 1 .

Ответ: M 0 ( — 5 , 1 ) .

Для полного понимания темы, необходимо знать некоторые нюансы.

Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 + C 2 = 0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.

Даны прямые x 3 + y — 4 = 1 и y = 4 3 x — 4 . Определить, имеют ли они общую точку.

Упрощая заданные уравнения, получаем 1 3 x — 1 4 y — 1 = 0 и 4 3 x — y — 4 = 0 .

Следует собрать уравнения в систему для последующего решения:

1 3 x — 1 4 y — 1 = 0 1 3 x — y — 4 = 0 ⇔ 1 3 x — 1 4 y = 1 4 3 x — y = 4

Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x 3 + y — 4 = 1 и y = 4 3 x — 4 определяют одну и ту же прямую. Поэтому нет точек пересечения.

Ответ: заданные уравнения определяют одну и ту же прямую.

Найти координаты точки пересекающихся прямых 2 x + ( 2 — 3 ) y + 7 = 0 и 2 3 + 2 x — 7 y — 1 = 0 .

По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:

2 x + ( 2 — 3 ) y + 7 = 0 2 ( 3 + 2 ) x — 7 y — 1 = 0 ⇔ 2 x + ( 2 — 3 ) y = — 7 2 ( 3 + 2 ) x — 7 y = 1 ⇔ ⇔ 2 x + 2 — 3 y = — 7 2 ( 3 + 2 ) x — 7 y + ( 2 x + ( 2 — 3 ) y ) · ( — ( 3 + 2 ) ) = 1 + — 7 · ( — ( 3 + 2 ) ) ⇔ ⇔ 2 x + ( 2 — 3 ) y = — 7 0 = 22 — 7 2

Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.

Второй способ решения.

Для начала нужно определить наличие пересечения прямых.

n 1 → = ( 2 , 2 — 3 ) является нормальным вектором прямой 2 x + ( 2 — 3 ) y + 7 = 0 , тогда вектор n 2 → = ( 2 ( 3 + 2 ) , — 7 — нормальный вектор для прямой 2 3 + 2 x — 7 y — 1 = 0 .

Необходимо выполнить проверку коллинеарности векторов n 1 → = ( 2 , 2 — 3 ) и n 2 → = ( 2 ( 3 + 2 ) , — 7 ) . Получим равенство вида 2 2 ( 3 + 2 ) = 2 — 3 — 7 . Оно верное, потому как 2 2 3 + 2 — 2 — 3 — 7 = 7 + 2 — 3 ( 3 + 2 ) 7 ( 3 + 2 ) = 7 — 7 7 ( 3 + 2 ) = 0 . Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.

Ответ: точек пересечения нет, прямые параллельны.

Найти координаты пересечения заданных прямых 2 x — 1 = 0 и y = 5 4 x — 2 .

Для решения составляем систему уравнений. Получаем

2 x — 1 = 0 5 4 x — y — 2 = 0 ⇔ 2 x = 1 5 4 x — y = 2

Найдем определитель основной матрицы. Для этого 2 0 5 4 — 1 = 2 · ( — 1 ) — 0 · 5 4 = — 2 . Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:

2 x = 1 5 4 x — y = 2 ⇔ x = 1 2 4 5 x — y = 2 ⇔ x = 1 2 5 4 · 1 2 — y = 2 ⇔ x = 1 2 y = — 11 8

Получили, что точка пересечения заданных прямых имеет координаты M 0 ( 1 2 , — 11 8 ) .

Ответ: M 0 ( 1 2 , — 11 8 ) .

Нахождения координат точки пересечения двух прямых в пространстве

Таким же образом находятся точки пересечения прямых пространства.

Когда заданы прямые a и b в координатной плоскости О х у z уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 1 = 0 а прямая b — A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 .

Когда точка М 0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0

Рассмотрим подобные задания на примерах.

Найти координаты точки пересечения заданных прямых x — 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0

Составляем систему x — 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A = 1 0 0 0 1 2 3 2 0 4 0 — 2 и расширенную T = 1 0 0 1 0 1 2 — 3 4 0 — 2 4 . Определяем ранг матрицы по Гауссу.

1 = 1 ≠ 0 , 1 0 0 1 = 1 ≠ 0 , 1 0 0 0 1 2 3 2 0 = — 4 ≠ 0 , 1 0 0 1 0 1 2 — 3 3 2 0 — 3 4 0 — 2 4 = 0

Отсюда следует, что ранг расширенной матрицы имеет значение 3 . Тогда система уравнений x — 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x — 27 — 4 = 0 в результате дает только одно решение.

Базисный минор имеет определитель 1 0 0 0 1 2 3 2 0 = — 4 ≠ 0 , тогда последнее уравнение не подходит. Получим, что x — 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0 ⇔ x = 1 y + 2 z = — 3 3 x + 2 y — 3 . Решение системы x = 1 y + 2 z = — 3 3 x + 2 y = — 3 ⇔ x = 1 y + 2 z = — 3 3 · 1 + 2 y = — 3 ⇔ x = 1 y + 2 z = — 3 y = — 3 ⇔ ⇔ x = 1 — 3 + 2 z = — 3 y = — 3 ⇔ x = 1 z = 0 y = — 3 .

Значит, имеем, что точка пересечения x — 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x — 2 z — 4 = 0 имеет координаты ( 1 , — 3 , 0 ) .

Ответ: ( 1 , — 3 , 0 ) .

Система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 имеет только одно решение. Значит, прямые a и b пересекаются.

В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.

Поэтому система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.

Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.

Заданы уравнения прямых x + 2 y — 3 z — 4 = 0 2 x — y + 5 = 0 и x — 3 z = 0 3 x — 2 y + 2 z — 1 = 0 . Найти точку пересечения.

Для начала составим систему уравнений. Получим, что x + 2 y — 3 z — 4 = 0 2 x — y + 5 = 0 x — 3 z = 0 3 x — 2 y + 2 z — 1 = 0 . решаем ее методом Гаусса:

1 2 — 3 4 2 — 1 0 — 5 1 0 — 3 0 3 — 2 2 1

1 2 — 3 4 0 — 5 6 — 13 0 — 2 0 — 4 0 — 8 11 — 11

1 2 — 3 4 0 — 5 6 — 13 0 0 — 12 5 6 5 0 0 7 5 — 159 5

1 2 — 3 4 0 — 5 6 — 13 0 0 — 12 5 6 5 0 0 0 311 10

Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.

Ответ: нет точки пересечения.

Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.

Заданы две прямые x = — 3 — λ y = — 3 · λ z = — 2 + 3 · λ , λ ∈ R и x 2 = y — 3 0 = z 5 в О х у z . Найти точку пересечения.

Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что

x = — 3 — λ y = — 3 · λ z = — 2 + 3 · λ ⇔ λ = x + 3 — 1 λ = y — 3 λ = z + 2 3 ⇔ x + 3 — 1 = y — 3 = z + 2 3 ⇔ ⇔ x + 3 — 1 = y — 3 x + 3 — 1 = z + 2 3 ⇔ 3 x — y + 9 = 0 3 x + z + 11 = 0 x 2 = y — 3 0 = z 5 ⇔ y — 3 = 0 x 2 = z 5 ⇔ y — 3 = 0 5 x — 2 z = 0

Находим координаты 3 x — y + 9 = 0 3 x + z + 11 = 0 y — 3 = 0 5 x — 2 z = 0 , для этого посчитаем ранги матрицы. Ранг матрицы равен 3 , а базисный минор 3 — 1 0 3 0 1 0 1 0 = — 3 ≠ 0 , значит, что из системы необходимо исключить последнее уравнение. Получаем, что

3 x — y + 9 = 0 3 x + z + 11 = 0 y — 3 = 0 5 x — 2 z = 0 ⇔ 3 x — y + 9 = 0 3 x + z + 11 = 0 y — 3 = 0

Решим систему методом Крамер. Получаем, что x = — 2 y = 3 z = — 5 . Отсюда получаем, что пересечение заданных прямых дает точку с координатами ( — 2 , 3 , — 5 ) .

Как найти ординату точки пересечения прямых заданных уравнениями

Найдите ординату точки пересечения прямых, заданных уравнениями и

Это задание ещё не решено, приводим решение прототипа.

Найдите ординату точки пересечения прямых, заданных уравнениями 3x + 2y = 6 и y = −x.

Решая совместно эти два уравнения, получаем, что x = 6, y = −6.

источники:

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/koordinaty-tochki-peresechenija-dvuh-prjamyh-prime/

http://ege.sdamgia.ru/test?likes=27690

Источник

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 121 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Добавить в вариант

Точки O(0; 0), A(10; 8), C(2; 6) и B являются вершинами параллелограмма. Найдите ординату точки B.

Точки O(0; 0), A(10; 8), B(8; 2) и C являются вершинами параллелограмма. Найдите ординату точки

Точки O(0; 0), B(8; 2), C(2; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.

Точки O(0; 0), A(10; 8), B(8; 2), C(2; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.

Найдите абсциссу точки пересечения прямой, заданной уравнением 3x + 2y  =  6, с осью Ox.

Найдите ординату точки пересечения прямой, заданной уравнением 3x + 2y  =  6, с осью Oy.

Найдите ординату точки пересечения прямых, заданных уравнениями 3x + 2y  =  6 и y = −x.

Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).

Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).

Найдите расстояние от точки A с координатами (4, 9) до оси абсцисс.

Найдите ординату точки, симметричной точке A(−5; 2) относительно оси Ox.

Найдите ординату точки, симметричной точке A(1, −4) относительно начала координат.

Найдите ординату середины отрезка, соединяющего точки и

Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A и B

Прямая a проходит через точки с координатами (0; 2) и (2; 0). Прямая b проходит через точку с координатами (0; 4) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Всего: 121 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Источник

Если две прямые не параллельны, то они обязательно пересекутся в одной точке. Найти координаты точки пересечения двух прямых можно как графическим, так и арифметическим способом, в зависимости от того, какие данные предоставляет задача.Вам понадобится

Если прямые уже начерчены на графике, найдите решение графическим способом. Для этого продолжите обе или одну из прямых так, чтобы они пересеклись. Затем отметьте точку пересечения и опустите из нее перпендикуляр на ось абсцисс (как правило, ох).

При помощи шкалы делений, отмеченных на оси, найдите значение х для этой точки. Если она находится на положительном направлении оси (справа от нулевой отметки), то ее значение будет положительным, в противном случае – отрицательным.

Точно также найдите ординату точки пересечения. Если проекция точки расположена выше нулевой отметки – она положительная, если ниже – отрицательная. Запишите координаты точки в виде (х, у) — это и есть решение задачи.

Если прямые заданы в виде формул у=kх+b, вы можете также решить задачу графическим способом: начертите прямые на координатной сетке и найдите решение описанным выше способом.

Попробуйте найти решение задачи, используя данные формулы. Для этого составьте из этих уравнений систему и решите ее. Если уравнения даны в виде у=kх+b, просто приравняйте обе части с х и найдите х. Затем подставьте значение х в одно из уравнений и найдите у.

Можно найти решение способом Крамера. В таком случае приведите уравнения к виду А1х+В1у+С1=0 и А2х+В2у+С2=0. Согласно формуле Крамера х=-(С1В2-С2В1)/(А1В2-А2В1), а у=-(А1C2-А2С1)/(А1В2-А2В1). Обратите внимание, если знаменатель равен нулю, то прямые параллельны или совпадают и, соответственно, не пересекаются.

Если вам даны прямые в пространстве в каноническом виде, перед тем, как начать поиск решения, проверьте, не параллельны ли прямые. Для этого оцените коэффициентыперед t, если они пропорциональны, например, x=-1+3t, y=7+2t, z=2+t и x=-1+6t, y=-1+4t, z=-5+2t, то прямые параллельны. Кроме того, прямые могут скрещиваться, в этом случае система не будет иметь решения.

Если вы выяснили, что прямые пересекаются, найдите точку их пересечения. Сначала приравняйте переменные из разных прямых, условно заменив t на u для первой прямой и на v для второй прямой. Например, если вам даныпрямые x=t-1, y=2t+1, z=t+2 и x=t+1, y=t+1, z=2t+8 вы получите выражения типа u-1=v+1, 2u+1=v+1, u+2=2v+8.

Выразите из одного уравнения u, подставьте в другое и найдите v (в данной задаче u=-2,v=-4). Теперь, чтобы найти точку пересечения, подставьте полученные значения вместо t (без разницы, в первое или второе уравнение) и получите координаты точки x=-3, y=-3, z=0.

Источник

#1658

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите значение $$x$$, при котором $$f(x)=-5$$.

#1659

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508903

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите значение $$x$$, при котором $$f(x)=-13,5$$.

#1667

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508904

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите значение $$x$$, при котором $$f(x)=14,5$$.

#1668

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508905

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите значение $$x$$, при котором $$f(x)=4,75$$.

#1669

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508906

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите значение $$x$$, при котором $$f(x)=-6,5$$.

#1670

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508907

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите значение $$x$$, при котором $$f(x)=-8$$.

#1671

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508908

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите значение $$x$$, при котором $$f(x)=16$$.

#1672

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508909

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите значение $$x$$, при котором $$f(x)=-7,25$$.

#1673

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508910

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите значение $$x$$, при котором $$f(x)=11,5$$.

10.

#849

Номер в банке заданий «Хижина математика»

Сложность «Средне»

На рисунке изображены графики функций вида $$y=kx+b$$. Найдите ординату точки пересечения этих графиков.

11.

#2206

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509213

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

12.

#2207

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509214

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.

13.

#2208

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509215

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.

14.

#2209

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509216

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.

15.

#2210

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509217

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.

16.

#2211

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509218

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.

17.

#2212

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509219

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

18.

#2213

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509220

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.

19.

#2214

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509221

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики функций вида $$y=kx+b$$, которые пересекаются в точке $$A$$. Найдите ординату точки $$A$$.

20.

#2215

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509222

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики функций вида $$f(x)=kx+b$$, которые пересекаются в точке $$A$$. Найдите ординату точки $$A$$.

21.

#2216

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509223

Официальное задание из открытого банка ЕГЭ

22.

#2217

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509224

Официальное задание из открытого банка ЕГЭ

23.

#2218

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509225

Официальное задание из открытого банка ЕГЭ

24.

#2219

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509226

Официальное задание из открытого банка ЕГЭ

25.

#2220

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509227

Официальное задание из открытого банка ЕГЭ

26.

#2221

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509228

Официальное задание из открытого банка ЕГЭ

27.

#809

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(7)$$.

28.

#810

Номер в банке заданий «Хижина математика»

Сложность «Легко»

Официальное задание из банка ФИПИ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(10)$$.

29.

#811

Номер в банке заданий «Хижина математика»

Сложность «Легко»

Официальное задание из банка ФИПИ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(-10)$$.

30.

#812

Номер в банке заданий «Хижина математика»

Сложность «Легко»

Официальное задание из банка ФИПИ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(-6)$$.

31.

#813

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508901

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(-12)$$.

32.

#814

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(8)$$.

33.

#815

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(7)$$.

34.

#816

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(5)$$.

35.

#817

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(12)$$.

36.

#818

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(8)$$.

37.

#819

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(6)$$.

38.

#820

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(11)$$.

39.

#821

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(11)$$.

40.

#361

Номер в банке заданий «Хижина математика»

Сложность «Легко»

На рисунке изображён график функции вида $$y=kx+b$$. Найдите значение $$f(3)$$.

41.

#1660

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508895

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(-5)$$.

42.

#1661

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508896

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(-9)$$.

43.

#1662

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508897

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(12)$$.

44.

#1663

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508898

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(-10)$$.

45.

#1664

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508899

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(-16)$$.

46.

#1665

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508900

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(8)$$.

47.

#1666

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 508902

Официальное задание из открытого банка ЕГЭ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(28)$$.

48.

#1941

Номер в банке заданий «Хижина математика»

Сложность «Легко»

9CC815

Официальное задание из банка ФИПИ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(7)$$.

49.

#1942

Номер в банке заданий «Хижина математика»

Сложность «Легко»

87429D

Официальное задание из банка ФИПИ

На рисунке изображён график функции $$f(x)=kx+b$$. Найдите $$f(5)$$.

50.

#1943

Номер в банке заданий «Хижина математика»

Сложность «Легко»

CFEAE8

Официальное задание из банка ФИПИ

На рисунке изображён график функции $$f(x)=kx+b$$. Найдите $$f(4)$$.

51.

#1944

Номер в банке заданий «Хижина математика»

Сложность «Легко»

5BF069

Официальное задание из банка ФИПИ

На рисунке изображён график функции $$y=kx+b$$. Найдите $$f(6)$$.

52.

#788

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509198

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

53.

#1851

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509199

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

54.

#840

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509197

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

55.

#1865

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509206

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики функций вида $$f(x)=kx+b$$, которые пересекаются в точке $$A$$. Найдите абсциссу точки $$A$$.

56.

#843

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509209

Официальное задание из открытого банка ЕГЭ

57.

#844

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509203

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

58.

#847

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509210

Официальное задание из открытого банка ЕГЭ

59.

#848

Номер в банке заданий «Хижина математика»

Сложность «Средне»

На рисунке изображены графики функций вида $$y=kx+b$$. Найдите абсциссу точки пересечения этих графиков.

60.

#2197

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509200

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

61.

#2198

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509201

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

62.

#2199

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509202

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

63.

#2200

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509204

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

64.

#1945

Номер в банке заданий «Хижина математика»

Сложность «Средне»

7D21DC

Официальное задание из банка ФИПИ

На рисунке изображены графики двух линейных функций, пересекающихся в точке $$A$$. Найдите абсциссу точки $$A$$.

65.

#2201

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509205

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики функций вида $$y=kx+b$$, которые пересекаются в точке $$A$$. Найдите абсциссу точки $$A$$.

66.

#1946

Номер в банке заданий «Хижина математика»

Сложность «Средне»

1DC3CC

Официальное задание из банка ФИПИ

На рисунке изображены графики двух линейных функций, пересекающихся в точке $$A$$. Найдите абсциссу точки $$A$$.

67.

#2202

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509207

Официальное задание из открытого банка ЕГЭ

68.

#2203

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509208

Официальное задание из открытого банка ЕГЭ

69.

#2204

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509211

Официальное задание из открытого банка ЕГЭ

70.

#2205

Номер в банке заданий «Хижина математика»

Сложность «Легко»

№ 509212

Официальное задание из открытого банка ЕГЭ

71.

#841

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509229

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

72.

#842

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509231

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

73.

#845

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509233

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

74.

#846

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509234

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

75.

#855

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509230

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

76.

#856

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509232

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

77.

#2222

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509235

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

78.

#2223

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509236

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

79.

#2224

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509237

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

80.

#2225

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509238

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

81.

#2226

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509239

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

82.

#2227

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509240

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения этих графиков.

83.

#851

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509245

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

84.

#852

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509247

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

85.

#2228

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509241

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

86.

#2229

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509242

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

87.

#2230

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509243

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

88.

#2231

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509244

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

89.

#2232

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509246

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

90.

#2233

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509248

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

91.

#2234

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509249

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

92.

#2235

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509250

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

93.

#2236

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509251

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

94.

#2237

Номер в банке заданий «Хижина математика»

Сложность «Средне»

№ 509252

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения этих графиков.

Источник