Как найти ординату точки пересечения двух функций

Заказать задачи по любым предметам можно здесь от 10 минут

Координаты точки пересечения графиков функций

Как найти?

1. Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие $ x $, а в правую остальные и найти корни, полученного уравнения.
2. Второй способ заключается в том, что нужно составить систему уравнений и решить её путём подстановки одной функции в другую
3. Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.

Случай двух линейных функций

Рассмотрим две линейные функции $ f(x) = k_1 x+m_1 $ и $ g(x) = k_2 x + m_2 $. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения $ x_1 $ и $ x_2 $ и найти $ f(x_1) $ и $ (x_2) $. Затем повторить тоже самое и с функцией $ g(x) $. Далее визуально найти координату точки пересечения графиков функций.

Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда $ k_1 neq k_2 $. Иначе, в случае $ k_1=k_2 $ функции параллельны друг другу, так как $ k $ — это коэффициент угла наклона. Если $ k_1 neq k_2 $, но $ m_1=m_2 $, тогда точкой пересечения будет $ M(0;m) $. Это правило желательно запомнить для ускоренного решения задач.

Пример 1

Пусть даны $ f(x) = 2x-5 $ и $ g(x)=x+3 $. Найти координаты точки пересечения графиков функций.

Решение

Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций $ k_1 = 2 $ и $ k_2 = 1 $. Замечаем, что $ k_1 neq k_2 $, поэтому существует одна точка пересечения. Найдём её с помощью уравнения $ f(x)=g(x) $: $$ 2x-5 = x+3 $$ Переносим слагаемые с $ x $ в левую часть, а остальные в правую: $$ 2x — x = 3+5 $$ $$ x = 8 $$ Получили $ x=8 $ абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим $ x = 8 $ в любое из уравнений хоть в $ f(x) $, либо в $ g(x) $: $$ f(8) = 2cdot 8 — 5 = 16 — 5 = 11 $$ Итак, $ M (8;11) $ — является точкой пересечения графиков двух линейных функций. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ M (8;11) $$

Пример 2

Дано $ f(x)=2x-1 $ и $ g(x) = 2x-4 $. Найти точки пересечения графиков функций.

Решение

Как найти? Опять же обращаем внимание на то, что угловые коэффициенты равны $ k_1 = k_2 = 2 $. Это означает, что линейные функции параллельны между собой, поэтому у них нет точек пересечения!

Ответы

Графики функций параллельны, нет точек пересечения.

 Случай двух нелинейных функций 

Пример 3

Найти координаты точки пересечения графиков функций: $ f(x)=x^2-2x+1 $ и $ g(x)=x^2+1 $

Решение

Как быть с двумя нелинейными функциями? Алгоритм простой: приравниваем уравнения друг к другу и находим корни: $$ x^2-2x+1=x^2+1 $$ Разносим по разным сторонам уравнения члены с $ x $ и без него: $$ x^2-2x-x^2=1-1 $$ $$ -2x=0 $$ $$ x=0 $$ Найдена абцисса искомой точки, но её недостаточно. Ещё нехватает ординаты $ y $. Подставляем $ x = 0 $ в любое из двух уравнений условия задачи. Например: $$ f(0)=0^2-2cdot 0 + 1 = 1 $$ $ M (0;1) $ — точка пересечения графиков функций

Ответ

$$ M (0;1) $$

Точки пересечения графиков функций

В алгебре и начале анализа можно встретить множество задач на поиск точек пересечения графиков функций с помощью их построения или другими методами. Благодаря определенному алгоритму действий, найти ответ достаточно просто. В большинстве случаев решение заключается в определении корней различного вида уравнений.

График функции (y = f(x)) является множеством точек ((x; y)), координаты которых связаны соотношением (y = f(x).)

Равенство (y = f(x)) называют уравнением данного графика. Таким образом, график функции представляет собой множество точек (x; y), где x — является аргументом, а y — определяется как значение функции, соответствующее данному аргументу.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В том случае, когда графики пересекаются в какой-то точке, можно сделать вывод о существовании общего решения системы уравнений. Определить координаты точки можно с помощью графического или аналитического метода. В первом случае требуется построить график уравнения с переменной. Аналитический метод поиска координат точек, в которых графики функций пересекаются, подразумевает решение уравнения, а найденные корни и являются искомыми точками.

Как найти координаты, примеры решения

Существует несколько способов решения подобных задач:

1. Поиск точек пересечения графиков функций заключается в приравнивании обеих функций друг к другу. При этом все члены с х переносят в левую сторону, а оставшиеся – в правую. Затем остается найти корни уравнения, которое получилось после преобразований.
2. Второй метод состоит в записи системы уравнения для ее последующего решения с помощью подстановки одной функции в другую.
3. Третий способ подразумевает построение графиков функций, чтобы определить точки их пересечения визуально.

В качестве примера можно рассмотреть две линейные функции:

(f(x) = k_1 x+m_1)

(g(x) = k_2 x + m_2)

Данные функции являются прямыми. Их можно графически изобразить, если принять какие-либо два значения (x_1) и (x_2) и найти (f(x_1)) и ((x_2)). Далее действия необходимо повторить с функцией (g(x)). Затем достаточно легко определить визуально координаты точки пересечения рассматриваемых функций.

Важно отметить, что для линейных функций характерна лишь одна точка пересечения только в том случае, когда (k_1 neq k_2). В противном случае (k_1=k_2), а функции будут параллельными друг другу, в связи с тем, что k является коэффициентом угла наклона. При( k_1 neq k_2) и (m_1=m_2) точка пересечения будет соответствовать (M(0;m)). Данная закономерность упрощает решение многих подобных задач.

(g(x)=x+3)

Требуется определить координаты точки, в которой пересекаются графики рассматриваемых функций.

Решение

В первую очередь стоит отметить, что функции являются линейными. Важно обратить внимание на коэффициент угла наклона рассматриваемых функций:

(k_1 = 2)

(k_2 = 1)

Заметим, что:

(k_1 neq k_2)

По этой причине имеется лишь одна точка пересечения графиков функций. Определить ее можно путем решения уравнения:

(f(x)=g(x))

(2x-5 = x+3)

Необходимо перенести члены с x в левую часть, а остальные — в правую:

(2x — x = 3+5)

(x =

В результате удалось найти x=8, что соответствует абсциссе точки пересечения графиков. Требуется определить ординату y с помощью подстановки x = 8 в любое из уравнений – в (f(x)), либо в (g(x)):

(f(8) = 2cdot 8 — 5 = 16 — 5 = 11)

Таким образом, M (8;11) – представляет собой точку, в которой пересекаются графики пары линейных функций.

Ответ: M (8;11)

(g(x) = 2x-4.)

Необходимо определить точки, в которых графики рассматриваемых функций пересекаются.

Решение

Угловые коэффициенты:

(k_1 = k_2 = 2)

Таким образом, линейные функции параллельны между собой, что объясняет отсутствие точек пересечения их графиков.

Ответ: графики функций параллельны, точки пересечения отсутствуют.

(g(x)=x^2+1)

Решение

В данном случае функции являются нелинейными. Поэтому алгоритм решения задачи будет несколько отличаться от предыдущих примеров. В первую очередь следует приравнять уравнения:

(x^2-2x+1=x^2+1)

Далее необходимо разнести в разные стороны уравнения члены с x и без него:

(x^2-2x-x^2=1-1)

(-2x=0)

(x=0)

Таким образом, будет определена абсцисса искомой точки. Затем необходимо найти ординату у. Для этого нужно подставить (x = 0) в какое-либо из двух начальных уравнений. К примеру:

(f(0)=0^2-2cdot 0 + 1 = 1)

M (0;1) является точкой, в которой пересекаются графики функций.

Ответ: M (0;1)

Приравнивание функций друг к другу и нахождение корней

Выяснить, имеют ли точки пересечения графики функций, можно путем сравнения соответствующих тождеств и решения уравнения. Однако при этом допускается получение различных равенств с неизвестными. Тогда целесообразно воспользоваться специальными методиками.

Когда уравнение относится к первой степени или является линейным, решение получить достаточно просто. Метод заключается в переносе переменных величин в одну часть уравнения, а известных – в другую. Алгоритм действий:

• раскрытие скобок, приведение подобных коэффициентов;
• перенос членов с неизвестными в одну сторону, а с известными – в другую;
• математические преобразования;
• определение корня.

Квадратные уравнения решают с помощью одного из способов:

• разложение на множители;
• выделение полного квадрата;
• поиск дискриминанта;
• теорема Виета.

В первом случае представляется возможным понизить степень при неизвестной величине. Второй метод заключается в выделении квадрата по одной из формул сокращенного умножения. Каждая из этих методик реализуема при наличии знаний соответствующих тождеств, в том числе правил разложения на множители.

Третий способ состоит в поиске корней через дискриминант (Д), который является дополнительным параметром, позволяющим сразу решить задачу. Дискриминант определяется с помощью формулы:

((-S)^2-4PU)

В том случае, когда Д>0, переменная может иметь пару значений, которые превращают равенство в справедливое тождество. Если Д=0, то корень является единственным. Когда Д<0, искомое тождество с неизвестными не имеет решений.

Квадратные уравнения решают таким образом:

• выполнение необходимых алгебраических преобразований, в том числе раскрытие скобок и приведение подобных слагаемых;
• выбор наиболее оптимального способа решения и его реализация;
• проверка корней с помощью их подстановки в начальное выражение.

Существует несколько методик решения тождеств кубического и биквадратного типов:

• понижение степени, то есть разложение на множители;
• замена переменной.

Первый вариант решения подразумевает выполнение преобразований для последующего применения одной из формул сокращенного умножения. Такой способ применяют нечасто. Второй способ состоит в том, что при решении необходимо ввести переменную с более низкой степенью, которая упрощает выражение. Порядок действий при этом следующий:

• выполнение математических преобразований;
• выражение переменной через другую;
• решение квадратного или линейного уравнения;
• подстановка промежуточных корней, которые получилось найти на третьем шаге, во второй;
• вычисление искомых корней;
• проверка;
• исключение ложных решений;
• запись ответа.

Путем составления системы уравнений

Данный метод определения точек пересечения графиков функций предполагает запись системы уравнения. К примеру:

Решение системы уравнений представляет собой пару чисел (х, у), являющуюся одновременно решением для первого и второго уравнения системы. Решить систему уравнений – значит, отыскать все ее решения, либо установить их отсутствие.

Порядок действий при решении системы уравнений можно рассмотреть на примере:

Решение будет иметь следующий вид:

Данные уравнения являются линейными, поэтому график каждого из них представляет собой прямую. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и является решением системы уравнений.

Решение системы представляет сбой единственную пару чисел:

Если подставить данные числа в любое из уравнений, то получится справедливое равенство. Таким образом, имеется единственное решение линейной системы. Можно записать отчет: (-1;0).

В процессе решения линейной системы можно столкнуться с разными ситуациями:

• система обладает единственным решением, прямые пересекаются;
• решения системы отсутствуют. прямые параллельны;
• система обладает бесчисленным множеством решений, прямые совпадают.

При рассмотрении частного случая системы p(x; y) и q(x; y) являются линейными выражениями от x и y.

В задачах нередко требуется решить нелинейную систему уравнений. К примеру, необходимо решить следующую систему:

Решение имеет следующий вид:

График первого уравнения будет иметь вид прямой, а второго – являться окружностью. Можно построить первый график по точкам:

Центр окружности в точке О(0; 0), радиус равен 1.

Графики пересекаются в точке А(0; 1) и в точке В(-1; 0).

Ответ: (0; 1); (-1; 0).

Можно решить систему графическим способом:

В первую очередь необходимо построить график первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 2. График второго уравнения является параболой, которая смещена относительно начала координат на 2 вверх, то есть ее вершина – точка (0; 2).

Графики обладают одной общей точкой А(0; 2). Данная точка является решением системы. Если подставить два числа в уравнение, можно проверить корректность ответа и записать его. Ответ: (0; 2).

В качестве еще одного примера можно решить следующую систему:

Первым шагом является построение графика первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 1.

Далее необходимо построить график функции:

График будет являться ломанной:

Далее следует сместить ее на 1 вниз по оси oy. В результате получится график функции:

При помещении обоих графиков в одну систему координат получится следующая ситуация:

Таким образом, получились три точки пересечения: А(1; 0), т. В(-1; 0), т. С(0; -1)

Нахождение через графическое построений функций

Любой определенный график задают с помощью соответствующей функции. Найти точки, в которых пересекаются графики, можно путем решения уравнения, имеющего вид:

(f1(x)=f2(x))

Решение данного уравнения будет являться искомой точкой.

Построить график можно с помощью бумаги и ручки. В процессе необходимо обратить внимание на то, что количество точек пересечения пары графиков определяется видом функции. Линейные функции обладают лишь одной точкой пересечения, линейная и квадратная – двумя, квадратные – двумя, либо четырьмя.

В общем случае двух линейных функций можно предположить, что:

(y1=k1x+b1)

(y2=k2x+b2)

Для поиска точки пересечения графиков необходимо решить уравнение:

(y1=y2 или k1x+b1=k2x+b2)

После преобразований получится, что:

(k1x-k2x=b2-b1.)

Далее нужно выразить x:

(x=(b2-b1)/(k1-k2).)

При известной координате точки по оси абсцисс следует определить координату по оси ординат. Таким образом, можно найти координаты точки пересечения графиков:

(((b2-b1)/(k1-k2); k1(b2-b1)/(k1-k2)+b2))

График функции y = f (х) представляет собой множество точек плоскости, координаты (х, у) которых соответствуют выражению y = f(x). График функции наглядно иллюстрирует поведение и свойства функции. Для построения графика определяют несколько значений довода х и для них рассчитывают соответствующие значения функции y=f(x). Для больше точного и наглядного построения графика следует обнаружить его точки пересечения с осями координат.

С целью определить точку пересечения графика функции с осью y, нужно определить значение функции при х=0, то есть обнаружить f(0). В качестве примера можно рассмотреть график линейной функции, изображенной на рисунке:

В данном случае при х=0 ((y=a*0+b)) функция равна b. Таким образом, график пересекает ось ординат (ось Y) в точке (0,b). Когда пересекается ось абсцисс (ось Х) функция равна 0, то есть (y=f(x)=0). Для того чтобы определить х, следует решить уравнение (f(x)=0). В случае линейной функции получаем уравнение (ax+b=0), откуда и находим (x=-b/a). В результате можно сделать вывод, что ось Х пересекается в точке ((-b/a,0).)

При наличии квадратичной зависимости y от х, уравнение (f(x)=0) обладает двумя корнями. Таким образом, ось абсцисс пересекается два раза. В случае периодической зависимости y от х, например, (y=sin(x)), график функции обладает бесконечным количеством точек пересечения с осью Х. Проверить корректность расчета координат точек, в которых пересекаются графики функций, можно с помощью подстановки найденных значений х в выражение f(x). Значение выражения при любом из вычисленных х должно быть равно 0.

Решение:

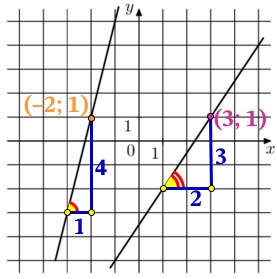
    На рисунке изображены прямые, линейных функции их вид имеет вид:

y = kx + b

    Найдём k и b функции справа. 
    k – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:

k=tg{color{Red}alpha}=frac{color{Blue} 3}{color{Blue} 2}=1,5

    Подставим в общий вид функции значение k и координаты точки (3; 1) найдём b:

y = kx + b
1 = 1,5·3 + b
1 = 4,5 + b
1 – 4,5 = b
–3,5 = b

    Функции справа имеет вид:

y = 1,5x – 3,5

    Найдём k и b функции слева. 

k=tg{color{Red}alpha}=frac{color{Blue} 4}{color{Blue} 1}=4

    Подставим в общий вид функции значение k и координаты точки (–2; 1) найдём b:

y = kx + b
1 = 4·(–2) + b
1 = –8 + b
1 + 8 = b
9 = b

    Функции слева имеет вид:

y = 4x + 9 

    В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:

1,5x – 3,5 = 4x + 9 
1,5x – 4x = 9 + 3,5
–2,5x = 12,5
x=frac{12,5}{–2,5}=-5

    Подставим значение х = –5, в любое уравнение и найдём ординату (y) точки пересечения прямых:

y = 4·(–5) + 9 = –20 + 9 = –11

Ответ: –11.

Как найти координаты точек пересечения графика функции: примеры решения

Ирина Алексеевна Антоненко

Эксперт по предмету «Математика»

Задать вопрос автору статьи

В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.

Первый способ

Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.

Пример 1

Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:

$5x = x- 2$;

$4x = -2$;

$x=-frac{1}{2}$

Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:

$y=-frac{1}{2} – 2 = — 2frac12$.

Точка пересечения будет $(-frac{1}{2};- 2frac12)$.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Второй способ

Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.

Пример 2

Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.

Решение:

Составим систему:

$begin{cases} y=2x^2-2x-1 \ y= x + 1 \ end{cases}$

Второе уравнение проще первого, поэтому подставим его вместо $y$:

$x+1 = 2x^2 – 2x-1$;

$2x^2 – 3x – 2 = 0$.

Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:

$x_1=2; x_2 = -frac{1}{2}$

Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:

$y_1= 2 + 1 = 3; y_2=1 — frac{1}{2} = frac{1}{2}$.

Точки пересечения будут $(2;3)$ и $(-frac{1}{2}; frac{1}{2})$.

Третий способ

«Как найти координаты точек пересечения графика функции: примеры решения» 👇

Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.

Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.

Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.

Пример 3

Найдите точку пересечения графиков на общем рисунке.

Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ

Решение:

Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 07.05.2023

В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.

Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций

Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).

Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:

Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный

Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).

Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.

Как отвечать на вопросы в задаче, когда уже определили функцию

— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример: