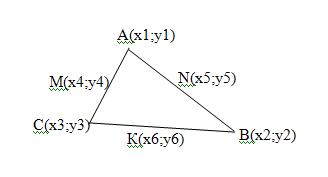Как найти ординату в четырехугольнике

Как найти ординату точки пересечения четырехугольника

Точки O(0; 0), A(10; 8), B(8; 2), C(2; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.

Противоположные стороны попарно равны, четырехугольник является параллелограммом, значит, точка P является серединой отрезка CB. Поэтому координаты точки P вычисляются следующим образом:

Как найти ординату точки пересечения четырехугольника

составить уравнения диагоналей и определить координаты точки пересечения их

координата середины отрезка равна полусумме координат его концов

саму реши задачу. ведь это совсем простенько

Это ромб с диагональю ОА ( Т х=5/2=2.5 у=7/2=3,5

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

1. Дано: http://bit.ly/OBACT35. Необходимо найти ординату точки пересечения Т прямых ОА и ВС.
2. Как известно, уравнение прямой, проходящей через две заданные точки М₁(х₁, у₁) и М₂(х₂, у₂), имеет вид (х – х₁) / (х₂ – х₁) = (у – у₁) / (у₂ – у₁).
3. Составим уравнения диагоналей ОА и ВС данного четырехугольника.
4. Уравнение прямой ОА имеет вид: (х – 0) / (6 – 0) = (у – 0) / (7 – 0) или 7 * х – 6 * у = 0. Аналогично, для ВС получим уравнение: (х – 5) / (1 – 5) = (у – 2) / (5 – 2) или 3 * х + 4 * у = 23.
5. Обозначим через х и у абсциссу и ординату точки Т, соответственно. Тогда, поскольку, точка Т является точкой пересечения прямых ОА и ВС, то х и у можно найти как решение системы линейных уравнений 7 * х – 6 * у = 0 и 3 * х + 4 * у = 23.
6. Первое уравнение позволяет получить х = (6/7) * у. Подставим это во второе уравнение: 3 * (6/7) * у + 4 * у = 23 или 3 * 6 * у + 4 * 7 * у = 23 * 7, откуда у = 161 : 46 = 3,5.

Ответ: Ордината точки Т равна 3,5.

Учитель математики:

Участник:Лосинская Наталья Викторовна
МОУ гимназия № 48
Тольятти, 2009
Искатели IDm033

Тема урока:

Четырехугольники на координатной плоскости.

Тип урока:

урок закрепления ранее изученного материала.

Цель урока:

Изучить свойство вершин параллелограмма на координатной плоскости.

Задачи:

1)отработка навыков по применению формул координат середины отрезка и расстояния между точками через решение задач;

2)выявление взаимосвязи тем геометрии «Четырехугольники» 8 кл. и «Метод координат» 9 кл.; применение метода координат для расширения объема знаний;

3)повторение теоретического материала по теме «Четырехугольники» в ходе решения задач;

4)совершенствование вычислительной культуры учащихся;

5)развитие навыков творческого мышления учащихся: развитие логического мышления,
памяти, умения анализировать и обобщать, сравнивать и находить аналогии;

6)воспитание культуры речи учащихся;

7)формирование положительных мотивов учения;

формирование навыков организации учебной деятельности учащихся.

Оборудование урока:

1)содержание задач учебника Л.С. Атанасяна «Геометрия 7-9»;

2)справочник, рабочая тетрадь, инструменты;

3)портрет Рене Декарта;

4)медиапрезентация «Метод координат».

Содержание урока:

1.Организационный момент (1 мин.)

2.Актуализация ранее полученных знаний (5 мин.)

3.Изучение нового материала (15 мин.)

4.Закрепление изученного материала (16 мин.)

5.Подведение итогов урока. Задание на дом.(3 мин.)

Ход урока:

I.Организационный момент

Учитель:

Эпиграфом урока сегодня будет высказывание Д. Пойа «Наиболее глубокий след оставляет то, что тебе удалось открыть».
Проверить справедливость этих слов нам поможет этот урок, на котором мы проследим связь двух тем «Четырехугольники» и «Метод координат», т.к. геометрия — это наука со взаимосвязанными темами. А поможет нам в этом прямоугольная система координат.

II. Актуализация ранее полученных знаний.

На фоне демонстрации презентация Метод координат учащиеся повторяют формулы координат середины отрезка и расстояния между точками.

«Не так уж и трудно задачи решать:

Проблема дает вдохновенье

Искусство же в том, чтоб суметь отыскать

Задачу, когда есть решенье».

П. Хэйн

Задача №1:

Доказать, что сумма абсцисс середин сторон треугольника равна сумме абсцисс вершин треугольника (аналогично для ординат).



Дано: треугольник ABC, M, N, K – середины AC, AB, BC, А(0;1), В(1;-4), С(5;2)

Доказать:

х4 + х5 + х6 = х1 + х2 + х3,

у4 + у5 + у6 = у1 + у2 + у3.

Доказательство:

х4 = (0 + 5)/2 = 2,5, х5 = (0 + 1)/2 = 0, 5, х6 = (1 + 5)/2 = 3;

х4 + х5 + х6 = 2,5 + 0,5 + 3 = 6, х1 + х2 + х3 = 0 + 1 + 5 = 6, ч.т.д.

Аналогично для ординат точек.

Задача №2

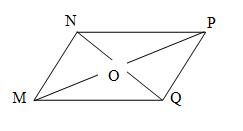
Дано: МNPQ – четырехугольник

М (1;1), N (6;1), Р(7;4), Q (2; 4).

Доказать: МNPQ — параллелограмм.

Вопрос: Какой признак параллелограмма мы будем использовать при решении задачи?

Ответ: Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Решение:

1) О – середина МР, то O(4; 2,5);

2)O – середина NQ, то O(4; 2,5);
тогда МNРQ – параллелограмм (по признаку параллелограмма).

III. Изучение нового материала.

Учитель:

Мы доказали, что МNPQ — параллелограмм. Теперь устно выполните мое задание: Чему равна сумма абсцисс точек, которые являются концами диагонали МР и NQ?

Ответ:х = 8 = 8.

Вопрос:Чему равна сумма ординат диагоналей МР и NQ?

Ответ:у = 5 = 5.

Учитель: Путем вычислений мы получили, что сумма абсцисс концов одной диагонали параллелограмма равна сумме абсцисс концов другой диагонали, аналогично для ординат точек. Случаен ли этот факт?

Задача :Начертите произвольный параллелограмм в прямоугольной системе координат и определите координаты вершин параллелограмма.
Каждый для своего чертежа найдите сумму абсцисс концов одной диагонали и сумму абсцисс концов другой диагонали. Сравните эти результаты.

Ответ:Равны, т.е. сумма абсцисс концов одной диагонали равна сумме абсцисс концов другой диагонали параллелограмма.
Учитель: Найдите сумму ординат концов диагоналей параллелограмма. Сравните эти числа.
Ответ: Равны, т.е. сумма ординат концов одной диагонали равна сумме ординат концов другой диагонали параллелограмма.
Учитель: Значит, говорить о случайности данного факта уже нельзя. Можно уже говорить о свойстве параллелограмма, если известны координаты вершин. Накопленные факты позволяют нам выдвинуть гипотезу.

ГИПОТЕЗА: В параллелограмме сумма абсцисс концов одной диагонали равна сумме абсцисс концов другой диагонали, сумма ординат концов одной диагонали равна сумме ординат концов другой диагонали.
Но пока это только гипотеза, истинность которой надо проверить доказательством.

Учитель: Какое свойство параллелограмма нам поможет в доказательстве?
Ответ: Диагонали параллелограмма точкой пересечения делятся пополам.
Учитель: Действительно, при доказательстве используется это свойство параллелограмма и формула координат середины отрезка.
Доказательство – будет частью вашего домашнего задания.

Учитель: Сформулируйте признак параллелограмма в декартовых координатах.
Ответ: Если в четырехугольнике сумма абсцисс концов одной диагонали равна сумме абсцисс концов другой диагонали, сумма ординат концов одной диагонали равна сумме ординат концов другой диагонали, то этот четырехугольник – параллелограмм.

IV. Закрепление нового материала.

Учитель: Теперь посмотрим как это свойство параллелограмма применяется при решении задач — на практике.
Устно выполним задание:
АВСD – параллелограмм: А(–4; –3), В(5; –2), С(1; 2). Найдите координаты вершины D.
Дано: АВСD – параллелограмм: А(–4; –3), В(5; –2), С(1; 2).

Найти: координаты вершины D.

Решение:
— 4 + 1 = х + 5,
— 3 + 2 = у + (-2),
х = -8,
у = 1
(по свойству параллелограмма).

Ответ:D(–8;1);

Учитель: Данная задача имела единственное решение. А сколько параллелограммов можно построить по трем точкам, не лежащим на одной прямой, если они являются вершинами параллелограмма?
Ответ: три параллелограмма.

Дополнительные задачи:

Задача № 1

Дано: АВСD – параллелограмм,
К – точка пересечения диагоналей,
А(–4; –3), В(5; –2), К(1; 2).

Найти: координаты вершин С и D.

Решение: 1)АВСВ – параллелограмм, К – середина АС и ВD, тогда 2) К – середина АС, то C(6;7); 3) ABCD – параллелограмм, тогда по свойству параллелограмма D(–3;6).

Ответ: C(6;7), D(–3;6).

Задача № 2:

Дано: ABCD – трапеция, AB|| DC, А(–4;–3), В(5;–2), С(6;7), D(–12;5), MN – средняя линия ABCD.

Найти: MN.

Учитель: Какие способы есть для решения данной задачи?

Ответ:

I. По определению средней линии трапеции.

II. По теореме о средней линии трапеции.

Учитель: Задание по вариантам:

I. Найти MN по определению средней линии трапеции;

II. МN по теореме о средней линии трапеции.

IV. Подведение итогов урока. Задание на дом.

Учитель: Сегодня на уроке мы проследили путь познания в математической науке:
накопление фактов › выдвижение гипотезы › проверка истинности доказательством › построение теории › выход в практику.
Мы с вами «открыли» свойство параллелограмма в декартовых координатах и учились применять это свойство при решении задач.

Задание на дом:

Доказательство свойства параллелограмма.

№ 951 (а) – доказать, что ABCD – прямоугольник.

№ 998 – ABCD – ромб.

Литература.

1. Л.С. Атанасян «Геометрия 7-9», М., 1998.

2. Ю.Г. Разбеглов «Путешествие по Пифагории или Тетрадь с печатной основой», 8 кл., Харьков, 1994.

3. Математика в школе № 5, 1995 Т.А. Иванова «Методология научного поиска — основа технологии развивающего обучения».

4. Математика в школе№ 3, 1994 Е. Феоктистов «Материал по теме «Декартовы координаты на плоскости».

муниципальное бюджетное общеобразовательное учреждение
городского округа Тольятти «Гимназия № 48 имени Героя России О.Н. Дологова»

(МБУ «Гимназия № 48»)

Четырехугольники

на координатной плоскости

(урок-исследование с постановкой проблемы)

9 класс

Учитель математики

высшей категории:

Лосинская Н.В.

Тема урока: «Четырехугольники
на координатной плоскости».

Тип урока: урок изучения нового материала на основе ранее
изученного.

Цель урока: развитие личности ребенка

Задачи:
1) отработка навыков по применению формул координат середины отрезка и
расстояния между

  точками через решение
задач;
2) выявление взаимосвязи тем геометрии «Четырехугольники» 8 кл. и
«Метод координат» 9 кл.;  

   применение метода
координат для расширения объема знаний;
3) изучить свойство вершин параллелограмма на координатной плоскости ;

4) совершенствование
вычислительной культуры учащихся;
5) развитие навыков творческого мышления учащихся: развитие логического мышления,
       

    памяти, умения
анализировать и обобщать, сравнивать и находить аналогии;
6) воспитание культуры речи учащихся;
7) формирование положительных мотивов учения;
формирование навыков организации учебной деятельности учащихся.

Виды деятельности на
уроке: накопление фактов › постановка
проблемы › выдвижение гипотезы › эксперимент › проверка истинности
доказательством › построение теории › выход в практику

Оборудование урока:
1) содержание задач учебника Л.С. Атанасяна «Геометрия 7-9»;
2) справочник,  инструменты;
3) портрет Рене Декарта;
4) медиапрезентация «Метод координат».

Содержание урока:

1. Организационный момент
   (1 мин.)
2. Актуализация ранее
   полученных знаний (5 мин.)
3. Изучение нового
   материала (15 мин.)
4. Закрепление изученного
   материала (16 мин.)
5. Подведение итогов урока.
   Задание на дом.(3 мин.)

Ход урока:

      I.  Организационный
момент.

Учитель: Эпиграфом урока сегодня будет высказывание Д. Пойа
«Наиболее глубокий след оставляет то, что тебе удалось открыть«.

Проверить справедливость этих слов нам поможет этот урок, на котором мы
проследим связь двух тем «Четырехугольники» и «Метод
координат», т.к. геометрия — это наука со взаимосвязанными темами. А
поможет нам в этом прямоугольная система координат.

II.               
Актуализация ранее
полученных знаний.

На фоне демонстрации презентации «Метод координат» учащиеся
повторяют формулы координат середины отрезка и расстояния между точками.

«Не так уж и трудно задачи решать:
Проблема дает вдохновенье
Искусство же в том, чтоб суметь отыскать
Задачу, когда есть решенье».

П. Хэйн

Задача №1: Доказать, что сумма абсцисс середин сторон
треугольника равна сумме абсцисс вершин треугольника (аналогично для ординат).

Вопрос: Какой признак параллелограмма мы будем использовать
при решении задачи?
Ответ: Если в четырехугольнике диагонали пересекаются и точкой
пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Решение:
1) О – середина МР,
то O(4; 2,5);

2)O – середина NQ,
то O(4; 2,5);

тогда МNРQ –
параллелограмм (по признаку параллелограмма).

III.            Изучение
нового материала.

Учитель: Мы доказали, что МNPQ — параллелограмм. Теперь устно
выполните мое задание: Чему равна сумма абсцисс точек, которые являются концами
диагонали МР и NQ?
Ответ:  х = 8 = 8.
Вопрос: Чему равна сумма ординат диагоналей МР и NQ?
Ответ: у = 5 = 5.

Учащиеся формулируют
проблему: Путем вычислений мы
получили, что сумма абсцисс концов одной диагонали параллелограмма равна сумме
абсцисс концов другой диагонали, аналогично для ординат точек. Случаен ли этот
факт?

Задача : Начертите
произвольный параллелограмм в прямоугольной системе координат и определите
координаты вершин параллелограмма.
Каждый для своего чертежа найдите сумму абсцисс концов одной диагонали и сумму
абсцисс концов другой диагонали. Сравните эти результаты.

Ответ: Равны, т.е. сумма абсцисс концов одной диагонали
равна сумме абсцисс концов другой диагонали параллелограмма.
Учитель: Найдите сумму ординат концов диагоналей параллелограмма.
Сравните эти числа.
Ответ: Равны, т.е. сумма ординат концов одной диагонали равна сумме
ординат концов другой диагонали параллелограмма.
Учитель: Значит, говорить о случайности данного факта уже нельзя. Можно
уже говорить о свойстве параллелограмма, если известны координаты вершин.
Накопленные факты позволяют нам выдвинуть гипотезу.

ГИПОТЕЗА:
В параллелограмме сумма абсцисс концов одной диагонали равна сумме абсцисс
концов другой диагонали, сумма ординат концов одной диагонали равна сумме
ординат концов другой диагонали.

Но пока это только
гипотеза, истинность которой надо проверить доказательством.

Учитель: Какое свойство параллелограмма нам поможет в
доказательстве?
Ответ: Диагонали параллелограмма точкой пересечения делятся пополам.
Учитель: Действительно, при доказательстве используется это свойство
параллелограмма и формула координат середины отрезка.
Доказательство  проводят учащиеся:

Пусть (х1,у1), (х2,у2),
(х3, у3), (х4,у4) – координаты вершин параллелограмма.

Координаты точки
пересечения диагоналей вычисляются по формуле середины отрезка:

Учитель: Сформулируйте признак параллелограмма в декартовых
координатах.
Ответ: Если в четырехугольнике сумма абсцисс концов одной диагонали
равна сумме абсцисс концов другой диагонали, сумма ординат концов одной
диагонали равна сумме ординат концов другой диагонали, то этот четырехугольник
– параллелограмм.

IV.         Закрепление нового материала.

Учитель: Теперь
посмотрим как это свойство параллелограмма применяется при решении задач — на
практике.

Выполним задание:
АВСD – параллелограмм: А(–4; –3), В(5; –2), С(1; 2). Найдите координаты
вершины D.
Дано: АВСD – параллелограмм: А(–4; –3), В(5; –2), С(1; 2).
Найти: координаты вершины D.
Решение:  — 4 + 1 = х + 5,         — 3 + 2 = у + (-2),

                     х =
-8,                      у = 1

                     (по
свойству параллелограмма).
Ответ: D(–8;1);

Учитель: Данная задача имела единственное решение. А сколько
параллелограммов можно построить по трем точкам, не лежащим на одной прямой,
если они являются вершинами параллелограмма?
Ответ: три параллелограмма.

Дополнительные задачи:

Задача № 1

Дано: АВСD – параллелограмм,
К – точка пересечения диагоналей,
А(–4; –3), В(5; –2), К(1; 2).
Найти: координаты вершин С и D.
Решение:
1) АВСВ – параллелограмм, К – середина АС и ВD,
тогда
2) К – середина АС, то C(6;7);
3) ABCD – параллелограмм, тогда по свойству параллелограмма D(–3;6).

Ответ: C(6;7),
D(–3;6).

Задача № 2:

Дано: ABCD – трапеция, AB|| DC,
А(–4;–3), В(5;–2), С(6;7), D(–12;5),
MN – средняя линия ABCD.
Найти: MN.

Учитель: Какие способы есть для решения данной задачи?
Ответ: I. По определению средней линии трапеции.
             II. По теореме о средней линии трапеции.
Учитель: Задание по вариантам:
I. Найти MN по определению средней линии трапеции;
II. МN по теореме о средней линии трапеции.

IV. Подведение итогов
урока. Задание на дом.

Учитель: Сегодня на уроке мы проследили путь познания в
математической науке:
накопление фактов › выдвижение гипотезы › проверка истинности доказательством ›
построение теории › выход в практику.

Мы с вами
«открыли» свойство параллелограмма в декартовых координатах и учились
применять это свойство при решении задач.

Задание на дом:

№ 951 (а) – доказать, что ABCD – прямоугольник.
№ 998 – ABCD – ромб.

Литература.

1.
Л.С. Атанасян «Геометрия 7-9», М., 2008.
2. Ю.Г. Разбеглов «Путешествие по Пифагории или Тетрадь с печатной
основой», 8 кл., Харьков.
3. Математика в школе № 5. Иванова «Методология научного поиска — основа
технологии развивающего обучения».
4. Математика в школе№ 3. Е. Феоктистов «Материал по теме «Декартовы
координаты на плоскости».

Анализ  урока показывает, что укрепляется база
знаний учащихся, совершенствуются их умения обобщать и систематизировать
материал, а самое главное, появляется интерес к математике. Важным для учеников
становится сам процесс приобретения знаний и его содержание, а не только
оценка. На уроке ученики умело применяют свои знания, открыли новые приемы
решений и рассуждений. При этом развивается логическое мышление, смысловая и
образная память, активизируется мыслительная деятельность, разносторонне
развивается личность учащегося. У ребят формируются умения аргументировано
доказывать свою точку зрения, отстаивать свою позицию, прислушиваться к мнению
других.

В системе обучения самое ценное и целесообразно
организованное проблемное обучение даёт больше всего эффективности в развитии
математического мышления, навыков применения знаний, умений делать выводы,
доказательства, проводить  исследования.

Если преподавание математики строится на проблемной основе, то предмет
совершенно естественно становится средством развития  и преподавательская
деятельность приобретает развивающий характер. Это и явилось главным аргументом
в пользу  применения  технологии проблемного обучения.

 Ничто не имеет большей  ценности на уроке, чем мысль ученика, его
собственный вывод, обобщение, догадка. Заставить его идти по пути собственных
открытий – значит максимально раскрыть перед ним весь спектр математических
знаний. Чем больше таких выводов учащиеся сделали сами, чем чаще на уроках они
самостоятельно проводят обобщения, тем глубже понимание материала, более прочно
его усвоение.

Проблемное обучение решает не только задачу развития мышления, но и
формирует научное мировоззрение. При проблемном обучении не только усвоение
становится творческим, но и преподавание приобретает подлинно творческий
характер.

Работу с учащимися необходимо строить именно с пробуждения интереса к
предмету, мобилизующего творческий потенциал ученика.