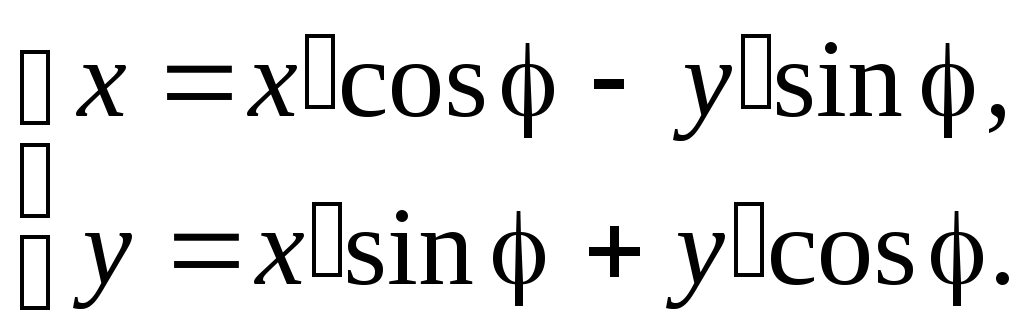Как найти ориентацию тройки векторов

Как найти ориентацию тройки векторов

Для дальнейшего изучения свойств пространства необходимо ввести определение ориентации пространства. Строгая теория, касающаяся этого понятия не очень сложна, но достаточно суха. В связи с этим ограничимся лишь некоторыми “качественными” пояснениями.

Итак, все упорядоченные некомпланарные тройки векторов могут быть разбиты на два непересекающихся класса: правые тройки и левые тройки.

Определение 1: Упорядоченная тройка некомпланарных векторов а 1 , а 2 , а 3 называется правой, если наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от а 1 к а 2 и от а 2 к а 3 кажутся происходящими против часовой стрелки. Если повороты происходят по часовой стрелке, то тройка – левая.

Есть и ещё один способ разделить эти два класса:

Правило правой руки: Совместите начала всех векторов тройки в одной точке. Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая.

Выбрав один из двух классов и назвав все входящие в него базисы “положительными” мы зададим ориентацию пространства.

Далее будем считать положительными правые тройки векторов. Все дальнейшие определения будем давать с учетом этого

Определение 2: Скалярное произведение ставит в соответствие паре векторов a и b число ( a , b )=| a | · | b | · cosφ a , b .

Свойства скалярного произведения:

1. коммутативность: ( a , b )=( b , a )

3. ( a , b )=0 a b

4. Дистрибутивность: ( a 1 + а 2 , b )= ( a 1 , b )+ ( a 2 , b )

5. ( а , λ ·b )= λ · ( a , b ) λ R .

Утверждение 1: В декартовом базисе если а =< x 1 , y 1 , z 1 >, b =< x 2 , y 2 , z 2 >, то ( a , b )= x 1 · x 2 + y 1 · y 2 + z 1 · z 2 .

Пример 1. Найти угол между векторами.

Определение 3: Векторным произведением упорядоченной пары векторов a и b называется вектор [ a , b ], такой что

1. | [ a , b ] |=S a , b , где S a , b – площадь параллелограмма, построенного на векторах a и b . (Если a || b , то S a , b =0.)
2. a[ a , b ] b .
3. a, b , [ a , b ] – правая тройка.

Свойства векторного произведения:

1. [ a , b ] = -[ b , a ]
2. [ a , b ] = θ ó a || b
3. [ a 1 + a 2 , b ] = [ a 1 , b ]+[ a 2 , b ]
4. λ·[ a , b ] = [λ ·a , b ] = [ a ,λ ·b ] λ R .

Утверждение 2: В декартовой системе координат (базис i , j , k ), a =< x 1 , y 1 , z 1 >, b =

=> [ a , b ] =

=

Пример 2. Вычислить площадь параллелограмма, построенного на векторах a и b.

Определение 4: Смешанным произведением упорядоченной тройки векторов a , b и c называется число , b , c> , т.ч. a , b , c >=([ a , b ], c ).

Утверждение 3: a , b , c >=V a , b , c , если a , b , c – правая тройка, или a , b , c >= -V a , b , c , если a , b , c – левая тройка. Здесь V a , b , c – объём параллелепипеда, построенного на векторах a , b и c . (Если a , b и c компланарны, то V a , b , c =0.)

Утверждение 4: В декартовой системе координат, если a =< x 1 , y 1 , z 1 >, b =< x 2 , y 2 , z 2 >,

с =< x 3 , y 3 , z 3 >, => a , b , c >=.

Пример 3. Проверка компланарности векторов.

Пример 4. Принадлежность 4 точек одной плоскости.

Пример 5. Вычислить объем тетраэдра и его высоту.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Вектор. Смешанное произведение векторов.

Также его называют тройным скалярным произведением векторов, скорее всего это связано с тем,

что результат — это скаляр (точнее — псевдоскаляр).

Смешанное произведение векторов — скалярное произведение вектора на векторное произведение векторов и .

Или другими словами:

Смешанным произведением векторов является число , состоящее из скалярного произведения вектора на векторное произведение векторов и . Смешанное произведение

векторов записывается следующим образом:

Геометрический смысл смешанного произведения векторов.

Геометрический смысл смешанного произведения векторов: если три вектора правые, то их

смешанное произведение равно объему параллелепипеда построенного на них:

.

В случае левой тройки , смешанное произведение указанных векторов равно объему

параллелепипеда со знаком “–“:

.

Если , и компланарны, то их смешанное произведение = 0.

Вывод: объем параллелепипеда, построенного на векторах , и равен модулю смешанного

произведения этих векторов:

Объем пирамиды, построенной на этой тройке этих векторов, находим по формуле:

Геометрические свойства смешанного произведения векторов.

1. Модуль смешанного произведения некомпланарных векторов равен объему

параллелепипеда, построенного на этих векторах. Произведение будет со знаком плюс, если

тройка векторов — правая, и будем иметь отрицательный знак, если тройка — левая,

2. Смешанное произведение =0 тогда и только тогда, когда векторы компланарны:

векторы компланарны.

Алгебраические свойства смешанного произведения векторов.

1. При перемене мест двух множителей смешанное произведение меняет знак на противоположный:

При циклической (круговой) перестановке множителей смешанное произведение остается без изменений:

2. Смешанное произведение линейно по любому множителю.

Первое свойство следует из первого геометрического свойства и свойств ориентации троек векторов, так

как от перестановки двух множителей местами, модуль смешанного произведения остается прежним, а

изменяется только ориентация тройки. При циклической перестановке векторов ориентация тройки

остается без изменений.

Второе свойство следует из линейности скалярного произведения и первого свойства.

Формула вычисления смешанного произведения векторов.

Теорема (формула вычисления смешанного произведения векторов):

Если у векторов в правом ортонормированном базисе координаты, ,

соответственно, то смешанное произведение их вычисляется по следующей формуле:

Из определения следует:

что и требовалось доказать.

Еще некоторые свойства смешанного произведения векторов.

1.

2.

3 .Три вектора компланарны в том случае, если

4. Тройка векторов будет правой только если . Ежели , то векторы, и

создают левую тройку векторов.

5.

6.

7.

8.

9.

10. Тождество Якоби:

Если векторы , и заданы своими координатами, то их

смешанное произведение можно найти по формуле, приведенной ниже:

Правая и левая тройки векторов

Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.

Остались вопросы?

Здесь вы найдете ответы.

Поможем выполнить
любую работу

Все еще сложно?

Наши эксперты помогут разобраться

Не получается написать работу самому?

Доверь это кандидату наук!

Ищещь ответ на вопрос с которым нужна помощь?

Ориентация тройки векторов

Упорядоченная
тройка некомпланарных векторов называется
правой,
если, глядя с конца третьего вектора на
плоскость первых двух, мы видим поворот
от первого вектора ко второму по
кратчайшему
пути происходящим против часовой
стрелки. В противном случае тройка
называется левой.
Так, на рис. 1.16 тройка

является левой.

Рис. 1.16

Свойства ориентации

1. {
— правая}

{
— левая}.

2. {
— правая}
{
— левая}.

3. {
— правая}
{
— правая}.

Перестановка
упорядоченного множества называется
циклической,
если каждый его элемент ставится на
место предыдущего (или последующего).
Как мы видим, при циклической перестановке
тройки векторов ее ориентация не
меняется.

Базисные векторы
правого ортонормированного базиса
будем обозначать

(так же, как и в школе). В дальнейшем мы
будем использовать только прямоугольные
системы координат, как правило, правые.

§ 3. Проекции

П
усть
в пространстве заданы плоскость

и прямая
,
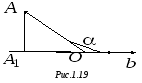
не параллельная этой плоскости. Проекцией
произвольной точки

на плоскость

параллельно прямой

называется точка

пересечения плоскости

и прямой, проходящей через

параллельно

(рис. 1.17).

П

роекцией
произвольной точки

на прямую

параллельно плоскость

называется
точка

пересечения прямой

и плоскости, проходящей через

параллельно

(рис. 1.18). Проекцией множества точек на
плоскость (или на прямую) называется
множество проекций всех точек этого
множества на заданную плоскость (или
прямую). Если плоскость

и прямая

перпендикулярны, то проекции называются
ортогональными.
В дальнейшем мы будем рассматривать
только ортогональные проекции. В этом
случае проекция точки

на прямую совпадает с основанием
перпендикуляра, проведенного из точки

к этой прямой.

Пусть в пространстве
задана прямая
.
Если на ней выбрать направление с помощью
вектора

(),
то прямая превратится в ось. Любой вектор
,
как и всякое множество, на эту ось можно
спроектировать. Полученный вектор будем
называть векторной проекцией вектора

на вектор

и обозначать
.
На рисунке 1.18
,
.

Алгебраической
проекцией
(или просто проекцией)
вектора

на

называется число

.

Проекции обладают
следующими свойствами.

1.
,
где

– угол между векторами

и
.

►

Если

острый угол, то (рис. 1.18)
;
если

– тупой, то (рис. 1.19)
.
Если же
—
прямой угол, то
..◄

2.
,
т.е. проекция суммы векторов равна сумме
их проекций.

►Выберем в
пространстве ортонормированный базис
так, чтобы
.
Если в этом базисе вектор

имеет координаты
,
то, нетрудно убедиться, что

(рис. 1.20).Тогда доказываемое свойство
вытекает из свойств координат векторов.◄

3.
,
т.е. при умножении вектора на число его
проекция умножается на это число.

Это свойство также
вытекает из свойств координат векторов.

§ 4. Преобразования систем координат на плоскости

Параллельный
перенос. Параллельным
переносом называется
такое преобразование системы координат,
при котором координатные оси «старой»
и «новой» систем сонаправлены (рис.1.20).
Выберем на плоскости произвольную точку

и обозначим

ее координаты в старой системе и

– в новой.
Пусть начало новой системы координат
– точка

– в старой системе имеет координаты
.
На рис. 1.17
,
значит,

(7)

Ф
ормулы
(7) и задают преобразование параллельного
переноса.

Преобразование
поворота.
При повороте системы координат начала
старой и новой систем совпадают, а
базисные векторы новой образуют с
базисными векторами старой некоторый
угол
.
Обозначим векторы старой системы, как
обычно,

и
,
а векторы новой –

и

(длины всех базисных векторов равны
единице). На рис. 1.21 видим:
,
.
Если

– произвольная
точка плоскости,

и

– ее
координаты соответственно в старой и
новой
системах координат, то

,

откуда, учитывая
единственность координат в выбранном
базисе, получаем

(8)

Формулы (8) задают
связь старых и новых координат точки
при преобразовании поворота.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Три некомпланарных вектора $overline{a}$,
$overline{b}$ и $overline{c}$, приведенных к общему началу, образуют так
называемую связку трех векторов (или тройку векторов).

Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.

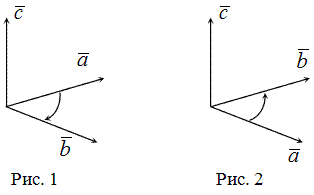
Тройка векторов $overline{a}$, $overline{b}$ и $overline{c}$ называется левой, если
поворот от вектора $overline{a}$ к вектору $overline{b}$, видимый с конца третьего вектора $overline{c}$,
осуществляется по ходу часовой стрелки (рис. 1).

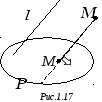
Тройка векторов $overline{a}$, $overline{b}$ и $overline{c}$ называется правой, если
поворот от вектора $overline{a}$ к вектору $overline{b}$, видимый с конца третьего вектора $overline{c}$,
осуществляется против хода часовой стрелки (рис. 2).