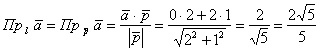Угол между векторами. Ортогональные проекции векторов
Угол между векторами
Углом между двумя ненулевыми векторами называется угол между равными им векторами, имеющими общее начало, не превосходящий по величине числа .
Пусть в пространстве даны два ненулевых вектора и
(рис.1.22). Построим равные им векторы
и
. На плоскости, содержащей лучи
и
, получим два угла
. Меньший из них, величина
которого не превосходит
, принимается за угол между векторами
и
.
Поскольку направление нулевого вектора не определено, то не определен и угол между двумя векторами, если хотя бы один из них нулевой. Из определения следует, например, что угол между ненулевыми коллинеарными векторами либо равен нулю (если векторы одинаково направлены), либо равен (если векторы противоположно направлены).
Ортогональные проекции векторов
Движение по любой прямой может быть в двух направлениях. Ориентированной прямой называется прямая, на которой выбрано направление, т.е. одно из направлений считается положительным, а противоположное — отрицательным. Для измерения длин отрезков на прямой задается масштабный отрезок, который принимается за единицу.
Ориентированная прямая с заданным масштабным отрезком называется осью.
Любой ненулевой вектор , принадлежащий прямой, называется направляющим вектором для данной прямой, поскольку задает на ней ориентацию. Направление вектора
принимается за положительное, а направление противоположного вектора
— за отрицательное. Кроме того, длину вектора
— можно принять за величину масштабного отрезка на этой прямой. Поэтому можно сказать, что любой ненулевой вектор определяет ось — прямую, содержащую этот вектор, задавая на ней направление и масштабный отрезок.
Ортогональной проекцией вектора на ось, задаваемую вектором
, называется его проекция на ось вдоль прямой (или вдоль плоскости), перпендикулярной данной оси. Ортогональную проекцию вектора
на ось, задаваемую вектором
, будем обозначать
.
Ортогональную проекцию вектора на прямую
(см. разд. 1.2.2 и рис. 1.13) будем обозначать
.
Ортогональную проекцию вектора а на плоскость (см. разд. 1.2.2 и рис. 1.14) будем обозначать
.
Разность между вектором и его ортогональной проекцией называют ортогональной составляющей:
— — ортогональная составляющая вектора
относительно вектора
;
— — ортогональная составляющая вектора
относительно прямой
;
— — ортогональная составляющая вектора
относительно плоскости
.
На рис. 1.23 изображены ортогональные проекции вектора :
— на прямую (или на ось
, задаваемую вектором
) вдоль прямой
(рис.1.23,а);
— на прямую (или на ось
, задаваемую вектором
) вдоль плоскости
(рис.1.23,б);
— на плоскость вдоль прямой
(рис.1.23,в).
На рис. 1.23 изображены ортогональные составляющие вектора :
— относительно оси (вектора
):
(рис.1.23,а);
— относительно плоскости (рис.1.23,в).
Для ортогональных проекций справедлива следующая теорема (см. теорему 1.1 в разд. 1.5).
Теорема 1.2 (об ортогональных проекциях вектора).
1. Если на плоскости заданы две взаимно перпендикулярные прямые и
, то любой вектор
на плоскости можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е.
(рис. 1.24,а).
2. Если в пространстве заданы три попарно перпендикулярные прямые и
, пересекающиеся в одной точке, то любой вектор
в пространстве можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е.
(рис. 1.24,6).
3. Квадрат длины вектора на плоскости или в пространстве равен сумме квадратов длин своих ортогональных проекций, т.е.
Первые два утверждения представляют собой частные случаи теоремы 1.1. Третье утверждение следует из теоремы Пифагора (для треугольника (рис. 1.24,а) или треугольников
и
(рис. 1.24,6)).
В формулировке теоремы 1.2 прямые можно заменить осями, задаваемыми попарно ортогональными векторами.
На рис.1.24,а проекции вектора на оси одновременно являются ортогональными составляющими:
и
. На рис. 1.24,6 вектор
является проекцией вектора
на плоскость
, содержащую прямые
и
:
, а вектор
является ортогональной составляющей вектора
относительно плоскости
.
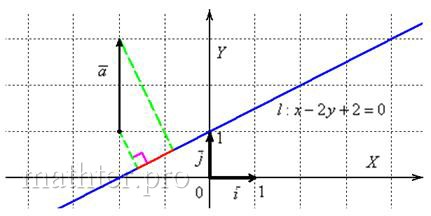
Алгебраическое значение длины проекции
Пусть – угол между ненулевым вектором
и осью, задаваемой вектором
, т.е. угол между ненулевыми векторами
и
.
Алгебраическим значением длины ортогональной проекции вектора на ось, задаваемую вектором
, называется длина его ортогональной проекции
, взятая с положительным знаком, если угол
не превышает
, и с отрицательным знаком, если угол
больше
, т.е.:
Например, для проекций, изображенных на рис. 1.25, , поскольку угол
между векторами
и
острый, a
, так как угол
между векторами
и
тупой.
Некоторые свойства проекций векторов переносятся на алгебраические значения их длин, в частности:
1. — алгебраическое значение длины ортогональной проекции суммы векторов равно сумме алгебраических значений длин ортогональных проекций слагаемых;
2. — алгебраическое значение длины ортогональной проекции произведения вектора на число равно произведению этого числа на алгебраическое значение длины ортогональной проекции вектора
Замечания 1.4.
1. Из определения алгебраического значения длины ортогональной проекции следует (см. также рис.1.25), что , т.е. алгебраическое значение длины ортогональной проекции ненулевого вектора на ось равна произведению длины этого вектора на косинус угла между вектором и осью.
Ортогональную проекцию вектора на ось, задаваемую вектором
, можно представить в виде
Если — единичный вектор, то
.
2. Равенство можно использовать как определение косинуса угла между ненулевыми векторами
и
(или, что то же самое, косинуса угла между осями, заданными ненулевыми векторами
и
(рис. 1.26)).
3. Углом между ненулевым вектором и прямой
называется угол
между вектором
и его ортогональной проекцией
на прямую
. Величина угла
может быть найдена по формуле
4. Углом между ненулевым вектором и плоскостью
называется угол
между вектором
и его ортогональной проекцией
на плоскость
. Величина угла
может быть найдена по формуле
Пример 1.7. Основания и
равнобокой трапеции
равны
и
соответственно; точка
— середина стороны
(рис. 1.27). Найти алгебраические значения длин ортогональных проекций векторов
и
на ось, задаваемую вектором
.
Решение. Пусть — высота трапеции,
— точка пересечения прямых
и
. По свойству равнобокой трапеции
; из равенства треугольников
и
.
Обозначим через искомые алгебраические значения длин ортогональных проекций.Тогда из равенств
,
и свойства 1 алгебраических значений длин проекций следует:
Решая систему находим
, т.е.
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
ТЕОРЕМА
16.1. Пусть
в пространстве выбран ортонормированный
базис , в
котором . Тогда
Доказательство. По
определению координат вектора в базисе
имеем
и
,
поэтому
Используя
доказанные свойства скалярного
произведения, получаем
Поскольку
базис ортонормированный,
то и
,
значит, окончательно получим
Теорема
доказана.
Замечание
16.1. Если
рассматривается множество векторов,
параллельных некоторой плоскости (т.е.
двумерное векторное подпространство
пространства ),
то формула принимает
вид
где в
ортонормированном базисе двумерного
подпространства .
17 Задачи, решаемые с помощью скалярного произведения
Задача
17.1. Пусть
даны координаты вектора в
ортонормированном базисе. Найти длину
вектора .
Решение. Согласно
свойству 4. скалярного произведения
длина вектора находится по формуле ,
т.е. .
Но скалярное произведение векторов в
ортонормированном базисе
вычисляется
по формуле .
Поэтому получаем следующую формулу для
нахождения длины вектора, заданного
своими координатами в ортонормированном
базисе
Задача
17.2. Пусть
даны координаты векторов и
в
ортонормированном базисе.
Найти угол между векторами и
.
Решение. Из
определения скалярного произведения
получаем следующую формулу для нахождения
косинуса угла между векторами:
С
учетом формул и
приходим
к следующей формуле для нахождения угла
между векторами, заданных своими
координатами в ортонормированном базисе
Ортогональная проекция вектора на ось.
Задача
17.3. Пусть
даны два вектора и
. Найти
ортогональную проекцию вектора на
ось вектора .
Решение. По
формуле имеем
Следовательно,
получаем формулу для нахождения
ортогональной проекции вектора на
ось вектора
Ортогональная проекция вектора на плоскость.
Определение
17.1. Пусть
дан вектор и
некоторая плоскость .
Обозначим через ортогональные
проекции точек на
плоскость .
Вектор называется
ортогональной проекцией вектора на
плоскость и
обозначается .
Задача
17.3. Найти
ортогональную проекцию данного
вектора на
плоскость ,
перпендикулярную данному
вектору .
Решение. Пусть
данный вектор .
По определению ортогональной проекции
вектора на плоскость имеем (см
рисунок).
По правилу
многоугольника для сложения векторов,
получаем равенство
Заметим,
что и
,
поэтому .
По признаку коллинеарности векторов
получаем равенство .
Кроме того, ,
поэтому
Умножим
обе части этого равенства скалярно на
вектор .
Имеем числовое равенство
Учитывая,
что
Из
последнего равенства находим,
что
Поэтому
для нахождения ортогональной проекции
вектора на плоскость, перпендикулярную
заданному вектору имеем
18 Геометрический смысл координат вектора в ортонормированном базисе
Пусть
в пространстве выбран ортонормированный
базис ,
в котором .
Тогда .
Умножим обе части этого
равенства
скалярно сначала на вектор ,
потом на и
.
Получаем
Поскольку
базис ортонормированный, то ,
а поэтому имеем равенства
С
учетом формулы имеем
Из
равенств получаем
геометрический смысл координат вектора
в ортонормированном базисе:
координаты
вектора в ортонормированном базисе
равны ортогональным проекциям данного
вектора на оси
соответствующих базисных векторов.
Обозначим
через .
Тогда, используя формулу ,
равенства примут
вид
Числа называются
направляющими косинусами вектора в
ОНБ .
Подставим в
получаем
или
Таким
образом, сумма квадратов направляющих
косинусов любого ненулевого вектора
равна единице.
Заметим,
что если —
единичный, то его координаты в ОНБ равны
направляющим косинусам этого вектора
или, иначе, направляющие косинусы данного
вектора равны
координатам единичного вектора того
же направления.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
30.03.201527.55 Mб32Административное право России Конин Н.М..pdf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
In linear algebra and functional analysis, a projection is a linear transformation 


Definitions
A projection on a vector space 


When 





A projection on a Hilbert space that is not orthogonal is called an oblique projection.
Projection matrix
The eigenvalues of a projection matrix must be 0 or 1.
Examples
Orthogonal projection
The transformation P is the orthogonal projection onto the line m.
For example, the function which maps the point 


The action of this matrix on an arbitrary vector is
To see that 

.
Observing that 
Oblique projection
The transformation T is the oblique projection along k onto m. The range of T is m and the null space is k.
A simple example of a non-orthogonal (oblique) projection (for definition see below) is
Via matrix multiplication, one sees that
proving that 
The projection 


Properties and classification
Idempotence
By definition, a projection 

Complementarity of range and kernel
Let 





Then 
is the identity operator
on
.
- We have a direct sum
. Every vector
may be decomposed uniquely as
with
and
, and where
.
The range and kernel of a projection are complementary, as are 










Spectrum
In infinite dimensional vector spaces, the spectrum of a projection is contained in 
Only 0 or 1 can be an eigenvalue of a projection. This implies that an orthogonal projection 


If a projection is nontrivial it has minimal polynomial 

Product of projections
The product of projections is not in general a projection, even if they are orthogonal. If two projections commute then their product is a projection, but the converse is false: the product of two non-commuting projections may be a projection .
If two orthogonal projections commute then their product is an orthogonal projection. If the product of two orthogonal projections is an orthogonal projection, then the two orthogonal projections commute (more generally: two self-adjoint endomorphisms commute if and only if their product is self-adjoint).
Orthogonal projections
When the vector space 






.
A projection is orthogonal if and only if it is self-adjoint. Using the self-adjoint and idempotent properties of 





where 



The other direction, namely that if 
for every 



-
Proof of existence Let
be a complete metric space with an inner product, and let
be a closed linear subspace of
(and hence complete as well).
For every
the following set of non-negative norms
has an infimum, and due to the completeness of
it is a minimum. We define
as the point in
where this minimum is obtained.
Obviously
is in
. It remains to show that
satisfies
and that it is linear.
Let us define
. For every non-zero
in
, the following holds:
By defining
we see that
unless
vanishes. Since
was chosen as the minimum of the abovementioned set, it follows that
indeed vanishes. In particular, (for
):
.
Linearity follows from the vanishing of
for every
:
By taking the difference between the equations we have
But since we may choose
(as it is itself in
) it follows that
. Similarly we have
for every scalar
.
Properties and special cases
An orthogonal projection is a bounded operator. This is because for every 
Thus 
For finite dimensional complex or real vector spaces, the standard inner product can be substituted for 
Formulas
A simple case occurs when the orthogonal projection is onto a line. If 
(If 



by the properties of the dot product of parallel and perpendicular vectors.
This formula can be generalized to orthogonal projections on a subspace of arbitrary dimension. Let 





which can be rewritten as
The matrix 







The orthonormality condition can also be dropped. If 

The matrix 







In the general case, we can have an arbitrary positive definite matrix 



When the range space of the projection is generated by a frame (i.e. the number of generators is greater than its dimension), the formula for the projection takes the form:


If 



If the orthogonal condition is enhanced to 

All these formulas also hold for complex inner product spaces, provided that the conjugate transpose is used instead of the transpose. Further details on sums of projectors can be found in Banerjee and Roy (2014). Also see Banerjee (2004) for application of sums of projectors in basic spherical trigonometry.
Oblique projections
The term oblique projections is sometimes used to refer to non-orthogonal projections. These projections are also used to represent spatial figures in two-dimensional drawings (see oblique projection), though not as frequently as orthogonal projections. Whereas calculating the fitted value of an ordinary least squares regression requires an orthogonal projection, calculating the fitted value of an instrumental variables regression requires an oblique projection.
Projections are defined by their null space and the basis vectors used to characterize their range (which is the complement of the null space). When these basis vectors are orthogonal to the null space, then the projection is an orthogonal projection. When these basis vectors are not orthogonal to the null space, the projection is an oblique projection. Let the vectors 






This expression generalizes the formula for orthogonal projections given above.
Finding projection with an inner product
Let 




where the 







y is being projected onto the vector space V.
Canonical forms
Any projection 



where 





.
where 







Projections on normed vector spaces
When the underlying vector space 

Many of the algebraic results discussed above survive the passage to this context. A given direct sum decomposition of 















However, in contrast to the finite-dimensional case, projections need not be continuous in general. If a subspace 






The converse holds also, with an additional assumption. Suppose 











The above argument makes use of the assumption that both 












Applications and further considerations
Projections (orthogonal and otherwise) play a major role in algorithms for certain linear algebra problems:
- QR decomposition (see Householder transformation and Gram–Schmidt decomposition);
- Singular value decomposition
- Reduction to Hessenberg form (the first step in many eigenvalue algorithms)
- Linear regression
- Projective elements of matrix algebras are used in the construction of certain K-groups in Operator K-theory
As stated above, projections are a special case of idempotents. Analytically, orthogonal projections are non-commutative generalizations of characteristic functions. Idempotents are used in classifying, for instance, semisimple algebras, while measure theory begins with considering characteristic functions of measurable sets. Therefore, as one can imagine, projections are very often encountered in the context operator algebras. In particular, a von Neumann algebra is generated by its complete lattice of projections.
Generalizations
More generally, given a map between normed vector spaces 

References

|
This page uses content that though originally imported from the Wikipedia article Projection (linear algebra) might have been very heavily modified, perhaps even to the point of disagreeing completely with the original wikipedia article. The list of authors can be seen in the page history. The text of Wikipedia is available under the Creative Commons Licence. |
2.5.8. Как найти проекцию вектора на прямую?
Об ортогональной проекции вектора на вектор мы говорили ранее, и фактически было установлено
следующее:
Чтобы найти ортогональную проекцию вектора на прямую, нужно найти его проекцию на любой направляющий вектор этой прямой.
…возможно, не всем понятен термин «ортогональная» – это такая проекция, при которой на вектор «падают лучи света» строго
перпендикулярно по отношению к прямой (см. рис. ниже). Существует куча иных («косых») проекций, когда проецирование осуществляется под
другими углами, но для данной книги этот материал не столь актуален.
Решим символическую задачку:
Задача 85
Найти проекцию вектора на прямую
Решение: найдём какой-нибудь направляющий вектор прямой, проще и быстрее
взять стандартный вариант: .
Проекция вектора на прямую – есть его проекция на любой направляющий вектор этой прямой, по
соответствующей формуле:
Ответ:
Напоминаю, что проекция – это длина «тени» вектора (красный цвет):
Желающие могут взять любые точки прямой, найти направляющий вектор
и убедиться в том, что проекция
будет такой же, как вариант, со знАком «минус».
Ну вот и подошло к концу наше путешествие по основным задачам с «плоской» прямой, и никакого Кащея Бессмертного тут нет…. – Здесь есть я, с
новыми знаниями и задачами J Потому что Бабу-Ягу никто не отменял =)


| Оглавление |
Автор: Aлeксaндр Eмeлин

В линейной алгебре и функциональный анализ, проекция — это линейное преобразование P { displaystyle P}


Содержание
- 1 Определения
- 1.1 Матрица проекции
- 2 Примеры
- 2.1 Ортогональная проекция
- 2.2 Наклонная проекция
- 3 Свойства и классификация
- 3.1 Идемпотентность
- 3.2 Комплементарность диапазон и ядро
- 3.3 Спектр
- 3.4 Произведение проекций
- 3.5 Ортогональные проекции
- 3.5.1 Свойства и особые случаи
- 3.5.1.1 Формулы
- 3.5.1 Свойства и особые случаи
- 3.6 Косые проекции
- 3.7 Поиск проекции с внутренним продуктом
- 4 Канонические формы
- 5 Проекции на нормированных векторных пространствах
- 6 Приложения и дополнительные соображения
- 7 Обобщения
- 8 См. также
- 9 Примечания
- 10 Ссылки
- 11 Внешние ссылки
Определения
A проекция на векторное пространство V { displaystyle V}


Когда V { displaystyle V}





Матрица проекции
Собственные значения матрицы проекции должно быть 0 или 1.
Примеры
Ортогональная проекция
Например, функция, отображающая точку (x, y, z) { displaystyle (x, y, z)}


- P = [1 0 0 0 1 0 0 0 0]. { displaystyle P = { begin {bmatrix} 1 0 0 \ 0 1 0 \ 0 0 0 end {bmatrix}}.}
Действие этой матрицы на произвольный вектор:
- P (xyz) = (xy 0). { displaystyle P { begin {pmatrix} x \ y \ z end {pmatrix}} = { begin {pmatrix} x \ y \ 0 end {pmatrix}}.}
Чтобы увидеть что P { displaystyle P}

- P 2 (xyz) = P (xy 0) = (xy 0) = P (xyz) { displaystyle P ^ {2} { begin {pmatrix} x \ y \ z end {pmatrix} } = P { begin {pmatrix} x \ y \ 0 end {pmatrix}} = { begin {pmatrix} x \ y \ 0 end {pmatrix}} = P { begin {pmatrix} x \ y \ z end {pmatrix}}}
.
Заметим, что PT = P { displaystyle P ^ { mathrm {T}} = P}
Наклонная проекция
Простым примером неортогональной (наклонной) проекции (определение см. Ниже) является
- P = [0 0 α 1]. { displaystyle P = { begin {bmatrix} 0 0 \ alpha 1 end {bmatrix}}.}
Через умножение матриц можно увидеть, что
- P 2 = [0 0 α 1] [0 0 α 1] = [0 0 α 1] = P. { displaystyle P ^ {2} = { begin {bmatrix} 0 0 \ alpha 1 end {bmatrix}} { begin {bmatrix} 0 0 \ alpha 1 end {bmatrix}} = { begin { bmatrix} 0 0 \ alpha 1 end {bmatrix}} = P.}
доказывает, что P { displaystyle P}
Проекция P { displaystyle P}


Свойства и классификация

Идемпотентность
По определению проекция P { displaystyle P}

Комплементарность диапазона и ядра
Пусть W { displaystyle W}






- P { displaystyle P}
— оператор идентичности I { displaystyle I}
на U { displaystyle U}
- ∀ x ∈ U: P x = x { displaystyle forall x in U: Px = x}
.
- ∀ x ∈ U: P x = x { displaystyle forall x in U: Px = x}
- У нас есть прямая сумма W = U ⊕ V { displaystyle W = U oplus V}
. Каждый вектор x ∈ W { displaystyle x in W}
может быть разложен однозначно как x = u + v { displaystyle x = u + v}
с u = P x { displaystyle u = Px}
и v = x — P x = (I — P) x { displaystyle v = x-Px = (IP) x}
, и где u ∈ U, v ∈ V { displaystyle u in U, v in V}
.
Диапазон и ядро проекции дополняют друг друга, как и P { displaystyle P}










Спектр
В бесконечномерных векторных пространствах спектр проекции содержится в {0, 1} { displaystyle {0,1 } }
- (λ I — P) — 1 = 1 λ I + 1 λ (λ — 1) P. { displaystyle ( lambda IP) ^ {- 1} = { frac {1} { lambda}} I + { frac {1} { lambda ( lambda -1)}} P.}
Только 0 или 1 могут быть собственным значением проекции. Это означает, что ортогональная проекция P { displaystyle P}


Если проекция нетривиальна он имеет минимальный многочлен x 2 — x = x (x — 1) { displaystyle x ^ {2} -x = x (x-1)}

Произведение проекций
Произведение проекций, как правило, не является проекцией, даже если они ортогональны. Если две проекции коммутируют, то их произведение является проекцией, но обратное неверно: произведение двух некоммутирующих проекций может быть проекцией.
Если две ортогональные проекции коммутируют, то их произведение является ортогональной проекцией. Если продукт двух ортогональных проекций является ортогональным проектором, то эти два ортогональных проектора коммутируют (в более общем смысле: два самосопряженных эндоморфизма коммутируют тогда и только тогда, когда их произведение самосопряжено).
Ортогональные проекции
Когда векторное пространство W { displaystyle W}






- ⟨x, P y⟩ = ⟨P x, P y P = ⟨P x, y⟩ { displaystyle langle x, Py rangle = langle Px, Py rangle = langle Px, y rangle}
.
Проекция ортогональна тогда и только тогда, когда она самосопряженная. Используя самосопряженные и идемпотентные свойства P { displaystyle P}





- ⟨P x, y — P y⟩ = ⟨P 2 x, y — P y⟩ = ⟨P x, P (I — П) y⟩ знак равно ⟨п Икс, (п — п 2) y⟩ знак равно 0 { displaystyle langle Px, y-Py rangle = langle P ^ {2} x, y-Py rangle = langle Px, P (IP) y rangle = langle Px, (PP ^ {2}) y rangle = 0 ,}
где ⟨⋅, ⋅⟩ { displaystyle langle cdot, cdot rangle}




- ⟨x, P y⟩ = ⟨P x, y⟩ = ⟨Икс, P * Y⟩ { Displaystyle langle x, Py rangle = langle Px, y rangle = langle x, P ^ {*} y rangle}
для каждого x { displaystyle x}



-
Доказательство существования Пусть H { displaystyle H}
будет полным метрическим пространством с внутренний продукт, и пусть U { displaystyle U}
будет замкнутым линейным подпространством из H { displaystyle H}
(а значит, и полный).
Для каждого x { displaystyle x}
следующий набор неотрицательных норм {‖ x — u ‖ | u ∈ U} { displaystyle { | xu || u in U }}
имеет нижнюю границу , а из-за полноты U { displaystyle U}
это минимум. Мы определяем P x { displaystyle Px}
как точку в U { displaystyle U}
, где достигается этот минимум.
Очевидно, P x { displaystyle Px}
находится в U { displaystyle U}
. Осталось показать, что P x { displaystyle Px}
удовлетворяет ⟨x — P x, P x⟩ = 0 { displaystyle langle x-Px, Px rangle = 0 }
и что это линейно.
Определим a = x — P x { displaystyle a = x-Px}
. Для каждого ненулевого v { displaystyle v}
в U { displaystyle U}
выполняется следующее:
- ‖ a — ⟨a, v⟩ ‖ v ‖ 2 v ‖ 2 знак равно ‖ a ‖ 2 — ⟨a, v⟩ 2 ‖ v ‖ 2 { displaystyle | a — { frac { langle a, v rangle} { | v | ^ {2}}} v | ^ {2} = | a | ^ {2} — { frac {{ langle a, v rangle} ^ {2}} { | v | ^ { 2}}}}
Определив w = P x + ⟨a, v⟩ ‖ v ‖ 2 v { displaystyle w = Px + { frac { langle a, v rangle} { | v | ^ {2}}} v}
мы видим, что ‖ x — w ‖ < ‖ x − P x ‖ {displaystyle |x-w|<|x-Px|}
, если ⟨a, v⟩ { displaystyle langle a, v rangle}
исчезает. Поскольку P x { displaystyle Px}
был выбран как минимум из вышеупомянутого набора, следует, что ⟨a, v⟩ { displaystyle langle a, v rangle}
действительно исчезает. В частности, (для y = P x { displaystyle y = Px}
): ⟨x — P x, P x⟩ = 0 { displaystyle langle x-Px, Px rangle = 0}
.
Линейность следует из исчезновения ⟨x — P x, v⟩ { displaystyle langle x-Px, v rangle}
для каждого v ∈ U { displaystyle v in U}
:
- ⟨(x + y) — P (x + y), v⟩ = 0 { displaystyle langle left (x + y right) -P left (Икс + Y справа), v rangle = 0}
- ⟨(x — P x) + (y — P y), v⟩ = 0 { displaystyle langle left (x-Px right) + left (y-Py right), v rangle = 0}
Взяв разность между уравнениями, мы имеем
- ⟨P x + P y — P (x + y), v⟩ = 0 { displaystyle langle Px + Py-P left (x + y right), v rangle = 0}
Но поскольку мы можем выбрать v = P x + P y — P (x + y) { displaystyle v = Px + Py-P (x + y)}
(как в U { displaystyle U}
) следует, что П Икс + Р Y знак равно п (Икс + Y) { Displaystyle Px + Py = P (x + y)}
. Точно так же у нас есть λ п Икс = P (λ x) { displaystyle lambda Px = P ( lambda x)}
для каждого scalar λ { displaystyle lambda}
.
- ‖ a — ⟨a, v⟩ ‖ v ‖ 2 v ‖ 2 знак равно ‖ a ‖ 2 — ⟨a, v⟩ 2 ‖ v ‖ 2 { displaystyle | a — { frac { langle a, v rangle} { | v | ^ {2}}} v | ^ {2} = | a | ^ {2} — { frac {{ langle a, v rangle} ^ {2}} { | v | ^ { 2}}}}
Свойства и особые случаи
Ортогональная проекция — это ограниченный оператор. Это связано с тем, что для каждого v { displaystyle v}
- ‖ P v ‖ 2 = ⟨P v, P v ⟩ Знак равно ⟨п v, v⟩ ≤ ‖ п v ‖ ⋅ ‖ v ‖ { displaystyle | Pv | ^ {2} = langle Pv, Pv rangle = langle Pv, v rangle leq | Pv | cdot | v |}
Таким образом, ‖ P v ‖ ≤ ‖ v ‖ { displaystyle | Pv | leq | v |}
Для конечномерных комплексных или вещественных векторных пространств стандартный внутренний продукт можно заменить на ⟨⋅, ⋅⟩ { displaystyle langle cdot, cdot rangle}
Формулы
Простые случай возникает, когда ортогональная проекция находится на прямой. Если u { displaystyle u}
- P u = uu T. { displaystyle P_ {u} = uu ^ { mathrm {T}}.}
(Если u { displaystyle u}



- P ux = uu T x ∥ + uu T x ⊥ = u (sign (u T x ∥) ‖ x ∥ ‖) + u ⋅ 0 = x ∥ { displaystyle P_ {u} x = uu ^ { mathrm {T}} x _ { parallel} + uu ^ { mathrm {T}} x _ { perp} = u left ( mathrm {sign} (u ^ { mathrm {T}} x _ { parallel}) | x _ { parallel} | right) + u cdot 0 = x _ { parallel}}
по свойствам точечного произведения параллельного и перпендикулярного векторов.
Эту формулу можно обобщить на ортогональные проекции на подпространство произвольной размерности. Пусть u 1,…, uk { displaystyle u_ {1}, ldots, u_ {k}}





- PA = AAT { displaystyle P_ {A} = AA ^ { mathrm {T}}}
, который можно переписать как
- PA = ∑ i ⟨ui, ⋅ ⟩ Ui. { displaystyle P_ {A} = sum _ {i} langle u_ {i}, cdot rangle u_ {i}.}
Матрица AT { displaystyle A ^ { mathrm {T }}}







Условие ортонормальности также может быть отброшенным. Если u 1,…, uk { displaystyle u_ {1}, ldots, u_ {k}}

- PA = A (ATA) — 1 AT. { displaystyle P_ {A} = A (A ^ { mathrm {T}} A) ^ {- 1} A ^ { mathrm {T}}.}
Матрица A { displaystyle A }







В общем случае мы можем иметь произвольную положительно определенную матрицу D { displaystyle D}



- P A = A (A T D A) — 1 A T D. { displaystyle P_ {A} = A (A ^ { mathrm {T}} DA) ^ {- 1} A ^ { mathrm {T}} D.}
Когда создается пространство диапазона проекции по кадру (т. е. количество генераторов превышает его размер) формула для проекции принимает вид: PA = AA + { displaystyle P_ {A} = AA ^ {+ }}

Если [AB] { displaystyle { begin {bmatrix} AB end {bmatrix}}}



- I = [AB] [AB] — 1 [ATBT] — 1 [ATBT] = [AB] ([ATBT ] [AB]) — 1 [ATBT] = [AB] [ATAOOBTB] — 1 [ATBT] = A (ATA) — 1 AT + B (BTB) — 1 BT { displaystyle { begin {выровнено} I = { begin {bmatrix} AB end {bmatrix}} { begin {bmatrix} AB end {bmatrix}} ^ {- 1} { begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix}} ^ {- 1} { begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix}} = { begin {bmatrix} AB end {bmatrix}} left ({ begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix} } { begin {bmatrix} AB end {bmatrix}} right) ^ {- 1} { begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix}} \ = { begin {bmatrix} AB end {bmatrix }} { begin {bmatrix} A ^ { mathrm {T}} AO \ OB ^ { mathrm {T}} B end {bmatrix}} ^ {- 1} { begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix}} \ [4pt] = A (A ^ { mathrm {T}} A) ^ {- 1} A ^ { mathrm {T}} + B (B ^ { mathrm {T}} B) ^ {- 1} B ^ { mathrm {T}} end {align}}}
Если условие ортогональности улучшено до ATWB = ATWTB = 0 { displaystyle A ^ { mathrm {T}} WB = A ^ { mathrm {T}} W ^ { mathrm {T}} B = 0}

- I = [AB] [(ATWA) — 1 AT (BTWB) — 1 BT] W. { displaystyle I = { begin {bmatrix} AB end {bmatrix}} { begin {bmatrix} (A ^ { mathrm {T}} WA) ^ {- 1} A ^ { mathrm {T}} \ (B ^ { mathrm {T}} WB) ^ {- 1} B ^ { mathrm {T}} end {bmatrix}} W.}
Все эти формулы также верны для сложных внутренних пространств продукта при условии, что вместо транспонирования используется сопряженное транспонирование. Более подробную информацию о суммах проекторов можно найти в Banerjee and Roy (2014). Также см. Banerjee (2004) о применении сумм проекторов в основной сферической тригонометрии.
Наклонные проекции
Термин «наклонные проекции» иногда используется для обозначения неортогональных проекций. Эти проекции также используются для представления пространственных фигур на двухмерных чертежах (см. наклонная проекция ), хотя и не так часто, как ортогональные проекции. В то время как для вычисления подобранного значения регрессии обычных наименьших квадратов требуется ортогональная проекция, для вычисления подобранного значения регрессии инструментальных переменных требуется наклонная проекция.
Проекции определяются своим нулевым пространством и базисными векторами, используемыми для характеристики их диапазона (который является дополнением к нулевому пространству). Когда эти базисные векторы ортогональны нулевому пространству, тогда проекция является ортогональной проекцией. Когда эти базисные векторы не ортогональны нулевому пространству, проекция является наклонной проекцией. Пусть векторы u 1,…, uk { displaystyle u_ {1}, ldots, u_ {k}}






- P = A (B T A) — 1 B T. { displaystyle P = A (B ^ { mathrm {T}} A) ^ {- 1} B ^ { mathrm {T}}.}
Это выражение обобщает формулу для ортогональных проекций, приведенную выше.
Поиск проекции с помощью внутреннего продукта
Пусть V { displaystyle V}




- proj V y = y ⋅ ujuj ⋅ ujuj { displaystyle operatorname {proj} _ {V} y = { frac {y cdot u ^ {j}} {u ^ {j} cdot u ^ {j}}} u ^ {j}}
, где j { displaystyle j}








Канонические формы
Любая проекция P = P 2 { displaystyle P = P ^ {2}}



- P = I r ⊕ 0 d — r { displaystyle P = I_ {r} oplus 0_ { dr}}
, где r { displaystyle r}





- P = [1 σ 1 0 0] ⊕ ⋯ ⊕ [1 σ k 0 0] ⊕ я м ⊕ 0 s { displaystyle P = { begin {bmatrix} 1 sigma _ {1} \ 0 0 end {bmatrix}} oplus cdots oplus { begin {bmatrix} 1 sigma _ {k} \ 0 0 end {bmatrix}} oplus I_ {m} oplus 0_ {s}}
.
где σ 1 ≥ σ 2 ≥… ≥ σ k>0 { displaystyle sigma _ {1} geq sigma _ {2} geq ldots geq sigma _ {k}>0}







Проекции на нормированные векторные пространства
Когда основное векторное пространство X { displaystyle X}

Многие из алгебраических результатов, обсужденных выше, переживают переход к этому контексту. Разложение заданной прямой суммы X { displaystyle X}















Однако, в отличие от конечномерного случая, проекции не обязательно должны быть непрерывными в целом. Если подпространство U { displaystyle U}






Обратное также верно с дополнительным предположением. Предположим, что U { displaystyle U}











В приведенном выше аргументе используется предположение, что оба U { displaystyle U}












Applications и другие соображения
Проекции (ортогональные и другие) играют важную роль в алгоритмах для некоторых задач линейной алгебры:
Как указано выше, проекции являются частным случаем идемпотентов. Аналитически ортогональные проекции являются некоммутативными обобщениями характеристики ристические функции. Идемпотенты используются при классификации, например, полупростых алгебр, тогда как теория меры начинается с рассмотрения характеристических функций измеримых множеств. Поэтому, как можно догадаться, проекции очень часто встречаются в контекстных операторных алгебрах. В частности, алгебра фон Неймана порождается ее полной решеткой проекций.
Обобщения
В более общем смысле, если дана карта между нормированными векторными пространствами T: V → W, { displaystyle T двоеточие V to W,}

См. Также
Примечания
Источники
- Банерджи, Судипто; Рой, Аниндия (2014), Линейная алгебра и матричный анализ для статистики, Тексты в статистике (1-е изд.), Чепмен и Холл / CRC, ISBN 978-1420095388
- Данфорд, Нью-Йорк.; Шварц, Дж. Т. (1958). Линейные операторы. Часть I: Общая теория. Interscience.
- Мейер, Карл Д. (2000). Матричный анализ и прикладная линейная алгебра. Общество промышленной и прикладной математики. ISBN 978-0-89871-454-8.

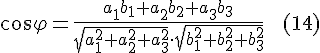
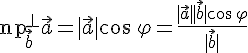










































![{displaystyle {begin{aligned}I&={begin{bmatrix}A&Bend{bmatrix}}{begin{bmatrix}A&Bend{bmatrix}}^{-1}{begin{bmatrix}A^{mathrm {T} }\B^{mathrm {T} }end{bmatrix}}^{-1}{begin{bmatrix}A^{mathrm {T} }\B^{mathrm {T} }end{bmatrix}}\&={begin{bmatrix}A&Bend{bmatrix}}left({begin{bmatrix}A^{mathrm {T} }\B^{mathrm {T} }end{bmatrix}}{begin{bmatrix}A&Bend{bmatrix}}right)^{-1}{begin{bmatrix}A^{mathrm {T} }\B^{mathrm {T} }end{bmatrix}}\&={begin{bmatrix}A&Bend{bmatrix}}{begin{bmatrix}A^{mathrm {T} }A&O\O&B^{mathrm {T} }Bend{bmatrix}}^{-1}{begin{bmatrix}A^{mathrm {T} }\B^{mathrm {T} }end{bmatrix}}\[4pt]&=A(A^{mathrm {T} }A)^{-1}A^{mathrm {T} }+B(B^{mathrm {T} }B)^{-1}B^{mathrm {T} }end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5726c62db8705af0b0cfcba21d9e4c4a3b9c0e03)