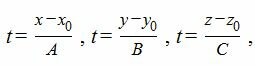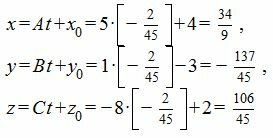На чтение 8 мин Просмотров 3.7к. Опубликовано 04.07.2019
Содержание
- Теоретические материалы
- Предупреждение
- Проекция точки на плоскость − теория, примеры и решения
- Проекция прямой на плоскость
- Угол между прямой и плоскостью
- Теорема о трех перпендикулярах
Теоретические материалы
Глава 9. Прямые и плоскости в пространстве
9.5. Наклонные и их проекции на плоскость. Угол наклонной с плоскостью
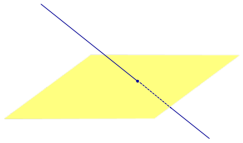
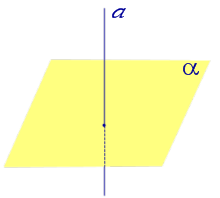
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.
Точка пересечения перпендикуляра (наклонной) с плоскостью называется основанием перпендикуляра (наклонной).
Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных к плоскости из одной и той же точки вне ее, называется проекцией наклонной на эту плоскость.
Если из одной и той же точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше;
3) (обратная) равные наклонные имеют равные проекции;
4) (обратная) большей наклонной соответствует большая проекция.
Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.
Перпендикуляр к плоскости меньше всякой наклонной, проведенной к той же плоскости из той же точки вне ее (катет меньше гипотенузы).
Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на данную плоскость.
Углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.
Угол между наклонной и ее проекцией на плоскость является наименьшим из всех углов, образуемых данной наклонной с прямыми, лежащими в данной плоскости.
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на плоскость − теория, примеры и решения
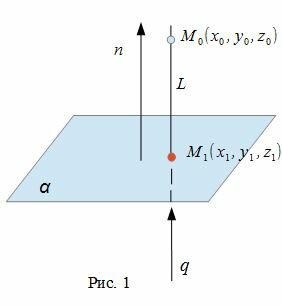
Для нахождения проекции точки M на плоскость α, необходимо:
- построить прямую L, проходящую через точку M и ортогональной плоскости α.
- найти пересечение данной плоскости α с прямой L(Рис.1).
Общее уравнение плоскости имеет вид:
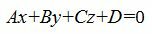 |
(1) |
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M(x, y, z) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
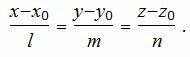 |
(2) |
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M(x, y, z) и ортогональной плоскости (1) имеет следующий вид:
 |
(3) |
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
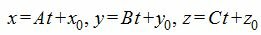 |
(4) |
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
A(At+x)+B(Bt+y)+C(At+z)+D=0,
A 2 t+Ax+B 2 t+By+C 2 t+Cz+D=0,
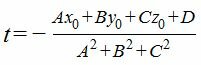 |
(5) |
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M на плоскость (1).
Пример 1. Найти проекцию M1 точки M(4, -3, 2) на плоскость
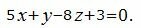 |
(6) |
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M и нормального вектора плоскости в (5), получим:
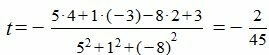 |
(7) |
Из выражений (7) находим:
Проекцией точки M(4, -3, 2) на плоскость (6) является точка:
Проекция прямой на плоскость
Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
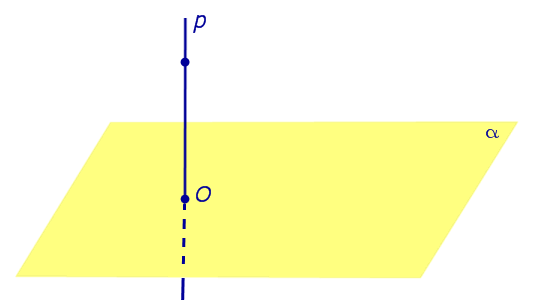
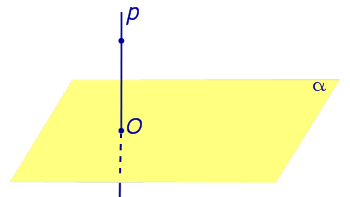
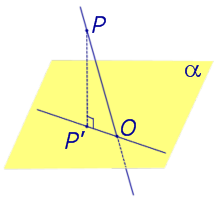
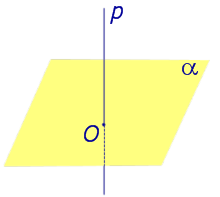
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
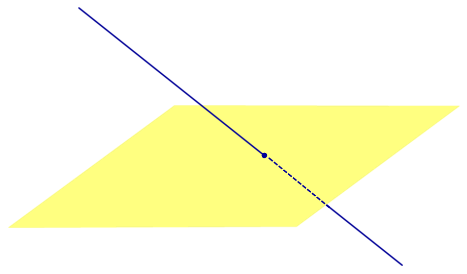
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
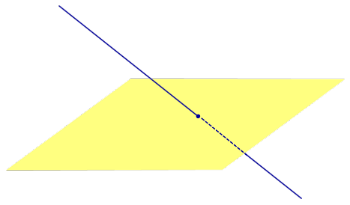
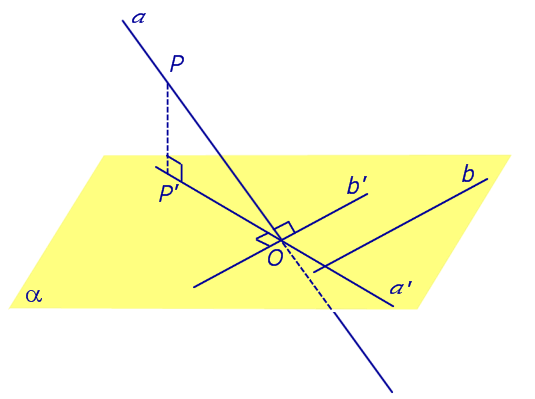
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
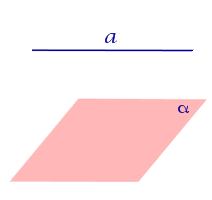
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
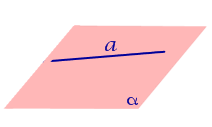
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
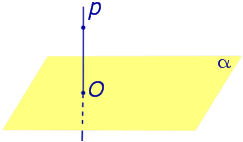
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
Угол между прямой и плоскостью
Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.
| Фигура | Рисунок | Свойство проекции |
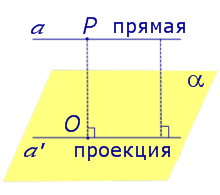
| Наклонная к плоскости α | 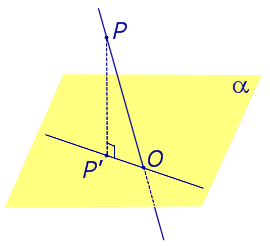 |
|
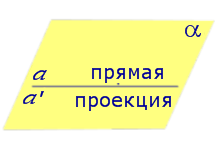
| Прямая, параллельная плоскости | 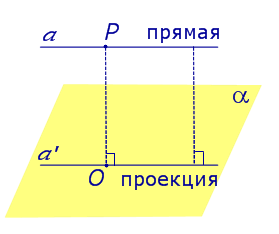 |
|
| Прямая, лежащая на плоскости | 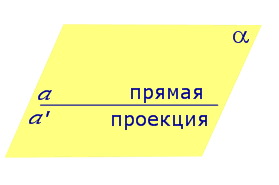 |
|
| Прямая, перпендикулярная к плоскости | 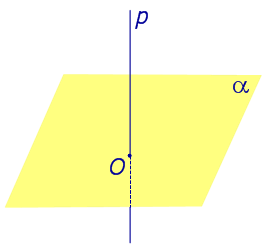 |
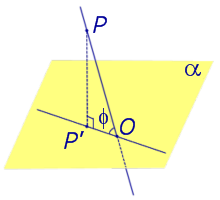
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O. )
На рисунке это угол φ
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( 
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O )
На рисунке это угол φ
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( 
Теорема о трех перпендикулярах
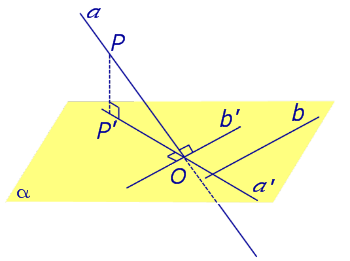
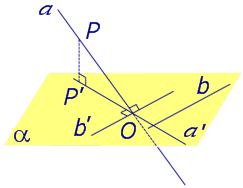
Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a’ на плоскость α перпендикулярна к прямой b.
Доказательство. Рассмотрим следующий рисунок 3.
На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P’ – это проекция точки P на плоскость α. Проведем через точку O прямую b’, параллельную прямой параллельную прямой b. Если прямая b проходит через точку O, то прямая b’, совпадет с прямой b.
Поскольку PP’ – перпендикуляр к плоскости α, то прямая PP’ перпендикулярна к прямой b’. Прямая a перпендикулярна к прямой b’ по условию. Таким образом, прямая b’ перпендикулярна к двум пересекающимся прямым PO и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b’ перпендикулярна к плоскости POP’, откуда вытекает, что прямая b’ перпендикулярна и к прямой a’, лежащей на плоскости POP’.
Теорема, обратная теореме о трех перпендикулярах. Если проекция a’ наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b.
Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.
Прямая a’ перпендикулярна к прямой b по условию обратной теоремы. Прямая PP’ перпендикулярна к прямой b’, поскольку PP’ – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым P’O и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости прямая b’ перпендикулярна к плоскости POP’. Тогда, в частности, прямая b’ перпендикулярна к прямой a, лежащей на плоскости POP’.
| Фигура | Рисунок | Определение |
| Наклонная к плоскости α | 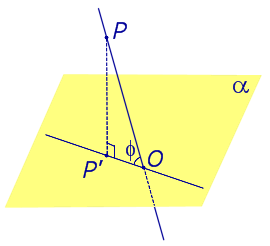 |
|
| Прямая, параллельная плоскости | 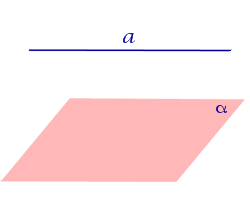 |
|
| Прямая, лежащая на плоскости |  |
|
| Прямая, перпендикулярная к плоскости | 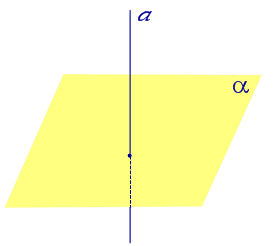 |
§ 10.Перпендикуляр и наклонная к плоскости.
Теорема о трёх перпендикулярах
Отрезок прямой, перпендикулярной данной плоскости, один конец которого принадлежит этой плоскости, а другой — данная точка, называется перпендикуляром, проведённым из данной точки на данную плоскость. Конец этого отрезка, принадлежащий плоскости, называется основанием перпендикуляра. Длина перпендикуляра, опущенного из данной точки на данную плоскость, называется расстоянием от этой точки до данной плоскости.
На рисунке 64 отрезок CD — перпендикуляр, проведённый из точки C на плоскость α, точка D — основание этого перпендикуляра; длина отрезка CD — расстояние от точки C до плоскости α. Это расстояние обозначают: | C, α | = | CD | или ρ(C; α). (Можно сказать, что через точку C проведён перпендикуляр CD к плоскости α или из точки C опущен перпендикуляр CD на плоскость α, или из точки D восставлен перпендикуляр DC к плоскости α.)
Рис. 64
Наклонной, проведённой из данной точки к данной плоскости, называется всякий отрезок, который соединяет данную точку с точкой на плоскости и не является перпендикуляром к этой плоскости. Конец этого отрезка, принадлежащий плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых к плоскости из одной точки, называется ортогональной проекцией наклонной на эту плоскость.
На рисунке 64 отрезок PO — перпендикуляр, проведённый из точки P на плоскость α; отрезок PH — наклонная, проведённая из точки P к плоскости α; отрезок OH — проекция этой наклонной на плоскость α; в плоскости α проведены прямые a и b через основание H наклонной PH.
Докажите самостоятельно следующие утверждения:
если из одной точки, не принадлежащей плоскости, проведены к этой плоскости перпендикуляр и наклонная, то длина наклонной больше длины перпендикуляра;
длина проекции наклонной меньше длины самой наклонной;
длины наклонных, проведённых из одной точки, не принадлежащей плоскости, равны тогда и только тогда, когда равны длины их проекций;
если из одной точки, не принадлежащей плоскости, проведены две наклонные к этой плоскости, то бó́льшей наклонной соответствует бó́льшая проекция. (Сформулируйте обратное утверждение.)
Обратите внимание! Данные утверждения аналогичны соответствующим утверждениям в планиметрии относительно перпендикуляра, наклонной и её проекции на прямую.
Наклонной к плоскости называют также любую прямую, пересекающую плоскость и не перпендикулярную к ней. В таком случае ортогональной проекцией наклонной является прямая. (Подробнее с параллельным проектированием вы познакомитесь в § 12.)
Докажите самостоятельно, что если AM — наклонная к плоскости α, то основания перпендикуляров, проведённых к плоскости α через все точки наклонной AM, принадлежат одной прямой. Эту прямую называют ортогональной проекцией наклонной AM на плоскость α. Доказанное утверждение подсказывает способ построения ортогональной проекции наклонной на данную плоскость.

Дано: AC — наклонная к плоскости α, m — прямая, лежащая в плоскости α, перпендикулярная проекции наклонной AC (рис. 65, а).
Доказать: m ⊥ AC.
Доказательство. Проведём AB ⊥ α (рис. 65, б). Тогда BC — ортогональная проекция наклонной AC на плоскость α. Рассмотрим прямую m и плоскость ABC. Имеем: m ⊥ BC (по условию) и m ⊥ AB (так как AB ⊥ α), т. е. прямая m перпендикулярна двум пересекающимся прямым плоскости ABC. Тогда по признаку перпендикулярности прямой и плоскости прямая m перпендикулярна самой плоскости ABC, а следовательно, и прямой AC, лежащей в этой плоскости. Теорема доказана. ▼
Справедлива и обратная теорема.

Дано: AC — наклонная к плоскости α, m — прямая плоскости α, перпендикулярная AC (рис. 65).
Доказать: m ⊥ BC (проекция наклонной AC).
Рис. 65
Доказательство. Проведём AB ⊥ α. Тогда BC — ортогональная проекция наклонной AC на плоскость α. Рассмотрим прямую m и плоскость ABC. Имеем: m ⊥ AB (так как AB — перпендикуляр к плоскости α) и m ⊥ AC (по условию). Таким образом, прямая m перпендикулярна двум пересекающимся прямым плоскости ABC. Тогда по признаку перпендикулярности прямой и плоскости прямая m перпендикулярна самой плоскости ABC, а следовательно, и прямой BC, лежащей в этой плоскости. Теорема доказана. ▼
Векторное доказательство теорем 16 и 17 проведено в пункте 23.3.
Обе эти теоремы можно объединить одним предложением:
наклонная к плоскости тогда и только тогда перпендикулярна прямой, лежащей в этой плоскости, когда проекция наклонной перпендикулярна данной прямой.
Или, иначе говоря:
для того чтобы проекция наклонной к плоскости была перпендикулярна прямой, лежащей в этой плоскости, необходимо и достаточно, чтобы сама наклонная была перпендикулярна данной прямой.
Придумайте ещё несколько аналогичных формулировок теоремы о трёх перпендикулярах и заодно подумайте: что это за «три перпендикуляра».
Заметим, что теорема о трёх перпендикулярах позволяет построить проекцию наклонной c к плоскости α, не опуская на эту плоскость перпендикуляра, если в плоскости α дана прямая b, перпендикулярная наклонной c. В таком случае достаточно через основание наклонной провести в плоскости α прямую a, перпендикулярную прямой b. Прямая a является искомой проекцией наклонной c на плоскость α. Этот приём часто используется при решении задач.
Рис. 66

Решение. Имеем BP ⊥ (ABC) ⇒ BP ⊥ AC. Кроме того, AC ⊥ BC (∠ ACB = 90°). Следовательно, по признаку перпендикулярности прямой и плоскости AC ⊥ (BCP). Тогда AC ⊥ BK. А так как KE ‖ AC и AC ⊥ BK, то KE ⊥ BK. Это означает, что ∠ BKE = 90°, т. е. ⧌ BKE — прямоугольный.
Рис. 67
ЗадаЧа 3.069. Через вершину прямого угла равнобедренного прямоугольного треугольника ABC проведена прямая CM, перпендикулярная его плоскости. Найти расстояние от точки M до прямой AB, если AC = 4 см, CM = 
Решение. Пусть точка K — середина гипотенузы AB треугольника ABC (рис. 67). Так как AC = CB, то CK ⊥ AB, и по теореме о трёх перпендикулярах отрезок MK перпендикулярен AB. Это означает, что длина отрезка MK — искомое расстояние от точки M до прямой AB.
Далее, так как MC ⊥ (ABC), то MC ⊥ CK (по определению прямой, перпендикулярной плоскости). Поэтому ⧌ MCK — прямоугольный, значит, MK2 = MC2 + CK2.
Так как ⧌ ABC — равнобедренный прямоугольный (∠ C = 90°) и CK — его медиана, то ⧌ CBK — равнобедренный прямоугольный (∠ K = 90°). Тогда CK2 = 

Перпендикуляр и наклонная
Урок геометрии в 10 классе

На одном из предыдущих уроков вы познакомились с понятием проекции точки на данную плоскость параллельно данной прямой.
На этом уроке вы продолжите изучение прямых и плоскостей; узнаете, как находится угол между прямой и плоскостью. Вы познакомитесь с понятием ортогональной проекции на плоскость и рассмотрите ее свойства. На уроке будут даны определения расстояния от точки до плоскости и от точки до прямой, угла между прямой и плоскостью. Будет доказана знаменитая теорема о трех перпендикулярах.
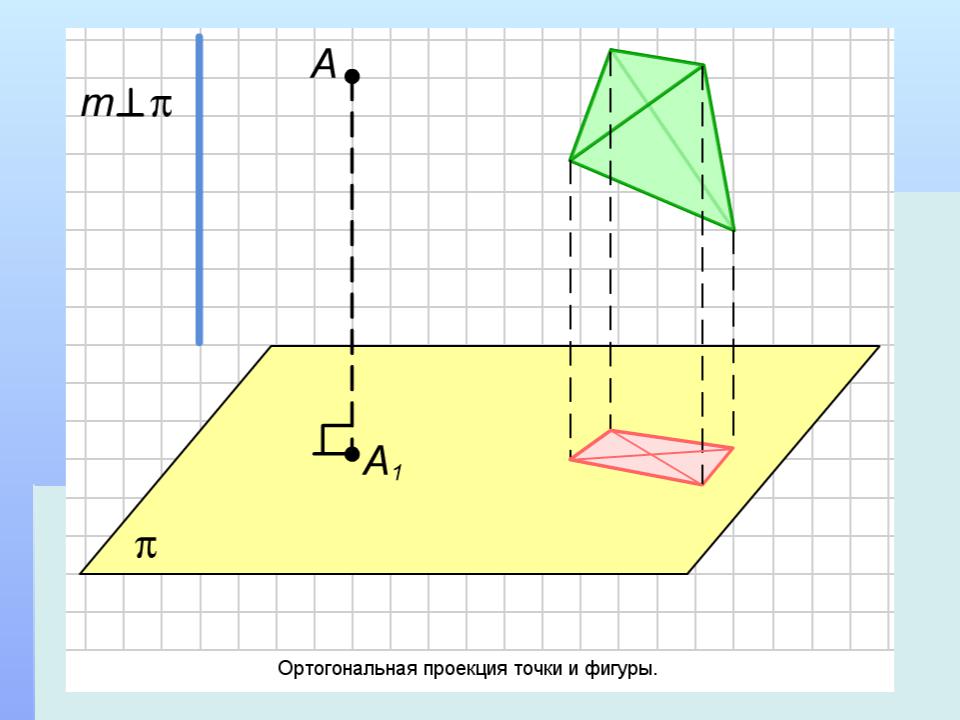
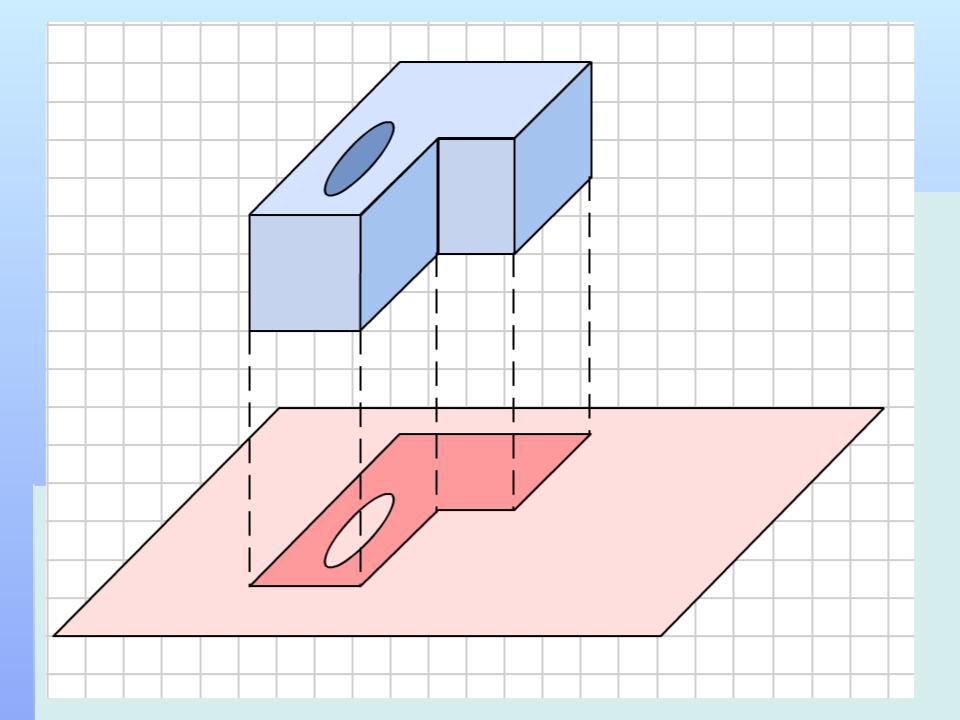
Ортогональная проекция
Ортогональная проекция точки и фигуры.
Ортогональная проекция детали.
Ортогональной проекцией точки А на данную плоскость называется проекция точки на эту плоскость параллельно
прямой, перпендикулярной этой плоскости. Ортогональная проекция
фигуры на данную плоскость p состоит из ортогональных проекций на плоскость p всех точек этой фигуры. Ортогональная проекция часто используется для изображения пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистическое изображение, чем произвольная параллельная проекция, особенно круглых тел.
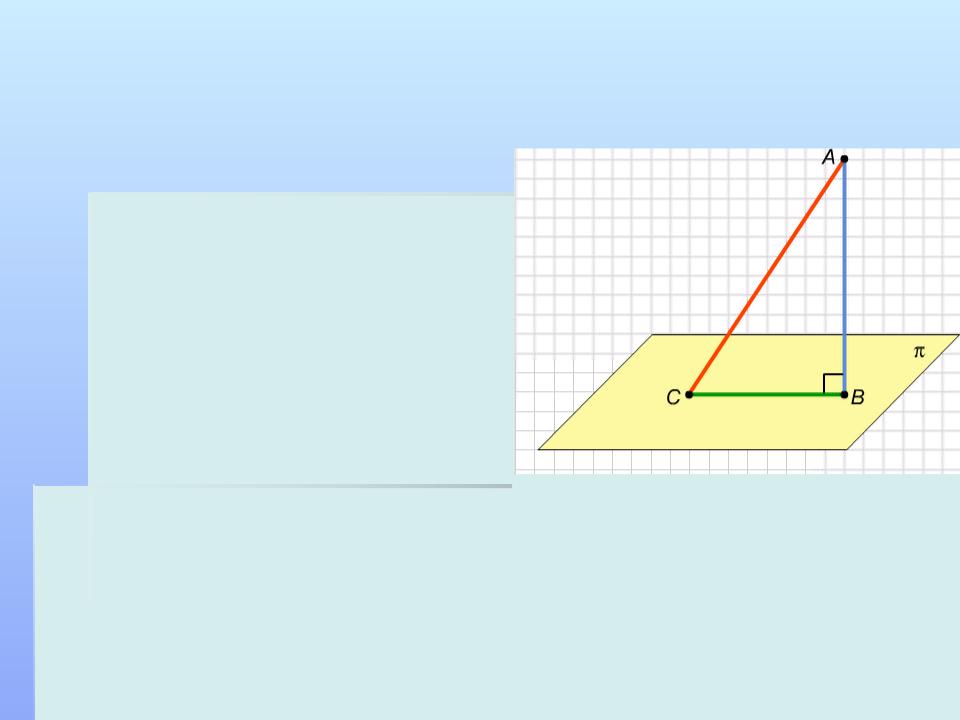
Перпендикуляр и наклонная
Пусть через точку А, не принадлежащую плоскости p, проведена прямая, перпендикулярная этой плоскости и пересекающая ее в точке В. Тогда
отрезок АВ называется
перпендикуляром, опущенным из точки
А на эту плоскость, а сама точка В — основанием этого перпендикуляра. Любой отрезок АС, где С —
произвольная точка плоскости p, отличная от В, называется наклонной к
этой плоскости.
Заметим, что точка В в этом определении является ортогональной
проекцией точки А, а отрезок АС — Перпендикуляр и наклонная. ортогональной проекцией наклонной AВ.
Ортогональные проекции обладают всеми свойствами обычных параллельных проекций, но имеют и ряд новых свойств.

Свойства ортогональной проекции
Пусть из одной точки к плоскости проведены перпендикуляр и несколько наклонных. Тогда справедливы следующие утверждения.
1. Любая наклонная длиннее как перпендикуляра, так и ортогональной проекции наклонной на эту плоскость.
2. Равные наклонные имеют и равные ортогональные проекции, и наоборот, наклонные, имеющие равные проекции, также равны.
3. Одна наклонная длиннее другой тогда и только тогда, когда ортогональная проекция первой наклонной длиннее ортогональной проекции второй наклонной.
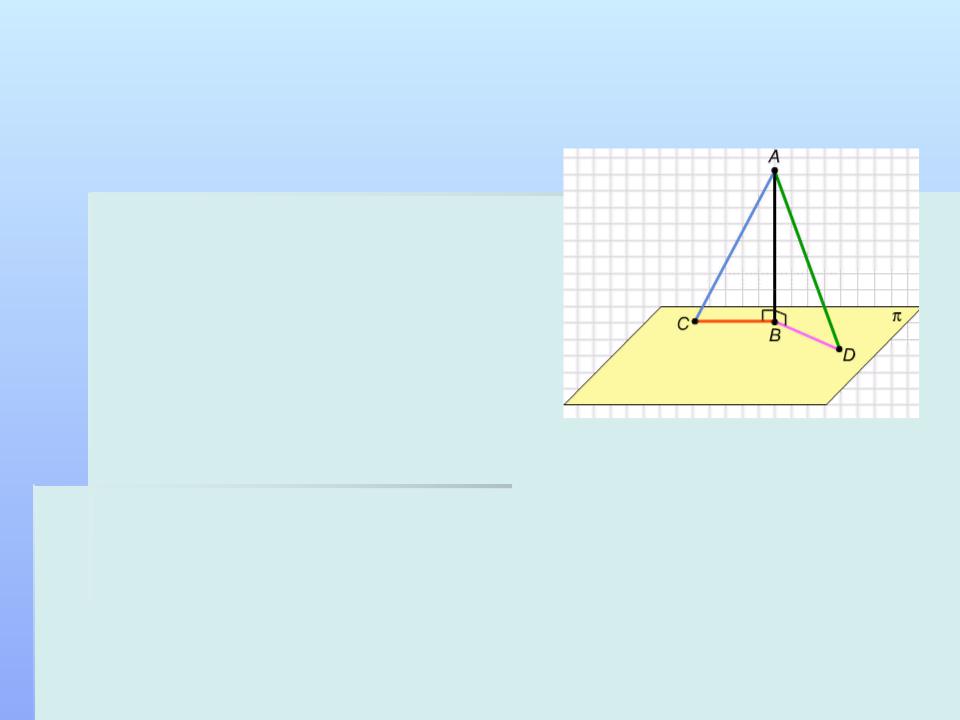
Свойства ортогональной проекции
Доказательство.
Пусть из точки А к плоскости p проведены перпендикуляр АВ и две наклонные АС и AD; тогда отрезки ВС и BD — ортогональные проекции этих отрезков на плоскость p.
Докажем первое утверждение: любая наклонная длиннее как перпендикуляра, так и ортогональной проекции наклонной на эту плоскость. Рассмотрим, например, наклонную AС и треугольник ABC, образованный перпендикуляром AВ, этой наклонной AС, и ее ортогональной проекцией ВС. Этот треугольник прямоугольный с прямым углом в вершине В и гипотенузой AС, которая, как мы знаем из планиметрии, длиннее каждого из катетов, т.е. и перпендикуляра AВ, и проекции ВС.
Из точки А к плоскости pi проведены перпендикуляр АВ и две наклонные AC и AD.
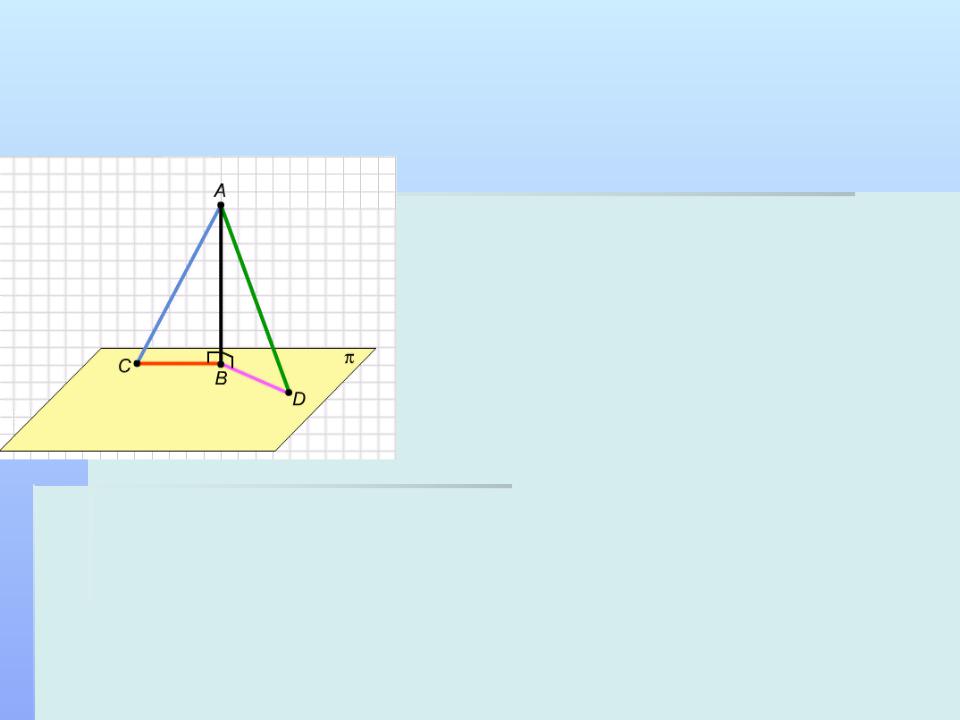
Свойства ортогональной проекции
Треугольники
ABC и ABD
равны по катету и гипотенузе.
Теперь докажем второе утверждение, а именно: равные наклонные имеют и равные ортогональные проекции, и наоборот, наклонные, имеющие равные проекции, также равны.
Рассмотрим прямоугольные треугольники AВС и ABD. Они
имеют общий катет AВ. Если наклонные AС и AD равны, то прямоугольные треугольники AВС и AВD равны по катету и гипотенузе, и тогда BC=BD. Обратно, если равны проекции ВС и BD, то эти же треугольники равны по двум катетам, и тогда у них равны и гипотенузы AС и AD.

Свойства ортогональной проекции
Докажем третье утверждение: одна наклонная длиннее другой тогда и только тогда, когда ортогональная проекция первой наклонной длиннее ортогональной проекции второй наклонной. Пусть, например, ВС > BD.
Отложим на отрезке ВС точку Е такую, что BD=BE. Тогда и AD=AE. В
треугольнике АСЕ угол AEC тупой и поэтому больше угла ACE, следовательно, сторона АС больше стороны АЕ, равной AD.
Обратно, пусть АС > AD. Возможны три случая: a) BC=BD; б) ВС < BD; с) ВС > BD. Если BC=BD, то по доказанному выше в пункте 2, AC=AD, что
противоречит условию. Если ВС < BD, как мы только что доказали, АС < AD, что опять противоречит условию.
Остается третья возможность: ВС > BD. Теорема доказана.
Если ВС больше BD,
то АС больше стороны
АЕ, равной AD.
Стереометрия
Глава 9. Прямые и плоскости в пространстве
9.5. Наклонные и их проекции на плоскость. Угол наклонной с плоскостью
Определение 1
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.
Определение 2
Точка пересечения перпендикуляра (наклонной) с плоскостью называется основанием перпендикуляра (наклонной).
Определение 3
Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных к плоскости из одной и той же точки вне ее, называется проекцией наклонной на эту плоскость.
Если из одной и той же точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше;
3) (обратная) равные наклонные имеют равные проекции;
4) (обратная) большей наклонной соответствует большая проекция.
Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.
Следствие
Перпендикуляр к плоскости меньше всякой наклонной, проведенной к той же плоскости из той же точки вне ее (катет меньше гипотенузы).
Определение 4
Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на данную плоскость.
Определение 5
Углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.
Теорема 5
Угол между наклонной и ее проекцией на плоскость является наименьшим из всех углов, образуемых данной наклонной с прямыми, лежащими в данной плоскости.
Пользуйтесь нашим приложением
Мы используем файлы cookie. Пользуясь сайтом, вы принимаете условия нашего соглашения. Принять Детальнее