Определение. Два множества F
и G векторов евклидова
пространства E
называются ортогональными, если каждый
вектор из F ортогонален
каждому вектору из G.
Определение. Пусть F
– подпространство E.
Совокупность всех векторов подпространства
E, ортогональных
подпространству F,
называется ортогональным дополнением
подпространства F.
Всякое ортогональное дополнение
является, в свою очередь, линейным
подпространством.
Всякое произвольное евклидово пространство
E разлагается в прямую
сумму своего произвольного подпространства
F и его ортогонального
дополнения
Примеры
1. Требуется найти базис ортогонального
дополнения
подпространства L,
натянутого на векторы
,
,

Будем считать, что базис, относительно
которого заданы векторы, ортонормированный.
По определению, если
,
то
.
Далее, каждый вектор
из
должен быть ортогонален к
.
Для этого достаточно, чтобы
.
Расписывая скалярные произведения,
получим три уравнения относительно
координат
вектора
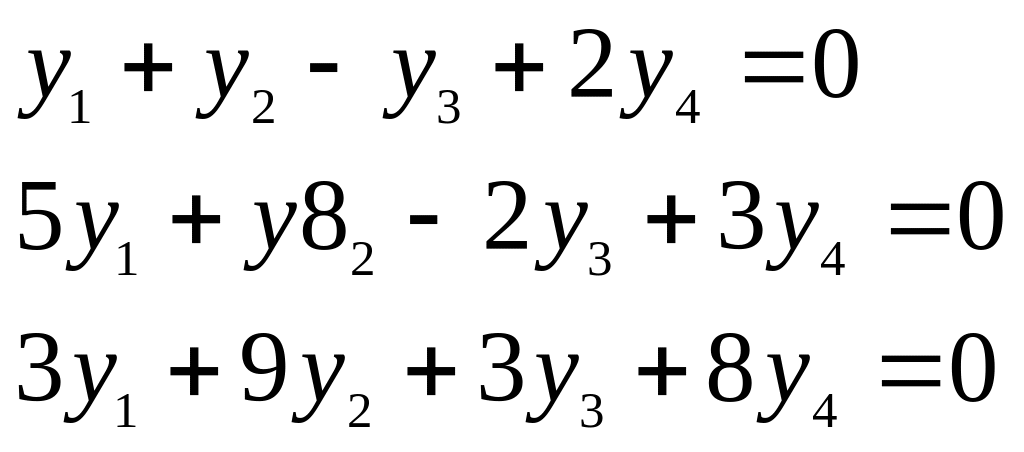
Совокупность решений этой системы и
образует ортогональное дополнение. За
базис в
можно принять любую фундаментальную
систему решений. Например, вектор
.
2. Линейное подпространство
задано уравнениями
Требуется найти уравнения, которые
задают ортогональное дополнение
.
Пусть
,
.
Тогда
.
Этому условию удовлетворяют два линейно
независимых вектора
и
,
которые образуют коэффициенты системы
уравнений, задающей F.
Далее,
.
Ранг системы равен 2. Значит
и, так как
,
то
.
Поэтому найденные векторы можно принять
за базис в
,
и
есть линейная оболочка данных векторов.
Далее задача решается так же как в
примере из § 3. Дословно повторяя решение,
получим следующую систему уравнений
которая и задает
.
5.3. Проектирование вектора на подпространства
Пусть
.
Тогда всякий вектор
можно представить в виде
,
где
и
.
Вектор
называется ортогональной проекцией
вектора x на
подпространство L, а
вектор
называется ортогональной составляющей
вектора
.
Пусть
и
— расстояние между векторами
,
тогда
Таким образом, ортогональная проекция
есть ближайший к
вектору подпространства L.
Часто используются следующие обозначения
,
.
Укажем в заключение как вычисляются
координаты вектора
.
Пусть
— базис в L. Так как
,
то
.
Поэтому
Отсюда имеем, что в случае ортонормированного
базиса
Примеры
1. Найти ортогональную проекцию
и ортогональную составляющую
вектора
на линейное подпространство L,
натянутое на векторы
.
Все векторы заданы координатами
относительно ортонормированного базиса.
,
,
,

Нетрудно убедиться, что
и что за базис можно принять векторы
и
.
Нам будет удобно перейти к ортонормированному
базису в L. Применяя
процедуру ортогонализации к векторам
и
,
получим ортонормированный базис в L:
,
Заметьте, что векторы
и
линейно выражаются через
и
и, значит, также принадлежат L.
Имеем теперь

2. Требуется найти расстояние от точки,
заданной вектором
до плоскости (линейного многообразия),
заданной системой уравнений
Расстояние между точкой
и множеством L
определится следующим образом
Для вычисления расстояния удобно перейти
к параметрическому уравнению плоскости.
Имеем
и поэтому всякий вектор
представляется в виде
где
— фиксированный радиус-вектор точки
плоскости;
и
— базис направляющего линейного
подпространства, которое задается
соответствующей однородной системой.
Решая уравнение, получим, например,
,
,

Затем
Векторы
и
принадлежат направляющему подпространству
M плоскости L.
Вектор
.
Так как
,
а
,
то
Правая часть этого неравенства и есть
искомое расстояние. Осталось вычислить
вектор
и найти его норму. Проделав для этого
аналогичные вычисления и вычислив длину
вектора, получим, что
.
3. Пусть
— ортонормированная система векторов
евклидова пространства En.
Нужно доказать, что для любого вектора
имеет место неравенство Бесселя
с равенством тогда и только тогда, когда
,
т.е. векторы
образуют ортонормированный базис в En.
Так как
— ортонормированная система, то ее
всегда можно векторами
достроить до ортонормированного базиса
в En.
Разложим вектор
по этому базису. Имеем
Далее,
или
С равенством тогда и только тогда, когда
.
Исключение составляют случаи, когда
или когда
принадлежит линейной оболочке векторов
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
В процессе решения системы уравнений Вы как-то её преобразовывали, при этом выяснялось, что некоторые уравнения являются линейными комбинациями остальных (или, как частный случай, сводятся к
|
||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
Хорошо. Посмотрите на матрицу системы как на два вектора (записанных в строку): Так как векторы Увидите — напишите «увидел».
|
||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
Да, увидел!
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
|||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
Решая эту систему у меня получились довольно странные и неприятные числа, но вроде бы правильные!
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
Вы пока получите эти два вектора (можно вынести Система уравнений, данная в задаче, определяет подпространство Мы нашли базис Получаем систему Теперь находим
|
||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
|||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
Да, в решении все понятно, огромное спасибо! Теперь проверим, что решение правильное. Значит, все правильно! Огромное спасибо за помощь и столь развернутое и понятное объяснение!
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
Рад был помочь. Выберите тот способ из описанных, который Вам больше всего понравился, и примените его к правильным данным.
|
||
|
|
|||
|
eco_fan |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/10/15 |
Как вы нашли векторы этой системы? Можете подробно расписать я имею ввиду векторы (0,-1,1,0),(-5, 7, 0,1)
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Пусть L – подпространство евклидового или унитарного пространства V. Тогда «XÎV $X0ÎL Ù $X^ÎL^ (причем единственные), такие что X = X0 + X^, X0 – Называется ортогональной проекцией вектора Х на подпространство L. X^ – Называется ортогональной составляющей вектора Х на подпространство L. Расстоянием Между двумя множествами M1 и M2 Называется кратчайшее из расстояний между элементами M1 и M2: r(M1, M2) = .
; r2(X, Y) = |X – Y|2 =
= |X – X0|2 + |X0 – Y|2 ³ ³ | X – X0 |2 = | X^ |2, где YÎL, т. е. Расстоянием между вектором и подпространством является длина его ортогональной составляющей. Для евклидового пространства углом между вектором Х и подпространством L Называется угол jÎ[0, p] такой, что
.
Преобразовав 
Рассмотрим – ортогональный базис в подпространстве L:
«XÎV X = X0 + X^ = a1E1 + a1E1 + … + aKEk + X^.
Умножим скалярно обе части равенства на Ei:
, т. е.

| < Предыдущая | Следующая > |
|---|
$begingroup$
The title could include «subpace with more than one base vector», because that’s what I’m having trouble with.
Say we have our subspace that is spanned by ${(1, 0 ,1),(1, 1, -1)} $ and we have the vector $(1, 2, 3)$. The subspace is already orthogonal, how do I find the orthogonal projection of the vector on the subspace?
Bernard
173k10 gold badges66 silver badges166 bronze badges
asked Feb 7, 2015 at 18:54
$endgroup$
$begingroup$
There is a general answer to this question that doesn’t depend on the vectors being given as orthogonal. Consider the orthogonal projection onto the span of ${ a_1,a_2,dots,a_n }$. Define $A$ to be the matrix whose $i$th column is $a_i$. Then the projection is the vector $Ax$ such that $Ax-b$ is orthogonal to $Ay$ for every vector $y$. That means:
$$y^T A^T (A x — b) = 0$$
for every vector $y$. It is not too hard to show that this implies $A^T (Ax — b)=0$, i.e. $A^T A x = A^T b$. The solution to this system is $x=(A^T A)^{-1} A^T b$, and the projection itself is $Ax=A (A^T A)^{-1} A^T b$.
When the columns of $A$ are orthonormal (meaning that they are orthogonal and have length $1$), $A^T A = I_n$, which makes the formula nicer: the projection is just $A A^T b$.
answered Feb 7, 2015 at 20:09
IanIan
99.1k4 gold badges83 silver badges148 bronze badges
$endgroup$
$begingroup$
The subspace is spanned by every vectors $vec v = a(101)+b(11-1)$. Now you want to know how much parallel is the vector $(123)$ to this subspace. Assuming that $(123) = a(101)+b(11-1)+c vec w$ with another «unimportant» vector $vec w$ that completes the orthonormal Basis.
Now take the scalar product with $(101)$ and you will see that $vec w (101) = 0,(11-1)(101) = 0$ due to orthogonality. Then you get $a$.
Multiplication with $(11-1)$ and $vec w (11-1) = 0$ will lead to the coefficient $b$.
answered Feb 7, 2015 at 19:07
kryomaximkryomaxim
2,8141 gold badge12 silver badges26 bronze badges
$endgroup$
1
$begingroup$
There is a formula for the projection on a subspace $E$ when it has an orthogonal basis (which is used in the Gram-Schmidt algorithm to find orthonormal bases: if $(u_1, dots, u_r)$ is such an othogonal basis, the projection of a vector $v$ onto $E,$ is:
$$operatorname{pr}_{_E} v=sum_{i=1}^r frac{langle u_i,vrangle}{langle u_i,u_irangle},u_i$$
Here, you obtain $operatorname{pr}_{_E} v=(2,0,2)$.
answered Feb 7, 2015 at 20:23
BernardBernard
173k10 gold badges66 silver badges166 bronze badges
$endgroup$
1
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.


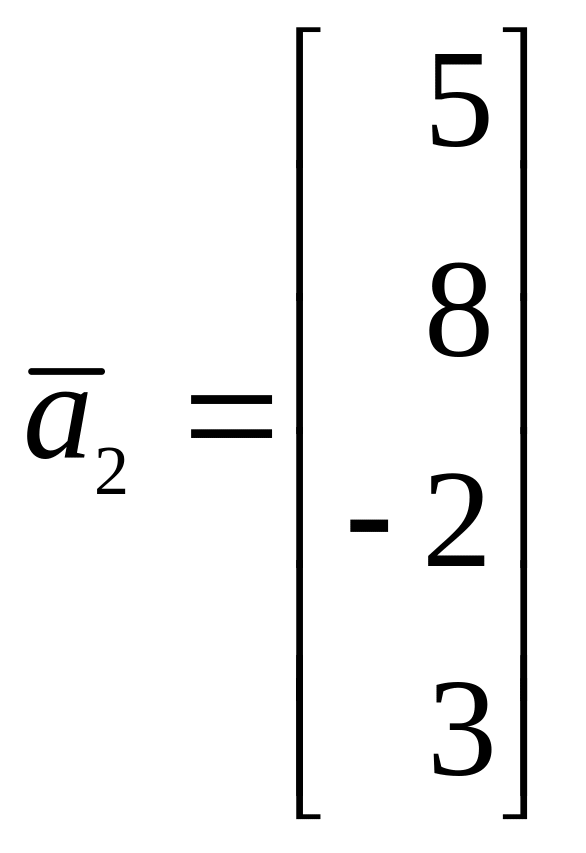
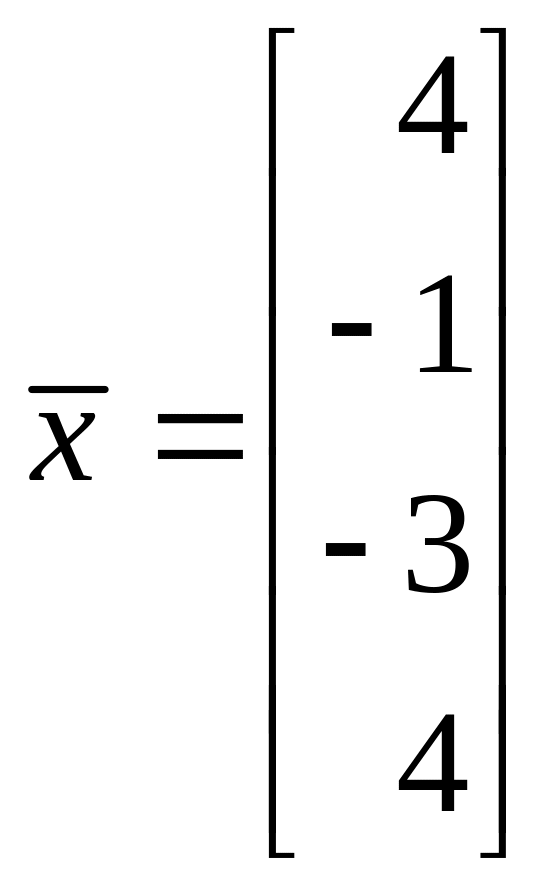
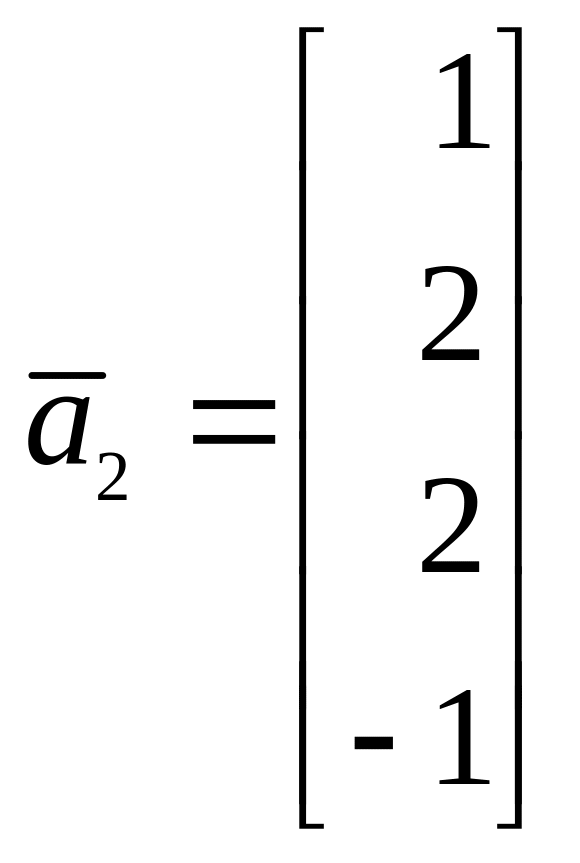
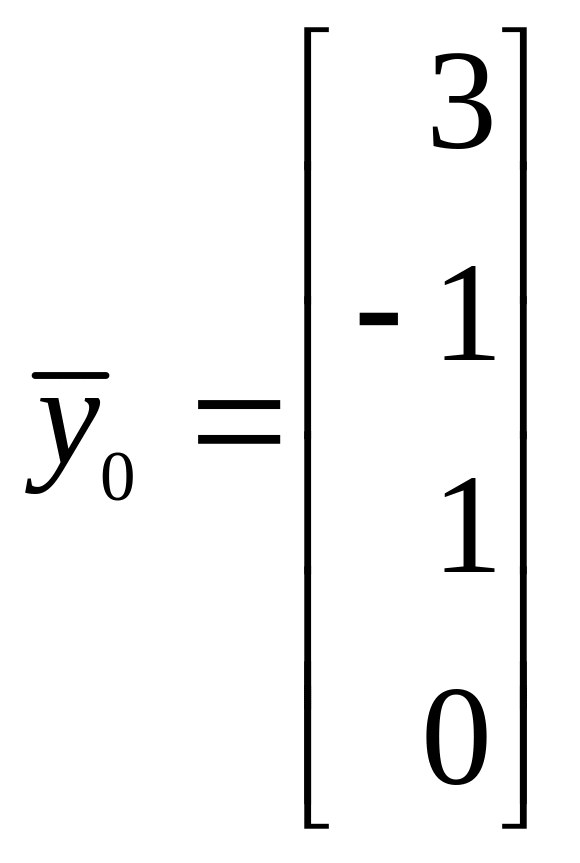

 ). Такие уравнения Вы выбрасывали. Приведите, пожалуйста, конечный вид системы после этих преобразований.
). Такие уравнения Вы выбрасывали. Приведите, пожалуйста, конечный вид системы после этих преобразований.
 .
.
 удовлетворяют системе, то
удовлетворяют системе, то 




 то ответ получается совсем некрасивым… Так и должно быть?
то ответ получается совсем некрасивым… Так и должно быть? за вектор, чтоб не было знаменателей).
за вектор, чтоб не было знаменателей). , к которому
, к которому  является ортогональным дополнением. Надо представить
является ортогональным дополнением. Надо представить  , где
, где  .
. и
и  . Так как
. Так как  , то
, то  , поэтому
, поэтому




 и
и  .
.

 .
. 



