Ортогональные векторы и условие ортогональности
В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.
Ортогональные векторы: определение и условие
Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .
Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.
Примеры решения задач на ортогональность векторов
Плоские задачи на ортогональность векторов
Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:
a ¯ × b ¯ = a x × b x + a y × b y = 0
Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; — 1 >ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) = 2 — 2 = 0
Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.
Задача 2. Докажем, что векторы a ¯ = < 3 ; — 1 >и b ¯ = < 7 ; 5 >ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 3 × 7 + ( — 1 ) × 5 = 21 — 5 = 16
Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.
Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.
Как решить?
Найдем скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = — 4 n = — 2
Ответ: векторы являются ортогональными при значении n = 2 .
Примеры пространственных задач на ортогональность векторов
При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; — 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .
Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; — 1 ; 10 >являются ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0
Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.
Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; — 8 >будут являться ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2
Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .
Ортогональность векторов. Перпендикулярность векторов.
Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).
 |
| рис. 1 |
Примеры задач на ортогональность векторов
Примеры плоских задач на ортогональность векторов
Так в случае плоской задачи для векторов a = < ax ; ay > и b = < bx ; by > , условие ортогональности запишется следующим образом:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16
Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = < ax ; ay ; az > и b = < bx ; by ; bz >, условие ортогональности запишется следующим образом:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 — 8 = 2 n — 4
2 n — 4 = 0
2 n = 4
n = 2
Ответ: вектора a и b будут ортогональны при n = 2.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Угол между векторами. Ортогональные проекции векторов
Угол между векторами
Углом между двумя ненулевыми векторами называется угол между равными им векторами, имеющими общее начало, не превосходящий по величине числа .
Пусть в пространстве даны два ненулевых вектора и (рис.1.22). Построим равные им векторы и . На плоскости, содержащей лучи и , получим два угла . Меньший из них, величина которого не превосходит , принимается за угол между векторами и .
Поскольку направление нулевого вектора не определено, то не определен и угол между двумя векторами, если хотя бы один из них нулевой. Из определения следует, например, что угол между ненулевыми коллинеарными векторами либо равен нулю (если векторы одинаково направлены), либо равен (если векторы противоположно направлены).
Ортогональные проекции векторов
Движение по любой прямой может быть в двух направлениях. Ориентированной прямой называется прямая, на которой выбрано направление, т.е. одно из направлений считается положительным, а противоположное — отрицательным. Для измерения длин отрезков на прямой задается масштабный отрезок, который принимается за единицу.
Ориентированная прямая с заданным масштабным отрезком называется осью.
Любой ненулевой вектор , принадлежащий прямой, называется направляющим вектором для данной прямой, поскольку задает на ней ориентацию. Направление вектора принимается за положительное, а направление противоположного вектора — за отрицательное. Кроме того, длину вектора — можно принять за величину масштабного отрезка на этой прямой. Поэтому можно сказать, что любой ненулевой вектор определяет ось — прямую, содержащую этот вектор, задавая на ней направление и масштабный отрезок.
Ортогональной проекцией вектора на ось, задаваемую вектором , называется его проекция на ось вдоль прямой (или вдоль плоскости), перпендикулярной данной оси. Ортогональную проекцию вектора на ось, задаваемую вектором , будем обозначать .
Ортогональную проекцию вектора на прямую (см. разд. 1.2.2 и рис. 1.13) будем обозначать .
Ортогональную проекцию вектора а на плоскость (см. разд. 1.2.2 и рис. 1.14) будем обозначать .
Разность между вектором и его ортогональной проекцией называют ортогональной составляющей:
— — ортогональная составляющая вектора относительно вектора ;
— — ортогональная составляющая вектора относительно прямой ;
— — ортогональная составляющая вектора относительно плоскости .
На рис. 1.23 изображены ортогональные проекции вектора :
— на прямую (или на ось , задаваемую вектором ) вдоль прямой (рис.1.23,а);
— на прямую (или на ось , задаваемую вектором ) вдоль плоскости (рис.1.23,б);
— на плоскость вдоль прямой (рис.1.23,в).
На рис. 1.23 изображены ортогональные составляющие вектора :
— относительно оси (вектора ): (рис.1.23,а);
— относительно плоскости (рис.1.23,в).
Для ортогональных проекций справедлива следующая теорема (см. теорему 1.1 в разд. 1.5).
Теорема 1.2 (об ортогональных проекциях вектора).
1. Если на плоскости заданы две взаимно перпендикулярные прямые и , то любой вектор на плоскости можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е. (рис. 1.24,а).
2. Если в пространстве заданы три попарно перпендикулярные прямые и , пересекающиеся в одной точке, то любой вектор в пространстве можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е. (рис. 1.24,6).
3. Квадрат длины вектора на плоскости или в пространстве равен сумме квадратов длин своих ортогональных проекций, т.е.
Первые два утверждения представляют собой частные случаи теоремы 1.1. Третье утверждение следует из теоремы Пифагора (для треугольника (рис. 1.24,а) или треугольников и (рис. 1.24,6)).
В формулировке теоремы 1.2 прямые можно заменить осями, задаваемыми попарно ортогональными векторами.
На рис.1.24,а проекции вектора на оси одновременно являются ортогональными составляющими: и . На рис. 1.24,6 вектор является проекцией вектора на плоскость , содержащую прямые и : , а вектор является ортогональной составляющей вектора относительно плоскости .
Алгебраическое значение длины проекции
Пусть – угол между ненулевым вектором и осью, задаваемой вектором , т.е. угол между ненулевыми векторами и .
Алгебраическим значением длины ортогональной проекции вектора на ось, задаваемую вектором , называется длина его ортогональной проекции , взятая с положительным знаком, если угол не превышает , и с отрицательным знаком, если угол больше , т.е.:
Например, для проекций, изображенных на рис. 1.25, 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAE8AAAAVBAMAAAD1D64kAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/cBBpYEhURAxkWFx4MHQtTUEJQAAAVlJREFUKM9jYKAAsBGrkKsATaB5AhZVRUpK+mKoQty3/LCpZDCu3YAqYDiB9QZWq4tBBHsEnO/PwCaNx6X7l8FYcgwMIgwMJlomWhOYnZarNECFmZ3KDMAMOzeogBQDgzwDQ46gZ4s420GRwANQhRsNHB9AWHbOEIWiDAyCDGDFFxuYJKZCTWSWZjAMgOoxUUZWKMTAsLCA6QNIqBWIeQWAZsJcl/IYVWFgAJMCA0No6FpQWDgwOMI9lHId6kYUhQwMJ4D44AGGe3B1YKvZ5MAeBylUnABRCAIHDdhEmZCdyMBwiYFNBkgJTuAWYeAHupEtBBTHiQX94qVgeSNPWDgk8IAiVd7LMYBVUFCBYVMCyFieW55fNEDS+9zgieTOQgOw1ZAY5xC3WQBJZJygkGJfhoikORUMEDeCAbvoTvypVB4a0twK+FPppkcvoTpucDoQl7CnRuOTBQA/mUGNQvQK+QAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, поскольку угол между векторами и острый, a , так как угол между векторами и тупой.
Некоторые свойства проекций векторов переносятся на алгебраические значения их длин, в частности:
1. — алгебраическое значение длины ортогональной проекции суммы векторов равно сумме алгебраических значений длин ортогональных проекций слагаемых;
2. — алгебраическое значение длины ортогональной проекции произведения вектора на число равно произведению этого числа на алгебраическое значение длины ортогональной проекции вектора
1. Из определения алгебраического значения длины ортогональной проекции следует (см. также рис.1.25), что , т.е. алгебраическое значение длины ортогональной проекции ненулевого вектора на ось равна произведению длины этого вектора на косинус угла между вектором и осью.
Ортогональную проекцию вектора на ось, задаваемую вектором , можно представить в виде
Если — единичный вектор, то .
2. Равенство можно использовать как определение косинуса угла между ненулевыми векторами и (или, что то же самое, косинуса угла между осями, заданными ненулевыми векторами и (рис. 1.26)).
3. Углом между ненулевым вектором и прямой называется угол между вектором и его ортогональной проекцией на прямую . Величина угла может быть найдена по формуле
4. Углом между ненулевым вектором и плоскостью называется угол между вектором и его ортогональной проекцией на плоскость . Величина угла может быть найдена по формуле
Пример 1.7. Основания и равнобокой трапеции равны и соответственно; точка — середина стороны (рис. 1.27). Найти алгебраические значения длин ортогональных проекций векторов и на ось, задаваемую вектором .
Решение. Пусть — высота трапеции, — точка пересечения прямых и . По свойству равнобокой трапеции ; из равенства треугольников и .
Обозначим через искомые алгебраические значения длин ортогональных проекций.Тогда из равенств
и свойства 1 алгебраических значений длин проекций следует:
http://ru.onlinemschool.com/math/library/vector/orthogonality/
http://mathhelpplanet.com/static.php?p=ugol-mezhdu-vektorami-i-ortogonalnye-proektsii-vektorov
Угол между векторами. Ортогональные проекции векторов
Угол между векторами
Углом между двумя ненулевыми векторами называется угол между равными им векторами, имеющими общее начало, не превосходящий по величине числа .
Пусть в пространстве даны два ненулевых вектора и
(рис.1.22). Построим равные им векторы
и
. На плоскости, содержащей лучи
и
, получим два угла
. Меньший из них, величина
которого не превосходит
, принимается за угол между векторами
и
.
Поскольку направление нулевого вектора не определено, то не определен и угол между двумя векторами, если хотя бы один из них нулевой. Из определения следует, например, что угол между ненулевыми коллинеарными векторами либо равен нулю (если векторы одинаково направлены), либо равен (если векторы противоположно направлены).
Ортогональные проекции векторов
Движение по любой прямой может быть в двух направлениях. Ориентированной прямой называется прямая, на которой выбрано направление, т.е. одно из направлений считается положительным, а противоположное — отрицательным. Для измерения длин отрезков на прямой задается масштабный отрезок, который принимается за единицу.
Ориентированная прямая с заданным масштабным отрезком называется осью.
Любой ненулевой вектор , принадлежащий прямой, называется направляющим вектором для данной прямой, поскольку задает на ней ориентацию. Направление вектора
принимается за положительное, а направление противоположного вектора
— за отрицательное. Кроме того, длину вектора
— можно принять за величину масштабного отрезка на этой прямой. Поэтому можно сказать, что любой ненулевой вектор определяет ось — прямую, содержащую этот вектор, задавая на ней направление и масштабный отрезок.
Ортогональной проекцией вектора на ось, задаваемую вектором
, называется его проекция на ось вдоль прямой (или вдоль плоскости), перпендикулярной данной оси. Ортогональную проекцию вектора
на ось, задаваемую вектором
, будем обозначать
.
Ортогональную проекцию вектора на прямую
(см. разд. 1.2.2 и рис. 1.13) будем обозначать
.
Ортогональную проекцию вектора а на плоскость (см. разд. 1.2.2 и рис. 1.14) будем обозначать
.
Разность между вектором и его ортогональной проекцией называют ортогональной составляющей:
— — ортогональная составляющая вектора
относительно вектора
;
— — ортогональная составляющая вектора
относительно прямой
;
— — ортогональная составляющая вектора
относительно плоскости
.
На рис. 1.23 изображены ортогональные проекции вектора :
— на прямую (или на ось
, задаваемую вектором
) вдоль прямой
(рис.1.23,а);
— на прямую (или на ось
, задаваемую вектором
) вдоль плоскости
(рис.1.23,б);
— на плоскость вдоль прямой
(рис.1.23,в).
На рис. 1.23 изображены ортогональные составляющие вектора :
— относительно оси (вектора
):
(рис.1.23,а);
— относительно плоскости (рис.1.23,в).
Для ортогональных проекций справедлива следующая теорема (см. теорему 1.1 в разд. 1.5).
Теорема 1.2 (об ортогональных проекциях вектора).
1. Если на плоскости заданы две взаимно перпендикулярные прямые и
, то любой вектор
на плоскости можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е.
(рис. 1.24,а).
2. Если в пространстве заданы три попарно перпендикулярные прямые и
, пересекающиеся в одной точке, то любой вектор
в пространстве можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е.
(рис. 1.24,6).
3. Квадрат длины вектора на плоскости или в пространстве равен сумме квадратов длин своих ортогональных проекций, т.е.
Первые два утверждения представляют собой частные случаи теоремы 1.1. Третье утверждение следует из теоремы Пифагора (для треугольника (рис. 1.24,а) или треугольников
и
(рис. 1.24,6)).
В формулировке теоремы 1.2 прямые можно заменить осями, задаваемыми попарно ортогональными векторами.
На рис.1.24,а проекции вектора на оси одновременно являются ортогональными составляющими:
и
. На рис. 1.24,6 вектор
является проекцией вектора
на плоскость
, содержащую прямые
и
:
, а вектор
является ортогональной составляющей вектора
относительно плоскости
.
Алгебраическое значение длины проекции
Пусть – угол между ненулевым вектором
и осью, задаваемой вектором
, т.е. угол между ненулевыми векторами
и
.
Алгебраическим значением длины ортогональной проекции вектора на ось, задаваемую вектором
, называется длина его ортогональной проекции
, взятая с положительным знаком, если угол
не превышает
, и с отрицательным знаком, если угол
больше
, т.е.:
Например, для проекций, изображенных на рис. 1.25, , поскольку угол
между векторами
и
острый, a
, так как угол
между векторами
и
тупой.
Некоторые свойства проекций векторов переносятся на алгебраические значения их длин, в частности:
1. — алгебраическое значение длины ортогональной проекции суммы векторов равно сумме алгебраических значений длин ортогональных проекций слагаемых;
2. — алгебраическое значение длины ортогональной проекции произведения вектора на число равно произведению этого числа на алгебраическое значение длины ортогональной проекции вектора
Замечания 1.4.
1. Из определения алгебраического значения длины ортогональной проекции следует (см. также рис.1.25), что , т.е. алгебраическое значение длины ортогональной проекции ненулевого вектора на ось равна произведению длины этого вектора на косинус угла между вектором и осью.
Ортогональную проекцию вектора на ось, задаваемую вектором
, можно представить в виде
Если — единичный вектор, то
.
2. Равенство можно использовать как определение косинуса угла между ненулевыми векторами
и
(или, что то же самое, косинуса угла между осями, заданными ненулевыми векторами
и
(рис. 1.26)).
3. Углом между ненулевым вектором и прямой
называется угол
между вектором
и его ортогональной проекцией
на прямую
. Величина угла
может быть найдена по формуле
4. Углом между ненулевым вектором и плоскостью
называется угол
между вектором
и его ортогональной проекцией
на плоскость
. Величина угла
может быть найдена по формуле
Пример 1.7. Основания и
равнобокой трапеции
равны
и
соответственно; точка
— середина стороны
(рис. 1.27). Найти алгебраические значения длин ортогональных проекций векторов
и
на ось, задаваемую вектором
.
Решение. Пусть — высота трапеции,
— точка пересечения прямых
и
. По свойству равнобокой трапеции
; из равенства треугольников
и
.
Обозначим через искомые алгебраические значения длин ортогональных проекций.Тогда из равенств
,
и свойства 1 алгебраических значений длин проекций следует:
Решая систему находим
, т.е.
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Определение. Два множества F
и G векторов евклидова
пространства E
называются ортогональными, если каждый
вектор из F ортогонален
каждому вектору из G.
Определение. Пусть F
– подпространство E.
Совокупность всех векторов подпространства
E, ортогональных
подпространству F,
называется ортогональным дополнением
подпространства F.
Всякое ортогональное дополнение
является, в свою очередь, линейным
подпространством.
Всякое произвольное евклидово пространство
E разлагается в прямую
сумму своего произвольного подпространства
F и его ортогонального
дополнения
Примеры
1. Требуется найти базис ортогонального
дополнения
подпространства L,
натянутого на векторы
,
,

Будем считать, что базис, относительно
которого заданы векторы, ортонормированный.
По определению, если
,
то
.
Далее, каждый вектор
из
должен быть ортогонален к
.
Для этого достаточно, чтобы
.
Расписывая скалярные произведения,
получим три уравнения относительно
координат
вектора
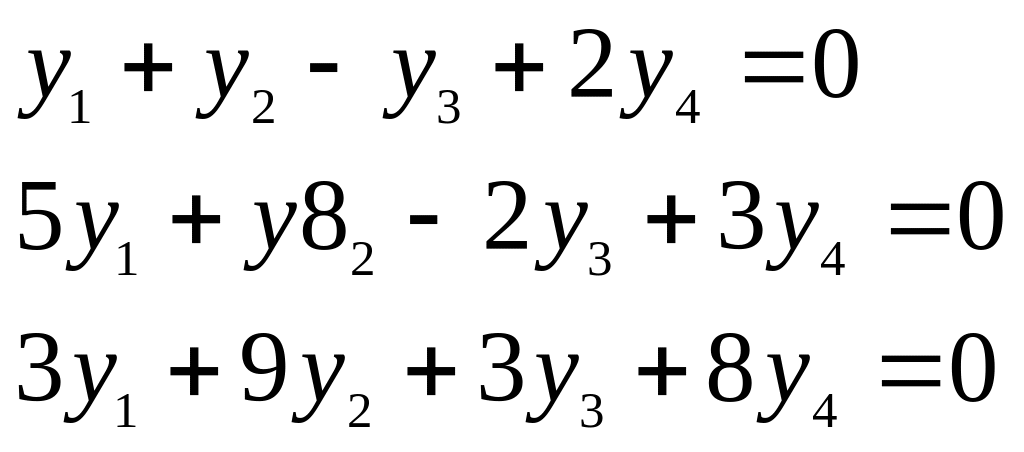
Совокупность решений этой системы и
образует ортогональное дополнение. За
базис в
можно принять любую фундаментальную
систему решений. Например, вектор
.
2. Линейное подпространство
задано уравнениями
Требуется найти уравнения, которые
задают ортогональное дополнение
.
Пусть
,
.
Тогда
.
Этому условию удовлетворяют два линейно
независимых вектора
и
,
которые образуют коэффициенты системы
уравнений, задающей F.
Далее,
.
Ранг системы равен 2. Значит
и, так как
,
то
.
Поэтому найденные векторы можно принять
за базис в
,
и
есть линейная оболочка данных векторов.
Далее задача решается так же как в
примере из § 3. Дословно повторяя решение,
получим следующую систему уравнений
которая и задает
.
5.3. Проектирование вектора на подпространства
Пусть
.
Тогда всякий вектор
можно представить в виде
,
где
и
.
Вектор
называется ортогональной проекцией
вектора x на
подпространство L, а
вектор
называется ортогональной составляющей
вектора
.
Пусть
и
— расстояние между векторами
,
тогда
Таким образом, ортогональная проекция
есть ближайший к
вектору подпространства L.
Часто используются следующие обозначения
,
.
Укажем в заключение как вычисляются
координаты вектора
.
Пусть
— базис в L. Так как
,
то
.
Поэтому
Отсюда имеем, что в случае ортонормированного
базиса
Примеры
1. Найти ортогональную проекцию
и ортогональную составляющую
вектора
на линейное подпространство L,
натянутое на векторы
.
Все векторы заданы координатами
относительно ортонормированного базиса.
,
,
,

Нетрудно убедиться, что
и что за базис можно принять векторы
и
.
Нам будет удобно перейти к ортонормированному
базису в L. Применяя
процедуру ортогонализации к векторам
и
,
получим ортонормированный базис в L:
,
Заметьте, что векторы
и
линейно выражаются через
и
и, значит, также принадлежат L.
Имеем теперь

2. Требуется найти расстояние от точки,
заданной вектором
до плоскости (линейного многообразия),
заданной системой уравнений
Расстояние между точкой
и множеством L
определится следующим образом
Для вычисления расстояния удобно перейти
к параметрическому уравнению плоскости.
Имеем
и поэтому всякий вектор
представляется в виде
где
— фиксированный радиус-вектор точки
плоскости;
и
— базис направляющего линейного
подпространства, которое задается
соответствующей однородной системой.
Решая уравнение, получим, например,
,
,

Затем
Векторы
и
принадлежат направляющему подпространству
M плоскости L.
Вектор
.
Так как
,
а
,
то
Правая часть этого неравенства и есть
искомое расстояние. Осталось вычислить
вектор
и найти его норму. Проделав для этого
аналогичные вычисления и вычислив длину
вектора, получим, что
.
3. Пусть
— ортонормированная система векторов
евклидова пространства En.
Нужно доказать, что для любого вектора
имеет место неравенство Бесселя
с равенством тогда и только тогда, когда
,
т.е. векторы
образуют ортонормированный базис в En.
Так как
— ортонормированная система, то ее
всегда можно векторами
достроить до ортонормированного базиса
в En.
Разложим вектор
по этому базису. Имеем
Далее,
или
С равенством тогда и только тогда, когда
.
Исключение составляют случаи, когда
или когда
принадлежит линейной оболочке векторов
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть L – подпространство евклидового или унитарного пространства V. Тогда «XÎV $X0ÎL Ù $X^ÎL^ (причем единственные), такие что X = X0 + X^, X0 – Называется ортогональной проекцией вектора Х на подпространство L. X^ – Называется ортогональной составляющей вектора Х на подпространство L. Расстоянием Между двумя множествами M1 и M2 Называется кратчайшее из расстояний между элементами M1 и M2: r(M1, M2) = .
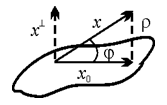
; r2(X, Y) = |X – Y|2 =
= |X – X0|2 + |X0 – Y|2 ³ ³ | X – X0 |2 = | X^ |2, где YÎL, т. е. Расстоянием между вектором и подпространством является длина его ортогональной составляющей. Для евклидового пространства углом между вектором Х и подпространством L Называется угол jÎ[0, p] такой, что
.
Преобразовав 
Рассмотрим – ортогональный базис в подпространстве L:
«XÎV X = X0 + X^ = a1E1 + a1E1 + … + aKEk + X^.
Умножим скалярно обе части равенства на Ei:
, т. е.

| < Предыдущая | Следующая > |
|---|
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
В процессе решения системы уравнений Вы как-то её преобразовывали, при этом выяснялось, что некоторые уравнения являются линейными комбинациями остальных (или, как частный случай, сводятся к
|
||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
Хорошо. Посмотрите на матрицу системы как на два вектора (записанных в строку): Так как векторы Увидите — напишите «увидел».
|
||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
Да, увидел!
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
|||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
Решая эту систему у меня получились довольно странные и неприятные числа, но вроде бы правильные!
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
Вы пока получите эти два вектора (можно вынести Система уравнений, данная в задаче, определяет подпространство Мы нашли базис Получаем систему Теперь находим
|
||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
|||
|
|
|||
|
SlayZar |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/11/13 |
Да, в решении все понятно, огромное спасибо! Теперь проверим, что решение правильное. Значит, все правильно! Огромное спасибо за помощь и столь развернутое и понятное объяснение!
|
|
|
|
|
svv |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
||
23/07/08 |
Рад был помочь. Выберите тот способ из описанных, который Вам больше всего понравился, и примените его к правильным данным.
|
||
|
|
|||
|
eco_fan |
Re: Найти ортогональную проекцию и ортогональную составляющую
|
|
14/10/15 |
Как вы нашли векторы этой системы? Можете подробно расписать я имею ввиду векторы (0,-1,1,0),(-5, 7, 0,1)
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы


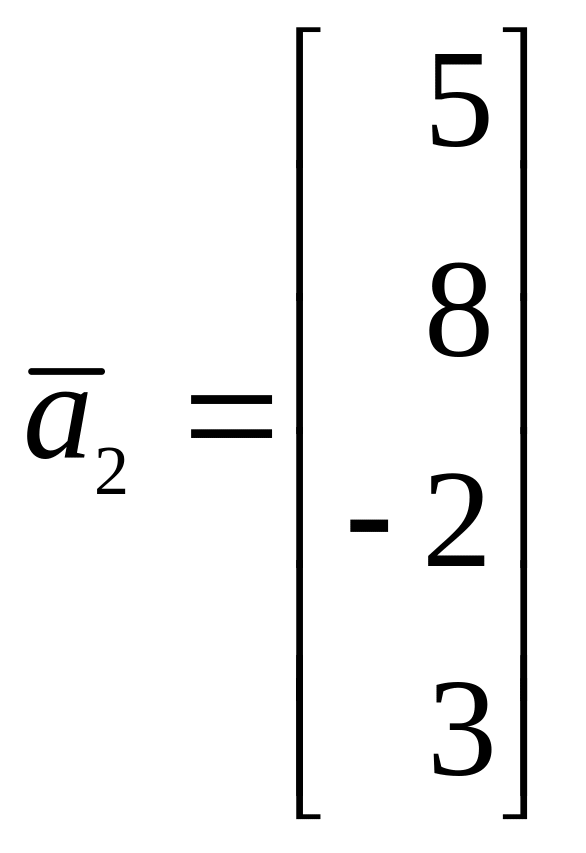
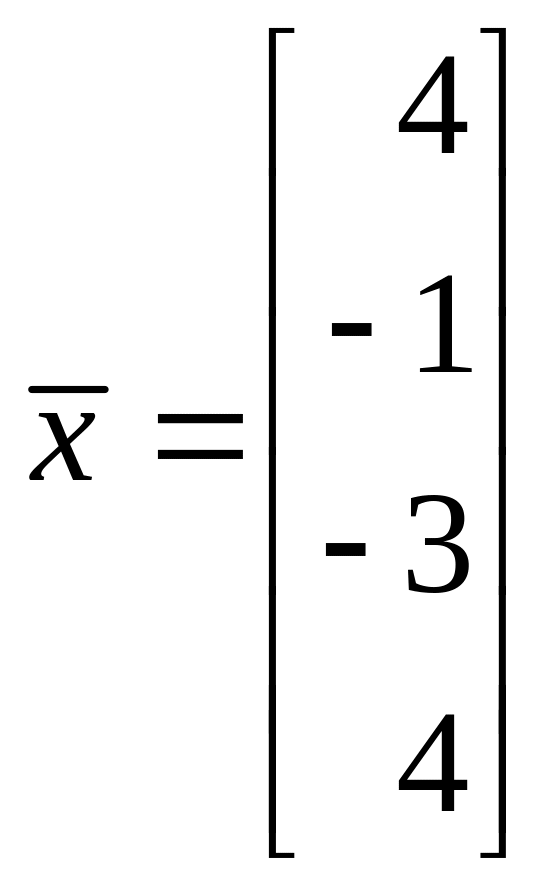
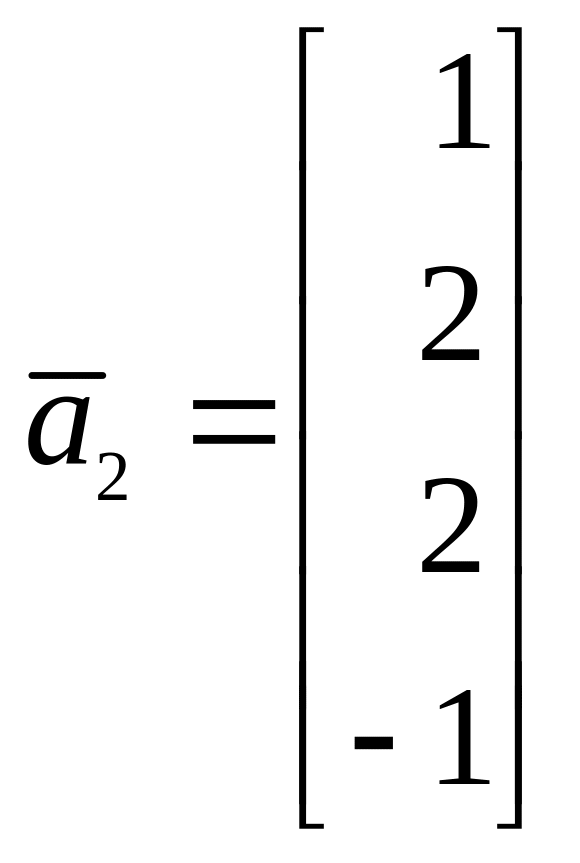
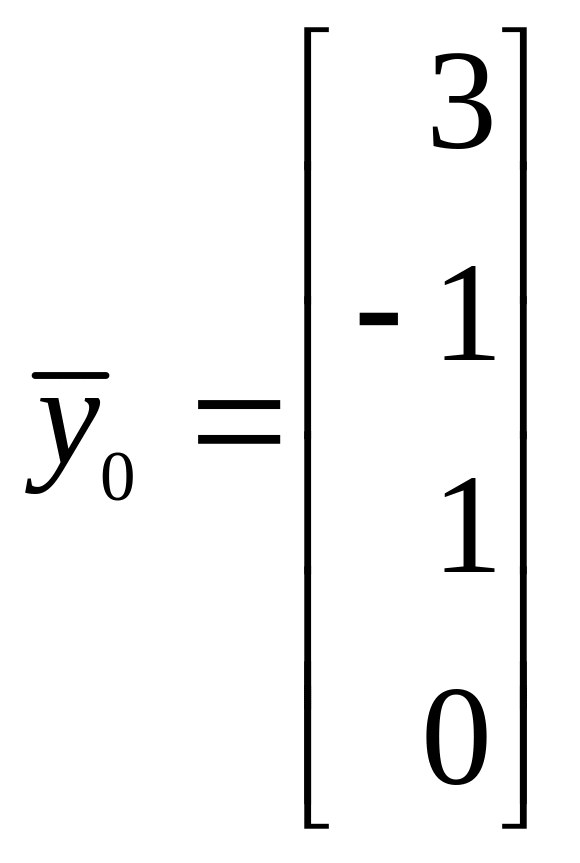

 ). Такие уравнения Вы выбрасывали. Приведите, пожалуйста, конечный вид системы после этих преобразований.
). Такие уравнения Вы выбрасывали. Приведите, пожалуйста, конечный вид системы после этих преобразований.
 .
.
 удовлетворяют системе, то
удовлетворяют системе, то 




 то ответ получается совсем некрасивым… Так и должно быть?
то ответ получается совсем некрасивым… Так и должно быть? за вектор, чтоб не было знаменателей).
за вектор, чтоб не было знаменателей). , к которому
, к которому  является ортогональным дополнением. Надо представить
является ортогональным дополнением. Надо представить  , где
, где  .
. и
и  . Так как
. Так как  , то
, то  , поэтому
, поэтому




 и
и  .
.

 .
. 



