Как найти ортогональные векторы в пространстве - Исправление недочетов и поиск решений вместе с Examum.ru

Ортогональность векторов. Перпендикулярность векторов.

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

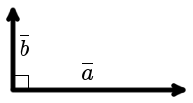рис. 1

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = < a_x ; a_y > и b = < b_x ; b_y > , условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 — 8 = 2 n — 4
2 n — 4 = 0
2 n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Ортогональные векторы

В данной публикации мы рассмотрим, какие векторы называются ортогональными, какое условие при этом должно выполняться. Также разберем примеры решения задач по этой теме.

Условие ортогональности векторов

Векторы a и b являются ортогональными, если угол между ними прямой (т.е. равен 90°).

Примечание: Скалярное произведение ортогональных векторов равняется нулю. Это и есть существенное условие их ортогональности.

a · b = 0

То есть, если в плоскости и , то

Примеры задач

Задание 1
Докажем, что векторы и ортогональны.

Решение:
a · b = 2 · (-2) + 4 · 1 = 0

Следовательно, заданные векторы являются ортогональными, так как их скалярное произведение равняется нулю.

Задание 2
При каком значении n векторы и ортогональны.

Решение:
a · b = 3 · 6 + (-9) · n = 0
18 – 9n = 0
n = 2

Таким образом, a и b ортогональны при n, равном двум.

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; — 1 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) = 2 — 2 = 0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a ¯ = < 3 ; — 1 >и b ¯ = < 7 ; 5 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 3 × 7 + ( — 1 ) × 5 = 21 — 5 = 16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = — 4 n = — 2

Ответ: векторы являются ортогональными при значении n = 2 .

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; — 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; — 1 ; 10 >являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; — 8 >будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

источники:

Ортогональные векторы

http://zaochnik.com/spravochnik/matematika/vektory/ortogonalnye-vektory-i-uslovie-ortogonalnosti/

Источник

Ортогональные векторы евклидова пространства и их свойства

Два вектора mathbf{u} и mathbf{v} евклидова пространства называются ортогональными (перпендикулярными), если их скалярное произведение равно нулю: langle mathbf{u},mathbf{v}rangle .

Система векторов $mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k$ называется ортогональной, если все ее векторы попарно ортогональны, т.е. $langle mathbf{u}_i, mathbf{v}_jrangle=0$ при ine j . Система векторов $mathbf{v}_1, mathbf{v}_2, ldots,mathbf{v}_k$ называется ортонормированной, если все ее векторы попарно Ортогональны и длина (норма) каждого вектора системы равна единице, т.е.

$langle mathbf{u}_i, mathbf{v}_jrangle=begin{cases}1,&i=j,\0,& ine j. end{cases}$

Говорят, что вектор mathbf{v} ортогонален (перпендикулярен) множеству , если он ортогонален каждому вектору из . Ортогональность векторов обозначается знаком перпендикуляра (perp) .

Свойства ортогональных векторов

1. Нулевой вектор ортогонален каждому вектору пространства.

2. Взаимно ортогональные ненулевые векторы линейно независимы.

В самом деле, пусть векторы $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ попарно ортогональны. Составим из них линейную комбинацию и приравняем ее нулевому вектору:

$lambda_1cdot mathbf{v}_1+lambda_2 mathbf{v}_2+ldots+lambda_k mathbf{v}_k=mathbf{o}.$

Умножим обе части равенства скалярно на вектор $mathbf{v}_1:$

$lambda_1langle mathbf{v}_1,mathbf{v}_1rangle+ lambda_2underbrace{langle mathbf{v}_1,mathbf{v}_2rangle}_{0}+ ldots+ lambda_kunderbrace{langle mathbf{v}_1, mathbf{v}_krangle}_{0}= underbrace{langle mathbf{v}_1,mathbf{o}rangle}_{0}.$

Следовательно, $lambda_1cdot|mathbf{v}_1|^2=0$ . Так как $mathbf{v}_1ne mathbf{o}$ , то lambda_1=o . Аналогично доказываем, что lambda_2=ldots= lambda_k=0 , т.е рассматриваемая линейная комбинация тривиальная. Значит, ортогональная система векторов $mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k$ линейно независима.

3. Если сумма взаимно ортогональных векторов равна нулевому вектору, то каждое из слагаемых равно нулевому вектору.

4. Если вектор mathbf{u} ортогонален каждому вектору системы $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ , то он также ортогонален и любой их линейной комбинации. Другими словами, если $mathbf{u}perp mathbf{v}_i,~ i=1,ldots,k$ , то $mathbf{u}perp operatorname{Lin} (mathbf{v}_1,ldots, mathbf{v}_k)$ .

5. Если вектор mathbf{u} ортогонален подмножеству евклидова пространства, то он ортогонален и линейной оболочке этого подмножества, т.e. mathbf{u}perp M~Rightarrow~ mathbf{u}perp operatorname{Lin}(M) .

6. Если $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ — ортогональная система векторов, то

$|mathbf{v}_1+mathbf{v}_2+ldots+mathbf{v}_k|^2= |mathbf{v}_1|^2+ |mathbf{v}_2|^2+ldots+|mathbf{v}_k|^2.$

Это утверждение является обобщением теоремы Пифагора.

Процесс ортогонализации Грама-Шмидта

Рассмотрим следующую задачу. Дана линейно независимая система $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ векторов конечномерного евклидова пространства. Требуется построить ортогональную систему $mathbf{w}_1,mathbf{w}_2, ldots,mathbf{w}_k$ векторов того же пространства так, чтобы совпадали линейные оболочки:

$operatorname{Lin}(mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k)= operatorname{Lin}(mathbf{w}_1, mathbf{w}_2,ldots,mathbf{w}_k).$

Решение задачи находится при помощи процесса ортогонализации Грама–Шмидта, выполняемого за шагов.

1. Положить $mathbf{w}_1=mathbf{v}_1$ .

2. Найти $mathbf{w}_2=mathbf{v}_2-alpha_{21}cdot mathbf{w}_1$ , где $alpha_{21}= frac{langle mathbf{v}_2, mathbf{w}_1rangle}{langle mathbf{w}_1, mathbf{w}_1 rangle}$ .

3. Найти $mathbf{w}_3=mathbf{v}_3-alpha_{31} mathbf{w}_1-alpha_{32} mathbf{w}_2$ , где $alpha_{31}=frac{langle mathbf{v}_3,mathbf{w}_1 rangle}{langle mathbf{w}_1, mathbf{w}_1rangle},~ alpha_{32}= frac{langle mathbf{v}_3,mathbf{w}_2 rangle}{langle mathbf{w}_2, mathbf{w}_2rangle}$ ; и т.д.

4. Найти $mathbf{w}_k=mathbf{v}_k-sum_{i=1}^{k-1}alpha_{ki}mathbf{w}_i$ , где $alpha_{ki}= frac{langle mathbf{v}_k,mathbf{w}_irangle}{langle mathbf{w}_i, mathbf{w}_irangle},~ i=1,ldots,k-1$ .

Поясним процесс ортогонализации. Искомый на втором шаге вектор $mathbf{w}_2$ представлен в виде линейной комбинации $mathbf{w}_2=mathbf{v}_2-alpha mathbf{w}_1$ . Коэффициент alpha подберем так, чтобы обеспечить ортогональность векторов $mathbf{w}_2$ и $mathbf{w}_1$ . Приравняем нулю скалярное произведение этих векторов $langle mathbf{w}_2,mathbf{w}_1rangle= langle mathbf{v}_2,mathbf{w}_1rangle- alpha langle mathbf{w}_1,mathbf{w}_1rangle=0$ . Отсюда получаем, что $alpha=alpha_{21}$ (см. пункт 2 алгоритма). Подбор коэффициентов $alpha_{ji}$ на j-м шаге алгоритма делается так, чтобы искомый вектор $mathbf{w}_j$ был ортогонален всем ранее найденным векторам $mathbf{w}_1, mathbf{w}_2,ldots,mathbf{w}_{j-1}$ .

Замечания 8.11

1. Векторы, найденные в процессе ортогонализации, обладают следующими свойствами:

а) $mathbf{w}_j perp operatorname{Lin}(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_{j-1}),quad j=2,ldots,k$ ;

б) $operatorname{Lin}(mathbf{w}_1)= operatorname{Lin}(mathbf{v}_1),quad operatorname{Lin}(mathbf{w}_1,mathbf{w}_2, ldots,mathbf{w}_{j})= operatorname{Lin}(mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_{j}),quad j=2,ldots,k$ .

Первое свойство следует из свойства 4 ортогональных векторов. Второе свойство следует из того, что каждый вектор системы $mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_{j}$ линейно выражается через векторы $mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_{j}$ , и наоборот.

2. В процессе ортогонализации любой вектор $mathbf{w}_j$ можно заменить на коллинеарный ему ненулевой вектор $lambdacdot mathbf{w}_j$ . При этом свойства, перечисленные в пункте 1, не нарушаются.

3. Если система $mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_{k}$ векторов линейно зависима, то в процессе ортогонализации будем получать (на некоторых шагах) нулевые векторы. Действительно, если подсистема $mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_{j}$ линейно зависима, то $mathbf{v}_jin operatorname{Lin} (mathbf{w}_1,ldots,mathbf{w}_{j-1})$ . Тогда вектор $mathbf{w}_j=mathbf{v}_j-sum_{i=1}^{j-1}alpha_{ji} mathbf{w}_i$ одновременно удовлетворяет двум условиям $mathbf{w}_jperp operatorname{Lin}(mathbf{w}_1,ldots, mathbf{w}_{j-1})$ и $mathbf{w}_jin operatorname{Lin}(mathbf{w}_1,ldots,mathbf{w}_{j-1})$ . Значит, это нулевой вектор $mathbf{w}_i=mathbf{o}$ .

Поэтому в данном случае формулы вычисления коэффициентов $alpha_{ji}$ на j-м шаге следует записывать в виде:

$alpha_{j,i}= begin{cases}dfrac{langle mathbf{v}_j,mathbf{w}_irangle}{langle mathbf{w}_i,mathbf{w}_irangle},& mathbf{w}_ine mathbf{o},\ 0,& mathbf{w}_i=mathbf{o}. end{cases}i=1,2,ldots,j-1.$

В остальном процесс ортогонализации остается неизменным.

4. Процесс ортогонализации можно дополнить процессом нормировки, разделив каждый вектор ортогональной системы $mathbf{w}_1, mathbf{w}_2,ldots,mathbf{w}_k$ на его длину:

$mathbf{e}_i=dfrac{1}{|,mathbf{w}_i,|}cdot mathbf{w}_i,quad i=1,2,ldots,k.$

В результате получим ортонормированную систему $mathbf{e}_1,mathbf{e}_2, ldots, mathbf{e}_k$ , отвечающую условию $operatorname{Lin}(mathbf{e}_1, ldots, mathbf{e}_k)= operatorname{Lin}(mathbf{v}_1,ldots,mathbf{v}_k)$ . Если исходная система векторов является линейно зависимой, то среди векторов ортогональной системы $mathbf{w}_1,mathbf{w}_2, ldots,mathbf{w}_k$ будут нулевые. Чтобы получить ортонормированную систему, нулевые векторы следует исключить, а остальные векторы нормировать.

Пример 8.18. Даны системы векторов евклидовых пространств:

а) $x=begin{pmatrix}1\0end{pmatrix}!,quad y=begin{pmatrix}2\0end{pmatrix}!,quad z=begin{pmatrix}0\1end{pmatrix}$ — элементы пространства $mathbb{R}^2$ со скалярным произведением (8.26):

$langle x,yrangle= x^Tcdot! begin{pmatrix}2&1\1&1end{pmatrix}!cdot y= 2cdot x_1cdot y_1+x_1cdot y_2+x_2cdot y_1+x_2cdot y_2,;$

б) p_1(x)=1,~ p_2(x),~ p_3(x)=x^2 — элементы пространства C[-1;1] со скалярным произведением (8.28):

$langle f,grangle= intlimits_{-1}^{1}f(x)g(x),dx,.$

Провести

ортогонализацию данных векторов.

Решение. а) Заметим, что система векторов x,,y,,z линейно зависимая, так как и пропорциональны, поэтому используем процесс ортогонализации Грама–Шмидта с учетом пункта 3 замечаний 8.11.

1. Полагаем mathbf{u}=x .

2. Вычисляем $alpha_{21}=frac{langle y,mathbf{u}rangle}{langle mathbf{u}, mathbf{u}rangle}= frac{2!cdot!2!cdot!1+ 1!cdot!0+ 0!cdot!2+0!cdot!0}{2!cdot!1!cdot!1+ 1!cdot!0+ 0!cdot!1+0!cdot!0}=2$ и находим $mathbf{v}=y-alpha_{21}mathbf{u}= begin{pmatrix}2\0end{pmatrix}-2! begin{pmatrix}1\0end{pmatrix}= begin{pmatrix} 0\0 end{pmatrix}$ . Получили нулевой вектор.

3. Вычисляем $alpha_{31}=frac{langle z,mathbf{u}rangle}{langle mathbf{u}, mathbf{u}rangle}= frac{2!cdot!0!cdot!1+ 0!cdot!0+ 1!cdot!1+1!cdot!0}{2!cdot!1!cdot!1+ 1!cdot!0+0!cdot!1+ 0!cdot!0}=frac{1}{2},;$ $alpha_{32}=0$ согласно пункту 3 замечаний 8.11, так как mathbf{v}=mathbf{o} , и находим

$mathbf{w}=z-alpha_{31}cdot mathbf{u}-alpha_{32}cdot mathbf{v}= begin{pmatrix} 0\1end{pmatrix}-frac{1}{2}cdot! begin{pmatrix}1\0end{pmatrix}- 0cdot! begin{pmatrix}0\0 end{pmatrix}= begin{pmatrix}-1/2\1end{pmatrix}!.$

Проверим условие ортогональности $langle mathbf{u},mathbf{w}rangle= 2cdot1cdot left(-frac{1}{2}right)+ 1cdot1+ 0cdotleft(-frac{1}{2}right)+0cdot1=0$ .

Для получения ортонормированной системы исключаем нулевой вектор mathbf{v}=mathbf{o} , а остальные нормируем (см. пункт 4 замечаний 8.11):

$begin{gathered} |mathbf{u}|= sqrt{langle mathbf{u},mathbf{u} rangle}= sqrt{2},;\[5pt] |mathbf{w}|= sqrt{langle mathbf{w},mathbf{w}rangle}= sqrt{2cdot!left(-frac{1}{2}right)!cdot!left(-frac{1}{2}right)+left(-frac{1}{2}right)!cdot1+ 1cdotleft(-frac{1}{2}right)+ 1cdot1}= sqrt{1/2},;\[5pt] widehat{mathbf{u}}= frac{1}{|mathbf{u}|}cdot mathbf{u}= frac{1}{sqrt{2}}cdot! begin{pmatrix}1\0end{pmatrix}= begin{pmatrix}1/sqrt{2}\ 0end{pmatrix}!,quad widehat{mathbf{w}}= frac{1}{|mathbf{w}|}cdot mathbf{w}= frac{1}{sqrt{1/2}}cdot! begin{pmatrix}-1/2\0end{pmatrix}= begin{pmatrix}-1/sqrt{2}\ sqrt{2}end{pmatrix}!. end{gathered}$

Таким образом, для системы трех векторов x,,y,,z построена ортогональная система из трех векторов mathbf{u},mathbf{v},mathbf{w} и ортонормированная система из двух векторов widehat{mathbf{u}},widehat{mathbf{w}} . Линейные оболочки этих трех систем совпадают между собой (и со всем пространством $mathbb{R}^2$ ).

б) 1. Полагаем q_1(x)=p_1(x)=1 .

2. Вычисляем $alpha_{21}= frac{langle p_2,q_1rangle}{langle q_1,q_1rangle}= Biggl(intlimits_{-1}^{1} xcdot1,dxBiggr):Biggl(intlimits_{-1}^{1}1cdot1,dxBiggr)= left.{frac{1}{2},x^2}right|_{-1}^{1}:2=0$ и находим q_2(x)=x-0!cdot!1=x .

3. Вычисляем

$begin{aligned} alpha_{31}&= frac{langle p_3,q_1rangle}{langle q_1,q_1rangle}= Biggl(intlimits_{-1}^{1} x^2cdot1,dxBiggr):2= left.{frac{1}{3},x^3}right|_{-1}^{1}= frac{2}{3} cdotfrac{1}{2}=frac{1}{3},;\[5pt] alpha_{32}&= frac{langle p_3,q_2rangle}{langle q_2,q_2 rangle}= Biggl(intlimits_{-1}^{1} x^2cdot x,dxBiggr):Biggl(intlimits_{-1}^{1}xcdot x,dxBiggr)= left.{frac{1}{4},x^4}right|_{-1}^{1}:left.{frac{1}{3},x^3}right|_{-1}^{1}=0 end{aligned}$

и находим $q_3(x)= x^2-alpha_{31}cdot1-alpha_{32}cdot x=x^2-frac{1}{3}$ .

Получили ортогональные многочлены $q_1(x)=1,~ q_2(x)=x,~ q_3(x)=x^2-frac{1}{3}$ . Выполним нормировку:

$begin{array}{lll}|q_1(x)|= sqrt{langle q_1(x),q_1(x)rangle}= sqrt{2},;&~ |q_2(x)|= sqrt{langle q_2(x),q_2(x)rangle}= sqrt{dfrac{2}{3}},;&~ |q_3(x)|= sqrt{langle q_3(x),q_3(x) rangle}= dfrac{2}{3}sqrt{dfrac{2}{5}},;\[10pt] widehat{q}_1(x)= dfrac{q_1(x)}{|q_1(x)|}= dfrac{1}{sqrt{2}},;&~ widehat{q}_2(x)= dfrac{q_2(x)}{|q_2(x)|}= sqrt{dfrac{3}{2}}cdot x,;&~ widehat{q}_3(x)= dfrac{q_3(x)}{|q_3(x)|}= dfrac{3}{2}sqrt{dfrac{5}{2}}! left(x^2-dfrac{1}{3}right)!.end{array}$

Получили ортонормированные многочлены (многочлены Лежандра).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Привет, всем!
Попытаюсь объяснить суть того, что мне нужно и сразу показать, то что я не понимаю. Приведу примеры как я шел от простого к сложному, чтобы понять как мне правильно сделать.
Начнем с простого примера.
Пусть задан единичный вектор в пространстве $R^2$ . Я хочу найти ортогональный ему вектор и тоже единичный . Цель, получить все ортогональные базисы в пространстве $R^2$ . Для этого составил систему уравнений:

— скалярное произведение

— нормировка
Число уравнений равно числу неизвестных, система нелинейная квадратичная и будет иметь два решения, что в принципе из опыта понятно, что любому вектору на плоскости могут быть два ортонормированных вектора, которые направленны в разные стороны.

Идем дальше. В пространстве $R^3$ для заданного вектора хотим тоже получить систему ортонормированных векторов. Цель таже, получить все системы ортонормированных базисов. И тут начинаются проблемы, так как мы имеем 6 неизвестных (ищем 2 вектора у каждого 3 компоненты) и всего 5 уравнений:

— скалярное произведение 1-го со 2-м
— скалярное произведение 1-го с 3-м
— скалярное произведение 3-го со 2-м

— нормировка 2-го
— нормировка 3-го

Попытаемся подсократить переменные. Для этого введем сферическую параметризацию от двух углов для 2-го и 3-го вектора (я имею ввиду вот так):

где $i=2,3$
таким образом мы имеем 4 неизвестных. Но так как уравнения, которые отвечают за нормировку уходят, то остаются 3 уравнения и 4 неизвестных. И тут тоже понятно, как и в предыдущем случае, что у любого вектора может быть бесконечно много двух ортонормированных векторов вращающихся в перпендикулярной ему плоскости. Причем как и в предыдущем случае, два вектора в плоскости существуют в двух вариантах, можно один вектор развернуть и будет уже другой базис.
Теперь сразу напишу, то что я хочу понять и сделать. Мне нужно уметь генерировать ортонормированный базис в комплексном 4х мерном пространстве $C^4$ !!! Что значит сгенерировать. Вернемся к 1-му примеру. Например, генерирую 1-ый вектор используя параметризацию . Отлично, теперь задавая один параметр — я могу решив уравнения для первого случая в пространстве $R^2$ получить решения для из уравнений, приведенных выше и параметризации . Таким образом, варьируя только и решая уравнения смогу получить все ортонормированные базисы в $R^2$
В 4х мерном комплексном пространстве, я даже теряюсь, какие мне параметры оставить, чтобы варьируя их получить все ортонормированные базисы. Если есть у кого-то идеи или может кто-то знает, где уже такой алгоритм есть, подскажите плиз.

Источник

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = {a_x; a_y} и b = {b_x; b_y}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b_y = 0

Пример 1. Доказать что вектора a = {1; 2} и b = {2; -1} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 2. Проверить являются ли вектора a = {3; -1} и b = {7; 5} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Пример 3. Найти значение числа n при котором вектора a = {2; 4} и b = {n; 1} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2n + 4
2n + 4 = 0
2n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b_y + a_z · b_z = 0

Пример 4. Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 5. Проверить являются ли вектора a = {2; 3; 1} и b = {3; 1; -9} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 6. Найти значение числа n при котором вектора a = {2; 4; 1} и b = {n; 1; -8} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 — 8 = 2n — 4
2n — 4 = 0
2n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Источник

При решении Примера
12–03была использована совокупность попарно
ортогональных векторов:,,…,.
Было доказано, что любой вектор ортогонален
сумме остальных векторов этой совокупности.

Определение:

(11.6)

Система
векторов называется ортогональной
системой,
если все
векторы этой системы попарно
ортогональны
между собой.

Замечание:
использование
понятия изоморфизм позволяет предвидеть
использование свойства попарной
ортогональности векторов при построении
базы в n-мерном
пространстве.

В Примере
12–03была доказана теорема, в которой
утверждается: во всякой совокупности
попарно ортогональных векторов:,,…,любой вектор ортогонален сумме остальных
векторов этой совокупности. Фактически
была доказана теорема:

Теорема:

(11.2)

Всякая
ортогональная система ненулевых
векторов линейно независима.

►Пусть
имеем систему ненулевые, попарно
ортогональных векторов:
,,…,
пространства E_n.
Допустим, существует линейная зависимость
этих векторов:

++..+=0,

умножим
это выражение скалярно на вектор
.
Так как вектор

перпендикулярен всем остальным векторам:

,…,,
то получим:
λ₁(e₁,e₁)=0.
Но, по свойству скалярного произведения,

→

=
0. Аналогично получим: все
=0,
то есть система векторов
,…,
линейно независима!

◄

Рассматривая
ортогональные системы векторов, а также
исследуя их линейную независимость в
пространстве
,
замечаем их сходство с векторами,,базы пространства,
используемой при построении прямоугольной
системы координат.
Ниже это сходство станет обоснованным
распространением свойств векторов
пространствав пространство.

§ 4. Ортонормированный базис евклидова пространства. Ортогональное дополнение.

При изучении
линейных векторных пространств
рассматривались способы построения
базиса произвольного пространства
.
Оказывается, любой базис пространстваможно преобразовать в ортогональный
базис пространства.

Теорема:

(11.3)

В
пространстве
всякий базис: g=(g₁,g₂,
… ,

)
можно преобразовать в ортогональный
базис некоторым невырожденным линейным
преобразованием.

►Пусть
в пространстве
имеем базис: g₁,g₂,
… ,.
Примем e₁=g₁.
Это равносильно невырожденному линейному
преобразованию: независимая система
векторов (g₁,g₂,
… ,)
преобразована в независимую систему
(e₁,g₂,
… ,).

Далее
примем: =λ₁e₁+g₂,

причем
e₂≠0,
так как векторы g₁,g₂
независимы. В этом случае реализуется
невырожденное преобразование, переводящее
независимую систему (e₁,g₂,
… ,)
в независимую систему (e₁,e₂,g₃
… ,).
Для нахождения числа

потребуем,
чтобы вектор e₂
был
ортогонален e₁:
получаем
выражение: =
–.

Пусть
уже построена система независимых
векторов (e₁,e₂,e₃
… ,e_n_—₁,).
Далее запишем выражение: =+
+…+

+,

причем
e_n≠0,
так как векторы (g₁,g₂,
… ,

)
независимы. В этом случае реализуется
невырожденное преобразование, переводящее
независимую систему (e₁,e₂,e₃
… ,e_n_—₁,)
в независимую систему (e₁,e₂,g₃
… , e_n_—₁,e_n).
Для нахождения чисел

потребуем,
чтобы вектор e_n
был
ортогонален каждому вектору
,

=1,2,…,(n-1):

=
–,

=1,2,…,(n-1).

Итак,
нами определен процесс, преобразующий
произвольный базис g=(g₁,g₂,
… ,

)
в ортогональную систему векторов

,,…,
—
ортогональный базис. ◄

Следствие:
Так как любой
вектор пространства
может быть включен в некоторый базис

пространства ,
то этот вектор может быть включен в
любой
ортогональный базис пространства .

Вектор
b
называют нормированным,
если (b,b)=1.
Если вектор a
≠
0, то
его можно нормировать: b
=a
=.

Если
в пространстве

построен ортогональный базис, его можно
нормировать. Так получаем ортогональный
и нормированный базис, короче:
ортонормированный
базис.

Пусть
в пространстве

определен ортонормированный базис, и
произвольные векторы записаны в виде:
x=
λ₁e₁+λ₂e₂+…+,

y=
μ₁e₁+μ₂e₂+…+.

В этом случае
скалярное произведение векторов имеет
простейшее выражение:

=
λ₁μ₁+λ₂μ₂+,…,+.
(1)

Верно
и обратное: если скалярное произведение
векторов в некотором базисе записывается
в виде (1),
то базис (e₁,
e₂,
… , e_n)
– ортонормированный.

Используя
полученные в настоящем параграфе
результаты, можно получить развитие
понятия изоморфизма евклидовых
пространств:

Теорема:

(11.4)

Любые
евклидовы пространства
и ,
имеющие одну и ту же размерность n,
изоморфны между собой.

►Пусть
в пространстве
имеем ортонормированный базис: (e₁,e₂,
… ,e_n),
а пространстве
ортонормированный базис: (e′₁,
e′₂,
… , e′_n).
Запишем векторы:

x=
λ₁e₁+λ₂e₂+…+, y=
μ₁e₁+μ₂e₂+…+,(2)

x′=
λ₁e′₁+λ₂e′₂+…+, y′=
μ₁e′₁+μ₂e′₂+…+.(3)

Выражения
(2)
и (3) определяют изоморфизм
и

как линейных пространств. В то же время
видим: (x,y)
=

=
(x′,y′),

что
определяет изоморфизм

и

как евклидовых
пространств.
◄

Далее
определим понятие ортогональное
дополнение. Пусть имеем подпространство
L₁размерности
k₁.
Ортогональным
дополнением
подпространства L₁
называют множество векторов L₂,
ортогональных каждому вектору L₁.

Если
можно представить евклидово пространство

в виде суммы: Е_n
= L₁+L₂,
где каждое из подпространств является
ортогональным дополнением другого, то
их пересечением является только нулевой
вектор. В этом случае сумма размерностей
подпространств равна размерности
пространства ,
то есть: n
= k₁+
k₂.
В этом случае говорят, что пространство

есть прямая
суммаподпространств
L₁+
L_2.
.

☺☺

Пример
12–07:Проверить, что
векторы =(1,-2,2,-3)
и=(2,-3,2,4)
ортогональны. Дополнить их до ортогонального
базиса.

Решение:

Замечание:
в условии не оговорено, в каком базисе
заданы векторы

и
,
но из имеющейся информации мы должны
считать, что эти векторы заданы в
ортонормированном базисе.

0). Учитывая
замечание, запишем:
==0.
Это значит, что векторыи— ортогональны. Поиск недостающих двух
векторов для построения ортогонального
базиса проведём двумя способами.

Способ
-1:

1). Запишем скалярное
произведение:
==0.
Значит векторыи— ортогональны.

2). Запишем любой
определитель, включающий строки
и,=,
не равный нулю. Это значит, что векторы,,=(0,0,1,0)
и=(0,0,0,1)
независимы и могут использоваться как
базис. Превратим его в ортогональный
базис:,,,.

3). Примем:
=,=.
Примем:=++,
где:

=
–=–=–,

=
–=–,
→ 99=99–11–6=(-23,40,65,9).

Чтобы не иметь
дробей, примем:
=(-23,40,65,9).

4). Примем:
=+++,
где:

=
–=,

=
–=–,

=
–=–.

Тогда
можем записать:
66·715=66·715+11·715–8·715–66=(-2057,-1210,
0, 121). Чтобы не иметь дробей, примем:=(-2057,-1210,
0, 121).

Ответ:
можно добавить:=(-23,40,65,9)
и=(-2057,-1210,
0, 121).

Замечание:
рассмотренный способ полезен своей
пугающей
громоздкостью
(!): это подсказывает, что поиск рациональных
способов решения задачи может избавить
исследователя от излишних затрат усилий.

Способ
-2:

1). Примем: вектор
=(x,y,1,0),
требуя выполнения условий:=0,=0
, или:

откуда: x=2
,y=2 →=(2,2,1,0).

2). Примем: вектор
a₄=
(1,x,y,z),
при условии:=0,=0,=0,
или:

откуда: x=–,y=–,z= –→=–(-5,2,6,1).

3).
Для удобства, примем: вектор =
(-5,2,6,1), так как ортогональность обеспечит
любой коллинеарный ему вектор!

Ответ:
можно добавить:=(2,2,1,0)
и=
(-5,2,6,1).

Замечание:
видим, что способ-2 сразу начинает поиск
ортогональных векторов, а способ-1
сначала импровизирует, соглашаясь
начать с любого базиса пространства, а
потом провести его ортогонализацию.

Пример
12–08:Задана система
векторов: =(2,1,3,-1),
=(7,4,3,-3)
,=(1,1,-6,0),=(5,7,7,8).
Применяя процесс ортогонализации,
построить ортогональный базис
подпространства-оболочки данной системы
векторов.

Решение:

1). Примем:
=,
и положим вектор=+,
где число
определяется выражением:

=–=–=–2
→ =–2=(3,2,-3,-1).

2). Примем:
=++,
где числаиопределяются выражениями:

=
–=–=1,
=
–=–=–1
→ =+–=(0,0,0,0),

это что вектор
является линейной комбинацией векторови
.
Этот вектор не должен участвовать в
ортогональном базисе!

3). Примем:
=++,
где числаиопределяются выражениями:

=
–=–=–2,
=
–=–=0
→ =–2=(1,5,1,10).

Ответ:
ортогональный базис:=(3,2,-3,-1),=(3,2,-3,-1)
и=(1,5,1,10).

Замечание:
пример интересен тем, что процесс
ортогонализации выделяет на очередном
шаге зависимый от уже включённых в базис
векторов: такой вектор из процесса
удаляется, как не удовлетворяющий
требованиям базиса.

Пример
12–09:
Доказать, что ортогональноедополнение

к линейному подпространству линейного векторного пространстваобладает свойствами:

1).
; 2).=;

3).
=; 4).=0
→=.

Решение:

1). Пусть в пространстве
выделен базис:,,…,.
Пусть подпространствообразовано совокупностью векторов:,,…,.
Это значит, что ортогональное дополнениеиспользует в качестве своего базиса
совокупность векторов:,…,.
Если теперь построить ортогональное
дополнениек подпространству,
получится подпространство с базисом,,…,,
что есть подпространство.
Из рисунка всё очевидно:

2). Пусть в пространстве
выделен базис:,,…,.
Доказательство пронаблюдаем, рассматривая
представленную ниже таблицу, в которой
отражены все элементы, используемые в
выражении=:

3). Пусть в пространстве
выделен базис:,,…,.
Доказательство пронаблюдаем, рассматривая
представленную ниже таблицу, в которой
отражены все элементы, используемые в
выражении=:

4). Пусть в пространстве
выделен базис:,,…,.
Доказательство пронаблюдаем, рассматривая
представленную ниже таблицу, в которой
отражены все элементы, используемые в
выражении=0
→=:

Замечание:
пример интересен тем, что процесс
доказательств можно хорошо иллюстрировать,
что особенно важно на первом этапе
освоения алгебраических абстракций
для тех, кто имеет слабо развитое образное
мышление!

Ответ:
доказательства представлены в рисунках.

☻

Соседние файлы в папке ЛА и АГ пособие

Источник