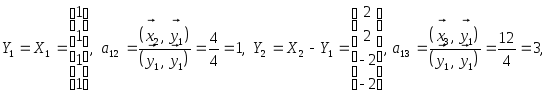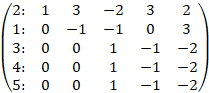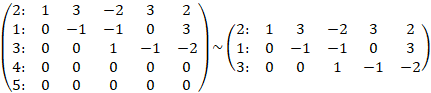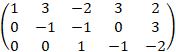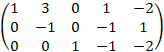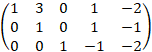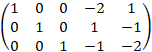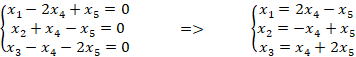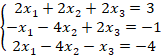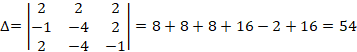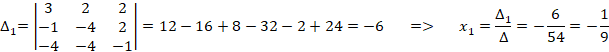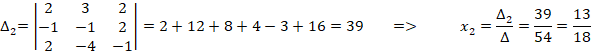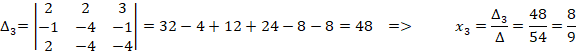Как найти ортогональный базис линейной оболочки

Определение
1.
Линейной
оболочкой
заданной
конечной совокупности

элементов векторного пространства
ⁿ
над полем К называется множество всех
линейных комбинаций этих элементов с
коэффициентами из поля К. При этом сама
совокупность

называется порождающей
системой
данной линейной оболочки, а сама линейная
оболочка обозначается символом
.

Линейные оболочки
обладают следующими свойствами:

.
Линейная оболочка элементов векторного
пространства
ⁿ
является подпространством М векторного
пространства
ⁿ.

Данный
результат следует из определения
линейной оболочки: сумма
двух векторов из линейной оболочки
будет принадлежать линейной оболочки
(одна из линейных комбинаций), произведение
вектора из линейной оболочки также
будет принадлежать линейной оболочки.

.
Линейная оболочка может совпадать со
всем пространством Rⁿ
(если образующая
система является базисом
в пространстве Rⁿ
)

.
Линейная оболочка

является наименьшим подпространством,
содержащим элементы
.
Все остальные подпространства могут
только содержать вектора порождающей
системы или их возможные комбинации.

.
Если какой-нибудь элемент из порождающей
системы элементов

есть линейная комбинация остальных
элементов этой системы, то его можно
удалить из порождающей системы, не
изменив при этом линейной оболочки.

.
Если координатная матрица системы
образующих

имеет ранг р, где
,
то любая линейно независимая система
,
является базисом линейной оболочки
,
а сама линейная оболочка будет
подпространством размерности р,
.

Примеры.

Если
a,
b,
с – геометрические векторы, лежащие
на одной прямой. В этом случае линейная
оболочка L(а,b,c)=
L(a).Здесь
линейная оболочка является одномерным
пространством, которое состоит из всех
вектор, лежащих на прямой, причем вектор
а
–является базисом.
Пусть
a,
b,
с – геометрические векторы, причем a,
b
не коллинеарны, с = а + b.
В этом случае линейная оболочка L(а,b,c)=
L(a,b).Здесь
линейная оболочка является двумерным
пространством, состоящем из всех
векторов, компланарных с векторами a
и b.
Вектора а,b
составляют базис в L(a,b).
Любой вектор из L
представляется в виде линейной комбинации
векторов а
и b.

Вообще,
в конечномерном пространстве R
всякое подпространство L

является линейной
оболочкой некоторой системы векторов.

Рассмотри
следующую задачу.
В евклидовом пространстве Eⁿ
задана линейная оболочка
,
где k

n.
Требуется:

1)Найти
размерность и базис линейной оболочки
;
2)Выделить в линейной оболочке

ортогональный базис и

достроить
его до
ортонормированного базиса евклидова

пространства
Eⁿ.

Если
схема решения первой задачи нам знакома,
то решение второй задачи строится на
следующем теоретическом результате.

Теорема
(Грама
– Шмидта)

Пусть

— система линейно независимых векторов
в евклидовом пространстве, где k

n,
являющихся образующей системой линейной
оболочки
.
Система векторов
,
описываемая формулами

,
. . .

где
коэффициенты

,
,

образует
ортогональный
базис
линейной оболочки
.

Доказательство.
Для
доказательства теоремы достаточно
доказать следующее утверждение: вектор

ортогонален вектору
.

Действительно,
умножая скалярно вектор

на вектор
,
получим

==0

Следствие.
Результат теоремы дает
алгоритм последовательной ортогонализации
системы линейно независимых элементов
( так
называемый
метод Грама — Шмидта).

Пример

В
евклидовом пространстве E⁴
линейная оболочка

задана образующей системой векторов

с координатами

Требуется:

а)
найти размерность и базис линейной
оболочки

б)
указать в линейной оболочке

ортонормированный базис

и
достроить его до ортонормированного
базиса евклидова

пространства
E⁴.

Решение.
Рассмотрим координатную матрицу
.
Так как

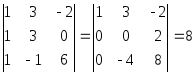
то
,
элементы

линейно независимы в E⁴
и образуют базис данной линейной
оболочки, являющейся подпространством
в E⁴.

Для
построения ортонормированного базиса
в E⁴
применим метод
ортогонализации
Грама-Шмидта. Получим

,

.

Записывая векторы
столбцами их координат, последовательно
найдем

Легко
проверить, что полученные элементы

попарно ортогональны. Найдем ортогональный
им вектор
.

Пусть
,
то неизвестные координаты

вектора Y₄
найдутся из условий

,,.

Так
как
,
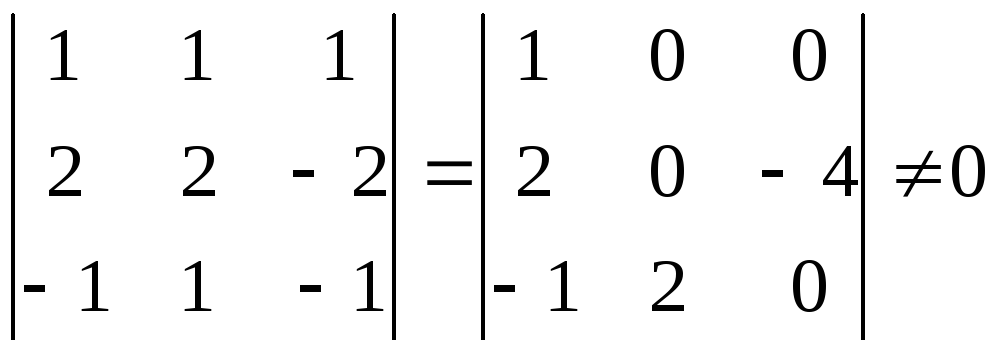
в последней системе неизвестные

можно взять в качестве базисных
неизвестных.

Если
для свободной (небазисной) неизвестной
,
то
.

Нормировав
найденные векторы
,
построим ортонормированный базис в E⁴:

Задача
решена.

В
завершении параграфа введем важное
определение.

Пусть

— — базис в Eⁿ
и векторы

представлены в этом базисе своими
разложениями

Тогда
скалярное произведение этих векторов
имеет вид

или в матричной форме
,
где

— столбцы координат векторов

в базисе

а симметричная матрица

составлена из скалярных произведений
базисных векторов:

В
общем случае в качестве элементов
матрицы А рассматривают скалярные
произведения произвольной системы
векторов а₁,
а₂,…,
а_n

Определение
3.
Определитель
матрицы А
скалярных произведений заданной системы
векторов
называют определителем
Грама.

Теорема
Произвольная
система
векторов,
заданных в ортонормированном
базисе,
будет линейно
независимой,
если ее определитель
Грама отличен от нуля.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Будем строить ортогональный базис $%f_1$%, $%f_2$%, $%f_3$%.

Полагаем $%f_1=e_1$%. Следующий вектор ищем в виде $%f_2=e_2+alpha f_1$%. Векторы должны быть ортогональны, откуда $%0=(f_1,f_2)=(e_1,e_2)+alpha(e_1,e_1)$%. Находим скалярные произведения: $%(e_1,e_1)=7$%; $%(e_1,e_2)=-5$%. Отсюда $%alpha=5/7$%. Чтобы избежать дробей, производим умножение на $%7$%, то есть полагаем $%f_2=7e_2+5f_1=(-9;12;3;-9)$%, и теперь можно сократить на $%3$%, окончательно имея $%f_2=(-3;4;1;-3)$% (в виде столбца).

Теперь ищем третий базисный вектор в виде $%f_3=e_3+beta f_1+gamma f_2$%, исходя из условий ортогональности $%0=(f_3,f_1)=(e_3,f_1)+beta(f_1,f_1)$% и $%0=(f_3,f_2)=(e_3,f_2)+gamma(f_2,f_2)$%. Скалярные произведения таковы: $%(f_1,f_1)=7$%; $%(f_2,f_2)=35$%; $%(e_3;f_1)=-8$%; $%(e_3;f_2)=24$%. Отсюда $%beta=8/7$% и $%gamma=-24/35$%. Производим домножение на 35, полагая $%f_3=35e_3+40f_1-24f_2=(-28;-21;21;7)$%, после чего сокращаем на 7, имея столбец $%f_3=(-4;-3;3;1)$%.

Искомый базис имеет вид $%f_1=(1;1;2;1)$%; $%f_2=(-3;4;1;-3)$%; $%f_3=(-4;-3;3;1)$%. Можно на всякий случай сделать проверку, убедившись в ортогональности построенной системы.

Источник

Итак, поднял свои старые конспекты, — действительно, для ответа на вопрос первого пункта нужно использовать процесс ортогонализации Грама-Шмидта. Нам заданы два вектора трёхмерного пространства (R^3), причём, насколько я понимаю, скалярное произведение считается по стандартной формуле (т.к. в условии не оговорено обратное). Так как параметр (i) в условии не пояснён, то будем считать его просто некоей константой.

Для начала отметим, что векторы линейно независимы. Показать это в нашем случае довольно просто. Обычно исследуют ранг матрицы, столбцы которой образуют заданные векторы. Но для двух векторов трёхмерного пространства можно использовать следующее утверждение: два вектора (a_1) и (a_2) будут линейно зависимыми, если существует константа (c neq 0) такая, что выполнено равенство (a_1=ccdot a_2). Если такой константы не существует, то векторы (a_1), (a_2) — линейно независимы. Допустим, такая константа есть в нашем случае, т.е. существует такое число (c neq 0), для которого выполнено равенство:

((1;i;1)=ccdot (0,i,0)), ((1;i;1)= (0;c i;0))

Векторы будут равными в том и только в том случае, когда равны их соответствующие координаты. Для равенства ((1;i;1)= (0;c i;0)) это означает следующее: (left{ begin{aligned} &1=0; \ & i=c i; \ & 1=0. end {aligned} right.). Первое и третье уравнения этой системы дают явное противоречие Поэтому нет такой константы, для которой равенство (a_1=ccdot a_2) выполнено. Вывод: векторы (a_1), (a_2) — линейно независимы.

Теперь перейдём к процессу ортогонализации. Нам нужно составить систему из двух векторов: (b_1), (b_2). Согласно процессу Грама-Шмидта, мы принимаем (b_1=a_1). Далее, (b_2=a_2-frac{a_2cdot b_1}{b_1cdot b_1}cdot b_1). Имеем:
(a_2cdot b_1=a_2 cdot a_1=(0;i;0)cdot (1;i;1)=0+i^2+0=i^2;)
(b_1cdot b_1=a_1 cdot a_1=|a_{1}|^{2}=1^2+i^2+1^2=i^2+2.)

Итак, (b_2=(0;i;0)-frac{i^2}{i^2+2}cdot (1;i;1)=left( -frac{i^2}{i^2+2}; frac{2i}{i^2+2}; -frac{i^2}{i^2+2} right))

Окончательно имеем: (b_1(1;i;1)), (b_2left( -frac{i^2}{i^2+2}; frac{2i}{i^2+2}; -frac{i^2}{i^2+2} right)).

«Именно то, что наиболее естественно, менее всего подобает человеку.» Братья Стругацкие, «Хромая судьба»

Источник

Задание №1

Дана матрица . Найти:

1) Базис линейной оболочки строк матрицы

2) Базис пространства решений системы

Решение:

Элементарными преобразованиями над строками матрицы приведем ее к ступенчатому виду:

Поменяем местами первую и вторую строки:

Умножим первую строку на 2 и сложим со второй, умножим первую строку на 3 и сложим с третьей, умножим первую строку на (-3) и сложим с четвертой, умножим первую строку на 3 и сложим с пятой

Умножим вторую строку на 4 и сложим с третьей, умножим вторую строку на (-1) и сложим с четвертой, умножим вторую строку на 3 и сложим с пятой

Разделим третью строку на (-6), разделим четвертую строку на 2, разделим пятую строку на (-5)

Умножим третью строку на (-1) и сложим с четвертой, умножим третью строку на (-1) и сложим с пятой

Строки матрицы 1, 2, 3 линейно независимы. Ранг матрицы равен 3, переменных 5, значит, базис пространства решений состоит из двух векторов. Примем переменные за базисные, а переменные за свободные. Выразим базисные переменные через свободные:

Сложим третью и вторую строки, умножим третью строку на 2 и сложим с первой

Умножим вторую строку на (-1)

Умножим вторую строку на (-3) и сложим с первой

Положим получим первый базисный вектор пространства решений:

Положим получим второй базисный вектор пространства решений:

Задание №2

Найти координаты столбца в ортогональном базисе:

Решение:

1) 1 способ

Представим вектор в виде линейной комбинации векторов

Последнему равенству соответствует система уравнений:

Решим систему уравнений по формулам Крамера:

2) Способ 2

Так как базис ортогональный, то координаты вектора в базисе можно найти по формулам:

Задание №3

Даны столбцы и . Найти столбец , ортогональный так, чтобы линейные оболочки и совпадали.

Решение:

Найдем вектор , применяя процесс ортогонализации:

Учитывая, что вектор есть линейная комбинация векторов и , то

Аналогично, вектор есть линейная комбинация векторов и , поэтому

Откуда получаем, что

Задание №4

Запишите матрицу линейного оператора в базисе , если известно, что ,

Решение:

-ый столбец матрицы оператора в базисе равен столбцу координат элемента в этом базисе:

Получаем

Задание №5

В стандартном базисе пространства найти матрицу оператора , если

, где

Решение:

Найдем образы базисных векторов

-ый столбец матрицы оператора в стандартном базисе равен столбцу координат элемента в этом базисе:

Источник

линейная-алгебра — Найти ортогональный базис

Используйте процесс Грама ― Шмидта, чтобы найти ортогональный базис в линейной оболочке следующей системы векторов: $%e_1=pmatrix$%, $%e_2=pmatrix$%, $%e_3=pmatrix$%.

задан 27 Окт ’14 16:00

1 ответ

Будем строить ортогональный базис $%f_1$%, $%f_2$%, $%f_3$%.

Сообщение 0201400 » 25 фев 2014, 20:20

Re: Найти ортогональный базис линейной оболочки

Жалоба
Цитата

Сообщение Алексей » 25 фев 2014, 23:00

Re: Найти ортогональный базис линейной оболочки

Жалоба
Цитата

Сообщение Алексей » 26 фев 2014, 19:39

Итак, поднял свои старые конспекты, — действительно, для ответа на вопрос первого пункта нужно использовать процесс ортогонализации Грама-Шмидта. Нам заданы два вектора трёхмерного пространства (R^3) , причём, насколько я понимаю, скалярное произведение считается по стандартной формуле (т.к. в условии не оговорено обратное). Так как параметр (i) в условии не пояснён, то будем считать его просто некоей константой.

Для начала отметим, что векторы линейно независимы. Показать это в нашем случае довольно просто. Обычно исследуют ранг матрицы, столбцы которой образуют заданные векторы. Но для двух векторов трёхмерного пространства можно использовать следующее утверждение: два вектора (a_1) и (a_2) будут линейно зависимыми, если существует константа (c neq 0) такая, что выполнено равенство (a_1=ccdot a_2) . Если такой константы не существует, то векторы (a_1) , (a_2) — линейно независимы. Допустим, такая константа есть в нашем случае, т.е. существует такое число (c neq 0) , для которого выполнено равенство:

Векторы будут равными в том и только в том случае, когда равны их соответствующие координаты. Для равенства ((1;i;1)= (0;c i;0)) это означает следующее: (left &1=0; \ & i=c i; \ & 1=0. end right.) . Первое и третье уравнения этой системы дают явное противоречие Поэтому нет такой константы, для которой равенство (a_1=ccdot a_2) выполнено. Вывод: векторы (a_1) , (a_2) — линейно независимы.

Теперь перейдём к процессу ортогонализации. Нам нужно составить систему из двух векторов: (b_1) , (b_2) . Согласно процессу Грама-Шмидта, мы принимаем (b_1=a_1) . Далее, (b_2=a_2-fraccdot b_1) . Имеем:
(a_2cdot b_1=a_2 cdot a_1=(0;i;0)cdot (1;i;1)=0+i^2+0=i^2;)
(b_1cdot b_1=a_1 cdot a_1=|a_|^=1^2+i^2+1^2=i^2+2.)

Ортогональный и ортонормированный базисы евклидова пространства

Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.

Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортогональным , если все образующие его векторы попарно ортогональны, т.е.

Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортонормированным , если его векторы попарно ортогональны и длина каждого из них равна единице:

Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.

В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис.

Выражение скалярного произведения через координаты сомножителей

Пусть [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис евклидова пространства, в котором векторы [math]mathbf[/math] и [math]mathbf[/math] имеют координаты [math]x_1,x_2,ldots,x_n[/math] и [math]y_1,y_2,ldots,y_n[/math] соответственно, т.е.

Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:

Преобразуем это выражение, используя операции с матрицами:

y=begin y_1&cdots& y_n end^T[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] , a [math]G(mathbf_1,mathbf_2,ldots, mathbf_n)[/math] — квадратная симметрическая матрица, составленная из скалярных произведений

которая называется матрицей Грама системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] .

Преимущества ортонормированного базиса

Для ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)[/math] ортонормированной системы [math]mathbf_1, mathbf_2,ldots, mathbf_n[/math] равна единичной матрице: [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)=E[/math] .

1. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] находится по формуле: [math]langle mathbf,mathbfrangle= x_1y_1+x_2y_2+ldots+x_ny_n[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] , а [math]y_1,ldots,y_n[/math] — координаты вектора [math]mathbf[/math] .

2. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] длина вектора [math]mathbf[/math] вычисляется по формуле [math]|mathbf|= sqrt[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] .

3. Координаты [math]x_1,ldots,x_n[/math] вектора [math]mathbf[/math] относительно ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] находятся при помощи скалярного произведения по формулам: [math]x_1=langle mathbf,mathbf_1rangle,ldots, x_n=langle mathbf,mathbf_nrangle[/math] .

В самом деле, умножая обе части равенства [math]mathbf= x_1 mathbf_1+ldots+x_n mathbf_n[/math] на [math]mathbf_1[/math] , получаем

Аналогично доказываются остальные формулы.

Изменение матрицы Грама при переходе от одного базиса к другому

Пусть [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] и [math](mathbf)= (mathbf_1,ldots,mathbf_n)[/math] — два базиса евклидова пространства [math]mathbb[/math] , a [math]S[/math] — матрица перехода от базиса [math](mathbf)[/math] к базису [math](mathbf)colon, (mathbf)=(mathbf)S[/math] . Требуется найти связь матриц Грама систем векторов [math](mathbf)[/math] и [math](mathbf)[/math]

По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] в разных базисах:

где [math]mathoplimits_)>,, mathoplimits_)>[/math] и [math]mathoplimits_)>,, mathoplimits_)>[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathoplimits_)>= S mathoplimits_)>,[/math] [math]mathoplimits_)>= S mathoplimits_)>[/math] , получаем тождество

Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому :

Записав это равенство для ортонормированных базисов [math](mathbf)[/math] и [math](mathbf)[/math] , получаем [math]E=S^TES[/math] , так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf_1,ldots,mathbf_n)= G(mathbf_1,ldots,mathbf_n)=E[/math] . Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^=S^T[/math] .

Свойства определителя Грама

Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.

1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.

Действительно, если система [math]mathbf_1, mathbf_2, ldots,mathbf_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math] , не равные нулю одновременно, что

Умножая это равенство скалярно на [math]mathbf_1[/math] , затем на [math]mathbf_2[/math] и т.д. на [math]mathbf_k[/math] , получаем однородную систему уравнений [math]G(mathbf_1,mathbf_2,ldots,mathbf_k)x=o[/math] , которая имеет нетривиальное решение [math]x=beginx_1&cdots&x_k end^T[/math] . Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.

Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.

Главный минор матрицы Грама системы [math]mathbf_1, mathbf_2,ldots,mathbf_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.

2. Определитель Грама [math]det_1,mathbf_2, ldots, mathbf_k)>[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] . Другими словами, если в процессе ортогонализации векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] получены векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , то

Действительно, в процессе ортогонализации по векторам [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] последовательно строятся векторы

После первого шага определитель Грама не изменяется

Выполним с определителем [math]det G(mathbf_1, mathbf_2, ldots,mathbf_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_)[/math] , а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_)[/math] . Получим определитель

Так как при этих преобразованиях определитель не изменяется, то

Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:

Вычислим правую часть этого равенства. Матрица [math]G(mathbf_1,mathbf_2,ldots, mathbf_k)[/math] Грама ортогональной системы [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] векторов является диагональной, так как [math]langle mathbf_i,mathbf_jrangle=0[/math] при [math]ine j[/math] . Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:

3. Определитель Грама любой системы [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] векторов удовлетворяет двойному неравенству

Докажем неотрицательность определителя Грама. Если система [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] , для которых по свойству 2:

Оценим теперь скалярный квадрат [math]langle mathbf_j,mathbf_jrangle[/math] . Выполняя процесс ортого-1нализации, имеем [math]mathbf_j= mathbf_j+ alpha_mathbf_1+ ldots+ alpha_mathbf_[/math] . Отсюда

Следовательно, по свойству 2 имеем

1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.

2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.

3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара :

Действительно, обозначив [math]a_1,a_2,ldots,a_n[/math] столбцы матрицы [math]A[/math] , элементы матрицы [math]A^TA[/math] можно представить как скалярные произведения (8.27): [math]langle a_i,a_jrangle= (a_i)^Ta_j[/math] . Тогда [math]A^TA=G(a_1,a_2,ldots,a_n)[/math] — матрица Грама системы [math]a_1,a_2,ldots,a_n[/math] векторов пространства [math]mathbb^n[/math] . По свойству 3, теореме 2.2 и свойству 1 определителя получаем доказываемое неравенство:

4. Если [math]A[/math] — невырожденная квадратная матрица, то любой главный минор матрицы [math]A^TA[/math] положителен. Это следует из пункта 2, учитывая представление произведения [math]A^TA=G(a_1,ldots,a_n)[/math] как матрицы Грама системы линейно независимых векторов [math]a_1,ldots,a_n[/math] — столбцов матрицы [math]A[/math] (см. пункт 3).

Изоморфизм евклидовых пространств

Два евклидовых пространства [math]mathbb[/math] и [math]mathbb'[/math] называются изоморфными [math](mathbbleftrightarrow mathbb’)[/math] , если они изоморфны как линейные пространства и скалярные произведения соответствующих векторов равны:

где [math](cdot,cdot)[/math] и [math](cdot,cdot)'[/math] — скалярные произведения в пространствах [math]mathbb[/math] и [math]mathbb'[/math] соответственно.

Напомним, что для изоморфизма конечномерных линейных пространств необходимо и достаточно, чтобы их размерности совпадали (см. теорему 8.3). Покажем, что это условие достаточно для изоморфизма евклидовых пространств (необходимость следует из определения). Как и при доказательстве теоремы 8.3, установим изоморфизм n-мерного евклидова пространства [math]mathbb[/math] с вещественным арифметическим пространством [math]mathbb^n[/math] со скалярным произведением (8.27). В самом деле, взяв в пространстве [math]mathbb[/math] какой-нибудь ортонормированный базис [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] , поставим в соответствие каждому вектору [math]mathbfin mathbb[/math] его координатный столбец [math]xin mathbb^n

(mathbfleftrightarrow x)[/math] . Это взаимно однозначное соответствие устанавливает изоморфизм линейных пространств: [math]mathbbleftrightarrow mathbb^n[/math] . В ортонормированном базисе скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] пространства [math]mathbb[/math] находится по формуле

(см. пункт 1 преимуществ ортонормированного базиса). Такое же выражение дает скалярное произведение (8.27) координатных столбцов [math]x[/math] и [math]y[/math] , т.е. скалярные произведения соответствующих элементов равны

Следовательно, евклидовы пространства [math]mathbb[/math] и [math]mathbb^n[/math] изоморфны.

Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]mathbb^n[/math] со стандартным скалярным произведением (8.27).

Источник