Как найти ортогональный вектор в пространстве - Исправление недочетов и поиск решений вместе с Examum.ru

Ортогональность векторов. Перпендикулярность векторов.

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

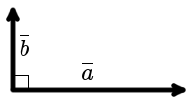рис. 1

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = < a_x ; a_y > и b = < b_x ; b_y > , условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 — 8 = 2 n — 4
2 n — 4 = 0
2 n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Ортогональные векторы

В данной публикации мы рассмотрим, какие векторы называются ортогональными, какое условие при этом должно выполняться. Также разберем примеры решения задач по этой теме.

Условие ортогональности векторов

Векторы a и b являются ортогональными, если угол между ними прямой (т.е. равен 90°).

Примечание: Скалярное произведение ортогональных векторов равняется нулю. Это и есть существенное условие их ортогональности.

a · b = 0

То есть, если в плоскости и , то

Примеры задач

Задание 1
Докажем, что векторы и ортогональны.

Решение:
a · b = 2 · (-2) + 4 · 1 = 0

Следовательно, заданные векторы являются ортогональными, так как их скалярное произведение равняется нулю.

Задание 2
При каком значении n векторы и ортогональны.

Решение:
a · b = 3 · 6 + (-9) · n = 0
18 – 9n = 0
n = 2

Таким образом, a и b ортогональны при n, равном двум.

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; — 1 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) = 2 — 2 = 0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a ¯ = < 3 ; — 1 >и b ¯ = < 7 ; 5 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 3 × 7 + ( — 1 ) × 5 = 21 — 5 = 16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = — 4 n = — 2

Ответ: векторы являются ортогональными при значении n = 2 .

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; — 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; — 1 ; 10 >являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; — 8 >будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

источники:

Ортогональные векторы

http://zaochnik.com/spravochnik/matematika/vektory/ortogonalnye-vektory-i-uslovie-ortogonalnosti/

Источник

Ортогональные векторы евклидова пространства и их свойства

Два вектора mathbf{u} и mathbf{v} евклидова пространства называются ортогональными (перпендикулярными), если их скалярное произведение равно нулю: langle mathbf{u},mathbf{v}rangle .

Система векторов $mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k$ называется ортогональной, если все ее векторы попарно ортогональны, т.е. $langle mathbf{u}_i, mathbf{v}_jrangle=0$ при ine j . Система векторов $mathbf{v}_1, mathbf{v}_2, ldots,mathbf{v}_k$ называется ортонормированной, если все ее векторы попарно Ортогональны и длина (норма) каждого вектора системы равна единице, т.е.

$langle mathbf{u}_i, mathbf{v}_jrangle=begin{cases}1,&i=j,\0,& ine j. end{cases}$

Говорят, что вектор mathbf{v} ортогонален (перпендикулярен) множеству , если он ортогонален каждому вектору из . Ортогональность векторов обозначается знаком перпендикуляра (perp) .

Свойства ортогональных векторов

1. Нулевой вектор ортогонален каждому вектору пространства.

2. Взаимно ортогональные ненулевые векторы линейно независимы.

В самом деле, пусть векторы $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ попарно ортогональны. Составим из них линейную комбинацию и приравняем ее нулевому вектору:

$lambda_1cdot mathbf{v}_1+lambda_2 mathbf{v}_2+ldots+lambda_k mathbf{v}_k=mathbf{o}.$

Умножим обе части равенства скалярно на вектор $mathbf{v}_1:$

$lambda_1langle mathbf{v}_1,mathbf{v}_1rangle+ lambda_2underbrace{langle mathbf{v}_1,mathbf{v}_2rangle}_{0}+ ldots+ lambda_kunderbrace{langle mathbf{v}_1, mathbf{v}_krangle}_{0}= underbrace{langle mathbf{v}_1,mathbf{o}rangle}_{0}.$

Следовательно, $lambda_1cdot|mathbf{v}_1|^2=0$ . Так как $mathbf{v}_1ne mathbf{o}$ , то lambda_1=o . Аналогично доказываем, что lambda_2=ldots= lambda_k=0 , т.е рассматриваемая линейная комбинация тривиальная. Значит, ортогональная система векторов $mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k$ линейно независима.

3. Если сумма взаимно ортогональных векторов равна нулевому вектору, то каждое из слагаемых равно нулевому вектору.

4. Если вектор mathbf{u} ортогонален каждому вектору системы $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ , то он также ортогонален и любой их линейной комбинации. Другими словами, если $mathbf{u}perp mathbf{v}_i,~ i=1,ldots,k$ , то $mathbf{u}perp operatorname{Lin} (mathbf{v}_1,ldots, mathbf{v}_k)$ .

5. Если вектор mathbf{u} ортогонален подмножеству евклидова пространства, то он ортогонален и линейной оболочке этого подмножества, т.e. mathbf{u}perp M~Rightarrow~ mathbf{u}perp operatorname{Lin}(M) .

6. Если $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ — ортогональная система векторов, то

$|mathbf{v}_1+mathbf{v}_2+ldots+mathbf{v}_k|^2= |mathbf{v}_1|^2+ |mathbf{v}_2|^2+ldots+|mathbf{v}_k|^2.$

Это утверждение является обобщением теоремы Пифагора.

Процесс ортогонализации Грама-Шмидта

Рассмотрим следующую задачу. Дана линейно независимая система $mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k$ векторов конечномерного евклидова пространства. Требуется построить ортогональную систему $mathbf{w}_1,mathbf{w}_2, ldots,mathbf{w}_k$ векторов того же пространства так, чтобы совпадали линейные оболочки:

$operatorname{Lin}(mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k)= operatorname{Lin}(mathbf{w}_1, mathbf{w}_2,ldots,mathbf{w}_k).$

Решение задачи находится при помощи процесса ортогонализации Грама–Шмидта, выполняемого за шагов.

1. Положить $mathbf{w}_1=mathbf{v}_1$ .

2. Найти $mathbf{w}_2=mathbf{v}_2-alpha_{21}cdot mathbf{w}_1$ , где $alpha_{21}= frac{langle mathbf{v}_2, mathbf{w}_1rangle}{langle mathbf{w}_1, mathbf{w}_1 rangle}$ .

3. Найти $mathbf{w}_3=mathbf{v}_3-alpha_{31} mathbf{w}_1-alpha_{32} mathbf{w}_2$ , где $alpha_{31}=frac{langle mathbf{v}_3,mathbf{w}_1 rangle}{langle mathbf{w}_1, mathbf{w}_1rangle},~ alpha_{32}= frac{langle mathbf{v}_3,mathbf{w}_2 rangle}{langle mathbf{w}_2, mathbf{w}_2rangle}$ ; и т.д.

4. Найти $mathbf{w}_k=mathbf{v}_k-sum_{i=1}^{k-1}alpha_{ki}mathbf{w}_i$ , где $alpha_{ki}= frac{langle mathbf{v}_k,mathbf{w}_irangle}{langle mathbf{w}_i, mathbf{w}_irangle},~ i=1,ldots,k-1$ .

Поясним процесс ортогонализации. Искомый на втором шаге вектор $mathbf{w}_2$ представлен в виде линейной комбинации $mathbf{w}_2=mathbf{v}_2-alpha mathbf{w}_1$ . Коэффициент alpha подберем так, чтобы обеспечить ортогональность векторов $mathbf{w}_2$ и $mathbf{w}_1$ . Приравняем нулю скалярное произведение этих векторов $langle mathbf{w}_2,mathbf{w}_1rangle= langle mathbf{v}_2,mathbf{w}_1rangle- alpha langle mathbf{w}_1,mathbf{w}_1rangle=0$ . Отсюда получаем, что $alpha=alpha_{21}$ (см. пункт 2 алгоритма). Подбор коэффициентов $alpha_{ji}$ на j-м шаге алгоритма делается так, чтобы искомый вектор $mathbf{w}_j$ был ортогонален всем ранее найденным векторам $mathbf{w}_1, mathbf{w}_2,ldots,mathbf{w}_{j-1}$ .

Замечания 8.11

1. Векторы, найденные в процессе ортогонализации, обладают следующими свойствами:

а) $mathbf{w}_j perp operatorname{Lin}(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_{j-1}),quad j=2,ldots,k$ ;

б) $operatorname{Lin}(mathbf{w}_1)= operatorname{Lin}(mathbf{v}_1),quad operatorname{Lin}(mathbf{w}_1,mathbf{w}_2, ldots,mathbf{w}_{j})= operatorname{Lin}(mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_{j}),quad j=2,ldots,k$ .

Первое свойство следует из свойства 4 ортогональных векторов. Второе свойство следует из того, что каждый вектор системы $mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_{j}$ линейно выражается через векторы $mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_{j}$ , и наоборот.

2. В процессе ортогонализации любой вектор $mathbf{w}_j$ можно заменить на коллинеарный ему ненулевой вектор $lambdacdot mathbf{w}_j$ . При этом свойства, перечисленные в пункте 1, не нарушаются.

3. Если система $mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_{k}$ векторов линейно зависима, то в процессе ортогонализации будем получать (на некоторых шагах) нулевые векторы. Действительно, если подсистема $mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_{j}$ линейно зависима, то $mathbf{v}_jin operatorname{Lin} (mathbf{w}_1,ldots,mathbf{w}_{j-1})$ . Тогда вектор $mathbf{w}_j=mathbf{v}_j-sum_{i=1}^{j-1}alpha_{ji} mathbf{w}_i$ одновременно удовлетворяет двум условиям $mathbf{w}_jperp operatorname{Lin}(mathbf{w}_1,ldots, mathbf{w}_{j-1})$ и $mathbf{w}_jin operatorname{Lin}(mathbf{w}_1,ldots,mathbf{w}_{j-1})$ . Значит, это нулевой вектор $mathbf{w}_i=mathbf{o}$ .

Поэтому в данном случае формулы вычисления коэффициентов $alpha_{ji}$ на j-м шаге следует записывать в виде:

$alpha_{j,i}= begin{cases}dfrac{langle mathbf{v}_j,mathbf{w}_irangle}{langle mathbf{w}_i,mathbf{w}_irangle},& mathbf{w}_ine mathbf{o},\ 0,& mathbf{w}_i=mathbf{o}. end{cases}i=1,2,ldots,j-1.$

В остальном процесс ортогонализации остается неизменным.

4. Процесс ортогонализации можно дополнить процессом нормировки, разделив каждый вектор ортогональной системы $mathbf{w}_1, mathbf{w}_2,ldots,mathbf{w}_k$ на его длину:

$mathbf{e}_i=dfrac{1}{|,mathbf{w}_i,|}cdot mathbf{w}_i,quad i=1,2,ldots,k.$

В результате получим ортонормированную систему $mathbf{e}_1,mathbf{e}_2, ldots, mathbf{e}_k$ , отвечающую условию $operatorname{Lin}(mathbf{e}_1, ldots, mathbf{e}_k)= operatorname{Lin}(mathbf{v}_1,ldots,mathbf{v}_k)$ . Если исходная система векторов является линейно зависимой, то среди векторов ортогональной системы $mathbf{w}_1,mathbf{w}_2, ldots,mathbf{w}_k$ будут нулевые. Чтобы получить ортонормированную систему, нулевые векторы следует исключить, а остальные векторы нормировать.

Пример 8.18. Даны системы векторов евклидовых пространств:

а) $x=begin{pmatrix}1\0end{pmatrix}!,quad y=begin{pmatrix}2\0end{pmatrix}!,quad z=begin{pmatrix}0\1end{pmatrix}$ — элементы пространства $mathbb{R}^2$ со скалярным произведением (8.26):

$langle x,yrangle= x^Tcdot! begin{pmatrix}2&1\1&1end{pmatrix}!cdot y= 2cdot x_1cdot y_1+x_1cdot y_2+x_2cdot y_1+x_2cdot y_2,;$

б) p_1(x)=1,~ p_2(x),~ p_3(x)=x^2 — элементы пространства C[-1;1] со скалярным произведением (8.28):

$langle f,grangle= intlimits_{-1}^{1}f(x)g(x),dx,.$

Провести

ортогонализацию данных векторов.

Решение. а) Заметим, что система векторов x,,y,,z линейно зависимая, так как и пропорциональны, поэтому используем процесс ортогонализации Грама–Шмидта с учетом пункта 3 замечаний 8.11.

1. Полагаем mathbf{u}=x .

2. Вычисляем $alpha_{21}=frac{langle y,mathbf{u}rangle}{langle mathbf{u}, mathbf{u}rangle}= frac{2!cdot!2!cdot!1+ 1!cdot!0+ 0!cdot!2+0!cdot!0}{2!cdot!1!cdot!1+ 1!cdot!0+ 0!cdot!1+0!cdot!0}=2$ и находим $mathbf{v}=y-alpha_{21}mathbf{u}= begin{pmatrix}2\0end{pmatrix}-2! begin{pmatrix}1\0end{pmatrix}= begin{pmatrix} 0\0 end{pmatrix}$ . Получили нулевой вектор.

3. Вычисляем $alpha_{31}=frac{langle z,mathbf{u}rangle}{langle mathbf{u}, mathbf{u}rangle}= frac{2!cdot!0!cdot!1+ 0!cdot!0+ 1!cdot!1+1!cdot!0}{2!cdot!1!cdot!1+ 1!cdot!0+0!cdot!1+ 0!cdot!0}=frac{1}{2},;$ $alpha_{32}=0$ согласно пункту 3 замечаний 8.11, так как mathbf{v}=mathbf{o} , и находим

$mathbf{w}=z-alpha_{31}cdot mathbf{u}-alpha_{32}cdot mathbf{v}= begin{pmatrix} 0\1end{pmatrix}-frac{1}{2}cdot! begin{pmatrix}1\0end{pmatrix}- 0cdot! begin{pmatrix}0\0 end{pmatrix}= begin{pmatrix}-1/2\1end{pmatrix}!.$

Проверим условие ортогональности $langle mathbf{u},mathbf{w}rangle= 2cdot1cdot left(-frac{1}{2}right)+ 1cdot1+ 0cdotleft(-frac{1}{2}right)+0cdot1=0$ .

Для получения ортонормированной системы исключаем нулевой вектор mathbf{v}=mathbf{o} , а остальные нормируем (см. пункт 4 замечаний 8.11):

$begin{gathered} |mathbf{u}|= sqrt{langle mathbf{u},mathbf{u} rangle}= sqrt{2},;\[5pt] |mathbf{w}|= sqrt{langle mathbf{w},mathbf{w}rangle}= sqrt{2cdot!left(-frac{1}{2}right)!cdot!left(-frac{1}{2}right)+left(-frac{1}{2}right)!cdot1+ 1cdotleft(-frac{1}{2}right)+ 1cdot1}= sqrt{1/2},;\[5pt] widehat{mathbf{u}}= frac{1}{|mathbf{u}|}cdot mathbf{u}= frac{1}{sqrt{2}}cdot! begin{pmatrix}1\0end{pmatrix}= begin{pmatrix}1/sqrt{2}\ 0end{pmatrix}!,quad widehat{mathbf{w}}= frac{1}{|mathbf{w}|}cdot mathbf{w}= frac{1}{sqrt{1/2}}cdot! begin{pmatrix}-1/2\0end{pmatrix}= begin{pmatrix}-1/sqrt{2}\ sqrt{2}end{pmatrix}!. end{gathered}$

Таким образом, для системы трех векторов x,,y,,z построена ортогональная система из трех векторов mathbf{u},mathbf{v},mathbf{w} и ортонормированная система из двух векторов widehat{mathbf{u}},widehat{mathbf{w}} . Линейные оболочки этих трех систем совпадают между собой (и со всем пространством $mathbb{R}^2$ ).

б) 1. Полагаем q_1(x)=p_1(x)=1 .

2. Вычисляем $alpha_{21}= frac{langle p_2,q_1rangle}{langle q_1,q_1rangle}= Biggl(intlimits_{-1}^{1} xcdot1,dxBiggr):Biggl(intlimits_{-1}^{1}1cdot1,dxBiggr)= left.{frac{1}{2},x^2}right|_{-1}^{1}:2=0$ и находим q_2(x)=x-0!cdot!1=x .

3. Вычисляем

$begin{aligned} alpha_{31}&= frac{langle p_3,q_1rangle}{langle q_1,q_1rangle}= Biggl(intlimits_{-1}^{1} x^2cdot1,dxBiggr):2= left.{frac{1}{3},x^3}right|_{-1}^{1}= frac{2}{3} cdotfrac{1}{2}=frac{1}{3},;\[5pt] alpha_{32}&= frac{langle p_3,q_2rangle}{langle q_2,q_2 rangle}= Biggl(intlimits_{-1}^{1} x^2cdot x,dxBiggr):Biggl(intlimits_{-1}^{1}xcdot x,dxBiggr)= left.{frac{1}{4},x^4}right|_{-1}^{1}:left.{frac{1}{3},x^3}right|_{-1}^{1}=0 end{aligned}$

и находим $q_3(x)= x^2-alpha_{31}cdot1-alpha_{32}cdot x=x^2-frac{1}{3}$ .

Получили ортогональные многочлены $q_1(x)=1,~ q_2(x)=x,~ q_3(x)=x^2-frac{1}{3}$ . Выполним нормировку:

$begin{array}{lll}|q_1(x)|= sqrt{langle q_1(x),q_1(x)rangle}= sqrt{2},;&~ |q_2(x)|= sqrt{langle q_2(x),q_2(x)rangle}= sqrt{dfrac{2}{3}},;&~ |q_3(x)|= sqrt{langle q_3(x),q_3(x) rangle}= dfrac{2}{3}sqrt{dfrac{2}{5}},;\[10pt] widehat{q}_1(x)= dfrac{q_1(x)}{|q_1(x)|}= dfrac{1}{sqrt{2}},;&~ widehat{q}_2(x)= dfrac{q_2(x)}{|q_2(x)|}= sqrt{dfrac{3}{2}}cdot x,;&~ widehat{q}_3(x)= dfrac{q_3(x)}{|q_3(x)|}= dfrac{3}{2}sqrt{dfrac{5}{2}}! left(x^2-dfrac{1}{3}right)!.end{array}$

Получили ортонормированные многочлены (многочлены Лежандра).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = {a_x; a_y} и b = {b_x; b_y}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b_y = 0

Пример 1. Доказать что вектора a = {1; 2} и b = {2; -1} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 2. Проверить являются ли вектора a = {3; -1} и b = {7; 5} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Пример 3. Найти значение числа n при котором вектора a = {2; 4} и b = {n; 1} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2n + 4
2n + 4 = 0
2n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z}, условие ортогональности запишется следующим образом:

a · b = a_x · b_x + a_y · b_y + a_z · b_z = 0

Пример 4. Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 5. Проверить являются ли вектора a = {2; 3; 1} и b = {3; 1; -9} ортогональными.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Пример 6. Найти значение числа n при котором вектора a = {2; 4; 1} и b = {n; 1; -8} будут ортогональны.

Решение:

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 — 8 = 2n — 4
2n — 4 = 0
2n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Источник

Условие ортогональности векторов
Примеры задач

Условие ортогональности векторов

Векторы a и b являются ортогональными, если угол между ними прямой (т.е. равен 90°).

a · b = 0

То есть, если в плоскости a = {a_x; a_y} и b = {b_x; b_y}, то a · b = a_x · b_x + a_y · b_y = 0

Примеры задач

Задание 1
Докажем, что векторы a = {2; 4} и b = {-2; 1} ортогональны.

Решение:
a · b = 2 · (-2) + 4 · 1 = 0

Следовательно, заданные векторы являются ортогональными, так как их скалярное произведение равняется нулю.

Задание 2
При каком значении n векторы a = {3; -9} и b = {6; n} ортогональны.

Решение:
a · b = 3 · 6 + (-9) · n = 0
18 – 9n = 0
n = 2

Таким образом, a и b ортогональны при n, равном двум.

Источник

Определение 1. Два вектора a
и b из E
называются ортогональными, если
их скалярное произведение равно нулю.

Определение 2. Система ненулевых
векторов b₁,
b₂, …, b_m
называется ортогональной
системой векторов, если
различные векторы этой системы попарно
ортогональны: b_ib_j
= 0 (i, j = 1,
2,…, m; i 
j).

Теорема 1. Ортогональная
система векторов линейно независима.

Доказательство. Пусть a₁,
a₂ , …, a_k
— ортогональная система ненулевых
векторов из V. Доказывая линейную
независимость системы a₁,
a₂ , …, a_k
допустим, что выполняется равенство:

₁a₁+ ₂a₂
+…+ _ka_k
= 0.

Скалярно умножим обе части этого
равенства на a_i , i
= 1, 2, …,k, получим в силу свойств 1, 2

₁(a₁a_i)
+ ₂(a₂a_i)
+…+ _i(a_ia_i)
+ … + _k(a_ka_i)
= 0.

В силу ортогональности системы отсюда
находим _i(a_ia_i)
= 0 . Так как a_i 
0 и скалярное произведение
невырожденное, то a_ia_i
 0. Таким образом

_i = 0 для всех i = 1, 2, …,k.
Таким образом система векторов a₁,
a₂ , …, a_k
линейно независима. 

Теорема 2. Для любой
линейно независимой системы
векторов a₁,
a₂, …, a_m
существует ортогональная система
векторов b₁,
b₂, …, b_m
таких, что каждый вектор b_j
(j = 1,
2,…, m)
линейная комбинация векторов b_j
(j = 1,
2,…, j).

Доказательство. Доказательство
проводим методом математической индукции
по k. При k =1 вторая система состоит
из одного вектора b₁ 
0 и поэтому ортогональна. Предположим,
что теорема справедлива для k1
векторов a₁, a₂
, …, a_k-₁, т.е. и
поэтим векторам найдена ортогональная
система ненулевых векторов b₁,
b₂ , …, b_k-₁
с указанными выше свойствами. Докажем
утверждение для k векторов. Для этого
ищем вектор b_k в виде:

b_k = ₁b₁+ ₂b₂
+…+ _k-1b_k-₁ a_k
,
(2)

где значения коэффициентов ₁
, ₂ ,…
, _k-1 находим
из условия ортогональности b_k
векторам b₁, b₂
, …, b_k-₁:

b_kb_i
= 0 , i = 1, 2, …,k —1,

которое можно записать в виде

₁(b₁b_i)+ ₂(b₂b_i)
+…+ _i(b_ib_i)
+…+ _k-1(b_k-₁b_i)+ a_kb_i=
0.

Так как по предположению b_jb_i
= 0 при всех i = 1, 2, …,k —1, i 
j, то находим

_i(b_ib_i)
+ a_kb_i=
0.

Так как b_i 
0, то b_i b_i
 0 и

_i = (a_kb_i)/(b_ib_i),
i = 1, 2, …,k —1.
(3)

При таком выборе коэффициентов _i
вектор b_k ортогонален
векторам b₁, b₂
, …, b_k-₁ и полученная
ситема векторов b₁, b₂
, …, b_k ортогональна.

Выразим вектор b_k через
вектора a₁, a₂
, …, a_k:

b_k = ₁a₁+ ₂(₂₁b₁+ a₂) + ₃(₃₁a₁+ ₃₂a₂
+ a₃) + … +_k-₁(_k-₁₁a₁+ _k-12a₂
+…+ _k-1k_—₂a_k-₂ a_k-₁)
a_k =

= (₁+ ₂₂₁+ ₃₃₁
+ … +_k-₁_k-₁₁)a₁+ (₂ +
₃₃₂
+ … + _k-₁_k-12)a₂ +…+ (_k-₂ _k-₁_k-1k_—₂)a_k-₂ _k-₁a_k-₁
a_k =

= _k₁a₁+ _k2a₂
+…+ _kk-1a_k-₁ a_k,

где _k₁
, _k2 ,
…, _kk-1 
Р. Вектор b_k
0. Действительно, если b_k= 0, то

_k₁a₁+ _k2a₂
+…+ _kk-1a_k-₁ a_k
= 0 .

Отсюда следует, что система a₁,
a₂ , …, a_k
линейно зависима, а это противоречит
условию.

Определение 3. Базис пространства
E_n
называется ортогональным, если он
образует ортогональную систему векторов.

Определение 4. Ортогональный базис
e₁, e₂,
…, e_n
называется ортонормированным, если
все его векторы единичную длину.

Теорема 4. Любое n-мерное
евклидово пространство обладает
ортогональным базисом.

Теорема 5. Любое n-мерное
евклидово пространство обладает
ортонормированным базисом.

Теорема 6. Скалярное
произведение векторов в ортонормированном
базисе равно сумме попарных произведений
соответствующих координат

Определение 7. Вектор a
евклидова пространства называется
нормированным, если его длина равна
единице, т.е. a
=1.

Определение 8. Ортогональный базис
евклидова пространства E_n
называется ортонормированным, если
все вектора базиса нормированные, т.е.
базис е₁, e₂,
…, е_n ортонормированный,
если выполняются условия:

1 е_ie_j
= 0, i, j = 1, 2, …,n, i 
j;

2 е_ie_i
= 1, i = 1, 2, …,n.

Теорема 7. Любое конечномерное
евклидово пространство Е_n
обладает ортонормированным базисом.

Доказательство. Скалярное произведение
в евклидовом пространстве невырожденное.
Поэтому по следствю теоремы 2 Е_n
обладает ортогональным базисом b₁,
b₂ , …, b_n
. Тогда легко показать, что система
векторов

е₁=

, e₂=

, …, е_n =

— линейно независима. Она образует
ортонормированный базис Е_n.
Действительно,

е_ie_j
=
,

если i, j = 1, 2, …,n, i 
j;

е_ie_i
=
,

i = 1, 2, …,n. 

Пример 1. Ортогонализовать систему
векторов a₁ = (1, 0, 0) , a₂
= =(1,1, 0), a₃
= (4, 2, 2) (скалярное
произведение определено в примере 1).
Пусть b₁ = (1, 0, 0).

По формуле (2) b₂ = ₁b₁
a₂, где коэффициент ₁находим по формуле (3): ₁=
(a₂b₁)/(b₁b₁)
= (1)/1
= 1. Тогда b₂ = b₁
a₂= (0, 1, 0).

По формуле (2) b₃ = ₁b₁+ ₂b₂
 a₃, где коэффициенты ₁, ₂находим
по формуле (3): ₁=
(a₃b₁)/(b₁b₁)
= 4/1 = 4.
₂= (a₃b₂)/(b₂b₂)
= (2)/1
= = 2. Тогда b₂ = 4b₁+ 2b₂ 
a₃= (0, 0, 2).

и ищем v₂ = (1,
1, 0), v₃ = (4, 2,
2) линейно независима и образует базис
пространства R³

Ортогональная система векторов a₁
= (1,0,0), a₂ = (0,1,0), a₃
= (0,0,2).

.5. Ортогональное дополнение.

Определение 1. Пусть L
— подпространство
евклидова пространства E.
Ортогональным дополнением
L называется множество
L^
всех векторов из E
ортогональных каждому вектору из
L: L^= {
bE

для любого вектора a

L имеем
b a = 0 }.

Теорема 1..
Для любого подпространства L
из E ортогональное
дополнение L^ есть
подпространство из
E.

Доказательство. По определению L^
E. Так как для
любого вектора a

L имеем
0 a
= 0, то 0 
L^
и L^
.

Проверим условия, входящие в определение
подпространства.

Пусть b,
c 
L^,
тогда для любого a

L имеем (b
+ c)
a = b
a + c
a = 0+ 0
= 0, и b
+ c

L^.
Пусть b

L^, R,
тогда для любого a

L имеем (b)
a =(b
a) =
0 = 0, и b

L^.

Отсюда по определению L^
— подпространство из E.


Теорема 2. Для
любого подпространства L
из E L
 L^
= {0}.

Доказать самостоятельно.

Теорема 3..
Если E —
конечномерное евклидово пространство,
то E прямая сумма
L и L^: E
= L 
L^.

Доказательство. Если L
= {0}, то
L^
= E. Если L

{0}, то
подпространство L имеет
базис e₁,
e₂,…,
e_k,
который в силу теоремы предыдущего
параграфа, можно считать ортогональным.
По теореме о базисах этот базис можно
дополнить до базиса пространства E
и полученный базис ортогонолизовать.
Получим ортогональный базис e₁,
e₂,…,
e_k,
e_k₊
₁,…,
e_n
пространства E. Тогда
любой вектор a

E представляется
единственным образом в виде:

a = ₁e₁
+ ₂e₂+…+ _ke_k+ _k₊
₁e_k₊
₁+…+
_n e_n
= b +
c;
b 
L, c
 L^.

Отсюда и теоремы 2 по определению прямой
суммы следует, что E
= L 
L^.


Следствие. Если E
— конечномерное евклидово пространство,
то dim E
= dim L
+ dim L^.

Теорема 4.
Пусть V — конечномерное векторное
пространство с невырожденным скалярным
призведением, L, L₁, L₂
— подпространства из V. Тогда
справедливы следующие свойства:

1 (L^)^
= L;

2 если L₁ L₂ , то
L₁^ L₂^;

3 (L₁+
L₂)^
= L₁^ L₂^;

4 (L₁
L₂)^
= L₁^+ L₂^.

Доказательство. 1
Eсли a  L ,
то ab =0 для любого b 
L^. Поэтому
a  L^
и L  (L^)^.
Докажем, что (L^)^
 L и тогда получим
(L^)^
= L.

Пусть a 
(L^)^
. Так как (L^)^
 V и по теореме
4 V = L  L^,
то a = b+ b
, где b  L
, b
 L^
. Поэтому bb
= 0. Так как a 
(L^)^
, то ab
= 0. Отсюда bb
= (a  b)b
= ab
ab
= 0 + 0 = 0. В силу невырожденности скалярного
произведения b
= 0 и a = b
L . Свойство доказано.

Свойства 2 — 4
рекомендуется доказать читателю
самостоятельно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник