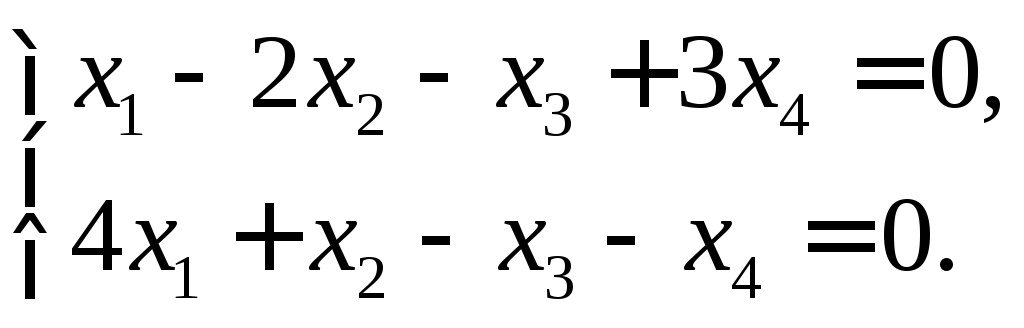Построить
ортонормированный базис подпространства
пространства
натянутого на систему векторов
и
Решение.Нам
требуется построить ортонормированный
базис евклидова пространствакоторое является линейной оболочкой
векторовПрименим к этим векторам процесс
ортогонализации.
Вначале возьмём
Вектор
будем искать в виде
Из условия перпендикулярности
получаем:
Следовательно,
Далее, следующий базисный вектор будем
искать в видеИз условий
и
получаем:
и
Отсюда
Таким образом, ортогональный базис
пространстватаков:
Ортонормированный базис получится,
если мы разделим каждый вектор на его
длину:
Пример.4 Дополнение системы векторов до ортогонального базиса.
Убедиться в том,
что векторы
ортогональны, и дополнить систему этих
векторов до ортогонального базиса.
Решение.Проверим ортогональность. Имеем:Следовательно,
Таким образом, мы можем положить
Другие векторы
ортогонального базиса удовлетворяют
условиями
Пусть
Условие
даёт систему
Найдём фундаментальную
систему решенийэтой системы. Вычтем
из второго уравнения первое, умноженное
на 4:
в правую часть:
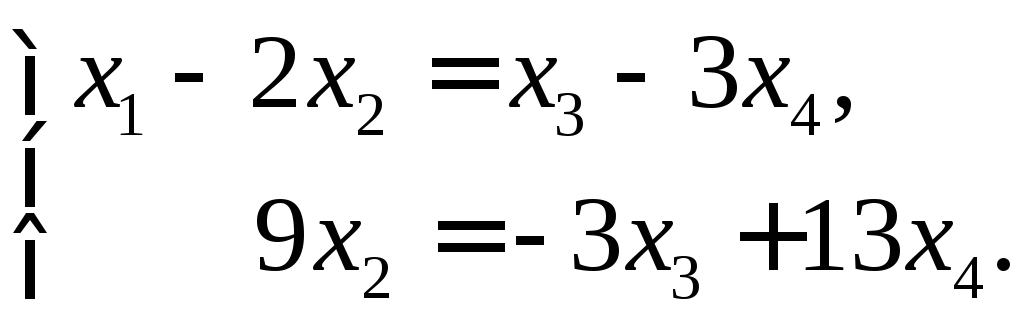
здесьсвободные, а переменные
–связанные. Придадим свободным
переменным значения: вначалезатем
и найдём
Составим таблицу:
|
|
|
|
|
|
1/3 |
|
1 |
0 |
|
|
|
0 |
1 |
Таким образом,
можно считать, что
Эти векторы перпендикулярны векторам
но не перпендикулярны друг другу.
Применим к ним процесс ортогонализации.
ПоложимТак как должно быть
то
Отсюда
Таким образом,
дополнением векторов
до ортогонального базиса будет служить,
например, система векторов
>>
d=eig(A)
%Функция
вычисляет собственные значения матрицы
A.
>>[U,D]=eig(A)
%Матрица
U
состоит правых собственных векторов,
удовлетворяющих соотношению A
* U=
U
* D.
Эти векторы нормированы так, что норма
каждого из них равна единице.
Упражнение.5
Линейное
преобразование, задано в некотором
базисе матрицей A.
Зная его собственные значения и
собственные векторы, найти матрицу из
ортонормированных собственных векторовU, проверить ее свойства
(является ли матрица ортогональной,
если нет, то почему, если да то почему).
Проверить результат с помощью функции
[U,D]=eig(A)
.
,
,
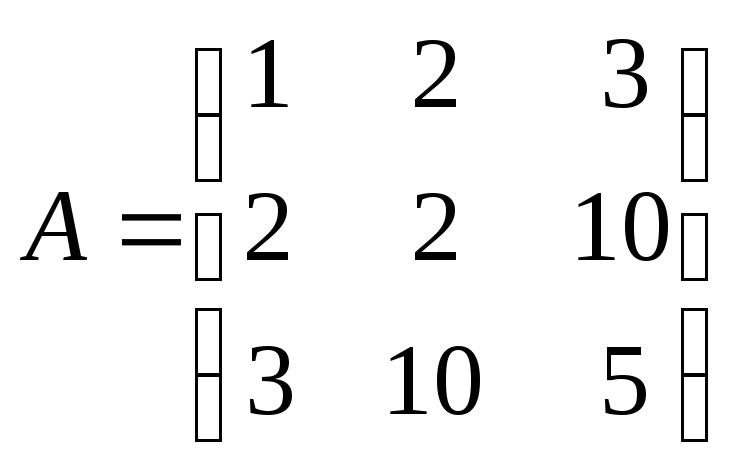

Проиллюстрировать
задачу.
-
Задание для самостоятельной работы
1. Выполнить в
тетради и в MATLAB все упражнения данного
практикума.
2. Решить задачи
средствами MATLAB.Продумать
решения каждой задачи средствами MATLAB.
Продумать геометрическую иллюстрацию.
Задачи.
Продумать
решения каждой задачи средствами MATLAB.
Продумать иллюстрации в MATLAB.
1.Привести
матрицу
оператора к диагональному виду и найти
соответствующий базис. Результаты
поверить с помощью функцииeig()
2.Для матрицы
диагональную матрицуDи
унитарную (ортогональную) матрицуUи проверить результат с помощью функцииeig()
3. Найти
собственные числа и собственные векторы
линейного оператора, заданного матрицей
Сначала найти на
листочке, затем с помощью встроенных
команд МАТЛАБ проверить себя.
4.В пространствеL3заданы векторыв некотором базисе. Доказать, что векторы
составляют базис, найти матрицу перехода
в базисе,
найти координаты векторав базисе
.
.
5.Заданы векторыв некотором базисе. Проверить, что
векторысоставляют базис. Применяя процесс
ортогонализации Шмидта построить новый
ортогональный базис..
Задачу сначала
решить на листочке. Опорные вычисления
проверяйте на МАТЛАБ. Затем сделать
графическую трехмерную иллюстрацию в
МАТЛАБ. Изобразите заданные векторы,
векторы нового базиса, орты нового
базиса, вспомогательные векторы
(демонстрирующие процесс ортогонализации).
В графическом окне выведите списком,
за какие цветные линии — векторы отвечают
за те или иные векторы из задачи.
Соседние файлы в папке МатЛаб — Алгебра
- #
- #
- #
- #
- #
- #
Векторные пространства
При проведении научных и прикладных исследование часто создаются модели, в которых рассматриваются точки и/или векторы определенных пространств. Например, в моделях шифров на эллиптических кривых используются аффинные и проективные пространства. К проективным прибегают тогда, когда необходимо ускорить вычисления, так как в формулах манипулирования с точками эллиптической кривой выводимых в рамках проективного пространства отсутствует операция деления на координату, которую в случае аффинного пространства обойти не удается.
Операция деления как раз одна из самых «дорогих» операций. Дело в том, что в алгебраических полях, а соответственно и в группах операция деления вообще отсутствует и выход из положения (когда не делить нельзя) состоит в том, что операцию деления заменяют умножением, но умножают не на саму координату, а на обращенное ее значение. Из этого следует, что предварительно надо привлекать расширенный алгоритм Евклида НОД и кое что еще. Одним словом, не все так просто как изображают авторы большинства публикаций о ЕСС. Почти все, что по этой теме опубликовано и не только в Интернете мне знакомо. Мало того, что авторы не компетентны и занимаются профанацией, оценщики этих публикаций плюсуют авторов в комментариях, т. е. не видят ни пробелов, ни явных ошибок. Про нормальную же статью пишут, что она уже 100500-я и от нее нулевой эффект. Так все пока на Хабре устроено, анализ публикаций делается огромный, но не качества содержания. Здесь возразить нечего — реклама двигатель бизнеса.
Линейное векторное пространство
Изучение и описание явлений окружающего мира с необходимостью приводит нас к введению и использованию ряда понятий таких как точки, числа, пространства, прямые линии, плоскости, системы координат, векторы, множества и др.
Пусть r = вектор трехмерного пространства, задает положение одной частицы (точки) относительно начала координат. Если рассматривать N элементов, то описание их положения требует задания 3∙N координат, которые можно рассматривать как координаты некоторого вектора в 3N-мерном пространстве. Если рассматривать непрерывные функции и их совокупности, то приходим к пространствам, размерность которых равна бесконечности. На практике часто ограничиваются использованием лишь подпространства такого бесконечномерного пространства функции координат, обладающего конечным числом измерений.
Пример 1. Ряд Фурье — пример использования пространства функций. Рассмотрим разложение произвольной функции в ряд Фурье
Его можно трактовать как разложение «вектора» f(x) по бесконечному набору «ортогональных» базисных векторов sinпх
Это пример абстрагирования и распространения понятия вектора на бесконечное число измерений. Действительно, известно, что при -π≤x≤π
Существо дальнейшего рассмотрения не пострадает, если мы отвлечемся от размерности абстрактного векторного пространства – будь — то 3, 3N или бесконечность, хотя для практических приложений больший интерес представляет конечномерные поля и векторные пространства.
Набор векторов r1, r2,… будем называть линейным векторным пространством L, если сумма любых двух его элементов тоже находится в этом наборе и если результат умножения элемента на число С также входит в этот набор. Оговоримся сразу, что значения числа С могут быть выбраны из вполне определенного числового множества Fр – поля вычетов по модулю простого числа р, которое считается присоединенным к L.
Пример 2. Набор из 8 векторов, составленных из n =5 -разрядных двоичных чисел
r0 = 00000, r1 = 10101, r2 = 01111, r3 = 11010, r4 = 00101, r5 = 10110, r6 = 01001, r7 = 11100 образует векторное пространство L, если числа С є <0,1>. Этот небольшой пример позволяет убедиться в проявлении свойств векторного пространства, включенных в его определение.
Суммирование этих векторов выполняется поразрядно по модулю два, т. е. без переноса единиц в старший разряд. Отметим, что если все С действительные (в общем случае С принадлежат полю комплексных чисел), то векторное пространство называют действительным.
Формально аксиомы векторного пространства и записываются так:
r1 + r2 = r2 + r1 = r3; r1, r2, r3 є L – коммутативность сложения и замкнутость;
(r1 + r2) + r3 = r1 + (r2 + r3) = r1 + r2 + r3 – ассоциативность сложения;
ri + r0 = r0 + ri = ri; ∀i, ri, r0 є L–существование нейтрального элемента;
ri +(- ri) = r0, для ∀i существует противоположный вектор (-ri) є L;
1∙ ri = ri ∙1 = ri существование единицы для умножения;
α (β∙ri) = (α∙β)∙ri; α, β, 1, 0 – элементы числового поля F, ri є L; умножение на скаляры ассоциативно; результат умножения принадлежит L;
(α + β) ri = α∙ri + β∙ri; для ∀i, ri є L, α, β – скаляры;
а (ri + rj) = ari + arj для всех а, ri, rj є L;
a∙0 = 0, 0∙ri = 0; (-1) ∙ ri = – ri.
Размерность и базис векторного пространства
При изучении векторных пространств представляет интерес выяснение таких вопросов, как число векторов, образующих все пространство; какова размерность пространства; какой наименьший набор векторов путем применения к нему операции суммирования и умножения на число позволяет сформировать все векторы пространства? Эти вопросы основополагающие и их нельзя обойти стороной, так как без ответов на них утрачивается ясность восприятия всего остального, что составляет теорию векторных пространств.
Оказалось, что размерность пространства самым тесным образом связана с линейной зависимостью векторов, и с числом линейно независимых векторов, которые можно выбирать в изучаемом пространстве многими способами.
Линейная независимость векторов
Набор векторов r1, r2, r3 … rр из L называют линейно независимым, если для них соотношение
выполняется только при условии одновременного равенства .
Все , k = 1(1)p, принадлежат числовому полю вычетов по модулю два
F = <0, 1>.
Если в некотором векторном пространстве L можно подобрать набор из р векторов, для которых соотношение выполняется, при условии, что не все одновременно, т.е. в поле вычетов оказалось возможным выбрать набор , k =1(1)р, среди которых есть ненулевые, то такие векторы называются линейно зависимыми.
Пример 3. На плоскости два вектора = T и = T являются линейно независимыми, так как в соотношении (T-транспонирование)
невозможно подобрать никакой пары чисел коэффициентов не равных нулю одновременно, чтобы соотношение было выполнено.
Три вектора = T , = T , = T образуют систему линейно зависимых векторов, так как в соотношении
равенство может быть обеспечено выбором коэффициентов , не равных нулю одновременно. Более того, вектор является функцией и (их суммой), что указывает на зависимость от и . Доказательство общего случая состоит в следующем.
Пусть хотя бы одно из значений , k = 1(1)р, например, , а соотношение выполнено. Это означает, что векторы , k = 1(1)р, линейно зависимы
Выделим явным образом из суммы вектор rр
Говорят, что вектор rр является л и н е й н о й комбинацией векторов или rр через остальные векторы выражается линейным образом, т.е. rр линейно зависит от остальных. Он является их функцией.
На плоскости двух измерений любые три вектора линейно зависимы, но любые два неколлинеарных вектора являются независимыми. В трехмерном пространстве любые три некомпланарных вектора линейно независимы, но любые четыре вектора всегда линейно зависимы.
Зависимость/независимость совокупности <> векторов часто определяют, вычисляя определитель матрицы Грама (ее строки скалярные произведения наших векторов). Если определитель равен нулю, среди векторов имеются зависимые, если определитель отличен от нуля — векторы в матрице независимы.
Определителем Грама (грамианом) системы векторов
в евклидовом пространстве называется определитель матрицы Грама этой системы:
где — скалярное произведение векторов
и .
Размерность и базис векторного пространства
Размерность s = d (L) пространства L определяется как наибольшее число векторов в L, образующих линейно независимый набор. Размерность – это не число векторов в L, которое может быть бесконечным и не число компонентов вектора.
Пространства, имеющие конечную размерность s ≠ ∞, называются конечномерными, если
s = ∞, – бесконечномерными.
Ответом на вопрос о минимальном числе и составе векторов, которые обеспечивают порождение всех векторов линейного векторного пространства является следующее утверждение.
Любой набор s линейно независимых векторов в пространстве L образует его б а з и с. Это следует из того, что любой вектор линейного s-мерного векторного пространства L может быть представлен единственным способом в виде линейной комбинации векторов базиса.
Зафиксируем и обозначим символом , i = 1(1)s, один из наборов, образующих базис пространства L. Тогда
Числа rki, i = 1(1)s называются координатами вектора в базисе , i = 1(1)s, причем rki = (, ).
Покажем единственность представления . Очевидно, что набор , является зависимым, так как , i = 1(1)s – базис. Другими словами, существуют такие не равные одновременно нулю, что .
При этом пусть , ибо если , то хоть одно из , было бы отлично от нуля и тогда векторы , i = 1(1)s, были бы линейно зависимы, что невозможно, так как это базис. Следовательно,
, будем иметь
Используя прием доказательства «от противного», допустим, что записанное представление не единственное в этом базисе и существует другое
Тогда запишем отличие представлений, что, естественно, выражается как
Очевидно, что правая и левая части равны, но левая представляет разность вектора с самим собой, т. е. равна нулю. Следовательно, и правая часть равна нулю. Векторы , i = 1(1)s линейно независимы, поэтому все коэффициенты при них могут быть только нулевыми. Отсюда получаем, что
а это возможно только при
Выбор базиса. Ортонормированность
Векторы называют нормированными, если длина каждого из них равна единице. Этого можно достичь, применяя к произвольным векторам процедуру нормировки.
Векторы называют ортогональными, если они перпендикулярны друг другу. Такие векторы могут быть получены применением к каждому из них процедуры ортогонализации. Если для совокупности векторов выполняются оба свойства, то векторы называются ортонормированными.
Необходимость рассмотрения ортонормированных базисов вызвана потребностями использования быстрых преобразований как одно –, так и многомерных функций. Задачи такой обработки возникают при исследовании кодов, кодирующих информационные сообщения в сетях связи различного назначения, при исследовании изображений, получаемых
посредством автоматических и автоматизированных устройств, в ряде других областей, использующих цифровые представления информации.
Определение. Совокупность n линейно независимых векторов n-мерного векторного
пространства V называется его базисом.
Теорема. Каждый вектор х линейного n-мерного векторного пространства V можно представить, притом единственным образом, в виде линейной комбинации векторов базиса. Векторное пространство V над полем F обладает следующими свойствами:
0·х = 0 (0 в левой части равенства – нейтральный элемент аддитивной группы поля F; 0 в правой части равенства – элемент пространства V, являющийся нейтральным единичным элементом аддитивной группы V, называемый нулевым вектором);
(– 1)·х = –х; –1є F; x є V; –x є V;
Если α·х = 0єV, то при х ≠ 0 всегда α = 0.
Пусть Vn(F) – множество всех последовательностей (х1, х2, …, хn) длины n с компонентами из поля F, т.е. Vn(F) = i =1(1)n >.
Сложение и умножение на скаляр определяются следующим образом:
x + y =(x1 + y1, x2 + y2, …, xn + yn);
α·х = (α·х1, α·х2,…, α·хn), где у = (у1, у2,…, уn),
тогда Vn(F) является векторным пространством над полем F.
Пример 4. В векторном пространстве rо = 00000, r1 = 10101, r2 = 11010, r3 = 10101 над полем F2 = <0,1>определить его размерность и базис.
Решение. Сформируем таблицу сложения векторов линейного векторного пространства
В этом векторном пространстве V= каждый вектор в качестве противоположного имеет самого себя. Любые два вектора, исключая rо, являются линейно независимыми, в чем легко убедиться
c1·r1 + c2·r2 = 0; c1·r1 + c3·r3 = 0; c2·r2 + c3·r3 = 0;
Каждое из трех соотношений справедливо только при одновременных нулевых значениях пар коэффициентов сi, сj є <0,1>.
При одновременном рассмотрении трех ненулевых векторов один из них всегда является суммой двух других или равен самому себе, а r1+r2+r3=rо.
Таким образом, размерность рассматриваемого линейного векторного пространства равна двум s = 2, d(L) = s = 2, хотя каждый из векторов имеет пять компонентов. Базисом пространства является набор (r1, r2). Можно в качестве базиса использовать пару (r1, r3).
Важным в теоретическом и практическом отношении является вопрос описания векторного пространства. Оказывается, любое множество базисных векторов можно рассматривать как строки некоторой матрицы G, называемой порождающей матрицей векторного пространства. Любой вектор этого пространства может быть представлен как линейная комбинация строк матрицы G ( как, например, здесь).
Если размерность векторного пространства равна k и равна числу строк матрицы G, рангу матрицы G, то очевидно, существует k коэффициентов с q различными значениями для порождения всех возможных линейных комбинаций строк матрицы. При этом векторное пространство L содержит q k векторов.
Множество всех векторов из ℤpn с операциями сложения векторов и умножения вектора на скаляр из ℤp есть линейное векторное пространство.
Определение. Подмножество W векторного пространства V, удовлетворяющее условиям:
Если w1, w2 є W, то w1+ w2 є W,
Для любых α є F и w є W элемент αw є W,
само является векторным пространством над полем F и называется подпространством векторного пространства V.
Пусть V есть векторное пространство над полем F и множество W ⊆ V. Множество W есть подпространство пространства V, если W по отношению к линейным операциям, определенным в V, есть линейное векторное пространство.
Таблица. Характеристики векторных пространств
Компактность матричного представления векторного пространства очевидна. Например, задание L векторов двоичных 50-разрядных чисел, среди которых 30 векторов образуют базис векторного пространства, требует формирования матрицы G[30,50], а описываемое количество векторов превышает 10 9 , что в поэлементной записи представляется неразумным.
Все базисы любого пространства L разбиваются подгруппой Р невырожденных матриц с det G > 0 на два класса. Один из них (произвольно) называют классом с положительно ориентированными базисами (правыми), другой класс содержит левые базисы.
В этом случае говорят, что в пространстве задана ориентация. После этого любой базис представляет собой упорядоченный набор векторов.
Если нумерацию двух векторов изменить в правом базисе, то базис станет левым. Это связано с тем, что в матрице G поменяются местами две строки, следовательно, определитель detG изменит знак.
Норма и скалярное произведение векторов
После того как решены вопросы о нахождении базиса линейного векторного пространства, о порождении всех элементов этого пространства и о представлении любого элемента и самого векторного пространства через базисные векторы, можно поставить задачу об измерении в этом пространстве расстояний между элементами, углов между векторами, значений компонентов векторов, длины самих векторов.
Действительное или комплексное векторное пространство L называется нормированным векторным пространством, если каждый вектор r в нем может быть сопоставлен действительному числу || r || – модулю вектора, норме. Единичный вектор – это вектор, норма которого равна единице. Нулевой вектор имеет компонентами нули.
Определение. Векторное пространство называется унитарным, если в нем определена бинарная операция, ставящая каждой паре ri, rj векторов из L в соответствие скаляр. В круглых скобках (ri, rj) записывается (обозначается) скалярное или внутреннее произведение ri и rj, причем
1. (ri, rj) = ri ∙ rj;
2. (ri, rj) = (rj ∙ ri)*, где * указывает на комплексное сопряжение или эрмитову симметрию;
3. (сri, rj) = с(ri ∙ rj) – ассоциативный закон;
4. (ri + rj, rk) = (ri ∙ rk)+ (rj ∙ rk)– дистрибутивный закон;
5. (ri, rk) ≥ 0 и из (ri, rj ) = 0 следует ri = 0.
Определение. Положительное значение квадратного корня называют нормой (или длиной, модулем) вектора ri. Если = 1, то вектор ri называют нормированным.
Два вектора ri, rj унитарного векторного пространства L взаимно ортогональны, если их скалярное произведение равно нулю, т.е. (ri, rj) = 0.
При s = 3 в линейном векторном пространстве в качестве базиса удобно выбирать три взаимно перпендикулярных вектора. Такой выбор существенно упрощает ряд зависимостей и вычислений. Этот же принцип ортогональности используется при выборе базиса в пространствах и других размерностей s > 3. Использование введенной операции скалярного произведения векторов обеспечивает возможность такого выбора.
Еще большие преимущества достигаются при выборе в качестве базиса векторного пространства ортогональных нормированных векторов – ортонормированного базиса. Если не оговорено специально, то далее всегда будем считать, что базис еi, i = 1(1)s выбран именно таким образом, т.е.
, где ij — символ Кронекера (1823 — 1891).
В унитарных векторных пространствах такой выбор всегда реализуем. Покажем реализуемость такого выбора.
Определение. Пусть S = есть конечное подмножество векторного пространства V над полем F.
Линейная комбинация векторов из S есть выражение вида а1∙v1 + а2∙v2 +…+ аn∙vn, где каждое аi ∊ F.
Оболочка для множества S (обозначение ) есть множество всех линейных комбинаций векторов из S. Оболочка для S есть подпространство пространства V.
Если U есть пространство в V, то U натянуто на S (S стягивает U), если =U.
Множество векторов S линейно зависимо над F, если в F существуют скаляры а1, а2,…, аn, не все нули, для которых а1∙v1+ а2∙v2 +…+ аn∙vn = 0. Если таких скаляров не существует, то множество векторов S линейно независимо над F.
Если векторное пространство V натянуто на линейно независимую систему векторов S (или система S стягивает пространство V), то система S называется базисом для V.
Приведение произвольного базиса к ортонормированному виду
Известно следующее утверждение [11]. Если ē i, i = 1(1)s – произвольная конечная или счетная система линейно независимых векторов в унитарном векторном пространстве, то существует ортонормированная система ē i, i = 1(1)s, порождающая то же самое линейное пространство (многообразие).
В основу процедуры приведения базиса к ортонормированному виду положен процесс ортогонализации Грама — Шмидта, который в свою очередь, реализуется рекуррентными формулами
В развернутом виде алгоритм ортогонализации и нормирования базиса содержит следующие условия:
Делим вектор ē 1, на его норму; получим нормированный вектор ē i=ē 1/(||ē 1 ||);
Формируем V2 = ē 2 — (ē 1, ē 2)e 1 и нормируем его, получим е 2. Ясно, что тогда
(е1, е2)
(е1, е2) – (е1, ē 2)( е1, е1) = 0;
Построив V3 = ē 3– (e1, ē 3)e1 – (e2, ē 3) e2 и нормируя его, получим е3.
Для него имеем сразу же (е1, е3) = (е2, е3) = 0.
Продолжая такой процесс, получим ортонормированный набор ē i, i = 1(1)s. Этот набор содержит линейно независимые векторы, поскольку все они взаимно ортогональны.
Убедимся в этом. Пусть выполняется соотношение
Если набор ē i, i = 1(1)s зависимый, то хотя бы один сj коэффициент не равен нулю сj ≠ 0.
Умножив обе части соотношения на еj, получаем
(ej, c1∙e1 ) + (ej, c2∙e2 )+ . + ( ej, cj∙ej ) +…+ ( ej, cs∙rs ) = 0.
Каждое слагаемое в сумме равно нулю как скалярное произведение ортогональных векторов, кроме (ej ,cj∙ej), которое равно нулю по условию. Но в этом слагаемом
(ej, ej) = 1 ≠ 0, следовательно, нулем может быть только cj.
Таким образом, допущение о том, что cj ≠ 0 неверно и набор является линейно независимым.
Пример 5. Задан базис 3-х мерного векторного пространства:
< , , >.
Скалярное произведение определено соотношением:
( , ) = x1∙y1+x2∙y2+x3∙y3+x4∙y4.
Процедурой ортогонализации Грама — Шмидта получаем систему векторов:
а1 = ; a2 = -4 /7= /7;
a3 = +½ — /5 = /10.
(a1,a2)= (1+4+9+0) = 14;
a1 E =a1/√14;
a2-(a1 E ,a2)∙a1 E =a2-(8/√14)(a1/√14)=a2 — 4∙a1/7;
Третий вектор читателю предлагается обработать самостоятельно.
Нормированные векторы получают вид:
a1 E =a1/√14;
a2 E = /√70;
a3 E = /√70;
Ниже в примере 6 дается подробный развернутый процесс вычислений получения ортонормированного базиса из простого (взятого наугад).
Пример 6. Привести заданный базис линейного векторного пространства к ортонормированному виду.
Дано: векторы базиса
Подпространства векторных пространств
Структура векторного пространства
Представление объектов (тел) в многомерных пространствах весьма непростая задача. Так, четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы, и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени «образность» и наглядность объекта или его частей способствует более успешному его изучению.
Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что рассмотрение многомерных и тем более бесконечномерных пространств и объектов в них лишает нас наглядности представлений, что весьма затрудняет исследование объектов в таких
пространствах. Даже, казалось бы, такие простые вопросы, как количественные характеристики элементов многогранников (число вершин, ребер, граней, и т. п.) в этих пространствах решены далеко не полностью.
Конструктивный путь изучения подобных объектов состоит в выделении их элементов (например, ребер, граней) и описании их в пространствах меньшей размерности. Так четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени
«образность» и наглядность объекта или его частей способствует более успешному их изучению.
Если L – расширение поля К, то L можно рассматривать как векторное (или линейное) пространство над полем К. Элементы поля L (т. е. векторы) образуют по сложению абелеву группу. Кроме того, каждый «вектор» а є L может быть умножен на «скаляр» r є K, и при этом произведение ra снова принадлежит L (здесь ra – просто произведение в смысле операции поля L элементов r и а этого поля). Выполняются также законы
r∙(a+b) = r∙a+r∙b, (r+s)∙a = r∙a + r∙s, (r∙s)∙a = r∙(s∙a) и 1∙а = а, где r,s є K, a,b є L.
Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что основным результатом при таком подходе является сокращение размерности выделяемых подпространств. Пусть в векторном линейном пространстве L выделены подпространства L1 и L2. В качестве базиса L1 выбирается меньший набор еi, i = 1(1)s1, s1 n – 1 способами. Следующий вектор v2 ≠ 0 не может быть выражен линейно через v1, т.е. может быть выбран q n – q способами и т.д.
Последний вектор vk ≠ 0 также линейно не выражается через предыдущие выбранные векторы v1,v2,…,vk и, следовательно, может быть выбран q n – q k – 1 способами. Общее число способов для выбора совокупности векторов v1,v2,…,vk, таким образом, определится как произведение числа выборов отдельных векторов, что и дает формулу (1). Для случая, когда k = п, имеем wп = wn, n и из формулы (I) получаем формулу (2).
Важные обобщающие результаты о размерностях подпространств.
Совокупность всех наборов длины n, ортогональных подпространству V1 наборов длины n, образует подпространство V2 наборов длины n. Это подпространство V2 называется нулевым пространством для V1.
Если вектор ортогонален каждому из векторов, порождающих подпространство V1, то этот вектор принадлежит нулевому пространству для V1.
Примером (V1) может служить множество 7-разрядных векторов порождающей матрицы (7,4)-кода Хемминга, с нулевым подпространством (V2) 7-разрядных векторов, образующих проверочную матрицу этого кода.
Если размерность подпространства (V1) наборов длины n равна k, то размерность нулевого подпространства (V2) равна n — k.
Если V2 — подпространство наборов длины n и V1 — нулевое пространство для V2, то (V2) — нулевое пространство для V1.
Пусть U∩V обозначает совокупность векторов, принадлежащих одновременно U и V, тогда U∩V является подпространством.
Пусть U⊕V обозначает подпространство, состоящее из совокупности всех линейных комбинаций вида au +bv, где u є U, v є V, a b — числа.
Сумма размерностей подпространств U∩V и U⊕V равна сумме размерностей подпространств U и V.
Пусть U2 — нулевое подпространство для U1, а V2 -нулевое пространство для V1. Тогда U2∩V2 является нулевым пространством для U1⊕V1.
Заключение
В работе рассмотрены основные понятия векторных пространств, которые часто используются при построении моделей анализа систем шифрования, кодирования и стеганографических, процессов, протекающих в них. Так в новом американском стандарте шифрования использованы пространства аффинные, а в цифровых подписях на эллиптических кривых и аффинные и
проективные (для ускорения обработки точек кривой).
Об этих пространствах в работе речь не идет (нельзя валить все в одну кучу, да и объем публикации я ограничиваю), но упоминания об этом сделаны не зря. Авторы, пишущие о средствах защиты, об алгоритмах шифров наивно полагают, что понимают детали описываемых явлений, но понимание евклидовых пространств и их свойств без всяких оговорок переносится в другие пространства, с другими свойствами и законами. Читающая аудитория вводится в заблуждение относительно простоты и доступности материала.
Создается ложная картина действительности в области информационной безопасности и специальной техники (технологий и математики).
В общем почин мною сделан, насколько удачно судить читателям.
Оглавление — Линейная алгебра
Ортогональный и ортонормированный базисы евклидова пространства
Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.
Базис [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е.
[math]langle mathbf{e}_i,mathbf{e}_jrangle=0[/math] при [math]ine j,~~ i=1,2,ldots,n,~~ j=1,2,ldots,n.[/math]
Базис [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] евклидова пространства называется ортонормированным, если его векторы попарно ортогональны и длина каждого из них равна единице:
[math]langle mathbf{e}_i,mathbf{e}_jrangle= begin{cases}1,&i=j,\ 0,&ine j end{cases}i=1,2,ldots,n,~~ j=1,2,ldots,n.[/math]
(8.31)
Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.
В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис.
Выражение скалярного произведения через координаты сомножителей
Пусть [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] — базис евклидова пространства, в котором векторы [math]mathbf{x}[/math] и [math]mathbf{y}[/math] имеют координаты [math]x_1,x_2,ldots,x_n[/math] и [math]y_1,y_2,ldots,y_n[/math] соответственно, т.е.
[math]mathbf{x}= x_1 mathbf{e}_1+x_2 mathbf{e}_2+ldots+ x_n mathbf{e}_n,qquad mathbf{y}= y_1 mathbf{e}_1+y_2 mathbf{e}_2+ldots+ y_n mathbf{e}_n.[/math]
Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:
[math]langle mathbf{x},mathbf{y}rangle= langle x_1 mathbf{e}_1+x_2 mathbf{e}_2+ldots+ x_n mathbf{e}_n,, y_1 mathbf{e}_1+y_2 mathbf{e}_2+ldots+ y_n mathbf{e}_n rangle= sum_{i=1}^{n}sum_{i=1}^{n}x_iy_jlangle mathbf{e}_i,mathbf{e}_jrangle.[/math]
Преобразуем это выражение, используя операции с матрицами:
[math]langle mathbf{x},mathbf{y}rangle= x^Tcdot G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)cdot y,[/math]
(8.32)
где [math]x=begin{pmatrix}x_1&cdots x_nend{pmatrix}^T,~ y=begin{pmatrix} y_1&cdots& y_n end{pmatrix}^T[/math] — координатные столбцы векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math], a [math]G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)[/math] — квадратная симметрическая матрица, составленная из скалярных произведений
[math]G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)= begin{pmatrix} langle mathbf{e}_1,mathbf{e}_1rangle& langle mathbf{e}_1,mathbf{e}_2rangle &cdots&langle mathbf{e}_1, mathbf{e}_nrangle\ langle mathbf{e}_2,mathbf{e}_1rangle& langle mathbf{e}_2, mathbf{e}_2rangle &cdots&langle mathbf{e}_2,mathbf{e}_nrangle\ vdots&vdots&ddots&vdots\ langle mathbf{e}_n,mathbf{e}_1rangle& langle mathbf{e}_n,mathbf{e}_2rangle &cdots&langle mathbf{e}_n,mathbf{e}_nrangle end{pmatrix}!.[/math]
(8.33)
которая называется матрицей Грама системы векторов [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math].
Преимущества ортонормированного базиса
Для ортонормированного базиса [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама [math]G(mathbf{e}_1, mathbf{e}_2,ldots,mathbf{e}_n)[/math] ортонормированной системы [math]mathbf{e}_1, mathbf{e}_2,ldots, mathbf{e}_n[/math] равна единичной матрице: [math]G(mathbf{e}_1, mathbf{e}_2,ldots,mathbf{e}_n)=E[/math].
1. В ортонормированном базисе [math]mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n[/math] скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] находится по формуле: [math]langle mathbf{x},mathbf{y}rangle= x_1y_1+x_2y_2+ldots+x_ny_n[/math], где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf{x}[/math], а [math]y_1,ldots,y_n[/math] — координаты вектора [math]mathbf{y}[/math].
2. В ортонормированном базисе [math]mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n[/math] длина вектора [math]mathbf{x}[/math] вычисляется по формуле [math]|mathbf{x}|= sqrt{x_1^2+x_2^2+ldots+x_n^2}[/math], где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf{x}[/math].
3. Координаты [math]x_1,ldots,x_n[/math] вектора [math]mathbf{x}[/math] относительно ортонормированного базиса [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] находятся при помощи скалярного произведения по формулам: [math]x_1=langle mathbf{x},mathbf{e}_1rangle,ldots, x_n=langle mathbf{x},mathbf{e}_nrangle[/math].
В самом деле, умножая обе части равенства [math]mathbf{x}= x_1 mathbf{e}_1+ldots+x_n mathbf{e}_n[/math] на [math]mathbf{e}_1[/math], получаем
[math]langle mathbf{x},mathbf{e}_1rangle= x_1underbrace{langlemathbf{e}_1, mathbf{e}_1 rangle}_{1}+ x_2underbrace{langle mathbf{e}_1,mathbf{e}_2 rangle}_{0}+ldots+ x_nunderbrace{langle mathbf{e}_n, mathbf{e}_n rangle}_{0}quad Leftrightarrowquad x_1=langle mathbf{x},mathbf{e}_1rangle.[/math]
Аналогично доказываются остальные формулы.
Изменение матрицы Грама при переходе от одного базиса к другому
Пусть [math](mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n)[/math] и [math](mathbf{f})= (mathbf{f}_1,ldots,mathbf{f}_n)[/math] — два базиса евклидова пространства [math]mathbb{E}[/math], a [math]S[/math] — матрица перехода от базиса [math](mathbf{e})[/math] к базису [math](mathbf{f})colon, (mathbf{f})=(mathbf{e})S[/math]. Требуется найти связь матриц Грама систем векторов [math](mathbf{e})[/math] и [math](mathbf{f})[/math]
По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] в разных базисах:
[math]langle mathbf{x},mathbf{y}rangle= {mathop{x}limits_{(mathbf{e})}}^Tcdot, G(mathbf{e}_1,ldots,mathbf{e}_n)cdot mathop{mathbf{y}}limits_{(mathbf{e})}= {mathop{x}limits_{(mathbf{f})}}^Tcdot, G(mathbf{f}_1,ldots,mathbf{f}_n)cdot mathop{mathbf{y}}limits_{(mathbf{f})},[/math]
где [math]mathop{x}limits_{(mathbf{e})},, mathop{x}limits_{(mathbf{f})}[/math] и [math]mathop{y}limits_{(mathbf{e})},, mathop{y}limits_{(mathbf{f})}[/math] — координатные столбцы векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathop{x}limits_{(mathbf{e})}= S mathop{x}limits_{(mathbf{f})},[/math] [math]mathop{y}limits_{(mathbf{e})}= S mathop{y}limits_{(mathbf{f})}[/math], получаем тождество
[math]{mathop{x}limits_{(mathbf{f})}}^Tcdot S^Tcdot, G(mathbf{e}_1,ldots,mathbf{e}_n)cdot Scdot mathop{mathbf{y}}limits_{(mathbf{f})}= {mathop{x}limits_{(mathbf{f})}}^Tcdot, G(mathbf{f}_1,ldots,mathbf{f}_n)cdot mathop{mathbf{y}}limits_{(mathbf{f})}.[/math]
Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому:
[math]G(mathbf{f}_1,ldots,mathbf{f}_n)= S^Tcdot G(mathbf{e}_1,ldots,mathbf{e}_n)cdot S.[/math]
Записав это равенство для ортонормированных базисов [math](mathbf{e})[/math] и [math](mathbf{f})[/math], получаем [math]E=S^TES[/math], так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf{e}_1,ldots,mathbf{e}_n)= G(mathbf{f}_1,ldots,mathbf{f}_n)=E[/math]. Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^{-1}=S^T[/math].
Свойства определителя Грама
Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.
1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.
Действительно, если система [math]mathbf{v}_1, mathbf{v}_2, ldots,mathbf{v}_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math], не равные нулю одновременно, что
[math]x_1cdot mathbf{v}_1+x_2cdot mathbf{v}_2+ldots+ x_kcdot mathbf{v}_k= mathbf{o}.[/math]
Умножая это равенство скалярно на [math]mathbf{v}_1[/math], затем на [math]mathbf{v}_2[/math] и т.д. на [math]mathbf{v}_k[/math], получаем однородную систему уравнений [math]G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)x=o[/math], которая имеет нетривиальное решение [math]x=begin{pmatrix}x_1&cdots&x_k end{pmatrix}^T[/math]. Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.
Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.
Главный минор матрицы Грама системы [math]mathbf{v}_1, mathbf{v}_2,ldots,mathbf{v}_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.
2. Определитель Грама [math]det{G (mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k)}[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k[/math]. Другими словами, если в процессе ортогонализации векторов [math]mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k[/math] получены векторы [math]mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k[/math], то
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots,mathbf{w}_k)= langle mathbf{w}_1,mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldotscdot langle mathbf{w}_k,mathbf{w}_krangle.[/math]
Действительно, в процессе ортогонализации по векторам [math]mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k[/math] последовательно строятся векторы
[math]mathbf{w}_1=mathbf{v}_1,quad mathbf{w}_2= mathbf{v}_2- alpha_{21} mathbf{w}_1,quad ldots,quad mathbf{w}_k= mathbf{v}_k- sum_{j=1}^{k-1}alpha_{kj} mathbf{w}_j.[/math]
После первого шага определитель Грама не изменяется
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{v}_2, ldots,mathbf{v}_k).[/math]
Выполним с определителем [math]det G(mathbf{w}_1, mathbf{v}_2, ldots,mathbf{v}_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_{21})[/math], а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_{21})[/math]. Получим определитель
[math]det G(mathbf{w}_1,mathbf{v}_2-alpha_{21}mathbf{w}_1,ldots,mathbf{v}_k)= det G(mathbf{w}_1,mathbf{w}_2, mathbf{v}_3, ldots,mathbf{v}_k).[/math]
Так как при этих преобразованиях определитель не изменяется, то
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2,mathbf{v}_3, ldots,mathbf{v}_k).[/math]
Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots,mathbf{w}_k).[/math]
Вычислим правую часть этого равенства. Матрица [math]G(mathbf{w}_1,mathbf{w}_2,ldots, mathbf{w}_k)[/math] Грама ортогональной системы [math]mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k[/math] векторов является диагональной, так как [math]langle mathbf{w}_i,mathbf{w}_jrangle=0[/math] при [math]ine j[/math]. Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:
[math]det G(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k)= langle mathbf{w}_1, mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldots langle mathbf{w}_k, mathbf{w}_krangle.[/math]
3. Определитель Грама любой системы [math]mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k[/math] векторов удовлетворяет двойному неравенству
[math]0leqslant det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k) leqslant langle mathbf{v}_1, mathbf{v}_1ranglecdot langle mathbf{v}_2,mathbf{v}_2ranglecdot ldots langle mathbf{v}_k, mathbf{v}_krangle.[/math]
Докажем неотрицательность определителя Грама. Если система [math]mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf{w}_1,mathbf{w}_2, ldots, mathbf{w}_k[/math], для которых по свойству 2:
[math]det G(mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots, mathbf{w}_k)= |mathbf{w}_1|^2cdot |mathbf{w}_2|^2cdot ldotscdot |mathbf{w}_k|^2>0.[/math]
Оценим теперь скалярный квадрат [math]langle mathbf{v}_j,mathbf{w}_jrangle[/math]. Выполняя процесс ортого-1нализации, имеем [math]mathbf{v}_j= mathbf{w}_j+ alpha_{j,1}mathbf{w}_1+ ldots+ alpha_{j,j-1}mathbf{w}_{j-1}[/math]. Отсюда
[math]langle mathbf{v}_j,mathbf{w}_jrangle= langle mathbf{w}_j,mathbf{w}_jrangle+ sum_{i=1}^{j-1}alpha_{i,i}^2 langle mathbf{w}_j,mathbf{w}_jrangle geqslant langle mathbf{w}_j, mathbf{w}_jrangle.[/math]
Следовательно, по свойству 2 имеем
[math]langle mathbf{v}_1,mathbf{v}_1ranglecdot langle mathbf{v}_2,mathbf{v}_2 ranglecdot ldotscdot langle mathbf{v}_k,mathbf{v}_kranglegeqslant langle mathbf{w}_1, mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldotscdot langle mathbf{w}_k, mathbf{w}_krangle= det G(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k).[/math]
Замечания 8.12
1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.
2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.
3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара:
[math](det{A})^2leqslant prod_{i=1}^{n}Bigl(a_{i,1}^2+ a_{i,2}^2+ldots+ a_{i,n}^2Bigr).[/math]
Действительно, обозначив [math]a_1,a_2,ldots,a_n[/math] столбцы матрицы [math]A[/math], элементы матрицы [math]A^TA[/math] можно представить как скалярные произведения (8.27): [math]langle a_i,a_jrangle= (a_i)^Ta_j[/math]. Тогда [math]A^TA=G(a_1,a_2,ldots,a_n)[/math] — матрица Грама системы [math]a_1,a_2,ldots,a_n[/math] векторов пространства [math]mathbb{R}^n[/math]. По свойству 3, теореме 2.2 и свойству 1 определителя получаем доказываемое неравенство:
[math]begin{aligned} (det{A})^2&= det{A}cdotdet{A}= det{A^T}cdotdet{A}= det(A^TA)= det G(a_1,a_2,ldots,a_n)leqslant\[2pt] &leqslant |a_1|^2cdot |a_2|^2cdot ldotscdot |a_n|^2= prod_{i=1}^{n}Bigl(a_{i,1}^2+ a_{i,2}^2+ldots+ a_{i,n}^2Bigr). end{aligned}[/math]
4. Если [math]A[/math] — невырожденная квадратная матрица, то любой главный минор матрицы [math]A^TA[/math] положителен. Это следует из пункта 2, учитывая представление произведения [math]A^TA=G(a_1,ldots,a_n)[/math] как матрицы Грама системы линейно независимых векторов [math]a_1,ldots,a_n[/math] — столбцов матрицы [math]A[/math] (см. пункт 3).
Изоморфизм евклидовых пространств
Два евклидовых пространства [math]mathbb{E}[/math] и [math]mathbb{E}'[/math] называются изоморфными [math](mathbb{E}leftrightarrow mathbb{E}’)[/math], если они изоморфны как линейные пространства и скалярные произведения соответствующих векторов равны:
[math]left.{begin{matrix}mathbf{u}leftrightarrow mathbf{u}’\ mathbf{v}leftrightarrow mathbf{v}’end{matrix}}right}quad Rightarrowquad langle mathbf{u},mathbf{v}rangle= langle mathbf{u}’,mathbf{v}’rangle’.[/math]
‘
где [math](cdot,cdot)[/math] и [math](cdot,cdot)'[/math] — скалярные произведения в пространствах [math]mathbb{E}[/math] и [math]mathbb{E}'[/math] соответственно.
Напомним, что для изоморфизма конечномерных линейных пространств необходимо и достаточно, чтобы их размерности совпадали (см. теорему 8.3). Покажем, что это условие достаточно для изоморфизма евклидовых пространств (необходимость следует из определения). Как и при доказательстве теоремы 8.3, установим изоморфизм n-мерного евклидова пространства [math]mathbb{E}[/math] с вещественным арифметическим пространством [math]mathbb{R}^n[/math] со скалярным произведением (8.27). В самом деле, взяв в пространстве [math]mathbb{E}[/math] какой-нибудь ортонормированный базис [math](mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n)[/math], поставим в соответствие каждому вектору [math]mathbf{x}in mathbb{E}[/math] его координатный столбец [math]xin mathbb{R}^n~ (mathbf{x}leftrightarrow x)[/math]. Это взаимно однозначное соответствие устанавливает изоморфизм линейных пространств: [math]mathbb{E}leftrightarrow mathbb{R}^n[/math]. В ортонормированном базисе скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] пространства [math]mathbb{E}[/math] находится по формуле
[math]langle mathbf{x},mathbf{y}rangle= x_1cdot y_1+x_2cdot y_2+ldots+x_ncdot y_n[/math]
(см. пункт 1 преимуществ ортонормированного базиса). Такое же выражение дает скалярное произведение (8.27) координатных столбцов [math]x[/math] и [math]y[/math], т.е. скалярные произведения соответствующих элементов равны
[math]langle mathbf{x},mathbf{y}rangle= x_1cdot y_1+x_2cdot y_2+ldots+x_ncdot y_n=x^Tcdot y.[/math]
Следовательно, евклидовы пространства [math]mathbb{E}[/math] и [math]mathbb{R}^n[/math] изоморфны.
Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]mathbb{R}^n[/math] со стандартным скалярным произведением (8.27).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Все курсы > Линейная алгебра > Занятие 2
Продолжим работать в том же ноутбуке⧉
Определение
С понятием вектора тесно связано понятие векторного или линейного пространства (vector space, linear space).
По большому счету, векторное пространство — это множество векторов, которые мы можем складывать (vector addition) и умножать на число или скаляр (scalar multiplication).
В частности, сложение и умножение на число двумерных (состоящих из двух компонентов) векторов дает нам двумерный вектор, трехмерных — трехмерный и так далее.
$$ begin{bmatrix} 3 \ 4 end{bmatrix} + 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} = begin{bmatrix} 5 \ 8 end{bmatrix} $$
При этом сложить, например, двумерный и трехмерный вектор нельзя
$$ begin{bmatrix} 3 \ 4 end{bmatrix} + begin{bmatrix} 4 \ 3 \ 3 end{bmatrix} = ? $$
Также нельзя сформировать векторное пространство из двумерных векторов, лежащих только в первой четверти координатной плоскости. Хотя для таких векторов будет задана операция сложения, при умножении на отрицательный скаляр мы можем выйти за пределы первой четверти.
Поэтому говорят, что векторное пространство должно быть замкнуто относительно операций сложения и умножения на скаляр (closed under vector addition and scalar multiplication).
Двумерное пространтсво вещественных чисел принято обозначать $R^2$, трехмерное $R^3$, n-мерное — $R^n$.
Отметим, что вектор $begin{bmatrix} 1 \ 2 \ 0 end{bmatrix}$ — это вектор в $R^3$ с нулевым третьим компонентом.
Линейная комбинация векторов
Любой вектор внутри одного пространства (например, $R^2$) можно представить как линейную комбинацию конечного числа векторов (linear combination of a finite set of vectors).
$$ 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} + 3 cdot begin{bmatrix} 2 \ 1 end{bmatrix} = begin{bmatrix} 8 \ 7 end{bmatrix} $$
Под линейной комбинацией, как вы видите, понимается опять же сложение векторов и их умножение на число.
Аксиомы векторных пространств
Операции в векторных пространствах должны отвечать следующим правилам:
- $ mathbf u + (mathbf v + mathbf w) = (mathbf u + mathbf v) + mathbf w $
- $ mathbf v + mathbf w = mathbf w + mathbf v $
- Существует нулевой вектор $ mathbf 0 Rightarrow mathbf 0 + mathbf v = mathbf v, forall mathbf v $
- Для каждого $ mathbf v $ существует $ -mathbf v Rightarrow mathbf v + (-mathbf v) $
- $ a(b mathbf v) = (ab) mathbf v $
- $ 1 mathbf v = mathbf v $
- $ a(mathbf v + mathbf w) = a mathbf v + a mathbf w $
- $ (a + b) mathbf v = a mathbf v + b mathbf v $
Этим правилам могут отвечать не только векторы действительных чисел в пространстве $R^n$ (Евклидово пространство), но и, в частности, векторы функций. В этом случае речь идет о функциональных пространствах (function spaces).
Видео про абстрактные векторные пространства⧉.
Примечание. Некоторые понятия, упомянутые в видео выше, в частности, линейные преобразования (linear transformations), ядро матрицы (null space) и собственные векторы и значения (eigenvectors and eigenvalues) будут рассмотрены на более поздних занятиях.
Серия видео про алгебраические структуры⧉.
Внутреннее произведение
Скалярное произведение (dot product) является частным случаем внутреннего произведения (inner product) для евклидового пространства.
Приведем простой пример того, почему скалярное произведение может не подойти для векторов, состоящих, например, из комплексных чисел $mathbb C$. Ранее мы сказали, что скалярное произведение вектора самого на себя есть квадрат длины этого вектора, т.е. $mathbf x^T mathbf x = || mathbf x ||^2 $, и нам бы хотелось, чтобы квадрат длины был положителен.
Для действительных векторов это условие выполняется всегда, так как мы возводим в квадрат каждый компонент (вещественное число) такого вектора. Теперь рассмотрим комплексный вектор
$$ mathbf z = begin{bmatrix} 1 \ i end{bmatrix} in mathbb C^2 $$
По правилам скалярного произведения квадрат его длины был бы равен
$$ mathbf z^T mathbf z = begin{bmatrix} 1 & i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + i cdot i = 1-1 = 0 $$
Для того чтобы квадрат ненулевого вектора не был равен нулю в векторных пространствах комплексных чисел скалярное (а точнее внутреннее) произведение задано как $overline{mathbf z}^T mathbf z$, где $overline{mathbf z}$ является комплексно сопряженным (complex conjugate) к $mathbf z$ вектором. Тогда,
$$ overline{mathbf z}^T mathbf z = begin{bmatrix} 1 & -i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + (-i) cdot i = 1+1 = 2 $$
Векторное подпространство
Определение
Подпространством (subspace) векторного пространства $K$ называется множество $S$ его элементов, само являющееся векторным пространством относительно введенных в $K$ операций сложения и умножения на число.
Другими словами, чтобы $S$ было подпространством $K$ для каждого $mathbf v, mathbf w in S, K$ и $a in mathbb{R}$ должно выполняться ${ mathbf v + mathbf w, a mathbf v } in S, K$.
Например, выше мы сказали, что векторы $R^2$ первой четверти координатной плоскости не могут образовывать векторное пространство, потому что мы не можем задать для них операцию умножения на число, результатом которой был бы вектор только в этой четверти.
При этом, если мы возьмем на пространстве $R^2$ подпространство всех векторов, лежащих на прямой линии и проходящих через начало координат, то такое подпространство будет отвечать аксиомам векторных пространств.
Примечание. $R^1$ нельзя назвать подпространством $R^2$, потому что у векторов $R^1$ только один компонент, а у векторов $R^2$, даже тех, которые лежат на одной линии, их два.
Пересечение подпространств
Если $S$ и $T$ — подпространства, то $S cap T$ тоже подпространство. Возьмем $mathbf v, mathbf w in S, T$. Тогда $mathbf v + mathbf w in S, T$ и $a mathbf v in S,T$, так как $S$ и $T$ отвечают свойствам подпространств.
Ортогональные подпространства
Подпространство $S$ будет ортогонально подпространству $T$, если каждый вектор в $S$ ортогонален каждому вектору в $T$.
$$ forall mathbf v in S perp forall mathbf w in T $$
Ортогональное дополнение
Если внутри некоторого пространства $K$ существует подпространство $S$, и внутри этого же пространства $K$ можно найти другое ортогональное ему подпространство $S^{perp}$, то такое подпространство называется ортогональным дополнением (orthogonal complement) подпространства $S$.
Более формально, пусть $S$ — подпространство $K$. Тогда ортогональным дополнением $S^{perp}$ будет множество всех векторов $mathbf w in K$, для которых скалярное произведение $mathbf w cdot mathbf v = 0$ для любого $mathbf v in S$.
$$ S^{perp} = { mathbf w in K hspace{5pt} | hspace{5pt} mathbf w cdot mathbf v = 0, hspace{5pt} forall mathbf v in S hspace{2pt} } $$
Покажем, что $S^{perp}$ также является подпространством. Возьмем два вектора $mathbf a, mathbf b in S^{perp} $. Для того чтобы $S^{perp}$ было подпространством, нам нужно продемонстрировать замкнутость относительно сложения и умножения на скаляр.
$$ mathbf a + mathbf b underset{mathord{?}}{in} S^{perp} $$
$$ c cdot mathbf a underset{mathord{?}}{in} S^{perp} $$
Начнем со сложения. По определению ортогонального дополнения
$$ mathbf a cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$
$$ mathbf b cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$
Тогда,
$$ (mathbf a + mathbf b) cdot mathbf v = mathbf a cdot mathbf v + mathbf b cdot mathbf v = mathbf 0 + mathbf 0 = mathbf 0 $$
Другими словами, мы показали, что сумма векторов принадлежащих $ S^{perp} $ также ортогонально вектору $mathbf v in S$, а значит принадлежит $ S^{perp} $, $ mathbf a + mathbf b in S^{perp} $. Перейдем к умножению на скаляр.
$$ c cdot mathbf a cdot mathbf v = c cdot ( mathbf a cdot mathbf v) = c cdot mathbf 0 = mathbf 0 $$
Это доказывает, что $ c cdot mathbf a in S^{perp} $.
Таким образом, ортогональное дополнение подпространства само является векторным подпространством.
Отметим, что нулевой вектор всегда принадлежит ортогональному дополнению, поскольку при $c = 0$
$$ c cdot mathbf a = 0 cdot mathbf a = mathbf 0 rightarrow mathbf 0 in S^{perp} $$
Обратите внимание, что нулевой вектор также присутствует в подпространстве $S$, $mathbf 0 in S$.
Более того, $S cap S^{perp} = { mathbf 0 } $. Это легко доказать. Возьмем некоторый вектор $mathbf x$, который одновременно принадлежит $ S $ и $ S^{perp} $, $mathbf x in S, S^{perp}$.
Тогда по определению ортогонального дополнения должно выполняться $mathbf x cdot mathbf x = 0 $. Такому условию отвечает только нулевой вектор.
Линейная независимость векторов
Когда один вектор можно выразить через умножение другого вектора на число говорят, что эти векторы линейно зависимы (linearly dependent). С двумя линейно независимыми (linearly independent) векторами $ mathbf v_1, mathbf v_2 $ такого сделать не получится.
$$ mathbf v_2 neq k mathbf v_1 $$
где k — некоторое число.
Рассмотрим пример трех векторов. Чтобы эти три вектора были линейно независимы, не должно быть возможности выразить третий вектор через линейные комбинации (сложение и умножение на скаляр) первых двух.
$$ mathbf v_3 neq k_1 mathbf v_1 + k_2 mathbf v_2 $$
Если так сделать нельзя, мы попадаем в трехмерное пространство, если можно — останемся на плоскости.
Линейная оболочка
Линейная оболочка (linear span) — это множество всех возможных линейных комбинаций с помощью данного набора векторов.
Если у нас два линейно независимых (двумерных) вектора, то оболочка — $R^2$ (плоскость), если три (трехмерных) вектора, но один из них линейно зависим, то по-прежнему $R^2$.
Оболочка — это ответ на вопрос, какие векторы можно построить с помощью сложения и умножения на скаляр $n$ n-мерных векторов. Линейно зависимый вектор находится внутри оболочки, создаваемой комбинациями других линейно независимых векторов.
Базис пространства
Имея два двумерных линейно независимых вектора (например, $begin{bmatrix} 1 \ 2 end{bmatrix}$ и $begin{bmatrix} 3 \ 1 end{bmatrix}$), мы можем представить любой другой вектор в пространстве $ R^2 $, сложив эти два вектора и умножив их на скаляр. Такие векторы называются базисом пространства (basis of a vector space) $ R^2 $, по сути его координатами.
В целом, базисом называется такое множество линейно независимых векторов внутри векторного пространства, с помощью которых можно выразить любой другой вектор этого пространства.
Базис можно представить как некоторую систему координат, которой пользуются все векторы данного пространства.
Повторим пример с единичными векторами $mathbf i$ и $mathbf j$.
|
i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([—0.07, 3]) plt.ylim([—0.07, 3]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Приведенный выше базис называется стандартным (standard, natural basis). Это самый «экономный» или удобный способ представить все остальные векторы этого пространства.
При этом выбор такого базиса конечно условен, ничто не мешает мне перейти к другой системе координат, то есть другому базису.
Можно сказать, что координаты вектора имеют смысл только если мы знаем в какой системе координат (каком базисе) они выражены. При этом верно и то, что вектор существует в пространстве вне зависимости от системы координат или базиса.
Смена базиса
Предположим, что у нас есть два вектора исходного стандартного базиса $ mathbf g_1 $ и $ mathbf g_2 $ (на рисунке ниже изображены зеленым цветом). Кроме этого, у нас есть вектор $mathbf r$ (красный). Эти векторы имеют следующие координаты
$$ mathbf g_1 = begin{bmatrix} 1 \ 0 end{bmatrix}, mathbf g_2 = begin{bmatrix} 0 \ 1 end{bmatrix}, mathbf r_g = begin{bmatrix} 3 \ 4 end{bmatrix} $$
Если векторы нового базиса ортогональны (это важно), то мы можем выразить координаты вектора $mathbf r$ в новом базисе. Новым базисом будут следующие векторы $ mathbf b_1 $ и $ mathbf b_2 $ (черные):
$$ mathbf b_1 = begin{bmatrix} 2 \ 1 end{bmatrix}, mathbf b_2 = begin{bmatrix} -2 \ 4 end{bmatrix} $$
Посмотрим на эти векторы на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
g1 = np.array([1, 0]) g2 = np.array([0, 1]) r = np.array([3, 4]) b1 = np.array([2, 1]) b2 = np.array([—2, 4]) ax = plt.axes() plt.xlim([—2.5, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, g1[0], g1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, g2[0], g2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b1[0], b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, b2[0], b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) plt.show() |
Убедимся, что векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $ перпендикулярны (ортогональны).
Найдем скалярные и векторные проекции красного вектора $ mathbf r $ на векторы $ mathbf b_1 $ и $ mathbf b_2 $.
|
scalar_proj_r_on_b1 = np.dot(r, b1) / np.linalg.norm(b1) vector_proj_r_on_b1 = scalar_proj_r_on_b1 * (b1 / np.linalg.norm(b1)) scalar_proj_r_on_b1.round(1), vector_proj_r_on_b1 |
|
scalar_proj_r_on_b2 = np.dot(r, b2) / np.linalg.norm(b2) ** 2 vector_proj_r_on_b2 = scalar_proj_r_on_b2 * b2 scalar_proj_r_on_b2.round(1), vector_proj_r_on_b2 |
Посмотрим на векторные проекции.
|
plt.figure(figsize = (6, 6)) ax = plt.axes() plt.xlim([—2, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, vector_proj_r_on_b1[0], vector_proj_r_on_b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, vector_proj_r_on_b2[0], vector_proj_r_on_b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) plt.show() |
В сумме векторные проекции должны дать вектор $ mathbf r_g $ в исходном базисе.
|
vector_proj_r_on_b1 + vector_proj_r_on_b2 |
В новом же базисе вектор $ mathbf r_b $ можно выразить, как скалярные проекции вектора $ mathbf r $ на векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $.
|
np.array([scalar_proj_r_on_b1, scalar_proj_r_on_b2]).round(1) |
Другими словами,
$$ mathbf r_b approx begin{bmatrix} 4,5 \ 2,2 end{bmatrix} $$
Ортонормированный базис
Если угол между векторами базиса равен 90 градусов, то такой базис называют ортогональным (orthogonal). Если одновременно это единичные (нормализованные) векторы, то такой базис называется ортонормированным (orthonormal).
Ортонормированный базис называют стандартным базисом пространства $R^n$.
$$ forall { mathbf q_1, …, mathbf q_k } in R^n $$
$$ mathbf q_i^T cdot mathbf q_j = begin{cases} 0, i not= j \ 1, i=j end{cases} $$
Хотя векторы базиса не обязательно должны быть ортогональными и иметь единичную норму, во многих случаях это удобно.
Видео про линейную оболочку⧉.
Подведем итог
Мы ввели понятие векторного пространства, подпространства, линейной комбинации векторов, понятия базиса, линейной независимости векторов и линейной оболочки.
Перейдем к изучению матриц и начнем этот путь с рассмотрения линейных преобразований.