Как найти ортонормированный базис системы векторов - Исправление недочетов и поиск решений вместе с Examum.ru

Построить
ортонормированный базис подпространства
пространства
натянутого на систему векторови

Решение.Нам
требуется построить ортонормированный
базис евклидова пространствакоторое является линейной оболочкой
векторовПрименим к этим векторам процесс
ортогонализации.

Вначале возьмём

Векторбудем искать в видеИз условия перпендикулярностиполучаем:Следовательно,Далее, следующий базисный вектор будем
искать в видеИз условийиполучаем:и

Отсюда
Таким образом, ортогональный базис
пространстватаков:Ортонормированный базис получится,
если мы разделим каждый вектор на его
длину:

Пример.4 Дополнение системы векторов до ортогонального базиса.

Убедиться в том,
что векторы
ортогональны, и дополнить систему этих
векторов до ортогонального базиса.

Решение.Проверим ортогональность. Имеем:Следовательно,Таким образом, мы можем положитьДругие векторыортогонального базиса удовлетворяют
условиямиПустьУсловиедаёт систему

Найдём фундаментальную
систему решенийэтой системы. Вычтем
из второго уравнения первое, умноженное
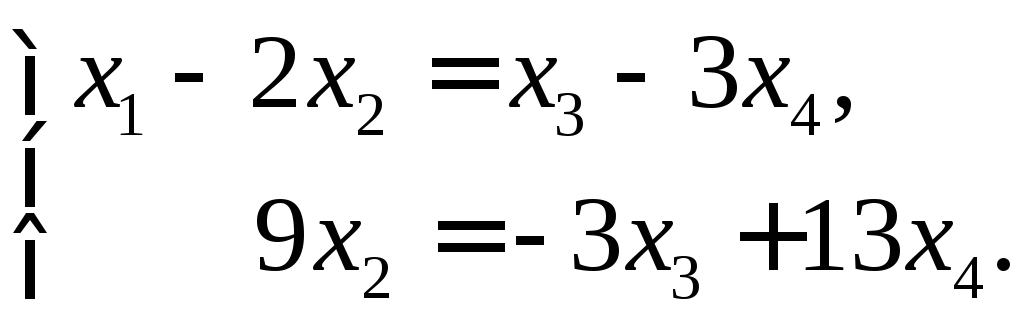
на 4:Перенесёмв правую часть:Переменныездесьсвободные, а переменные–связанные. Придадим свободным
переменным значения: вначалезатеми найдёмСоставим таблицу:


1/3	1	0
	0	1

Таким образом,
можно считать, что
Эти векторы перпендикулярны векторамно не перпендикулярны друг другу.
Применим к ним процесс ортогонализации.
ПоложимТак как должно бытьтоОтсюда

Таким образом,
дополнением векторов
до ортогонального базиса будет служить,
например, система векторов

>>
d=eig(A)
%Функция
вычисляет собственные значения матрицы
A.

>>[U,D]=eig(A)
%Матрица
U
состоит правых собственных векторов,
удовлетворяющих соотношению A
* U=
U
* D.
Эти векторы нормированы так, что норма
каждого из них равна единице.

Упражнение.5

Линейное
преобразование, задано в некотором
базисе матрицей A.
Зная его собственные значения и
собственные векторы, найти матрицу из
ортонормированных собственных векторовU, проверить ее свойства
(является ли матрица ортогональной,
если нет, то почему, если да то почему).
Проверить результат с помощью функции
[U,D]=eig(A)
.

,
,,.

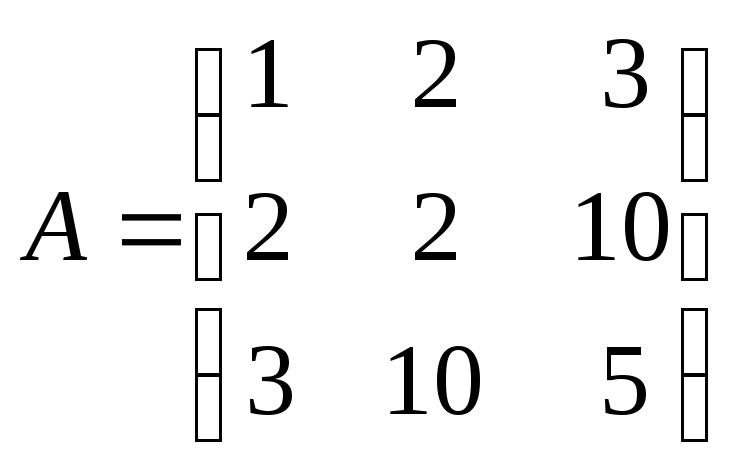
Проиллюстрировать
задачу.

Задание для самостоятельной работы

1. Выполнить в
тетради и в MATLAB все упражнения данного
практикума.

2. Решить задачи
средствами MATLAB.Продумать
решения каждой задачи средствами MATLAB.
Продумать геометрическую иллюстрацию.

Задачи.

Продумать
решения каждой задачи средствами MATLAB.
Продумать иллюстрации в MATLAB.

1.Привести
матрицулинейного
оператора к диагональному виду и найти
соответствующий базис. Результаты
поверить с помощью функцииeig()

2.Для матрицынайти
диагональную матрицуDи
унитарную (ортогональную) матрицуUи проверить результат с помощью функцииeig()

3. Найти
собственные числа и собственные векторы
линейного оператора, заданного матрицей.

Сначала найти на
листочке, затем с помощью встроенных
команд МАТЛАБ проверить себя.

4.В пространствеL³заданы векторыв некотором базисе. Доказать, что векторысоставляют базис, найти матрицу перехода
в базисе,
найти координаты векторав базисе..

5.Заданы векторыв некотором базисе. Проверить, что
векторысоставляют базис. Применяя процесс
ортогонализации Шмидта построить новый
ортогональный базис..

Задачу сначала
решить на листочке. Опорные вычисления
проверяйте на МАТЛАБ. Затем сделать
графическую трехмерную иллюстрацию в
МАТЛАБ. Изобразите заданные векторы,
векторы нового базиса, орты нового
базиса, вспомогательные векторы
(демонстрирующие процесс ортогонализации).
В графическом окне выведите списком,
за какие цветные линии — векторы отвечают
за те или иные векторы из задачи.

Соседние файлы в папке МатЛаб — Алгебра

Источник

Оглавление — Линейная алгебра

Ортогональный и ортонормированный базисы евклидова пространства

Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.

Базис [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е.

[math]langle mathbf{e}_i,mathbf{e}_jrangle=0[/math] при [math]ine j,~~ i=1,2,ldots,n,~~ j=1,2,ldots,n.[/math]

Базис [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] евклидова пространства называется ортонормированным, если его векторы попарно ортогональны и длина каждого из них равна единице:

[math]langle mathbf{e}_i,mathbf{e}_jrangle= begin{cases}1,&i=j,\ 0,&ine j end{cases}i=1,2,ldots,n,~~ j=1,2,ldots,n.[/math]

(8.31)

Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.

В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис.

Выражение скалярного произведения через координаты сомножителей

Пусть [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] — базис евклидова пространства, в котором векторы [math]mathbf{x}[/math] и [math]mathbf{y}[/math] имеют координаты [math]x_1,x_2,ldots,x_n[/math] и [math]y_1,y_2,ldots,y_n[/math] соответственно, т.е.

[math]mathbf{x}= x_1 mathbf{e}_1+x_2 mathbf{e}_2+ldots+ x_n mathbf{e}_n,qquad mathbf{y}= y_1 mathbf{e}_1+y_2 mathbf{e}_2+ldots+ y_n mathbf{e}_n.[/math]

Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:

[math]langle mathbf{x},mathbf{y}rangle= langle x_1 mathbf{e}_1+x_2 mathbf{e}_2+ldots+ x_n mathbf{e}_n,, y_1 mathbf{e}_1+y_2 mathbf{e}_2+ldots+ y_n mathbf{e}_n rangle= sum_{i=1}^{n}sum_{i=1}^{n}x_iy_jlangle mathbf{e}_i,mathbf{e}_jrangle.[/math]

Преобразуем это выражение, используя операции с матрицами:

[math]langle mathbf{x},mathbf{y}rangle= x^Tcdot G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)cdot y,[/math]

(8.32)

где [math]x=begin{pmatrix}x_1&cdots x_nend{pmatrix}^T,~ y=begin{pmatrix} y_1&cdots& y_n end{pmatrix}^T[/math] — координатные столбцы векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math], a [math]G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)[/math] — квадратная симметрическая матрица, составленная из скалярных произведений

[math]G(mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n)= begin{pmatrix} langle mathbf{e}_1,mathbf{e}_1rangle& langle mathbf{e}_1,mathbf{e}_2rangle &cdots&langle mathbf{e}_1, mathbf{e}_nrangle\ langle mathbf{e}_2,mathbf{e}_1rangle& langle mathbf{e}_2, mathbf{e}_2rangle &cdots&langle mathbf{e}_2,mathbf{e}_nrangle\ vdots&vdots&ddots&vdots\ langle mathbf{e}_n,mathbf{e}_1rangle& langle mathbf{e}_n,mathbf{e}_2rangle &cdots&langle mathbf{e}_n,mathbf{e}_nrangle end{pmatrix}!.[/math]

(8.33)

которая называется матрицей Грама системы векторов [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math].

Преимущества ортонормированного базиса

Для ортонормированного базиса [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама [math]G(mathbf{e}_1, mathbf{e}_2,ldots,mathbf{e}_n)[/math] ортонормированной системы [math]mathbf{e}_1, mathbf{e}_2,ldots, mathbf{e}_n[/math] равна единичной матрице: [math]G(mathbf{e}_1, mathbf{e}_2,ldots,mathbf{e}_n)=E[/math].

1. В ортонормированном базисе [math]mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n[/math] скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] находится по формуле: [math]langle mathbf{x},mathbf{y}rangle= x_1y_1+x_2y_2+ldots+x_ny_n[/math], где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf{x}[/math], а [math]y_1,ldots,y_n[/math] — координаты вектора [math]mathbf{y}[/math].

2. В ортонормированном базисе [math]mathbf{e}_1,mathbf{e}_2,ldots, mathbf{e}_n[/math] длина вектора [math]mathbf{x}[/math] вычисляется по формуле [math]|mathbf{x}|= sqrt{x_1^2+x_2^2+ldots+x_n^2}[/math], где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf{x}[/math].

3. Координаты [math]x_1,ldots,x_n[/math] вектора [math]mathbf{x}[/math] относительно ортонормированного базиса [math]mathbf{e}_1,mathbf{e}_2,ldots,mathbf{e}_n[/math] находятся при помощи скалярного произведения по формулам: [math]x_1=langle mathbf{x},mathbf{e}_1rangle,ldots, x_n=langle mathbf{x},mathbf{e}_nrangle[/math].

В самом деле, умножая обе части равенства [math]mathbf{x}= x_1 mathbf{e}_1+ldots+x_n mathbf{e}_n[/math] на [math]mathbf{e}_1[/math], получаем

[math]langle mathbf{x},mathbf{e}_1rangle= x_1underbrace{langlemathbf{e}_1, mathbf{e}_1 rangle}_{1}+ x_2underbrace{langle mathbf{e}_1,mathbf{e}_2 rangle}_{0}+ldots+ x_nunderbrace{langle mathbf{e}_n, mathbf{e}_n rangle}_{0}quad Leftrightarrowquad x_1=langle mathbf{x},mathbf{e}_1rangle.[/math]

Аналогично доказываются остальные формулы.

Изменение матрицы Грама при переходе от одного базиса к другому

Пусть [math](mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n)[/math] и [math](mathbf{f})= (mathbf{f}_1,ldots,mathbf{f}_n)[/math] — два базиса евклидова пространства [math]mathbb{E}[/math], a [math]S[/math] — матрица перехода от базиса [math](mathbf{e})[/math] к базису [math](mathbf{f})colon, (mathbf{f})=(mathbf{e})S[/math]. Требуется найти связь матриц Грама систем векторов [math](mathbf{e})[/math] и [math](mathbf{f})[/math]

По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] в разных базисах:

[math]langle mathbf{x},mathbf{y}rangle= {mathop{x}limits_{(mathbf{e})}}^Tcdot, G(mathbf{e}_1,ldots,mathbf{e}_n)cdot mathop{mathbf{y}}limits_{(mathbf{e})}= {mathop{x}limits_{(mathbf{f})}}^Tcdot, G(mathbf{f}_1,ldots,mathbf{f}_n)cdot mathop{mathbf{y}}limits_{(mathbf{f})},[/math]

где [math]mathop{x}limits_{(mathbf{e})},, mathop{x}limits_{(mathbf{f})}[/math] и [math]mathop{y}limits_{(mathbf{e})},, mathop{y}limits_{(mathbf{f})}[/math] — координатные столбцы векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathop{x}limits_{(mathbf{e})}= S mathop{x}limits_{(mathbf{f})},[/math] [math]mathop{y}limits_{(mathbf{e})}= S mathop{y}limits_{(mathbf{f})}[/math], получаем тождество

[math]{mathop{x}limits_{(mathbf{f})}}^Tcdot S^Tcdot, G(mathbf{e}_1,ldots,mathbf{e}_n)cdot Scdot mathop{mathbf{y}}limits_{(mathbf{f})}= {mathop{x}limits_{(mathbf{f})}}^Tcdot, G(mathbf{f}_1,ldots,mathbf{f}_n)cdot mathop{mathbf{y}}limits_{(mathbf{f})}.[/math]

Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому:

[math]G(mathbf{f}_1,ldots,mathbf{f}_n)= S^Tcdot G(mathbf{e}_1,ldots,mathbf{e}_n)cdot S.[/math]

Записав это равенство для ортонормированных базисов [math](mathbf{e})[/math] и [math](mathbf{f})[/math], получаем [math]E=S^TES[/math], так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf{e}_1,ldots,mathbf{e}_n)= G(mathbf{f}_1,ldots,mathbf{f}_n)=E[/math]. Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^{-1}=S^T[/math].

Свойства определителя Грама

Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.

1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.

Действительно, если система [math]mathbf{v}_1, mathbf{v}_2, ldots,mathbf{v}_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math], не равные нулю одновременно, что

[math]x_1cdot mathbf{v}_1+x_2cdot mathbf{v}_2+ldots+ x_kcdot mathbf{v}_k= mathbf{o}.[/math]

Умножая это равенство скалярно на [math]mathbf{v}_1[/math], затем на [math]mathbf{v}_2[/math] и т.д. на [math]mathbf{v}_k[/math], получаем однородную систему уравнений [math]G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)x=o[/math], которая имеет нетривиальное решение [math]x=begin{pmatrix}x_1&cdots&x_k end{pmatrix}^T[/math]. Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.

Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.

Главный минор матрицы Грама системы [math]mathbf{v}_1, mathbf{v}_2,ldots,mathbf{v}_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.

2. Определитель Грама [math]det{G (mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k)}[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k[/math]. Другими словами, если в процессе ортогонализации векторов [math]mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k[/math] получены векторы [math]mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k[/math], то

[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots,mathbf{w}_k)= langle mathbf{w}_1,mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldotscdot langle mathbf{w}_k,mathbf{w}_krangle.[/math]

Действительно, в процессе ортогонализации по векторам [math]mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k[/math] последовательно строятся векторы

[math]mathbf{w}_1=mathbf{v}_1,quad mathbf{w}_2= mathbf{v}_2- alpha_{21} mathbf{w}_1,quad ldots,quad mathbf{w}_k= mathbf{v}_k- sum_{j=1}^{k-1}alpha_{kj} mathbf{w}_j.[/math]

После первого шага определитель Грама не изменяется

[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{v}_2, ldots,mathbf{v}_k).[/math]

Выполним с определителем [math]det G(mathbf{w}_1, mathbf{v}_2, ldots,mathbf{v}_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_{21})[/math], а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_{21})[/math]. Получим определитель

[math]det G(mathbf{w}_1,mathbf{v}_2-alpha_{21}mathbf{w}_1,ldots,mathbf{v}_k)= det G(mathbf{w}_1,mathbf{w}_2, mathbf{v}_3, ldots,mathbf{v}_k).[/math]

Так как при этих преобразованиях определитель не изменяется, то

[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2,mathbf{v}_3, ldots,mathbf{v}_k).[/math]

Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:

[math]det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots,mathbf{w}_k).[/math]

Вычислим правую часть этого равенства. Матрица [math]G(mathbf{w}_1,mathbf{w}_2,ldots, mathbf{w}_k)[/math] Грама ортогональной системы [math]mathbf{v}_1,mathbf{v}_2, ldots,mathbf{v}_k[/math] векторов является диагональной, так как [math]langle mathbf{w}_i,mathbf{w}_jrangle=0[/math] при [math]ine j[/math]. Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:

[math]det G(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k)= langle mathbf{w}_1, mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldots langle mathbf{w}_k, mathbf{w}_krangle.[/math]

3. Определитель Грама любой системы [math]mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k[/math] векторов удовлетворяет двойному неравенству

[math]0leqslant det G(mathbf{v}_1,mathbf{v}_2,ldots,mathbf{v}_k) leqslant langle mathbf{v}_1, mathbf{v}_1ranglecdot langle mathbf{v}_2,mathbf{v}_2ranglecdot ldots langle mathbf{v}_k, mathbf{v}_krangle.[/math]

Докажем неотрицательность определителя Грама. Если система [math]mathbf{v}_1,mathbf{v}_2, ldots, mathbf{v}_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf{w}_1,mathbf{w}_2, ldots, mathbf{w}_k[/math], для которых по свойству 2:

[math]det G(mathbf{v}_1,mathbf{v}_2,ldots, mathbf{v}_k)= det G(mathbf{w}_1, mathbf{w}_2, ldots, mathbf{w}_k)= |mathbf{w}_1|^2cdot |mathbf{w}_2|^2cdot ldotscdot |mathbf{w}_k|^2>0.[/math]

Оценим теперь скалярный квадрат [math]langle mathbf{v}_j,mathbf{w}_jrangle[/math]. Выполняя процесс ортого-1нализации, имеем [math]mathbf{v}_j= mathbf{w}_j+ alpha_{j,1}mathbf{w}_1+ ldots+ alpha_{j,j-1}mathbf{w}_{j-1}[/math]. Отсюда

[math]langle mathbf{v}_j,mathbf{w}_jrangle= langle mathbf{w}_j,mathbf{w}_jrangle+ sum_{i=1}^{j-1}alpha_{i,i}^2 langle mathbf{w}_j,mathbf{w}_jrangle geqslant langle mathbf{w}_j, mathbf{w}_jrangle.[/math]

Следовательно, по свойству 2 имеем

[math]langle mathbf{v}_1,mathbf{v}_1ranglecdot langle mathbf{v}_2,mathbf{v}_2 ranglecdot ldotscdot langle mathbf{v}_k,mathbf{v}_kranglegeqslant langle mathbf{w}_1, mathbf{w}_1ranglecdot langle mathbf{w}_2,mathbf{w}_2ranglecdot ldotscdot langle mathbf{w}_k, mathbf{w}_krangle= det G(mathbf{w}_1,mathbf{w}_2,ldots,mathbf{w}_k).[/math]

Замечания 8.12

1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.

2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.

3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара:

[math](det{A})^2leqslant prod_{i=1}^{n}Bigl(a_{i,1}^2+ a_{i,2}^2+ldots+ a_{i,n}^2Bigr).[/math]

Действительно, обозначив [math]a_1,a_2,ldots,a_n[/math] столбцы матрицы [math]A[/math], элементы матрицы [math]A^TA[/math] можно представить как скалярные произведения (8.27): [math]langle a_i,a_jrangle= (a_i)^Ta_j[/math]. Тогда [math]A^TA=G(a_1,a_2,ldots,a_n)[/math] — матрица Грама системы [math]a_1,a_2,ldots,a_n[/math] векторов пространства [math]mathbb{R}^n[/math]. По свойству 3, теореме 2.2 и свойству 1 определителя получаем доказываемое неравенство:

[math]begin{aligned} (det{A})^2&= det{A}cdotdet{A}= det{A^T}cdotdet{A}= det(A^TA)= det G(a_1,a_2,ldots,a_n)leqslant\[2pt] &leqslant |a_1|^2cdot |a_2|^2cdot ldotscdot |a_n|^2= prod_{i=1}^{n}Bigl(a_{i,1}^2+ a_{i,2}^2+ldots+ a_{i,n}^2Bigr). end{aligned}[/math]

4. Если [math]A[/math] — невырожденная квадратная матрица, то любой главный минор матрицы [math]A^TA[/math] положителен. Это следует из пункта 2, учитывая представление произведения [math]A^TA=G(a_1,ldots,a_n)[/math] как матрицы Грама системы линейно независимых векторов [math]a_1,ldots,a_n[/math] — столбцов матрицы [math]A[/math] (см. пункт 3).

Изоморфизм евклидовых пространств

Два евклидовых пространства [math]mathbb{E}[/math] и [math]mathbb{E}'[/math] называются изоморфными [math](mathbb{E}leftrightarrow mathbb{E}’)[/math], если они изоморфны как линейные пространства и скалярные произведения соответствующих векторов равны:

[math]left.{begin{matrix}mathbf{u}leftrightarrow mathbf{u}’\ mathbf{v}leftrightarrow mathbf{v}’end{matrix}}right}quad Rightarrowquad langle mathbf{u},mathbf{v}rangle= langle mathbf{u}’,mathbf{v}’rangle’.[/math]

‘

где [math](cdot,cdot)[/math] и [math](cdot,cdot)'[/math] — скалярные произведения в пространствах [math]mathbb{E}[/math] и [math]mathbb{E}'[/math] соответственно.

Напомним, что для изоморфизма конечномерных линейных пространств необходимо и достаточно, чтобы их размерности совпадали (см. теорему 8.3). Покажем, что это условие достаточно для изоморфизма евклидовых пространств (необходимость следует из определения). Как и при доказательстве теоремы 8.3, установим изоморфизм n-мерного евклидова пространства [math]mathbb{E}[/math] с вещественным арифметическим пространством [math]mathbb{R}^n[/math] со скалярным произведением (8.27). В самом деле, взяв в пространстве [math]mathbb{E}[/math] какой-нибудь ортонормированный базис [math](mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n)[/math], поставим в соответствие каждому вектору [math]mathbf{x}in mathbb{E}[/math] его координатный столбец [math]xin mathbb{R}^n~ (mathbf{x}leftrightarrow x)[/math]. Это взаимно однозначное соответствие устанавливает изоморфизм линейных пространств: [math]mathbb{E}leftrightarrow mathbb{R}^n[/math]. В ортонормированном базисе скалярное произведение векторов [math]mathbf{x}[/math] и [math]mathbf{y}[/math] пространства [math]mathbb{E}[/math] находится по формуле

[math]langle mathbf{x},mathbf{y}rangle= x_1cdot y_1+x_2cdot y_2+ldots+x_ncdot y_n[/math]

(см. пункт 1 преимуществ ортонормированного базиса). Такое же выражение дает скалярное произведение (8.27) координатных столбцов [math]x[/math] и [math]y[/math], т.е. скалярные произведения соответствующих элементов равны

[math]langle mathbf{x},mathbf{y}rangle= x_1cdot y_1+x_2cdot y_2+ldots+x_ncdot y_n=x^Tcdot y.[/math]

Следовательно, евклидовы пространства [math]mathbb{E}[/math] и [math]mathbb{R}^n[/math] изоморфны.

Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]mathbb{R}^n[/math] со стандартным скалярным произведением (8.27).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

104. Построение ортонормированного базиса из собственных векторов самосопряженного оператора

1) Составить характеристическое уравнение линейного оператора |A — l.E| = 0.

2) Найдем все корни характеристического уравнения.

3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A — l.E)X=0.

4) Ортонормируем, полученный базис.

Пример. Линейный оператор A, действующий в евклидовом пространстве Е3, имеет в ортонормированном базисе E1, E2, E3 матрицу

Найти в Е3 ортонормированный базис из собственных векторов оператора A и составить матрицу оператора A в этом базисе.

Решение. 1) Составить характеристическое уравнение линейного оператора |A — l.E| = 0.

2) Найдем все корни характеристического уравнения: l1=-1, l2 = l3 = 1. Тогда матрица линейного оператора в ортонормированном базисе, составленном из собственных векторов имеет вид

3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A — l.E)X=0.

Пусть l1=-1. Матричное уравнение (A — l1E)X=0 принимает вид:

Пусть l2 = l3 = 1. Матричное уравнение (A — l1E)X=0 принимает вид:

4) Ортонормируем, полученный базис.

B1 = (1,-2,1), B2 = (2,1,0), B3 = A3 + k b2, , b3 =(-1/5, 2/5, 1/5).

Ортогональный и ортонормированный базисы евклидова пространства

Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортогональным , если все образующие его векторы попарно ортогональны, т.е.

Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортонормированным , если его векторы попарно ортогональны и длина каждого из них равна единице:

Выражение скалярного произведения через координаты сомножителей

Пусть [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис евклидова пространства, в котором векторы [math]mathbf[/math] и [math]mathbf[/math] имеют координаты [math]x_1,x_2,ldots,x_n[/math] и [math]y_1,y_2,ldots,y_n[/math] соответственно, т.е.

Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:

Преобразуем это выражение, используя операции с матрицами:

y=begin y_1&cdots& y_n end^T[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] , a [math]G(mathbf_1,mathbf_2,ldots, mathbf_n)[/math] — квадратная симметрическая матрица, составленная из скалярных произведений

которая называется матрицей Грама системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] .

Преимущества ортонормированного базиса

Для ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)[/math] ортонормированной системы [math]mathbf_1, mathbf_2,ldots, mathbf_n[/math] равна единичной матрице: [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)=E[/math] .

1. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] находится по формуле: [math]langle mathbf,mathbfrangle= x_1y_1+x_2y_2+ldots+x_ny_n[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] , а [math]y_1,ldots,y_n[/math] — координаты вектора [math]mathbf[/math] .

2. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] длина вектора [math]mathbf[/math] вычисляется по формуле [math]|mathbf|= sqrt[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] .

3. Координаты [math]x_1,ldots,x_n[/math] вектора [math]mathbf[/math] относительно ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] находятся при помощи скалярного произведения по формулам: [math]x_1=langle mathbf,mathbf_1rangle,ldots, x_n=langle mathbf,mathbf_nrangle[/math] .

В самом деле, умножая обе части равенства [math]mathbf= x_1 mathbf_1+ldots+x_n mathbf_n[/math] на [math]mathbf_1[/math] , получаем

Аналогично доказываются остальные формулы.

Изменение матрицы Грама при переходе от одного базиса к другому

Пусть [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] и [math](mathbf)= (mathbf_1,ldots,mathbf_n)[/math] — два базиса евклидова пространства [math]mathbb[/math] , a [math]S[/math] — матрица перехода от базиса [math](mathbf)[/math] к базису [math](mathbf)colon, (mathbf)=(mathbf)S[/math] . Требуется найти связь матриц Грама систем векторов [math](mathbf)[/math] и [math](mathbf)[/math]

По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] в разных базисах:

где [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] и [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>,[/math] [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>[/math] , получаем тождество

Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому :

Записав это равенство для ортонормированных базисов [math](mathbf)[/math] и [math](mathbf)[/math] , получаем [math]E=S^TES[/math] , так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf_1,ldots,mathbf_n)= G(mathbf_1,ldots,mathbf_n)=E[/math] . Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^<-1>=S^T[/math] .

Свойства определителя Грама

Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.

1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.

Действительно, если система [math]mathbf_1, mathbf_2, ldots,mathbf_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math] , не равные нулю одновременно, что

Умножая это равенство скалярно на [math]mathbf_1[/math] , затем на [math]mathbf_2[/math] и т.д. на [math]mathbf_k[/math] , получаем однородную систему уравнений [math]G(mathbf_1,mathbf_2,ldots,mathbf_k)x=o[/math] , которая имеет нетривиальное решение [math]x=beginx_1&cdots&x_k end^T[/math] . Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.

Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.

Главный минор матрицы Грама системы [math]mathbf_1, mathbf_2,ldots,mathbf_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.

2. Определитель Грама [math]det_1,mathbf_2, ldots, mathbf_k)>[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] . Другими словами, если в процессе ортогонализации векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] получены векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , то

Действительно, в процессе ортогонализации по векторам [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] последовательно строятся векторы

После первого шага определитель Грама не изменяется

Выполним с определителем [math]det G(mathbf_1, mathbf_2, ldots,mathbf_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_<21>)[/math] , а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_<21>)[/math] . Получим определитель

Так как при этих преобразованиях определитель не изменяется, то

Вычислим правую часть этого равенства. Матрица [math]G(mathbf_1,mathbf_2,ldots, mathbf_k)[/math] Грама ортогональной системы [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] векторов является диагональной, так как [math]langle mathbf_i,mathbf_jrangle=0[/math] при [math]ine j[/math] . Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:

3. Определитель Грама любой системы [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] векторов удовлетворяет двойному неравенству

Докажем неотрицательность определителя Грама. Если система [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] , для которых по свойству 2:

Оценим теперь скалярный квадрат [math]langle mathbf_j,mathbf_jrangle[/math] . Выполняя процесс ортого-1нализации, имеем [math]mathbf_j= mathbf_j+ alpha_mathbf_1+ ldots+ alpha_mathbf_[/math] . Отсюда

Следовательно, по свойству 2 имеем

3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара :

Действительно, обозначив [math]a_1,a_2,ldots,a_n[/math] столбцы матрицы [math]A[/math] , элементы матрицы [math]A^TA[/math] можно представить как скалярные произведения (8.27): [math]langle a_i,a_jrangle= (a_i)^Ta_j[/math] . Тогда [math]A^TA=G(a_1,a_2,ldots,a_n)[/math] — матрица Грама системы [math]a_1,a_2,ldots,a_n[/math] векторов пространства [math]mathbb^n[/math] . По свойству 3, теореме 2.2 и свойству 1 определителя получаем доказываемое неравенство:

Изоморфизм евклидовых пространств

Два евклидовых пространства [math]mathbb[/math] и [math]mathbb'[/math] называются изоморфными [math](mathbbleftrightarrow mathbb’)[/math] , если они изоморфны как линейные пространства и скалярные произведения соответствующих векторов равны:

где [math](cdot,cdot)[/math] и [math](cdot,cdot)'[/math] — скалярные произведения в пространствах [math]mathbb[/math] и [math]mathbb'[/math] соответственно.

(mathbfleftrightarrow x)[/math] . Это взаимно однозначное соответствие устанавливает изоморфизм линейных пространств: [math]mathbbleftrightarrow mathbb^n[/math] . В ортонормированном базисе скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] пространства [math]mathbb[/math] находится по формуле

(см. пункт 1 преимуществ ортонормированного базиса). Такое же выражение дает скалярное произведение (8.27) координатных столбцов [math]x[/math] и [math]y[/math] , т.е. скалярные произведения соответствующих элементов равны

Следовательно, евклидовы пространства [math]mathbb[/math] и [math]mathbb^n[/math] изоморфны.

Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]mathbb^n[/math] со стандартным скалярным произведением (8.27).

источники:

http://mathhelpplanet.com/static.php?p=ortogonalnyi-i-ortonormirovannyi-bazisy-evklidova-prostranstva

Источник

From Wikipedia, the free encyclopedia

In mathematics, particularly linear algebra, an orthonormal basis for an inner product space V with finite dimension is a basis for whose vectors are orthonormal, that is, they are all unit vectors and orthogonal to each other.^[1]^[2]^[3] For example, the standard basis for a Euclidean space $mathbb {R} ^{n}$ is an orthonormal basis, where the relevant inner product is the dot product of vectors. The image of the standard basis under a rotation or reflection (or any orthogonal transformation) is also orthonormal, and every orthonormal basis for $mathbb {R} ^{n}$ arises in this fashion.

For a general inner product space an orthonormal basis can be used to define normalized orthogonal coordinates on Under these coordinates, the inner product becomes a dot product of vectors. Thus the presence of an orthonormal basis reduces the study of a finite-dimensional inner product space to the study of $mathbb {R} ^{n}$ under dot product. Every finite-dimensional inner product space has an orthonormal basis, which may be obtained from an arbitrary basis using the Gram–Schmidt process.

In functional analysis, the concept of an orthonormal basis can be generalized to arbitrary (infinite-dimensional) inner product spaces.^[4] Given a pre-Hilbert space an orthonormal basis for is an orthonormal set of vectors with the property that every vector in can be written as an infinite linear combination of the vectors in the basis. In this case, the orthonormal basis is sometimes called a Hilbert basis for Note that an orthonormal basis in this sense is not generally a Hamel basis, since infinite linear combinations are required.^[5] Specifically, the linear span of the basis must be dense in but it may not be the entire space.

If we go on to Hilbert spaces, a non-orthonormal set of vectors having the same linear span as an orthonormal basis may not be a basis at all. For instance, any square-integrable function on the interval [-1,1] can be expressed (almost everywhere) as an infinite sum of Legendre polynomials (an orthonormal basis), but not necessarily as an infinite sum of the monomials $x^{n}.$

A different generalisation is to pseudo-inner product spaces, finite-dimensional vector spaces equipped with a non-degenerate symmetric bilinear form known as the metric tensor. In such a basis, the metric takes the form with positive ones and negative ones.

Examples[edit]

For $mathbb {R} ^{3}$ , the set of vectors ${displaystyle left{e_{1}=(1,0,0),e_{2}=(0,1,0),e_{3}=(0,0,1)right},}$ is called the standard basis and forms an orthonormal basis of $mathbb {R} ^{3}$ with respect to the standard dot product. Note that both the standard basis and standard dot product rely on viewing $mathbb {R} ^{3}$ as the Cartesian product

Proof: A straightforward computation shows that the inner products of these vectors equals zero, ${displaystyle leftlangle e_{1},e_{2}rightrangle =leftlangle e_{1},e_{3}rightrangle =leftlangle e_{2},e_{3}rightrangle =0}$ and that each of their magnitudes equals one, ${displaystyle left|e_{1}right|=left|e_{2}right|=left|e_{3}right|=1.}$ This means that ${displaystyle left{e_{1},e_{2},e_{3}right}}$ is an orthonormal set. All vectors ${displaystyle (x,y,z)in mathbb {R} ^{3}}$ can be expressed as a sum of the basis vectors scaled

${displaystyle (x,y,z)=xe_{1}+ye_{2}+ze_{3},}$

so ${displaystyle left{e_{1},e_{2},e_{3}right}}$ spans $mathbb{R} ^{3}$ and hence must be a basis. It may also be shown that the standard basis rotated about an axis through the origin or reflected in a plane through the origin also forms an orthonormal basis of $mathbb{R} ^{3}$ .
For $mathbb {R} ^{n}$ , the standard basis and inner product are similarly defined. Any other orthonormal basis is related to the standard basis by an orthogonal transformation in the group O(n).
For pseudo-Euclidean space ${displaystyle mathbb {R} ^{p,q},}$ , an orthogonal basis ${displaystyle {e_{mu }}}$ with metric instead satisfies ${displaystyle eta (e_{mu },e_{nu })=0}$ if , ${displaystyle eta (e_{mu },e_{mu })=+1}$ if , and ${displaystyle eta (e_{mu },e_{mu })=-1}$ if . Any two orthonormal bases are related by a pseudo-orthogonal transformation. In the case , these are Lorentz transformations.
The set ${displaystyle left{f_{n}:nin mathbb {Z} right}}$ with ${displaystyle f_{n}(x)=exp(2pi inx),}$ where denotes the exponential function, forms an orthonormal basis of the space of functions with finite Lebesgue integrals, ${displaystyle L^{2}([0,1]),}$ with respect to the 2-norm. This is fundamental to the study of Fourier series.
The set ${displaystyle left{e_{b}:bin Bright}}$ with ${displaystyle e_{b}(c)=1}$ if and ${displaystyle e_{b}(c)=0}$ otherwise forms an orthonormal basis of ${displaystyle ell ^{2}(B).}$
Eigenfunctions of a Sturm–Liouville eigenproblem.
The column vectors of an orthogonal matrix form an orthonormal set.

Basic formula[edit]

If is an orthogonal basis of then every element xin H may be written as

${displaystyle x=sum _{bin B}{frac {langle b,xrangle }{lVert brVert ^{2}}}b.}$

When is orthonormal, this simplifies to

${displaystyle x=sum _{bin B}langle b,xrangle b}$

and the square of the norm of can be given by

${displaystyle |x|^{2}=sum _{bin B}|langle x,brangle |^{2}.}$

Even if is uncountable, only countably many terms in this sum will be non-zero, and the expression is therefore well-defined. This sum is also called the Fourier expansion of and the formula is usually known as Parseval’s identity.

If is an orthonormal basis of then is isomorphic to ${displaystyle ell ^{2}(B)}$ in the following sense: there exists a bijective linear map ${displaystyle Phi :Hto ell ^{2}(B)}$ such that

Incomplete orthogonal sets[edit]

Given a Hilbert space and a set of mutually orthogonal vectors in we can take the smallest closed linear subspace of containing Then will be an orthogonal basis of which may of course be smaller than itself, being an incomplete orthogonal set, or be when it is a complete orthogonal set.

Existence[edit]

Using Zorn’s lemma and the Gram–Schmidt process (or more simply well-ordering and transfinite recursion), one can show that every Hilbert space admits an orthonormal basis;^[6] furthermore, any two orthonormal bases of the same space have the same cardinality (this can be proven in a manner akin to that of the proof of the usual dimension theorem for vector spaces, with separate cases depending on whether the larger basis candidate is countable or not). A Hilbert space is separable if and only if it admits a countable orthonormal basis. (One can prove this last statement without using the axiom of choice.)

Choice of basis as a choice of isomorphism[edit]

For concreteness we discuss orthonormal bases for a real, dimensional vector space with a positive definite symmetric bilinear form .

One way to view an orthonormal basis with respect to phi is as a set of vectors ${displaystyle {mathcal {B}}={e_{i}}}$ , which allow us to write ${displaystyle v=v^{i}e_{i}}$ for vin V , and ${displaystyle v^{i}in mathbb {R} }$ or ${displaystyle (v^{i})in mathbb {R} ^{n}}$ . With respect to this basis, the components of phi are particularly simple:
${displaystyle phi (e_{i},e_{j})=delta _{ij}.}$

We can now view the basis as a map ${displaystyle psi _{mathcal {B}}:Vrightarrow mathbb {R} ^{n}}$ which is an isomorphism of inner product spaces: to make this more explicit we can write

${displaystyle psi _{mathcal {B}}:(V,phi )rightarrow (mathbb {R} ^{n},delta _{ij}).}$

Explicitly we can write ${displaystyle (psi _{mathcal {B}}(v))^{i}=e^{i}(v)=phi (e_{i},v)}$ where $e^{i}$ is the dual basis element to $e_{i}$ .

The inverse is a component map

${displaystyle C_{mathcal {B}}:mathbb {R} ^{n}rightarrow V,(v^{i})mapsto sum _{i=1}^{n}v^{i}e_{i}.}$

These definitions make it manifest that there is a bijection

${displaystyle {{text{Space of orthogonal bases }}{mathcal {B}}}leftrightarrow {{text{Space of isomorphisms }}Vleftrightarrow mathbb {R} ^{n}}.}$

The space of isomorphisms admits actions of orthogonal groups at either the side or the $mathbb {R} ^{n}$ side. For concreteness we fix the isomorphisms to point in the direction ${displaystyle mathbb {R} ^{n}rightarrow V}$ , and consider the space of such maps, ${displaystyle {text{Iso}}(mathbb {R} ^{n}rightarrow V)}$ .

This space admits a left action by the group of isometries of , that is, such that , with the action given by composition:

This space also admits a right action by the group of isometries of $mathbb {R} ^{n}$ , that is, ${displaystyle R_{ij}in {text{O}}(n)subset {text{Mat}}_{ntimes n}(mathbb {R} )}$ , with the action again given by composition: ${displaystyle C*R_{ij}=Ccirc R_{ij}}$ .

As a principal homogeneous space[edit]

The set of orthonormal bases for $mathbb {R} ^{n}$ with the standard inner product is a principal homogeneous space or G-torsor for the orthogonal group and is called the Stiefel manifold ${displaystyle V_{n}(mathbb {R} ^{n})}$ of orthonormal -frames.^[7]

In other words, the space of orthonormal bases is like the orthogonal group, but without a choice of base point: given the space of orthonormal bases, there is no natural choice of orthonormal basis, but once one is given one, there is a one-to-one correspondence between bases and the orthogonal group.
Concretely, a linear map is determined by where it sends a given basis: just as an invertible map can take any basis to any other basis, an orthogonal map can take any orthogonal basis to any other orthogonal basis.

The other Stiefel manifolds ${displaystyle V_{k}(mathbb {R} ^{n})}$ for k<n of incomplete orthonormal bases (orthonormal -frames) are still homogeneous spaces for the orthogonal group, but not principal homogeneous spaces: any -frame can be taken to any other -frame by an orthogonal map, but this map is not uniquely determined.

References[edit]

^ Lay, David C. (2006). Linear Algebra and Its Applications (3rd ed.). Addison–Wesley. ISBN 0-321-28713-4.
^ Strang, Gilbert (2006). Linear Algebra and Its Applications (4th ed.). Brooks Cole. ISBN 0-03-010567-6.
^ Axler, Sheldon (2002). Linear Algebra Done Right (2nd ed.). Springer. ISBN 0-387-98258-2.
^ Rudin, Walter (1987). Real & Complex Analysis. McGraw-Hill. ISBN 0-07-054234-1.
^ Roman 2008, p. 218, ch. 9.
^ Linear Functional Analysis Authors: Rynne, Bryan, Youngson, M.A. page 79
^ «CU Faculty». engfac.cooper.edu. Retrieved 2021-04-15.

Roman, Stephen (2008). Advanced Linear Algebra. Graduate Texts in Mathematics (Third ed.). Springer. ISBN 978-0-387-72828-5. (page 218, ch.9)
Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.

External links[edit]

This Stack Exchange Post discusses why the set of Dirac Delta functions is not a basis of L²([0,1]).

Источник

Пример.4 Дополнение системы векторов до ортогонального базиса.

Упражнение.5

Задание для самостоятельной работы

Задачи.

Ортогональный и ортонормированный базисы евклидова пространства

Выражение скалярного произведения через координаты сомножителей

Преимущества ортонормированного базиса

Изменение матрицы Грама при переходе от одного базиса к другому

Свойства определителя Грама

Изоморфизм евклидовых пространств

104. Построение ортонормированного базиса из собственных векторов самосопряженного оператора

Ортогональный и ортонормированный базисы евклидова пространства

Выражение скалярного произведения через координаты сомножителей

Преимущества ортонормированного базиса

Изменение матрицы Грама при переходе от одного базиса к другому

Свойства определителя Грама

Изоморфизм евклидовых пространств

Examples[edit]

Basic formula[edit]

Incomplete orthogonal sets[edit]

Existence[edit]

Choice of basis as a choice of isomorphism[edit]

As a principal homogeneous space[edit]

See also[edit]

References[edit]

External links[edit]