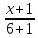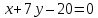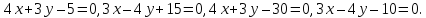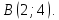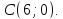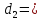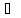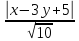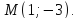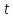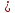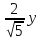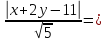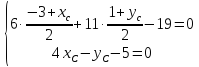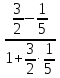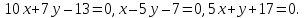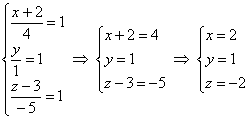Содержание:
- Формула
- Примеры нахождения орта вектора
Формула
Чтобы найти орт $bar{e}$ вектора
$bar{a}$, нужно вектор
$bar{a}$ поделить на его
длину:
$$bar{e}=frac{bar{a}}{|bar{a}|}$$
Если вектор задан на плоскости своими координатами
$bar{a}=left(a_{x} ; a_{y}right)$, то его орт вычисляется по формуле:
$$bar{e}=frac{bar{a}}{|bar{a}|}=frac{a_{x} cdot bar{i}+a_{y} cdot bar{j}}{sqrt{a_{x}^{2}+a_{y}^{2}}}=left(frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}}} ; frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}}}right)$$
Если вектор задан в пространстве и имеет координаты
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$, то его орт вычисляется по формуле:
$$bar{e}=frac{bar{a}}{|bar{a}|}=frac{a_{x} cdot bar{i}+a_{y} cdot bar{j}+a_{z} cdot bar{k}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}=$$
$$=left(frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} ; frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} ; frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}right)$$
Примеры нахождения орта вектора
Пример
Задание. На плоскости задан вектор
$bar{a}=(-2 ; 2)$ . Найти его орт.
Решение. Для нахождения орта заданного вектора воспользуемся формулой:
$$bar{e}=frac{bar{a}}{|bar{a}|}=frac{a_{x} cdot bar{i}+a_{y} cdot bar{j}}{sqrt{a_{x}^{2}+a_{y}^{2}}}$$
Подставляя заданные координаты, получим:
$$bar{e}=frac{-2 cdot bar{i}+2 cdot bar{j}}{sqrt{(-2)^{2}+2^{2}}}=frac{-2 cdot bar{i}+2 cdot bar{j}}{sqrt{4+4}}=frac{-2 cdot bar{i}+2 cdot bar{j}}{sqrt{8}}=$$
$$=frac{-2 cdot bar{i}+2 cdot bar{j}}{2 sqrt{2}}=-frac{1}{sqrt{2}} cdot bar{i}+frac{1}{sqrt{2}} cdot bar{j}$$
Таким образом, искомый орт вектора $bar{a}$
имеет координаты $bar{e}=left(-frac{1}{sqrt{2}} ; frac{1}{sqrt{2}}right)$
Ответ. $bar{e}=left(-frac{1}{sqrt{2}} ; frac{1}{sqrt{2}}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны точки
$A(3 ;-1 ; 4)$ и $B(2 ; 0 ; 2)$ . Найти орт вектора
$overline{A B}$
Решение. Найдем координаты вектора
$overline{A B}$, для этого из координат конца вектора (точки
$B$ ) вычтем соответствующие координаты начала (точки
$A$ ):
$$overline{A B}=(2-3 ; 0-(-1) ; 2-4)=(-1 ; 1 ;-2)$$
Для нахождения орта полученного вектора воспользуемся формулой
$$bar{e}=frac{a_{x} cdot bar{i}+a_{y} cdot bar{j}+a_{z} cdot bar{k}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$$
Подставим в неё координаты вектора $overline{A B}$, будем иметь:
$$bar{e}=frac{-1 cdot bar{i}+1 cdot bar{j}-2 cdot bar{k}}{sqrt{(-1)^{2}+1^{2}+(-2)^{2}}}=frac{-1 cdot bar{i}+1 cdot bar{j}-2 cdot bar{k}}{sqrt{1+1+4}}=$$
$$=frac{-1 cdot bar{i}+1 cdot bar{j}-2 cdot bar{k}}{sqrt{6}}=-frac{1}{sqrt{6}} cdot bar{i}+frac{1}{sqrt{6}} cdot bar{j}-frac{2}{sqrt{6}} cdot bar{k}$$
Таким образом, орт вектора $overline{A B}$ имеет координаты $bar{e}=left(-frac{1}{sqrt{6}} ; frac{1}{sqrt{6}} ;-frac{2}{sqrt{6}}right)$
Ответ. $bar{e}=left(-frac{1}{sqrt{6}} ; frac{1}{sqrt{6}} ;-frac{2}{sqrt{6}}right)$
Читать дальше: как найти вектор по точкам.
Определение.
Любой ненулевой вектор, перпендикулярный
прямой называется её нормальным
вектором,
и обозначается
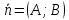
Теорема.
Алгебраическое уравнение 1-й степени
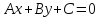
где
коэффициенты
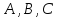
одновременно не равные нулю, являетсяуравнением
прямой на плоскости
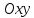
а вектор
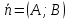
Верно
обратное:
на координатной плоскости
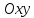
любой прямой с нормальным вектором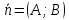
может быть записано в виде алгебраического
уравнения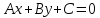
Определение.
Уравнение прямой вида
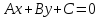
где
коэффициенты
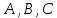
одновременно не равные нулю, называетсяобщим
уравнением прямой.
Известно,
что прямая определяется двумя точками.
Пусть
и
–
точки, лежащие на прямой
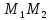
–
произвольная точка этой прямой. Тогда
векторы
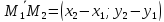
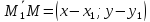
пропорциональны. Получаемуравнение
прямой, проходящей через две точки:
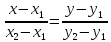
Определение.
Вектор,
параллельный прямой, называется
направляющим
вектором прямой.
Определение.
Пусть
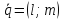
предыдущего уравнения получаемканоническое
уравнение прямой:
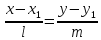
Определение.
В
тех же обозначениях, параметрическое
уравнение прямой
имеет вид:
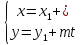
Определение.
Уравнение прямой вида
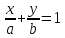
где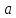
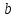
действительные числа, называетсяуравнением
прямой в отрезках.
Теорема.
Пусть
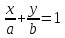
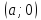
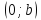
прямой с осями координат.
Определение.
Уравнение прямой вида

где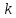
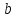
называетсяуравнением
прямой с угловым коэффициентом,
коэффициент
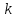
коэффициентом данной
прямой.
Теорема.
Пусть
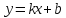
Тогда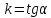
где угол
α
равен углу наклона данной прямой к оси
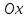
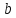
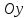
Если
известны угловые коэффициенты
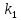
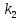
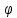
формуле:
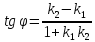
Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:
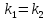
Признаком
перпендикулярности двух прямых является
соотношение:
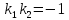
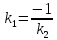
Теорема.
(Связь нормального вектора прямой с её
направляющим вектором и её угловым
коэффициентом.)
1)
Если
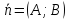
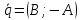
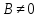
то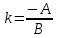
2)
Если
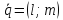
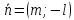
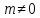
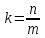
3)
Если
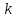
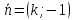
–
направляющий вектор.
Взаимное
расположение двух прямых на плоскости.
Две
прямые на плоскости могут пересекаться,
совпадать или быть параллельными.
Теорема.
Пусть прямые заданы общими уравнениями:
L1: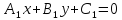
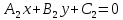
Тогда:
1)
если
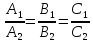
то прямые совпадают, и система уравнений
имеет
бесконечное множество решений;
2)
если
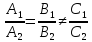
уравнений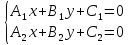
3)
если
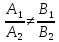
точки их пересечения являются единственным
решением системы уравнений
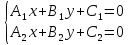
Определение.
Уравнение вида
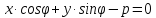
где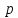
координат, называетсянормальным
уравнением прямой,
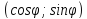
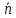
Чтобы
привести прямую к указанному виду,
разделим общее уравнение прямой на
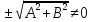
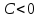
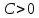
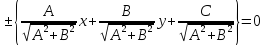
Теорема.
Орт нормального вектора
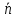
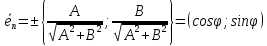
где
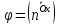
Теорема.
Расстояние от прямой до произвольной
точки
находится
по формуле:
Чтобы
найти расстояние
между двумя параллельными прямыми,
нужно взять произвольную точку на одной
из прямых и найти расстояние от нее до
другой прямой.
Чтобы
найти множество
точек, равноудаленных от двух прямых
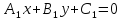
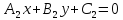
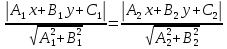
Раскрывая
модули в случае параллельных прямых,
получаем параллельную им прямую, лежащую
между данными прямыми, а в случае
пересекающихся прямых – биссектрисы
углов,
образованных пересечением прямых.
Определение.
Совокупность прямых, проходящих через
некоторую точку S,
называется пучком
прямых с центром S.
Теорема.
Если
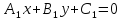
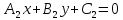
в точкеS,
то уравнение:
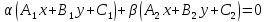
где
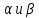
одновременно нулю, определяют прямую,
также проходящую через точкуS.
Более
того, в указанном уравнении числа всегда
возможно подобрать так, чтобы оно
определяло любую (заранее назначенную)
прямую, проходящую через точку S,
иначе говоря, любую прямую пучка с
центром S.
Поэтому уравнение вида называется
уравнением пучка с центром S.
Решение
типовых задач
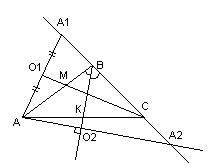
Задача
№1:
Даны
уравнения двух сторон параллелограмма
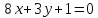
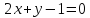
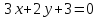
Определить координаты вершин этого
параллелограмма.
Решение:
Найдём
координаты т.
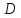
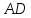
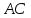
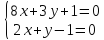
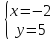
т.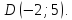
Подставим
координаты т.
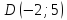
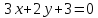
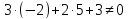
т.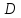
следовательно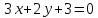
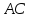
Найдём
координаты т.
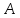
как точки пересечения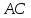
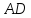
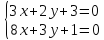
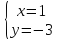
т.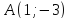
Найдём
координаты т.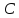
как точки пересечения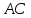
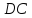
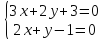

т.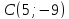
Найдём
координаты т.B:
в параллелограмме диагонали делят друг
друга пополам:
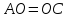
Найдём координаты т.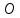
т.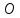
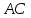
следовательно, т.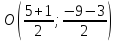
т.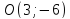
но т.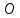
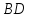
следовательно,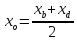
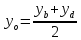
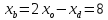
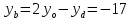
т.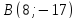
Ответ:
Задача
№2:
Дана
прямая
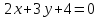
Составить уравнение прямой, проходящей
через точку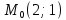
-
параллельно
данной прямой. -
перпендикулярно
к данной прямой.
Решение:
-
Искомая
прямая параллельна прямой
,
поэтому её уравнение имеет вид:.
Найдём
т.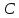
точка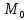
координаты удовлетворяют записанному
уравнению: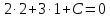
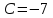
Итак, прямая принимает вид: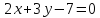
-
Т.к.
заданная и искомые прямые перпендикулярны,
то их угловые коэффициенты удовлетворяют
условию:
.
Найдём
угловой коэффициент прямой
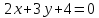
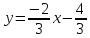
итак,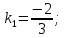
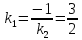
Запишем уравнение искомой прямой: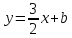
Точка
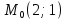
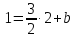
Уравнение
прямой принимает вид:
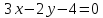
Ответ:
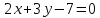
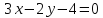
Задача
№3:
Определить,
при каких значениях a
и b
две прямые
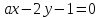
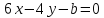
-
имеют
одну общую точку; -
параллельны;
-
совпадают.
Решение:
-
Прямые
имеют одну общую точку, когда они не
параллельны (их коэффициенты при x
и y
не пропорциональны):
;
-
Прямые
параллельны, когда коэффициенты при x
и y
пропорциональны:
;
.
-
Прямые
совпадают, когда все их коэффициенты
пропорциональны:
;
.
Задача
№4:
Найти
проекцию точки
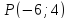
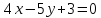
Решение:
Проведём
через т.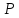
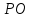
перпендикулярную прямой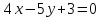
Точка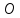
проекцией.
Прямая
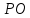
её направляющим вектором служит
нормальный вектор прямой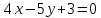
т.е.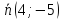
Запишем
уравнение прямой
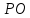
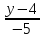
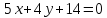
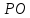
Найдём
координаты т.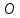
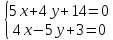
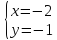
т.
Ответ:
Задача
№5:
Найти
точку
симметричную точке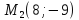
точки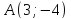
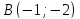
Решение:
Составим
уравнение
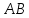
как прямой проходящей через 2 точки:
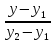
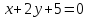
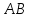
Найдём
уравнение прямой
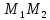
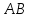
Нормальный
вектор
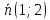
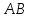
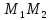
поэтому используем каноническое
уравнение прямой: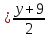
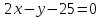
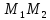
Найдём
координат т.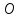
как точки пересечения прямых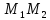
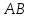
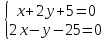
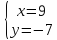
т.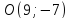
Так
как точка

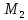
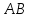
следовательно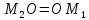
то есть т.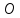
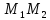
Найдём координаты точки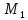
зная начало и середину отрезка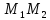
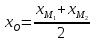
, тогда
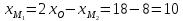
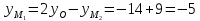
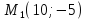
Ответ:
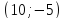
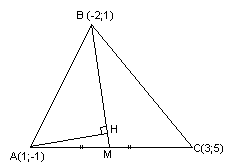
Задача
№6:
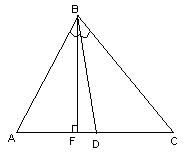
Даны
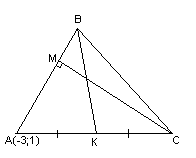
вершины треугольника
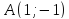
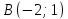
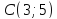
Составить уравнение перпендикуляра,
опущенного из вершины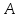
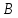
Решение:
Найдём
координаты т.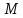
как середины отрезка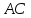
т.
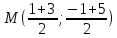
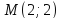
Запишем
уравнение медианы
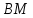
как прямой, проходящей через две известные
точки:
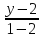
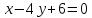
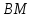
Нормальный
вектор для
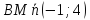
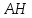
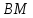
тогда уравнение примет вид:
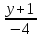
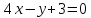
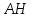
Ответ:
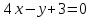
Задача
№7:
Даны
вершины треугольника

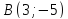
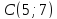
Составить уравнение перпендикуляра,
опущенного из вершины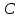
вершине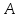
Решение:
Пусть
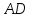
Найдём
координаты т.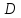
Тогда:
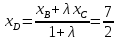
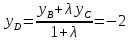
т.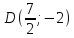
Уравнение
биссектрисы
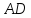
=
⇒
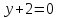
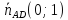
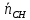
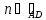
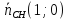
Точка
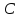
поэтому уравнение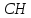
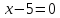
Ответ:
Задача
№8:
Две
стороны квадрата лежат на прямых
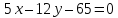
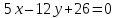
Вычислить его площадь.
Решение:
-
Выберем
на прямой
некоторую точку
:
пусть
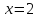
тогда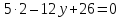
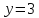
т.е.
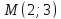
-
Найдём
расстояние от точки
до прямой
:
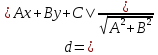
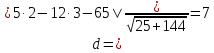
где
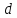
-
т.е.
.
Ответ:
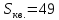
Задача
№9:
Даны
две противоположные вершины квадрата
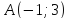
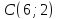
Составить уравнения его сторон.
Решение:
Зная
вершины

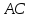
как прямой проходящей через две точки: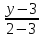
– уравнение прямой
Т.к.
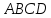
биссектрисами, поэтому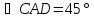
найдём угловой коэффициент
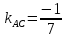
Зная
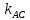

найдём угловой коэффициент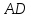
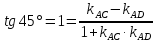
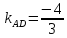
Уравнение
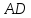
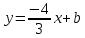
Найдём
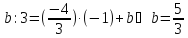
Тогда уравнение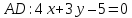
Т.к.
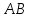
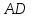
угловой коэффициент
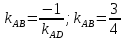
Уравнение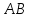
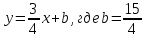
тогда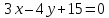
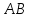
Т.к.
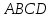
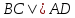
то уравнение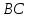
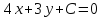
Зная,
что точка
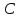
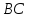
найдём свободный член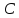
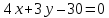
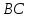
Аналогично
найдём уравнение стороны
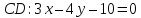
Ответ:
Задача
№10:
Вычислить
площадь треугольника, отсекаемого
прямой
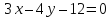
Решение:
Запишем
уравнение прямой
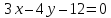
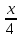
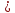
Из
этого уравнения следует, что длины
отрезков
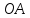
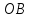
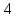
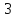
поэтому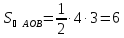
Ответ:
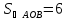
Задача
№11:
Составить
уравнения сторон треугольника, зная
одну из его вершин

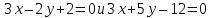
Решение:
Выясним,
что точка
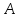
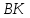
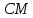
Найдём
координаты точки
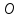
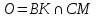
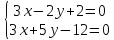
т.
Продолжим
медиану
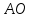
и на её продолжении отложим отрезок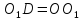
Соединим точку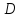
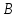
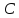
Полученный четырёхугольник
пересекаясь в точке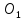
делятся пополам).
Найдём
координаты точки
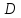
как конца отрезка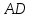

Найдём
уравнение прямой
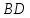
зная, что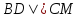

Найдём
координаты вершины
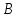
как точки пересечения прямых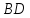
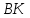
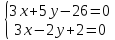
т.
Точка
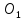
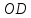
поэтому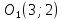
Найдём
координаты точки
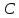
как конца отрезка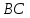
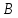
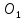
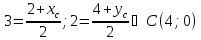
Зная
координаты всех вершин треугольника
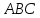
найдём уравнения его сторон, как прямых
проходящих через две точки.
Ответ:
Задача
№12:
Составить
уравнения сторон треугольника, зная
одну из его вершин
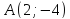
Решение:
Очевидно,
что точка

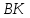
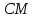
Найдём точку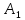
симметричную точке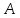
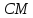
Можно доказать, что точка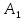
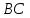
Опустим из т.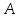
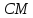
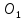
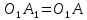
Т.к.
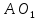
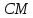
то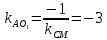
точка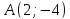
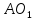
поэтому её уравнение примет вид:
Координаты
точки
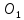
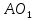
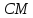
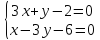
т.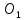
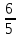
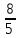
Найдём
координаты точки
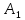
как конца отрезка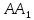
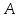
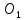
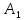
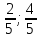
Аналогично
найдём точку
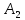
симметричную т.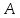
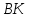
Точка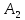
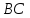
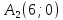
Тогда
уравнение стороны
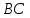
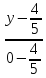
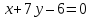
Найдём
координаты точек
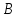
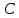
как точек пересечения прямой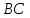
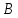
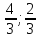
Зная
координаты вершин треугольника
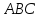
найдём уравнения его сторон.
Ответ:
Задача
№13:
Составить
уравнения биссектрис углов, образованных
двумя пересекающимися прямыми:
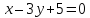
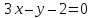
Решение:
Известно
свойство: биссектриса есть геометрическое
место точек, равноудалённых от сторон
угла.
Пусть
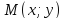
тогда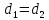
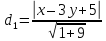
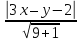
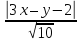
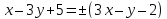
Тогда
уравнения биссектрис примут вид:
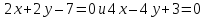
Ответ:
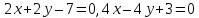
Задача
№14:
Составить
уравнение биссектрисы угла между прямыми
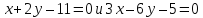
в котором лежит точка
Решение:
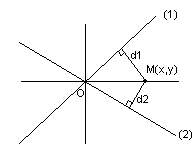
Найдём
отклонение точки
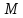
прямых, для этого приведём их уравнения
к нормальному виду: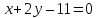
нормирующий множитель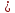
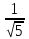
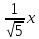
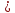
Найдём
отклонение
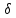
т.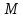
нормального уравнения подставим
координаты т.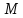
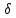
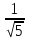
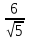
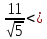
Аналогично
найдём отклонение
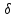
т.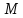
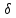
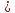
Отклонения имеют разные знаки, поэтому
при раскрытии модулей (см. решение
предыдущей задачи) справа ставим знак
«минус».
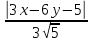
Уравнение
биссектрисы принимает вид:
Ответ:
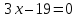
Задача
№15:
На
прямой
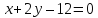
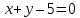
Решение:
Точки
равноудалённые от прямых
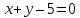
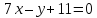
лежат на биссектрисах углов, образованных
этими прямыми. Аналогично решению
предыдущих задач найдём их:
Тогда
искомые точки являются точками пересечения
этих биссектрис и прямой
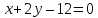
поэтому найдём их, решая системы: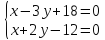
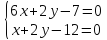
Ответ:
Задача
№16:
Составить
уравнения сторон треугольника, зная
одну из его вершин
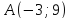
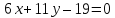
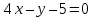
проведённых из различных вершин.
Решение:
Убедимся,
что точка
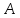
высоте.
Найдём
уравнение стороны
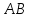
зная, что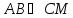
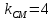
тогда уравнение примет вид:
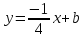
зная координаты т.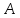
принадлежащей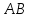
найдём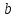
тогда уравнение примет вид: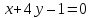
Найдём
координаты т.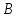
как точки пересечения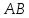
медианы
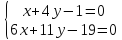
Пусть
точка
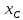
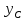
найдём их. Точка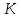
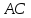
поэтому
Точка
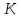
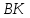
точка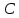
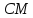
поэтому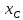
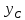
Откуда
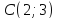
найдём уравнения всех его сторон.
Ответ:
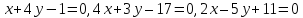
Задача
№17:
Через
точку
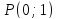
заключённый между прямыми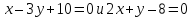
делился бы в точке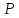
Решение:
Обозначим
через
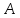
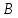
искомой прямой и пусть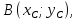
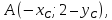
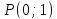
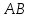
Координаты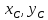
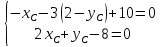
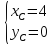
Составим
уравнение искомой прямой, которая
проходит через две точки, например,
Ответ:
Задача
№18:
Составить
уравнения сторон треугольника
зная одну из его вершин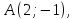
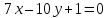
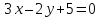
проведённых из одной вершины. Решить
задачу, не вычисляя координат вершин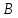
Решение:
Можно
проверить, что т.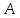
ни биссектрисе.
Найдём уравнение стороны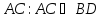
поэтому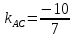
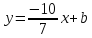
зная координаты т.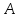
найдём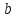
Итак,
уравнение
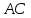
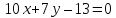
Рассмотрим
пучок с центром в т.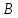
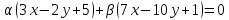
Пусть
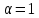
тогда уравнение пучка примет вид:
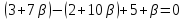
(1)
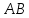
пучка, причём координаты т.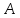
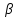
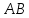
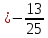
поэтому уравнение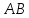
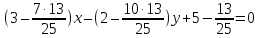
т.е.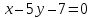
Найдём
угол между прямыми
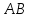
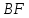
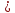
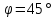
Тогда
угол
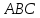
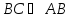
—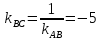
С другой стороны найдём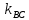
Итак,
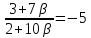
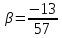
Найдём
уравнение стороны
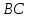
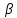
стороны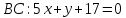
Ответ:
Образовательным
результатом после изучения данной темы
является сформированность компонент,
заявленных во введении, совокупности
компетенций (знать, уметь, владеть) на
двух уровнях: пороговый и продвинутый.
Пороговый уровень соответствует оценке
«удовлетворительно», продвинутый
уровень соответствует оценкам «хорошо»
или «отлично» в зависимости от результатов
защиты кейс-заданий.
Для
самостоятельной диагностики данных
компонент вам предлагаются следующие
задания.
Орт:
- это вектор,
- он лежит на оси,
- направлен туда же, куда направлена ось,
- его длина равна единице.
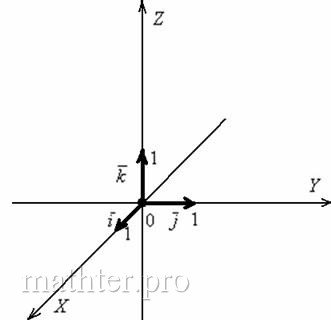
На рисунке 1 изображены орты для двумерного а) и трехмерного б) случаев.
Рис. 1. Единичные векторы – орты, располагаются на осях координат
Орты сонаправлены с осями, на которых они лежат:
- Орт ( vec{i} ) направлен вдоль оси Ox;
- Орт ( vec{j} ) направлен вдоль оси Oy;
- Орт ( vec{k} ) направлен вдоль оси Oz;
Орты обладают единичной длиной:
[ |vec{i}| = |vec{j}| = |vec{k}| = 1]
Все три орта взаимно перпендикулярны. Перпендикулярные векторы часто называют ортогональными.
Любые два орта из трех, лежат в одной плоскости:
- Орты ( vec{i} ) и ( vec{j} ) лежат в плоскости xOy;
- Орты ( vec{i} ) и ( vec{k} ) лежат в плоскости xOz;
- Орты ( vec{j} ) и ( vec{k} ) лежат в плоскости yOz;
Векторы, лежащие в одной плоскости, называют компланарными. Об этом подробно написано «здесь» (откроется в новой вкладке).
Координаты вектора можно указать двумя способами. Либо, перечислив эти координаты в скобках, либо, с помощью разложения вектора по ортам.
Пример:
Сравните два способа обозначения вектора
[ vec{a} = left{ -2; 7; -5 right} ]
и
[vec{a} = -2 cdot vec{i} + 7cdot vec{j} – 5 cdot vec{k} ]
5.4.1. Канонические уравнения прямой
Для лёгкого понимания темы целесообразно освоить или вспомнить уравнение «плоской» прямой, поскольку будет очень много похожих вещей. Но будут и отличия, на одно из которых вы уже наверняка обратили внимание. Я выделил прописной буквой окончание слова «уравнениЯ», подчеркивая, что оно находится ВО МНОЖЕСТВЕННОМ ЧИСЛЕ. И это не случайно: особенность пространственной прямой состоит в том, что она задаётся не одним уравнением, а некоторым множеством уравнений.
Теперь о совпадениях: пространственную прямую точно так же обозначают строчными латинскими буквами , как вариант, с подстрочными индексами:
. Либо двумя точками, принадлежащими данной прямой:
.
И точно так же – её можно задать несколькими способами. Начнём с канонов, точки и направляющего вектора:
Если известна некоторая точка пространства , принадлежащая прямой, и направляющий вектор
данной прямой, то канонические уравнения этой прямой выражаются формулами:
Приведённая запись предполагает, что координаты направляющего вектора не равны нулю. Что делать, если одна или две координаты нулевые, мы рассмотрим чуть позже.
Задача 143
Составить канонические уравнения прямой по точке и направляющему вектору
Решение: по соответствующим формулам:
Ответ:
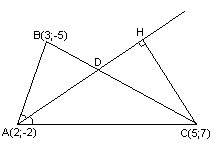
Что следует отметить в этом очень простом примере? Во-первых, полученные уравнения НЕ НАДО сокращать на единицу:
Сократить, точнее, можно, но это режет глаз и создаёт неудобства в ходе решения задач.
А во-вторых, проверка, которая очень легко (и быстро!) выполняется устно:
Сначала смотрим на знаменатели уравнений и сверяемся – правильно ли там записаны координаты направляющего вектора ? Нет, не подумайте, у нас не урок в детском садике «Тормозок», эта мера позволит исключить ошибку по невнимательности. Никто не застрахован от «наваждения», или вдруг вы условие неправильно переписали?
Далее подставляем координаты точки в найденные уравнения:
– получены верные равенства, значит, координаты точки
удовлетворяют нашим уравнениям, и сама точка действительно принадлежит данной прямой.
Довольно часто требуется найти какую-нибудь другую точку , принадлежащую данной прямой. Как это сделать? Берём полученные уравнения
и мысленно «отщипываем», например, левый кусочек:
. Теперь этот кусочек приравниваем к любому числу (помним, что ноль уже был), например, к единице:
.
Так как , то и два других «куска» тоже должны быть равны единице. По сути, нужно решить систему:
Проверим, удовлетворяет ли точка уравнениям
:
– получены верные равенства, значит, точка
действительно принадлежит данной прямой.
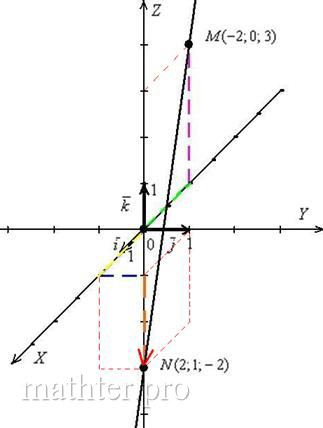
Выполним чертёж в прямоугольной системе координат:
Заодно вспомним, как правильно откладывать точки в пространстве. Строим точку :
– от начала координат в отрицательном направлении оси откладываем отрезок первой координаты
(зелёный пунктир);
– вторая координата нулевая, поэтому «не уходим» с оси
ни влево, ни вправо;
– в соответствие с третьей координатой отмеряем три единицы вверх (фиолетовый пунктир). Строим точку
:
– отмеряем две единицы «на себя» (желтый пунктир), одну единицу вправо (синий пунктир) и две единицы вниз (коричневый пунктир). Коричневый пунктир и сама точка наложились на координатную ось, заметьте, что они находятся в нижнем полупространстве и расположены ПЕРЕД осью
.
Сама прямая проходит над осью
и, если меня не подводит глазомер, над осью
. Не подводит, убедился аналитически. Если бы прямая
проходила ЗА осью
, то следовало бы стереть частичку линии
сверху и снизу точки скрещивания.
У прямой бесконечно много направляющих векторов, например:
(красная стрелка). Получился в точности исходный вектор
, но это чистая случайность (такую уж я выбрал точку
). Любой коллинеарный вектор, например,
тоже будет направляющим вектором данной прямой (вспоминаем, как их получить)
Разберёмся с частными случаями, когда одна или две координаты направляющего вектора нулевые. Попутно продолжим тренировать пространственное воображение. Изобразите в тетради декартову систему координат . Напоминаю удобный масштаб: 2 клетки = 1 ед. – по осям
и диагональ одной клетки = 1 ед. – по оси
.
Теперь я буду рассказывать о прямых, а вы их мысленно представляйте! Рассмотрим все шесть случаев:
1) Для точки и направляющего вектора
канонические уравнения прямой распадаются на три отдельных уравнения:
или короче:
Что это за прямая?
Поскольку направляющий вектор коллинеарен орту
, то такая прямая будет параллельна оси
, в частности, уравнения
задают саму ось абсцисс. В чём смысл уравнений
? «Игрек» и «зет» ВСЕГДА (при любом «икс») равны нулю. А это ось
. Кроме того, есть и другая интерпретация – ведь перед нами уравнения двух плоскостей! Уравнение
задаёт координатную плоскость
, а уравнение
– плоскость
. Смотрим на чертёж и ищем их пересечение!
Задача 144
Составить уравнения прямой по точке и вектору
.
Решение и ответ в одну строчку:
Какому условию удовлетворяет каждая точка этой прямой? «Иксовая» координата может быть любой: (на практике данное уравнение, как правило, не записывают). А вот «игрековая» и «зетовая» координата постоянны, равны конкретным числам:
.
Самостоятельно осмысливаем два «родственных» случая:
2) Канонические уравнения прямой, проходящей через точку параллельно вектору
, выражаются формулами
.
Такие прямые будут параллельны координатной оси , в частности, уравнения
(
любое) задают координатную саму ось ординат.
3) Канонические уравнения прямой, проходящей через точку параллельно вектору
, выражаются формулами
. Данные прямые параллельны координатной оси
, а уравнения
(
любое) задают саму ось аппликат.
Обкатываем вторую тройку:
4) Для точки и направляющего вектора
канонические уравнения прямой распадаются на пропорцию
и уравнение плоскости
.
Задача 145
Составить уравнения прямой по точке и вектору
.
Решение и ответ в одну строчку:
Разберём суть полученной записи. Уравнение задаёт плоскость, причём данная плоскость будет параллельна «родной» координатной плоскости
. Из пропорции
легко выразить уравнение «плоской» прямой, единственное, эта прямая будет находиться не на плоскости
, а на высоте
.
Если высота нулевая: , то уравнения принимают вид
, и вот это уже в точности наша «плоская» прямая, лежащая в плоскости
.
Таким образом, рассмотренный случай задаёт прямую, параллельную координатной плоскости . Действительно, задумайтесь, ведь направляющий вектор
параллелен данной плоскости, ибо «зетовая» координата равна нулю.
Аналогично – читаем, вдумываемся и представляем:
5) Прямая, заданная точкой и направляющим вектором
, параллельна координатной плоскости
, и её канонические уравнения выражаются формулами:
. В частности, уравнения
определяют прямую, лежащую в плоскости
.
6) Прямая, заданная точкой и направляющим вектором
, параллельна координ атной плоскости
, и её канонические уравнения выражаются формулами:
. В частности, уравнения
определяют прямую, лежащую в плоскости
.
Настала пора закусить – составляем уравнения и вникаем в их смысл:
Задача 146
Записать канонические уравнения прямой, если известна точка и направляющий вектор данной прямой:
а) ;
б) .
в) Прямая проходит через точку параллельно оси
.
Это задание для самостоятельного решения, ответы в конце книги.


| Оглавление |
Автор: Aлeксaндр Eмeлин

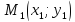
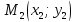
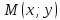


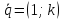
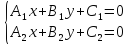
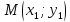
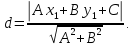

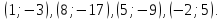
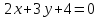 ,
,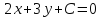 .
.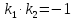 .
.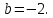
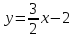
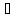
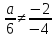 ;
;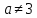
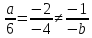 ;
;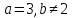 .
.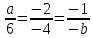 ;
;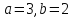 .
.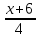
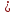
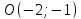
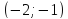
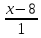
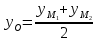
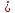
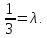
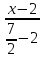
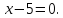
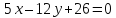 некоторую точку
некоторую точку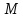 :
: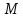 до прямой
до прямой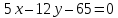 :
: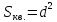 т.е.
т.е.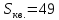 .
.