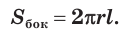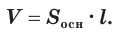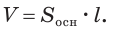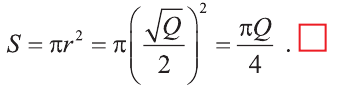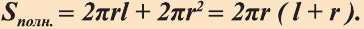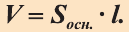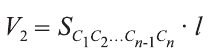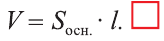Содержание:
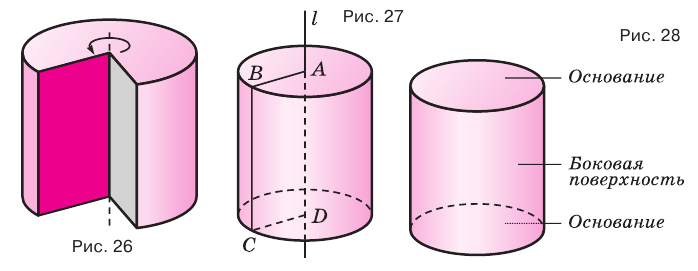
Цилиндром называется тело, полученное вращением прямоугольника вокруг оси, проходящей через его сторону (рис. 26). На рисунке 27 показано образование цилиндра при вращении прямоугольника
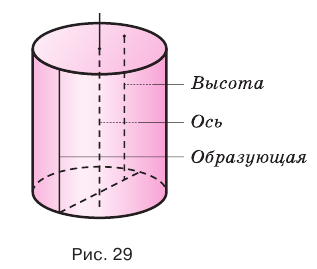
Образующая цилиндра является его высотой.
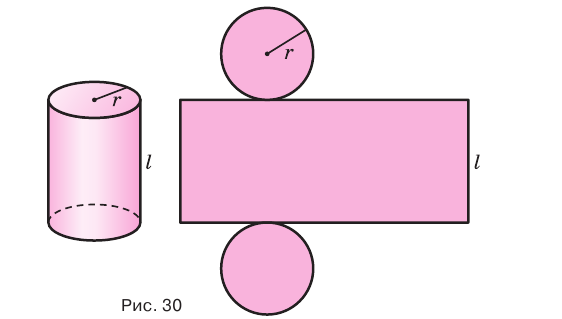
Поверхность цилиндра можно развернуть на плоскость, в результате получится прямоугольник, представляющий боковую поверхность цилиндра, и два круга, представляющих его основания. На рисунке 30 показан цилиндр и его развертка.
Теорема 4.
Боковая поверхность цилиндра равна произведению длины окружности основания и образующей:
На плоскости важной конфигурацией, которая часто встречается в задачах, является сочетание окружности с прямой. Подобной пространственной конфигурацией является сочетание цилиндра с плоскостью.
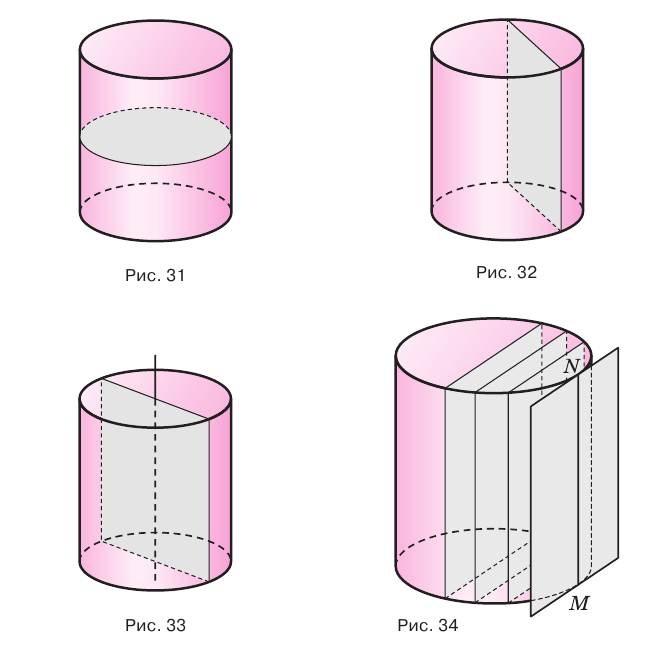
Если цилиндр пересечь плоскостью, параллельной основанию, то получится круг, равный основанию (рис. 31), а если плоскостью, перпендикулярной основанию, то — прямоугольник, одна сторона которого равна высоте цилиндра (рис. 32). Осевое сечение цилиндра, т. е. сечение плоскостью, проходящей через ось цилиндра, является прямоугольником, стороны которого равны высоте цилиндра и диаметру его основания (рис. 33).
Будем двигать плоскость, проходящую через ось цилиндра, параллельно самой себе (рис. 34). При этом две противолежащие стороны прямоугольника-сечения цилиндра, являющиеся хордами оснований, будут уменьшаться, а две другие стороны, которые являются образующими цилиндра, — сближаться до того момента, пока не совпадут. Получим плоскость, содержащую образующую 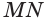
Теорема 5.
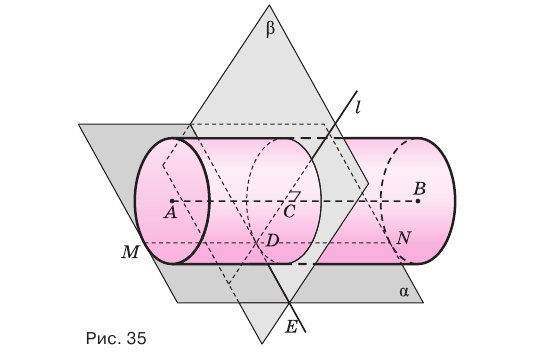
Если плоскость касается цилиндра по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 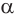
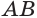
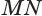
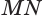
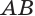
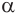
Проведем прямую 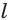
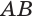
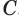
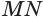
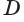
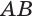
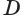
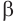
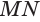
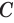
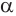
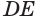
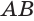
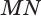
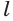
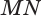
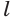
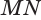
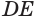
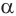
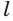
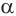
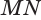
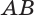
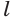
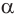
Теорема 5 выражает свойство касательной плоскости цилиндра.
Теорема 6.
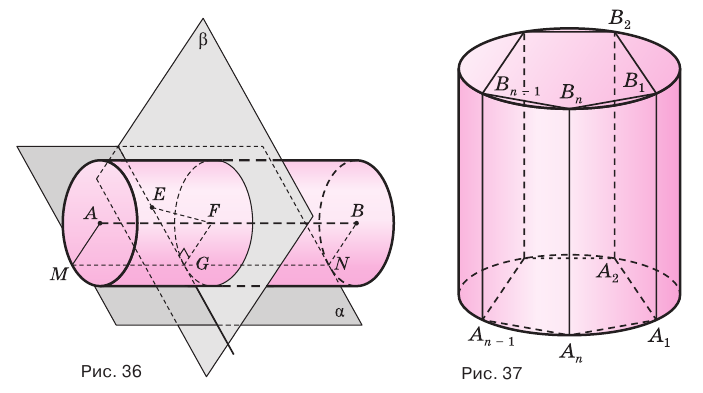
Плоскость касается цилиндра, если она проходит через его образующую и перпендикулярна плоскости, содержащей эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 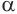
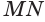
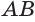
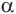
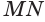
Пусть 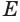
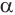
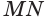
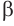
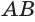
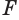
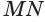
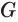
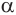
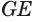
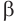
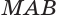
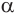
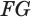
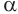
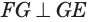
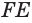
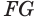
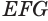
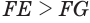
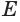
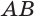
Теорема 6 выражает признак касательной плоскости цилиндра.
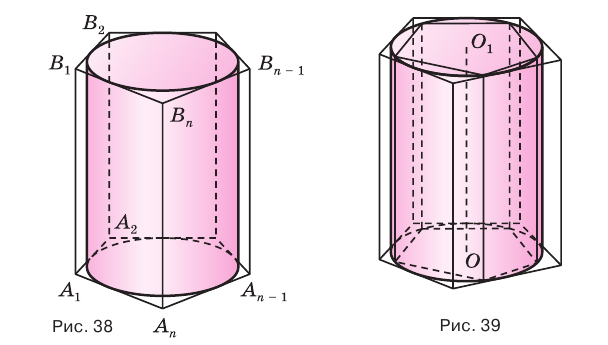
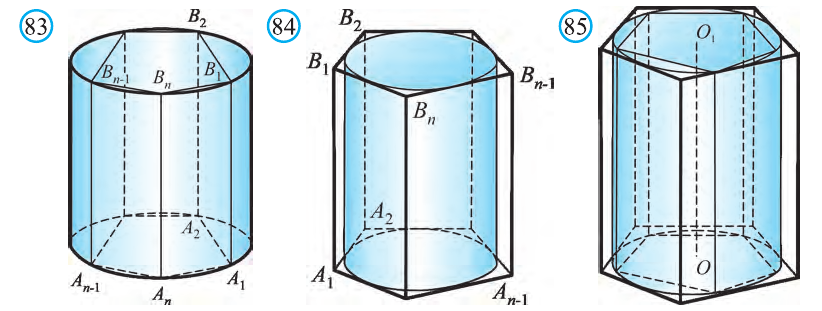
Пусть имеется цилиндр (рис. 37). Впишем в одно из оснований цилиндра многоугольник 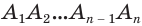
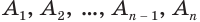
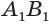
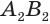
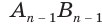
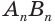
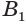
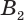
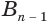
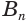
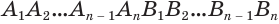
Если цилиндр описан около призмы, то основания цилиндра описаны около оснований призмы, а боковая поверхность цилиндра содержит боковые ребра призмы.
Подобным образом вводится понятие призмы, описанной около цилиндра, и цилиндра, вписанного в призму (рис. 38). Если призма описана около цилиндра, то ее основания описаны около оснований цилиндра, а боковые грани касаются боковой поверхности цилиндра.
Теорема 7.
Объем цилиндра равен произведению площади его основания и образующей:
Доказательство:
Пусть имеется цилиндр с осью 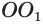
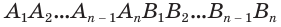
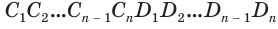
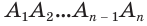
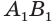
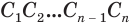
Будем количество 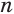
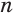
В описанном процессе высота 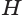
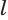
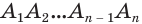
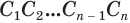
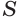
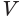
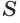
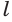
Поверхность цилиндра
Ещё один важный класс пространственных фигур — тела вращения. Цилиндр является одним из них, мы познакомимся с ним глубже. Свойства цилиндра похожи на свойства призм, мы последовательно изучим их.
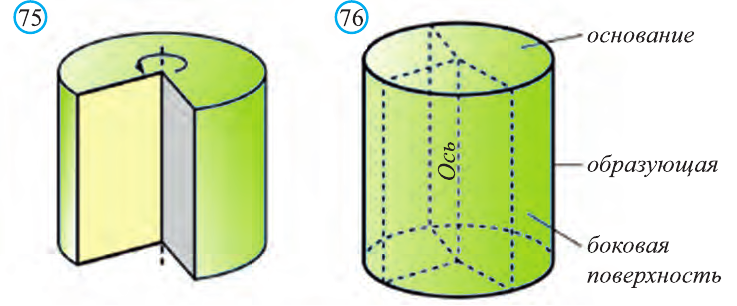
Тело, полученное вращением прямоугольника вокруг одной из его сторон называют цилиндром (точнее, прямой круговой цилиндр) (рис. 75). При вращении прямоугольника одна его сторона остаётся неподвижной. Её называют осью цилиндра. Поверхность, образованную при вращении противоположной стороны прямоугольника называют цилиндрической поверхностью, а саму сторону образующей цилиндра. Две другие стороны прямоугольника при этом вращении образуют два равных круга, которые называют основаниями цилиндра (рис. 76).
Замечание. Тело, полученное вращением прямоугольника вокруг одной из его сторон называют прямым круговым цилиндром. Более широкое понятие цилиндра вводят следующим образом.
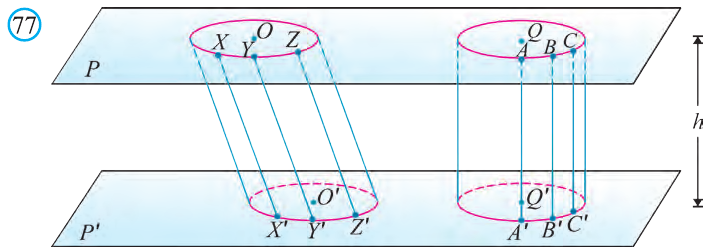
Пусть в пространстве параллельный перенос переводит плоскую фигуру F1, в фигуру F2. Тело, состоящее из этих фигур и отрезков, соединяющих их соответствующие точки, называют цилиндром (рис. 77).
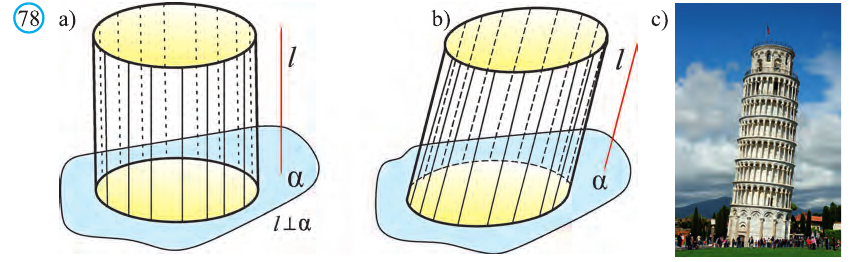
Если при параллельном переносе образующая перпендикулярна плоскости фигуры F1 , цилиндр называют прямым (рис. 78.а), в противном случае наклонным цилиндром (рис. 78.b). На рисунке 78.с изображена Пизанская башня, имеющая вид наклонного цилиндра.
Если фигура F1 является кругом, то цилиндр называют круговым цилиндром.
Только прямой круговой цилиндр является телом вращения. В дальнейшем мы будем рассматривать прямые круговые цилиндры, которые для краткости будем называть цилиндрами.
Основания цилиндра являясь равными кругами, лежат на параллельных плоскостях. Перпендикуляр, опущенный из некоторой точки одного основания на другое, называют его высотой.
Расстояние между параллельными плоскостями равно высоте цилиндра. Ось цилиндра также является его высотой.
Образующие цилиндра параллельны и равны. Точно также, длины высоты, оси и образующих цилиндра будут равны между собой.
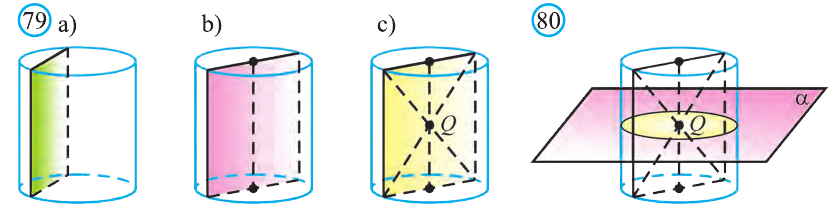
Сечением цилиндра плоскостью параллельной его оси является прямоугольник (рис.79.а). Две противоположные его стороны — это образующие цилиндра, а две другие стороны — соответствующие параллельные хорды оснований цилиндра.
В частности, осевое сечение также прямоугольник, образованный сечением цилиндра плоскостью, проходящей через его ось (рис. 79.b).
Диагонали осевого сечения цилиндра проходят через точку являющуюся серединой отрезка, соединяющего центры оснований цилиндра. Следовательно, эта точка Q есть центр симметрии цилиндра (рис. 79.с).
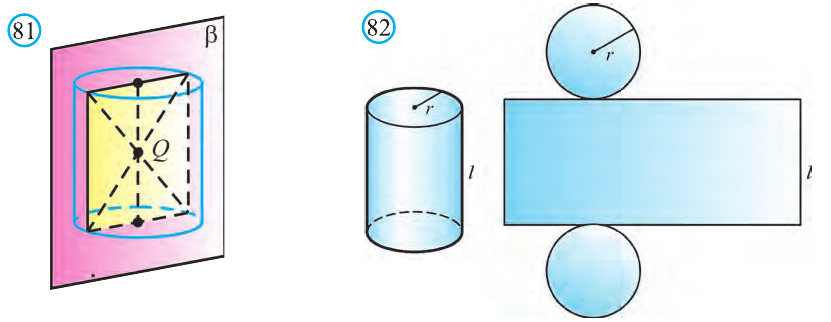
Плоскость, проходящая через точку Q перпендикулярно оси цилиндра является его плоскостью симметрии (рис. 80). Любая плоскость, проходящая через ось цилиндра также будет ось симметрии цилиндра (рис. 81).
Пример:
Осевое сечение цилиндра — квадрат, площадь которого Q. Найдите площадь основания цилиндра.
Решение:
Сторона квадрата равна 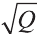
основания. Поэтому его площадь равна
Докажите самостоятельно эту теорему пользуясь рисунком 82.
Следствие. Полная поверхность цилиндра равна сумме его боковой поверхности и площадей двух его оснований:
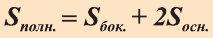
Пусть дан произвольный цилиндр. Впишем в одно из его оснований многоугольник 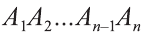
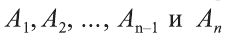
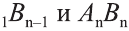
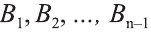
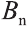
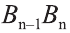
Ясно, что если вокруг основания призмы можно описать окружность, то вокруг призмы можно описать цилиндр.
Аналогично вводятся понятия призмы, описанной вокруг цилиндра и цилиндра, вписанного в призму (рис. 84). Если призма описана вокруг цилиндра, то основание призмы будет описано вокруг основания цилиндра и боковые грани призмы будут касаться боковой поверхности цилиндра.
Ясно, что если в основание призмы можно вписать окружность, то вокруг цилиндра можно описать призму.
Объём цилиндра
Теорема. Объём цилиндра равен произведению площади его основания и образующей цилиндра:
Доказательство. Пусть дан цилиндр с осью ОО1 (рис. 85). Впишем в него призму 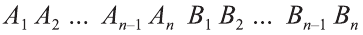
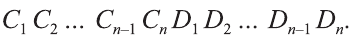
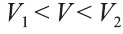
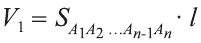
Будем всё больше и больше увеличивать число n сторон оснований призм. Тогда объём вписанной призмы будет увеличиваться, а объём описанной призмы уменьшаться. Если число n сторон увеличивать неограниченно, то разность между объёмами будет стремится к нулю. Число, к которому приближаются объёмы вписанной и описанной призм, принимают за объём данной призмы. При этом площади многогранников 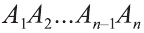
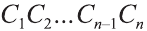
Исторические сведения:
В произведении Абу Райхна Беруни «Книга о началах искусства астрономии» («Астрономия») как введение в стереометрию в разделе о геометрии приводятся следующие определения фигур:
Куб — физическая фигура, похожая на кубик для игры в нарды, ограниченная с шести сторон квадратами.
Призма — представляет собой фигуру, ограниченную по бокам плоскостями в форме квадрата или прямоугольника, а сверху и снизу -двумя треугольниками. В этом определении Беруни приведено описание частного вида призмы, а именно треугольной призмы.
Книга Беруни «Канон Масьуда» написана в 1037 году. В ней приведены правила нахождения объёмов параллелепипеда и призмы: «Если тело не четырёхугольное или другого вида, то его расчёт таков: найди площадь, умножь его на глубину, в итоге получишь объём». В произведении Абу Али ибн Сино «Книга знания» в разделе «Основы изучения геометрических тел» дано описание тела и треугольной призмы. А также описаны условия взаимного равенства двух призм. Ибн Сино даёт следующее определение призмы: «Призма — тело, ограниченное двумя плоскими треугольными сторонами.»
В произведении Аль Каши «Книга счёта» приведёт много примеров расчета площадей поверхностей и объёмов тел. Благодаря своим глубоким знаниям в математике, геометрии, тригонометрии, механике и астрономии он пользовался вниманием и уважением Улугбека. Аль Каши наряду с многоугольниками изучачл призмы, пирамиды, цилиндры, конусы, усечённые конусы.
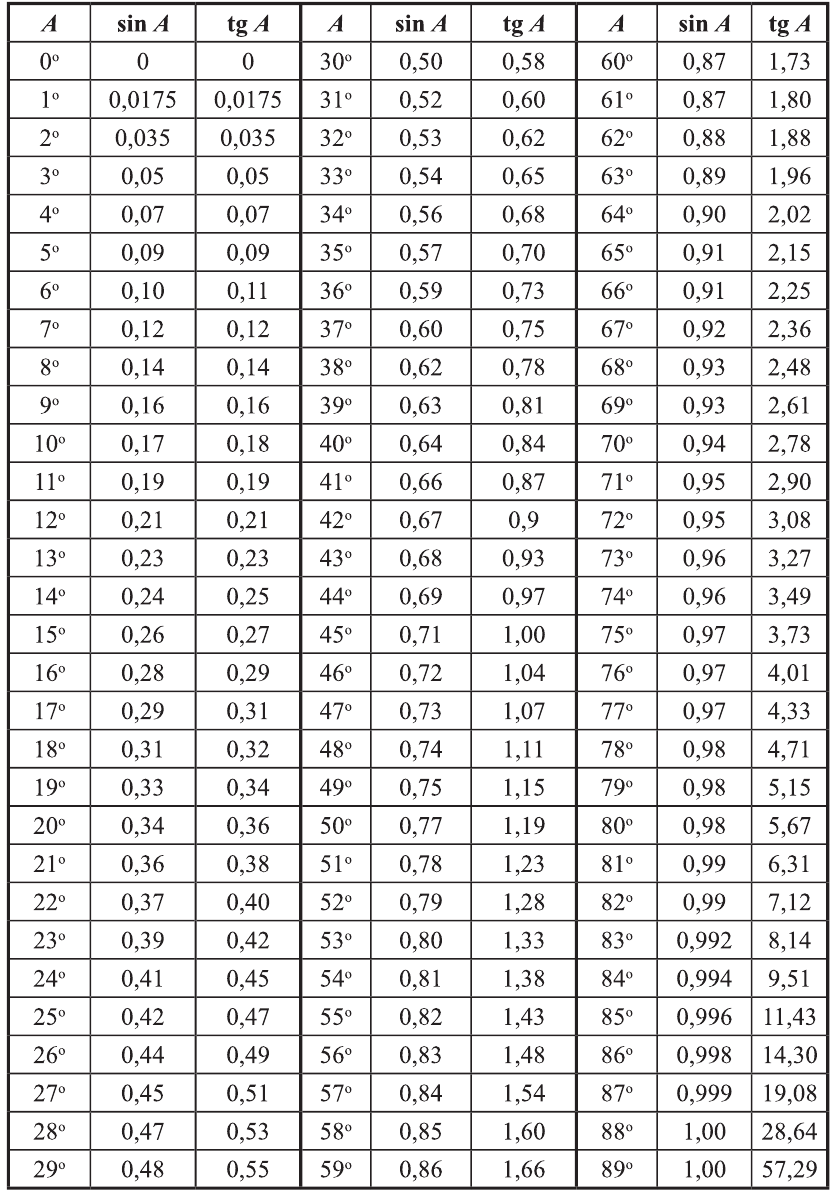
Таблица приближенных значений тригонометрических функций:
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Возникновение геометрии
- Призма в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
Рисуем цилиндр карандашом
Начинающим художникам необходимо усвоение академического рисунка. Невозможен переход сразу к сложным предметам и фигурам, так как именно база академического рисунка закладывает основные знания, которые применяются в дальнейшем при работе над любым изображением. Освоение академического рисунка начинается с изучения построения геометрических тел, которое является базой для рисования.
Стоит помнить, что все объекты представляют собой сочетание простых геометрических тел. Поэтому необходимо уметь правильно передавать эти фигуры на бумаге, правильно компоновать их, применяя законы перспективы для изображения предмета объемным. Каждый начинающий художник должен уметь качественно выполнять линейно-конструктивный рисунок, уметь правильно штриховать предмет и знать законы светотени.
Основной фигурой вместе с кубом и шаром является цилиндр. Поэтому мы сегодня рисуем цилиндр.
Рисуем цилиндр — необходимые материалы
Для работы Вам понадобятся следующие материалы:
- простые карандаши разной твердости;
- ластик;
- плотная бумага.
Напоминаем, что любые построения мы всегда начинаем твердыми карандашами. Такие карандаши позволят выполнить построение точно, так как рисует тонкие линии, при этом такие карандаши не создают грязи в процессе работы и легче стираются. Уделите внимание бумаге. Плотность бумаги должна быть высокой, бумага должна быть гладкой. Мы советуем нашим ученикам работать на бумаге для черчения.
Ластик следует подбирать мягкий, без вкраплений в текстуру. Также в дальнейшем может возникнуть необходимость использования клячки с целью облегчения тона, но мы советуем использовать её уже на итоговых этапах работы, так как это может помешать дальнейшему наслоению штриха.
Рисуем цилиндр карандашом — пропорции
При выполнении академического рисунка мы не используем линейку, весь процесс рисования направлен на то, чтобы развивался глазомер. На начальных этапах работы Вы можете использовать Ваш карандаш в качестве измерительного предмета. Для этого карандаш следует держать на вытянутой руке. Кончик карандаша — верхняя точка, на нижней точке предмета следует зажать карандаш пальцем. Далее Вы вкладываете высоту в ширину цилиндра. Таким образом Вы можете понять соотношения сторон и проверить свое построение.
Первый этап рисунка цилиндра — построение основы
Построение цилиндра достаточно простое. Самый сложный этап — изображение раскрытия эллипсов, которые являются основой цилиндра.
Но для начала нам следует обозначить центральную ось, которая в дальнейшем будет служить основой для построение. Всегда помним о композиции. Уже на этапе построение оси компонуем цилиндр на листе. Рисуем три перпендикулярных линии. Сразу закладываем высоту цилиндра. Верхняя и линия линия будут служить нам ориентирами для верхней и нижней плоскости.
Пропорционально измеряем ширину цилиндра и рисуем параллельные друг-другу и оси прямые. Эти прямые будут являться гранями цилиндра, задавать его ширину. С помощью такого построения мы сразу обозначили пропорции предмета и следуя им, уже не допустим ошибок.
Второй этап рисунка цилиндра — построение эллипсов
Переходим к наиболее сложному и важному этапу рисунка — построение эллипсов. Эллипсы являются основанием цилиндра. На первых этапах проще всего изображать их двумя полудугами, которые соединяются между собой.
Второй способ — это вписывание окружности в квадрат. Для этого Вам необходимо построить квадраты в соответствии с пропорциональными искажениями. Центральная ось должна быть центром эллипсов и при этом оставаться перпендикулярной им.
При изображении эллипсов, Вам следует усвоить такое понятие, как раскрытие. Правило — чем дальше эллипс от линии горизонта, тем более он раскрыт (более круглый), чем ближе к линии горизонта, тем он уже. Уделите внимание вращению эллипсов. Возможно, изначально они будут получаться кривыми и волнистыми, только постоянная практика поможет Вам достичь идеальных форм.
Грани
Теперь ослабляем уже нарисованные линии, но не слишком сильно. Прежде всего, отделяем друг от друга передний и задний планы цилиндра. Для этого нужно потолще прорисовать линии всех видимых элементов. При этом самые толстые линии будут только на нижних и верхних дугах. Заднюю линию эллипса (видимую) тоже нужно выделить, но не настолько жирно. Главное – чтобы она осталась чёткой.
Так, нарисованные линии можно разделить на три группы: толстые – на переднем плане, на заднем – тонкие, и практически незаметные вспомогательные линии.
Окружности основания цилиндра прорисовываются насквозь – невидимые линии (которые должны быть внутри) исчезнут на этапе штриховки. Благодаря этому можно увидеть различия между верхним и нижним основаниями.
Штриховка
После того, как разобрались с линиями, берём мягкий карандаш и приступаем к тонированию изображения, и так постепенно создаётся объём. Начать стоит с техники диагональной штриховки, и с самых тёмных участков.
Чтобы грамотно выполнить штриховку и правильно создать объём у фигуры, нужно знать элементы светотени, из которых состоит изображение: блик, свет, полутень, тень, рефлекс.
- Блик – самый светлый участок, его штриховать не нужно;
- Свет – штриховка очень слабая, едва заметная;
- Полутень – в этом цилиндре будет основным тоном;
- Тень – предполагает самую тёмную и плотную штриховку;
- Рефлекс – располагается у края предмета, этот тон примерно такой же, как и полутень.
То есть, свет от блика распределяется по поверхности, постепенно переходя в полутень. А за счёт цилиндрической формы начинающему художнику гораздо проще понять логику и последовательность распределения тонов светотени. Самое сложное – штриховка должна быть такой, чтобы переходы между участками светотени были плавными, даже незаметными.
Свет в целом и создаёт форму геометрического объекта, поэтому от добросовестности и правильности работы напрямую зависит итоговое изображение. Этот этап работы требует сосредоточенности и аккуратности: штриховка должна быть равномерной, поэтому важно периодически следить за соблюдением пропорций и корректной градацией тонов.
Для итогового восприятия рисунка и формирования объёмного пространства не менее важен и фон. Его штриховать не нужно.
После завершения этапа штриховки стоит проверить свою работу на предмет ошибок. Для этого следует отойти на некоторое расстояние от мольберта (на пару метров) – главное, чтобы рисунок был чётко виден. Правило простое: чем больше рисунок, тем дальше нужно отойти. При такой смене ракурса обнаружатся все допущенные ошибки, как в построении, так и в штриховке. То же самое следует повторить после корректировки работы.
Развитие навыков
Это – простейший вариант расположения геометрической фигуры на плоскости, идеально подходящий для новичков. Как только он покажется лёгким, можно будет усложнять задачу: рисовать цилиндр в пространстве, а также в горизонтальном или наклонном положениях.
Did you find apk for android? You can find new Free Android Games and apps.
ЦЕЛЬ И ПОСТАНОВКА ЗАДАНИЯ. Научиться изображать цилиндр в перспективе.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ. Рассмотрите цилиндр на рис. 3.81 и его ортогональные проекции на рис. 3.82. Цилиндр – геометрическое тело, относящееся к так называемым телам вращения, т. е. цилиндр можно получить путем вращения прямоугольника вокруг одной из его сторон. Основаниями цилиндра являются окружности. Ось вращения цилиндра соединяет центры окружностей оснований и перпендикулярна им.
Приступая к рисунку вертикального цилиндра, сначала наметьте на листе вертикальную линию – ось цилиндра и перпендикулярные ей горизонтальные линии – большие оси эллипсов верхнего и нижнего оснований (рис. 3.83). Проведите вертикальные образующие цилиндра (рис. 3.84). Изображая эллипсы оснований, помните, что чем дальше находится основание от линии горизонта, тем больше его раскрытие. В нашем примере, когда цилиндр расположен ниже горизонта, раскрытие нижнего основания больше раскрытия верхнего основания цилиндра (рис. 3.85). Завершите рисунок, изобразив вертикальные сечения цилиндра двумя перпендикулярными плоскостями (рис. 3.86).
Последовательность изображения горизонтального цилиндра такая же, что и вертикального: наметьте ось цилиндра и перпендикулярные ей большие оси эллипсов оснований. Проведите образующие. Большая ось цилиндра и его образующие должны сходиться на линии горизонта в одну точку схода (рис. 3.87). Изобразите эллипсы оснований, учитывая, что большая ось ближнего к зрителю основания будет длиннее, чем большая ось дальнего основания, а раскрытие ближнего эллипса – меньше, чем раскрытие дальнего (рис. 3.88).
Завершите рисунок, изобразив сечения цилиндра горизонтальной и вертикальными плоскостями (рис. 3.89). Если вашего опыта пока недостаточно, чтобы правильно найти направление оси цилиндра и раскрытие эллипсов оснований, вы можете воспользоваться рисунком куба. Вертикальные боковые грани куба задают габариты оснований цилиндра, горизонтальные ребра идут в одну точку схода с большой осью и образующими цилиндра, а также определяют его длину (рис. 3.90). Изображая цилиндр в произвольном положении, помните, что его ось вращения всегда перпендикулярна большим осям эллипсов оснований.
Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
Прямоугольник
AOO1A1
вращается вокруг стороны
OO1
.
OO1
— ось симметрии цилиндра и высота цилиндра.
AA1
— образующая цилиндра, длина которой равна длине высоты цилиндра.
(AO) — радиус цилиндра.
Полученная цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги — основаниями цилиндра.
Осевое сечение цилиндра — это сечение цилиндра плоскостью, которая проходит через ось цилиндра. Это сечение является прямоугольником.
При сечении цилиндра плоскостью, параллельной оси цилиндра (т. е. перпендикулярной основанию), также получается прямоугольник.
На рисунке изображён цилиндр, пересечённый плоскостью, которая параллельна оси цилиндра
OO1
.
— прямоугольник.
(OA = OB = R) — радиусы.
(OC) — расстояние от оси цилиндра до плоскости сечения.
Дуга (AB) равна центральному углу (AOB).
При сечении цилиндра плоскостью, параллельной основанию, в сечении получаем круг, равный основаниям цилиндра.
Если представить, что боковая цилиндрическая поверхность разрезана по образующей
AA1
и развёрнута, получаем прямоугольник.
Сторона
AA1
равна высоте (H), а другую сторону образует развёрнутая окружность основания длиной
2πR
.
Так как развёртка — прямоугольник, то боковая поверхность определяется по формуле:
Основания цилиндра — два круга с общей площадью
2⋅πR2
.
Полная поверхность цилиндра определяется по формуле:
.
План урока:
Понятие цилиндра
Понятие конуса
Усеченный конус
Понятие цилиндра
Построим на некоторой плоскости α окружность L, центр которой находится в точке О, а ее радиус обозначим как r. Далее через каждую точку этой окруж-ти проведем прямую, которая будет перпендикулярна к α. Все вместе эти прямые образуют поверхность, которую принято называть цилиндрической поверхностью (может использоваться сокращение поверх-ть). Введем несколько понятий:
- Окружность, построенная в плос-ти α, именуется основанием цилиндрической поверх-ти;
- Каждая прямая, проходящая через эту окруж-ть L и перпендикулярная α – это образующая цилиндрической поверх-ти;
- Прямая, проходящая через точку О и также перпендикулярная α, именуется осью цилиндрической поверх-ти.
Примечание. Заметьте, что в стереометрии при изображении окружности на плос-ти она выглядит как эллипс (овал).
Заметим, что так как все образующие и ось цилиндрической поверх-ти перпендикулярны одной и той же плос-ти α, то они будут параллельны друг другу.
Далее проведем плос-ть β, параллельную α. Так как образующие и ось пересекали α, то они должны пересекать и β. В результате они образуют в плос-ти β какую-то плоскую линию L1. Докажем, что L1 – это также окружность.
Действительно, пусть ось цилиндрической поверх-ти пересекает плос-ти α и β в точках О и О1 соответственно. Произвольная образующая пересекает эти же плос-ти в точках А и А1:
Так как ОО1||АА1, то ОО1А1А – это плоский четырехугольник. ОО1⊥α и ОО1⊥β, поэтому углы ∠АОО1 и ∠А1О1О – прямые. АА1⊥α и АА1⊥β, поэтому прямыми будут и углы ∠ОАА1 и ∠О1А1А. Получается, что ОО1А1А – это прямоугольник, и поэтому отрезки ОА и О1А1 одинаковы:
Итак, точка А1 находится на расстоянии r от О1. Аналогично и для любой другой точки на линии L1 можно показать, что она находится на расстоянии r от О1. То есть все точки L1 равноудалены от О1, и поэтому L1 – это окруж-ть с центром в точке О1, ч. т. д.
Обратите внимание, что окруж-ти L и L1 имеют одинаковые радиусы, то есть это одинаковые окруж-ти.
Объемная фигура, образованная окруж-тями L и L1, именуется цилиндром. Рассмотрим его основные элементы:
- круги L1 и L – это основания цилиндра;
- отрезок ОО1 – ось цилиндра;
- отрезки образующих, заключенные между основаниями, именуются образующими цилиндра;
- часть цилиндрической поверх-ти, заключенную между основаниями цилиндра, именуют боковой поверхностью цилиндра.
Напомним, что отрезки параллельных прямых, заключенные между параллельными плос-тями, имеют одинаковую длину. Отсюда вытекает тот факт, что образующие цилиндра одинаковы.
Введем ещё два термина:
- длина образующей именуется высотой цилиндра;
- радиус оснований цилиндра именуется радиусом цилиндра.
Отметим, что на самом деле мы рассмотрели только частный случай цилиндра – так называемый прямой круговой цилиндр. Его основания – это круги (поэтому он именуется круговым), а его образующие образуют с основаниями прямой угол(поэтому он именуется прямым). Можно построить наклонный цилиндр (его также называют косым), у которого образующие не перпендикулярны основанию. Также существуют и цилиндры, у которых основаниями являются не окруж-ти, а другие фигуры, например параболы:
В принципе любую призму (а значит и любой параллелепипед) можно считать цилиндром. Однако в дальнейшем в курсе школьной стереометрии под цилиндром будет подразумеваться исключительно прямой круговой цилиндр, если специально не оговорено иное.
В реальной жизни очень многие предметы имеют форму цилиндра. Колонны в зданиях, ножки стульев, бочки, рулоны бумаги представляют собой цилиндры. Даже дерево можно условно считать цилиндром.
Рассмотрим сечение цилиндра плос-тью, перпендикулярной его основаниям.
Пусть сечение пересекает нижнее основание цилиндра в точках А1 и В1. Тогда перпендикуляры к основанию, проходящие через эти точки, будут принадлежать этому сечению. Но эти перпендикуляры – одновременно и образующие цилиндра А1А и В1В. Значит, сечение проходит и через точки А и В. Раз АА1 и ВВ1 – перпендикуляры к обоим основаниям цилиндра, то
Итак, в четырехугольнике АВВ1А1 все углы прямые, то есть он представляет собой прямоугольник. Более того, можно утверждать, что любое сечение, проходящее через образующую цилиндра, будет прямоугольником, ведь такое сечение будет перпендикулярно основаниям, так как оно содержит перпендикуляр к ним. Сечение, проходящее через цилиндрическую ось, именуется осевым сечением. Оно также имеет форму прямоугольника.
Далее рассмотрим сечение цилиндра плос-тью, параллельной основаниям:
Пусть секущей будет плос-ть γ, а нижнее основание располагается в плос-ти α. Тогда по определению фигура, «зажатая» между этими двумя плос-тями – это цилиндр, а потому сечение должно иметь форму круга. Получается, что сечение γ разбивает цилиндр на два цилиндра.
Рассмотрим боковую поверх-ть цилиндра. Она представляет собой замкнутую поверхность. Если ее условно «разрезать» по образующей цилиндра и развернуть, то получится прямоугольник:
Длина одной стороны такого прямоугольника (он называется разверткой боковой поверх-ти цилиндра) – это длина образующей цилиндра, то есть его высота. Длина второй стороны совпадает с длиной окруж-ти, лежащей в основании цилиндра. Если радиус цилиндра обозначен как r, то длина этой окруж-ти составляет 2πr. Тогда площадь боковой поверх-ти можно рассчитать как площадь прямоугольника:
Площадь полной поверх-ти цилиндра – это сумма площадей его оснований и его боковой поверх-ти. Так как площадь круга рассчитывается по формуле
Рассмотрим ещё несколько важных понятий. В цилиндр может быть вписана прямая призма. В таком случае основания призмы находятся в тех же плос-тях, что и основания цилиндра, а её боковые грани – это образующие цилиндра.
Если плос-ть содержит образующую цилиндра, но не пересекает его основания, то такая плос-ть именуется касательной к цилиндру. Можно сказать, что касательная плос-ть – это такая плос-ть, которая имеет ровно по одной общей точке с каждым основанием цилиндром.
Если каждая боковая грань призмы – это касательная к цилиндру, а основания призмы находятся в тех же плос-тях, что и основания цилиндра, то говорят, что цилиндр вписан в призму.
Естественно, что если цилиндр вписан в призму, то его основания оказываются вписанными в те многоугольники, которые являются основаниями призмы. Если же призма вписана в цилиндр, то основания цилиндра – это уже окруж-ти, описанные около этих многоугольников.
Рассмотрим несколько задач, в которых фигурируют цилиндры.
Задание. Найдите боковую и полную площади цилиндра, если его радиус составляет 2 м, а высота – 3 м.
Задание. Какова длина диагонали осевого сечения цилиндра, с высотой 4 м и радиусом 1,5 м?
Решение. Осевое сечение цилиндра – это прямоугольник, обозначим его как АВСD. Сторона АВ – это высота цилиндра, а AD – это диаметр нижнего основания, ведь AD проходит через центр окруж-ти О. Тогда длина AD вдвое больше радиуса цилиндра:
Задание. Осевое сечение цилиндра – это квадрат, площадь которого обозначена буквой Q. Какова площадь основания цилиндра?
Решение. Обозначим сторону сечения-квадрата буквой а. Зная площадь сечения, легко найдем и сторону:
Задание. Высота цилиндра составляет 8 см, а его радиус – 5 см. Через его образующую проведено сечение, которое имеет форму квадрата. Каково расстояние между этим сечением и осью цилиндра?
Решение. Обозначим сечение как АВСD. Так как и это сечение, и ось цилиндра перпендикулярны основаниям цилиндра, то они должны быть параллельны друг другу. Расстояние между ними – это длина перпендикуляра О1К, опущенного из центра основания на сторону ВС:
Отрезок АВ имеет длину 8 см, ведь это высота цилиндра. Так как АВСD – квадрат, то и ВС имеет такую же длину. ВС – это хорда в окруж-ти с центром в точке О1. Напомним, что перпендикуляр к хорде, опущенный из центра окруж-ти, делит ее пополам, поэтому
Задание. Диаметр цилиндра равен его высоте. На верхнем основании, центр которого находится в точке О, отмечены точки А и В так, что ∠АОВ составляет 60°. Отрезок АА1 – образующая цилиндра. Найдите тангенс угла ∠ВА1А.
Решение. Рассмотрим ∆АОВ. Он равнобедренный, ведь радиусы АО и ОВ одинаковы. Но если в равнобедренном треугольнике один из углов составляет 60°, то и все углы будут также будут по 60°, то есть это равносторонний треугольник. Тогда, если радиус цилиндра обозначен как r, то
Понятие конуса
Построим на плос-ти α окруж-ть L с центром в точке О. Далее через О проведем перпендикуляр к α и отметим на нем точку Р. Если мы отрезками соединим точку Р с каждой точкой окруж-ти L, то получим поверх-ть, которая именуется конической поверхностью. При этом:
- прямая ОР – это ось конической поверх-ти;
- прямые, соединяющие Р с точками на окруж-ти L, именуются образующими конической поверх-ти;
- сама точка Р – это вершина конической поверх-ти.
Объемное тело, ограниченное окруж-тью L и конической поверх-тью, именуется конусом. Соответственно вершина конической поверх-ти, её ось и образующие будут одновременно являться вершиной, осью и образующими конуса. Окруж-ть L – это основание конуса.
Ещё несколько терминов:
- коническая поверх-ть конуса именуется его боковой поверх-тью;
- если же к этой площади прибавить ещё и площадь основания, то в итоге получится полная площадь конуса;
- отрезок ОР – это не только ось конуса, но и высота конуса.
Как и в случае с цилиндром, мы в данном случае рассматриваем особый случай конуса – прямой круговой конус. В более общем случае ось конуса может не быть перпендикуляром к плос-ти основания (так называемый косой конус). Также в его основании может находиться не окруж-ть, а другая плоская фигура.
В общем случае любая пирамида может рассматриваться как частный случай конуса. Однако в рамках школьного курса под конусом подразумевается исключительно прямой круговой конус, если только не обговорено иное.
Докажем важное утверждение:
Действительно, рассмотрим две произвольные образующие РА и РВ у конуса с вершиной Р, у которой О – центр основания:
Так как ось ОР перпендикулярна основанию, то ∆РОА и ∆РОВ – прямоугольные. У них общий катет РО, а катеты АО и ОВ одинаковы как радиусы окруж-ти. Тогда ∆РОА и ∆РОВ равны, поэтому одинаковы и образующие РА и РВ, ч. т. д.
Заметим, что конус получается при вращении прямоугольного треуг-ка вокруг его катета. Так, на следующем рисунке конус получается при вращении ∆РОА с прямым углом О относительно катета РО:
Если сечение конуса проходит через его ось, то оно именуется осевым сечением. Ясно, что это сечение будет являться треуг-ком, причем две его стороны – это образующие конуса, а третья сторона диаметр основания. Образующие конуса одинаковы, поэтому осевое сечение будет равнобедренным треуг-ком.
Теперь рассмотрим сечение, параллельное плос-ти основания. Пусть оно пересекает ось РО в какой-то точке О1. Также пусть А1 – точка пересечения образующей АР исходного конуса с секущей плос-тью α:
Заметим, что раз ось РО перпендикулярна основанию, то она также будет перпендикулярна и секущей плос-ти, ведь основание и плос-ть α параллельны. Тогда ∠РО1А1 будет прямым.
Теперь рассмотрим ∠РОА и ∠РО1А1. Они прямоугольные и у них есть общие угол ∠АРО. Значит, это подобные треуг-ки. Обозначим радиус ОА как r, а длину А1О1 как r1. Тогда из подобия получаем:
Рассмотрим теперь другую образующую ВР, которая пересекает секущую плос-ть в точке В1. Отрезки АО и ОВ одинаковы. Повторяя предыдущие рассуждения, легко доказать подобие ∆РОВ и ∆РО1В1, откуда можно вычислить длину О1В1:
Получили, что точки А1и В1 находятся на одинаковом расстоянии r1 от точки О1. Мы выбрали точки А и В произвольно, поэтому для любых двух точек, принадлежащих сечению конуса, можно утверждать, что они равноудалены от точки О1. Это значит, что все точки сечения лежат на окруж-ти с центром в точке О1 и радиусом r1, то есть сечение имеет форму окруж-ти.
Как определить площадь боковой поверхности конуса? Для этого ее надо «разрезать» вдоль одной из образующих и развернуть на плос-ти. В результате получится круговой сектор.
Напомним, что площадь сектора может быть рассчитана по формуле
Теперь обозначим длину образующей буквой l, а радиус основания конуса как r. Тогда
Для вычисления полной площади конуса к боковой поверх-ти необходимо добавить ещё и площадь основания:
Усеченный конус
Ранее мы уже изучали сечение конуса плос-тью, параллельной его основанию. Такое сечение разбивает конус на две фигуры. Одна из них – это конус меньших размеров, а вторая именуется усеченным конусом:
Введем несколько понятий и отметим очевидные факты:
- боковая поверхность усеченного конуса – это коническая поверх-ть;
- у усеченного конуса есть два основания, имеющих форму окруж-ти;
- те отрезки образующих конической поверх-ти, которые заключены между основаниями усеченного конуса, именуются образующими усеченного конуса;
- отрезок, соединяющий центры оснований, именуется высотой усеченного конуса, или его осью.
В предыдущем параграфе мы уже выяснили, что радиусы оснований усеченного конуса связаны с высотами исходного конуса и того конуса, который получается при проведении секущей плос-ти:
Заметим, что любые две образующие усеченного конуса одинаковы. Действительно, пусть усеченный конус с образующими АА1 и ВВ1 получен их исходного конуса с образующими АР и ВР:
Заметим, что осевое сечение усеченного конуса – это равнобедренная трапеция:
Действительно, построим осевое сечение исходного конуса, которое пройдет через образующие РА и РВ. Пусть эти образующие пересекают плос-ть верхнего основания усеченного конуса в точках А1 и В1 соответственно. Тогда АА1В1В будет осевым сечением усеченного конуса. Точки А, А1, В1 и В располагаются в одной плос-ти РАВ, то есть АА1В1В – плоский четырехугольник. Его стороны АВ и А1В1 не могут пересекаться, ведь они принадлежат параллельным основаниям, поэтому АВ||А1В1. Стороны АА1 и ВВ1 одинаковы как образующие, при этом прямые АА1 и ВВ1 непараллельны, ведь они пересекаются в точке Р. В итоге получается, что АА1В1В – равнобедренная трапеция. Отдельно отметим, что ось ОО1 делит эту равнобедренную трапецию на две прямоугольных трапеции.
Теперь выведем формулы для рассчета площади боковой поверх-ти усеченного конуса. Ясно, что развертка усеченного конуса – это часть развертки поверх-ти исходного конуса:
Нам надо найти площадь фигуры АА1А1’А’ (показана желтым цветом). Ее можно найти как разность площадей секторов РАА’и РА1А1’. Но эти площади можно вычислить по формуле боковых поверх-тей конусов:
Обозначим длину образующей АА1 как l. Далее выразим А1P через r, r1 и l. ∆АОР и ∆РА1О1 подобны, поэтому можно записать:
Подставляем полученное выражение в (1) и получаем:
Чтобы посчитать полную площадь поверх-ти усеченного конуса, необходимо к боковой поверх-ти добавить площади верхнего и нижнего основания:
Рассмотрим несколько задач про конусы.
Задание. Высота конуса составляет 15 см, а его радиус – 8 см. Вычислите длину его образующей.
Решение. Обозначим вершину конуса буквой Р, буквой О – центр основания, а буквой А – произвольную точку на окруж-ти. Тогда высотой конуса будет отрезок ОР, радиусом – отрезок ОА, а образующей окажется отрезок АР:
Высота ОР перпендикулярна плос-ти основания, поэтому ∠РОА – прямой, а ∆РОА – прямоугольный. Тогда АР можно найти по теореме Пифагора:
Задание. Угол между образующей конуса и плос-тью основания составляет 30°, а длина образующей – 12 см. Какова площадь основания конуса?
Решение. Обозначим образующую как АР, а высоту конуса как ОР. Тогда радиус ОА будет проекцией АР на плос-ть основания, то именно ∠РАО будет составлять 30°:
Для вычисления площади основания надо найти радиус АО. Это можно сделать через прямоугольный ∆РОА:
Задание. Осевое сечение конуса имеет площадь 6, а площадь основания равна 8. Вычислите его высоту.
Решение. Пусть осевым сечением будет ∆РАВ, а РО – искомая высота:
Зная площадь основания, легко найдем радиус конуса ОА, а потом и диаметр АВ:
Так как РО – высота для ∆РАВ, то площадь этого треуг-ка может быть рассчитана так:
Задание. Найдите площадь боковой и полной поверх-ти конуса, если образующая имеет длину 8, а радиус основания составляет 5.
Решение. В этой задаче надо просто применить формулу для вычисления площадей:
Задание. Дан конус. Развертка его конической поверх-ти – это сектор, чья дуга составляет 60°. Р – вершина конуса, а РAB – осевое сечение. Вычислите ∠АРВ.
Решение. Длину образующих РА и РВ обозначим как L. Сначала находим длину дуги АА’:
Теперь искомый нами ∠АРВ можно найти с помощью теоремы косинусов, записанной для ∆АРВ:
Задание. Найдите длину образующей усеченного конуса, если радиусы его оснований составляют 6 см и 3 см, а его высота – 4 см.
Решение. Обозначим искомую образующую как АВ, а буквами О и О1 обозначим центры нижнего и верхнего оснований соответственно:
При изучении осевого сечения усеченного конуса мы уже выяснили, что АВО1О – прямоугольная трапеция. Опустим в ней высоту ВН, которая будет иметь ту же длину, что и высота конуса ОО1:
Ответ: 5 см.
Задание. Радиусы оснований усеченного конуса обозначены буквами R и r (R > r). Образующая конуса образует с нижним основанием угол 45°. Составьте формулу, по которой можно найти площадь осевого сечения этого конуса.
Решение. Осевым сечением будет равнобедренная трапеция А1АВВ1:
Проведем высоту А1Н. Вычислим АН:
Теперь площадь трапеции А1АВВ1 можно посчитать по формуле:
Задание. Основания усеченного конуса – окружности с радиусами 6 и 7 см. Длина образующей – 5 см. Вычислите площадь его боковой и полной поверх-ти.
Решение. Здесь надо просто подставить данные из условия в формулы для вычисления площадей:
Ответ: 65π см2, 150π см2.
Сегодня мы узнали две новые объемные фигуры – цилиндр и конус. Эти фигуры иногда называют телами вращения, ведь они получаются вращением плоских фигур вокруг одной из их сторон. Важно помнить, что у всех тел вращения есть такие элементы, как основание (иногда не одно), ось и образующие.