Как найти осевое сечение усеченного конуса

Как найти площадь осевого сечения усеченного конуса

Чтобы решить данную задачу, необходимо вспомнить, что такое усеченный конус и какими свойствами он обладает. Обязательно сделайте чертеж. Это позволит определить, какую геометрическую фигуру представляет собой сечение конуса. Вполне возможно, что после этого решение задачи уже не будет представлять для вас сложности.

Инструкция

Круглый конус – тело, полученное путем вращения треугольника вокруг одного из его катетов. Прямые, исходящие из вершины конуса и пересекающие его основание, называются образующими. Если все образующие равны, то конус является прямым. В основании круглого конуса лежит круг. Перпендикуляр, опущенный на основание из вершины, является высотой конуса. У круглого прямого конуса высота совпадает с его осью. Ось – это прямая, соединяющая вершину с центром основания. Если горизонтальная секущая плоскость кругового конуса параллельна основанию, то его верхнее основание представляет собой круг.

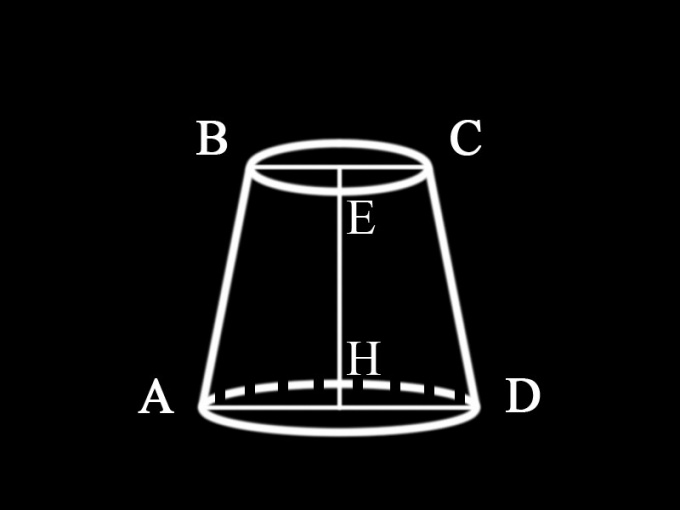
Поскольку в условии задачи не оговорено, какой именно конус дается в данном случае, можно сделать вывод, что это круглый прямой усеченный конус, горизонтальное сечение которого параллельно основанию. Его осевое сечение, т.е. вертикальная плоскость, которая проходит через ось круглого усеченного конуса, представляет собой равнобочную трапецию. Все осевые сечения круглого прямого конуса равны между собой. Следовательно, чтобы найти площадь осевого сечения, требуется найти площадь трапеции, основаниями которой являются диаметры оснований усеченного конуса, а боковые стороны – его образующие. Высота усеченного конуса является одновременно высотой трапеции.

Площадь трапеции определяется по формуле:S = ½(a+b) h, где S – площадь трапеции;a – величина нижнего основания трапеции;b – величина ее верхнего основания;h – высота трапеции.

Поскольку в условии не оговорено, какие именно величины даны, можно считать, что диаметры обеих оснований и высота усеченного конуса известны: AD = d1 – диаметр нижнего основания усеченного конуса;BC = d2 – диаметр его верхнего основания; EH = h1 – высота конуса.Таким образом, площадь осевого сечения усеченного конуса определяется: S1 = ½ (d1+d2) h1

Источники:

• площадь усеченного конуса

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Усеченный конус

Определение

Усеченным
конусом называется часть конуса,
заключенная между основанием и плоскостью,
параллельной основанию( рис.166).

AA₁—
образующая, OO₁—
высота, круги с центрами O
и O₁,
радиусами R и r
— основания .

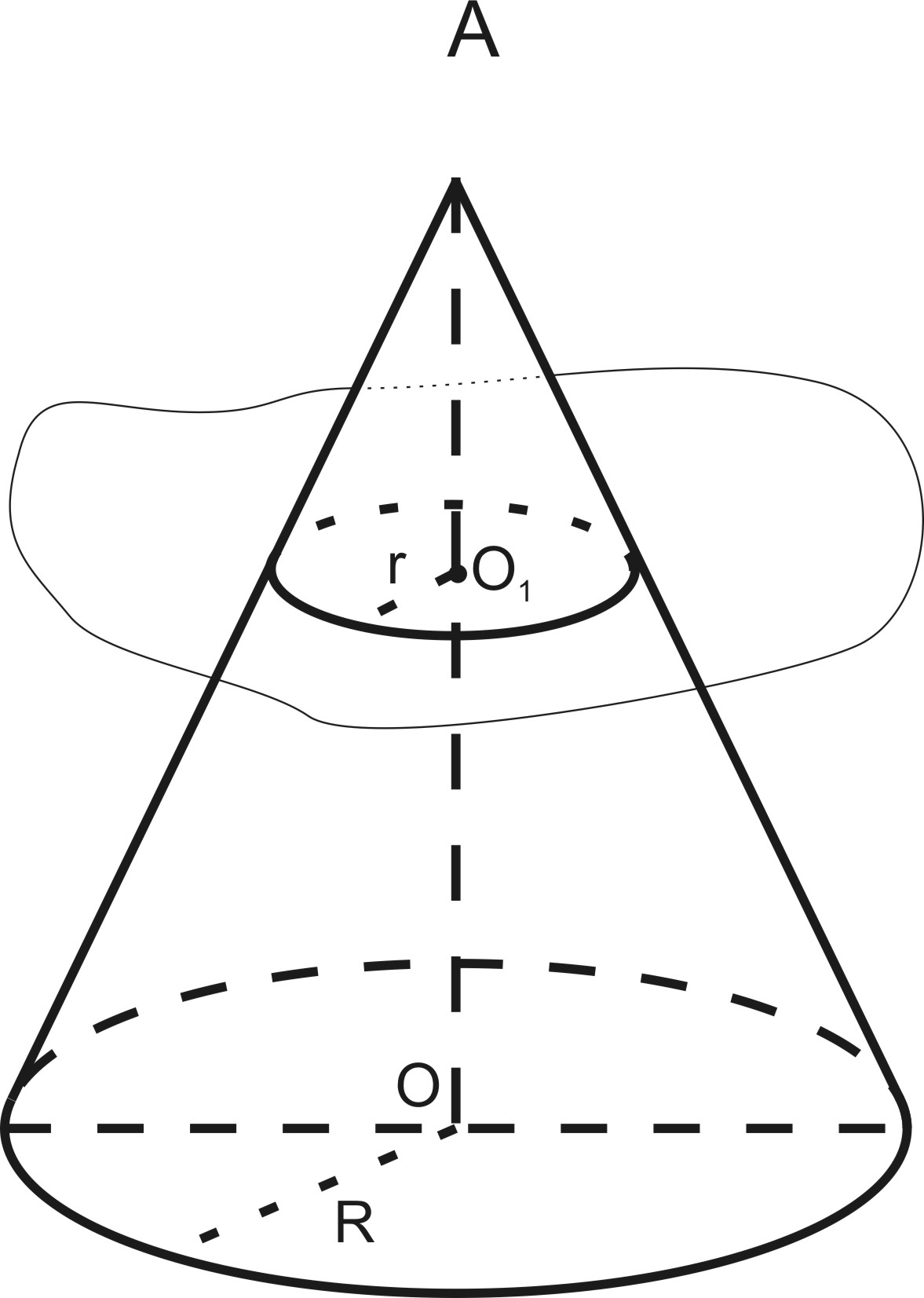
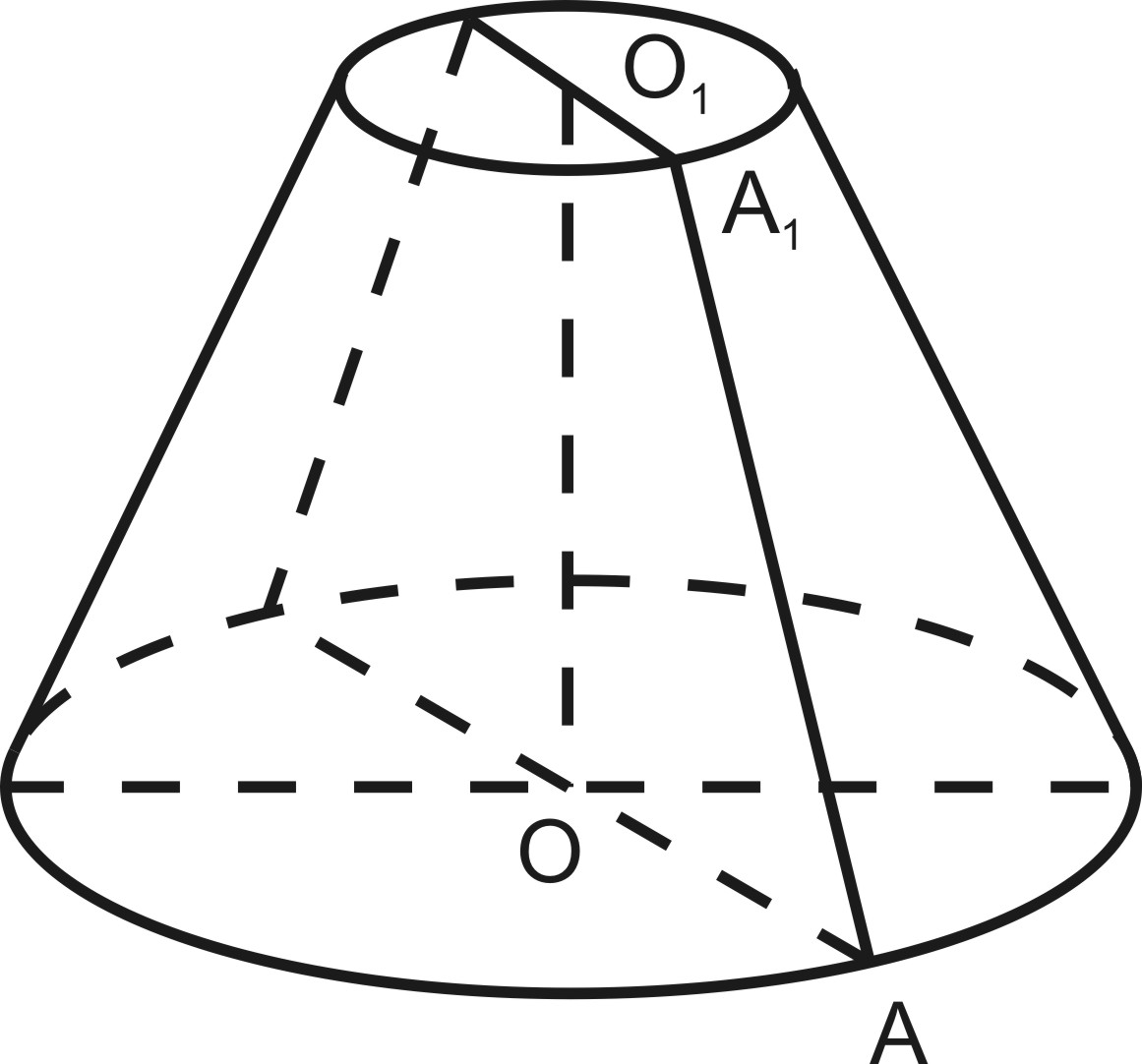
Осевое
сечение усеченного конуса –
равнобедренная трапеция, полученная
при пересечении плоскости, проходящей
через ось усеченного конуса

перпендикулярно его основанию).

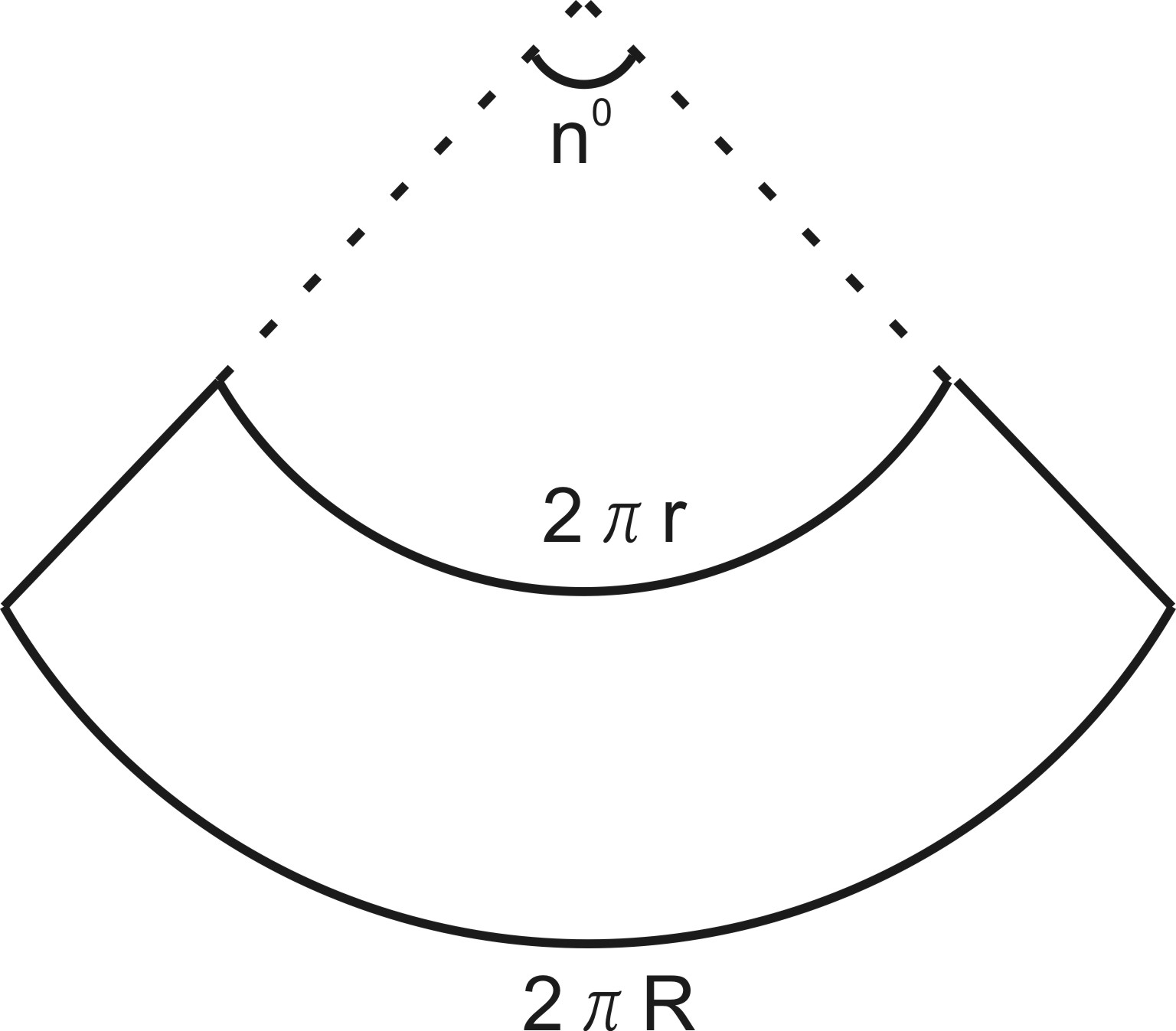
Развертка
боковой поверхности усеченного конуса—
часть кругового кольца.

Чтобы
получить развертку боковой поверхности
усеченного конуса, дополним

его
до полного конуса и сделаем развертку
полного конуса, а затем рассмотрим

на
этой развертке развертку конуса с тем
же центральным углом и меньшим радиусом,
получим часть кольца

Сфера и шар. Элементы сферы и шара

Определения

1.Сферой называется
множество всех точек пространства,
находящихся на положительном расстоянии
R от данной точки.

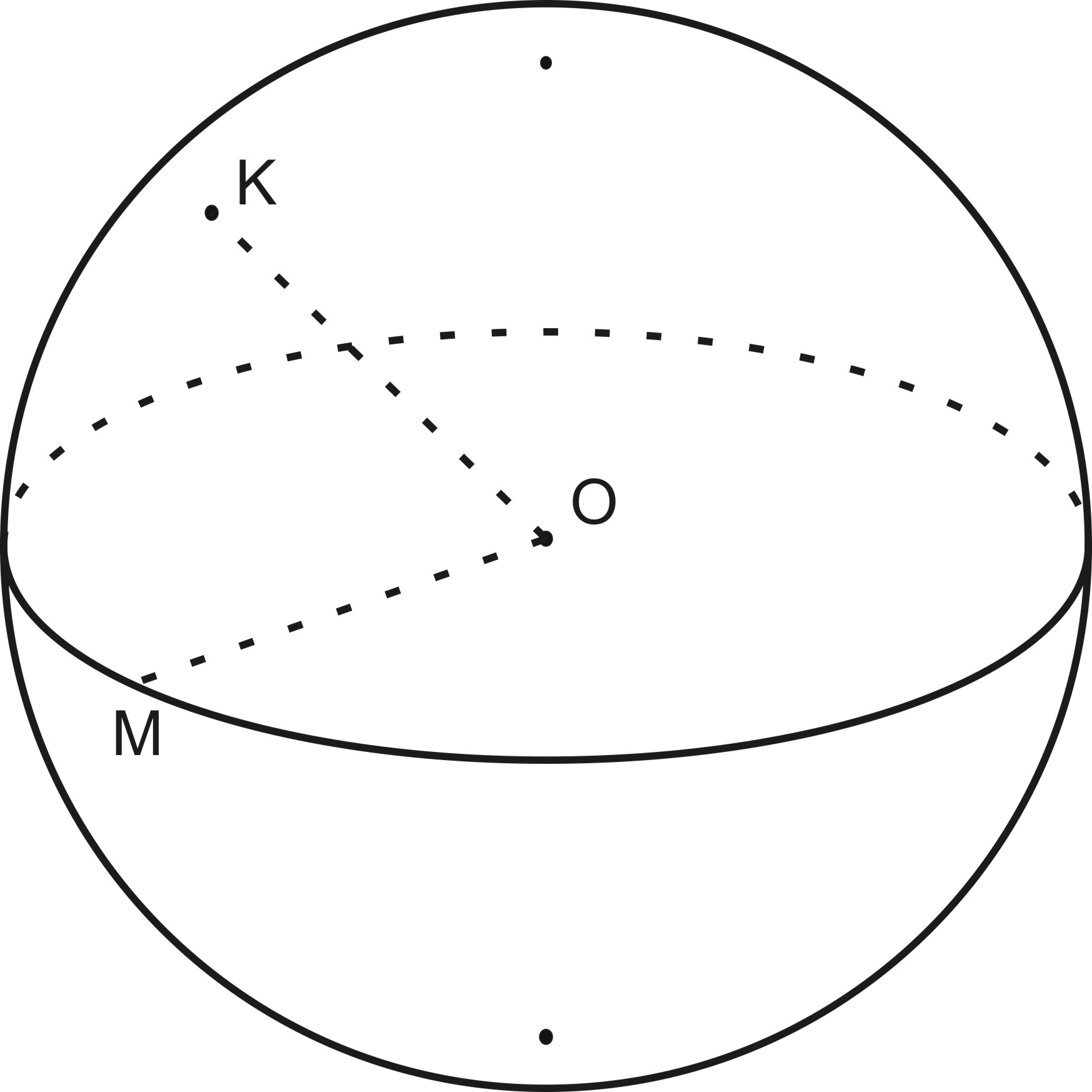
2.Центр сферы – данная точка O
(рис.168), отрезок OM
–радиус сферы.

Любой отрезок, соединяющий центр сферы
с точкой сферы называется радиусом
сферы.

3.Шаром называется множество
всех точек пространства, находящихся
на расстоянии, не больше положительного
R от данной точки
или

шар – это часть пространства,
ограниченная сферой.

Радиус шара – это радиус
ограничивающей его сферы.

Шар можно получить при вращении
полукруга вокруг оси, которая содержит
диаметр полукруга.

Отрезок, соединяющий две точки сферы,
называется хордой сферы.

Хорда, проходящая через центр сферы
называется диаметром сферы.

Уравнение сферы

Пусть задана прямоугольная система
координат. Составим уравнение сферы с
центром в точке S(a;
b; c) и радиусом
R.

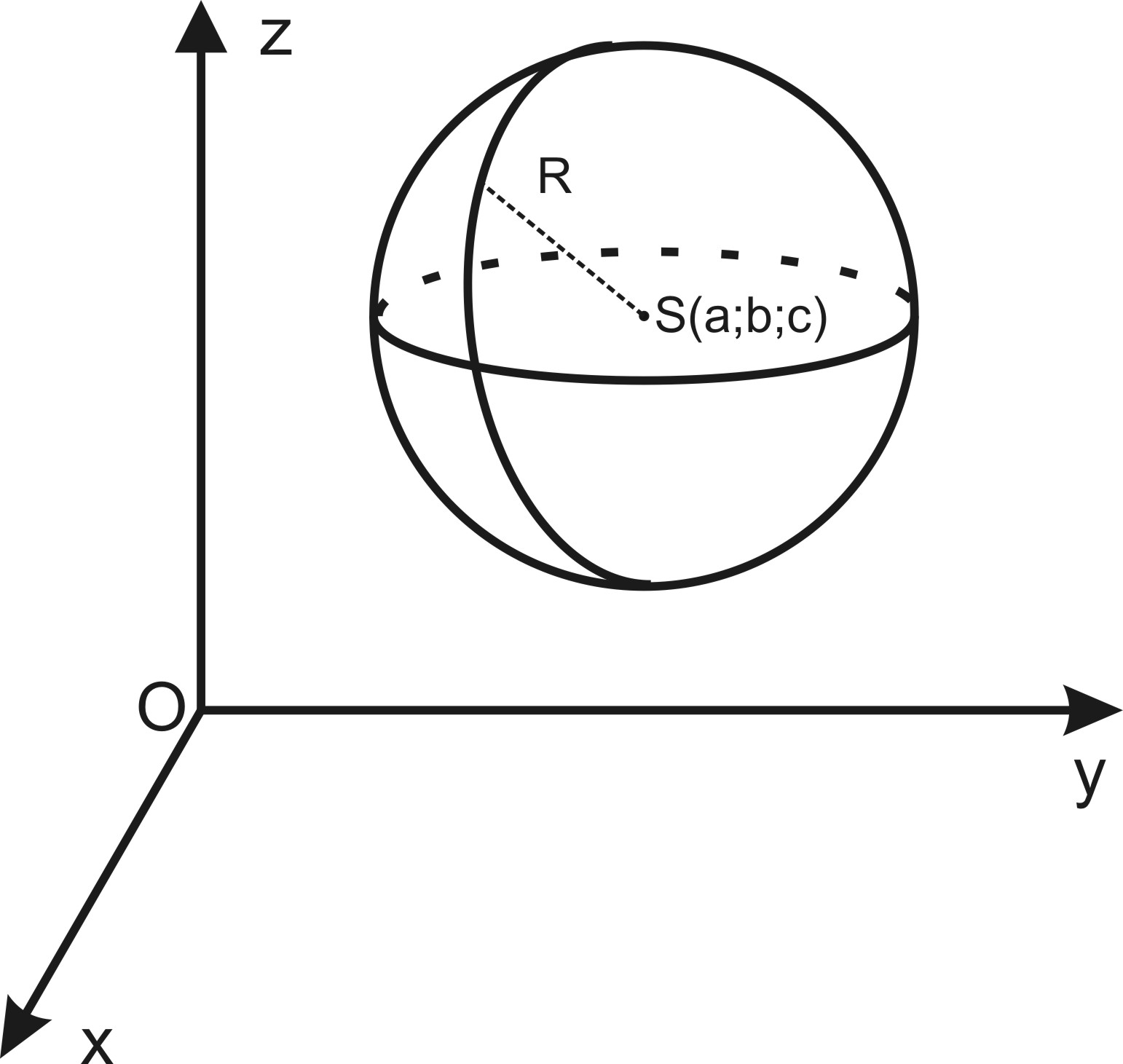
Для каждой точки M ( x;y;z),
принадлежащей сфере и только для таких
точек, выполняется равенство:

SM = R.

Пользуясь формулой расстояния между
двумя точками, получим

(x-a) ²
+( y- b ) ²
+ (z — c )
² = R ² (1) .

Уравнение (1) и есть уравнение сферы с
центром в точке (a; b;
c) и радиусом R.

Если a=b=c=0,
то получим уравнение сферы с центром в
начале координат

x-² +y
² + z ² = R
² .

Сечение шара плоскостью

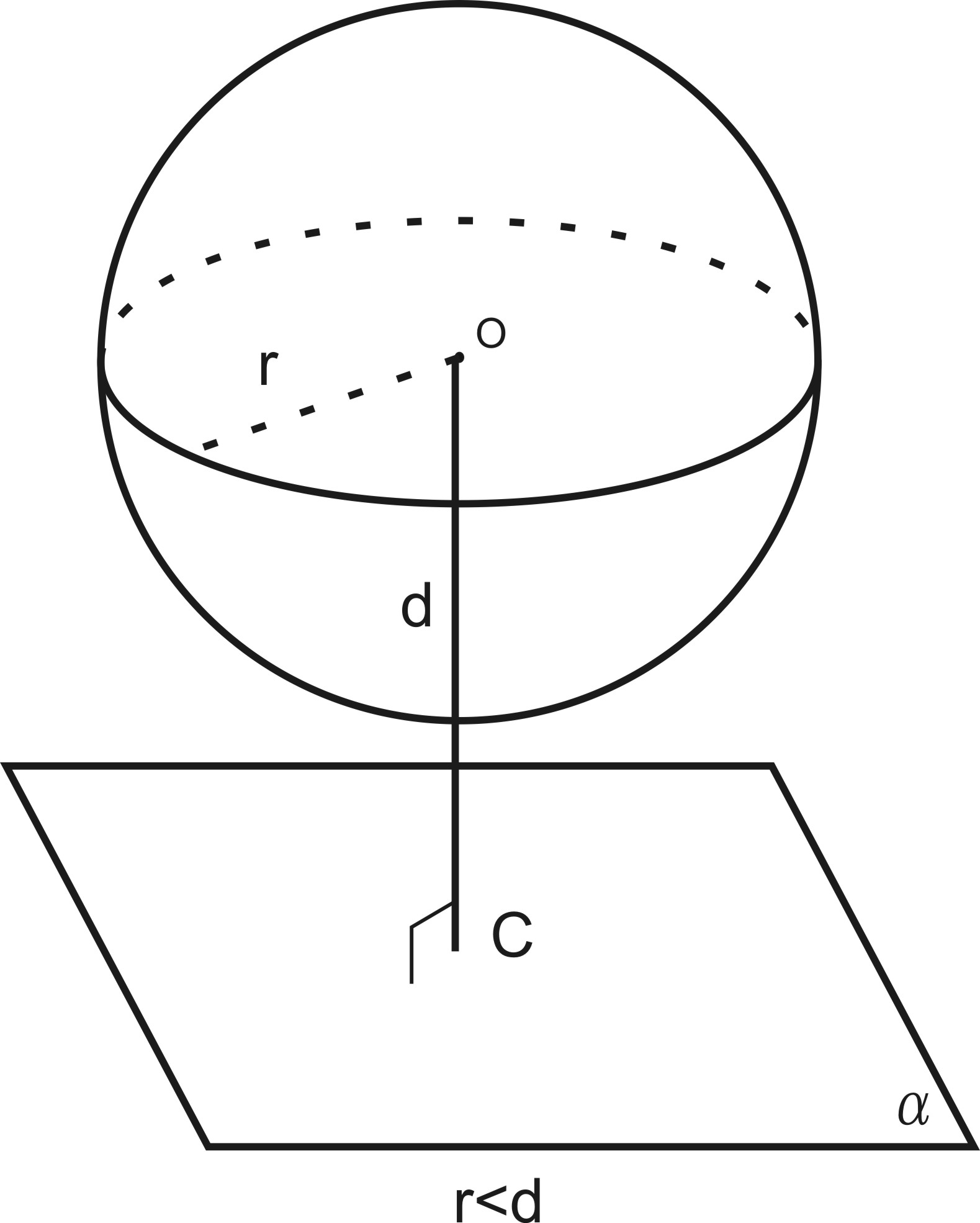
Рассмотрим сферу с центром в точке O
и плоскость α .

Проведем ОС

α.
Пусть OC = d.

Если d > r,
то сфера и плоскость общих точек не
имеют.

Если d < r,
то сфера и плоскость имеют общие точки.

Теорема

Сечение сферы плоскостью – окружность.

Доказательство

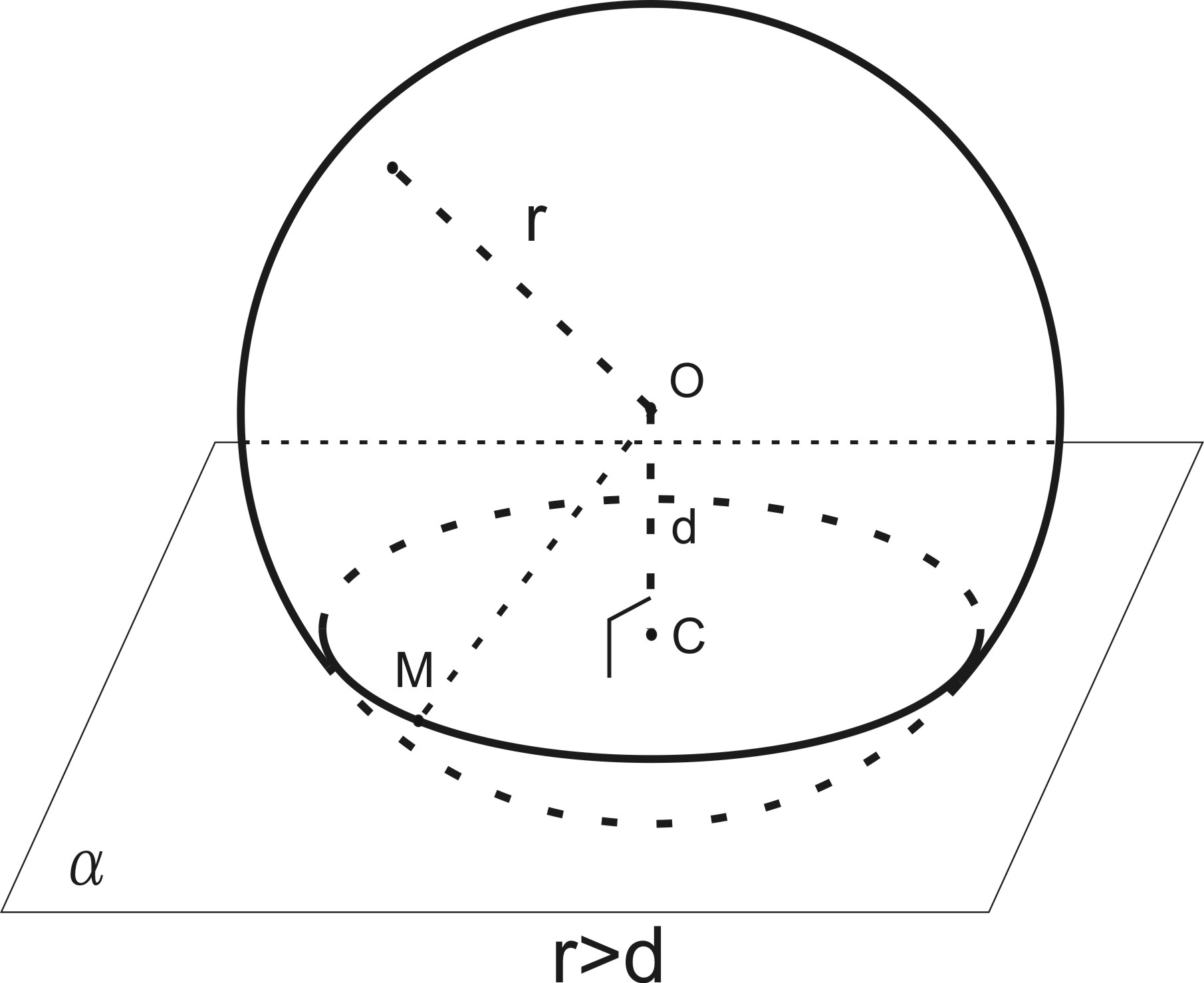
Пусть M – любая точка
пересечения сферы с плоскостью α (
рис.170). Соединим ее с точкой С и проведем
радиус OM. По определению
перпендикуляра к плоскости ОС

СM.

По теореме Пифагора CM =

,
где OC = d, r
– радиус сферы.

Величины
r и d –
постоянные, следовательно, для любой
точки пересечения сферы и плоскости
расстояние до точки C
есть величина постоянная, следовательно,
по определению окружности – эта линия
есть окружность.

Доказательство закончено.

Следствие
1

Сечение
шара плоскостью есть круг.

Следствие
2

Сечения
шара плоскостью, равноудаленные от
центра, равны

Следствие
3

Сечения
шара плоскостью тем больше, чем
ближе оно расположено к центру.

Определение1

Сечения
шара плоскостью, проходящей через центр
шара, называется большим кругом,
а его окружность – окружностью большого
круга.

Определение2

Точки
пересечения сферы с диаметром,
перпендикулярным большому кругу,
называются полюсами сферы.

Следствие
4

Два
больших круга пересекаются по диаметру.

Следствие
5

Сечением шара плоскостью
является точка, если расстояние
от центра шара до плоскости равно радиусу
шара.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Круглый конус в геометрии является симметричной пространственной фигурой, имеющей ось вращения. Одной из важных его характеристик является площадь сечения осевого. В данной статье приведем формулу площади сечения осевого конуса прямого с круглым основанием и усеченного.

О какой фигуре будет идти речь?

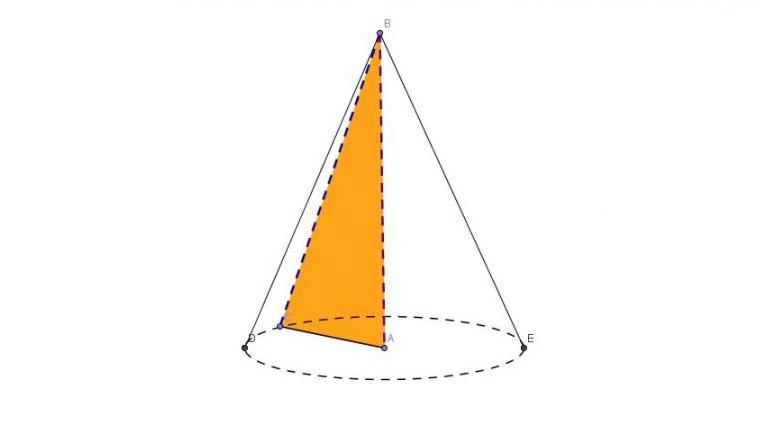
Круглый конус — это фигура, которую можно получить следующим образом. Необходимо взять треугольник с углом прямым и его вокруг одного из катетов вращать. Тогда получится показанная ниже объемная фигура.

Отрезок AC на рисунке называется радиусом основания, который «рисует» при вращении с центром в точке A круг. Катет AB — это высота конуса. Очевидно, что отрезок AB перпендикулярен основанию и является частью оси вращения фигуры. Точка B — это высота рассматриваемой фигуры. Отрезок BE называется образующей, или генератрисой конуса. Совокупность всех генератрис образует боковую поверхность конуса. Она является конической. Ограничивающая основание окружность называется направляющей, или директрисой конуса.

Поскольку генератриса, радиус и высота являются гипотенузой и катетами рассмотренного прямоугольного треугольника, то для них можно записать формулу:

g² = r² + h²

Здесь g — генератриса, r — радиус, h — высота.

Осевое сечение конуса и его площадь

Чтобы записать для конуса формулу площади сечения осевого, сначала следует познакомиться с самим сечением. Оно получается так: нужно взять секущую плоскость, расположить ее параллельно оси конуса. Затем необходимо разрезать конус плоскостью на две одинаковые части таким образом, чтобы в плоскость сечения попала вершина фигуры.

Несложно себе представить, что в результате описанной операции получится равнобедренный треугольник. Равные стороны треугольника будут такие же, как длины генератрис. А третья сторона будет равна диаметру основания.

Формула площади осевого сечения конуса (фото см. выше) не отличается сложностью. Она соответствует формуле расчета этой величины для описанного треугольника. Поскольку у треугольника площадь равна произведению основания на высоту, которое следует поделить пополам, то искомое равенство для осевого сечения примет вид:

S = h*r

Эта формула говорит о том, что S в два раза больше площади прямоугольного треугольника, вращением которого был получен конус.

Усеченный конус и его осевое сечение

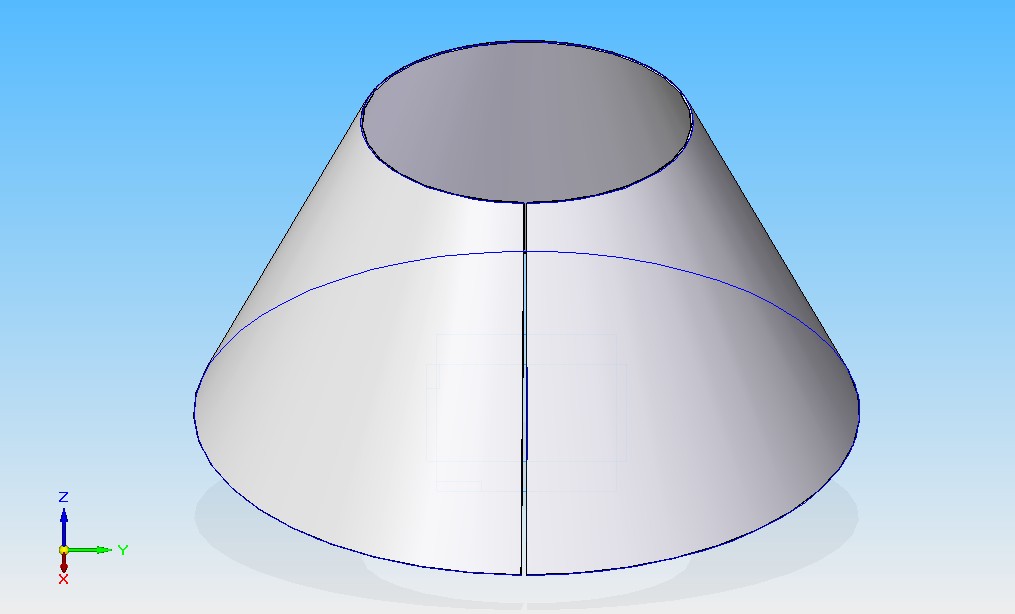
Усеченный конус получается из обычного при помощи секущей плоскости, которая параллельна его основанию. Полученная при этом фигура под плоскостью будет усеченным конусом. Он показан на рисунке.

Помимо боковой поверхности, эта фигура состоит из двух оснований, которые представляют собой большой и малый круги. Обозначим их радиусы как r₁ и r₂. Расстояние между основаниями называется высотой, обозначим ее буквой h.

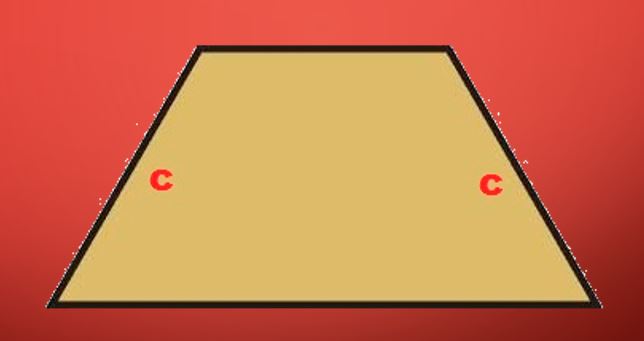
Осевое сечение рассматриваемого конуса будет четырехугольником, две стороны которого являются образующими. А две другие стороны будут параллельны друг другу и равны 2*r₁ и 2*r₂ соответственно. Этот четырехугольник будет равнобедренной трапецией, которая показана на рисунке ниже.

Этот факт позволяет использовать выражение для трапеции, чтобы записать формулу площади сечения усеченного осевого конуса . Она примет вид:

S = (2*r₁ + 2*r₂)/2*h = h*(r₁ + r₂)

То есть площадь S равна произведению суммы радиусов оснований усеченного конуса на его высоту.

Для решения геометрических задач также может потребоваться формула связи между генератрисой фигуры и ее параметрами r₁, r₂ и h. Соответствующее выражение приобретает вид:

g² = h² + (r₁ — r₂)²

Получить ее достаточно просто самостоятельно, если рассмотреть прямоугольный треугольник внутри конуса, построенный на сторонах g, h и (r₁ — r₂).

Задача на определение площади сечения осевого конуса усеченного

Покажем, как находить площадь осевого сечения на примере усеченного конуса.

Известно, что высота указанной фигуры составляет 10 см. Также известно, что для конуса осевого сечения площадь равна разности площадей оснований. Зная, что диаметры оснований отличаются ровно в два раза, необходимо найти площадь этого сечения по оси.

В соответствии с условием задачи можно записать два уравнения:

r₁ = 2*r₂;

h*(r₁ + r₂) = pi*(r₁² — r₂²)

Значение высоты известно из условия. Таким образом, мы имеем 2 равенства и 2 неизвестные величины. Решаем эту систему:

h*(2*r₂ + r₂) = pi*((2*r₂) ² — r₂²) =>

3*pi*r₂² — 3*h*r₂ = 0

Мы получили неполное квадратное уравнение, которое следует решить относительно переменной r₂. Уравнение имеет 2 корня, но решение r₂ = 0 не является физическим, поэтому запишем только одно единственное значение для малого радиуса:

r₂ = h/pi

Тогда большой радиус r₁ будет равен:

r₁ = 2*h/pi

Подставляя эти равенства в формулу площади осевого сечения конуса, получаем:

S = h*(r₁ + r₂) = 3*h²/pi

Подставляем численное значение h и записываем ответ: S ≈ 95,54 см².

В данной публикации мы рассмотрим определение и основные элементы усеченного конуса. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

• Определение усеченного конуса

• Основные элементы усеченного конуса

Определение усеченного конуса

Усеченный конус (конический слой) – это геометрическая фигура в пространстве; часть конуса, оставшаяся между его основанием и секущей плоскостью, параллельной этому основанию.

Примечание: В рамках данной публикации мы будем рассматривать самый распространенный вид усеченного конуса – прямой круговой.

Усеченный конус образуется путем вращения на 360° прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию, или равнобедренной трапеции вокруг своей оси симметрии на 180°.

На рисунке ниже конус образован путем вращения равнобедренной трапеции ABCD вокруг оси O₁O₂.

Основные элементы усеченного конуса

• R – радиус бОльшего основания конуса, являющегося кругом, с центром в точке O₁ и диаметром AD.
• r – радиус меньшего основания конуса с центром в точке O₂, диаметр – отрезок BC.
• h (O₁O₂) – высота конуса; одновременно является высотой трапеции ABCD и осью симметрии обеих фигур.
• l (AB, CD и т.д.) – образующие конуса; это отрезки, соединяющие две точки на окружностях двух его оснований (с минимально возможным расстоянием). Одновременно являются боковыми сторонами трапеции (осевого сечения конуса).
• Осевое сечение усеченного конуса – это равнобедренная трапеция ABCD, образованная в результате пересечения конуса плоскостью, проходящей через его ось.
• Поверхность усеченного конуса – боковая поверхность и поверхность двух его оснований. Формулы для расчета площади поверхности, а также объема усеченного конуса представлены в отдельных публикациях.

Развёртка боковой поверхности усеченного конуса выглядит следующим образом:

Длина бОльшей (меньшей) дуги равна длине окружности соответствующего основания конуса (2πR или 2πr).

Усеченный конус.

МБОУ «СШ № 43»г.Иваново,

учитель математики Шляпцева Н.Н.

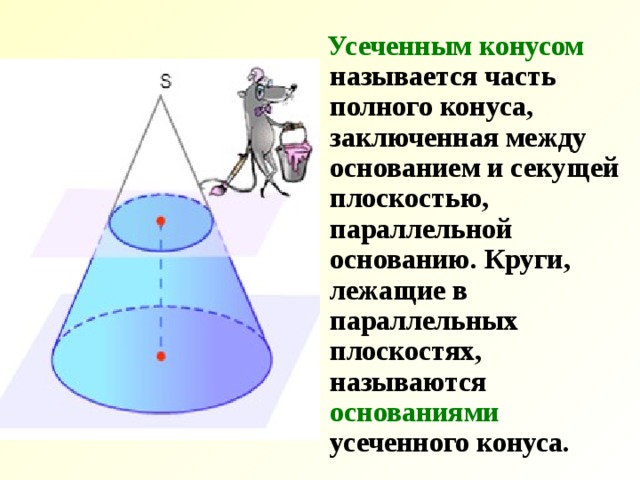
Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей плоскостью, параллельной основанию. Круги, лежащие в параллельных плоскостях, называются основаниями усеченного конуса.

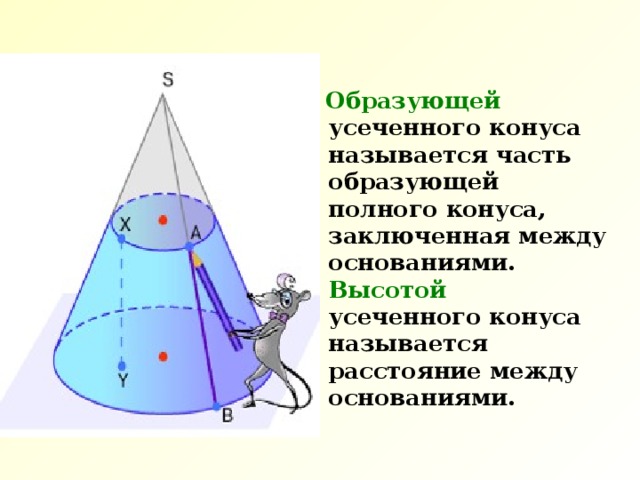
Образующей усеченного конуса называется часть образующей полного конуса, заключенная между основаниями. Высотой усеченного конуса называется расстояние между основаниями.

?

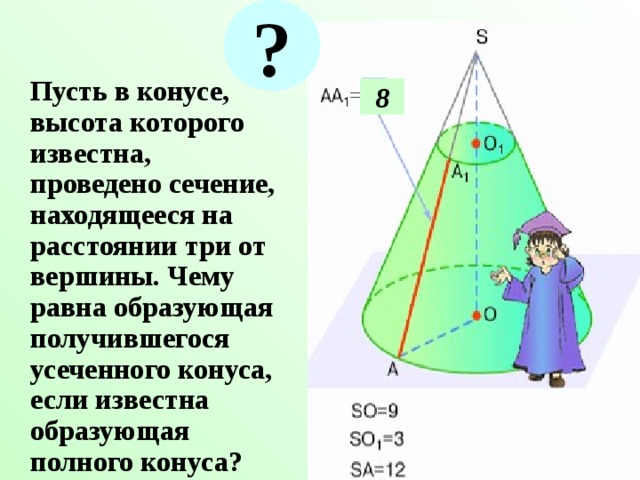
Пусть в конусе, высота которого известна, проведено сечение, находящееся на расстоянии три от вершины. Чему равна образующая получившегося усеченного конуса, если известна образующая полного конуса?

8

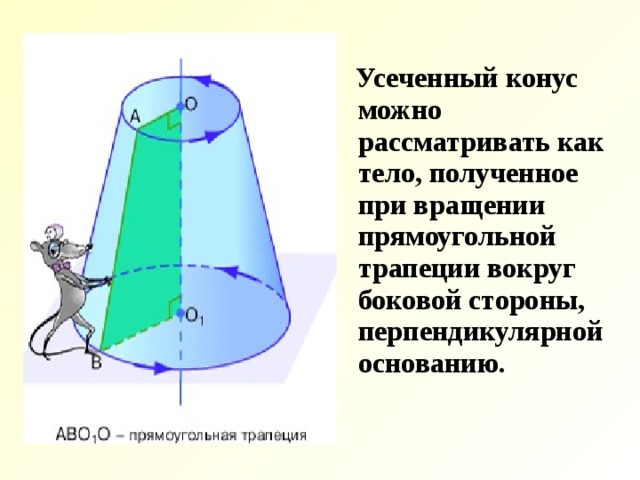
Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.

8

?

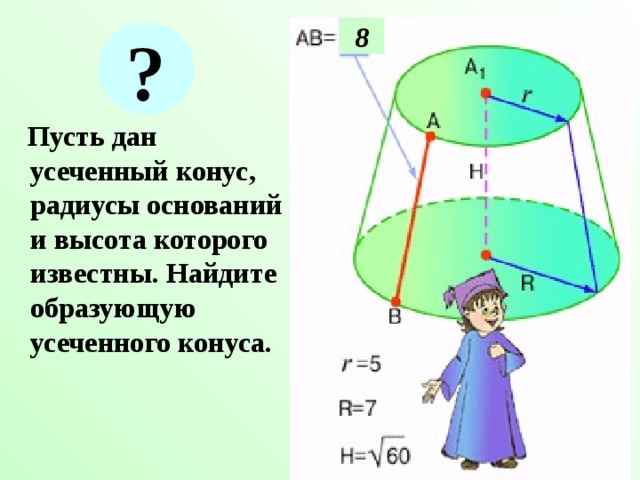
Пусть дан усеченный конус, радиусы оснований и высота которого известны. Найдите образующую усеченного конуса.

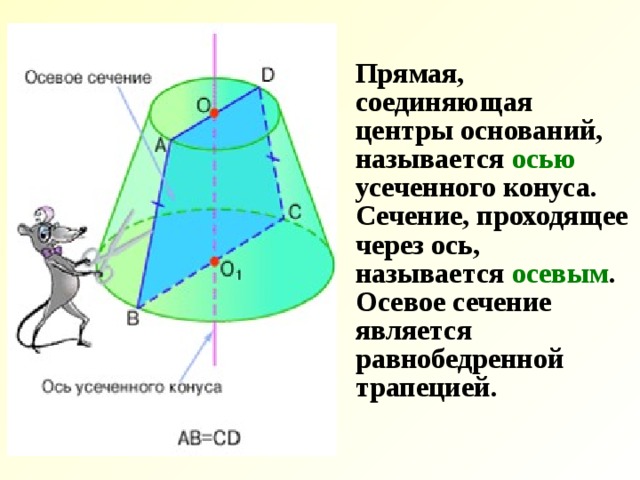
Прямая, соединяющая центры оснований, называется осью усеченного конуса. Сечение, проходящее через ось, называется осевым . Осевое сечение является равнобедренной трапецией.

36

?

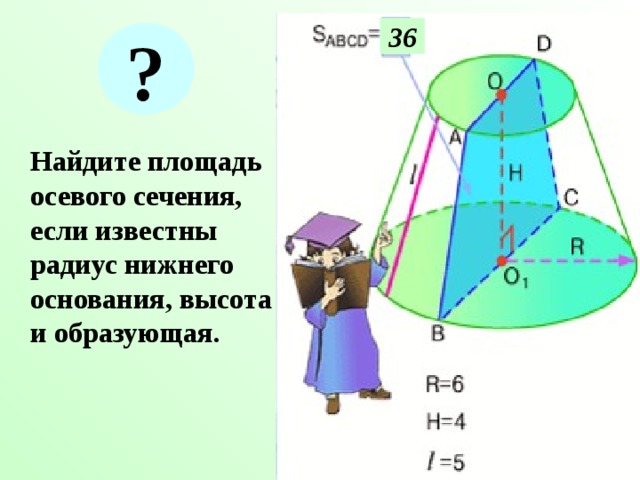
Найдите площадь осевого сечения, если известны радиус нижнего основания, высота и образующая.

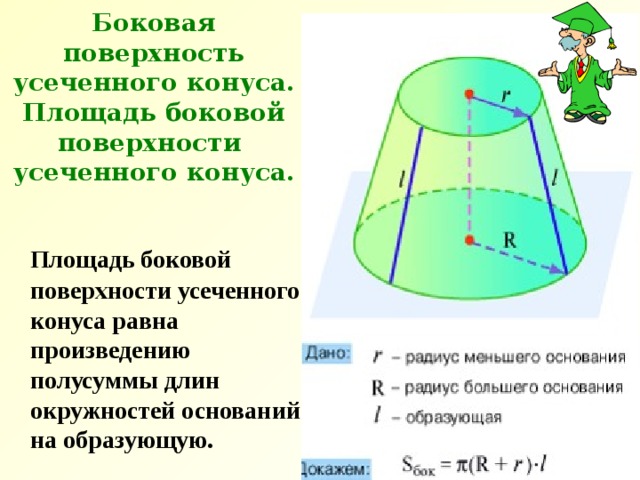
Боковая поверхность усеченного конуса. Площадь боковой поверхности усеченного конуса.

Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

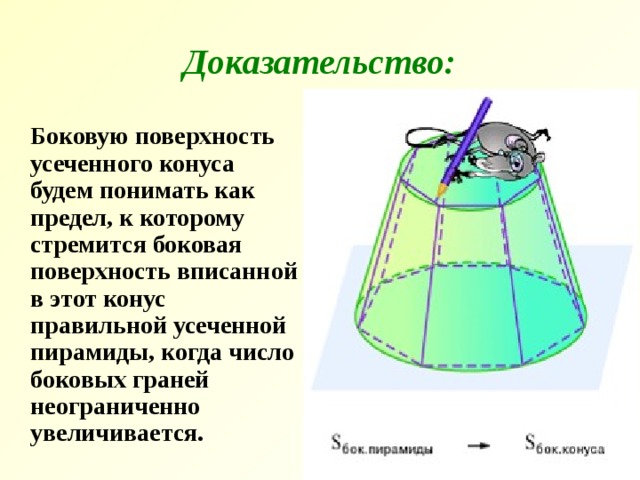
Доказательство:

Боковую поверхность усеченного конуса будем понимать как предел, к которому стремится боковая поверхность вписанной в этот конус правильной усеченной пирамиды, когда число боковых граней неограниченно увеличивается.

Доказательство:

Впишем в конус правильную пирамиду. Ее боковая поверхность состоит из трапеций.

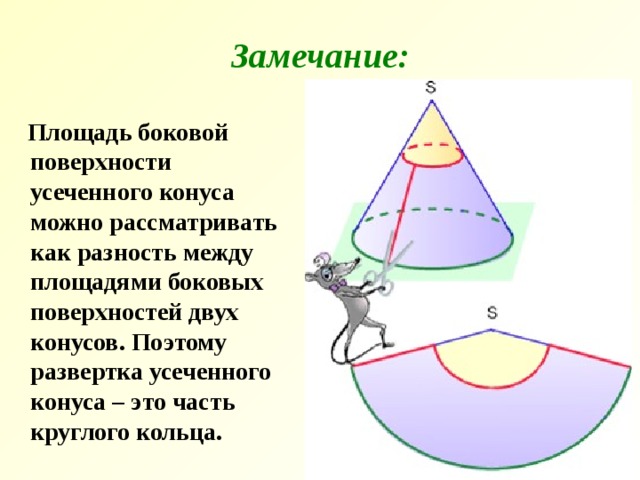
Замечание:

Площадь боковой поверхности усеченного конуса можно рассматривать как разность между площадями боковых поверхностей двух конусов. Поэтому развертка усеченного конуса – это часть круглого кольца.

?

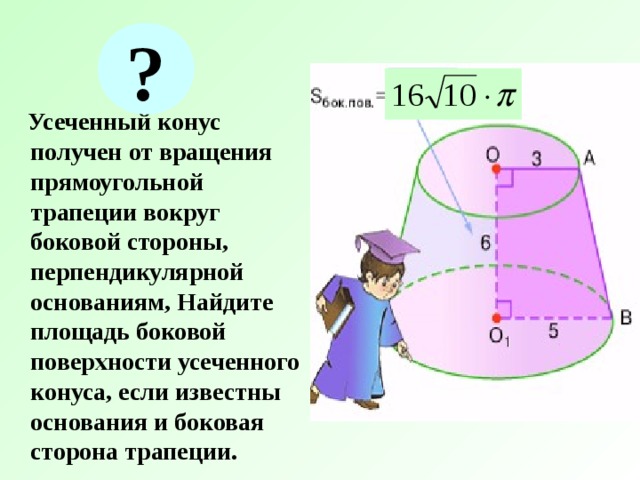
Усеченный конус получен от вращения прямоугольной трапеции вокруг боковой стороны, перпендикулярной основаниям, Найдите площадь боковой поверхности усеченного конуса, если известны основания и боковая сторона трапеции.

Задача.

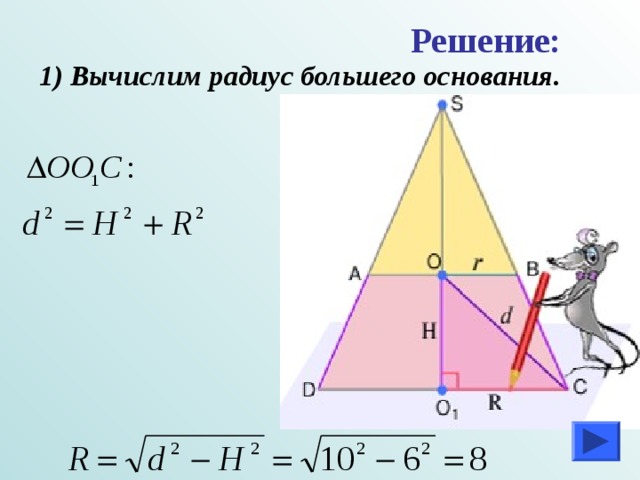
• Радиус меньшего основания усеченного конуса равен 5, высота равна 6, а расстояние от центра меньшего основания до окружности большего основания равно 10. Найдите площадь боковых поверхностей усеченного и полного конусов.

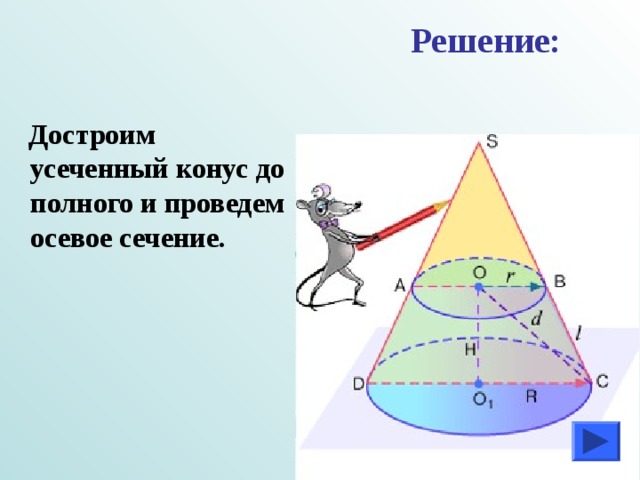
Решение:

Достроим усеченный конус до полного и проведем осевое сечение.

Решение:

1) Вычислим радиус большего основания.

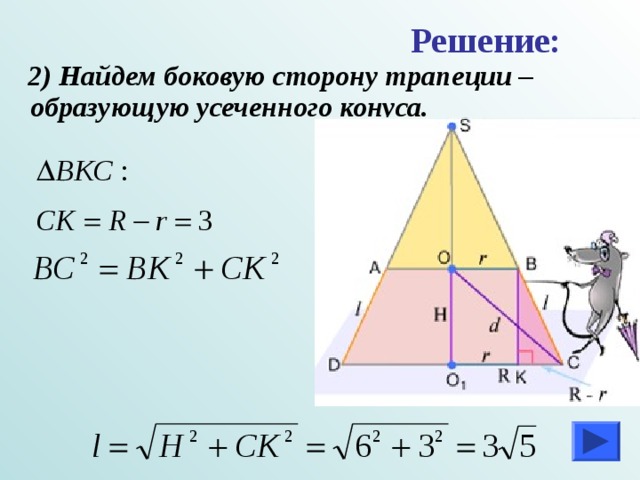
Решение:

2) Найдем боковую сторону трапеции –образующую усеченного конуса.

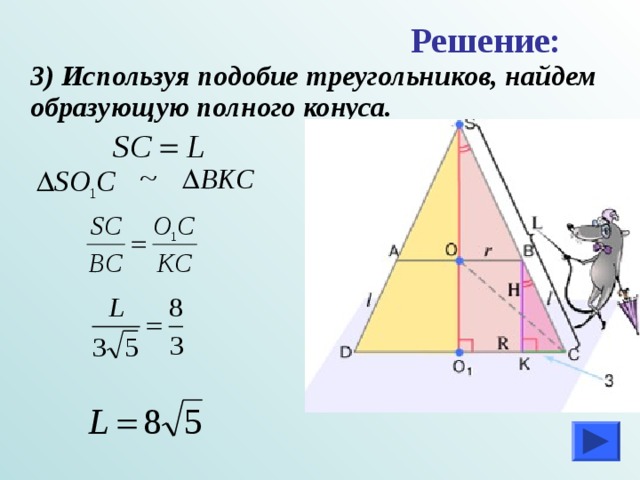
Решение:

3) Используя подобие треугольников, найдем образующую полного конуса.

~

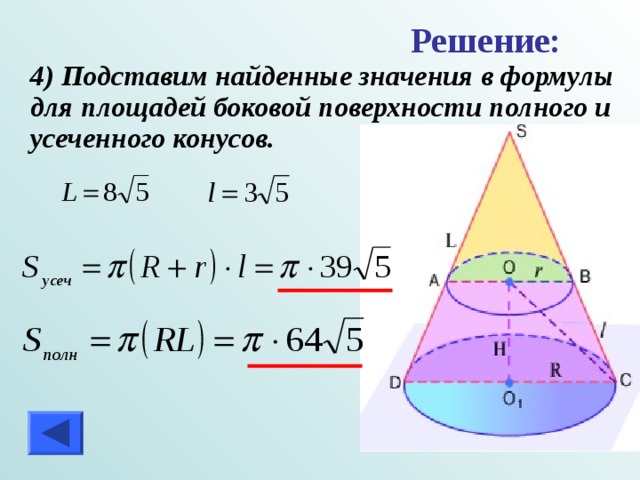
Решение:

4) Подставим найденные значения в формулы для площадей боковой поверхности полного и усеченного конусов.

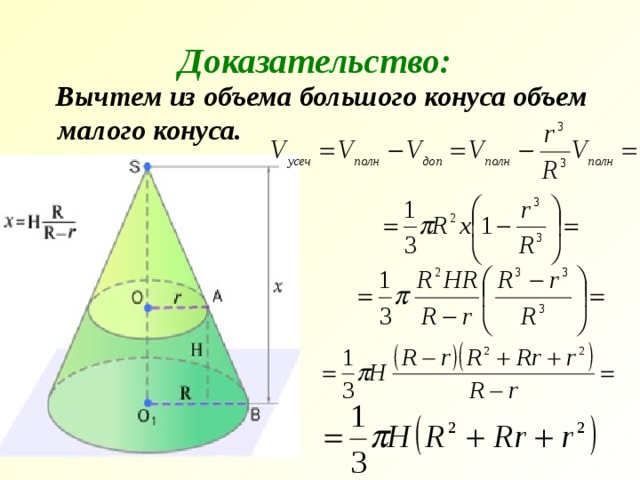
Формула объема усеченного конуса.

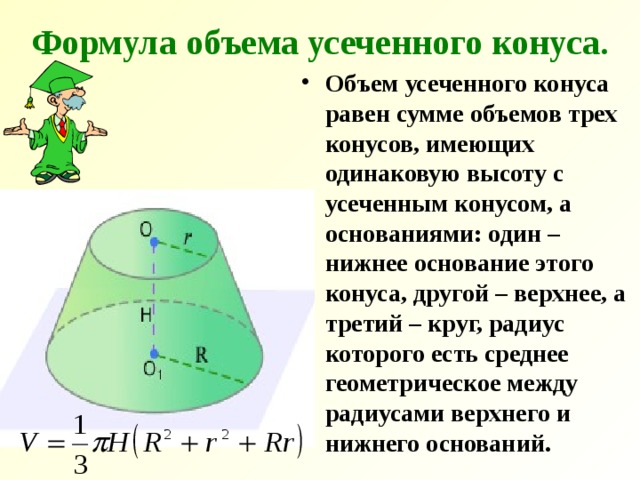
• Объем усеченного конуса равен сумме объемов трех конусов, имеющих одинаковую высоту с усеченным конусом, а основаниями: один – нижнее основание этого конуса, другой – верхнее, а третий – круг, радиус которого есть среднее геометрическое между радиусами верхнего и нижнего оснований.

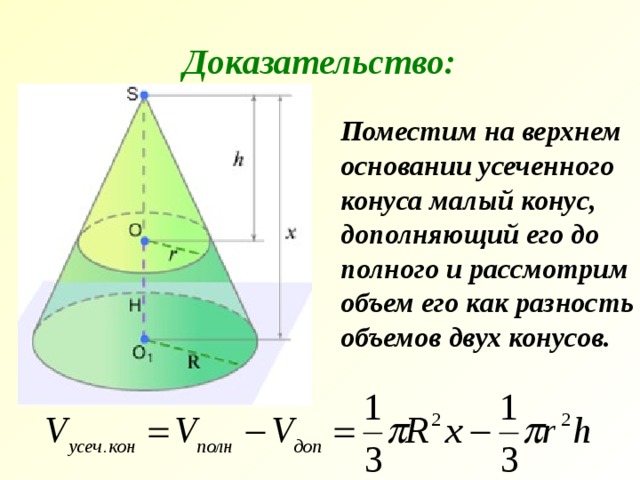
Доказательство:

Поместим на верхнем основании усеченного конуса малый конус, дополняющий его до полного и рассмотрим объем его как разность объемов двух конусов.

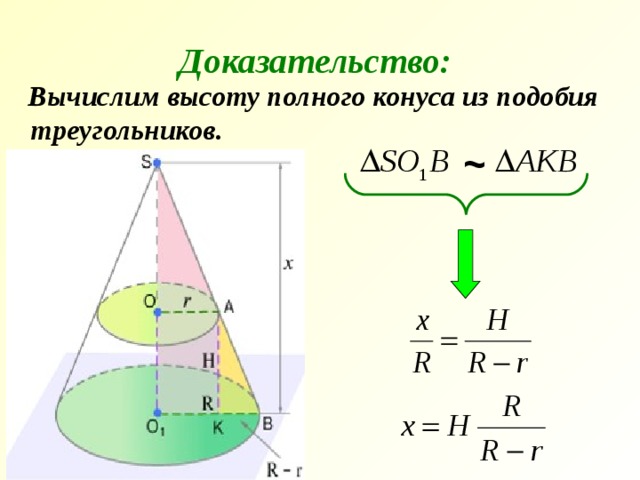
Доказательство:

Вычислим высоту полного конуса из подобия треугольников.

~

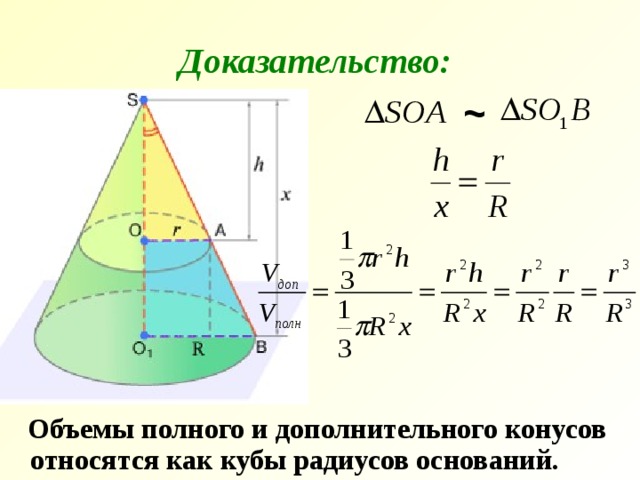
Доказательство:

~

Объемы полного и дополнительного конусов относятся как кубы радиусов оснований.

Доказательство:

Вычтем из объема большого конуса объем малого конуса.

?

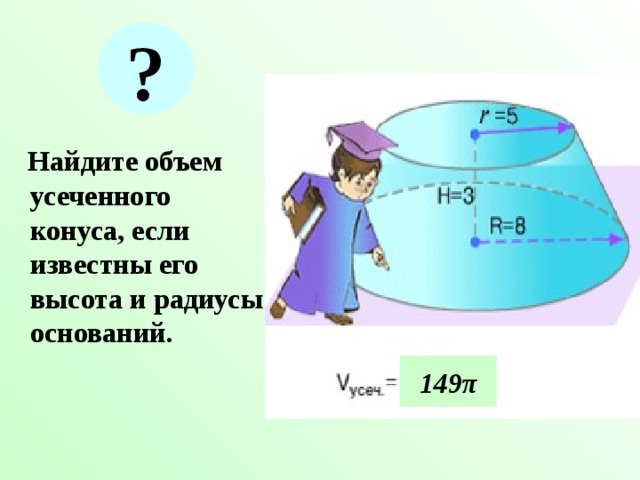
Найдите объем усеченного конуса, если известны его высота и радиусы оснований.

149 π

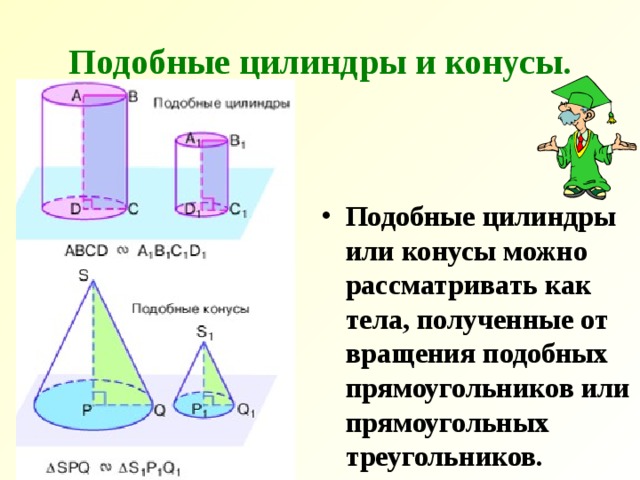
Подобные цилиндры и конусы.

• Подобные цилиндры или конусы можно рассматривать как тела, полученные от вращения подобных прямоугольников или прямоугольных треугольников.

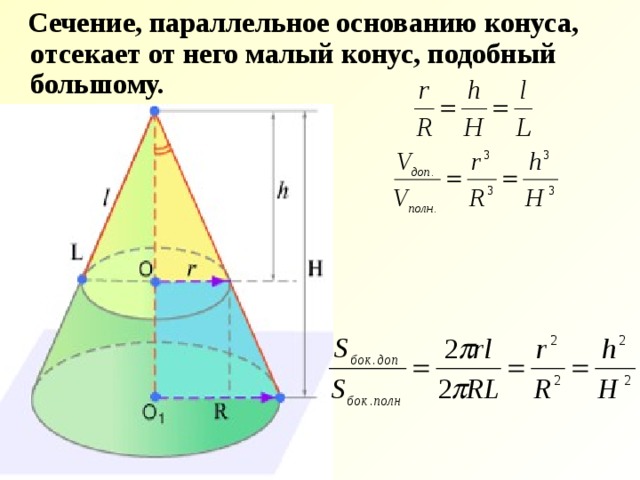
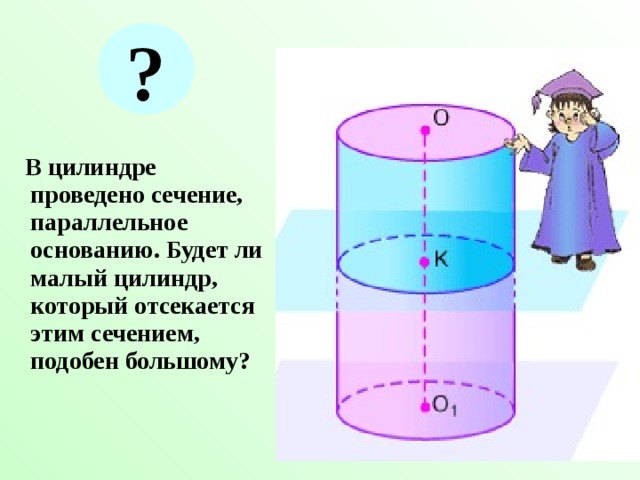
Сечение, параллельное основанию конуса, отсекает от него малый конус, подобный большому.

?

В цилиндре проведено сечение, параллельное основанию. Будет ли малый цилиндр, который отсекается этим сечением, подобен большому?

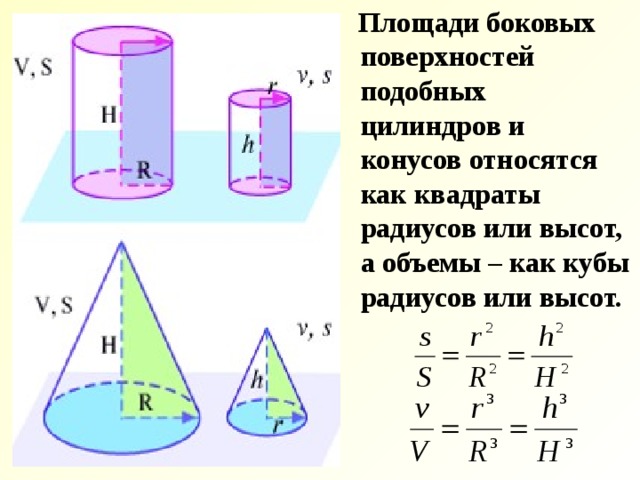
Площади боковых поверхностей подобных цилиндров и конусов относятся как квадраты радиусов или высот, а объемы – как кубы радиусов или высот.

?

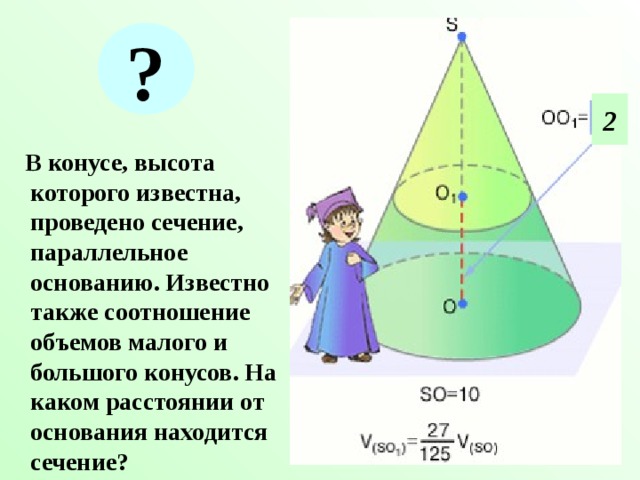
2

В конусе, высота которого известна, проведено сечение, параллельное основанию. Известно также соотношение объемов малого и большого конусов. На каком расстоянии от основания находится сечение?

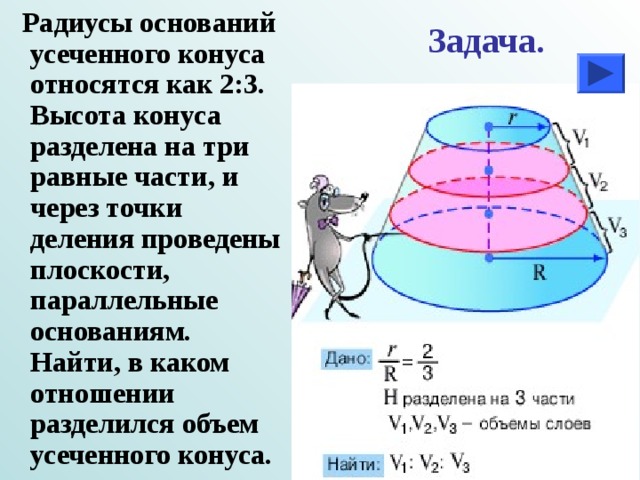
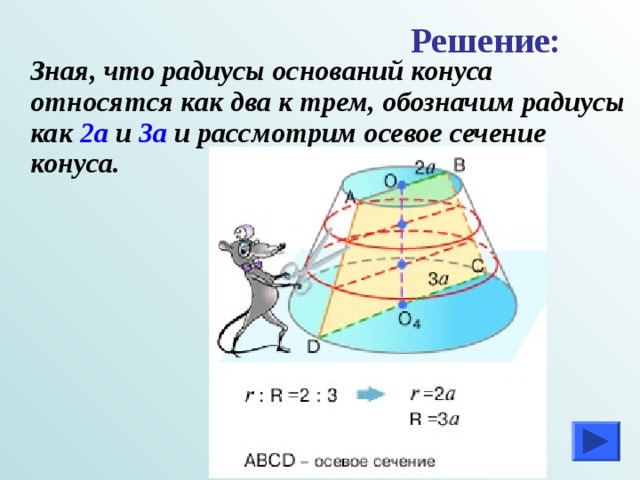
Радиусы оснований усеченного конуса относятся как 2:3. Высота конуса разделена на три равные части, и через точки деления проведены плоскости, параллельные основаниям. Найти, в каком отношении разделился объем усеченного конуса.

Задача.

Решение:

Зная, что радиусы оснований конуса относятся как два к трем, обозначим радиусы как 2а и 3а и рассмотрим осевое сечение конуса.

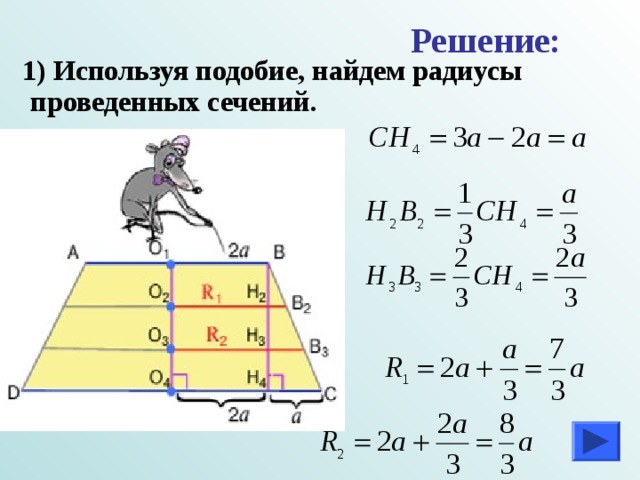
Решение:

1) Используя подобие, найдем радиусы проведенных сечений.

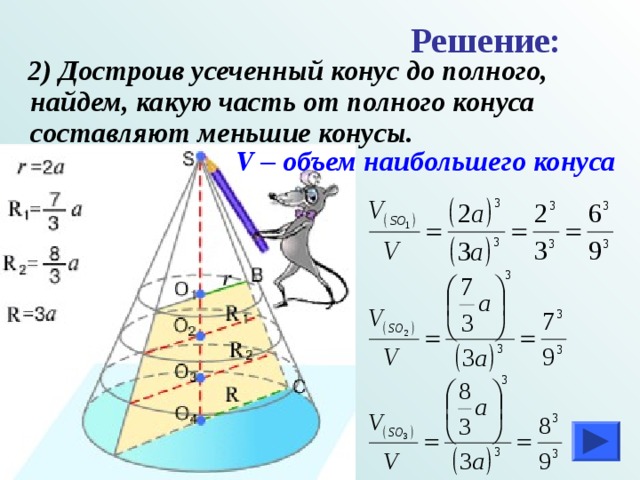
Решение:

2) Достроив усеченный конус до полного, найдем, какую часть от полного конуса составляют меньшие конусы.

V – объем наибольшего конуса

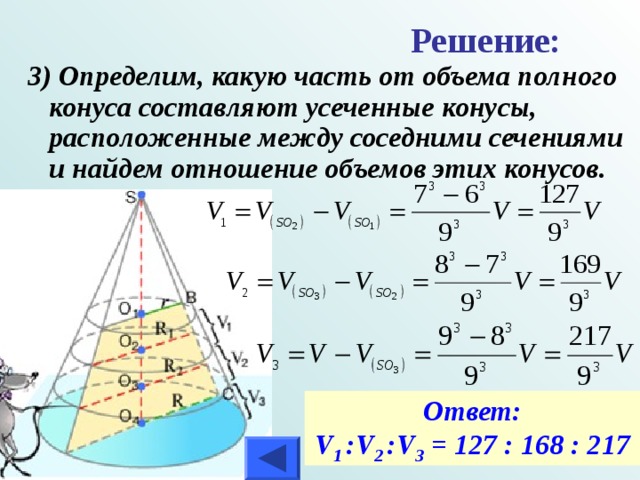
Решение:

3) Определим, какую часть от объема полного конуса составляют усеченные конусы, расположенные между соседними сечениями и найдем отношение объемов этих конусов.

Ответ:

V 1 :V 2 :V 3 = 127 : 168 : 217