Как найти ошибку измерения силы в физике

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с  точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением 
шкалы линейки совпадает второй край стола  (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.  

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения 
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: .  То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой  (эпсилон): 

     (5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения –  плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм — Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора. 
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:   и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
3. вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2: 

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 — с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
2. Цена деления шкалы равна значению наименьшего деления шкалы.
3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

• Заказать решение задач по физике

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы: 

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

Динамометр (силомер) — прибор, предназначенный для измерения сил. Действие такого прибора основано на том, что упругие деформации пропорциональны прикладываемым силам.

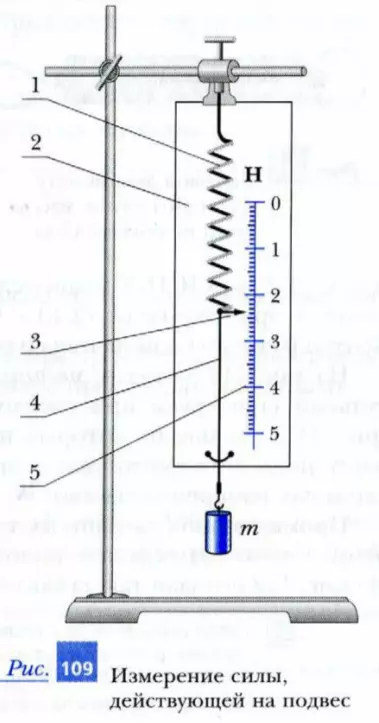
На рис. 109 показан динамометр, используемый в школах при выполнении лабораторных работ по физике. Он состоит из пружины 1, один конец которой прикреплен к основанию 2. К другому концу пружины прикреплена стрелка 3 и проволока 4 с крючком па конце. На основание 2 нанесена шкала 5, пользуясь которой можно определить силу, растягивающую пружину. Отметка «0» на шкале соответствует нерастянутому состоянию пружины. Этот динамометр предназначен для измерения сил в ньютонах. Об атом свидетельствует буква Н (или N) над шкалой.

На шкалы динамометров цифры нанесены только против некоторых штрихов. Как же узнать значения деформирующих пружину сил, если стрелка динамометра не совпадает с оцифрованным штрихом? Для этого нужно прежде всего узнать цену деления шкалы прибора (т. е. на сколько изменяется значение силы, когда стрелка смещается на одно деление – расстояние между двумя соседними штрихами). После этого подсчитывают число делений между двумя соседними оцифрованными штрихами. Например, на рис. 109 между штрихами, около которых стоят цифры 2 и 3, находится 10 делений. Следовательно, цена деления этого динамометра равна (3 – 2) / 10 = 0,1 Н на деление. Стрелка динамометра отстоит на 4 деления от штриха с цифрой 2. Поэтому модуль деформирующих пружину сил равен 2 Н + 4 · 0,1 Н = 2,4 Н.

Найденное значение силы упругости не является истинным. Динамометр, как и всякий прибор, имеет погрешность. В паспорте школьного динамометра, рассчитанного на измерение сил в пределах от 0 до 5 Н, говорится, что погрешность прибора Δ_пр = 0,05 Н в любом месте шкалы. С учетом погрешности отсчета, равной Δ_о = 0,05, получаем, что общая погрешность Δ = Δ_пр + Δ_о = 0,10 Н. Следовательно, истинное значение измерешюй силы лежит в промежутке от (2,40 — 0,10) Н = 2,3 Н до (2,40 + 0,10) Н = 2,5 Н. Кратко результат измерения силы можно записать в виде: 2,3 Н ≤ F ≤ 2,5 Н.

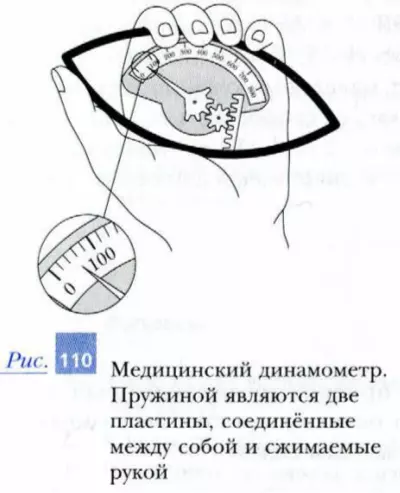
На рисунке 110 показан медицинский динамометр для измерения мускульной силы руки при сжатии кисти в кулак. Имеются динамометры (рис. 111), на шкалы которых нанесены деления, позволяющие измерять массу подвешиваемого тела непосредственно в килограммах (или других единицах измерения массы).

Когда динамометр с подвешенным телом покоится относительно Земли, динамометр показывает вес тела. При этом вес тела по модулю пропорционален его массе (P = m · g). Это и позволяет задать цену деления шкалы динамометра в единицах массы, а сам прибор использовать для измерения массы.

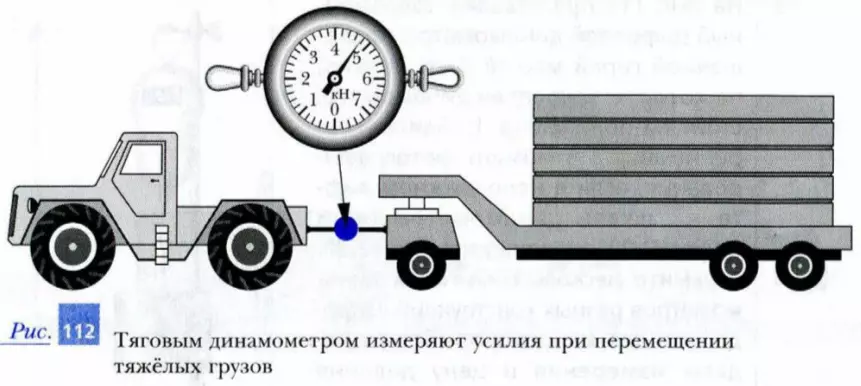
Промышленность выпускает динамометры, предназначенные для измерения сил от сотых долей ньютона до нескольких десятков килоньютонов. На рис. 112 показан так называемый тяговый динамометр.

Итоги

Динамометр – прибор для измерения сил.

Принцип действия динамометров основан на однозначной зависимости модуля упругих деформаций от модуля деформирующих сил.

Точность измерения сил определяется погрешностью динамометра, которая указывается в паспорте прибора.

Вопросы

1. Что такое динамометр? На чем основан принцип действия динамометра?
2. Как изготовить простейший динамометр и отградуировать его?
3. Как определить погрешность измерения сил динамометром?

Упражнения

1. Определите массу гири, показанной на рис. 109. Указание: модуль ускорения свободного падения считайте равным 10 м/с². Погрешность динамометра Δ = 0,10 Н.

2. Определите модуль силы, с которой трактор, показанный на рис. 112, тянет прицеп. Указание: погрешность тягового динамометра считайте равной цене деления между соседними штрихами на его шкале.

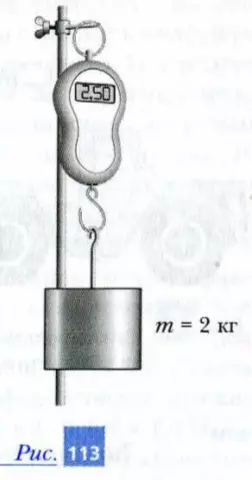
* 3. На рис. 113 представлен современный цифровой динамометр с подвешенной гирей массой 2 кг. Штатив, на котором закреплен динамометр, стоит на полу лифта. Найдите ускорение лифта в момент фотографирования, если в неподвижном лифте на шкале динамометра были цифры 2,00, а в движущемся – 2,50.

4. Возьмите несколько бытовых динамометров разных конструкций. Определите для каждого прибора пределы измерения и цену деления шкалы. Проведите взвешивание одного и того же тела разными динамометрами. Сравните результаты с учетом погрешности измерений.

5. Приготовьте напольные весы. Установите их в кабине лифта, стоящего на первом этаже, встаньте на них и зафиксируйте показание. Нажмите кнопку верхнего этажа, наблюдайте за изменением показаний весов в моменты, соответствующие: а) началу разгона лифта; б) равномерному движению; в) началу торможения перед остановкой. Объясните причины изменений в показаниях весов. Повторите эксперимент при спуске лифта с верхнего этажа на первый. Сопоставьте результаты экспериментов, объясните различия.

Ошибки измерений физических величин

По
способу выражения точности результатов
измерения различают абсолютную
и относительную
ошибки.

Абсолютной
ошибкой
измерения x
некоторой величины называют модуль
разности между измеренным значением x
и истинным значением a
измеряемой
величины:

x
= a
– x.
(1)

Абсолютная ошибка
имеет размерность измеряемой величины
и указывает на необходимую поправку в
данном результате измерения. При этом
она определяет неточность в измерении
величины вне зависимости от её значения.

Относительной
ошибкой
измерения 
называют отношение абсолютной ошибки
измерения к истинному значению измеряемой
величины:

 = x/a
. (2)

Относительная
ошибка безразмерна или иногда выражается
в процентах:

 = (x/a)100%
. (3)

Если абсолютная
ошибка определяет неточность в измерении
величины безотносительно к значению
самой величины, то относительная ошибка
даёт непосредственное представление
о точности проведённых измерений, так
как определяет, какую долю составляет
ошибка в полученном результате. Например,
абсолютная ошибка в 1 грамм (x
= 1 г) при измерении массы тела в 10 кг даёт
неточность всего 
= (10^-3/10)100%
= 0,01%, в то время как такая же абсолютная
ошибка в определении массы тела в 10
г даёт неточность уже 
= (10^-3/10^-2)100%
= 10%.

По характеру
проявления различают три вида ошибок:
грубые ошибки
(промахи), систематические ошибки и
случайные ошибки.

Промахи
– допущенные грубые ошибки, когда
некоторые измерения вдруг резко
выделяются из большого ряда полученных
измерений. Они могут возникать вследствие
недостатка внимания экспериментатора,
непредсказуемого поведения прибора
(внешние наводки, нестабильность
источника питания и т.д.) и множества
других причин, которые практически
невозможно учесть. Такие измерения
обычно просто отбрасываются, хотя, надо
сказать, существуют критерии, позволяющие
разобраться в том, является ли данное
измерение промахом или же естественным
случайным отклонением от среднего
значения, т.е. измерением, которое нельзя
отбрасывать (такие критерии разбираются
в приведённой в конце этих методических
указаний литературе). Обычно, всё же
даже неверный отброс случайного
измерения, как “промаха”, не приводит
к заметному изменению оценок неточностей
измеряемой величины.

Систематические
ошибки связаны
с факторами, действующими одинаково
при многократном повторении одних и
тех же измерений. Они возникают по
нескольким причинам. 1). Из-за погрешности
метода измерений, который может не
учитывать некоторых факторов, влияющих
на результат измерений. Например, это
– не учёт при измерениях длины тела её
зависимости от температуры, не принятие
во внимание “потери веса” тела в воздухе
из-за наличия выталкивающей силы и т.д.
Во многих случаях величину и знак такой
систематической ошибки можно установить
и ввести соответствующие поправки.
Поправка, разумеется, равна систематической
ошибке измерения, взятой с обратным
знаком. 2). Из-за неизвестных, непредполагаемых
свойств измеряемого объекта (например,
наличие в нём пустот, несимметричность
считающегося симметричным объекта и
т.д.). Эти ошибки исключаются только,
если провести измерения изучаемой
величины другим методом и в других
условиях эксперимента. 3). Из-за
индивидуальных погрешностей, допускаемых
в процессе измерений наблюдателем.
Например, наблюдатели по-разному
внимательны, обладают разной скоростью
реакции, а это приводит к систематическим
ошибкам при слежении за “уходом нуля”
приборов, при регистрации временных
интервалов секундомером и т.д. Устранить
индивидуальные систематические
погрешности можно только повторением
этих измерений другими наблюдателями.
4). Из-за ошибок, которые вносят погрешности
измерительных приборов. Погрешности
измерительных приборов будут подробно
разобраны в следующем разделе.

Случайные
погрешности определяются
сложной совокупностью причин. Они
обнаруживаются при всё большем числе
повторных измерений в виде некоторого
разброса результатов измерений, причём
невозможно предсказать результат
очередного измерения. Но это не означает,
что случайная ошибка не подчиняется
никаким закономерностям. Законы её
изменения носят статистический характер.
Далее отдельно будет дано математическое
обоснование определения этой ошибки.

Соседние файлы в папке физика_1

• #

  28.03.2016210.94 Кб2380.doc

• #

  28.03.2016169.47 Кб2182.doc

• #

  28.03.2016592.38 Кб2688.doc

• #

  28.03.2016163.33 Кб239.doc

• #
• #
• #
• #

Как определять погрешности измерений

Измерение – нахождение значения физической величины
опытным путем с                   помощью средств измерений.

Прямое
измерение
– определение значения физической
величины непосредственно средствами измерения.

Косвенное
измерение
– определение значения физической
величины по формуле, связывающей ее с другими физическими величинами, определяемыми
прямыми измерениями.

          А,  В, С, … — физические величины.

          А_пр. – приближенное значение физической величины.

         А – абсолютная погрешность измерения физической
величины.

          — относительная погрешность измерения
физической величины.

          _иА
– абсолютная
инструментальная погрешность, определяемая конструкцией прибора.

          _оА – абсолютная погрешность отсчета, она равна в
большинстве случаев

                     половине цены деления; при
измерении времени – цене деления секундомера или часов.

          Абсолютную погрешность измерения
обычно округляют до одной значащей цифры:

         

          Численное значение результата
измерений округляют так, чтобы его последняя цифра оказалась в том же разряде,
что и цифра погрешности:

          

          
Результат
измерения записывается так:

       %

                                                    

      
Определение погрешности методом среднего арифметического

          При многократных
измерениях величины погрешность можно оценить следующим образом:

1.    
Определить среднее
значение величины А:

 (при трех
измерениях).

2.Определить отклонение каждого значения от среднего:

       

     3.Определить среднее значение отклонения,
его и принимают за абсолютную погрешность:

   4.Определить
относительную погрешность и выразить ее в процентах:

№ опыта
1
2
3

          Многократные измерения
предпочтительнее, так как при их проведении возможна компенсация случайных
факторов, влияющих на результат. Обычно многократные измерения проводят, слегка
изменяя условия опыта, но предполагая, что значение величины А не изменяются

Определение
погрешности косвенных измерений

          При косвенных измерениях значение
физической величины находится путем    расчетов по формуле.

      Относительную погрешность
определяют так, как показано в таблице:

Формула величины	Формула относительной погрешности
1.
2. 3.
4.

     Абсолютную погрешность определяют
по формуле:

(  выражается десятичной дробью)

    Пример:  пусть измеряется сопротивление проводника. .

   Результаты прямых измерений:     

    Тогда ;                                                                                                    
,    ;                                                                
,       ;                                             
,     ,   .

Графическое
представление результатов эксперимента

                                   Правила  построения
 графиков

          Для построения графиков выпускают
специальную бумагу-миллиметровку.

          При выборе масштабов по осям
координат следует руководствоваться следующими правилами:

         — значение независимой переменной
откладывают вдоль оси абсцисс, функции – вдоль оси ординат;

         — цена наименьшего деления масштабной
сетки должна быть сравнимой с величиной погрешности измерения;

         — точка пересечения оси абсцисс и оси
ординат не обязательно должна иметь координаты (0,0).

          При построении графиков следует
иметь в виду, что по результатам опытов мы получаем не точку, а прямоугольник
со сторонами  и.

  

                    
В

                                                                                             
 

                                                                                           

                                                                                           

                       0                                                                        
А

          При выполнении простых лабораторных
работ достаточно обвести экспериментальную точку кружком или пометить
крестиком, не указывая доверительных интервалов.

          Этот кружок или крестик будут
обозначать, что данная точка получена с каким-то приближением и истинное
значение измеряемой величины лежит где-то в ее окрестности. 

Правила
приближенных вычислений

 1. Основное
правило округления.

Если первая
отброшенная цифра равна 5 или больше, то последнюю из сохраняемых цифр
увеличивают на единицу; если первая отброшенная цифра меньше 5, то последнюю из
сохраняемых цифр оставляют без изменения, например:

                              

 2. При сложении и
вычитании приближенных чисел
в полученном результате сохраняют столько десятичных знаков, сколько их в числе
с наименьшим количеством десятичных знаков, например:

      

 3. При умножении
и делении приближенных чисел
в полученном результате нужно сохранить столько значащих цифр, сколько их имеет
приближенное число с наименьшим количеством значащих цифр, например:

                        

 4. При возведении
в квадрат приближенного числа
нужно в результате сохранять столько значащих цифр, сколько их имеет возводимое
в степень число, например:

                   

 5. При извлечении
квадратного корня в результате
нужно сохранять столько значащих цифр, сколько их имеет подкоренное число,
например:

                   

 6. При вычислении
промежуточных результатов в
них следует сохранять на одну цифру больше, чем требуют правила 2-5. Причем при
подсчете значащих цифр запасные цифры не учитываются. В окончательном
результате запасная цифра отбрасывается   по основному правилу округления.

 7. При нахождении
углов или тригонометрических функций значение соответствующего угла записывают с точностью до градуса, если
значение тригонометрической функции имеет две значащие цифры; если угол задан с
точностью до градусов, то в значении тригонометрической функции сохраняют две
значащие цифры, например:

                   

1. Введение (измерения и погрешности измерений)

Физика как наука родилась более 300 лет назад, когда Галилей по сути создал научный изучения физических явлений: физические законы устанавливаются и проверяются экспериментально путем накопления и сопоставления опытных данных, представляемых набором чисел, формулируются законы языком математики, т.е. с помощью формул, связывающих функциональной зависимостью числовые значения физических величин. Поэтому физика- наука экспериментальная, физика- наука количественная.

Познакомимся с некоторыми характерными особенностями любых измерений.

Измерение- это нахождение числового значения физической величины опытным путем с помощью средств измерений (линейки, вольтметра, часы и т.д.).

Измерения могут быть прямыми и косвенными.

Прямое измерение- это нахождение числового значения физической величины непосредственно средствами измерений. Например, длину — линейкой, атмосферное давление- барометром.

Косвенное измерение- это нахождение числового значения физической величины по формуле, связывающей искомую величину с другими величинами, определяемыми прямыми измерениями. Например сопротивление проводника определяют по формуле R=U/I, где U и I измеряются электроизмерительными приборами.

Рассмотрим пример измерения.

Измерим длину бруска линейкой (цена деления 1 мм). Можно лишь утверждать, что длина бруска составляет величину между 22 и 23 мм. Ширина интервала “неизвестности составляет 1мм, те есть равна цене деления. Замена линейки более чувствительным прибором, например штангенциркулем снизит этот интервал, что приведет к повышению точности измерения. В нашем примере точность измерения не превышает 1мм.

Поэтому измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный. Неопределенность в измерении характеризуется погрешностью — отклонением измеренного значения физической величины от ее истинного значения.

Перечислим некоторые из причин, приводящих к появлению погрешностей.

1. Ограниченная точность изготовления средств измерения.

2. Влияние на измерение внешних условий (изменение температуры, колебание напряжения.).

3. Действия экспериментатора (запаздывание с включением секундомера, различное положение глаза.).

4. Приближенный характер законов, используемых для нахождения измеряемых величин.

Перечисленные причины появления погрешностей неустранимы, хотя и могут быть сведены к минимуму. Для установления достоверности выводов, полученных в результате научных исследований существуют методы оценки данных погрешностей.

2. Случайные и систематические погрешности

Погрешности, возникаемые при измерениях делятся на систематические и случайные.

Систематические погрешности- это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней.

Причины возникновения систематических погрешностей:

1) несоответствие средств измерения эталону;

2) неправильная установка измерительных приборов (наклон, неуравновешенность);

3) несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают;

4) несоответствие измеряемого объекта с предположением о его свойствах (наличие пустот и т.д).

Случайные погрешности- это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.

3. Абсолютные и относительные погрешности

Для количественной оценки качества измерений вводят понятия абсолютной и относительной погрешностей измерений.

Как уже говорилось, любое измерение дает лишь приближенное значение физической величины, однако можно указать интервал, который содержит ее истинное значение:

А_пр— DА < А_ист < А_пр+DА

Величина DА называется абсолютной погрешностью измерения величины А. Абсолютная погрешность выражается в единицах измеряемой величины. Абсолютная погрешность равна модулю максимально возможного отклонения значения физической величины от измеренного значения. А_пр— значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений.

Но для оценки качества измерения необходимо определить относительную погрешность e. e= DА/А_пр или e= (DА/А_пр)*100%.

Если при измерении получена относительная погрешность более 10%, то говорят, что произведена лишь оценка измеряемой величины. В лабораториях физического практикума рекомендуется проводить измерения с относительной погрешностью до 10%. В научных лабораториях некоторые точные измерения (например определение длины световой волны), выполняются с точностью миллионных долей процента.

4. Погрешности средств измерений

Эти погрешности называют еще инструментальными или приборными. Они обусловлены конструкцией измерительного прибора, точностью его изготовления и градуировки. Обычно довольствуются о допустимых инструментальных погрешностях, сообщаемых заводом изготовителем в паспорте к данному прибору. Эти допустимые погрешности регламентируются ГОСТами. Это относится и к эталонам. Обычно абсолютную инструментальную погрешность обозначают DиА.

Если сведений о допустимой погрешности не имеется (например у линейки), то в качестве этой погрешности можно принять половину цены деления.

При взвешивании абсолютная инструментальная погрешность складывается из инструментальных погрешностей весов и гирь. В таблице приведены допустимые погрешности наиболее часто

встречающихся в школьном эксперименте средств измерения.

Средства измерения	Предел измерения	Цена деления	Допустимая погрешность
линейка ученическая	до 50 см	1 мм	1 мм
линейка демонстрационная	100 см	1 см	0.5 см
лента измерительная	150 см	0.5 см	0.5 см
мензурка	до 250 мл	1 мл	1 мл
гири 10,20, 50 мг			1 мг
гири 100,200 мг			2 мг
гири 500 мг			3 мг
гири 1 г			4 мг
гири 2 г			6 мг
гири 5 г			8 мг
гири 10 г			12 мг
гири 20 г			20 мг
гири 50 г			30 мг
гири 100 г			40 мг
штангенциркуль	150 мм	0.1 мм	0.05 мм
микрометр	25 мм	0.01 мм	0.005 мм
динамометр	4 Н	0.1 Н	0.05 Н
весы учебные	200 г		0.1 г
Секундомер	0-30 мин	0.2 с	1с за 30 мин
барометр-анероид	720-780 мм рт.ст.	1 мм рт.ст	3 мм рт.ст
термометр лабораторный	0-100 градусов С	1 градус	1 градус
амперметр школьный	2 А	0.1 А	0.08 А
вольтметр школьный	6 В	0.2 В	0.16 В

5. Класс точности электроизмерительных приборов

Стрелочные электроизмерительные приборы по допустимым значениям погрешностям делятся на классы точности, которые обозначены на шкалах приборов числами 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Класс точности g_пр прибора показывает, сколько процентов составляет абсолютная погрешность от всей шкалы прибора.

g_пр = (D_иА/А_макс)*100%.

Например абсолютная инструментальная погрешность прибора класса 2,5 составляет 2,5% от его шкалы.

Если известен класс точности прибора и его шкала, то можно определить абсолютную инструментальную погрешность измерения

DиА=(g_пр * А_макс)/100.

Для повышения точности измерения стрелочным электроизмерительным прибором надо выбирать прибор с такой шкалой, чтобы в процессе измерения располагались во второй половине шкалы прибора.

6. Погрешность отсчета

Погрешность отсчета получается от недостаточно точного отсчитывания показаний средств измерений.

В большинстве случаев абсолютную погрешность отсчета принимают равной половине цены деления. Исключения составляют измерения стрелочными часами (стрелки передвигаются рывками).

Абсолютную погрешность отсчета принято обозначать DоА

7. Полная абсолютная погрешность прямых измерений

При выполнении прямых измерений физической величины А нужно оценивать следующие погрешности: DиА, DоА и DсА (случайную). Конечно, иные источники ошибок, связанные с неправильной установкой приборов, несовмещение начального положения стрелки прибора с 0 и пр. должны быть исключены.

Полная абсолютная погрешность прямого измерения должна включать в себя все три вида погрешностей.

Если случайная погрешность мала по сравнению с наименьшим значением, которое может быть измерено данным средством измерения (по сравнению с ценой деления), то ее можно пренебречь и тогда для определения значения физической величины достаточно одного измерения. В противном случае теория вероятностей рекомендует находить результат измерения как среднее арифметическое значение результатов всей серии многократных измерений, погрешность результата вычислять методом математической статистики. Знание этих методов выходит за пределы школьной программы.

8. Запись окончательного результата прямого измерения

Окончательный результат измерения физической величины А следует записывать в такой форме;

А=А_пр+ DА, e= (DА/А_пр)*100%.

А_пр— значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений. DА- полная абсолютная погрешность прямого измерения.

Абсолютную погрешность обычно выражают одной значащей цифрой.

Пример: L=(7,9 + 0,1) мм, e=13%.

9. Погрешности косвенных измерений

При обработке результатов косвенных измерений физической величины, связанной функционально с физическими величинами А, В и С, которые измеряются прямым способом, сначала определяют относительную погрешность косвенного измерения e= DХ/Х_пр, пользуясь формулами, приведенными в таблице (без доказательств).

Абсолютную погрешность определяется по формуле DХ=Х_пр*e,

где e выражается десятичной дробью, а не в процентах.

Окончательный результат записывается так же, как и в случае прямых измерений.

Вид функции	Формула
Х=А+В+С
Х=А-В
Х=А*В*С
Х=Аn
Х=А/В
Х=

Пример: Вычислим погрешность измерения коэффициента трения с помощью динамометра. Опыт заключается в том, что брусок равномерно тянут по горизонтальной поверхности и измеряют прикладываемую силу: она равна силе трения скольжения.

С помощью динамометра взвесим брусок с грузами: 1,8 Н. F_тр=0,6 Н

μ=0,33. Инструментальная погрешность динамометра (находим по таблице) составляет Δ _и =0,05Н, Погрешность отсчета (половина цены деления)

Δ _о =0,05Н. Абсолютная погрешность измерения веса и силы трения 0,1 Н.

Относительная погрешность измерения (в таблице 5-я строчка)

, следовательно, абсолютная погрешность косвенного измерения μ составляет 0,22*0,33=0,074

Ответ: