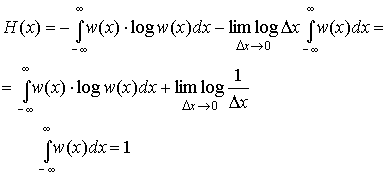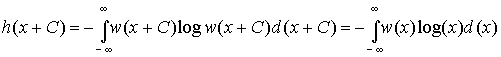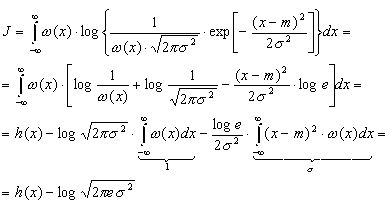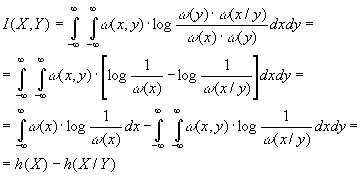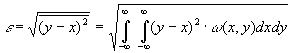This example shows how to compute and compare the statistics of the signal quantization error when using various rounding methods. Quantization occurs when a data type cannot represent a value exactly. In these cases, the value must be rounded to the nearest value that can be represented by the data type.
First, a random signal is created that spans the range of the quantizer object. Next, the signal is quantized, respectively, with rounding methods 'fix', 'floor', 'ceil', 'nearest', and 'convergent', and the statistics of the signal are estimated.
The theoretical probability density function of the quantization error is computed with the errpdf function, the theoretical mean of the quantization error is computed with the errmean function, and the theoretical variance of the quantization error is computed with the errvar function.
Create Uniformly Distributed Random Signal
Create a uniformly distributed random signal that spans the domain -1 to 1 of the fixed-point quantizer object q.
q = quantizer([8 7]); r = realmax(q); u = r*(2*rand(50000,1) - 1); xi = linspace(-2*eps(q),2*eps(q),256);
Fix: Round Towards Zero
With 'fix' rounding, the probability density function is twice as wide as the others. For this reason, the variance is four times that of the others.
q = quantizer('fix',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
The theoretical variance is eps(q)^2/3 and the theoretical mean is 0.
Floor: Round Towards Negative Infinity
'floor' rounding is often called truncation when used with integers and fixed-point numbers that are represented using two’s complement notation. It is the most common rounding mode of DSP processors because it requires no hardware to implement. 'floor' does not produce quantized values that are as close to the true values as 'round' will, but it has the same variance. Using 'floor', small signals that vary in sign will be detected, whereas in 'round' they will be lost.
q = quantizer('floor',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
The theoretical variance is eps(q)^2/12 and the theoretical mean is -eps(q)/2.
Ceil: Round Towards Positive Infinity
q = quantizer('ceil',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
The theoretical variance is eps(q)^2/12 and the theoretical mean is eps(q)/2.
Round: Round to Nearest; In a Tie Round to Largest Magnitude
'round' is more accurate than 'floor', but all values smaller than eps(q) get rounded to zero and are lost.
q = quantizer('nearest',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
The theoretical variance is eps(q)^2/12 and the theoretical mean is 0.
Convergent: Round to Nearest; In a Tie Round to Even
'convergent' rounding eliminates the bias introduced by ordinary 'round' caused by always rounding the tie in the same direction.
q = quantizer('convergent',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
The theoretical variance is eps(q)^2/12 and the theoretical mean is 0.
Compare Nearest and Convergent Rounding
The error probability density function for convergent rounding is difficult to distinguish from that of round-to-nearest by looking at the plot.
The error probability density function of convergent is
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
while the error probability density function of round is
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
The error probability density function of convergent is symmetric, while round is slightly biased towards the positive.
The only difference is the direction of rounding in a tie.
x = (-3.5:3.5)'; [x convergent(x) nearest(x)]
ans = 8×3
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
See Also
quantizer | quantize | Rounding
Будем
рассматривать квантование
с равномерным шагом x=const, т.е. равномерное
квантование.
Как было отмечено в §
3.1.1. в процессе квантования неизбежно
возникает ошибка квантования .
Последовательность ошибок квантования
(kt), возникающая при квантовании
процесса с дискретным временем, называется
шумом квантования. Обычно шум квантования
предполагают стационарным эргодическим
случайным процессом.
Чаще всего
интерес представляют максимальное
значение ошибки квантования, ее среднее
значение , равное математическому
ожиданию шума и среднеквадратическое
отклонение ,
равное квадратному корню из дисперсии
шума
(она характеризует мощность шума
квантования). Все эти величины зависят
от способа округления, применяемого
при квантовании, кроме того
и
зависят от закона распределения w()
мгновенных значений сигнала в пределах
шага квантования.
Считая шаг квантования
x малым по сравнению с диапазоном
изменения сигнала, плотность w(x) в
пределах этого шага можно принять
равномерной, т.е.
.
Различают
квантование с округлением, с усечением
и с усечением модуля.
При квантовании
с округлением истинному значению отсчета
приписывает ближайший разрешенный
уровень квантования независимо от того,
находится он сверху или снизу. Очевидно,
что при этом
|
max=0.5x; |
(3.31а) |
Квантование
с округлением требует определенной
сложности в реализации. Проще выполняется
квантование с усечением, при котором
истинному значению отсчета приписывается
ближайший нижний уровень. При
этом
|
max=x; |
т.е.
максимальное значение погрешности в 2
раза больше, а
,
что приводит к накоплению погрешности
квантования при дальнейшей обработке
квантованной последовательности.
Промежуточное
положение по точности и сложности
реализации занимает квантование с
усечением модуля, которое для положительных
отсчетов является таким же, как и
квантование с усечением. Отрицательным
отсчетам приписывается ближайший
верхний уровень. При этом
то
есть накопление погрешностей не
происходит, но в 2 раза увеличивается
максимальная погрешность, и в 2 раза —
мощность шума квантования
.
Выбирая достаточно большее число уровней
квантования N, шаг квантования.
,
а следовательно и все рассмотренные
погрешности можно сделать необходимо
малыми. При неравномерном законе
распределения мгновенных значений
сигнала квантования с постоянным шагом
не
является оптимальным по критерию
минимума среднеквадратической ошибки
.
Квантуя участки с менее вероятными
значениями сигнала с большим шагом
значение
можно
уменьшить, при этом же количестве уровней
квантования.
3.3. Информация в непрерывных сообщениях
Для
того, чтобы оценить потенциальные
возможности передачи сообщений
по непрерывным каналам, необходимо
вести количественные информационные
характеристики непрерывных сообщений
и каналов.
Обобщим с этой целью понятие энтропии
и взаимной
информации
на ансамбли непрерывных сигналов.
Пусть
Х — случайная величина (сечение или
отсчет случайного процесса), определенная
в некоторой непрерывной области и ее
распределение вероятностей характеризуется
плотностью w(х).
Разобьем область
значений Х на небольшие интервалы
протяженностью x. Вероятность Рк
того, что хк<x<xк+
x, приблизительно равна w(хк)
x т.е.
|
Рк=Р( |
(3.32) |
причем
приближение тем точнее, чем меньше
интервал x. Степень положительности
такого события.
Если
заменить истинные значения Х в пределах
интервала x значениями хк
в начале интервала, то непрерывный
ансамбль заменится дискретным и его
энтропия в соответствии с (1.4)
определится, как
или
с учетом (3.32)
|
|
(3.33) |
Будем
теперь увеличивать точность определения
значения х, уменьшения интервал x. В
пределе при x0 получим
энтропию непрерывной случайной величины.
|
|
(3.34) |
Второй
член в полученном выражении стремится
к
и
совершенно не зависит от распределения
вероятностей Х. Это означает, что
собственная информация любой непрерывной
случайной величины бесконечно велика.
Физический смысл такого результата
становиться понятным, если учесть, что
в конечном диапазоне непрерывная
величина может принимать бесконечное
множество значений, поэтому вероятность
того, что ее реализация будет точно
равна какому-то наперед заданному
конкретному значению является бесконечно
малой величиной 0. В результате энтропия,
определенная в соответствии с (1.4),
характеризующая среднюю степень
неожиданности появления возможных
реализаций для любой непрерывной
случайной величины не зависит от ее
закона распределения и всегда равна
бесконечности. Поэтому для описания
информационных свойств непрерывных
величин необходимо ввести другие
характеристики. Это можно сделать, если
обратить внимание на то, что первое
слагаемое выражении (3.34) является
конечным и однозначно определяется
плотностью распределения вероятности
w(x). Его называют дифференциальной
энтропией и обозначают h(x):
|
|
(3.35) |
Дифференциальная
энтропия обладает следующими свойствами.
1.
Дифференциальная энтропия в отличии
от обычной энтропии дискретного источника
не является мерой собственной информации,
содержащейся в ансамбле значений
случайной величины Х. Она зависит от
масштаба Х и может принимать отрицательные
значения. Информационный смысл имеет
не сама дифференциальная энтропия, а
разность двух дифференциальных энтропий,
чем и объясняется ее название.
2.
Дифференциальная энтропия не меняется
при изменении всех возможных значений
случайной величины Х на постоянную
величину. Действительно, масштаб Х при
этом не меняется и
справедливо равенство
|
|
(3.36) |
Из
этого следует, что h(x) не зависит от
математического ожидания случайной
величины, т.к. изменяя все значения Х на
С мы тем самым изменяем на С и ее среднее,
то есть математическое ожидание.
3.
Дифференциальная энтропия аддитивна,
то есть для объединения ХY независимых
случайный величин Х и Y справедливо:
h(XY)=
h(X)+ h(Y).
Доказательство этого свойства
аналогично доказательству (1.8) аддитивности
обычной энтропии.
4. Из всех
непрерывных величин Х с фиксированной
дисперсией 2
наибольшую дифференциальную энтропию
имеет
величина с гауссовским распределением,
т.е.
|
|
(3.37) |
Доказательство
свойства проведем в два этапа: сначала
вычислим h(x) для гауссовского распределения,
задаваемого плотностью.
где
м — математическое ожидание,
а затем
докажем неравенство (3.37).
Подставив
(3.38) в (3.35) найдем<
Для
доказательства неравенства (3.37) зададимся
произвольным распределением (х) с
дисперсией 2
и математическим ожиданием m и вычислим
интеграл J вида
|
|
Но
в силу неравенства (1.7)
с учетом правила изменения основания
логарифмов (log t = log e ln t)
имеем:
|
|
|
|
так |
Таким
образом
,
откуда
.
Но
как только что было показано,
—
это дифференциальная энтропия гауссовского
распределения. Доказанное неравенство
и означает, что энтропия
гауссовского распределения
максимальна.
Попытаемся теперь
определить с помощью предельного
перехода взаимную
информацию между двумя непрерывными
случайными величинами X и Y. Разбив
области определения Х и Y соответственно
на небольшие интервалы x и y, заменим
эти величины дискретными так же, как
это делалось при выводе формулы
(3.34).
Исходя из выражения
(1.14) можно определить взаимную информацию
между величинами Х и Y .
|
|
(3.39) |
При
этом предельном переходе никаких явных
бесконечностей не появилось, т.е. взаимная
информация оказывается величиной
конечной, имеющей тот же смысл, что и
для дискретных сообщений.
С
учетом того, что
|
(x,y)= (y) |
равенство
(3.39) можно представить в виде
|
|
(3.40) |
Здесь
h(X) — определенная выражением (3.35)
дифференциальная энтропия Х, а
|
|
(3.41) |
h(X/Y)
— условная дифференциальная энтропия.
Можно показать, что во всех случаях
h(X/Y)h(X).
Формула
(3.40) имеет ту же форму, что и (1.13), а
отличается лишь заменой энтропии
дифференциальной энтропией. Легко
убедиться, что основные свойства 1 и 2
(см. пункт 1.3) взаимной информации,
описываемые равенствами (1.15)(1.17),
остаются справедливыми и в этом случае.
3.4 -энтропия
и -производительность
источника непрерывных сообщений
Как
было показано в § 3.3, в одном отсчете
любого непрерывного сообщения содержится
бесконечное количество собственной
информации. И тем не менее, непрерывные
сообщения (телефонные разговоры,
телепередачи) успешно передаются по
каналам связи. Это объясняется тем, что
на практике никогда не требуется
абсолютно точного воспроизведения
переданного сообщения, а для передачи
даже с очень высокой, но ограниченной
точностью, требуется конечное количество
информации, также как и при передаче
дискретных сообщений. Данное обстоятельство
и положено в основу определения
количественной меры собственной
информации, источников непрерывных
сообщений. В качестве такой меры,
принимается минимальное количество
информации, необходимое для воспроизведения
непрерывного сообщения с заданной
точностью. Очевидно, что при таком
подходе собственная информация зависит
не только от свойств источника сообщений,
но и от выбора параметра , характеризующего
точность воспроизведения. Возможны
различные подходы к определению в
зависимости от вида и назначения
передаваемой информации. Наиболее часто
в информационной технике в качестве
используют среднеквадратическое
отклонение между принятым у и переданным
х сигналами, отражающими непрерывные
сообщения, т.е.
|
|
(3.42) |
где
Х и Y – ансамбли сигналов, отражающих
исходное и воспроизведенное сообщения.
Два
варианта сообщения или сигнала,
различающиеся не более, чем на заданное
значение 0,
называются эквивалентными. Взаимная
информация
I(X,Y) между двумя эквивалентными процессами
X(t) и Y(t) может быть определена в соответствии
с (3.40) как
|
I(X,Y)=h(X)-h(X/Y), |
где
h(X) и h(X/Y) – соответственно дифференциальная
и условная дифференциальная энтропии.
Из приведенного выражения видно,
что величина I(X,Y) зависит не только от
собственного распределения (х) ансамбля
Х (см. (3.35)), но и от условного распределения
(x/y) (см. (3.41)), которое определяется
способом преобразования процесса X в
Y. Для характеристики собственной
информации, содержащейся в одном отсчете
процесса Х, нужно устранить ее зависимость
от способа преобразования сообщения Х
в эквивалентное ему сообщение Y. Этого
можно добиться, если под количеством
собственной информации или — энтропией
H(Х)
процесса Х понимать минимизированную
по всем распределениям (X/Y) величину
I(X,Y), при которой сообщения Х
и Y еще эквивалентны, т.е.
|
|
(3.43) |
Таким
образом,
— энтропия
определяет минимальное количество
информации, содержащейся в одном отсчете
непрерывного
сообщения,
необходимое для воспроизведения его с
заданной верностью.
Если ансамбль
сообщений Х представляет собой процесс
с дискретным
временем
с непрерывными отсчетами, то под
— производительностью источника понимают
величину
|
|
(3.44) |
где
с
– количество отсчетов сообщения,
выдаваемых в единицу времени.
В том
случае, когда Х — непрерывный случайный
процесс с ограниченным спектром, вся
информация, содержащаяся в его значениях,
эквивалентна информации, содержащейся
в отсчетах процесса, следующих друг за
другом с интервалом
,
(fm-граничная
частота спектра), т.е. со
скоростью
|
c=2 |
(3.45) |
При
этом
— производительность
источника или процесса по-прежнему
определяется выражением (3.44), где величина
с
рассчитывается из условия (3.45).
В том
случае, если следующие друг за другом
отсчеты процесса коррелированны
(взаимозависимы), величина Н(Х)
в (3.43) должна вычисляться с учетом
вероятностных связей между отсчетами.
Итак,
— производительность источника
непрерывных сообщений представляет
собой минимальное количество информации,
которое нужно создать источнику в
единицу времени, для воспроизведения
его сообщений с заданной верностью.
— производительность называют также
скоростью создания информации при
заданном критерии верности.
Максимально
возможная — производительность
непрерывного
источника Х обеспечивается при гауссовском
распределении Х с дисперсией
(при
этом условии h(X) максимальна (см. (3.37)).
Оценим значение
.
Рассмотрим случай, когда непрерывное
сообщение X(t) представляет собой
стационарный гауссовский процесс с
равномерным энергетическим спектром,
ограниченным частотой Fc,
и с заданной мощностью (дисперсией) Рх,
а критерий эквивалентности задан в
виде (3.42).
Будем считать, что заданная верность
воспроизведения обусловлена действием
аддитивной статистически не связанной
с сигналом помехи (t) с математическим
ожиданием М[]=0 и дисперсией (мощностью)
.
Исходный сигнал Х рассматриваем
как сумму воспроизводящего сигнала Y и
помехи:
|
X=Y+. |
При
этом, поскольку (x/y)= (y+/y)= (/y)=
(), то h(X/Y) полностью определяется
шумом воспроизведения (t). Поэтому max
h(X/Y)=max h(). Так как шум воспроизведения
имеет фиксированную дисперсию
,
то дифференциальная энтропия имеет
максимум (3.37) при гауссовском
распределении шума
|
|
В
свою очередь дифференциальная энтропия
гауссовского источника с дисперсией
.
|
|
Следовательно,
— энтропия на один отсчет
сообщения
|
|
(3.46) |
Величина
характеризует
минимальное отношение сигнал-шум, при
котором сообщения X(t) и Y(t) еще
эквивалентны.
Согласно теореме
Котельникова
шаг
дискретизации
,
а c=2
Fc.
При этом равномерность спектра сообщения
обеспечивает некоррелированность
отстоящих на t друг от друга отсчетов,
а гауссовский характер распределения
X(t) — их независимость. Следовательно,
в соответствии с (3.44)
|
|
или с учетом (3.46)
|
|
(3.47) |
Количество
информации,
выданное таким источником за время Тс
|
|
(3.48) |
Интересно
отметить, что правая часть выражения
(3.48) совпадает с наиболее общей
характеристикой сигнала, называемой
его объемом, если принять динамический
диапазон сигнала D=log
0.
Это означает, что объем сигнала равен
максимальному количеству информации,
которое может содержаться в сигнале
длительностью Тс.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычислите ошибку квантования
В этом примере показано, как вычислить и сравнить статистику ошибки квантования сигнала при использовании различных методов округления.
Во-первых, случайный сигнал создается, который порождает линейную оболочку столбцов квантизатора.
Затем сигнал квантуется, соответственно, с округлением методов ‘фиксируют’, ‘ставят в тупик’, ‘перекрывают’, ‘самый близкий’, и ‘конвергентный’, и статистические данные сигнала оцениваются.
Теоретическая функция плотности вероятности ошибки квантования будет вычислена с ERRPDF, теоретическое среднее значение ошибки квантования будет вычислено с ERRMEAN, и теоретическое отклонение ошибки квантования будет вычислено с ERRVAR.
Равномерно распределенный случайный сигнал
Сначала мы создаем равномерно распределенный случайный сигнал, который охватывает область-1 к 1 из квантизаторов фиксированной точки, на которые мы посмотрим.
q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1); % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);
Фиксация: вокруг по направлению к нулю.
Заметьте, что с округлением ‘фиксации’, функция плотности вероятности вдвое более широка, чем другие. Поэтому отклонение в четыре раза больше чем это других.
q = quantizer('fix',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 3 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
Пол: вокруг к минус бесконечность.
Пол, округляющийся, часто называется усечением, когда используется с целыми числами и числами фиксированной точки, которые представлены в дополнении two. Это — наиболее распространенный режим округления процессоров DSP, потому что это требует, чтобы никакое оборудование не реализовало. Пол не производит квантованные значения, которые являются как близко к истинным значениям, когда ROUND будет, но это имеет то же отклонение, и маленькие сигналы, которые варьируются по знаку, будут обнаружены, тогда как в ROUND они будут потеряны.
q = quantizer('floor',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = -eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
Потолок: вокруг к плюс бесконечность.
q = quantizer('ceil',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
Вокруг: вокруг к самому близкому. Вничью, вокруг к самой большой величине.
Вокруг более точно, чем пол, но все значения, меньшие, чем eps (q), округлены, чтобы обнулить и потеряны — также.
q = quantizer('nearest',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Конвергентный: вокруг к самому близкому. Вничью, вокруг к даже.
Конвергентное округление устраняет смещение, введенное обычным «раундом», вызванным, всегда округляя связь в том же направлении.
q = quantizer('convergent',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Сравнение самых близких по сравнению с конвергентным
Функция плотности вероятности появления ошибки для конвергентного округления затрудняет, чтобы различать от того из раунда-к-самому-близкому путем рассмотрения графика.
Ошибка p.d.f. из конвергентных
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
в то время как ошибка p.d.f. из раунда
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
Обратите внимание на то, что ошибка p.d.f. из конвергентных симметрично, в то время как вокруг немного склоняется к положительному.
Единственной разницей является направление округления вничью.
x=(-3.5:3.5)'; [x convergent(x) nearest(x)]
ans =
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
Постройте функцию помощника
Функция помощника, которая использовалась, чтобы сгенерировать графики в этом примере, описана ниже.
type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m')) %#ok<*NOPTS>
function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT Plot function for QERRORDEMO.
% QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
% used by the example function QERRORDEMO, where Q is the quantizer
% whose attributes are being analyzed; F_T is the theoretical
% quantization error probability density function for quantizer Q
% computed by ERRPDF; XI is the domain of values being evaluated by
% ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
% computed by ERRMEAN; V_T is the theoretical quantization error
% variance of quantizer Q computed by ERRVAR; and ERR is the error
% generated by quantizing a random signal by quantizer Q.
%
% See QERRORDEMO for examples of use.
% Copyright 1999-2014 The MathWorks, Inc.
v=10*log10(var(err));
disp(['Estimated error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')
Ошибка квантования E = em — ea — это разность между реальной продолжительностью события ea и его измеренной продолжительностью em. У вас нет возможности узнать реальную продолжительность события, следовательно, нельзя и обнаружить ошибку квантования, основываясь на отдельном значении. Однако можно доказать наличие ошибки квантования, исследуя группы родственных статистик. Мы уже рассматривали пример, в котором удалось выявить ошибку квантования. В примере 7.5 наличие ошибки квантования удалось определить, заметив, что:
Ошибку квантования легко выявить, исследуя вызов базы данных и выполняемые им события ожидания в системе с низкой загрузкой, где минимизировано влияние других факторов, способных нарушить отношение e и c + Eela.
Рассмотрим фрагмент файла трассировки Oracle8i, который демонстрирует эффект ошибки квантования:
Данный вызов выборки инициировал ровно три события ожидания. Мы знаем, что приведенные значения c, e и ela должны быть связаны таким приблизительным равенством:
В системе с низкой загрузкой величина, на которую отличаются левая и правая части приблизительного равенства, указывает на общую ошибку квантования, присутствующую в пяти измерениях (одно значение c, одно значение e и три значения ela):
С учетом того, что отдельному вызову gettimeofday в большинстве систем соответствует лишь несколько микросекунд ошибки, вызванной влиянием измерителя, получается, что ошибка квантования вносит значительный вклад в «разность» длиной в одну сантисекунду в данных трассировки.
Следующий фрагмент файла трассировки Oracle8i демонстрирует простейший вариант избыточного учета продолжительности, в результате которого возникает отрицательная величина неучтенного времени:
WAIT #96: nam=’db file sequential read’ ela= 0 p1=1 p2=1691 p3=1
FETCH #96:c=1,e=0,p=1,cr=4,cu=0,mis=0,r=1,dep=1,og=4,tim=116694789 В данном случае E = -1 сантисекунда:
При наличии «отрицательной разности» (подобного только что рассмотренному) невозможно все объяснить эффектом влияния измерителя, ведь этот эффект может быть причиной появления только положительных значений неучтенного времени. Можно было бы подумать, что имел место двойной учет использования процессора, но и это не соответствует действительности, т. к. нулевое значение ela свидетельствует о том, что время занятости процессора вообще не учитывалось для события ожидания. В данном случае ошибка квантования имеет преобладающее влияние и приводит к излишнему учету времени для выборки.
В данном случае E = 640 мкс:
В Oracle9i разрешение временной статистики улучшено, но и эта версия отнюдь не защищена от воздействия ошибки квантования, что видно в предложенном ниже фрагменте файла трассировки для E > 0:
Некоторая часть этой ошибки, несомненно, является ошибкой квантования (невозможно, чтобы общее время использования процессора данной выборкой действительно равнялось нулю). Несколько микросекунд следует отнести на счет эффекта влияния измерителя.
Наконец, рассмотрим пример ошибки квантования E < 0 в данных трассировки Oracle9i:
Возможно, в данном случае имел место двойной учет использования процессора. Также вероятно, что именно ошибка квантования внесла основной вклад в полученное время вызова выборки. Избыточный учет 8784 микросекунд говорит о том, что фактический общий расход процессорного времени вызовом базы данных составил, вероятно, всего около (10000 — 8784) мкс = 1,216 мкс.
Диапазон значений ошибки квантования
Величину ошибки квантования, содержащейся во временных статистиках Oracle, нельзя измерить напрямую. Зато можно проанализировать статистические свойства ошибки квантования в данных расширенной трассировки SQL. Во-первых, величина ошибки квантования для конкретного набора данных трассировки ограничена сверху. Легко представить ситуацию, в которой ошибка квантования, вносимая такими характеристиками продолжительности, как e и ela, будет максимальной. Наибольшего значения данная ошибка достигает в том случае, когда в последовательности значений e и ela все отдельные ошибки квантования имеют максимальную величину и их знаки совпадают.
На рис. 7.9 показан пример возникновения описанной ситуации: имеется восемь очень непродолжительных системных вызовов, причем все они попадают на такты интервального таймера. Фактическая длительность каждого события близка к нулю, но измеренная длительность каждого такого события равна одному такту системного таймера. В итоге суммарная фактическая продолжительность всех вызовов близка к нулю, а общая измеренная продолжительность равна 8 тактам. Для такого набора из n = 8 системных вызовов ошибка квантования по существу равна nrx, где rx — это разрешение интервального таймера, с помощью которого измеряется характеристика x.
Думаю, вы обратили внимание, что изображенный на рис. 7.9 случай выглядит надуманно и изобретен исключительно для прояснения вопроса. В реальной жизни подобная ситуация чрезвычайно маловероятна. Вероятность, что n ошибок квантования будут иметь одинаковые знаки, равна всего 0,5n. Вероятность того, что n=8 последовательных
Рис. 7.9. Наихудший вариант накопления ошибки квантования для последовательности измеренных продолжительностей
ошибок квантования будут отрицательными, равна всего 0,00390625 (т. е. приблизительно четыре шанса из тысячи). Для 266 значений шанс совпадения знаков у всех ошибок квантования меньше, чем один из 1080.
Для больших наборов значений длительностей совпадение знаков всех ошибок квантования практически невозможно. Но это не единственное, в чем состоит надуманность ситуации, изображенной на рис. 7.9. Она также предполагает, что абсолютная величина каждой ошибки квантования максимальна. Шансы наступления такого события еще более иллюзорны, чем у совпадения всех знаков ошибок. Например, вероятность того, что величина каждой из n имеющихся ошибок квантования превышает 0,9, равна (1 — 0,9)n. Вероятность того, что величина каждой из n = 266 ошибок квантования превысит 0,9, составляет всего 1 из 10266.
Вероятность того, что все n ошибок квантования имеют одинаковый знак и абсолютная величина всех из них больше m, чрезвычайно мала и равна произведению рассмотренных ранее вероятностей:
P (значения всех n ошибок квантования больше m или меньше -m)=
= (0.5)n(1- m)n
Ошибки квантования для продолжительностей (например, значений e и ela в Oracle) — это случайные числа в диапазоне:
-rx < E < rx где rx — это разрешение интервального таймера, с помощью которого измеряется характеристика x (x- это e или ela).
Так как положительные и отрицательные ошибки квантования возникают c равной вероятностью, средняя ошибка квантования для выбранного набора статистик стремится к нулю даже для больших файлов трассировки. Опираясь на теорему Лапласа (Pierre Simon de Laplace, 1810), можно предсказать вероятность того, что ошибки квантования для статистик e и ela будут превышать указанное пороговое значение для файла трассировки, содержащего определенное количество статистик.
Я начал работать над вычислением вероятности того, что общая ошибка квантования файла трассировки (включая ошибку, вносимую статистикой c) будет превышать заданную величину, однако мое исследование еще не завершено. Мне предстоит получить распределение ошибки квантования для статистики c, что, как я уже говорил, осложняется особенностями получения этой статистики в процессе опроса. Результаты этих изысканий планируется воплотить в одном из будущих проектов.
К счастью, относительно ошибки квантования есть и оптимистические соображения, которые позволяют не слишком расстраиваться по поводу невозможности определения ее величины:
• Во многих сотнях файлов трассировки Oracle, проанализированных нами в hotsos.com, общая продолжительность неучтенного вре-
Что означает «один шанс из десяти в [очень большой] степени»?
Для того чтобы представить себе, что такое «один шанс из 1080», задумайтесь над следующим фактом: ученые утверждают, что в наблюдаемой вселенной содержится всего около 1080 атомов (по данным http:// www.sunspot.noao.edu/sunspot/pr/answerbook/universe.html#q70, http:/ /www.nature.com/nsu/020527/020527-16.html и др.). Это означает, что если бы вам удалось написать на каждом атоме нашей вселенной 266 равномерно распределенных случайных чисел от -1 до +1, то лишь на одном из этих атомов можно было бы ожидать наличия всех 266 чисел с одинаковым знаком.
Представить вторую упомянутую вероятность — «один шанс из 10266»-еще труднее. На этот раз представим себе три уровня вложенных вселенных. То есть что каждый из 1080 атомов нашей вселенной сам по себе является вселенной, состоящей из 1080 вселенных, каждая из которых в свою очередь содержит 1080 атомов. Теперь у нас достаточно атомов для того, чтобы представить себе возможность возникновения ситуации с вероятностью «один из 10240». Даже во вселенных третьего уровня вложенности вероятность появления атома, для которого все 266 его случайных чисел по абсолютной величине больше 0,9, составит один из 100 000 000 000 000 000 000 000 000.
мени в случае корректного сбора данных (см. главу 6) чрезвычайно редко превышала 10% общего времени отклика.
Несмотря на то, что и ошибка квантования, и двойной учет использования процессора могут привести к такому результату, файл трассировки чрезвычайно редко содержит отрицательное неучтенное время, абсолютная величина которого превышала бы 10% общего времени отклика.
В случаях, когда неучтенное время оценивается более чем в 25% времени отклика для корректно собранных данных трассировки, такой объем неучтенного времени почти всегда объясняется одним из двух явлений, описанных в последующих разделах.
Наличие ошибки квантования не лишает нас возможности правильно диагностировать основные причины проблем производительности при помощи файлов расширенной трассировки SQL в Oracle (даже в файлах трассировки Oracle8i, в которых вся статистика приводится с точностью лишь до сотых долей секунды).
Ошибка квантования становится еще менее значимой в Oracle9i благодаря повышению точности измерений.
В некоторых случаях влияние ошибки квантования способно привести к утрате доверия к достоверности данных трассировки Oracle. Наверное, ничто не может так подорвать боевой дух, как подозрение в недостоверности данных, на которые вы полагаетесь. Думаю, что лучшим средством, призванным укрепить веру в получаемые данные, должно служить четкое понимание влияния ошибки квантования.
| Следующая > |
|---|