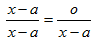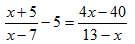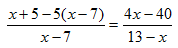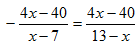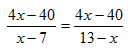Как найти ошибку в примере

Введение

Тема сегодняшнего урока посвящена тому, как найти вычислительную ошибку. Вы когда-нибудь ошибались в вычислениях? Не ошибается только тот, который ничего не делает. С другой стороны, из этого можно сделать один очень важный вывод: уметь искать свои ошибки не менее важно, чем решать задачу. Задача, решенная с ошибкой, и задача, не решенная вовсе, чаще всего будут значить одинаково, то есть ничего. Поэтому сегодня мы попробуем научиться отыскивать ошибки в своих вычислениях и исправлять.

Сразу возникает следующая проблема. Хорошо, когда вы уверены, что в вашем примере есть ошибка, и рано или поздно вы ее найдете. А вот как самому во время контрольной работы или экзамена догадаться, что в примере есть ошибка? Ведь можно час искать ошибку в примере, а потом выяснится, что ее нет. Сегодня мы познакомимся с некоторыми довольно простыми соображениями, которые позволяют проверять, есть ли в примере ошибка.

Метод последней цифры

Одно из таких соображений называется последняя цифра (или анализ последней цифры). Рассмотрим несколько примеров, иллюстрирующих данный подход.

Например:

1) 346757 + 23546 = 369575

Даже не считая в столбик можно сразу увидеть, что в этом примере есть ошибка, потому что если проверить по последним цифрам 7 + 6 = 13, то есть число должно оканчиваться на 3, а оканчивается на 5 – значит, где-то есть ошибка. Нужно вернуться к своим вычислениям и эту ошибку найти.

346757 + 23546  369575

2) 2465313 = 6546371

Можно сразу сказать, что в вычислении допущена ошибка. Почему? Потому что если перемножить последние цифры 5 и 3, то получается 15, число должно оканчиваться на 5, а у нас оканчивается на 1.

2465 313  6546371

3). 347 + 234  235 = 47806

Опять без подсчетов в столбик можно сказать, что здесь допущена ошибка. Как видите, этот пример содержит два действия. Попробуем сделать все действия с последними цифрами. Как вы помните, порядок действия у нас таков: сначала делаем умножение, потом сложение. Мы умножаем 4 на 5 – и получается 20, на конце числа должен стоять 0, к 0 прибавляем 7, должно получиться 7, а у нас на конце числа 6, значит, в примере допущена ошибка. Где именно, мы не знаем, может, была допущена ошибка в умножении или в сложении, но то, что ошибка есть, мы уже поняли.

347 + 234  235  47806

4) (345 4567 – 9873)  237 – 366 = 12948371

Первым действием мы 5 умножаем на 7 и получаем 35, на конце 5. Вторым действием вычитаем: 5 минус число, оканчивающееся на 3, и получаем 2 на конце. Умножаем это на 237, дважды семь – получаем 14, после третьего действия получаем на конце 4. Наконец, вычитаем из 14 число 6, получаем 8, которое должно стоять на конце. Значит, ответ 12948371 неправильный.

(345  4567 – 9873)  237 – 366  12948371

Нужно быть очень аккуратными, если в вашем выражении присутствует знак деления.

1) 28 : 4 = 7

Если разделить это выражение просто, то получится 7. С другой стороны, если мы попробуем проверить это равенство по методу последней цифры, 8 разделить на 4 равно 2, что не подходит к уравнению. Метод последней цифры к делению не применяется. Если по последней цифре все совпало, это еще ничего не значит. Это значит, что мы не нашли противоречия в данном случае, но ошибка все же может быть.

Например:

2) 2 2 = 14

Понятно, что это уравнение изначально неправильное, но, если проверить по последней цифре, два умножить на два будет 4, и у нас в конце уравнения стоит 4. Поэтому, если по последней цифре не сошлось, значит, в уравнении есть ошибка. Если же сошлось, это ничего не значит, может, ошибка есть, а может, и нет.

2 2  14

Итак, давайте подведем краткий итог первого метода. Если у вас решен пример на вычисление, который не содержит деления, а содержит только натуральные числа, то вы можете проверить себя, проделав все вычисления устно только с последними цифрами. Если результат сошелся, значит, с большой вероятностью, ошибки нет. Если же результат не сошелся, то ищем ошибку.

Метод округления

Давайте рассмотрим следующий пример: 143 147 = 221.

По проверке последней цифры, 3 умножить на 7, получаем 21, в конце числа 1, все в порядке, казалось бы, ошибки нет. С другой стороны, давайте сделаем простой предварительный подсчет. Если 100 умножить на 100, уже получится 10000, но у нас числа больше, чем 100, и мы получили в произведении только 221. Конечно, где-то закралась ошибка.

100  100 = 10000

143  147  221

Такая очень грубая прикидка, такое округление, позволяет нам понять, что пример решен неверно.

2) 2342 + 23426 = 234648

Опять же мы можем прикинуть по последней цифре и выяснить, что 2 плюс 6 – это 8, казалось бы, ошибки нет. С другой стороны, сделаем грубую прикидку: каждое число округлим до тысяч: 2 тысячи плюс 23 тысячи получается 25 тысяч, а в уравнении 234 тысячи. Значит, в примере где-то есть ошибка.

2000 + 23000 = 25000

3) 73462 – 2346 = 5362

Этот пример показателен тем, что вы можете найти ошибку, пользуясь и первым методом, и вторым. Действительно, если вычесть из 12 число 6, получаем 6, а в ответе последняя цифра 2. Уже неправильно. С другой стороны, давайте опять округлим до тысяч: 73 тысячи минус 2 тысячи получается 71 тысяча, а у нас примере 5 тысяч.

73000 – 2000 = 71000

4) 27  27 = 729

С последней цифрой все в порядке, семью семь – сорок девять, оканчивается на 9. Давайте сделаем округление: 30  30 = 900.

То есть ответ вроде правильный. Метод округления ошибку не выявляет. И этот пример действительно решен верно.

5) 342 + 253  175 = 306777

Обратите внимание, что с последней цифрой все в порядке: 3 умножить на 5 будет 15, то есть оканчивается на 5 плюс еще 2 – и будет 7. Но давайте снова округлим до сотен.

300 + 300  200 = 60300

Сами видите, что в левой части 60300, а в правой – 306 тысяч, равенство неверное. Значит, где-то допущена ошибка, при этом мы не знаем, где именно.

Таким образом, если мы хотим сделать проверку нашего примера с помощью прикидки или округления, мы должны сделать следующее: берем каждое число нашего примера и округляем его, то есть приравниваем его к ближайшему круглому числу. Проводим все вычисления с округленными числами и сравниваем тот ответ, который мы получаем с тем, который получился у нас в исходном примере. Естественно, ответы не должны полностью совпасть. Если они получились неравными, не паникуйте. Но они должны получиться близкими друг к другу. Если в примере ответ получился 102, а после округления ответ получился 1000000, значит, вы где-то ошиблись. Если же ответ у вас получился 102, а после округления 100, скорее всего, все правильно. Посмотрим еще на один пример: 33 ⋅ 33 = 1089.

Давайте округлим: 30  30 = 900. О чем же говорит такой ответ? Формально, как вы видите, у нас в ответе 4 цифры, а при округлении получилось 3 цифры. То есть вроде бы мы ошиблись на целый порядок, наверное, ошибка есть. Но, если вы присмотритесь к этим числам, вы увидите, что эти числа близки: 900 и 1000. Если вы видите, что разница в количестве цифр есть, но реально она не велика, возможно, никакого противоречия нет. В данном случае пример верный.

Еще один маленький совет. Если задача имеет какой-то практический смысл, старайтесь проверять, подходит ответ под этот смысл или нет. Например, если в задаче требуется найти скорость велосипедиста, а у вас после вычисления получилось 500 км/ч, скорее всего, вы ошиблись. Или предположим, вам нужно посчитать, сколько молока в литрах привезли на завод в сумме двух цистернах, а у вас получилось 3 литра. Наверное, это все-таки маловато для двух цистерн, так что тоже, скорее всего, у вас ошибка.

Итоги

Давайте подведем краткие итоги сегодняшнего урока. Сегодня мы познакомились с некоторыми методами, которые позволяют проверить, правильным ли получился ваш ответ. Эти методы не дают стопроцентной гарантии того, что вы отыщете ошибку. Даже если с помощью каждого из методов все получается в порядке, возможно, в примере есть ошибка. С другой стороны, проверка каждого из этих методов занимает не очень много времени, и поэтому, если даже в трех случаях из десяти какой-то из этих методов даст вам возможность найти ошибку, это уже будет хорошо.

Список рекомендованной литературы

1. Гельфман Э. Г., Холодная О. В. Математика: учебник для 5 класса. – М.: БИНОМ. Лаборатория знаний. – 2012.
2. Шварцбурд С. И. Внеклассная работа по математике в 4-5 классах. – М.: Просвещение. – 2012.
3. Виленкин Н. Я., Жохов В. И. Математика. 5 класс, 31-е изд., стер. – М.: 2013.

Рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «lifehacker.ru» (Источник)
2. Интернет-портал «kp.ru» (Источник)
3. Интернет-портал «5klass.net» (Источник)

Домашнее задание

1. Каким методом вы обычно пользуетесь, что найти вычислительную ошибку в примере?
2. В чем заключается метод последней цифры? Приведите пример.
3. В чем заключается метод округления (прикидки)? Приведите пример.

Математические софизмы и задания «Найди ошибку»

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

«Правильно понятая ошибка – это путь к открытию»

И. П. Павлов

ВВЕДЕНИЕ

Бесконечно разнообразны ошибки, которые совершались и совершаются в различных математических рассуждениях. Рассмотреть такие ошибки полезно по двум причинам: во-первых, хорошо ознакомившись с какой-нибудь такой ошибкой, мы защитим себя от повторения такой ошибки в будущем; во- вторых, сам процесс разыскания ошибки легко сделать весьма увлекательным, и изучение ошибок становится средством поднять интерес к изучению математики.

Рассуждение, в котором допущена та или иная ошибка, в большинстве случаев легко довести до получения явно неверного вывода. Получается видимость доказательства какой-нибудь нелепости, или так называемый софизм.

Разбор и решение любого рода математических задач, а в особенности нестандартных, помогает развивать смекалку и логику.

Цель исследования софизмов заключается в приобщении к критическому мышлению, умению не только воспроизводить определенные логические мыслительные процессы, но и критически осмысливать каждый этап рассуждений в соответствии с усвоенными принципами математического мышления.

Наверняка, каждый человек слышал хоть раз в жизни подобную фразу:

«Дважды два равно пяти» или «Два равно трем». На самом деле таких примеров очень много. Что они обозначают? Имеют ли какое-то логическое объяснение или это вымысел?

Именно это я хочу рассмотреть в этой работе, название которой «Математические софизмы и задания «Найди ошибку». Целью моей работы является исследование разнообразных математических софизмов для формирования критического мышления, приобретения необходимых в жизни навыков правильного мышления и разбор собственных заданий «Найди ошибку» по различным темам курса алгебры и геометрии. 1

СОФИЗМЫ

Софизм (в переводе с греческого sophisma — уловка, выдумка, головоломка), формально кажущийся правильным, но по существу ложное умозаключение, основанное на преднамеренном неправильном подборе исходных положений. Каков бы не был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах выполняются «запрещенные» действия или не учитываются условия применимости теорем, форму и правил. Иногда рассуждения ведутся с использованием ошибочного чертежа или опираются на приводящие к ошибочным заключениям «очевидности». Встречаются софизмы, содержащие и другие ошибки.

ИСТОРИЯ СОФИЗМОВ

В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости математических рассуждений и содействовали более глубокому уяснению понятий методов математики. Роль софизмов в развитии математики сходно с той ролью, какую играют непреднамеренные ошибки математических исследований, допускаемые выдающимися математиками. Именно уяснение ошибок математических рассуждение часто содействовало развитию математики. Пожалуй, особенно поучительна в этом отношении история аксиомы Евклида о параллельных прямых. Сформировать эту аксиому можно так: через данную точку лежащую вне данной прямой, можно провести не более одной прямой, параллельной данной. Это утверждение на протяжении более двух тысяч лет пытались доказать, но все попытки не увенчались успехом. Полученные «доказательства» оказались ошибочными. И все же, несмотря на ошибочность этих «доказательств», они принесли большую пользу развитию геометрии. Они подготовили одно из величайших достижений в области геометрии и всей математики – создание неевклидовой геометрии. Честь разработки новой геометрии принадлежит Н.И. Лобачевскому и венгерскому математику Яношу Бойяи.

Понятие софизмов включает в себя несколько видов софизмов: арифметические, алгебраические и геометрические.

АРИФМЕТИЧЕСКИЕ СОФИЗМЫ

Арифметические софизмы — это числовые выражения, имеющие неточность или ошибку, незаметную с первого взгляда. Рассмотрим такие примеры.

Пример 1

« 5 = 6 »

Решение:

Попытаемся доказать, что 5 = 6. С этой целью возьмем числовое тождество:

35 + 10 – 45 = 42 + 12 – 54.

Вынесем общие множители левой и правой частей за скобки. Получим:

5 (7 + 2 – 9) = 6 (7 + 2 – 9).

Разделим обе части этого равенства на общий множитель

Получаем 5 = 6.

Где ошибка?

Ответ: общий множитель (7 + 2 – 9) = 0, а делить на 0 нельзя.

Пример 2

« 2 * 2 = 5 »

Решение:

Имеем числовое равенство (верное): 4 : 4 = 5 : 5.

Вынесем за скобки в каждой части его общий множитель. Получим:

4 (1 : 1) = 5 (1 : 1).

Числа в скобках равны, поэтому

4 = 5 или 2 * 2 = 5.

Где ошибка?

Ответ: допущена ошибка в вынесении общего множителя за скобки в левой и правой частях тождества 4 : 4 = 5 : 5. Общий множитель нельзя вынести.

АЛГЕБРАИЧЕСКИЕ СОФИЗМЫ

Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией, к числу старейших ветвей этой науки. Задачи, а также методы, отличающие ее от других отраслей математики, создавались постепенно, начиная с древности. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приемов для решения однотипных арифметических задач. Приемы эти заключаются обычно в составлении и решении уравнений, т.е. алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.

Пример 1

«Любое число равно его половине»

Возьмем два равных числа а и b, а =b обе части этого равенства умножим на а и затем вычтем из произведений по b² . Получим: а² – b² = ab — b² или (а + b)(a — b)=b(a — b).

Отсюда а + b = b, или а + а = а, так как b = a.

Значит, 2а = а, .

Где ошибка?

Ответ: нельзя делить на (а – b), так как ( a – b) = 0.

Пример 2

«Любое число равно нулю»

Возьмем произвольное положительное число а и рассмотрим сумму х и бесконечного числа слагаемых, равных а:

х = а + а + а + а + … . (1)

Очевидно, что мы можем представить эту сумму как

х = а + (а + а + а +…), (2)

в которой сумма, стоящая в скобках, так же ровна х, как сумма бесконечного числа слагаемых, равных а. Так что можем записать, что х = а + х, откуда заключаем, что а=0

Где ошибка?

Ответ: ошибка допущена в равенстве (1), в котором бесконечная сумма чисел а обозначена конечным числом х.

Пример 3

«Всякое число равно своему удвоенному значению»

Запишем очевидное для любого числа а тождество:

а² – а² = а² – а².

Вынесем множитель а в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получим:

а (а — а) = ( а + а) ( а – а ). (1)

Разделив обе части на ( а – а ), получим:

а = а + а , а = 2а.

Где ошибка?

Ответ: используется распространенная ошибка, а именно деление на 0 в неравенстве (1) (а—а=0).

Пример 4

«Все числа равны между собой»

Возьмем любые два числа х , у.

Рассмотрим тождество:

х² — 2ху + у² = у² — 2ху + х². Имеем: ( х – у )² = ( у – х )².

отсюда: х – у = у – х или 2х = 2у, а значит, х = у.

Где ошибка?

Ответ: ошибка заключается в том, что из равенства ( х – у )² = (у – х )² следует, что х = у, а это равенство справедливо для любых чисел х, у.

Пример 5

Если «а» больше «b», в тогда «а» всегда больше, чем «2b».

Возьмем два произвольных положительных числа а и b, такие, что а > b. Умножив это неравенство на b, получим новое неравенство аb > bb, а отняв от обеих его частей аа, получим неравенства аb – аа > bb – аа, которое равносильно следующему: а ( b – a ) > ( b + a ) ( b — a ). (1)

После деления обеих частей неравенства (1) на (b – а), получим а > b + a (2).

А прибавив к этому неравенству почленно исходное неравенство а > b, имеем 2а > 2b + a, откуда а > 2b. Итак, если а > b, то а > 2b.

Где ошибка?

Ответ: ошибка совершена при переходе от равенства (1) к (2). Так как а > b, то b – a < 0, следовательно, при делении неравенства (1) на b – а, мы должны

поменять знак неравенства на противоположный.

Пример 6

« 8 = 6 »

Решим систему уравнений:

Решим подстановкой у из второго уравнения в первое, получаем

х + 8 – х = 6, откуда 8 = 6.

Где ошибка?

Ответ: второе уравнение системы можно записать как х + 2у = 8, так что исходная система запишется в виде:

В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система не имеет ни одного решения.

Графически это означает, что прямые у = 3 — и у = 4 — параллельны и не совпадают. Перед тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.

Пример 7

«Неравные числа равны»

Возьмем два неравных между собой произвольных числа а и b.

Пусть их разность равна с, то есть а – b = с. Умножив обе части этого равенства на ( а – b ), получим ( а – b )² = с ( а – b ). Раскрыв скобки, придем к равенству а² – 2аb + b² = ca – cb. После преобразования получаем а² – аb — ас= аb – b² – bc. Выносим общий множитель а слева и общий множитель b справа, получим: а ( а – b – c ) = b ( a – b – c ).

Разделив последнее равенство на ( а – b – c ), получаем : а = b.

Где ошибка?

Ответ: здесь ошибка совершена при переходе от равенства а ( а – b – c ) = b ( a – b – c ) к равенству а = b. Действительно, согласно условию разность двух произвольных чисел а и b равна с, то есть а – b = с, откуда а – b — c = 0. Можно записать равенство а ( а – b – c ) = b ( a – b – c ) в виде: а*0 = b*0. Переход от этого равенства к равенству, а=b осуществляется путем деления обеих частей на равное нулю число а – b – с = 0.Следовательно, здесь мы имеем деление нуля на нуль, которое не имеет смысла, поскольку равенство, а*0=b*0 выполняется при любых а и b. Поэтому, вывод о том, что числа а и b равны, неверен.

Пример 8

« 7 = 13 »

Рассмотрим уравнение: . (1)

Оно может быть решено следующим образом. Приведя левую часть уравнения к общему знаменателю, получим

= , откуда – = , или

= . (2)

Поскольку числители дробей в левой и в правой частях уравнения равны, то для того чтобы имело место равенство обеих частей уравнения, необходимо, чтобы были равны и знаменатели дробей. Таким образом, приходим к равенству

7 = 13.

Где ошибка? Ответ: область допустимых значений исходного уравнения (1) состоит из всех значений переменой х, кроме х=7, х=13. В этом софизме неявно подразумевается, что равенство (2) является не уравнением, а тождеством, равным при любых значениях х, что неверно. Поэтому, утверждение софизма неверно.

ГЕОМЕТРИЧЕСКИЕ СОФИЗМЫ

Геометрические софизмы – это умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.

Пример 1

«Катет равен гипотенузе»

Доказательство

Угол С равен 90°, ВД — биссектриса угла СВА, СК = КА, ОК перпендикулярно СА, О – точка пересечения прямых ОК и ВД, ОМ перпендикулярно АВ, ОL перпендикулярно ВС. Имеем: ∆LВО равен ∆МВО, ВL=ВМ, ОМ = ОL = СК = КА, ∆КОА = ∆ОМА (ОА- общая сторона, КА = ОМ, ∠ОКА и ∠ОМА- прямые), ∠ОАК= ∠МОА, ОК=МА=СL, ВА= ВМ+МА, ВС=ВL+LС, но ВМ=ВL, МА=СL, и потому ВА=ВС.

В

M

L

С К D A

К D

Где ошибка?

Ответ: ошибка заключается в том, что рассуждения, о том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к катету АС, находится вне треугольника АВС.

Пример 2

«Отрезки параллельных прямых, заключенные между сторонами угла, равны»

Рассмотрим произвольный угол с вершиной в точке Е и пересечем их стороны двумя параллельными прямыми, отрезки которых АВ и СD заключены между сторонами этого угла.

Как известно параллельные прямые отсекают от сторон угла пропорциональные отрезки, следовательно, откуда АЕ · DE = BE · CE.

Умножив обе части последнего равенства на отличную от нуля разность

АВ – СD , запишем AE · DE · AB – AE · DE · CD = AE · DE · CD – BE · CE · CD,

ИлиАВ (AE · DE – BE · CE) = CD (AE · DE – BE · CE).

Разделив обе части последнего равенства на (AE · DE – BE · CE) получим равенство АВ = СD.

Е

D А

B С

Где ошибка?

Ответ: так как АЕ · DE = BE · CE, то АЕ · DE – ВЕ · СЕ = 0, то ошибка в делении на 0.

Пример 3

«Катет прямоугольного треугольника равен его гипотенузе»

Пусть BO (рис.1) – биссектриса угла B, D – середина катета AC, DO ┴ AC, OE ┴ BC, OF ┴ BA.

Так как О — на биссектрисе угла B,

то Δ BFO = Δ BEO (по гипотенузе и острому углу). Поэтому

BF = BE. (1)

Далее, OA = OC, ибо каждая точка перпендикулярна к отрезку AC,

9проходящего через середину AC, равноудалена от А и С. Так как ОF = OE,

то Δ AOF = Δ СОЕ, и поэтому АF = СЕ. (2)

С

n DD D

кладывая почленно (1) и (2), получим AB = CB, то есть катет равен гипотенузе, что и требовалось доказать.

n O

O O

В В

E A C

F F О Е

А D С Рис. 2

Рис. 1

Где ошибка? Ответ: точка О не может быть внутри Δ ABC. Тогда можно показать, что если точка О лежит вне Δ ABC или на его стороне, то опять AB = CB (рис.2). Именно, показываем, что BF = BE, АF = СЕ. Отсюда AB = CB.

Пример 4

«Прямой угол равен тупому!»

Пусть угол АDC — прямой, угол DCВ — тупой, СВ=DА, СМ=DМ, АF=ВА, МО ┴ СD, FО ┴ АВ. Следовательно, ∆DMO = ∆СМО (по двум катетам). Поэтому, ∠ МDО= ∠ МСО. (1) OD=ОС, ∆ AFO =∆ ВFО (по двум катетам).

Следовательно, АО=ОВ и ∆ АDО= ∆ ВСО (по трем сторонам).

Значит, ∠АDО = ∠ВСО. (2)

A F B

D M C

O

∠АDO –∠ МDО =∠ ВСО – ∠МСО, то есть ∠АDC=∠ BCD.

Таким образом, прямой угол равен тупому углу. Что и требовалось доказать.

ЗАДАНИЯ «НАЙДИ ОШИБКУ»

В процессе изучения и исследования математических софизмов мне стало интересно, а как можно предупредить ошибки учеников моего класса в решении примеров на уроках. Ведь часто при неправильном решении получается явно неверный результат, который не могут увидеть сами ученики. Поэтому, я заинтересовалась заданиями с ошибками в решении. Используя учебную литературу, я попробовала самостоятельно составить задания, в которых есть ошибка.

Пример 1

Решить неравенство:

( 4 — х² )³ ( х – 3 )² ≥ 0.

( х²-4)³ ( х – 3 )² ≤ 0,

( х – 2 )³( х + 2 ) ³ ( х – 3 ) ² ≤ 0.

Найдем нули выражения

х – 2 =0, х + 2 =0, х – 3 = 0,

х = 2, х = -2, х = 3.

— + — +

х

-2 2 3

х (-∞; -2] υ [2; 3]

Где ошибка?

Ответ: в выражении второй множитель в квадрате. Поэтому, при переходе через точку х=3 знак выражения не должен измениться.

+ — + +

х

-2 2 3

х [-2; 2] Ответ: [-2; 2]

Пример 2

Найти производную функции f(х) = sin⁶ .

f‘ꞌ(х) = (sin⁶)’ =6sin⁵ · · · (5х²-6х) = =6sin⁵ = 3sin⁵ .

Где ошибка?

Ответ: ошибка заключается в нахождении производной степенной функции.

f‘ꞌ(х) = (sin⁶)’ =6sin⁵ · · · (5х²-6х) = =6sin⁵ =sin⁵ .

Пример 3 Решить биквадратное уравнение:

9х⁴ – 2х² — 7 = 0.

Введем замену х² =z, решаем квадратное уравнение:

9z² — 2z – 7 = 0, k=

Д₁ = k² — ac = (-1)²— 9 · (-7) = 1 +63 = 64 > 0, имеет 2 корня

z_1,2 = =

z₁₌ -1, z₂= ,

х² = — 1, х² = ,

не имеет решения, х = ± .

Где ошибка? Ответ: при нахождении корней уравнения допущена ошибка: k=-1, а в формуле корней знак не изменен. Правильное решение:

z_1,2 = = ,

z₁= 1,z₂=- ,

х²= 1 , х² = — ,

х = ± 1, не имеет решения. Ответ: ± 1

Пример 4

Решить тригонометрические уравнения:

а) 2соsх = 1.

соsх = ,

х = аrccos + 2n, n Z,

x = + 2n, n Z.

Где ошибка?

Ответ: ошибка заключается в неправильном определении табличного значения косинуса.

х = аrccos + 2 n, n Z

x = + 2 n, n Z

б) 3sin ²x — 2sinx -1 = 0.

Введем замену sinx=t , тогда получим и решим квадратное уравнение:

3t² -2t -1 = 0.

По свойству коэффициентов a+ b +c = 0 получаем:

t₁ = 1, t₂ = — ,

sinx= 1, sinx= — ,

х =(-1)ⁿ + n, n Z. х= (-1)ⁿarcsin(- ) + n, n Z,

х= — (-1)ⁿ arcsin + n, n Z.

Где ошибка?

Ответ: 1) ошибка заключается в нахождении корня тригонометрического уравнения sinx= 1. Это частный случай. Поэтому, х = + 2n, n Z.

2) ошибка при определении корня уравнения sinx= — . Отрицательное значение синуса увеличивает степень числа (-1) на единицу.

Правильный ответ: х= (-1)ⁿ⁺¹ arcsin + n, n Z

Пример 5. Задача.

Стороны параллелограмма АВСD относятся как 2:3, а его периметр равен 20 см, угол между сторонами равен 60°. Найдите его площадь.

А В

С D

Решение.

АВ : АD = 2 : 3.

х – коэффициент пропорциональности,

тогда АВ = 2х (см), АD = 3х (см)., Р_АВCD = 2(АВ + АD), получим

(2х + 3х) · 2 = 20,

5х = 10,

х = 2 (см).

АВ = 2 · 2 = 4 (см), АD = 2 · 3 = 6 (см).

S_АВCD = аbsinα = АВ · АD · sin60°,

S_АВCD = 4 · 6 · = 12 (cм²).

Где ошибка?

Ответ: ошибка в определении значения синуса. Правильно sin60° = .

Поэтому, S_АВCD = 4 · 6 · = 12 (cм²).

ЗАКЛЮЧЕНИЕ

Исследовать софизмы очень интересно и необычно. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными.

Изучая и исследуя математические софизмы, я научилась контролировать логические рассуждения при решении задач и примеров.. Поэтому, я могу найти ошибку в своем решении и увидеть ошибку в решении других учеников во время урока.

Мне было очень интересно изучать и исследовать математические софизмы, а особенно придумывать новые задания, содержащие ошибку и анализировать их.

Такие задания помогут мне еще лучше подготовиться к государственному экзамену по математике и сдаче ЕНТ.

Литература

1. М. Б. Балк, Г. Д. Балк, «Математика после уроков», «Просвещение», Москва, 1971

2. сайт ppt4.web.rumatematisheskie—sofizmy.htlm

3. А. Н. Шыныбеков, учебник «Геометрия 8», «Атамура», Алматы, 2004

4. А. Н. Шыныбеков, учебник «Алгебра 8», «Атамура», Алматы, 2004

5. А. Е. Абылкасомова, З .А Жумагулова, К. Д. Шойынбеков,

6. В. Е. Корчевский, учебник «Алгебра и начала анализа 10», «Мектеп», Алматы, 2014

7. И. П. Рустюмова, С. Т. Рустюмова, «Тренажер по математике для подготовки к Единому Национальному Тестированию (ЕНТ)», Алматы,2011

Просмотров работы: 108

«Алгоритм
нахождения и исправления ошибок

 в проверочных работах  по математике»

Ковалёва Г.И. 

МБОУ «СШ №15»

Найди ошибку в выражении:        15+6=22                56-20=46

1. 
Выпиши выражение, в
котором была допущена ошибка, с правильным ответом:

                                                             
 15+6=21                 56-20=36

2. 
Придумай и запиши два
подобных выражения:

                      14+7=21     13+8=21                                      
    47-30=17     93-40=53

Найди ошибку в неравенстве:      45-15>45+15

1. 
Выпиши неравенство, в
котором была допущена ошибка, с правильным решением:

                                                  
45-15 <45+15

2. 
Придумай и запиши подобное
неравенство:

                                                       
34-20 <34+20

Найди ошибку в сравнении величин:     1м = 20см                

1.  Выпиши сравнение, в котором была допущена ошибка, с
правильным решением и объяснением данного решения:

         1м
>20см                         1м = 100см             100см >20см

Найди ошибку в решении задачи:

1. 
Читай задачу, останавливаясь на каждой смысловой точке,
делая при этом пометки в черновике.

2.     
Выполни решение с помощью рисунка,
чертежа, краткой записи, пояснения, вопросов.

3.     
Сравни свое решение задачи
с правильным решением

4.     
Придумай и реши подобную
задачу.

Найди ошибку в геометрическом задании:

Ø Если
ошибка в нахождении периметра или площади многоугольника:

1.      Начерти
фигуру на черновике

2.     
Обозначь каждую сторону
многоугольника

3.     
Вспомни, что ты знаешь о
сторонах данной фигуры

4.     
Вспомни формулу нахождения
периметра или площади  данной фигуры

5.     
Найди периметр или площадь
данной фигуры

6.     
Сравни свой ответ с
правильным решением

Ø
Если есть ошибки в построении геометрической фигуры:

1.    
обратись за помощью к
учителю

Задания на поиск ошибки, как инструмент формирования
регулятивных УУД

Проверь работу ученика 5 Екласса Иванова Вани.		I	II
1) 185х+272х=457х	1
2) 230у-175у=55у	2
3) 156а+79а+21а+44а=300а	3
4) 35х+17х+65+33х=150х	4
5) 55а+а=56а	5
6) 1307у-500у+93=807у+93	6
7) 14+17с-8с=14+9с	7
Отметка

Задание на поиск ошибки по теме: «Упрощение выражений» (5 класс)
Критерии оценивания
менее 4 верных заданий — отметка «2»
4-5 верных заданий – отметка «3»
6 верных заданий — отметка «4»
7 верных заданий — отметка «5»

— Мне было все понятно — Я испытывал небольшие затруднения, которые сумел преодолеть — Мне нужно еще поработать над этой темой — Мне не понятно, без помощи учителя я не справлюсь

Проверь работу ученика 5 Екласса Иванова Вани.		I	II
1) 2	1
2) 72	2
3) 9 =90+972=1062	3
4) 321+266+134=321+300=621	4
5)	5
6) 3 =621-27=594	6
7)	7
Отметка

Критерии оценивания
менее 4 верных заданий — отметка «2»
4-5 верных заданий – отметка «3»
6 верных заданий — отметка «4»
7 верных заданий — отметка «5»

— Мне было все понятно — Я испытывал небольшие затруднения, которые сумел преодолеть — Мне нужно еще поработать над этой темой — Мне не понятно, без помощи учителя я не справлюсь

Проверь работу ученика 7 Д класса Иванова Вани.		I	II
1) 15ас – 7с — ас = с ( 15а -7-а )	1
2) 2х 2у + ху = 2ху( х )	2
3) 16а3с2х — 2ас2 =2 ас2 ( 8ас – 1 )	3
4) 6х2у( х –у) + ( у – х )= (х-у)(6х2у -1)	4
5) 35ас – 14 ас2 + 4 = а ( 35с – 14с2 + 4 )	5
6) 49 – а2= ( 7 – а )( 7 + а )	6
7) 16х4у2 – 64 =( 4х2у – 8 )( 4х2у + 8 )	7
Отметка

Критерии оценивания
менее 4 верных заданий — отметка «2»
4-5 верных заданий – отметка «3»
6 верных заданий — отметка «4»
7 верных заданий — отметка «5»

— Мне было все понятно — Я испытывал небольшие затруднения, которые сумел преодолеть — Мне нужно еще поработать над этой темой — Мне не понятно, без помощи учителя я не справлюсь

Проверь работу ученика 7 Д класса Иванова Вани.		I	II
1)Треугольники равны по стороне и двум прилежащим углам	1
2) Если треугольник равносторонний, то все его углы равны	2
3) Треугольники равны по двум сторонам и углу между ними	3
4) Медиана в равнобедренном треугольнике всегда является биссектрисой и высотой.	4
5) Треугольники равны по стороне и двум прилежащим углам	5
6) Треугольники равны по трем сторонам	6
7) Если треугольник равносторонний, то он равнобедренный.	7
Отметка

— Мне было все понятно — Я испытывал небольшие затруднения, которые сумел преодолеть — Мне нужно еще поработать над этой темой — Мне не понятно, без помощи учителя я не справлюсь

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/245757-zadanija-na-poisk-oshibki-kak-instrument-form

Со скольки лет надо начинать изучать математику? Все в этом мире меняется. То, что наши предшественники могли понять только к двадцати годам, люди сейчас понимают уже в 15 и ранее. Современный мир таков, что все молодеет. Зачем нам изучать математику? Почему именно математика? Математика — это одна из тех наук, основы, которой была заложены не год, не два и даже не сто лет назад. Математика с нами уже несколько тысяч лет. Писать шпаргалки или не писать? «Писать шпаргалки или не писать?» — вот в чём вопрос. Математика — предмет серьёзный и решение задач требует хорошего знания формул. Поэтому, ответ теоретиков и учащихся — писать стоит. Шпаргалки не для нас Как известно из многих источников есть цвета, которые очень хорошо располагают к себе человека, действуя на подсознание человека, это голубой и зеленый цвет. Вот в таких тонах и желательно одеваться на экзамен. Математика — часть нашей жизни Не раз приходилось слышать фразу о том, что математика — страна без границ. Несмотря на свою банальность, фраза о математике имеет под собой очень веские основания. Математика в жизни человека занимает особое место. Математика в решении строительных задач Математика используется повсеместно, для решения задач из самых разных областей. В том числе, и для решения задач строительства. Подготовка к контрольной работе, концентрация Контрольная работа, это отличный способ проверить свои знания и навыки, полученные за время обучения. Контрольные работы по математике отличаются повышенной сложностью. Решение задач и оформление контрольных работ по дисциплине математика Все большее количество людей, сейчас предпочитают учиться удаленно, таким образом нужно уделять много внимания правильному оформлению сделанных контрольных работ.

Как найти ошибку в софизме? Примеры софизмов Подготовил Бакушкин Иван Как найти ошибку в софизме? Зачастую найти ошибку в софизме очень сложно. К тому же не существовал алгоритм нахождения ошибки в софизме. Но я, проанализировав софизмы, составил алгоритм, который может помочь в нахождении ошибки во многих софизмах. Внимательно прочитать условие предложенной вам задачи (Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат, получается, из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки)   Установить темы, которые отражены в софизме (Ученики, учителя привыкли, что задания, предполагаемые в учебнике, не содержат ошибок в условии и, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения)   Воспроизвести вслух точные формулировки утверждений (Установить темы, которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них. И если вы увидели эти темы, попытайтесь зрительно разбить «большой софизм» на маленькие)   Выяснить, соблюдены ли все условия применимости теорем, правил, формул, логичности (Воспроизвести вслух точные формулировки утверждений, используемых в софизме. Например: 2 * 2 =5. Если произнести эту фразу вслух, то мы можем услышать ошибку, услышав самого себя, или более подробно разобраться в смысле софизма)   Проверять преобразования. После каждого перехода проверить полученный результат обратным действием (Выяснить, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Действительно, некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости некоторых теорем. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускаются. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам»)   Следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока (Работать блоками. Следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока. Удобнее проследить за одним блоком, чем за целым преобразованием) Примеры софизмов «Двусмысленность произношения» Сто сорок да сто сорок будет двести сорок. «Рассуждение о женщинах» TranslateПеревод Если у вас будет женщина, то вам потребуется время и деньги: a. Женщина=Время*Деньги Время-деньги, поэтому: a. Время=Деньги Из этого следует: a. Женщина=Деньги*Деньги b. Женщина=Деньги в квадрате c. Деньги- это и есть все ваши проблемы: d. Деньги=Корень из проблем i. Из этого следует: ii. Женщина=Корень из проблем в квадрате Вывод: Женщина=ПРОБЛЕМЫ «Апельсин- планета» Земля, Марс ит. д. — круглые. Значит, все планеты круглые. Апельсин тоже круглый, значит апельсин – планета. «Нет конца» Движущийся предмет должен дойти до половины своего пути прежде, чем он достигнет его конца. Затем он должен пройти половину оставшейся половины, затем половину этой четвертой части и т.д. до бесконечности. Предмет будет постоянно приближаться к конечной точке, но так никогда ее не достигнет. «Продолжительность учебного года» Можно доказать, что учителя и ученики целый год ничего не делают. Для простоты будем считать, что в году 360 дней, из них 52 воскресных дня. Если не считать других выходных дней, останется 308 учебных дней. Ночью школа не работает, следовательно, половина количества суток пропадает, остается 154 учебных дня. В большинстве школ занятия продолжаются только до полудня, вследствие чего учебное время уменьшается вдвое. Получаем 77 учебных дней. Будем считать, что на каникулы выпадает только 60 дней, тогда для занятий останется всего 17 дней в году. «Песенка английских студентов» Чем больше учишься, тем больше знаешь. Чем больше знаешь, тем больше забываешь. Чем больше забываешь, тем меньше знаешь. Чем меньше знаешь, тем меньше забываешь. Но чем меньше забываешь, тем больше знаешь. Так для чего учиться? « Единица равна нулю» Возьмем уравнение х-а = 0 Разделив обе его части на х-а, получим Откуда сразу же получаем требуемое равенство 1=0 Ошибка заключается в том, что на 0 делить нельзя (1). «Семь равно тринадцати» Рассмотрим уравнение Оно может быть решено следующим образом. Приведя левую часть уравнения к общему знаменателю, будем иметь Откуда следует или Поскольку числители дробей в левой и правой частях уравнения равны, то для того чтобы имело место равенство обеих частей уравнения, необходимо, чтобы были равны и знаменатели дробей. Таким образом, приходим к равенству 7=13 Ошибка состоит в том, что область допустимых значений исходного уравнения (1) состоит из всех значений переменой х кроме х=7, х=13. В этом софизме неявно подразумевается, что равенство(2) является не уравнением, а тождеством равным при любых значениях х, что неверно. Поэтому утверждение софизма не имеет места. «Один рубль не равен ста копейкам» Возьмем верное равенство: 1 р. = 100 к., Возведем его по частям в квадрат, получим: 1 р. = 10000 к. Таким образом, один рубль не равен ста копейкам. (Ошибка: умножение величины на себя не имеет смысла, в квадрат возводятся только числа). «2×2=5» Найти ошибку в рассуждении: Имеем верное числовое равенство: 4:4=5:5. Вынесем за скобки в каждой части его общий множитель. Получим: 4(1:1)=5(1:1). Числа в скобках равны, поэтому 4=5 или . (Ошибка: ошибка допущена в левой и правой частях тождества 4:4=5:5 при вынесении общего множителя за скобки.)