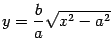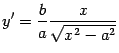Как найти оси симметрии для гиперболы - Исправление недочетов и поиск решений вместе с Examum.ru

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Математическая гипербола.

Функция заданная формулой (y=frac{k}{x}), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac{k}{x}) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти

гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти

2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$yneqcolor{red} {frac{1}{x}}+0$$
(frac{1}{x}) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

$$y=color{red} {frac{1}{x+2}}-1$$

Дробь (color{red} {frac{1}{x+2}}) отбрасываем
Остается y≠ -1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Пример №3:

$$begin{align*}
&y=frac{2+x}{1+x} \\
&y=frac{color{red} {1+1}+x}{1+x} \\
&y=frac{1}{1+x}+frac{1+x}{1+x}\\
&y=frac{1}{1+x}+1\\
&y=frac{1}{color{red} {1+x}}+1
end{align*}$$

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red}{frac{1}{1+x}}+1$$

(color{red}{frac{1}{1+x}}) Дробь убираем.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

$$y=frac{1}{x}$$

Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

$$y=frac{1}{x}$$

Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

$$f(-x)=frac{1}{-x}=-frac{1}{x}=-f(x)$$

6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:

$$y=frac{-1}{x-1}-1$$

а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red} {frac{-1}{x-1}}-1$$

Дробь (color{red} {frac{-1}{x-1}}) удаляем.

Остается y≠ -1 это вторая асимптота.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).

д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.

8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама

Источник

Гипербола: определение, свойства, построение

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек F_1 и F_2 есть величина постоянная (2a) , меньшая расстояния (2c) между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.

Фокальное свойство гиперболы

Точки F_1 и F_2 называются фокусами гиперболы, расстояние 2c=F_1F_2 между ними — фокусным расстоянием, середина отрезка F_1F_2 — центром гиперболы, число — длиной действительной оси гиперболы (соответственно, — действительной полуосью гиперболы). Отрезки F_1M и F_2M , соединяющие произвольную точку гиперболы с ее фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение $e=frac{c}{a}$ , где $c=sqrt{a^2+b^2}$ , называется эксцентриситетом гиперболы. Из определения (2a<2c) следует, что e>1 .

Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1.$

(3.50)

Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F_1 к точке F_2 ); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Гипербола и фокальное свойство гипербол

Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов F_1(-c,0) и F_2(c,0) . Для произвольной точки M(x,y) , принадлежащей гиперболе, имеем:

$left||overrightarrow{F_1M}|-|overrightarrow{F_2M}|right|=2a.$

Записывая это уравнение в координатной форме, получаем:

$sqrt{(x+c)^2+y^2}-sqrt{(x-c)^2+y^2}=pm2a.$

Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:

$frac{x^2}{a^2}-frac{y^2}{b^2}=1,,$

где $b=sqrt{c^2-a^2}$ , т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.

Директориальное свойство гиперболы

Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии $a^2!!not{phantom{|}},c$ от нее (рис.3.41,а). При a=0 , когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.

Гиперболу с эксцентриситетом e=1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство гиперболы). Здесь и — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

Директрисы гиперболы и директориальное свойство

В самом деле, например, для фокуса F_2 и директрисы d_2 (рис.3.41,а) условие $frac{r_2}{rho_2}=e$ можно записать в координатной форме:

$sqrt{(x-c)^2+y^2}=eleft(x-frac{a^2}{c}right)$

Избавляясь от иррациональности и заменяя $e=frac{c}{a},~c^2-a^2=b^2$ , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса F_1 и директрисы d_1 :

$frac{r_1}{rho_1}=e quad Leftrightarrow quad sqrt{(x+c)^2+y^2}= eleft(x+frac{a^2}{c} right).$

Уравнение гиперболы в полярной системе координат

Уравнение правой ветви гиперболы в полярной системе координат F_2rvarphi (рис.3.41,б) имеет вид

$r=frac{p}{1-ecdotcosvarphi}$ , где $p=frac{p^2}{a}$ — фокальный параметр гиперболы.

В самом деле, выберем в качестве полюса полярной системы координат правый фокус F_2 гиперболы, а в качестве полярной оси — луч с началом в точке F_2 , принадлежащий прямой F_1F_2 , но не содержащий точки F_1 (рис.3.41,б). Тогда для произвольной точки M(r,varphi) , принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем F_1M-r=2a . Выражаем расстояние между точками M(r,varphi) и F_1(2c,pi) (см. пункт 2 замечаний 2.8):

$F_1M=sqrt{(2c)^2+r^2-2cdot(2c)^2cdot rcdotcos(varphi-pi)}=sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}.$

Следовательно, в координатной форме уравнение гиперболы имеет вид

$sqrt{r^2+4cdot ccdot rcdotcosvarphi+4cdot c^2}-r=2a.$

Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:

$r^2+4crcdotcosvarphi+4c^2=4a^2+4ar+r^2 quad Leftrightarrow quad aleft(1-frac{c}{a}cosvarphiright)r=c^2-a^2.$

Выражаем полярный радиус и делаем замены $e=frac{c}{a},~b^2=c^2-a^2,~p=frac{b^2}{a}$ :

$r=frac{c^2-a^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{b^2}{a(1-ecosvarphi)} quad Leftrightarrow quad r=frac{p}{1-ecosvarphi},$

что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( e>1 для гиперболы, 0leqslant e<1 для эллипса).

Геометрический смысл коэффициентов в уравнении гиперболы

Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение y=0 , находим абсциссы точек пересечения: x=pm a . Следовательно, вершины имеют координаты (-a,0),,(a,0) . Длина отрезка, соединяющего вершины, равна . Этот отрезок называется действительной осью гиперболы, а число — действительной полуосью гиперболы. Подставляя x=0 , получаем y=pm ib . Длина отрезка оси ординат, соединяющего точки (0,-b),,(0,b) , равна . Этот отрезок называется мнимой осью гиперболы, а число — мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.

Замечания 3.10.

1. Прямые x=pm a,~y=pm b ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).

2. Прямые $y=pmfrac{b}{a},x$ , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).

Для равносторонней гиперболы, описываемой уравнением $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ (т.е. при a=b ), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат Ox'y' (рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид $y'=frac{a^2}{2x'}$ (гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).

Асимптоты гиперболы и равносторонняя гипербола

В самом деле, повернем каноническую систему координат на угол $varphi=-frac{pi}{4}$ (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами

$left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y',\ y&=-frac{sqrt{2}}{2}cdot x'+frac{sqrt{2}}{2}cdot y'end{aligned}right. quad Leftrightarrow quad left{!begin{aligned}x&=frac{sqrt{2}}{2}cdot(x'+y'),\ y&=frac{sqrt{2}}{2}cdot(y'-x')end{aligned}right.$

Подставляя эти выражения в уравнение $frac{x^2}{a^2}-frac{y^2}{a^2}=1$ равносторонней гиперболы и приводя подобные члены, получаем

$frac{frac{1}{2}(x'+y')^2}{a^2}-frac{frac{1}{2}(y'-x')^2}{a^2}=1 quad Leftrightarrow quad 2cdot x'cdot y'=a^2 quad Leftrightarrow quad y'=frac{a^2}{2cdot x'}.$

3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.

Действительно, если точка M(x,y) принадлежит гиперболе $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ . то и точки M'(x,y) и M''(-x,y) , симметричные точке относительно координатных осей, также принадлежат той же гиперболе.

Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.

4. Из уравнения гиперболы в полярных координатах $r=frac{p}{1-ecosvarphi}$ (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси ( r=p при $varphi=frac{pi}{2}$ ).

5. Эксцентриситет характеризует форму гиперболы. Чем больше , тем шире ветви гиперболы, а чем ближе к единице, тем ветви гиперболы уже (рис.3.43,а).

Действительно, величина gamma угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника: $operatorname{tg}frac{gamma}{2}=frac{b}{2}$ . Учитывая, что $e=frac{c}{a}$ и c^2=a^2+b^2 , получаем

$e^2=frac{c^2}{a^2}=frac{a^2+b^2}{a^2}=1+{left(frac{b}{a}right)!}^2=1+operatorname{tg}^2frac{gamma}{2}.$

Чем больше , тем больше угол gamma . Для равносторонней гиперболы (a=b) имеем e=sqrt{2} и $gamma=frac{pi}{2}$ . Для e>sqrt{2} угол gamma тупой, а для 1<e<sqrt{2} угол gamma острый (рис.3.43,а).

Эксцентриситет гиперболы и сопряжённая гипербола

6. Две гиперболы, определяемые в одной и той же системе координат уравнениями $frac{x^2}{a^2}-frac{y^2}{b^2}=1$ и $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы $-frac{x^2}{a^2}+frac{y^2}{b^2}=1$ приводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение $frac{(x-x_0)^2}{a^2}-frac{(y-y_0)^2}{b^2}=1$ определяет гиперболу с центром в точке O'(x_0,y_0) , оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение $-frac{(x-x_0)^2}{a^2}+frac{(y-y_0)^2}{b^2}=1$ определяет сопряженную гиперболу с центром в точке O'(x_0,y_0) .

Параметрическое уравнение гиперболы

Параметрическое уравнение гиперболы в канонической системе координат имеет вид

$begin{cases}x=acdotoperatorname{ch}t,\y=bcdotoperatorname{sh}t,end{cases}tinmathbb{R},$

где $operatorname{ch}t=frac{e^t+e^{-t}}{2}$ — гиперболический косинус, a $operatorname{sh}t=frac{e^t-e^{-t}}{2}$ гиперболический синус.

Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству $operatorname{ch}^2t-operatorname{sh}^2t=1$ .

Построение гиперболы в канонической системе координат

Пример 3.21. Изобразить гиперболу $frac{x^2}{2^2}-frac{y^2}{3^2}=1$ в канонической системе координат Oxy . Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.

Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: a=2 — действительная полуось, b=3 — мнимая полуось гиперболы. Строим основной прямоугольник со сторонами 2a=4,~2b=6 с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя x=4 в уравнение гиперболы, получаем

$frac{4^2}{2^2}-frac{y^2}{3^2}=1 quad Leftrightarrow quad y^2=27 quad Leftrightarrow quad y=pm3sqrt{3}.$

Следовательно, точки с координатами (4;3sqrt{3}) и (4;-3sqrt{3}) принадлежат гиперболе. Вычисляем фокусное расстояние

$2cdot c=2cdotsqrt{a^2+b^2}=2cdotsqrt{2^2+3^2}=2sqrt{13}$

эксцентриситет $e=frac{c}{a}=frac{sqrt{13}}{2}$ ; фокальныи параметр $p=frac{b^2}{a}=frac{3^2}{2}=4,!5$ . Составляем уравнения асимптот $y=pmfrac{b}{a},x$ , то есть $y=pmfrac{3}{2},x$ , и уравнения директрис: $x=pmfrac{a^2}{c}=frac{4}{sqrt{13}}$ .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Гипербола

Гиперболой называется
геометрическое место точек плоскости,
для каждой из которых абсолютная величина
разности расстояний до двух фиксированных
точек той же плоскости, называемых
фокусами гиперболы, есть величина
постоянная.

Так же, как и в случае эллипса, для
получения уравнения гиперболы выберем
подходящую систему координат. Начало
координат расположим на середине отрезка
между фокусами, ось
направим
вдоль этого отрезка, а ось ординат —
перпендикулярно к нему.

Пусть расстояние между фокусами

и

гиперболы равно
,
а абсолютная величина разности расстояний
от точки гиперболы до фокусов равна
.

— текущая точка гиперболы (рис. 5).

Рис.5.

Так как разность двух сторон треугольника
меньше третьей стороны, то
,
то есть
,

.
По условию, фокусы
,
.

По определению гиперболы

Это уравнение запишем в виде

Обе части возведем в квадрат:

После приведения подобных членов и
деления на 4, приходим к равенству

Опять обе части возведем в квадрат:

Раскрывая скобку и приводя подобные
члены, получим

С учетом того, что

уравнение принимает вид

Разделим обе части уравнения на
и
получим уравнение
(4)

Уравнение (4) называется каноническим
уравнением гиперболы.

Гипербола обладает двумя взаимно
перпендикулярными осями симметрии, на
одной из которых лежат фокусы гиперболы,
и центром симметрии. Если гипербола
задана каноническим уравнением, то ее
осями симметрии служат координатные
оси Ox
и
,
а начало координат — центр симметрии
гиперболы.

Проведем построение гиперболы, заданной
уравнением (4). Заметим, что из-за симметрии
достаточно построить кривую только в
первом координатном угле. Выразим из
канонического уравнения y
как функцию х,
при условии, что
,

и построим график этой функции.

Область определения – интервал
,
,
функция монотонно растет. Производная

существует во всей области определения,
кроме точки. Следовательно, график —
гладкая кривая (без углов). Вторая
производная

во всех точках интервала

отрицательна, следовательно, график —
выпуклый вверх.

Проверим график на наличие асимптоты
при
.
Пусть асимптота имеет уравнение
.
Тогда по правилам математического
анализа

Выражение под знаком предела домножим
и разделим на
.
Получим

Итак, график функции имеет асимптоту

.
Из симметрии гиперболы следует, что

— тоже асимптота. (рис. 6).

Рис.6.График
функции

Окончательно, используя симметрию
гиперболы, получаем кривую рисунка 7.

Рис.6.Гипербола

Точки пересечения гиперболы, заданной
каноническим уравнением (4) с осью

называются
вершинами гиперболы, отрезок между
ними называется действительной осью
гиперболы. Отрезок оси ординат между
точками (0;-b) и (0; b)
называется мнимой осью. Числа
и

называются
соответственно действительной и
мнимой полуосями гиперболы. Начало
координат называется ее центром.
Величина

называется эксцентриситетом
гиперболы.

Из равенства

следует, что у гиперболы
.
Эксцентриситет
характеризует
угол между асимптотами, чем
ближе
к
1, тем меньше этот угол.????

Замечание
12.4 В отличие от эллипса в каноническом
уравнении гиперболы соотношение между
величинами
и

может
быть произвольным. В частности, при
мы
получим равностороннюю гиперболу,
известную из школьного курса математики.
Ее уравнение имеет знакомый вид
,
если взять
,
а оси
и

направить по биссектрисам четвертого
и первого координатных углов (рис. 7).

Рис.7.Равносторонняя
гипербола

Для отражения на рисунке качественных
характеристик гиперболы достаточно
определить ее вершины, нарисовать
асимптоты и нарисовать гладкую кривую,
проходящую через вершины, приближающуюся
к асимптотам и похожую на кривую рисунка
7.

Пример 2.4 Постройте гиперболу
,
найдите ее фокусы и эксцентриситет.

Решение. Разделим обе части уравнения
на 4. Получим каноническое уравнение

.
Проводим асимптоты

и строим гиперболу (рис. 8).

Рис.8.Гипербола

Из формулы

получим
.

Тогда фокусы —
,
,

Пример 12.5 Постройте гиперболу
.
Найдите ее фокусы и эксцентриситет.

Решение. Преобразуем уравнение к
виду

Данное уравнение не является каноническим
уравнением гиперболы, так как знаки
перед
и

противоположны знакам в каноническом
уравнении. Однако, если переобозначить
переменные
,

,
то в новых переменных получим каноническое
уравнение

Действительная ось этой гиперболы лежит
на оси
,
то есть на оси
исходной
системы координат, асимптоты имеют
уравнение
,
то есть уравнение

в исходных координатах. Действительная
полуось равна 5, мнимая — 2. В соответствии
с этими данными проводим построение
(рис. 12.14).

Рис.9.Гипербола
с уравнением

,
фокусы лежат на действительной оси —
,

,
где координаты указаны в исходной
системе координат.

Соседние файлы в папке модуль2

Источник

Способы построения гиперболы самостоятельно

Содержание:

Гипербола в математике — что это такое
Как построить гиперболу самостоятельно
Построение гиперболы по фокусам
Как построить гиперболу по точкам
Как построить график гиперболы по уравнению

Гипербола в математике — что это такое

определение 1

Гипербола представляет собой линию, определяемую в некой декартовой прямоугольной системе координат каноническим уравнением:

(frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref9})

Согласно записанному правилу, все точки гиперболы (|x| geq a). Таким образом, данные точки расположены за пределами вертикальной полосы ширины (2a), как показано на рисунке. Ось абсцисс канонической системы координат имеет точки пересечения с гиперболой. Координаты этих точек соответствуют: ((a, 0)) и ((-a, 0)). Такие точки называют вершинами гиперболы.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Ось ординат не имеет общих точек с гиперболой. В состав гиперболы входят две части, которые не связаны между собой. Они носят название ветвей гиперболы. Числа «a» и «b» являются соответственно вещественной и мнимой полуосями гиперболы.

Ось ординат не имеет общих точек с гиперболой

Источник: univerlib.com

Определение 2

Ветви гиперболы — это две отдельные кривые, из которых состоит гипербола.

Определение 3

Ближайшие друг к другу точки двух ветвей гиперболы являются вершинами гиперболы.

Определение 4

Большая ось гиперболы — наименьшее расстояние между двумя ее ветвями.

Определение 5

Центр гиперболы — это середина ее большой оси.

Определение 6

Большая полуось гиперболы — расстояние, на которое удалены центр и одна из вершин, обозначается «а».

Определение 7

Фокальное расстояние гиперболы — расстояние, на которое удалены друг от друга центр и один из фокусов, обозначается «с».

Оба фокуса гиперболы расположены на продолжении большой оси и равноудалены от центра гиперболы.

Определение 8

Прямая, включающая в себя большую ось гиперболы, носит название действительной, или поперечной, оси гиперболы.

Определение 9

Прямая в виде перпендикуляра к действительной оси, которая пересекает центр гиперболы — мнимая, или сопряженная ось гиперболы.

Определение 10

Отрезок между фокусом гиперболы и гиперболой, который перпендикулярен к действительной оси, — это фокальный параметр.

Определение 11

Прицельный параметр — расстояние от фокуса до асимптоты гиперболы, обозначается «b».

Определение 12

Перицентрическое расстояние — расстояние, на которое фокус удален от ближайшей вершины гиперболы, обозначается ({displaystyle r_{p}}r_{p}).

Перечисленные характеристики гиперболы взаимосвязаны. Справедливы следующие соотношения:

({displaystyle c^{2}=a^{2}+b^{2}}{displaystyle c^{2}=a^{2}+b^{2}})
({displaystyle varepsilon =c/a}{displaystyle varepsilon =c/a})
({displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)}{displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)})
({displaystyle r_{p}=aleft(varepsilon -1right)}{displaystyle r_{p}=aleft(varepsilon -1right)})
({displaystyle a={frac {p}{varepsilon ^{2}-1}}}{displaystyle a={frac {p}{varepsilon ^{2}-1}}})
({displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}}{displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}})
({displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}}{displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}})
({displaystyle p={frac {b^{2}}{a}}}p={frac {b^{2}}{a}})

Определение 13

Оси симметрии гиперболы представляют собой оси канонической системы координат, а начало канонической системы является центром симметрии.

Когда требуется исследовать форму гиперболы, следует начать с поиска ее пересечения с произвольной прямой, пересекающей начало координат. Уравнение прямой можно задать в виде:

(y=kx)

Такой выбор связан с тем, что прямая (x=0 ) не пересекает гиперболу. Абсциссы точек пересечения можно вычислить с помощью уравнения:

(frac{x^{2}}{a^{2}}-frac{k^{2}x^{2}}{b^{2}}=1)

Таким образом, при (b^{2}-a^{2}k^{2} > 0) получим:

(x=pm frac{ab}{sqrt{b^{2}-a^{2}k^{2}}})

Полученное равенство позволит рассчитать координаты точек пересечения:

((ab/v, abk/v))

((-ab/v, -abk/v))

В данном случае:

(v=(b^{2}-a^{2}k^{2})^{1/2})

Руководствуясь свойством симметрии, можно проанализировать смещение первой из точек при изменении k, как показано на рисунке.

смещение первой из точек при изменении k

Источник: univerlib.com

Числитель дроби (ab/v) является постоянной величиной, а знаменатель характеризуется максимальным значением, если (k=0). Таким образом, самую маленькую абсциссу имеет вершина ((a, 0)). При увеличении (k ) знаменатель убывает, и x растет, стремясь к бесконечности, когда k приближается к числу (b/a).

Прямая (y=bx/a) с угловым коэффициентом (b/a) не имеет точек пересечения с гиперболой, как и прямые с большими угловыми коэффициентами. Какая-либо прямая, обладающая меньшим положительным угловым коэффициентом, пересекает гиперболу.

При сдвиге прямой от горизонтального положения по часовой стрелке, k будет уменьшаться, (k^{2}) — увеличиваться, и прямая будет иметь удаляющиеся точки пересечения с гиперболой до тех пор, пока не займет положения с угловым коэффициентом (-b/a).

К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из вышесказанного следует вывод, что гипербола имеет вид, изображенный на рисунке.

гипербола имеет вид

Источник: univerlib.com

Определение 14

Асимптоты гиперболы являются прямыми, описываемыми уравнениями (y=bx/a) и (y=-bx/a ) в канонической системе координат.

Предположим, что уравнения асимптот имеют вид:

(bx-ay=0)

(bx+ay=0)

Расстояния от точки (M(x, y)) до асимптот составят

(h_{1}=frac{|bx-ay|}{sqrt{a^{2}+b^{2}}},)( h_{2}=frac{|bx+ay|}{sqrt{a^{2}+b^{2}}})

В том случае, когда точка M расположена на гиперболе:

(b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2})

(h_{1}h_{2}=frac{|b^{2}x^{2}-a^{2}y^{2}|}{a^{2}+b^{2}}=frac{a^{2}b^{2}}{a^{2}+b^{2}})

Определение 15

Произведение расстояний от точки гиперболы до асимптот является постоянным и соответствует (a^{2}b^{2}/(a^{2}+b^{2})).

Из данного определения можно вывести ключевое свойство, которым обладают асимптоты гиперболы.

Определение 16

В том случае, когда точка совершает движение по гиперболе таким образом, что ее абсцисса по абсолютной величине неограниченно возрастает, расстояние от точки до одной из асимптот стремится к нулю.

В действительности получим, что хотя бы одно из расстояний (h_{1}) или (h_{2}) при этих условиях должно неограниченно увеличиваться. Если предположить, что утверждение не справедливо, то произведение не было бы постоянной величиной.

Введем такое число с, что:

(c^{2}=a^{2}+b^{2})

и (c > 0)

Определение 17

Фокусы гиперболы — точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат.

Фокусы гиперболы

Источник: univerlib.com

Отношение (varepsilon=c/a), как и для эллипса, называется эксцентриситетом. У гиперболы (varepsilon > 1).

Расстояния от произвольной точки (M(x, y)) на гиперболе до каждого из фокусов определяются абсциссой (x):

(r_{1}=|F_{1}M|=|a-varepsilon x|, r_{2}=|F_{2}M|=|a+varepsilon x|)

Расстояния от произвольной точки

Источник: univerlib.com

Следует отметить, что равенства eqref{ref11} можно представить в более подробной форме:

для правой ветви гиперболы ((x geq a): r_{1}=varepsilon x-a), ( r_{2}=varepsilon x+a);
для левой ветви гиперболы ((x leq -a): r_{1}= a-varepsilon x), ( r_{2}=-varepsilon x-a).

Таким образом, для правой ветви (r_{2}-r_{1}=2a), а для левой ветви (r_{1}-r_{2}=2a). В обоих случаях:

(|r_{2}-r_{1}|=2a)

Определение 18

Директрисы гиперболы — прямые, заданные в канонической системе координат уравнениями: (x=frac{a}{varepsilon}), ( x=-frac{a}{varepsilon}).

Директрисы расположены поблизости от центра в отличие от вершин. Из этого можно сделать вывод, что директрисы не имеют точек пересечения с гиперболой. Директриса и фокус, которые расположены по одну сторону от центра, считаются соответствующими друг другу.

Определение 19

Для того чтобы точка (M) была расположена на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы 2a.

С целью доказательства достаточности данного условия его следует записать в виде:

(sqrt{(x-c)^{2}+y^{2}}=pm 2a+sqrt{(x+c)^{2}+y^{2}})

Следующие действия отличаются от доказательства соответствующего утверждения для эллипса только тем, что нужно воспользоваться равенством:

(c^{2}=a^{2}+b^{2}), а не (c^{2}=a^{2}-b^{2})

Определение 20

Для того чтобы точка была расположена на гиперболе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету (varepsilon).

равнялось эксцентриситету

Источник: univerlib.com

Можно доказать, к примеру, необходимость условия для фокуса (F_{2}(-c, 0).) Предположим, что (M'(x, y)) является точкой гиперболы. Расстояние от (M’) до директрисы с уравнением (x=-a/varepsilon) равно:

(d’=left|x+frac{a}{varepsilon}right|=frac{1}{varepsilon}|varepsilon x+a|)

Таким образом:

(r’/d’=varepsilon).

Уравнение касательной к гиперболе в точке (M_{0}(x_{0}, y_{0})), которая принадлежит данной гиперболе, можно записать так же, как подобное уравнение в случае эллипса. Уравнение касательной к гиперболе:

(frac{xx_{0}}{a^{2}}-frac{yy_{0}}{b^{2}}=1)

Определение 21

Касательная к гиперболе в точке (M_{0}(x_{0}, y_{0})) представляет собой биссектрису угла между отрезками, которые соединяют рассматриваемую точку с фокусами.

Как построить гиперболу самостоятельно

Построение графика гиперболы следует начать с изображения прямоугольной системы координат Декарта. Алгоритм действий:

На листе бумаги нарисовать горизонтальную прямую. Выполнить действие следует таким образом, чтобы конец прямой с правой стороны был обозначен с помощью стрелки. Данная прямая является осью (X) и носит название абсциссы.
На середине оси ( Х) необходимо опустить перпендикуляр. Конец полученной прямой в верхней части нужно обозначить стрелкой. В результате получена ось (Y), которую называют ординатой.
На следующем шаге необходимо пронумеровать шкалу. С правой стороны на оси (Х) расположены положительные значения (Х) в порядке возрастания — от 1 и выше. С левой стороны — отрицательные. В верхней части на оси (Y) расположены положительные значения (Y) в порядке возрастания. В нижней части — отрицательные.

Примечание

Точка, в которой пересекаются абсцисса и ордината является началом координат, то есть числом 0. От данной точки следует откладывать все значения (Х) и (Y).

С помощью прямоугольной системы координат плоскость поделена на четыре части, которые называют четвертями и нумеруют против часовой стрелки. Для того чтобы построить график, требуется определить точки. Каждая точка координатной плоскости определяется парой чисел ((x;y)). Данные числа представляют собой координаты точки, где:

(х) — абсцисса точки;
(y) — ордината.

Гипербола представляет собой график функции, которая задана формулой:

(y=k/x)

где (k) — является каким-то коэффициентом, не равным нулю;

(x) — представляет собой независимую переменную.

Гипербола включает в себя две части, расположенные симметрично в разных четвертях. Данные части носят название ветвей гиперболы. При (k>0), ветви расположены в 1 и 3 четвертях. При (k<0), ветви гиперболы размещены во 2 и 4 четвертях.

Принцип построения гиперболы можно рассмотреть на примере, когда функция задана следующей формулой:

(y=3/х)

Так как коэффициент 3 обладает положительным значением, гипербола, соответственно, будет находиться в 1 и 3 четвертях. Можно взять произвольно значения (Х) и найти значения (Y). Таким образом, получатся координаты точек, с помощью которых можно изобразить гиперболу. Важно отметить, что (Х) не должно иметь нулевое значение, так как на 0 делить нельзя.

Поскольку мы знаем, что гипербола располагается в двух четвертях, то берем как положительные значения, так и отрицательные. Предположим, что (Х) равен: -6, -3, -1, 1, 3, 6. Далее можно рассчитать ординаты путем подстановки каждого значение (Х) в начальную формулу:

(y=3/-6)

(у=3/-3)

(у=3/-1)

(у=3/1)

(у=3/3)

(у=3/6)

В результате, значения ( Y) равны: -0.5, -1, -3, 3, 1, 0.5.

Полученные 6 точек с координатами необходимо отложить на системе координат. Далее точки соединяют с помощью кривых линий, как изображено на рисунке. В итоге получилась гипербола.

получилась гипербола

Источник: sovetclub.ru

Построение гиперболы по фокусам

Гиперболу можно построить, зная заданные вершины (А) и (В) и фокусное расстояние (FF1). Алгоритм построения следующий:

В первую очередь фокусное расстояние следует разделить пополам, чтобы получить точку 0.
Далее с левой стороны от фокуса (F) можно отметить ряд произвольных точек 1, 2, 3, 4 и так далее, расстояние между которыми постепенно увеличивается.
Затем нужно начертить вспомогательные окружности с центром в фокусе (F), имеющие радиусы (R1=1B), (R2=2B), (R3=3B), (R4=4B) и так далее.
На следующем этапе можно изобразить вспомогательные окружности с центром в фокусе (F1) и радиусами (r1=1A), (r2=2A), (r3=3A), (r4=4A) и так далее.
При пересечении вспомогательных окружностей определяется положение точек гиперболы. (С), (С1 )представляют собой точки, которые образованы в результате пересечения окружностей радиусов (R1) и (r1). Точки (D,D1) являются точками, в которых пересекаются окружности (R2) и (r2).
Полученные точки остается соединить с помощью плавной кривой линии, чтобы получить правую ветвь гиперболы.
Аналогичным способом следует выполнить построение левой ветви гиперболы.

FA1

FA2

FA3

FA4

FA5

FA6

FA7

FA8

FA9

FA10

Источник: graph.power.nstu.ru

Как построить гиперболу по точкам

Исходя из определения гиперболы, разница между расстояниями (r1) и (r2) для всех ее точек является постоянной величиной. Таким образом, переход от одной точки гиперболы к другой осуществляется путем увеличения или уменьшения данных характеристик. Алгоритм действий:

В первую очередь следует отложить точки (А1) и (А2). Точка ( А2) является точкой касания двух окружностей, центр одной из которых расположен в фокусе ( F1), а радиус составляет F1A2. Другая окружность обладает центром в фокусе (F2) и радиусом (F2A2).
Следующие точки гиперболы можно определить при пересечении пар окружностей с радиусами, которые равны:

пересечении пар окружностей

Источник: natalibrilenova.ru.

Пересечении пар окружностей с

Источник: natalibrilenova.ru.

Таким образом, новые значения радиусов превышают предыдущие на одинаковую величину. Чем ближе расположены точки, тем точнее будет построен график гиперболы.

Как построить график гиперболы по уравнению

Каноническое уравнение гиперболы записывают таким образом:

Каноническое уравнение гиперболы

Источник: mathter.pro

где («a») и («b») являются положительными действительными числами, причем, («а») может быть больше или меньше, чем («b»).

Важно отметить, что гипербола обладает двумя симметричными ветвями и двумя асимптотами.

Построение гиперболы можно рассмотреть на примере. Предположим, что она задана следующим уравнением:

построение гиперболы

Источник: mathter.pro

Рассматриваемое уравнение необходимо привести к каноническому виду:

Рассматриваемое уравнение

Источник: mathter.pro

Так как в правой части требуется получить единицу, необходимо обе части начального уравнения поделить на 20:

правой части требуется получить единицу

Источник: mathter.pro

Правая

Источник: mathter.pro

Далее следует сократить обе дроби:

Далее следует сократить обе дроби

Источник: mathter.pro

следует сократить обе дроби

Источник: mathter.pro

Затем нужно выделить квадраты в знаменателях:

Затем нужно выделить квадраты в знаменателях

Источник: mathter.pro

В результате получено каноническое уравнение:

В результате получено каноническое уравнение

Источник: mathter.pro

Существует два подхода к построению гиперболы:

геометрический;
алгебраический.

С практической точки зрения, эффективнее воспользоваться расчетами. В первую очередь следует определить асимптоты:

Источник: mathter.pro

Асимптоты равны:

Источник: mathter.pro

На втором этапе можно определить вершины гиперболы, которые соответствуют точкам на оси абсцисс с координатами:

Источник: mathter.pro

При у=0, каноническое уравнение гиперболы примет вид:

Источник: mathter.pro

Таким образом:

Источник: mathter.pro

Вершины гиперболы:

Источник: mathter.pro

Затем необходимо определить дополнительные точки. В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Согласно каноническому уравнению, можно выразить:

Источник: mathter.pro

В результате получим две функции. Первая функция определяет верхние дуги гиперболы:

Источник: mathter.pro

Вторая функция выражает нижние дуги гиперболы:

Источник: mathter.pro

Напрашивается нахождение точек с абсциссами:

Источник: mathter.pro

На последнем этапе следует изобразить асимптоты, вершины, дополнительные точки, симметричные точки в других координатных четвертях:

Источник: mathter.pro

После того, как все точки соединены, будет изображена гипербола.

После того, как все точки соединены, будет изображена гипербола

Источник: mathter.pro

Источник

Гипербола

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Функция заданная формулой (y=frac), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

гипербола, где k y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=frac<1>-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

Дробь (color <frac<1>>) отбрасываем
Остается y≠ -1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Находим вторую асимптоту.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

Находим вторую асимптоту.

Остается y≠ -1 это вторая асимптота.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: 8 класс, База знаний, Уроки Tag: Гипербола Leave a comment

Что такое гипербола

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие гиперболы

Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы в алгебре выглядит так:

, где a и b — положительные действительные числа.

Кстати, канонический значит принятый за образец.

В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.

Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.

Вспомним особенности математической гиперболы:

Две симметричные ветви.
Две асимптоты. Асимптота — это прямая, которая обладает таким свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Их значение помогает найти специальное уравнение асимптот гиперболы.

Если гипербола задана каноническим уравнением, то асимптоты можно найти так:

Пример 1. Построить гиперболу, которая задана уравнением 5(x^2) — 4(y^2) = 20.

Приведем данное уравнение к каноническому виду (x^2)/(a^2) — (y^2)/(b^2) = 1.

Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:

Сокращаем обе дроби в уме или при помощи трехэтажной дроби:

Выделяем квадраты в знаменателях:

Готово. Можно начертить гиперболу.

Можно было сделать проще и дроби левой части 5(x^2)/20 — 4(y^2)/20 = 1 сразу сократить и получить (x^2)/4 — (y^2)/5 = 1. Нам повезло с примером, потому что число 20 делится и на 4 и на 5. Рассмотрим пример посложнее.

Пример 2. Построить гиперболу, которая задана уравнением 3(x^2)/20 — 8(y^2)/20 = 1.

Произведем сокращение при помощи трехэтажной дроби:
Воспользуемся каноническим уравнением
- Найдем асимптоты гиперболы. Вот так:
  Важно! Без этого шага ветви гиперболы «вылезут» за асимптоты.
- Найдем две вершины гиперболы, которые расположены на оси абсцисс в точках A1(a; 0), A2(-a; 0).

Если y = 0, то каноническое уравнение (x^2)/(a^2) — (y^2)/(b^2) = 1 превращается в (x^2)/(a^2) = 1, из чего следует, что x^2 = a^2 -> x = a, x = -a.

Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).

Найдем дополнительные точки — хватит двух-трех.

В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.

Способ такой же, как при построении эллипса. Из полученного канонического уравнения

на черновике выражаем:

Уравнение распадается на две функции:

— определяет верхние дуги гиперболы (то, что ищем);

— определяет нижние дуги гиперболы.

Далее найдем точки с абсциссами x = 3, x = 4:

Изобразим на чертеже полученные асимптоты y = (√5/2)x, y = -(√5/2)x, вершины A1(2; 0), A2(-2; 0), дополнительные C1, C2 и симметричные им точки в других координатных четвертях. Аккуратно соединяем соответствующие точки у каждой ветви гиперболы.

Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.

Действительная ось гиперболы — отрезок А1А2.

Расстояние между вершинами — длина |A1A2| = 2a.

Действительная полуось гиперболы — число a = |OA1| = |OA2|.

Мнимая полуось гиперболы — число b.

В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.

Форма гиперболы

Повторим основные термины и узнаем, какие у гиперболы бывают формы.

Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.

Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.

Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.

Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.

Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.

Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.

Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Фокальное свойство гиперболы

Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).

Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение e = a/c, где c = √(a^2 + b^2), называется эксцентриситетом гиперболы. Из определения (2a 1 .

Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:

Рассмотрим, как это выглядит на прямоугольной системе координат:

пусть центр O гиперболы будет началом системы координат;
прямую, которая проходит через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F1 к точке F2);
прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:

Запишем это уравнение в координатной форме:

Избавимся от иррациональности и придем к каноническому уравнению гиперболы:

, т.е. выбранная система координат является канонической.

Если рассуждать в обратном порядке, можно убедиться, что все точки, координаты которых удовлетворяют уравнению (x^2)/(a^2) — (y^2)/(b^2) = 1, и только они, принадлежат геометрическому месту точек, называемому гиперболой. Именно поэтому аналитическое определение гиперболы эквивалентно его геометрическому определению.

Директориальное свойство гиперболы

Директрисы гиперболы — это две прямые, которые проходят параллельно оси.

ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.

Директориальное свойство гиперболы звучит так:

Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.

Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

На самом деле для фокуса F2 и директрисы d2 условие

можно записать в координатной форме так:

Избавляясь от иррациональности и заменяя e = a/c, c^2 — a^2 = b^2, мы придем к каноническому уравнению гиперболы. Аналогичные рассуждения можно провести для фокуса F1 и директрисы d1:

Построение гиперболы

Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.

Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.

В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:

Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:

Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.

По определению эксцентриситет гиперболы равен

Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.

Так как b^2 = c^2 — a^2, то величина b изменится.

При этом ε -> 1, b -> 0 и мнимые вершины B1, B2 стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы выражается в пределе в отрезок A1A2, а сама гипербола выражается в два луча на оси абсцисс: (-∞; -a] и [a; ∞).

При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.

Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.

Из определения следует, что в равносторонняя гиперболе a = b, поэтому ее каноническое уравнение выглядит так: x^2 — y^2 = a^2

Действительно, ε = c/a = √2, откуда c^2 = 2a^2 и b^2 = c^2 — a^2 = a^2. И так как а и b положительные числа, получаем a = b.

2.4 Гипербола

Гиперболой Называется геометрическое место точек на плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.

Обозначим эту постоянную через 2А, расстояние между фокусами через 2С, а оси координат выберем так же, как в разделе 2.3.

Пусть М(Х, У) – произвольная точка гиперболы (рисунок 2.4).

По определению гиперболы F2M – F1М = ±2A. (Знак плюс в правой части надо выбрать, если F2M > F1М, и минус, если F2M A).

Исследуем формулу гиперболы.

1. Уравнение (2.7) содержит квадраты текущих координат, следовательно, оси координат являются осями симметрии гиперболы. Ось симметрии, на которой находятся фокусы, называется фокальной осью, точка пересечения осей симметрии – центром гиперболы. Для гиперболы, заданной уравнением (2.7), фокальная ось совпадает с осью ОХ, а центр – с началом координат.

В этом случае координаты фокусов гиперболы имеют вид F1(с,0), F2(-с,0).

2. Точки пересечения с осями симметрии. Точки пересечения гиперболы с осями симметрии называются Вершинами гиперболы. Полагая в уравнении (2.7) У = 0, найдем абсциссы точек пересечения с осью ОХ:

или X2 = А2, откуда Х = ±А.

Итак, точки и являются вершинами гиперболы.

Если же в уравнении (2.7) принять x = 0, получим

или У2 = –B2,

Т. е. для У мы получили мнимые значения. Это означает, что гипербола не пересекает ось ОY.
В соответствии с этим ось симметрии, пересекающая гиперболу, называется действительной осью (фокальная ось); ось симметрии, которая не пересекает гиперболу, – ее мнимой осью. Для гиперболы, заданной уравнением (2.7), действительной осью симметрии является ось ОХ, а мнимой осью – ось ОY. Длина отрезка А1А2 = 2А, число А называется действительной полуосью гиперболы. Отложим на мнимой оси гиперболы по обе стороны от центра симметрии O отрезки ОВ1 и ОВ2 длиною B, тогда отрезок В1B2 = 2B называют мнимой осью, а величину B – мнимой полуосью гиперболы.

Из уравнения (2.7) видно, что , следовательно, |X| ³ A. Кривая имеет форму, изображенную на рисунке 2.5. Она располагается вне прямоугольника со сторонами, равными 2А и 2B, с центром в начале координат, и состоит из двух отдельных ветвей, простирающихся в бесконечность (см. рисунок 2.5). Диагонали этого прямоугольника определяются уравнениями

(2.8)

И являются Асимптотами гиперболы.

Если A = B, гипербола называется равносторонней.

Замечание 1. Если мнимая ось гиперболы равна 2А и расположена на оси ОХ, а действи-тельная ось равна 2B и расположена на оси ОY, то уравнение такой гиперболы (рисунок 2.6) имеет вид (каноническое уравнение гиперболы, если ее фокальная ось – ось Y)

(2.9)