Как посчитать высоту равнобедренного треугольника
Онлайн калькулятор
Чтобы вычислить высоту равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину двух равных сторон (a) и длину основания (b)
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину основания (b) и угол α
- длину основания (b) и угол β
Введите их в соответствующие поля и получите результат.
Если известны длина стороны а и основания b
Чему равна высота h равнобедренного треугольника если длина сторон , а длина основания
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и длина основания b?
Формула
h = √ a 2 — ( b /2) 2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
h = √ 10 2 — ( 5 /2) 2 = √ 100 — 6.25 ≈ 9.68 см
Если известны длина стороны а и угол α
Чему равна высота h равнобедренного треугольника если длина сторон , а угол
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
Пример
Если сторона a = 5 см, а ∠α = 45°, то:
h = 5⋅sin 45 ≈ 3,53 см
Если известны длина стороны а и угол β
Чему равна высота h равнобедренного треугольника если длина сторон , а угол
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
Пример
Если сторона a = 5 см, а ∠β = 30°, то:
Если известны длина стороны b и угол α
Чему равна высота h равнобедренного треугольника если длина основания , а угол
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол α?
Формула
Пример
Если сторона b = 20 см, а ∠α = 35°, то:
Если известны длина стороны b и угол β
Чему равна высота h равнобедренного треугольника если длина основания , а угол
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол β?
Равнобедренный треугольник: свойства, признаки и формулы
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
Равнобедренным называется треугольник, у которого две стороны равны.
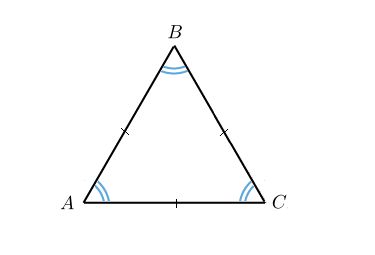
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Значит, ∠A = ∠C = 80°.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.
Высота и сторона «A» равнобедренного треугольника
Свойства
Так как высота равнобедренного треугольника, опущенная на основание, является одновременно и биссектрисой и медианой, следовательно, она делит основание и угол при вершине на две равные части, образуя прямоугольный треугольник со сторонами a и b/2. Из теоремы Пифагора в таком треугольнике можно найти само основание, а затем рассчитать все остальные возможные данные. (рис.88.2) h^2+(b/2)^2=a^2 b=√(a^2-h^2 )/2
Чтобы вычислить периметр равнобедренного треугольника, надо к двум боковым сторонам прибавить основание или приведенный выше радикал через высоту. P=2a+b=2a+√(a^2-h^2 )/2
Площадь равнобедренного треугольника через высоту и основание по определению вычисляется как половина их произведения. Заменив основание на соответствующее ему выражение, получаем площадь через высоту и боковую сторону равнобедренного треугольника. S=hb/2=(h√(a^2-h^2 ))/4
В равнобедренном треугольнике равны не только боковые стороны, но и углы при основании, а так как в сумме они дают всегда 180 градусов, то любой из углов можно найти, зная другой. Первый угол вычисляется по теореме косинусов, приведенной для равных боковых сторон, а второй можно найти через разность от 180. (рис.88.1) cosα=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cosβ=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 ) α=(180°-β)/2 β=180°-2α
Центральные медиана и биссектриса, опущенные на основание совпадают с высотой, а боковые медианы, высоты и биссектрисы можно найти по следующим формулам для равнобедренных треугольников. Чтобы вычислить их через высоту и боковую сторону, нужно заменить основание на эквивалентное ему выражение. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2
Высота, опущенная на боковую сторону, через высоту, опущенную на основание и боковую сторону равнобедренного треугольника. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a=(√(a^2-h^2 ) √((4a^2-a^2+h^2)))/2a=√((a^2-h^2)(3a^2+h^2))/2
Биссектрисы, направленные в боковые стороны, также могут быть выражены через боковую сторону и центральную высоту треугольника . (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=√(a(a^2-h^2)(2a+√(a^2-h^2 )) )/(a+√(a^2-h^2 ))
Средняя линия проводится параллельно любой стороне треугольника, соединяя середины боковых в ее отношении сторон. Таким образом, она всегда оказывается равна половине параллельной ей стороны. Вместо неизвестного основания в формулу можно подставить используемый радикал, чтобы найти среднюю линию через высоту и боковую сторону равнобедренного треугольника(рис. 88.5) M_b=b/2=√(a^2-h^2 )/2 M_a=a/2
Радиус окружности, вписанной в равнобедренный треугольник, начинается от точки на пересечении биссектрис и уходит перпендикулярно в любую из сторон. Чтобы его найти через высоту и боковую сторону треугольника, надо заменить основание в формуле на радикал. (рис. 88.6) r=1/2 √(((a^2-h^2)(2a-√(a^2-h^2 )))/(2a+√(a^2-h^2 )))
Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы путем подстановки радикала через высоту и боковую сторону вместо основания. (рис. 88.7) R=a^2/√(3a^2-h^2 )
http://skysmart.ru/articles/mathematic/chto-takoe-ravnobedrennyj-treugolnik
http://geleot.ru/education/math/geometry/calc/triangle/isosceles_triangle_height_and_sides_a
|
Равнобедренный треугольник — это треугольник, у которого 2 стороны равны. Равные стороны — это рёбра, а 3 сторона — основание. Вариант 1 Если известно, чему равна боковая сторона, а также высота, опущенная на основание. Как известно, высота перпендикулярна основанию, а в случае с равнобедренным треугольником она разбивает его на 2 равных прямоугольных треугольника. Можно по теореме Пифагора найти половину основания, а затем это значение умножить на 2. Вот формула: b = 2√(a² — h²) Вариант 2 Если известно, чему равна боковая сторона и один из углов. Нужно воспользоваться теоремой синусов: a/sinα = b/sinβ = c/sinγ. c = (a*sinγ)/sinα. Так как в равнобедренном треугольнике углы при основании равны, то легко можно найти 2 оставшихся угла, исходя из того, что сумма 3 углов равна 180 градусов. система выбрала этот ответ лучшим Алиса в Стране 5 лет назад К сожалению у нас нет условия задачи, из которой было бы ясно — на основании каких данных мы должны искать основание нашего равнобедренного треугольника (две стороны боковые которого равны между собой, а основание — это нижняя сторона, которая как раз двум другим не равна). Поэтому рассмотрим несколько вариантов. 1.) Допустим, мы знаем, чему равна боковая сторона и угол треугольника (любой из трех). Тогда мы сначала легко вычисляем два других угла треугольника, помня, что их сумма всегда равна 180 градусам, а затем применяем теорему синусов: следовательно с (основание) будет равно: 2.) Допустим, мы знаем чему равна боковая сторона и высота нашего треугольника. Тогда мы сначала находим половину его основания (она является катетом треугольника, полученного делением исходного равнобедренного треугольника его высотой на два прямоугольных треугольника), применив теорему Пифагора. где с — основание треугольника, которое мы ищем, h — его высота. Марина Вологда 5 лет назад Чтобы найти основание равнобедренного треугольника, необходимо вспомнить геометрию. Что такое равнобедренный треугольник — это треугольник, в котором две из трех сторон равны. Теперь вспомним что такое основание треугольника — это как раз третья сторона, которая не равна остальным двум. Так как у нас нет никаких данных задачи, значит следует указать только формулы, по которым можно найти основание. Основание можно найти применив теорему Пифагора по формуле: b = 2√(a² — h²) где h — это высота опущенная на основание; а -сторона треугольника. Чтобы понять, как правильно решать, вот примерная задача: А вот решение для задачи: JuliGor 9 лет назад Для того, чтобы найти основание равнобедренного треугольника? нам необходимо знать или один из углов, или же высоту треугольника, которая проводится к его основанию. Основание можно вычислить по следующей, вполне легкой формуле: где b — длина основания треугольника; a — длина стороны треугольника; B — это угол, который противоположен основанию. Alen4uk 5 лет назад Для начала вспомним, какой треугольник называется равнобедренным и из этих его свойств будем уже находить величину основания. Как видим из рисунка, равнобедренный треугольник- это треугольник, у которого две стороны равны и они называются боковыми. Третья же сторона является основанием этого треугольника. Равные стороны называются боковыми. Какие же свойства имеет равнобедренный треугольник, которые помогут нам найти его основание? Углы при основании у равнобедренного треугольника равны между собой. Высота, которую мы опускаем с верхнего угла на основание одновременно является и биссектрисой и медианой. Чтобы найти площадь равнобедренного треугольника нужно разделить на 2 произведение основания на высоту, проведенную к этому основанию. К сожалению, нам не даны условия задачи, поэтому можно использовать несколько формул. Все будет зависеть от данных задачи. Используя эти свойства, мы для нахождения основания можем использовать следующие формулы: Так же нам может помочь в решении теорема синусов. Бекки Шарп 5 лет назад При решении задач с равнобедренным треугольником нужно использовать свойства как равнобедренного треугольника, так и прямоугольного, поскольку высота равнобедренного треугольника делит его на 2 одинаковых прямоугольных. Основание равнобедренного треугольника ищется, когда есть какие-то исходные данные. Например известны сторона и угол. Тогда поступаем следующим образом: Находим третий угол ( 180 градусов минус сумму двух углов) и используем теорему косинусов: где АС -основание, АВ и ВС — стороны. Рассмотри задачу, когда известны стороны равнобедренного треугольника. Тогда основание ищется, используя теорему Пифагора. Вот здесь нам и понадобится разделить равнобедренный треугольник на два прямоугольных. В итоге основание АС будет равно — 2 квадратных корня из разности квадратов стороны АВ и высоты ВН. 127771 5 лет назад Для начала нужно понять, что такое равнобедренный треугольник, таким треугольником называют треугольник у которого две стороны равны. Ниже рисунок такого треугольника: К сожалению нет данных в вопросе. Например, если задана площадь и высота ВH. Тогда основание (на рисунке выше сторона АС) будет равна площадь разделить на высоту BH и умножить на 0,5. Если же нам известна одна сторона и высота треугольника, можно воспользоваться теоремой Пифагора. Ниже представлена формула, по которой можно вычислить основание: b = 2√(a² — h²). Возможно и другие варианты, например, если известна сторона и угол, тогда можно воспользоваться теоремой косинусов или синусов. Nelli4ka 5 лет назад Можно найти для начала значение половины основания, а затем умножить это значение на два. Смысл в том, что мы опускаем на основание из противоположного угла высоту (она в равнобедренном треугольнике совпадает с биссектрисой и медианой), получается два прямоугольных треугольника. Вспоминаем теорему Пифагора, вычисляем разницу между гипотенузой и высотой, извлекаем корень. Конечно, в этом случае по условиям задачи нам должно быть известно значение высоты. Если же известно значение боковой стороны и противоположного основанию угла, то легче всего пойти через формулу синусов: Также можно воспользоваться формулой косинусов: Бархатные лапки 5 лет назад Равнобедренный треугольник — это треугольник у которого две стороны одинаковые, они боковыми, а третья сторона — это основание. Чему равняется основание возможно узнать, если у нас есть данные чему равна одна боковая сторона (а вторая боковая будет равняться также) и высота. В этом случае воспользуемся такой формулой: b = 2(a — h). Как уже видно, для этого нам нужно знать значение боковой стороны и высоты (которая в равнобедренном треугольнике будет такая же как медиана и биссектриса). Но также можно решить эту задачку и другим способом, для этого должны знать чему равняется боковая сторона и один из углов. kkkaratisttt 5 лет назад В задачах такого типа всегда даётся вариант, где у вас известен один угол, если вы знаете одну сторону угла равнобедренного треугольника. То вы умножаете значения на два угла и высоту равнобедренного треугольника. Таким образом вы получите чему равно основание этого треугольника. Бисектриса тоже может вам помоч. Знаете ответ? |
Как найти основание треугольника
Часто в задачах по планиметрии и тригонометрии требуется найти основание треугольника. Для этой операции существует даже несколько методов.

Вам понадобится
- Калькулятор
Инструкция
Строгого определения понятия «основание треугольника» в геометрии не существует. Как правило, этим термином обозначается, сторона треугольника, к которой из противоположной вершины проведен перпендикуляр (опущена высота). Также этим термином принято называть «неравную» сторону равностороннего треугольника. Поэтому выберем из всего многообразия примеров, известного в математике под понятием «решение треугольников», варианты, в которых встречаются высоты и равносторонние треугольники.
Если известны высота и площадь треугольника, то для того чтобы найти основание треугольника (длину стороны, на которую опущена высота), воспользуемся формулой нахождения площади треугольника, утверждающей, что площадь любого треугольника можно посчитать, умножив половину длины основания на длину высоты:
S=1/2*c*h, где:
S — площадь треугольника,
с — длина его основания,
h — длина высоты треугольника.
Из этой формулы находим:
с=2*S/h.
Например, если площадь треугольника равняется 20 кв.см., а длина высоты — 10 см, то основание треугольника будет:
с=2*20/10=4 (см).
Если известны боковая сторона и периметр равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=Р-2*а, где:
Р — периметр треугольника,
а — длина боковой стороны треугольника,
с — длина его основания.
Если известны боковая сторона и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=а*√(2*(1-cosC)), где:
C — величина противоположного основанию угла равностороннего треугольника,
а — длина боковой стороны треугольника.
с — длина его основания.
(Формула является прямым следствием теоремы косинусов)
Имеется и более компактная запись этой формулы:
с=2*а*sin(B/2)
Если известны боковая сторона и величина смежного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей легко запоминающейся формуле:
с=2*а*cosA
A — величина смежного основанию угла равностороннего треугольника,
а — длина боковой стороны треугольника.
с — длина его основания.
Эта формула является следствием теоремы о проекциях.
Если известен радиус описанной окружности и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=2*R*sinC, где:
C — величина противоположного основанию угла равностороннего треугольника,
R — радиус описанной вокруг треугольника окружности,
с — длина его основания.
Эта формула является прямым следствием теоремы синусов.
Обратите внимание
Для начала абстрагируемся от частностей и посмотрим, как найти основание треугольника, не являющегося ни равносторонним, ни равнобедренным, ни прямоугольным. Так как основанием в такой фигуре может служить любая сторона, для начала выберем какую-то грань и «обзовём» её основанием. Соответственно, повернём треугольник так, чтобы он на ней стоял, и будем искать её длину.
Полезный совет
Как найти основание равнобедренного треугольника? Смотря, что дано в данном треугольнике. Если в равнобедренном треугольнике дана сторона и угол, который находится напротив основания, то можете провести из этого угла высоту треугольника. В результате, по свойству равностороннего треугольника вы получите два равных прямоугольника.
Источники:
- Медианы, биссектрисы и высоты треугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Равнобедренный треугольник это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона называется основанием треугольника. По определению, каждый правильный треугольник также является равнобедренным. Равнобедренный треугольник обладает следующими свойствами:
- углы при основании равны
- биссектриса, проведенная к основанию, является медианой и высотой
- медиана, проведенная к основанию, является биссектрисой и высотой
- высота, проведенная к основанию, является биссектрисой и медианой
.
Найти основание равнобедренного треугольника
зная сторону и высоту
Сторона равнобедренного треугольника a
Высота равнобедренного треугольника h
Как найти основание треугольника
Для того, чтобы найти основание треугольника, можно воспользоваться одной из формул, обязательно должны быть заданы для этой формулы площадь и высота. Вообще, в геометрии и тригонометрии нет четкого обозначения того, какая именно сторона является основанием, так как его можно перевернуть на любую из них. Чтобы найти основание треугольника, его для начала нужно обозначить, а именно выделить ту сторону, на противоположном от которой углу расположена высота. Это перпендикуляр по отношению к основанию, и в зависимости от типа треугольника, он может делить основание пополам.
Есть ряд основных формул, по которым можно найти основание треугольника, в том числе и равнобедренного. Основная формула выглядит так:
- S – площадь треугольника;
- С – длина основания треугольника, которую надо найти;
- h – высота треугольника.
Исходя из тех данных, которые у нас есть, можно найти основание треугольника, если дана площадь и высота.
Как найти основание равнобедренного треугольника
По этой же формуле можно найти основание равнобедренного треугольника. Если известна одна сторона и значение угла напротив основания, то можно вывести по формуле высоту треугольника и потом найти основание по общей формуле.
Как найти основание равностороннего треугольника через косинус
Если известны боковая сторона и величина противоположного основанию угла, можно найти основание треугольника через формулу, где используется значение косинуса.
- С – величина противоположного основанию угла равностороннего треугольника;
- А – длина боковой стороны треугольника;
- с – длина основания.
Эта формула для того, чтобы найти основание треугольника, основана на теореме косинусов и имеет более известную и более простую для применения формулу с=2*а*sin(B/2).
А еще интересно знать, стоит ли покупать евро, так как валюта постоянно дорожает.
Как найти основание треугольника
Строгого определения понятия «основание треугольника» в геометрии не существует. Как правило, этим термином обозначается, сторона треугольника, к которой из противоположной вершины проведен перпендикуляр (опущена высота). Также этим термином принято называть «неравную» сторону равностороннего треугольника. Поэтому выберем из всего многообразия примеров, известного в математике под понятием «решение треугольников», варианты, в которых встречаются высоты и равносторонние треугольники.
Если известны высота и площадь треугольника, то для того чтобы найти основание треугольника (длину стороны, на которую опущена высота), воспользуемся формулой нахождения площади треугольника, утверждающей, что площадь любого треугольника можно посчитать, умножив половину длины основания на длину высоты:
S=1/2*c*h, где:
S — площадь треугольника,
с — длина его основания,
h — длина высоты треугольника.
Из этой формулы находим:
с=2*S/h.
Например, если площадь треугольника равняется 20 кв.см., а длина высоты — 10 см, то основание треугольника будет:
с=2*20/10=4 (см).
Если известны боковая сторона и периметр равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=Р-2*а, где:
Р — периметр треугольника,
а — длина боковой стороны треугольника,
с — длина его основания.
Если известны боковая сторона и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=а*√(2*(1-cosC)), где:
C — величина противоположного основанию угла равностороннего треугольника,
а — длина боковой стороны треугольника.
с — длина его основания.
(Формула является прямым следствием теоремы косинусов)
Имеется и более компактная запись этой формулы:
с=2*а*sin(B/2)
Если известны боковая сторона и величина смежного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей легко запоминающейся формуле:
с=2*а*cosA
A — величина смежного основанию угла равностороннего треугольника,
а — длина боковой стороны треугольника.
с — длина его основания.
Эта формула является следствием теоремы о проекциях.
Если известен радиус описанной окружности и величина противоположного основанию угла равностороннего треугольника, то длину основания можно посчитать по следующей формуле:
с=2*R*sinC, где:
C — величина противоположного основанию угла равностороннего треугольника,
R — радиус описанной вокруг треугольника окружности,
с — длина его основания.
Эта формула является прямым следствием теоремы синусов.
- Медианы, биссектрисы и высоты треугольника
- Как вычислить основание равнобедренного треугольника
- Как найти основание у равнобедренного треугольника
- Как найти боковую сторону равнобедренного треугольника, если дано основание
Основание треугольника
Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение
Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
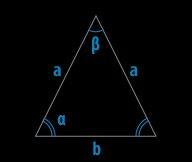
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
- Теорема о равенстве углов: в равнобедренном треугольнике углы при основании равны.
- Теорема о равенстве медианы, биссектрисы и высоты, проведенной к основанию. Теорема особенно подчеркивает, что из трех возможных медиан, высот и биссектрис, только проведенные к основанию окажутся равными между собой.
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.
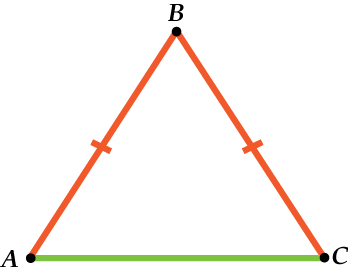
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.
Рис. 3. Равносторонний треугольник.
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.