Как найти основание пирамиды 5 класс - Исправление недочетов и поиск решений вместе с Examum.ru

Ответы к учебнику для 5 класса. А. Г. Мерзляк

Переход на главную страницу сайта

Вопросы к параграфу

1. Какие предметы дают представление о прямоугольном параллелепипеде?

Коробка, кирпич, спичечный коробок, ящик, пакет молока или сока, платяной шкаф и т.д.

2. Из каких фигур состоит поверхность прямоугольного параллелепипеда?

Из шести прямоугольников.

3. Сколько граней имеет прямоугольный параллелепипед?

Шесть граней.

4. Сколько пар противолежащих граней имеет прямоугольный параллелепипед?

У прямоугольного параллелепипеда три паны противолежащих граней.

5. Каким свойством обладают противолежащие грани прямоугольного параллелепипеда?

Противолежащие грани прямоугольного параллелепипеда равны.

6. Как называют стороны граней прямоугольного параллелепипеда?

Стороны граней прямоугольного параллелепипеда называют рёбрами.

7. Как называют вершины граней прямоугольного параллелепипеда?

Вершины граней прямоугольного параллелепипеда называют вершинами.

8. Сколько вершин имеет прямоугольный параллелепипед?

Прямоугольный параллелепипед имеет 8 вершин.

9. Сколько рёбер имеет прямоугольный параллелепипед?

Прямоугольный параллелепипед имеет 12 рёбер.

10. Какое общее название имеют длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину?

Измерения.

11. Какие названия измерений прямоугольного параллелепипеда используют для их различия?

Длина, ширина, высота.

12. Какую фигуру называют кубом?

Куб — это прямоугольный параллелепипед, у которого все измерения равны.

13. Из каких фигур состоит поверхность куба?

Из шести равных квадратов.

14. Из каких фигур состоит поверхность пирамиды?

Поверхность пирамиды состоит из боковых граней — треугольников, имеющих общую вершину, и основания.

15. Какую пирамиду называют треугольной? Четырёхугольной?

Треугольной пирамидой называют пирамиду, у основания которой три стороны, то есть основание является треугольником.

Четырехугольной пирамидой называют пирамиду, у основания которой четыре стороны, то есть основание является четырёхугольником.

16. Что называют вершиной пирамиды?

Вершиной пирамиды называют общую вершину боковых граней.

17. Что называют рёбрами основания пирамиды?

Стороны основания пирамиды называют рёбрами основания пирамиды.

18. Что называют боковыми рёбрами пирамиды?

Боковыми рёбрами пирамиды называют стороны боковых граней, не принадлежащие основанию.

Решаем устно

1. Вычислите:

13 • 4 • 25 = 13 • (4 • 25) = 13 • 100 = 1 300
4 • 5 • 78 • 5 = (4 • 5) • 78 • 5 = (20 • 5) • 78 = 100 • 78 = 7 800
125 • 943 • 8 = (125 • • 943 = 1 000 • 943 = 943 000

2. Упростите выражение:

3a • 16b = 48 ab
4m •9n •5k = 180 mnk
7a •2b •50c •8d = 5600 abcd

3. Раскройте скобки:

2(a + b) = 2a + 2b
(3 — b) • 5 = 3 • 5 — b • 5 = 15 — 5b
6m(7n + 8p) = 6m • 7n + 6m • 8p = 42 mn + 48 mp

4. Найдите периметр прямоугольника, площадь которого равна 28 см², а одна из его сторон — 7 см.

1) 28 : 7 = 4 (см) — длина второй стороны прямоугольника.

2) (4 + 7) • 2 = 11 • 2 = 22 (см) — периметр прямоугольника.

Ответ: периметр равен 22 см.

5. В магазине разложили 6 ц яблок в ящики так, что в каждом ящике оказалось по 12 кг яблок. Сколько ящиков заполнили яблоками?

6ц = 600 кг.

600 : 12 = 50 (ящиков) — заполнили яблоками.

Ответ: 50 ящиков.

6. Во сколько раз площадь квадрата, сторона которого равна 6 см, больше площади квадрата со стороной 2 см?

1) 6 • 6 = 36 (см²) — площадь квадрата со стороной 6 см.

2) 2 • 2 = 4 (см²) — площадь квадрата со стороной 2 см.

3) 36 : 2 = 18 (раз) — площадь квадрата со стороной 6 см больше площади квадрата со стороной 2 см.

Ответ: в 18 раз.

Упражнения

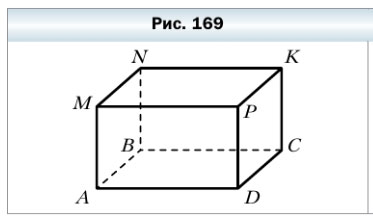
598. На рисунке 169 изображён прямоугольный параллелепипед ABCDMNKP. Назовите:

1) грани, которым принадлежит вершина С — ABCD, NKCB, PKCD

2) рёбра, равные ребру ВС — AD, MP, NK

3) верхнюю грань — MNKP

4) вершины, принадлежащие нижней грани — A, B, C, D

5) грани, имеющие общее ребро AM — AMNB, AMPD

6) грань, равную грани DPKC — AMNB

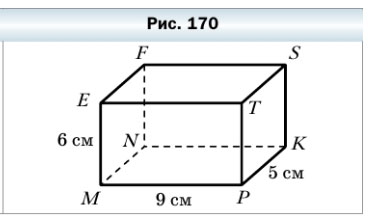
599. Измерения прямоугольного параллелепипеда MNKPEFST (рис. 170) равны 9 см, 5 см и 6 см. Вычислите сумму длин всех его рёбер и площадь его поверхности.

В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:

рёбро EM = FN = SK = TP = 6 см
рёбро MP = ET = FS = NK = 9 см
рёбро PK = MN = EF = TS = 5 см

6 • 4 + 9 • 4 + 5 • 4 = 24 + 36 + 20 = 80 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.

Поверхность прямоугольного параллелепипеда состоит из 6 граней:

площадь грани EFST = MNKP = 5 • 9 = 45 см²
площадь грани EFNM = TSKP = 6 • 5 = 30 см²
площадь грани ETPM = FSKN = 9 • 6 = 54 см²

45 • 2 + 30 • 2 + 54 • 2 = 90 + 60 + 108 = 258 (см²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.

Ответ: длина всех рёбер 80 см, площадь поверхности 258 см².

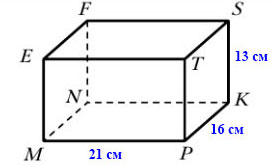
600. Найдите сумму длин всех рёбер прямоугольного параллелепипеда, измерения которого равны 13 см, 16 см, 21 см.

В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:

рёбро EM = FN = SK = TP = 13 см
рёбро MP = ET = FS = NK = 21 см
рёбро PK = MN = EF = TS = 16 см

13 • 4 + 16 • 4 + 21 • 4 = 52 + 64 + 84 = 200 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.

Ответ: длина всех рёбер 200 см.

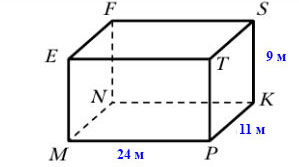
601. Найдите площадь поверхности прямоугольного параллелепипеда, измерения которого равны 9 м, 24 м, 11 м.

Поверхность прямоугольного параллелепипеда состоит из 6 граней:

площадь грани EFST = MNKP = 24 • 11 = 264 м²
площадь грани EFNM = TSKP = 9 • 11 = 99 м²
площадь грани ETPM = FSKN = 24 • 9 = 216 м²

264 • 2 + 99 • 2 + 216 • 2 = 528 + 198 + 432 = 1 158 (м²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.

Ответ: площадь поверхности 1 158 м².

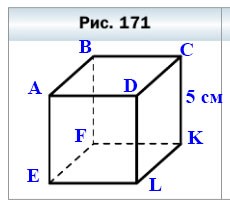
602. Вычислите площадь поверхности и сумму длин всех рёбер куба (рис. 171), ребро которого равно 5 см.

В кубе ABCDEFKL всего 12 рёбер и они все равны 5 см.

5 • 12 = 60 (см) — длина всех рёбер куба ABCDEFKL.

Поверхность куба состоит из 6 граней и они все равны 5 • 5 = 25 см²

25 • 6 = 150 (см²) — площадь поверхности куба ABCDEFKL.

Ответ: длина всех рёбер 60 см, площадь поверхности 150 см².

603. Найдите сумму длин всех рёбер и площадь поверхности куба, если его ребро равно 7 см.

В кубе ABCDEFKL всего 12 рёбер и они все равны 7 см.

7 • 12 = 84 (см) — длина всех рёбер куба ABCDEFKL.

Поверхность куба состоит из 6 граней и они все равны 7 • 7 = 49 см²

49 • 6 = 294 (см²) — площадь поверхности куба ABCDEFKL.

Ответ: длина всех рёбер 84 см, площадь поверхности 294 см².

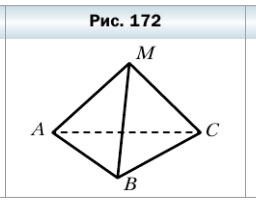
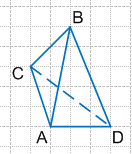
604. На рисунке 172 изображена пирамида МАВС. Укажите:

1) основание пирамиды — ABC

2) вершину пирамиды — M

3) боковые грани пирамиды — AMB, AMC, BMC

4) боковые рёбра пирамиды — AM, BM, CM

5) рёбра основания пирамиды — AB, BC, AC

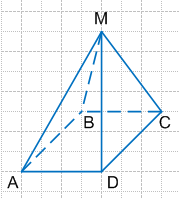
605. На рисунке 173 изображена пирамида SABCD. Укажите:

1) основание пирамиды — ABCD

2) вершину пирамиды — S

3) боковые грани пирамиды — ADS, DCS, CBS, ABS

4) боковые рёбра пирамиды — AS, BS, CS, DS

5) рёбра основания пирамиды — AB, BC, CD, DA

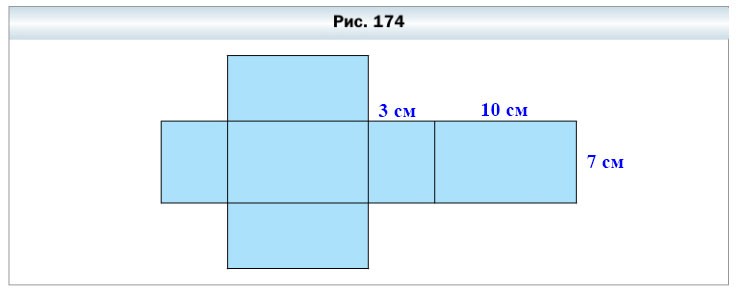
606. На рисунке 174 изображена развёртка прямоугольного параллелепипеда.

1) Из скольких прямоугольников состоит развёртка? — из 6 прямоугольников.

2) Сколько пар равных прямоугольников содержит развёртка? — 3-х пары равных прямоугольников.

3) Какова площадь этой развёртки, если измерения параллелепипеда равны 10 см, 7 см и 3 см?

S = (10 • 7) • 2 + (3 • 10) • 2 + (7 • 3) • 2 = 70 • 2 + 30 • 2 + 21 • 2 = 140 + 60 + 42 = 242 см²

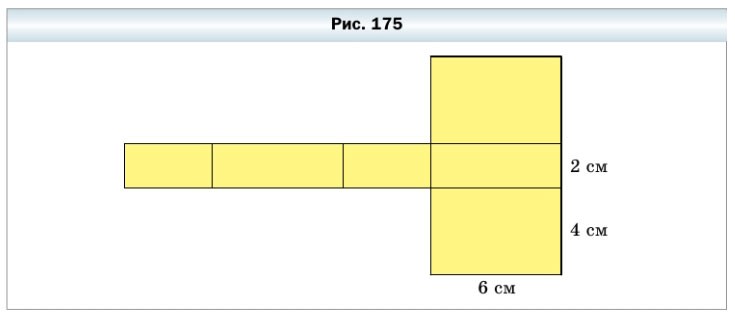
607. Вычислите площадь поверхности прямоугольного параллелепипеда, развёртка которого изображена на рисунке 175.

S = (6 • 4) • 2 + (6 • 2) • 2 + (4 • 2) • 2 = 24 • 2 + 12 • 2 + 8 • 2 = 48 + 24 + 16 = 88 см²

Ответ: площадь поверхности равна 88 см².

608. Высота прямоугольного параллелепипеда равна 20 см, что на 5 см больше его ширины и в 3 раза меньше его длины. Вычислите площадь поверхности параллелепипеда.

1) 20 — 5 = 15 (см) — ширина прямоугольного параллелепипеда.

2) 20 • 3 = 60 (см) — длина прямоугольного параллелепипеда

3) (60 • 20) • 2 + (60 • 15) • 2 + (20 • 15) • 2 = 1 200 • 2 + 900 • 2 + 300 • 2 = 2 400 + 1 800 + 600 = 4 800 (см²) — площадь поверхности прямоугольного параллелепипеда.

Ответ: S = 4 800 см².

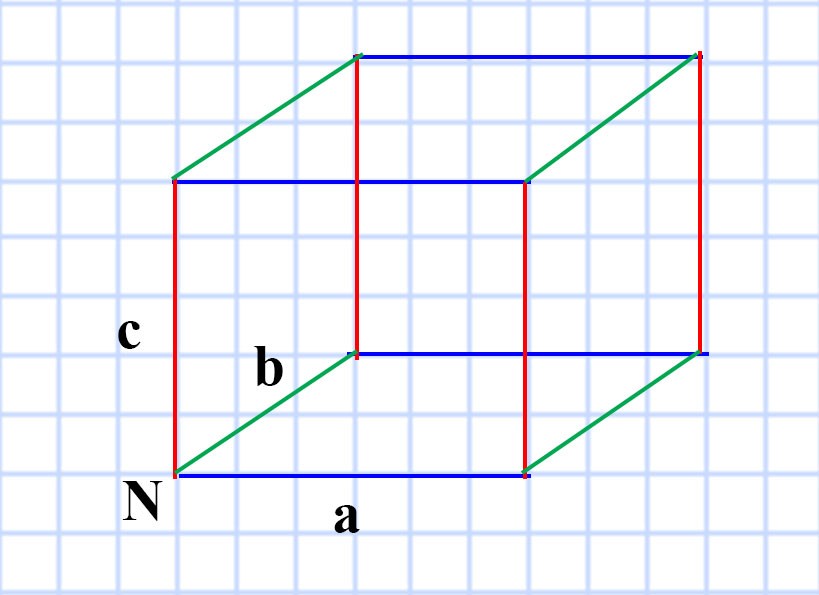
609. Сумма длин всех рёбер прямоугольного параллелепипеда равна 28 см. Найдите сумму длин трёх его рёбер, имеющих общую вершину.

В прямоугольном параллелепипеде всего 12 ребер. Причём:

4 ребра равны длине a — рёбра синего цвета
4 ребра равны ширине b — рёбра зелёного цвета
4 ребра равны ширине c — рёбра красного цвета

Мы знаем, что сумма длин всех рёбер этого прямоугольного параллелепипеда равна 28 см.

Значит, можно записать:

4a + 4b + 4с = 28
4 (a + b + с ) = 28
a + b + с = 28 : 4
a + b + с = 7 (см)

Так как рёбра a, b и с сходятся в общей вершине N, то искомая сумма длин трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину равна 7 см.

Ответ: 7 см.

610. Прямоугольный параллелепипед и куб имеют равные площади поверхностей. Длина параллелепипеда равна 18 м, что в 2 раза больше, чем его ширина, и на 8 м больше, чем его высота. Найдите ребро куба.

1) 18 : 2 = 9 (м) — ширина параллелепипед.

2) 18 — 8 = 10 (м) — высота параллелепипеда.

3) (18 • 9) • 2 + (18 • 10) • 2 + (10 • 9) • 2 = 162 • 2 + 180 • 2 + 90 • 2 = 324 + 360 + 180 = 864 (м²) — площадь поверхности параллелограмма.

Значит площадь поверхности куба равна 864 м². Так как у куба всего 6 граней и все они одинаковы, то можно найти площадь грани куба.

4) 864 : 6 = 144 (м²) — площадь грани куба.

Для того, чтобы найти длину ребра куба, надо подобрать такое число, квадрат которого будет равняться числу 144. Это число 12 (12 • 12 = 144).

Значит длина ребра куба равна 12 м.

Ответ: 12 метров.

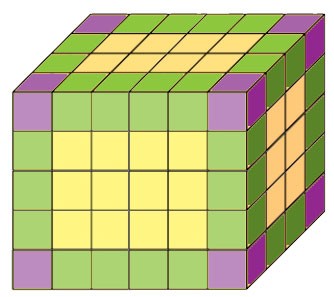
611. Брусок, имеющий форму прямоугольного параллелепипеда с измерениями 4 см, 5 см и 6 см, покрасили со всех сторон и разрезали на кубики с ребром 1 см. Сколько получилось кубиков, у которых:

1) окрашено три грани — 8 кубиков (фиолетовые), которые расположены по вершинам прямоугольного параллелепипеда.

2) окрашено две грани — 36 кубков (зелёные), которые расположены по рёбрам параллелепипеда, но не являются его вершинами (4 • 4 + 3 • 4 + 2 • 4 = 16 + 12 + 8 = 36):

по 4 кубика на 4 рёбрах длиной 6 см
по 3 кубика на 4 рёбрах длиной 5 см
по 2 кубика на 4 рёбрах длиной 4 см

3) окрашено одна грань — 52 кубика (жёлтые), которые не примыкают ни к вершинам, ни к рёбрам параллелепипеда (12 • 2 + 8 • 2 + 6 • 2 = 24 + 16 + 12 = 52):

4 • 3 = 12 кубиков на двух гранях размерами 6 см х 5 см
4 • 2 = 8 кубиков на двух гранях размерами 6 см х 4 см
3 • 2 = 6 кубиков на двух гранях размерами 5 см х 5 см

Упражнения для повторениях

612. Скорость космического корабля «Восток», на котором Юрий Гагарин совершил свой полёт, равна 8 км/с.

1) За сколько минут он пролетал 960 км?

960 : 8 = 120 (с) — нужно кораблю для преодоления 960 км.

120 с = 2 мин

Ответ: 2 минуты.

2) Какое расстояние он пролетал за 1 ч?

1 ч = 60 мин = 3 600 с

8 • 3 600 = 28 800 (км) — пролетает корабль за 1 час.

Ответ: 28 800 км.

613. Из листа картона можно вырезать шесть одинаковых квадратов. Сколько листов картона надо для того, чтобы вырезать 50 таких квадратов?

50 = 6 • 8 + 2

Значит нужно 8 + 1 = 9 листов.

Ответ: 9 листов.

614. Поезд отправился со станции в 16 ч со скоростью 54 км/ч. В 19 ч с этой же станции в противоположном направлении отправился второй поезд. В 24 ч расстояние между ними было равно 642 км. С какой скоростью двигался второй поезд?

1) 24 — 16 = 8 (часов) — двигался первый поезд.

2) 54 • 8 = 432 (км) — проехал первый поезд за 8 часов.

3) 24 — 19 = 5 (часов) — двигался второй поезд.

4) 642 — 432 = 210 (км) — проехал второй поезд за 5 часов.

5) 210 : 5 = 42 (км/ч) — скорость второго поезда.

Ответ: 42 км/ч.

615. Решите уравнение:

Задача от мудрой совы

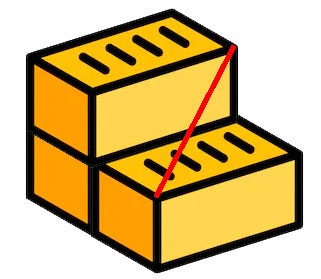
616. Как с помощью линейки измерить диагональ кирпича, имея ещё несколько таких кирпичей? (Диагональ параллелепипеда — это отрезок, соединяющий две его вершины, не принадлежащие одной грани.)

Для этого нам потребуется как минимум 3 кирпича:

Сложим кирпичи лесенкой
Линейкой измерим расстояние так, как показано на рисунке.
Измеренное расстояние будет точно соответствовать длине диагонали кирпича.

Ответы к учебнику для 5 класса. А. Г. Мерзляк

Переход на главную страницу сайта

Источник

Цели урока:

Познавательные:

Познакомить учащихся с геометрическим телом —
пирамидой.

Обучающие:

Уметь из данных многогранников находить
пирамиду,
Уметь находить основание и боковые грани
пирамиды,
Уметь давать название пирамидам.

Развивающие:

Развитие логического мышления, умения
самостоятельно работать, умения говорить и
слушать

Воспитательные:

Выработка привычки к постоянной занятости
каким-либо полезным делом,
Воспитание отзывчивости, трудолюбия,
аккуратности.

Оборудование: модели многогранников,
карточки для устного счета, линейка, цветные
мелки.

План урока

Организационный момент 3 мин
Устная работа 7 мин
Объяснение нового материала 10 мин
Отработка нового материала 15 мин
Резерв
Итоги урока 2 мин
Домашнее задание 3 мин

Ход урока

I. Организационный момент

II. Устная работа

Решить устно:

А 46-11³/₈

М 42•²/₃

Д 10:6

П 2•19

И 14+23⁷/₈

А ²/₃+³/₈

Р 82-45

И 8:¹/₃

Составьте слово, расположив ответы примеров в
порядке убывания, и вы узнаете тему нашего урока.

Работа в парах. Из предложенных
геометрических тел найдите многогранники.
Почему выбранные вами многогранники являются
многогранниками? С какими многогранниками вы уже
знакомы?

(На каждую парту выдаются модели
геометрических тел).

III. Объяснение нового материала

Как уже вы знаете, тема нашего урока
“Пирамида”, поэтому мы сегодня должны
познакомиться с этим геометрическим телом.

( В тетрадях записывается число, классная
работа, тема урока).

“Пирамида” — слово греческого
происхождения, означает “костер”, “огонь”.

Где вы встречались с пирамидой?

Ответы: На уроках истории (пирамида Хеопса).
В архитектуре (крыши домов, музей современного
искусства в Париже). Также можно встретить
пирамиду в виде сувениров, свечей, упаковки.

Одним из интересных фактов является то, что
продукты, находящиеся в упаковке в виде пирамиды,
лучше и дольше сохраняются.

Важным и интересным семейством многогранником
являются пирамиды.

(Работа с моделями пирамид).

У пирамиды различают боковые грани —
треугольники, сходящиеся в одной вершине и основание
— многоугольник, противолежащий этой вершине. В
основании пирамиды может лежать многоугольник с
любым количеством сторон. Называют пирамиду по
числу сторон ее основания: треугольная,
четырехугольная, шестиугольная и т.д.

(Продемонстрировать)

Простейшей пирамидой и даже простейшим
многогранником является треугольная пирамида,
которая называется тетраэдром . Тетраэдр
изображен в учебнике на с.314 рис. 275; начертите ее в
тетради. Обозначьте ее.

Какую форму имеют ее грани? ( Треугольники).
Сколько граней у пирамиду? (4) Назовите их.
Сколько боковых граней у пирамиды? ( 3) Назовите
их.
Назовите основание пирамиды.
Сколько ребер у пирамиды? (6) Назовите их.
Сколько боковых ребер у пирамиды? ( 3) Назовите
их.
Сколько вершин? (4) Назовите их.
Сколько ребер выходит из каждой вершины? (3)

Каждую грань можно считать основанием. Ни у
одного многогранника не может быть меньшего
числа граней, вершин или ребер, чем у треугольной
пирамиды.

IY. Отработка нового материала

Работа в группах.

(У каждой группы на столе пирамида, таблица и
текст к таблице).

Заполнить таблицу.

Вопросы	Ответы
1. Число вершин пирамиды.
2. Число вершин основания пирамиды.
3. Число ребер у пирамиды.
4. Число ребер боковых граней пирамиды.
5. Число ребер в основании пирамиды.
6. Число боковых граней.
7. Число сторон основания.
8. Название пирамиды.

По данным таблицы заполните пропуски в тексте.

Число вершин пирамиды на _______________ больше числа
вершин в ее основании.

Ребер боковых граней _________________, сколько их в
основании.

Число боковых граней _________________ числу сторон
основания.

После выполнения группами задания проверить
выводы.

Ответы:

Число вершин пирамиды на единицу больше
числа вершин в ее основании.

Ребер боковых граней столько же , сколько
их в основании.

Число боковых граней равно числу сторон
основания.

Работа с классом.

1. С. 314 №1264 (рис. а и в).

2. Назовите пирамиду на рис. 276. Укажите ее
основание и боковые грани. Начертите пирамиду в
тетради.

3. С.314 №1267.

4. Нужно изготовить каркасную модель
треугольной пирамиды, все ребра которой равны 7
см. Сколько потребуется проволоки?

Ответ:(6•7=42)

Y. Резерв. №1265, 1271(1)

YI. Итоги урока

С чем мы сегодня познакомились и что вы узнали
нового?

(Каждый ученик высказывается по данному
вопросу).

YII. Домашнее задание

П. 10.4, на “3” №1264 (рис. б), 1266;

на “4” №1264 (рис. б), 1266, №1268;

на “5” №1264 (рис. б), 1266, №1268, №1270.

Источник

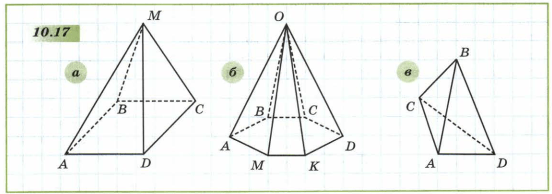
Назовите пирамиду (рис.10.17, а−в). Укажите ее основание и боковые грани. Начертите все пирамиды в тетради.

reshalka.com

ГДЗ учебник по математике 5 класс Бунимович. 40. Параллелепипед и пирамида. Номер №685

Решение а

Четырехугольная пирамида MABCD имеет:
основание: ABCD;
боковые грани: MAB, MBC, MCD, MAD.

Решение б

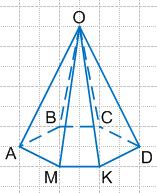
Шестиугольная пирамида OABCDKM имеет:
основание: ABCDKM;
боковые грани: OAB, OBC, OCD, ODK, OKM, OAM.

Решение в

Трехугольная пирамида BACD имеет:
основание: ACD;
боковые грани: BAC, BAD, BCD.

Источник

Основание правильной пирамиды является правильный многоугольник – равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды – это площадь этой плоской фигуры.

Площадь основания правильной пирамиды
- Площадь основания правильной треугольной пирамиды
- Площадь основания правильной четырехугольной пирамиды
- Площадь основания правильной шестиугольной пирамиды
Площадь основания любой пирамиды
Примеры решения задач
- Задача 1
- Задача 2
- Задача 3

Площадь основания правильной пирамиды

Правильная пирамида может быть трех видов:

треугольная,
четырехугольная,
шестиугольная.

Соответственно у правильной треугольной пирамида основание – равносторонний треугольник. У правильной четырехугольной пирамиды основание – квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:

Площадь основания правильной треугольной пирамиды

В основании равносторонний треугольник – находим его площадь:

$displaystyle S=frac{a^2 sqrt{3}}{4}$ , где – сторона треугольника.

Основание треугольной пирамиды

Площадь основания правильной четырехугольной пирамиды

В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:

, где – сторона квадрата.

Основание четырехугольной пирамиды

Площадь основания правильной шестиугольной пирамиды

Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:

$displaystyle S=frac{3a^2 sqrt{3}}{2}$

Основание шестиугольной пирамиды

Площадь основания любой пирамиды

Площадь основания любой пирамиды – это площадь ее основания.

Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье “Площадь треугольника”.

В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.

Теперь давайте решим несколько задач для нахождения площади основания пирамиды

Примеры решения задач

Задача 1

Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.

Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: $S=frac{a^2 sqrt{3}}{4}$ . Нам дана сторона , тогда $S=frac{2^2 sqrt{3}}{4} = sqrt{3}$

Ответ:

Задача 2

Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 м². Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?

Решение:

Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: $S=frac{3a^2 sqrt{3}}{2}$ . Подставим в нее значение стороны . Получим: $S=frac{3 cdot 6^2 sqrt{3}}{2}=54 sqrt{3}$ м².

Теперь подсчитаем, сколько нам понадобится досок: $N=frac{54 sqrt{3}}{0,5 sqrt{3}}=108$ .

Ответ: 108 досок.

Задача 3

Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Решение: иными словами – нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой – высотой. Определяем площадь по формуле:

$S=frac{a^2}{2}=frac{4^2}{2}=8$ .

Ответ: 8

Источник

Описание презентации по отдельным слайдам:

1 слайд

«Учитель года – 2019»
Открытый урок
Учитель математики
МБОУ «Школа №174»
Шемякова Анжелика Давидовна
5 слайд

24.01.2019
Классная работа.
Тема:
Пирамида.
Цели урока:
1. Дать определение пирамиды.
2. Назвать элементы пирамиды.
3. Научиться чертить пирамиду.
6 слайд

П И Р А М И Д А
ПИ – очень важное число в математике
РА – Бог Солнца в Древнем Египте
МИ – одна из семи нот
ДА – положительный ответ
ПИ-РА-МИ-ДА
7 слайд

Пирамида в жизни:
8 слайд

Путешествие в Египет
9 слайд

Достопримечательности:
10 слайд

Рис.163, стр.148
Треугольная пирамида
Четырёхугольная пирамида
Пятиугольная пирамида
11 слайд

№604, с.151
На рис.171 изображена пирамида МАВС. Укажите:

1)основание пирамиды;
2)вершину пирамиды;
3)боковые грани пирамиды;
4)боковые рёбра пирамиды;
5) рёбра основания пирамиды.
12 слайд

Определение
Пирамида — это ___________________________, в основании которого — ______________________, а остальные (боковые) грани — _________________________, имеющие общую вершину.

многогранник
многоугольник
треугольники
13 слайд

Рис.165, 166, стр.148,149
15 слайд

24.01.2019
Классная работа.
Тема:
Пирамида.
Цели урока:
1. Дать определение пирамиды.
2. Назвать элементы пирамиды.
3. Научиться чертить пирамиду.
16 слайд

ПИРАМИДА УСПЕХА
Позитивное настроение
Негативное настроение
Позитивное настроение
17 слайд

ПИРАМИДА УСПЕХА
Позитивное настроение
Мне было легко
Мне было трудно
Мне было легко
18 слайд

ПИРАМИДА УСПЕХА
Позитивное настроение
Мне было легко
Хорошо понял
Хорошо понял
Мало, что понял
Ничего не понял
19 слайд

ПИРАМИДА УСПЕХА
Позитивное настроение
Мне было легко
Хорошо понял
Совсем не отвечал
Активно работал
Отвечал иногда
Активно работал
20 слайд

ПИРАМИДА УСПЕХА
Позитивное настроение
Мне было легко
Хорошо понял
Активно работал
21 слайд

§22(с.148-149),
№ 605, склеить модель пирамиды из развёртки и выполнить практическую работу
Домашнее задание:
22 слайд

1) ЗАДАНИЕ: заполните таблицу
23 слайд

2) ЗАДАНИЕ: заполните пропуски
Число вершин пирамиды на ________ больше числа вершин в её основании.
Рёбер боковых граней _____________, сколько их в основании.
Число боковых граней _____________ числу сторон основания.

Источник