Пирамидой называют многогранник, одна грань которого – многоугольник, а остальные грани – треугольники с общей вершиной. Многоугольник называют основанием пирамиды, а треугольники – боковыми гранями.
Высотой пирамиды называют перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания.
На рисунке 9.53 изображена четырехугольная пирамида 











1. Если все боковые ребра пирамиды равны или наклонены к плоскости основания под одним и тем же углом, то основание высоты пирамиды, проведенной из ее вершины, совпадает с центром окружности, описанной около основания пирамиды.
2. Если боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом (двугранные углы при основании равны), то основание высоты пирамиды, проведенной из ее вершины, совпадает с центром окружности, вписанной в основание пирамиды.
3. Если две боковые грани пирамиды перпендикулярны плоскости основания, то боковое ребро, содержащее эти грани, является высотой пирамиды.
Объем пирамиды высоты 

Площадь поверхности пирамиды находят по формуле:

Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты пирамиды, проведенной из ее вершины, совпадает с центром окружности, вписанной в основание пирамиды (или описанной около основания пирамиды, так как центры этих окружностей совпадают).
На рисунке 9.54 изображена правильная четырехугольная пирамида, а на рисунке 9.55 – правильная треугольная.
Высоту боковой грани правильной пирамиды, проведенную из ее вершины, называют апофемой. На рисунке 9.54 отрезок 
Любую треугольную пирамиду называют тетраэдром.
Тетраэдр называется правильным, если все его ребра равны.
На рисунке 9.56 изображен правильный тетраэдр.
Площадь боковой поверхности правильной пирамиды находят по формуле:

где 
Усеченной пирамидой называют многогранник, вершинами которого служат вершины основания пирамиды и вершины ее сечения плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники.
Высотой усеченной пирамиды называют перпендикуляр, заключенный между плоскостями ее оснований.
На рисунке 9.57 изображена треугольная усеченная пирамида, а на рисунке 9.58 – правильная четырехугольная усеченная пирамида.
Объем усеченной пирамиды находят по формуле:

где 


Пример 1. Основанием пирамиды является правильный треугольник со стороной 

Решение. Так как две боковые грани 





Объем пирамиды найдем по формуле 9.11 . Получим: 

Ответ: 

Пример 2. Вычислите объем правильного тетраэдра с ребром, равным 
Решение. Так как тетраэдр правильный (рис. 9.60), то его высота опускается в центр треугольника 

Тогда 


Найдем высоту тетраэдра. Рассмотрим треугольник



Объем тетраэдра вычислим по формуле 9.11 , где 

Ответ: 
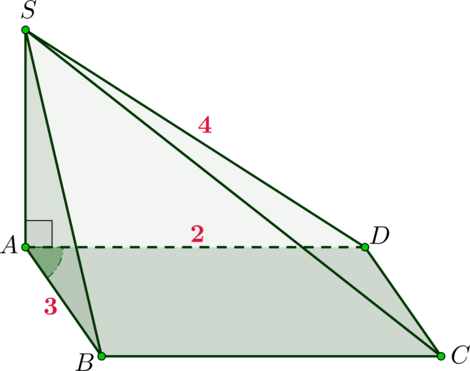
Пример 3. В основании пирамиды лежит прямоугольный треугольник с гипотенузой, равной 


Решение. Основанием пирамиды является треугольник 





Рассмотрим прямоугольный треугольник 






Рассмотрим прямоугольный треугольник 



Найдем площадь треугольника:



По формуле 9.11 найдем объем пирамиды: 
Ответ: 
Пример 4. Основанием пирамиды служит треугольник со сторонами 


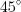
Решение. Основанием пирамиды (рис. 9.62) служит равнобедренный треугольник 





Тогда 



Площадь треугольника 





Угол 






Согласно формуле 9.11 найдем объем пирамиды:


Ответ: 
Пример 5. Апофема правильной четырехугольной пирамиды (рис. 9.63) равна 

Решение. Так как пирамида правильная, то четырехугольник 
Точка 

Поскольку 



По формуле 9.13 найдем площадь боковой поверхности пирамиды: 
Ответ: 
Пример 6. Основание пирамиды – ромб с острым углом 


Решение. Так как вершина пирамиды равноудалена от всех сторон ромба, то основание высоты пирамиды (точка 


С другой стороны, площадь ромба можем найти и по формуле 



Из теоремы Пифагора 

По формуле 9.11 найдем объем пирамиды:

Ответ: 
Пример 7. Боковое ребро правильной четырехугольной усеченной пирамиды наклонено к плоскости основания под углом 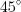


Решение. Так как основания усеченной пирамиды – квадраты со сторонами 





По теореме Пифагора найдем диагонали квадратов:


Так как диагонали точкой пересечения делятся пополам, то 

Рассмотрим диагональное сечение пирамиды – трапецию 








По формуле 9.14 найдем объем пирамиды:


Ответ: 

1. Решение задач, связанных с пирамидой, необходимо начинать с построения высоты пирамиды.
2. Различайте правильную треугольную пирамиду и правильный тетраэдр:
1) у правильной треугольной пирамиды основание – правильный треугольник, а боковые ребра хоть и равны между собой, но не обязательно, что они равны ребрам основания пирамиды;
2) правильный тетраэдр – это треугольная пирамида, у которой все ребра равны.
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Правильная и прямоугольная пирамиды»
(blacktriangleright) Пирамида называется прямоугольной, если одно из ее боковых ребер ((SR)) перпендикулярно основанию (оно же будет и высотой).
Грани, образованные этим ребром, будут представлять собой прямоугольные треугольники ((triangle SMR, triangle SPR)).
(blacktriangleright) Пирамида называется правильной, если в основании лежит правильный многоугольник (все углы равны и все стороны равны) и выполнено одно из эквивалентных условий:
(sim) боковые ребра равны;
(sim) высота пирамиды проходит через центр описанной около основания окружности;
(sim) боковые ребра наклонены к основанию под одинаковым углом.
(blacktriangleright) Заметим, что у правильных многоугольников центры описанной и вписанной окружностей совпадают.
(blacktriangleright) Заметим, что у правильной пирамиды все боковые грани – равные равнобедренные треугольники.
Высота этих треугольников, проведенная из вершины пирамиды, называется апофемой.
Задание
1
#2854
Уровень задания: Равен ЕГЭ
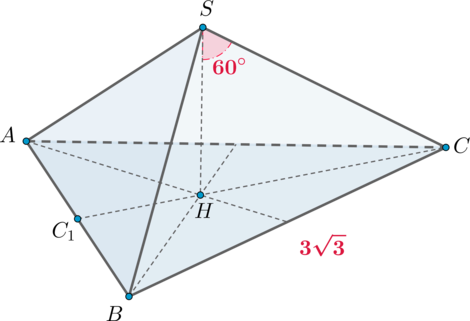
Дана правильная треугольная пирамида (SABC) с вершиной (S). Известно, что сторона основания пирамиды равна (3sqrt3), а угол между ее высотой и боковым ребром равен (60^circ). Найдите объем пирамиды.
Пусть (SH) – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания, то есть в точку пересечения медиан (высот, биссектрис).
Пусть (CC_1) – высота (а значит и медиана) основания. Тогда [CC_1=dfrac{sqrt3}2AB.] Так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то [CH=dfrac23CC_1=dfrac{sqrt3}3AB.] Из прямоугольного (triangle SHC): [mathrm{tg},60^circ=dfrac{CH}{SH}quadRightarrowquad
SH=dfrac{CH}{sqrt3}=dfrac13AB.] Следовательно, объем пирамиды равен [V=dfrac13cdot SHcdot S_{ABC}=dfrac13cdot
dfrac13cdot 3sqrt3cdot dfrac12cdot 3sqrt3cdot
dfrac{sqrt3}2cdot 3sqrt3=dfrac{27}4=6,75.]
Ответ: 6,75
Задание
2
#2856
Уровень задания: Равен ЕГЭ
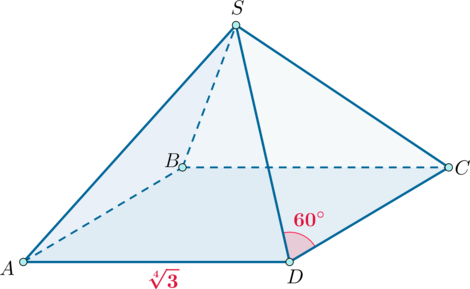
Дана правильная четырехугольная пирамида (SABCD) с вершиной (S). Угол между боковым ребром и стороной основания равен (60^circ), а (AB=sqrt[4]3). Найдите площадь боковой поверхности этой пирамиды.
Так как пирамида правильная, то все боковые грани представляют собой равные равнобедренные треугольники. Так как у них угол при основании равен (60^circ), то они являются равносторонними, то есть все боковые ребра пирамиды равны стороне основания. Площадь правильного треугольника со стороной (a) вычисляется по формуле (dfrac{sqrt3}4a^2), следовательно, площадь боковой поверхности [S_{text{бок. пов-ти}}=4cdot dfrac{sqrt3}4AS^2=sqrt3AS^2=sqrt3cdot sqrt3=3.]
Ответ: 3
Задание
3
#2858
Уровень задания: Равен ЕГЭ
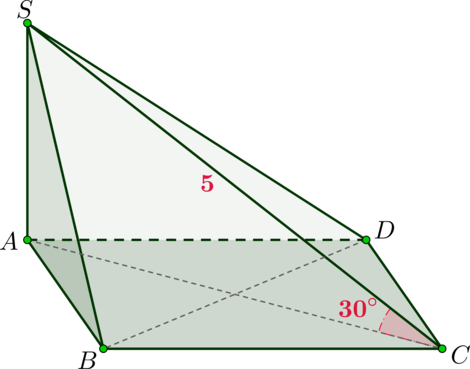
Дана прямоугольная пирамида (SABCD), причем (SA) – высота пирамиды, а (ABCD) – ромб. Диагональ (BD) ромба равна (8sqrt3), а боковое ребро (SC) равно (5). Найдите объем пирамиды, если также известно, что угол между (SC) и плоскостью основания равен (30^circ).
Так как (SA) – высота, то она перпендикулярна плоскости основания, следовательно, по определению (AC) является проекций (SC) на плоскость основания. А так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость, то (angle SCA) – угол между (SC) и основанием.
Так как (SA) перпендикулярна основанию, то она перпендикулярна любой прямой из основания, следовательно, (triangle SAC) прямоугольный. Значит, (AS) как катет, лежащий против угла (30^circ), равен половине (SC), то есть (AS=2,5).
По теореме Пифагора из этого же треугольника [AC=sqrt{SC^2-SA^2}=2,5sqrt3.] Так как площадь ромба равна полупроизведению диагоналей, то объем [V=dfrac13cdot SAcdot dfrac12cdot ACcdot BD=25.]
Ответ: 25
Задание
4
#1865
Уровень задания: Равен ЕГЭ
В прямоугольной пирамиде (SABCD): (SB) – высота пирамиды, (ABCD) – прямоугольная трапеция с прямыми углами (angle BAD) и (angle ABC). Найдите объем пирамиды, если (angle SAB = 60^circ), (angle SCB = 30^circ), (AD = 2cdot AB), а (AB = sqrt3).
(triangle ABS) и (triangle CBS) – прямоугольные треугольники (Rightarrow) (SB = ABcdotmathrm{tg},60^circ = sqrt3cdotsqrt3 = 3) (Rightarrow) (BC = SBcdot mathrm{ctg},30^circ = 3sqrt3) (Rightarrow) (S_{ABCD} = frac{1}{2}cdot(AD + BC)cdot AB = frac{1}{2}cdot(2sqrt3 + 3sqrt3)cdotsqrt3 = 7,5) (Rightarrow) [V_{text{пир.}} = frac{1}{3}cdot SBcdot S_{ABCD} = frac{1}{3}cdot3cdot7,5 = 7,5]
Ответ: 7,5
Задание
5
#3113
Уровень задания: Равен ЕГЭ
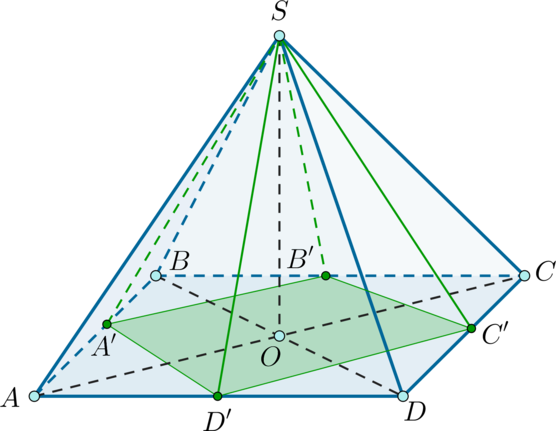
Дана правильная четырехугольная пирамида, объем которой равен (7). Найдите объем пирамиды, вершина которой совпадает с вершиной исходной пирамиды, а вершины основания совпадают с серединами сторон основания исходной пирамиды.
Рассмотрим рисунок. Пусть (SABCD) – исходная пирамида, (A’, B’, C’,
D’) – середины отрезков (AB, BC, CD, DA) соответственно. (SO) – высота пирамиды (SABCD). [V_{SABCD}=dfrac13cdot SOcdot AB^2] Заметим, что (SO) – также высота пирамиды (SA’B’C’D’).
Так как (ABC) – прямоугольный треугольник, то (AC=sqrt{AB^2+BC^2}=sqrt2AB). Так как (A’B’) – средняя линия в (triangle ABC), то [A’B’=frac12AC=dfrac{sqrt2}2AB] Так как (A’B’parallel AC, A’D’parallel BD), а (ACperp BD), то (A’B’perp
A’D’), следовательно, (A’B’C’D’) – квадрат. Следовательно, [V_{SA’B’C’D’}=dfrac13cdot SOcdot A’B’^2=dfrac13cdot SOcdot
dfrac12AB^2=
dfrac12V_{SABCD}=3,5.]
Ответ: 3,5
Задание
6
#2857
Уровень задания: Сложнее ЕГЭ
Дана прямоугольная пирамида (SABCD), в основании которой лежит параллелограмм со сторонами (AD) и (AB), соответственно равными (2) и (3), и углом между ними (arcsin dfrac{sqrt3}4), а боковое ребро (SA) перпендикулярно основанию. Найдите объем пирамиды, если (SD=4).
Пусть (angle DAB=arcsin dfrac{sqrt3}4), следовательно, (sinangle DAB=dfrac{sqrt3}4).
Так как (SA) перпендикулярно основанию, то оно перпендикулярно любой прямой из основания, следовательно, (triangle SAD) – прямоугольный. Также по определению (SA) является высотой пирамиды. Следовательно, по теореме Пифагора [SA=sqrt{SD^2-AD^2}=2sqrt3.] Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними, следовательно, объем пирамиды равен [V=dfrac13cdot SAcdot ABcdot ADcdot sinangle DAB=3.]
Ответ: 3
Задание
7
#2853
Уровень задания: Сложнее ЕГЭ
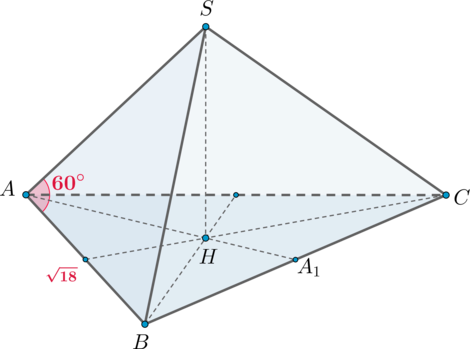
Дана правильная треугольная пирамида (SABC) с основанием (ABC), сторона которого равна (sqrt{18}). Найдите объем пирамиды, если угол (SAB) равен (60^circ).
Пусть (SH) – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания, то есть в точку пересечения медиан (высот, биссектрис). Также боковые грани представляют собой равнобедренные треугольники. Так как в равнобедренном (triangle
ASB) угол при основании равен (60^circ), то треугольник равносторонний, следовательно, (AS=AB=sqrt{18}).
Пусть (AA_1) – высота основания. Следовательно, [AA_1=dfrac{sqrt3}2AB.] Так как (AA_1) – медиана, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то [AH=dfrac23AA_1=dfrac{sqrt3}3AB.] Следовательно, по теореме Пифагора [SH=sqrt{AS^2-AH^2}=dfrac{sqrt6}3AB.] Тогда объем пирамиды равен [V=dfrac13cdot SHcdot S_{ABC}=
dfrac13cdot dfrac{sqrt6}3ABcdot dfrac12cdot ABcdot dfrac{sqrt3}2AB=9.]
Ответ: 9
Задания из раздела «Геометрия в пространстве» по теме «Правильная и прямоугольная пирамида» являются обязательной частью ЕГЭ по математике. Понимать, как найти правильный ответ, и оперативно справляться с ними должны учащиеся с различным уровнем подготовки. Школьники, которые знают принцип решения задач с правильной треугольной и четырехугольной пирамидой, смогут выполнять задания с любым количеством действий и рассчитывать на получение достойных баллов по итогам сдачи аттестационного испытания.
Выбирайте образовательный портал «Школково» для успешной сдачи единого государственного экзамена!
Часто во время подготовки к аттестационному испытанию учащиеся сталкиваются с проблемой поиска подходящего источника. Школьный учебник далеко не всегда присутствует под рукой, когда это необходимо. А поиск требуемых формул для вычисления, к примеру, объема прямоугольной пирамиды, бывает достаточно сложным даже в Интернете в онлайн-режиме.
Для того чтобы подобные задания не вызывали затруднений, готовьтесь к единому государственному экзамену вместе с математическим порталом «Школково». Мы предлагаем принципиально новый подход к построению занятий с выпускниками. Наш портал помогает учащимся выявить наиболее сложные разделы и улучшить собственные знания.
Что такое правильная и прямоугольная пирамида, как вычисляются объем и площадь пирамиды, какие базовые теоремы и важные нюансы нужно знать для выполнения заданий — всю эту информацию вы найдете в разделе «Теоретическая справка». Этот материал систематизирован и изложен нашими специалистами с учетом их богатого опыта максимально просто и понятно.
Чтобы задачи ЕГЭ на площадь поверхности правильной пирамиды не вызывали особых сложностей, мы предлагаем также попрактиковаться в выполнении соответствующих упражнений. Найти подобные задания вы можете в разделе «Каталог».

УСТАЛ? Просто отдохни
План урока:
Понятие пирамиды
Правильная пирамида
Усеченная пирамида
Типичные задачи на пирамиды
Понятие пирамиды
Построим на некоторой плос-ти α произвольный многоугольник А1А2…Аn. Далее отметим в пространстве точку Р, не принадлежащую плос-ти α. Соединив точку Р с вершинами многоуг-ка получим многогранник, который именуется пирамидой (в различной литературе может использоваться сокращение пирам-а).
Та единственная точка Р, не находящаяся в одной плос-ти со всеми остальными вершинами, именуется вершиной пирам-ы. Многоугольник, образованный остальными вершинами – это основание пирамиды.
Основанием пирам-ы может быть многоугольник с любым количеством сторон. Если в основании лежит, например, пятиугольник, то и пирам-у называют пятиугольной. Если же в основании находится десятиугольник, то это будет уже десятиугольная пирам-а. В общем случае пирам-у, у которой в основании располагается n-угольник, именуется n-угольной. Ясно, что треугольная пирам-а и тетраэдр – это по сути одна и та же фигура.
Все грани пирам-ы, за исключением ее основания, именуются боковыми гранями. Понятно, что каждая боковая грань – это треугольник. Ребра пирамиды, выходящие из ее вершины, именуются боковыми ребрами пирамиды.
Посчитаем количество ребер, вершин и граней пирам-ы. Если она n-угольная, то у неё (n + 1) вершин (n точек в основании и ещё одна точка, не лежащая в основании). Также у нее (n + 1) граней, из них одна – это основание, а остальные n – боковые грани пирамиды (по одной на каждую сторону n-угольника). Наконец, у пирам-ы n ребер находятся в плос-ти основания, а ещё n ребер являются боковыми. Итого имеем 2n ребер. Теперь можно убедиться, что теорема Эйлера для пирам-ы выполняется:
Из вершины пирам-ы можно опустить перпендикуляр на плос-ть основания. Он будет именоваться высотой пирамиды.
Как и в случае с призмой, можно подсчитать площадь боковой поверхности призмы, которую обозначают как Sбок. Если же к ней ещё добавить и площадь основания (Sосн), то в сумме получится уже площадь полной поверхности призмы (Sполн). Эту связь между величинами можно представить в виде формулы:
Правильная пирамида
Особый интерес и в геометрии, и в реальной жизни представляют так называемые правильные пирамиды. Их отличают две особенности:
1) в их основании находится правильный многоугольник;
2) высота пирам-ы падает на основание в точке, являющейся центром этого правильного многоуг-ка.
Напомним, что центром правильного многоуг-ка считается центр описанной около него окружности, который одновременно является и центром вписанной окружности.
Действительно, опустим из вершины Р правильной пирам-ы высоту РО. Тогда О будет центром описанной окружности:
Примечание. На рисунках, показывающих объемные фигуры, окружности искажают свою форму и выглядят как эллипсы, то есть овалы.
Построим из О радиусы ОА1, ОА2, ОА3,… Они все будут одинаковы, ведь это радиусы одной и той же окружности. Также заметим, что высота правильной пирамиды РО будет перпендикулярна каждому из этих радиусов, ведь она перпендикулярна и всей плос-ти. Это значит, что ∆РОА1, ∆РОА2, ∆РОА3… – прямоугольные. При этом у них есть общий катет РО, а катеты ОА1, ОА2, ОА3… одинаковы. Значит, эти треугольники равны. Отсюда и вытекает, что их гипотенузы, то есть боковые ребра РА1, РА2, РА3…, также одинаковы, ч. т. д.
Заметим, что можно доказать и почти противоположное утверждение – если у пирам-ы боковые ребра одинаковы, а в основании находится правильный многоуг-к, то она является правильной. Для доказательства предположим, что ребра РА1, РА2, РА2… одинаковы. Опустим из Р высоту, которая упадет в некоторую точку О. Теперь соединим эту точку с вершинами А1, А2, А3… Получатся прямоугольные ∆РОА1, ∆РОА2, ∆РОА3… У них есть общий катет (высота РО) и одинаковые гипотенузы. Значит, эти треугольники равны, и потому одинаковы отрезки ОА1, ОА2, ОА3… Это значит, что точка О равноудалена от вершин многоуг-ка, и если из нее провести окружность радиусом ОА1, то она также пройдет через остальные вершины многоуг-ка. То есть эта окружность окажется описанной. Это и означает, что точка О – центр многоуг-ка, и тогда вся пирам-а оказывается по определению правильной.
Из равенства боковых ребер напрямую вытекает и тот факт, что все боковые грани правильной пирам-ы – одинаковые равнобедренные треугольники. Высоты, проведенные в этих равнобедренных треугольниках к основанию правильной пирамиды, именуются апофемами.
Ещё раз уточним, что понятие апофемы применимо только к правильной пирам-е. У других пирамид тоже можно на боковых гранях провести высоты к основанию, но они просто не будут называться апофемами пирамиды.
Ясно, что раз в правильной пирам-е все боковые грани – равные друг другу равнобедренные треуг-ки, то и их высоты, то есть апофемы, одинаковы. Также можно утверждать, что каждая апофема делит ребра, на которое она падает, пополам, ведь высоты в равнобедренном треуг-ке – это ещё и медианы.
Апофема используется для вычисления площади боковой поверхности пирам-ы, так как существует такая теорема:
Докажем ее. Пусть у правильной n-угольной пирам-ы в основании находится многоуг-к со стороной а. Тогда его периметр Р вычисляется так:
Каждая боковая грань пирам-ы – это треугольник. Проведем на них апофемы, которые одновременно окажутся и высотами для этих треугольников. Если мы обозначим длину апофемы как d, то площадь каждой грани можно рассчитать по простейшей формуле площади треугольника:
Усечённая пирамида
Возьмем произвольную пирам-у, а далее секущую плоскость, которая будет параллельна основанию, причем она будет пересекать ребра РА1, РА2, РА3… в точках В1, В2, В3… соответственно. В результате, отбросив «верхушку» пирам-ы, мы получим новую фигуру, которая именуется усеченной пирамидой.
У усеченной пирам-ы уже не одна, а две грани считаются основаниями, и они параллельны друг другу. Большее из них именуют нижним основанием, а меньшее – верхним основанием.
Докажем, что боковые грани любой усеченной пирам-ы – это трапеции. Действительно, обозначим плос-ть верхнего основания как α, нижнее основание как β, а произвольную грань как γ:
Нам надо доказать, что А1А2В2В1 – это трапеция. Действительно, прямые А1А2 и В1В2 не могут скрещиваться, ведь они располагаются в единой плос-ти γ. Не могут они и пересекаться, ведь тогда точка их пересечения была бы общей для плос-тей α и β, а эти плос-ти параллельны. Остается один вариант: А1А2||В1B2. Две другие стороны грани, А1В1 и А2В2, будут пересекаться в точке Р, вершине исходной пирам-ы. Тогда по определению две четырехугольник А1А2В2В1 будет трапецией, ведь у него две стороны параллельны, а две другие – нет.
Отдельно отметим, что усеченная пирам-а, полученная из правильной пирам-ы, также называется правильной, а высоты ее боковых граней также именуются апофемами. Докажем одну теорему:
Действительно, пусть из правильной пирам-ы с вершиной в Р получена правильная усеченная пирамида с основаниями А1А2А3…An и В1В2В3…Bn:
Так как исходная пирам-а – правильная, то ее грани – равные равнобедренные треугольники, у которых одинаковы углы при основаниях:
Мы уже знаем, что грани А1А2В2В1 и А2А3В3В2 – трапеции. Раз у них одинаковы углы при основании, то можно утверждать, что эти трапеции – равнобедренные. Это значит, что любые два боковых ребра, находящиеся на одной грани, одинаковы. Значит, одинаковы вообще все боковые ребра. Получается, что все боковые грани – это равнобедренные трапеции с одинаковыми основаниями, боковыми сторонами и углами при основании. Этого достаточно для того, чтобы считать эти трапеции равными, ч. т. д.
Из этой теоремы вытекает тот факт, что стороны многоуг-ка, образующего верхнее основание, одинаковы. Более того, углы этого многоуг-ка равны таким же углам в нижнем основании. Например, ∠А1А2А3 = ∠В1В2В3. Действительно, мы знаем, что А1А2||В1В2 и А2А3||B2B3, и потому стороны углов ∠А1А2А3 = ∠В1В2В3 оказываются сонаправленными лучами.
Так как в нижнем многоуг-ке А1А2А3…An все углы одинаковы (ведь он правильный), то и в верхнем многоуг-ке В1В2В3…Bn также будут одинаковы углы. В итоге можно утверждать, что верхнее основание усеченной пирамиды является правильным многоуг-ком, также как и нижнее.
Отметим ещё один факт. При построении секущей плос-ти пирам-а делится на две части. Нижняя из них – это усеченная пирам-а, а верхняя – это обычная пирам-а, меньшая исходной. Докажем, что если исходная пирам-а РА1А2А3…Рn была правильной, то оставшаяся после отсечения «верхушка» также будет правильной пирам-ой. Мы уже выяснили, что ее основание В1В2В3…Вn– правильный многоуг-к. Отрезки РА1, РА2, РА3… одинаковы как боковые ребра исходной правильной пирам-ы. В свою очередь отрезки А1В1, А2В2, А3В3 одинаковы как боковые ребра правильной усеченной пирам-ы. Но отсюда получается, что одинаковы также и отрезки РВ1, РВ2, РВ3… Значит, в пирам-е РВ1В2В3…Вn в основании лежит правильный многоуг-к, а ее боковые ребра одинаковы. Из этого вытекает, что эта пирам-а – правильная.
Ещё одна теорема позволяет вычислять площадь боковой поверхности правильной усеченной пирам-ы:
Действительно, каждая грань такой пирам-ы – это трапеция. Обозначим длину ее верхнего основания буквой а, а нижнего – буквой b.Тогда, если основания пирам-ы – это многоуг-ки с n сторонами, периметр этих оснований будет вычисляться так:
Теперь проведем на каждой боковой грани апофему, чья длина будет обозначаться как d. Тогда, используя формулы площади трапеции, сможем вычислить площадь грани:
Типичные задачи на пирамиды
Рассмотрим несколько задач, в которых фигурируют пирам-ы. Перед просмотром решения попытайтесь решить их самостоятельно.
Задание. Существует ли пирамида, у которой ровно 999 ребер?
Решение. Если в основании пирам-ы находится n-угольник, то у нее 2n ребер. Так как n– целое число, то 2n будет уже четным числом. То есть количество ребер у любой пирам-ы всегда четно. Поэтому не существует пирам-ы с 999 ребрами, ведь 999 – нечетное число.
Задание. Верно ли, что всякий правильный тетраэдр одновременно является и правильной пирам-ой? И наоборот, является ли каждая правильная треугольная пирам-а правильным тетраэдром?
Решение. Напомним, что правильный тетраэдр – это тетраэдр, у которого все ребра одинаковы. Если одну из вершин тетраэдра принять за вершину пирам-ы, то получится, что в ее основании равносторонний треугольник, который, как мы знаем, является правильным многоуг-ком. Также окажется, что все боковые ребра пирам-ы также одинаковы. Это значит, что она – правильная.
Теперь посмотрим на произвольную правильную треугольную пирам-у. Будет ли она обязательно правильным тетраэдром? Нет, ведь ее боковые ребра могут отличаться по длине от ребер, находящихся в основании. Например, в основании может находиться равносторонний треуг-к со стороной 5 см, а боковое ребро правильной пирамиды может иметь длину 10 см. Таким образом, можно считать правильный тетраэдр лишь частным случаем правильной пирам-ы.
Задание. В основании пирам-ы находится ромб со стороной 5 см.Одна из его диагоналей имеет длину 8 см. Высота пирам-ы имеет длину 7 см и проходит через точку, в которой пересекаются диагонали ромба. Вычислите длину боковых ребер.
Решение.
Обозначим ромб в основании как АВСD, а вершину пирам-ы буквой Р. Пусть диагонали пересекаются в точке О, тогда РО – высота. Также пусть диагональ АС равна 8 см. По свойству ромба О будет серединой диагоналей, поэтому
Отрезок OD будет иметь ту же длину 3 см, ведь О – середина BD.
Так как высота РО перпендикулярна всем прямым в плос-ти основания, то ∆АОР, ∆ВОР, ∆СОР, ∆DOP – прямоугольные, и боковые ребра пирам-ы будут гипотенузами этих треугольников. Вычислим АР по теореме Пифагора:
Задание. В основании пирам-ы лежит квадрат, а одно из ее боковых ребер перпендикулярно основанию. Одна из боковых граней образует с плос-тью основания угол в 45°. Длина длиннейшего ребра пирам-ы составляет 12 см. Определите высоту пирам-ы и площадь ее боковой поверхности.
Решение.
Обозначим квадрат, находящийся в основании, как АВСD, а вершину пирам-ы как Р. Пусть ребро PD перпендикулярно основанию. Тогда PD⊥AD и PD⊥CD. Ясно, что PD как раз и является искомой нами высотой пирам-ы.
Теперь надо понять, какие углы в пирам-е составляют 45° и какое ребро равно 12 см. Грани ADP и СDP проходят через перпендикуляр PDк основанию, а потому они перпендикулярны основанию. Значит, угол в 45° с основанием образует либо грань АВР, либо грань СВР.
Заметим, что АВ⊥AD (это смежные стороны квадрата), а AD – это проекция ребра АР на основание. Тогда по теореме о трех перпендикулярах АВ⊥АР. Аналогично из того факта, что ВС⊥СD, вытекает, что ВС⊥СР. Также заметим, что ∆ADP и ∆СDP прямоугольные, имеют общий катет PD и одинаковые катеты AD и CD (это стороны квадрата). Значит, это равные треугольники, и
∠PAD = ∠PCD
Грань АВР пересекается c основанием по прямой АВ, причем AD⊥АВ и АР⊥АВ. Значит, ∠РАD – это угол между гранью АВР и основанием. Аналогично и ∠РСD является углом между гранью СВР и основанием. Но эти углы одинаковы. Значит, каждый из этих углов будет равен 45°, иначе в пирам-е не останется угла между плос-тями, который мог бы составлять 45°.
Ясно, что ребро АР длиннее ребра РD, ведь в прямоугольном ∆ADP АР – это гипотенуза, а РD катет (гипотенуза всегда длиннее катета). Теперь заметим, что ∆РАВ и ∆РСВ – также прямоугольные, ведь АВ⊥АР и ВС⊥СР. Но в них гипотенузой является уже РВ, то есть РВ длиннее АВ, ВС, АР и РС. Так как отрезки AD и AC равны АВ как стороны квадрата, получаем, что именно ребро РВ – длиннейшее в пирам-е, то есть его длина составляет 12 см.
В прямоугольном ∆ADP∠PAD = 45°. Это значит, что ∆ADP является прямоугольным и равнобедренным, то есть AD = PD. Обозначим искомую нами длину РD как x. Теперь проведем диагональ BD:
Её длину можно вычислить из ∆ADB:
Итак, высоту нашли, теперь нужно рассчитать боковую площадь. Но для этого предварительно найдем АР из ∆АРD:
Такую же длину имеет и РС, ведь ∆АРD и ∆СРD равны.
Мы уже выяснили, что каждая боковая грань – прямоугольный треугольник. Зная длины катетов, легко найдем площадь каждой грани:
Задание. В правильной шестиугольной пирам-е ребро при основании равно 3 см. Высота этой пирам-ы составляет 4 см. Вычислите длину апофемы этой пирам-ы, а также угол, который ее боковые грани образуют с основанием.
Решение.
Основание пирам-ы обозначим как АВСDEF, а вершину как Р. Пусть РО – высота, тогда О – центр описанной окружности. Напомним, что у правильного шестиугольника радиус описанной окружности совпадает с длиной его стороны, то есть
Теперь надо найти угол между гранью АВР и основанием. Они пересекаются по прямой АВ. РН⊥АВ, ведь РН – апофема. ОН – это проекция РН на основание. Так как АВ⊥РН, то по обратной теореме о трех перпендикулярах и ОН⊥АВ. Значит, ∠ОНР и является искомым углом между гранью АВР и основанием. Для его вычисления применим тригонометрию к ∆ОНР:
Задание. В правильной шестиугольной пирам-е все ребра имеют длину, равную единице. Найдите угол между прямыми АР и BD:
Решение. Для нахождения угла между АР и BD, у которых нет общей точки, можно вычислить угол между прямыми, которые будут им параллельны. Легко заметить, что АЕ||BD. Докажем это, рассмотрев основание пирам-ы:
Каждый угол правильного шестиугольника составляет 120°. В частности, это относится к ∠F и ∠С. ∆АFЕ – равнобедренный, ведь его стороны FE и AF одинаковы. Тогда и углы при основании будут одинаковыми. Найдем их:
Аналогично можно определить, что все углы четырехугольника АВDE прямые, то он представляет собой прямоугольник. Его противоположные стороны параллельны, в частности, АЕ||BD. Это означает, что искомый нами угол – это ∠РАЕ:
Для его вычисления необходимо вычислить длины сторон ∆РАЕ. Ребра РА и РЕ по условию равны единице. Длину ЕА найдем из ∆FAE, применив теорему косинусов:
Задание. В правильной шестиугольной пирам-е боковые ребра имеют длину 2, а ребра в основании равны 1. Вычислите угол между плос-тями РFA и PDE:
Решение. Сначала надо найти прямую, по которой эти две грани пересекаются. Мы видим одну их общую точку – Р. Продолжим ребра FA и ED до тех пор, пока они не пересекутся в некоторой точке К. Эта точка K также будет общей для плос-тей, проходящих через грани PFA и РЕD. Значит, они пересекаются по прямой РК:
Найдем углы в ∆КЕF, помня при этом, что все в шестиугольнике АВСDEF составляют по 120°:
Получили, что все углы в ∆КЕF составляют по 60°, то есть он равносторонний, и поэтому стороны KE и KF одинаковы. Но также одинаковы и грани FA и DE. Отсюда получаем и равенство отрезков АК и DK:
Теперь сравним ∆АРК и ∆KPD. КР – их общая сторона, АР = РD как боковые ребра правильной пирам-ы, и АК = DK. Получается, что эти треугольники равны.
Далее в ∆АРК опустим высоту АН. Из равенства ∆АРК и ∆KPD вытекает, что и HD будет высотой в ∆PHD, ведь в равных треугольниках высоты должны делить равные стороны в одном и том же отношении. Тогда по определению двугранного угла ∠AHD и будет искомым углом между гранями, ведь KP – линия их пересечения, АН⊥KP и DH⊥KP.
∆AKP – равнобедренный, ведь отрезки АК и АР оказались одинаковыми. Значит, АН не только высота, но и медиана. Поэтому
Отрезок AD окажется диаметром окружности, описанной около шестиугольника. Мы знаем, что радиус такой окружности равен длине стороны шестиугольника, то есть единице. Тогда диаметр будет вдвое больше:
Сегодня мы познакомились с ещё одним видом многогранника –пирамидой. Они нередко встречаются в задачах ЕГЭ, посвященных стереометрии. Особо часто используются правильные пирамиды, поэтому важно помнить их основные свойства.

Основание пирамиды — ромб, один из углов которого 60 градусов. Каждая боковая грань образует с плоскостью основания угол, равный 30 градусов. Найдите площадь основания пирамиды, если высота пирамиды равна 6 см.
Если можно с пояснением!

Светило науки — 320 ответов — 9151 помощь
Обозначим пирамиду АВСДS(смотри рисунок). Проведём высоту ОК в треугольнике АОД. Найдём её значение через тангенс угла наклона грани и высоту пирамиды. Прямоугольные треугольники ОКД и АОД-подобны по по острому углу АДВ. Он равен 60 градусов, поскольку ВД-биссектриса угла АВС=120. Находим АО и ОД, затем площадь треугольника АОД, ромб состоит из четырёх таких треугольников. Ответ площадь основания равна 288корней из3.