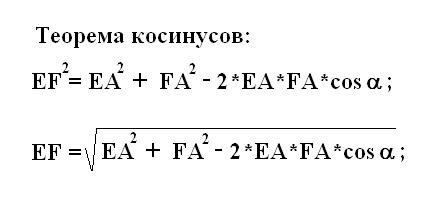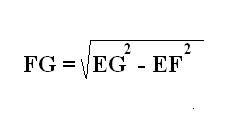Периметр любого прямоугольника составляет 2а+2с. То есть сумме удвоенных произведений противоположных сторон. Кроме того, по свойствам прямоугольника известно, что у него противоположные стороны попарно равны. То есть а=а, с=с. Отсюда имеем: 2а, 2с.
По условию задачи, 2а=1/5*400. то есть 2а=80.
Подставляем 2а в формулу периметра прямоугольника: 2а+2с. Получаем 80+2с=200. Отсюда находим с: с=(200-80):2. с=60. Вот мы нашли одну сторону прямоугольника (с).
Теперь находим сторону а. При этом снова используем формулу периметра прямоугольника, подставив туда найденное значение с. Получаем:
2а+2с=200
2а+120=200
2а=200-120
2а=80
а=40
Вот мы нашли вторую сторону (а).
Итак, стороны прямоугольника равны: а=40, с=60.
Проверка:
Находим периметр, имея заданные стороны (а и с)
Р=2а+2с. Подставляем известные нам а и с. Получаем:
Р=2*40+2*60
Р=80+120
Р=200
Итак, у нас периметр получился равным 200 см., что соответсвует условиям задачи. Значит, найденные значения а и с у нас правильные. а=40, с=60
Совет 1: Как обнаружить стороны, если вестим периметр
Периметром плоской фигуры называют сумму длин всех ее сторон. Но обнаружить стороны фигуры, зная только периметр – не неизменно выполнимая задача. Зачастую требуются добавочные данные.
Инструкция
1. Для квадрата либо ромба задача обнаружить стороны из периметра решается дюже примитивно. Вестимо, что у этих 2-х фигур по 4 стороны и все они равны между собой, следственно периметр p квадрата и ромба равен 4a, где a – сторона квадрата либо ромба. Тогда длина стороны равна одной четвертой периметра: a = p/4.
2. Легко разрешима эта задача и для равностороннего треугольника. У него три идентичных по длине стороны , следственно периметр p равностороннего треугольника равен 3a. Тогда сторона равностороннего треугольника a = p/3.
3. Для остальных фигур потребуются добавочные данные. Скажем, дозволено обнаружить стороны прямоугольника, зная его периметр и площадь. Представим, что длина 2-х противолежащих сторон прямоугольника равна a, а длина 2-х других сторон – b. Тогда периметр p прямоугольника равен 2(a+b), а площадь s равна ab. Получим систему уравнений с двумя неведомыми:p = 2(a+b)s = ab.Выразим из первого уравнения а: а = p/2 – b. Подставим во второе уравнение и обнаружим b: s = pb/2 – b². Дискриминант этого уравнения D = p²/4 – 4s. Тогда b = (p/2±D^1/2)/2. Отбросьте тот корень, тот, что будет поменьше нуля, и подставьте в выражение для стороны a.
Совет 2: Как обнаружить дискриминант
Если вы знаете значение дискриминанта, то вы можете сказать, что решили квадратное уравнение, потому как его корни будут обнаружены дюже легко.
Вам понадобится
- -формула дискриминанта квадратного уравнения;
- -умение таблицы умножения
Инструкция
1. Удостоверитесь, что перед вами квадратное уравнение. Это уравнение вида ax²+bx+c=0, где a, b, c – всякие действительные числа, а х – переменная.
2. Разглядите показатель b, стоящий перед x. Если b – нечетное, то ищем дискриминант. Если b представляет собой четное число, то для больше простого вычисления корней комфортно искать дискриминант, деленный на 4.
3. Находим дискриминант по формуле: D = b²-4ac. Соответственно, для дискриминанта, деленного на 4, формула примет дальнейший вид: D/4 = b²/4 – ac.
Видео по теме
Полезный совет
Дискриминант квадртаного уравнения может быть позитивным, негативным, либо равняться 0.
Совет 3: Как обнаружить стороны прямоугольника
Частный случай параллелограмма – прямоугольник – знаменит только в геометрии Евклида. У прямоугольника равны все углы, и всякий из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон дозволено обнаружить стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника базируется на дополнительных построениях и использовании свойств получаемых фигур.
Инструкция
1. Постройте прямоугольник EFGH. Запишите знаменитые данные: диагональ прямоугольника EG и угол α, полученный от пересечения 2-х равных диагоналей FH и EG. Постройте на рисунке диагонали и подметьте между ними угол α.
2. Буквой А подметьте точку пересечения диагоналей. Разглядите образованный построениями треугольник EFА. Согласно свойству прямоугольника его диагонали равны и делятся напополам точкой пересечения А. Вычислите значения FА и EА. Потому что треугольник EFА является равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.
3. Дальше вычислите первую сторону EF прямоугольника . Данная сторона является третьей неведомой стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле обнаружьте сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА равна EА и косинус знаменитого угла между ними α. Вычислите и запишите полученное значение EF.
4. Обнаружьте вторую сторону прямоугольника FG. Для этого разглядите иной треугольник EFG. Он является прямоугольным, где знамениты гипотенуза EG и катет EF. Согласно теореме Пифагора обнаружьте 2-й катет FG по соответствующей формуле.
5. В соответствии со свойствами прямоугольника его противолежащие ребра равны. Таким образом сторона GH равна обнаруженной стороне EF, а HЕ = FG. Запишите в результат все вычисленные стороны прямоугольника .
Совет 4: Как обнаружить периметр равностороннего треугольника
Равносторонний треугольник наравне с квадратом является, вероятно, самой примитивный и симметричной фигурой в планиметрии. Разумеется, все соотношения, объективные для обыкновенного треугольника, правильны также и для равностороннего. Впрочем для положительного треугольника все формулы становятся гораздо проще.
Вам понадобится
- калькулятор, линейка
Инструкция
1. Дабы обнаружить периметр равностороннего треугольника измерьте длину одной из его сторон и умножьте итог измерения на три. В виде формулы это правило дозволено записать дальнейшим образом:Прт = Дс * 3,где:Прт – периметр равностороннего треугольника,Дс – длина всякий из его сторон.Периметр треугольника получится в тех же единицах измерения, что и длина его стороны.
2. Пример.Длина стороны равностороннего треугольника равна 10 мм. Требуется определить его периметр.Решение.Прт = 10 * 3 = 30 (мм)
3. Потому что равносторонний треугольник владеет высокой степенью симметрии, то для вычисления его периметра довольно одного из параметров. Скажем, площади, высоты, радиуса вписанной либо описанной окружности.
4. Если вестим радиус вписанной окружности равностороннего треугольника, то для вычисления его периметра воспользуйтесь дальнейшей формулой:Прт = 6 * ?3 * r, где: r – радиус вписанной окружности.Это правило следует из того, что радиус вписанной окружности равностороннего треугольника выражается через длину его стороны дальнейшим соотношением:r = ?3/6 * Дс.
5. Дабы вычислить периметр положительного треугольника через радиус описанной окружности, примените формулу:Прт = 3 * ?3 * R,где: R – радиус описанной окружности.Данная формула легко выводится из того факта, что радиус описанной окружности верного треугольника выражается через длину его стороны дальнейшим соотношением: R = ?3/3 * Дс.
6. Для вычисления периметра равностороннего треугольника через вестимую площадь воспользуйтесь дальнейшим соотношением:Sрт = Дст? * ?3 / 4,где: Sрт – площадь равностороннего треугольника.Отсель дозволено вывести: Дст? = 4 * Sрт / ?3, следственно: Дст = 2 * ?(Sрт / ?3).Подставляя это соотношение в формулу периметра через длину стороны равностороннего треугольника, получаем:Прт = 3 * Дст = 3 * 2 * ?(Sрт / ?3) = 6 * ?Sст / ?(?3) = 6?Sст / 3^?.
Видео по теме
Совет 5: Как обнаружить площадь и периметр квадрата
Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон идентичной длины и четырех прямых углов, всякий из которых равен 90°. Определение площади либо периметра четырехугольника, причем всякого, требуется не только при решении задач по геометрии, но и в повседневной жизни. Эти знания могут стать пригодными, скажем, во время ремонта при расчете необходимого числа материалов – покрытий для пола, стен либо потолка, а также для разбивки газонов и грядок и т.д.
Инструкция
1. Для определения площади квадрата умножьте величину длины на величину ширины. Потому что в квадрате длина и ширина идентичны, то значение одной стороны довольно построить в квадрат. Таким образом, площадь квадрата равна длине его стороны, возведенной в квадрат. Единицей измерения площади могут быть квадратные миллиметры, сантиметры, дециметры, метры, километры.Дабы определить площадь квадрата, дозволено воспользоваться формулойS = aa, где S – площадь квадрата,а – сторона квадрата.
2. Пример № 1. Комната имеет форму квадрата. Сколько ламината (в кв.м) понадобится для того, дабы всецело покрыть пол, если длина одной стороны комнаты составляет 5 метров.Запишите формулу: S = aa. Подставьте в нее указанные в условии данные.Потому что а = 5 м, следственно, площадь будет равнаS (комнаты) = 5х5= 25 кв.м, значит, и S (ламината) = 25 кв.м.
3. Периметр представляет собой всеобщую длину границы фигуры. В квадрате периметр – это длина всех четырех, причем идентичных, сторон. То есть, периметр квадрата представляет собой сумму всех его четырех сторон. Дабы вычислить периметр квадрата, довольно знать длину одной его стороны. Измеряется периметр в миллиметрах, сантиметрах, дециметрах, метрах, километрах.Для определения периметра имеется формула:P = a + а + а + а илиP = 4a, гдеР – периметр,а – длина стороны.
4. Пример № 2. Для отделочных работ помещения в форме квадрата требуются потолочные плинтуса. Вычислите всеобщую длину (периметр) плинтусов, если величина одной стороны комнаты равна 6 метров. Запишите формулу P = 4a.Подставьте в нее указанные в условии данные:Р (комнаты) = 4 х 6 = 24 метра.Следственно, длина потолочных плинтусов тоже будет равна 24 метров.
Видео по теме
Как найти стороны прямоугольника, если известен его периметр в см и одна сторона больше другой на i см?
i = a — b ⇒ a = i + b
P = 2(a + b) ⇒ a = P : 2 — b
i + b = P : 2 — b ⇒ b = ( 0,5 P — i ) : 2 = 0,25 P — 0,5 i
a = i + 0,25 P — 0,5 i = 0,25 P + 0,5 i
Итого площадь прямоугольника можно найти по формуле:
a = 0,25 P + 0,5 i
b = 0,25 P — 0,5 i
P — периметр прямоугольника в см (сантиметрах);
a — длина одной из сторон прямоугольника в см (сантиметрах);
b — длина другой стороны прямоугольника в см (сантиметрах);
i — на сколько см (сантиметров) длина стороны a больше длины стороны b.
Например:
Периметр прямоугольника равен 44 см, одна сторона больше другой на 2 см. Найдите стороны прямоугольника.
Краткое решение:
a = 0,25 P + 0,5 i = 0,25 • 44 + 0,5 • 2 = 12 см
b = 0,25 P — 0,5 i = 0,25 • 44 — 0,5 • 2 = 10 см
Периметр прямоугольника равен 58 см, одна сторона больше другой на 5 см. Найдите стороны прямоугольника.
Краткое решение:
a = 0,25 P + 0,5 i = 0,25 • 58 + 0,5 • 5 = 17 см
b = 0,25 P — 0,5 i = 0,25 • 58 — 0,5 • 5 = 12 см
Периметр прямоугольника равен 18 см, одна сторона больше другой на 3 см. Найдите стороны прямоугольника.
Краткое решение:
a = 0,25 P + 0,5 i = 0,25 • 18 + 0,5 • 3 = 6 см
b = 0,25 P — 0,5 i = 0,25 • 18 — 0,5 • 3 = 3 см
Школьная математика » Блог » Как найти стороны прямоугольника при известных периметре и площади
В этой статье я хочу рассмотреть две математические задачи повышенной сложности для 4 класса.
Видеоурок по теме этой статьи можно посмотреть по ссылке.
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
С этими задачами, я уверен, без труда справится более старший школьник, знакомый с решением системы уравнений и квадратных уравнений. Кстати, подобная задача есть в учебнике по геометрии Атанасяна, глава VI № 454 пункт б за 8 класс.
Но почему же эти задачи указаны в математических сборниках как задачи для 4 класса, в котором еще не изучают алгебраические понятия и методы решения? Нет ли здесь ошибки?
Нет, никакой ошибки здесь нет. Эти, и аналогичные им задачи можно решить и без использования алгебраических знаний.
Первое, что приходит на ум – это по значению периметра прямоугольника (а периметр – это удвоенная сумма двух его сторон) найти сумму двух сторон, а после простым подбором определить два числа, произведение которых равно данной по условию площади прямоугольника, а сумма – половине периметра.
Я хочу показать вам математически точное решение, которое безо всяких подборов приводит к правильному результату.
Нахождение сторон прямоугольника при известных периметре и площади
Рассмотрим первую задачу:
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Как известно, периметр прямоугольника находится по формуле ({color{red} P=2cdot (a+b)}) , площадь – по формуле ({color{red} S=acdot b}) .
Так как периметр прямоугольника – это удвоенное произведение суммы двух сторон прямоугольника, то мы можем найти эту сумму, разделив значение периметра на 2:
({color{red} a + b = 24 : 2 = 12}) см.
А дальше мы рассуждаем так.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – четное число, то очевидно, что прямоугольник с максимально возможным значением площади при сумме его двух сторон, равной 12, – это квадрат со стороной ({color{red} 12 : 2 = 6}) см.
Тогда площадь этого квадрата равна
({color{red}S_{k}=6cdot 6=36}) см2.
По условию нашей задачи площадь прямоугольника составляет 32 см2. Находим разницу между полученной площадью квадрата и заданной площадью прямоугольника.
({color{red} S–S _{k}=36-32=4}) см2.
Это значит, что нам нужно изменить стороны рассматриваемого квадрата со стороной 6 см так, чтобы уменьшилась его площадь, но не изменился периметр.
Так как квадрат имеет самую большую площадь среди прямоугольников с одинаковым периметром, то для уменьшения площади нам нужно увеличить разницу между его длиной и шириной. То есть, ширину уменьшить, а длину увеличить на одно и то же число.
Но на какое?
Площадь 4 см2 – это квадрат со стороной 2 см. Это и есть нужное нам число.
Тогда, ширина искомого прямоугольника будет равна:
({color{red} a=6-2=4}) см
а длина:
({color{red} b=6+2=8}) см.
Проверим найденные длины сторон, определив периметр и площадь полученного прямоугольника:
({color{red} P=2cdot (4+8)=2cdot 12=24}) см
({color{red} S=4cdot 8=32}) см2.
Задача решена верно.
Теперь рассмотрим вторую задачу.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
Находим полупериметр, то есть, сумму двух сторон прямоугольника.
({color{red} a+b=46:2=23}) см.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – нечетное число, значит, нам нужен такой прямоугольник, разница между значениями ширины и длины которого в натуральных числах минимальна, то есть, единица. Это прямоугольник со сторонами 11 и 12, т.к. ({color{red} 23=11+12}).
Площадь такого прямоугольника равна:
({color{red}S_{2}=11cdot 12=132}) см2.
Разница между полученной площадью и заданной по условию задачи составляет:
({color{red}S_{2}-S=132-126=6}) см2.
6 см2 – это площадь прямоугольника со сторонами 2 и 3 см. Чтобы уменьшить площадь нашего прямоугольника со сторонами 11 см и 12 см, нужно увеличить разницу между значениями этих сторон, а именно, уменьшить его короткую сторону, то есть, ширину. При этом длину также нужно увеличить на это же число, чтобы сохранить значение периметра.
Для этого ширину 11 мы уменьшаем на одноименное значение, то есть, тоже на ширину прямоугольника с площадью 6 см2, а именно, на 2.
Кстати, подумайте и напишите в комментарии к этой статье, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью (например, в этой задаче как прямоугольник 2 на 3, а не 1 на 6, а в первой – как квадрат 2 на 2, а не прямоугольник 1 на 4), и почему ширину уменьшаем именно на ширину (в этой задаче 11 – 2, а не 11 – 3).
Находим ширину искомого прямоугольника:
({color{red} a=11-2=9}) см.
Длину нужно увеличить также на это число, чтобы не изменился периметр прямоугольника:
({color{red} b=12+2=14}) см.
Проведем проверку:
({color{red} P=2cdot (9+14)=2cdot 23=46}) см.
({color{red}S=9cdot 14=126}) см2.
И эта задача решена тоже верно.
На этом все. Не забудьте написать в комментарии ответы на вопросы, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью, и почему ширину уменьшаем именно на ширину.
Вам также пригодится:
Четырехугольник, у которого все углы прямые, противоположные стороны равны и параллельны друг другу, называется прямоугольником. Стороной прямоугольника является отрезок, соединяющий две вершины фигуры. Длинная сторона считается длиной, короткая сторона — шириной прямоугольника, прилегающие стороны перпендикулярны, они являются его высотами.
Расчет длины стороны прямоугольника через диагональ и сторону
Отрезок, соединяющий 2 противолежащие вершины прямоугольника, является его диагональю. В прямоугольнике две диагонали одинаковой длины. Каждая из них делит прямоугольник на два прямоугольных треугольника, гипотенузой которых является диагональ, а катетами — стороны прямоугольника. Соответственно, квадрат диагонали можно вычислить через теорему Пифагора: d2 = a2 + b2, а сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон:
2d2 = 2a2 + 2b2
где d — диагональ, а, b — стороны прямоугольника.
Если дана диагональ прямоугольника и одна из его сторон, находим длину другой стороны, как корень из разности: квадрат диагонали минус квадрат известной стороны:
a = √d2 — b2
b = √d2 — a2
где d — диагональ, а, b — стороны прямоугольника.
Расчет стороны прямоугольника через периметр и сорону
Периметр прямоугольника равняется сумме всех его сторон. Если известны длина (а) и ширина (b) прямоугольника, его периметр (Р) будет равен удвоенной сумме сторон, т.к. его противоположные стороны равны:
Р = 2a + 2b = 2 (а + b)
Если известны периметр и одна из сторон прямоугольника, другую находим по формуле:
a = (P — 2b) / 2
b = (P — 2a) / 2
Р — периметр, a — длина, b — ширина прямоугольника
Т.е. сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.
Расчет стороны прямоугольника через площадь и сторону
Чтобы рассчитать площадь прямоугольника (S), необходимо его длину а умножить на ширину b:
S = аb
Если известна площадь прямоугольника и одна из его сторон, длину другой находим путем деления площади на длину известной стороны:
a = S / b
b = S / a
где S — площадь прямоугольника, a, b — его стороны.