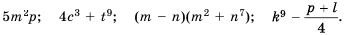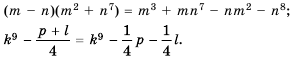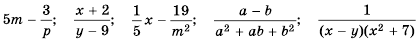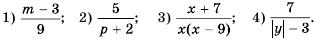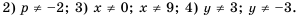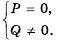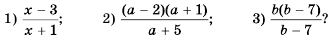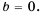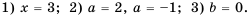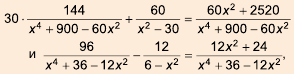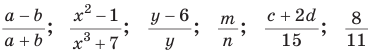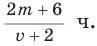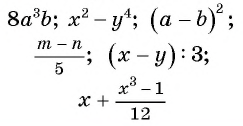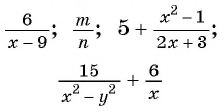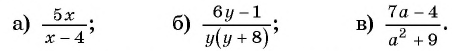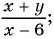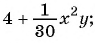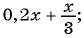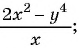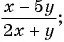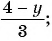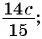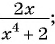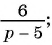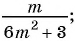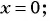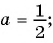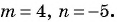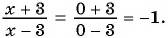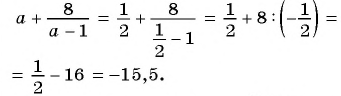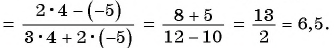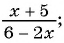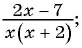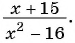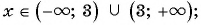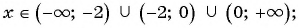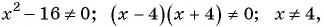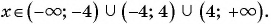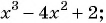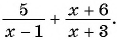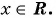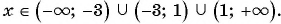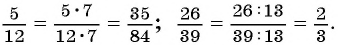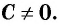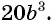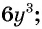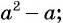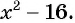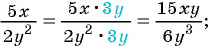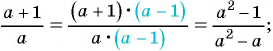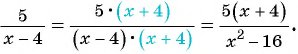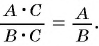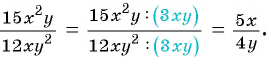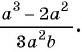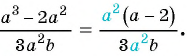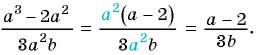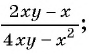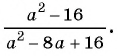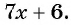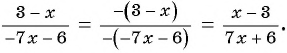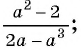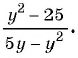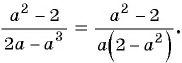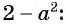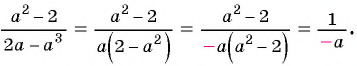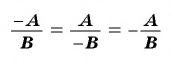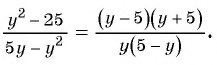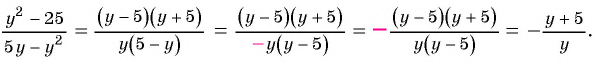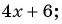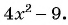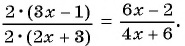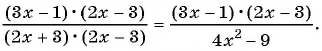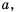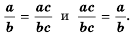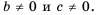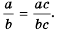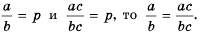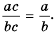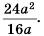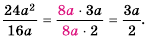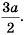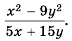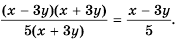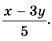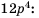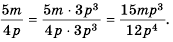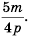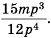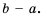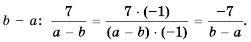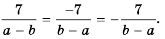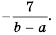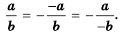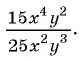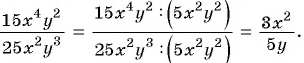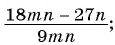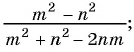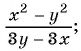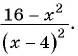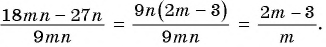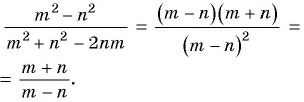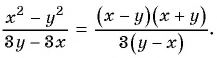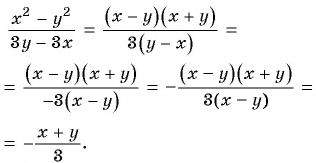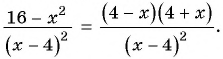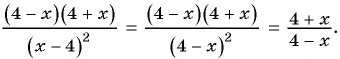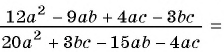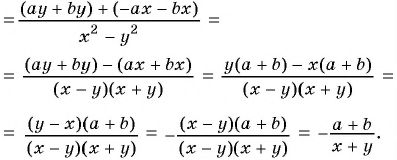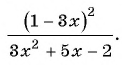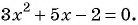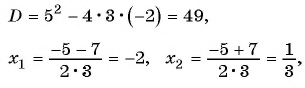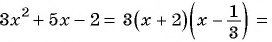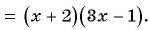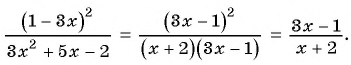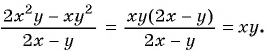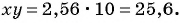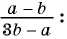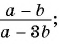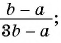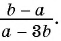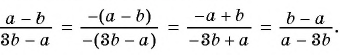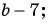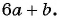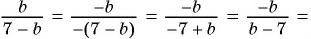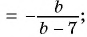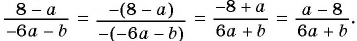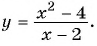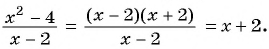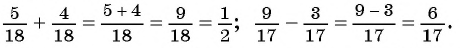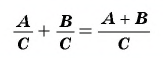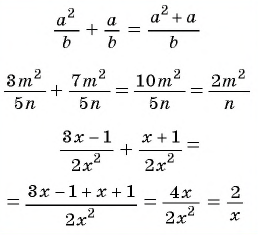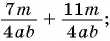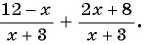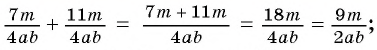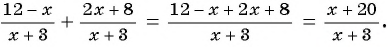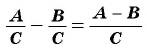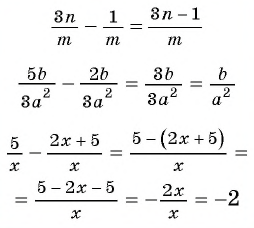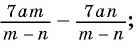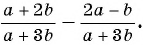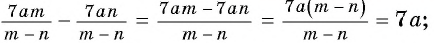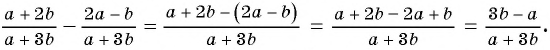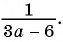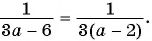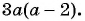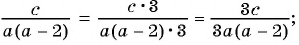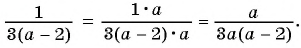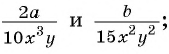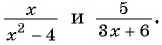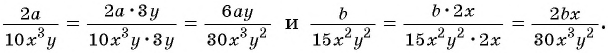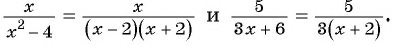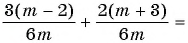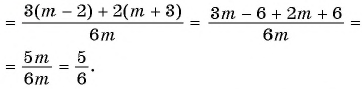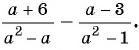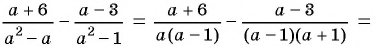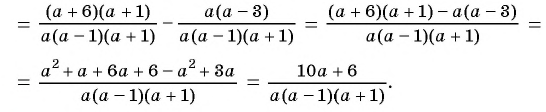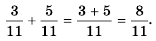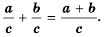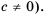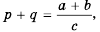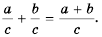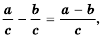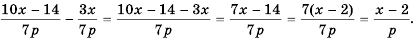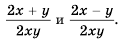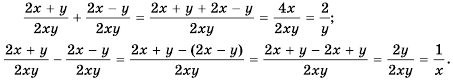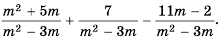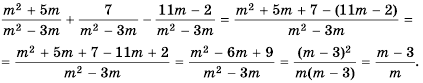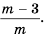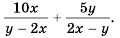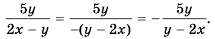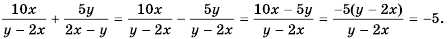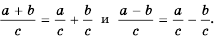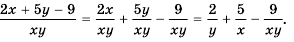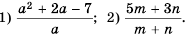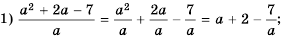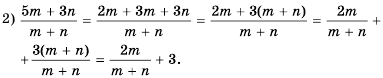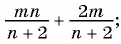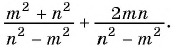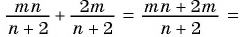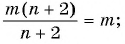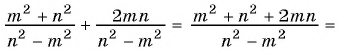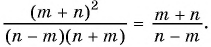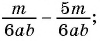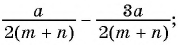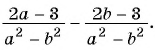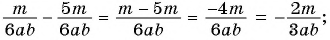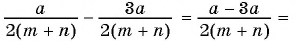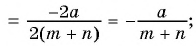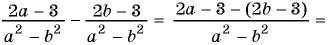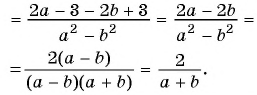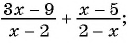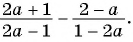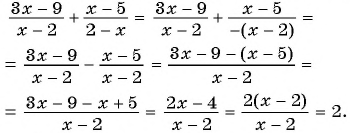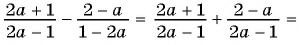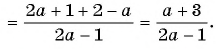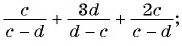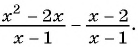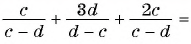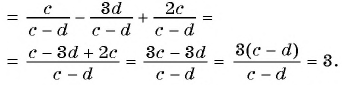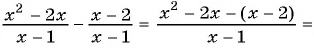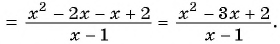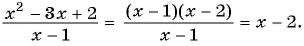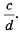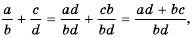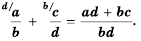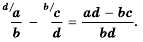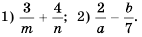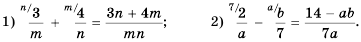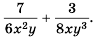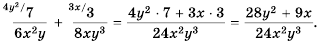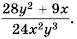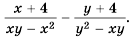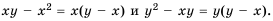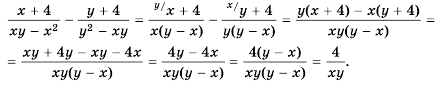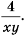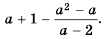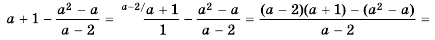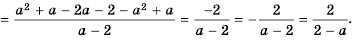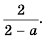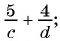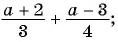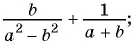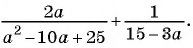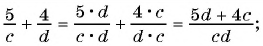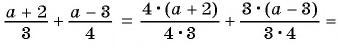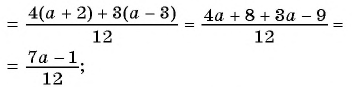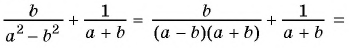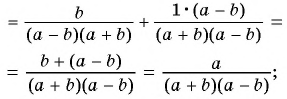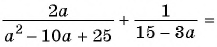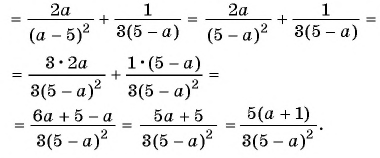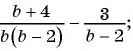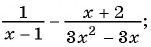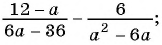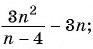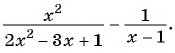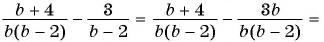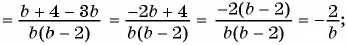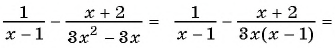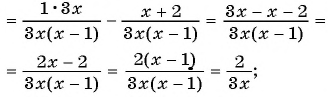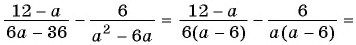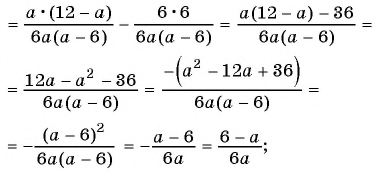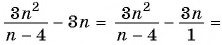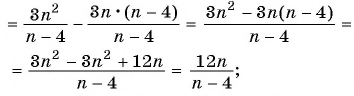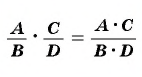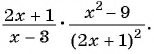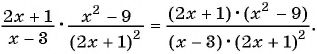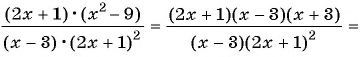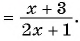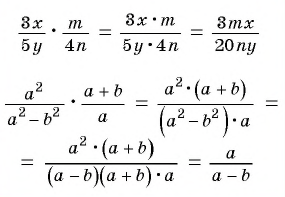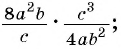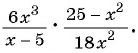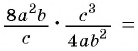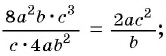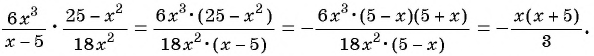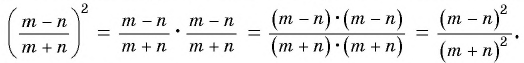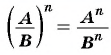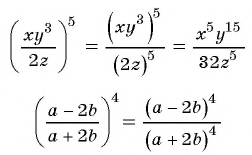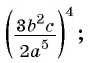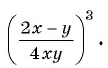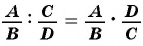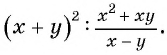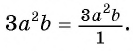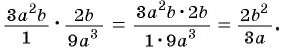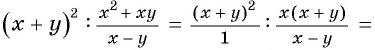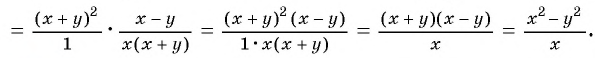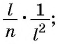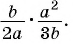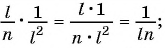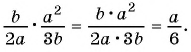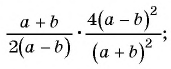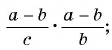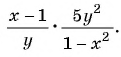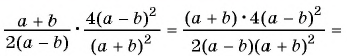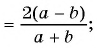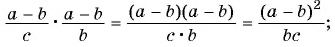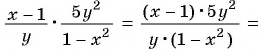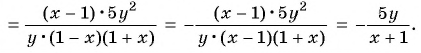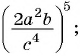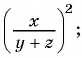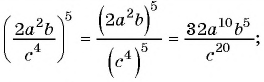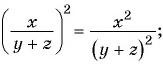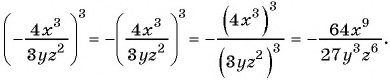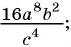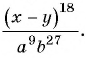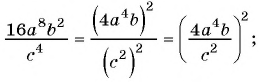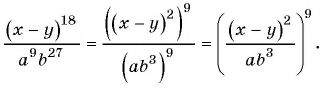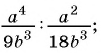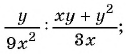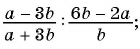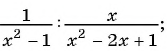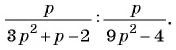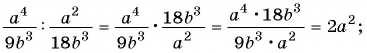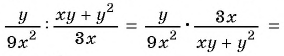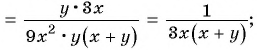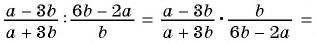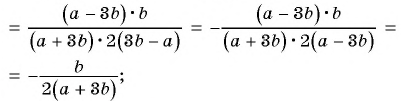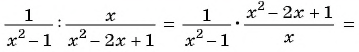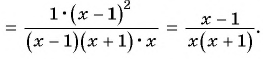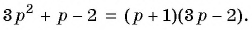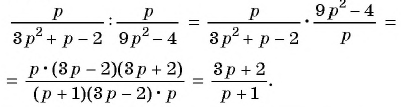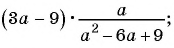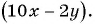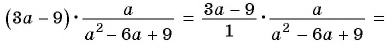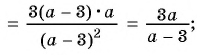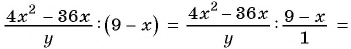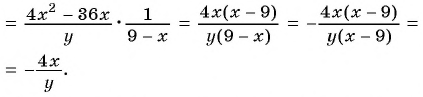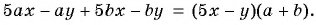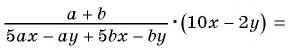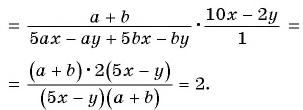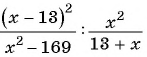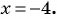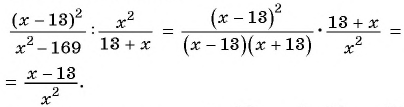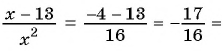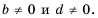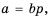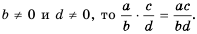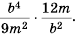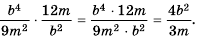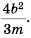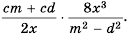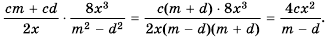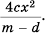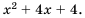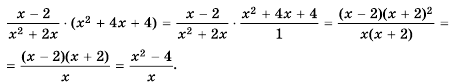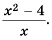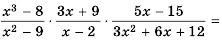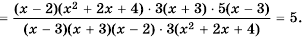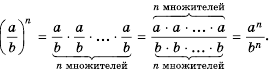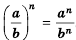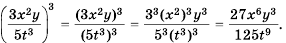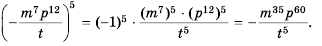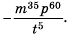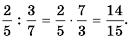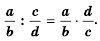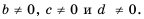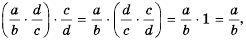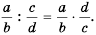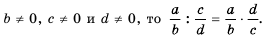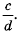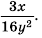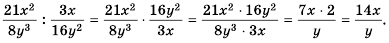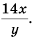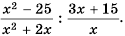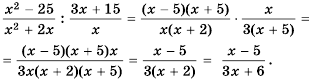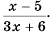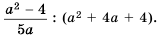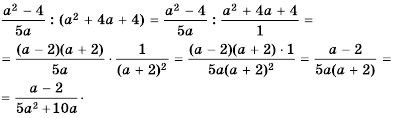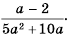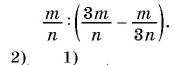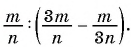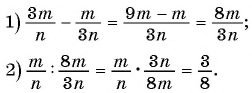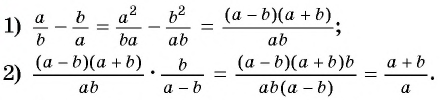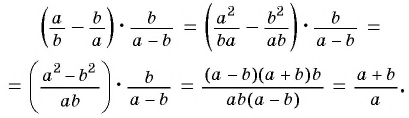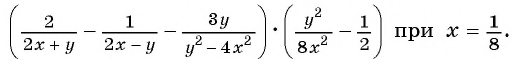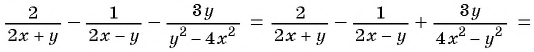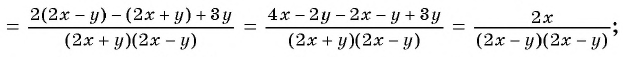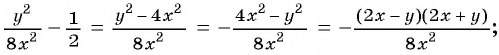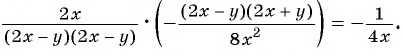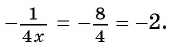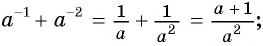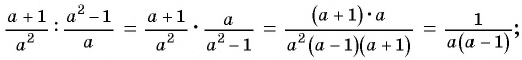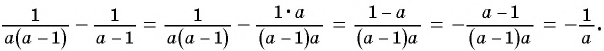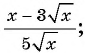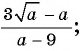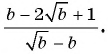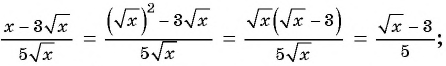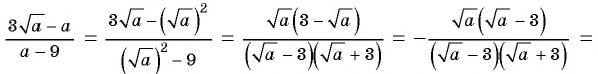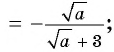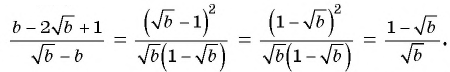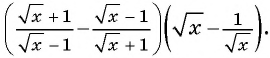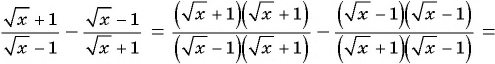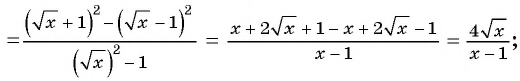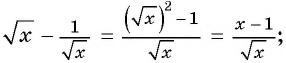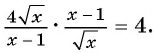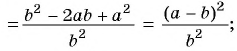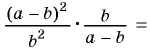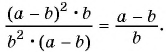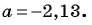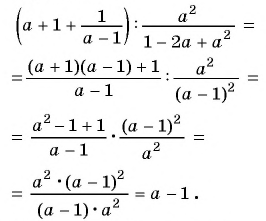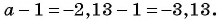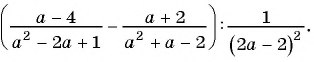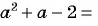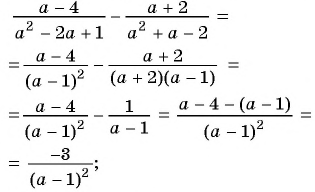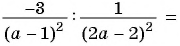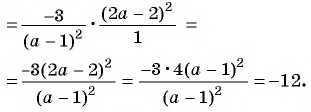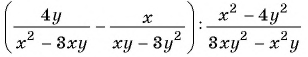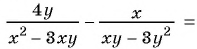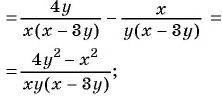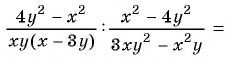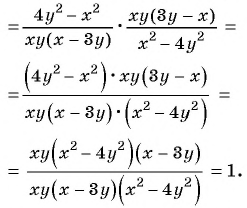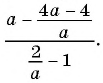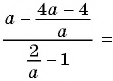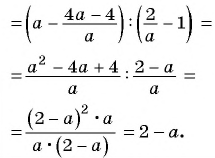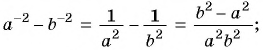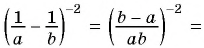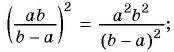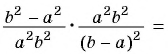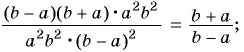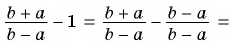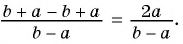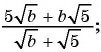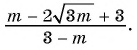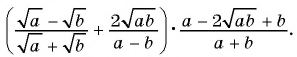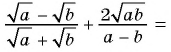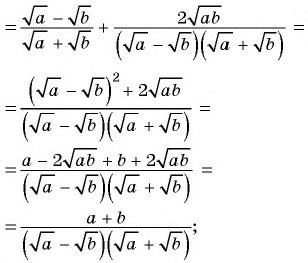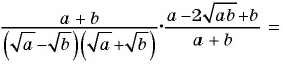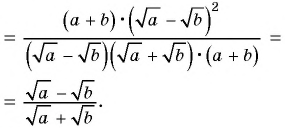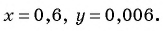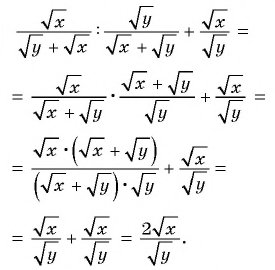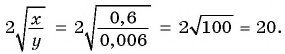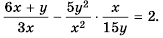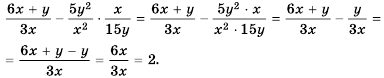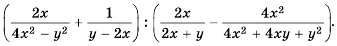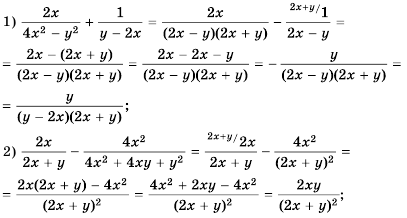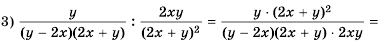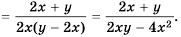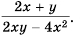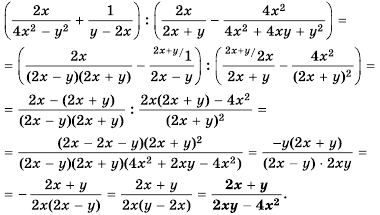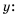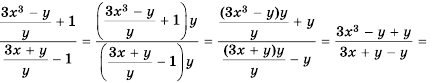Основное свойство рациональных чисел достаточное простое для понятия. Пользоваться основным свойством дроби вы будите постоянно во всех классах и темах математики, поэтому важно его сейчас разобрать и понять.
Основное свойство дроби, приведение к общему знаменателю.
Определение:
Если числитель и знаменатель умножить на одно и тоже число, которое не равно нулю, то получится равная ей дробь.
Запишем формулу основного свойства рациональных чисел:
(bf begin{align}frac{p}{q}=frac{p times n}{q times n}end{align})
Где p,q и n –целые числа ((q neq 0, n neq 0)).
По этой формуле приводят к общему знаменателю дроби. Умножаем на одно и тоже число числитель и знаменатель дроби.
Рассмотрим дробь, пример:
(begin{align}
&frac{1}{2}=frac{1 times 4}{2 times 4}=frac{4}{8} \\
&frac{1}{2}=frac{4}{8} \\
end{align})
Разберем данные дроби на рисунке.
Видим, если мы круг раздели на две равные части и закрасим 1 часть из 2, то закрашенная часть круга будет равна 4 равным частям из 8.
В чем заключается смысл основного свойства, мы разобрали на примере. А теперь запишем краткие правила основного свойства дроби общего знаменателя:
- Числитель и знаменатель дроби умножаем на число отличное от нуля.
- Проверяем равны ли исходная дробь с полученной.
Основное свойство дроби, сокращение дробей.
Определение:
Если у дроби числитель и знаменатель делим на общий множитель, не равный нулю, то получиться равная ей дробь.
Запишем формулу основного свойства дроби.
(bf begin{align}frac{p times n}{q times n}=frac{p}{q}end{align})
Где p,q и n –целые числа ((q neq 0, n neq 0)).
Такой вид формулы основного свойства дроби называется сокращением дробей. Мы имеем право сократить числитель и знаменатель на общий множитель.
Рассмотрим ту же самую дробь, но в обратном порядке.
(begin{align}
&frac{4}{8}=frac{1 times 4}{2 times 4}=frac{1}{2} \\
&frac{4}{8}=frac{1}{2} \\
end{align})
На рисунке запись дробей будет выглядеть так:
Основное свойство рациональных чисел сокращения дроби состоит из простых правил:
- Расписать числитель и знаменатель дроби на простые множители, найти среди них общий для числителя и знаменателя.
- Сократить числитель и знаменатель дроби на общий множитель.
- Проверяем равны ли исходная дробь с полученной.
Пример:
Пользуясь основным свойством дроби, найдите значение a, при котором верно равенство: а) (frac{a}{6}=frac{8}{48}) б) (frac{56}{70}=frac{8}{a})
Решение:
а) (frac{a}{6}=frac{8}{48})
Если мы внимательно посмотрим, то заметим, что знаменатель с числа 6 поменялся на число 48. Возникает вопрос: На какие число надо умножить 6, чтобы получить число 48? Ответ на 8, то есть первую дробь (frac{a}{6}) числитель и знаменатель умножили на 8 и получили вторую дробь (frac{8}{48}). Выглядит это так:
(begin{align}frac{a}{6}=frac{a times 8}{6 times 8}=frac{8}{48}end{align})
Тогда возникает вопрос: Какое число скрывается под переменной а, при умножении на которую получаем 8. Не трудно догадаться, переменная a=1. Подставим и проверим:
(begin{align}frac{1}{6}=frac{1 times 8}{6 times 8}=frac{8}{48}end{align})
А теперь рассмотрим, как решить пропорцию математически, ведь не всегда в выражении будут легкие числа.
(begin{align}
&frac{a}{6}=frac{8}{48} \\
&a=frac{8 times 6}{48} \\
&a=frac{48}{48} \\
&a=1 \\
end{align})
Ответ: 1
б) (frac{56}{70}=frac{8}{a})
Смотрим внимательно, видим, что в числители было число 56, а потом стало число 8. На какое число надо поделить 56, чтобы получить 8? Ответ на 7.
(frac{56}{70}=frac{8 times 7}{10 times 7}=frac{8}{10}=frac{8}{a})
Видим, что a=10. Теперь решим выражение (frac{56}{70}=frac{8}{a}) как пропорцию.
(begin{align}
&frac{56}{70}=frac{8}{a} \\
&a times 56=8 times 70 \\
&a=frac{8 times 70}{56} \\
&a=frac{560}{56} \\
&a=10
end{align})
Ответ: 10
Содержание:
Вы уже знакомы с целыми рациональными выражениями, то есть с выражениями, которые не содержат деления на выражение с переменной, например:
Любое целое выражение можно представить в виде многочлена стандартного вида, например:
В отличие от целых выражений, выражения
содержат деление на выражение с переменной. Такие выражения называют дробными рациональными выражениями. Целые рациональные и дробные рациональные выражения называют рациональными выражениями.
Рациональные выражения — это математические выражения, содержащие действии сложения, вычитания, умножения, деления и возведения в степень с целым показателем.
Определение рациональной дроби
Рациональное выражение вида 
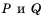
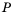
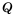
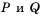
Целое рациональное выражение имеет смысл при любых значениях входящих в него переменных, так как при нахождении его значения выполняют действия сложения, вычитания, умножения и деления на число, отличное от нуля, что всегда выполнимо.
Рассмотрим дробное рациональное выражение — 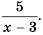
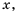
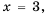
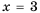
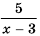
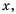
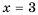
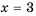
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных в выражении.
Эти значения образуют область определения выражения, или область допустимых значений переменных в выражении.
Пример:
Найдите допустимые значения переменной в выражении:
Решение:
1) Выражение имеет смысл при любых значениях переменной 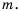
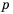
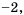
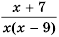
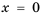
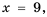
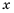
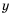
Кратко ответы можно записать следующим образом: 1) 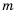
Рассмотрим условие равенства дроби нулю. Так как 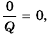
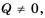
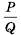
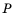
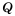
Пример:
При каких значениях переменной равно нулю значение дроби:
Решение:
1) Числитель дроби равен нулю при 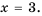
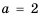

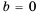
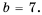
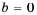
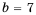
Ответ.
А еще раньше
Древнегреческий математик Диофант (прибл. 
записанных символикой того времени.
Выдающийся английский ученый Исаак Ньютон (1643-1727) в своей монографии «Универсальная арифметика» (1707 г.) определяет дробь следующим образом: «Запись одной из двух величин под другой, ниже которой между ними проведена черта, означает часть или же величину, возникающую при делении верхней величины на нижнюю». В этой работе Ньютон рассматривает не топько обычные дроби, но и рациональные.
Определение: Дробь, числитель и знаменатель которой — многочлены, называется рациональной дробью.
Например, выражения
являются рациональными дробями.
Рациональная дробь является рациональным выражением. Выражения, составленные из чисел, переменных с помощью действий сложения, вычитания, умножения, деления, возведения в натуральную степень, называют рациональными выражениями.
Если рациональное выражение не содержит деления на выражение с переменными, то оно называется целым рациональным выражением.
Рассмотрим задачу: Туристы в первый день проплыли на лодке по течению реки 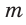
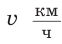
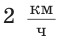
Решение:
Так как за два дня туристы преодолели 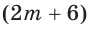
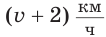
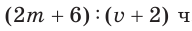
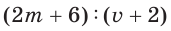
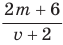
Ответ:
При решении этой задачи получили дробь, в числителе и знаменателе которой записаны многочлены. Такая дробь называется рациональной.
Целые рациональные выражения
Например, выражения 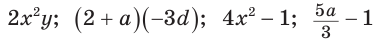
Рациональное выражение, содержащее деление на выражение с переменными, называют дробным рациональным выражением.
Дробные рациональные выражения
Например, выражения 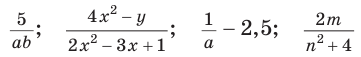
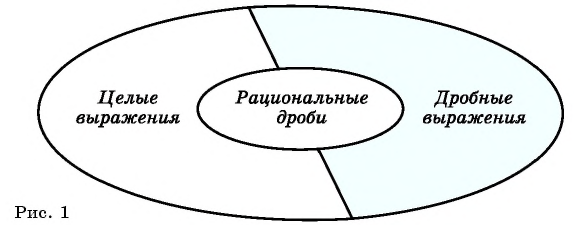
Связь между понятиями «рациональная дробь», «целое рациональное выражение» и «дробное рациональное выражение» иллюстрирует рисунок 1.
Целые рациональные выражения имеют смысл при любых значениях входящих в них переменных.
Например, областью определения выражения 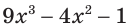
Рациональные выражения:
Дробные рациональные выражения имеют смысл при всех значениях переменных, кроме тех, которые обращают знаменатели дробей в нуль.
Например, выражение 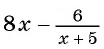
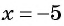
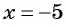
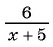
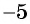
Рациональная дробь 
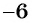
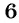
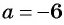
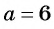
Областью определения рациональной дроби является множество всех значений входящих в нее переменных, кроме тех, которые обращают ее знаменатель в нуль.
Пример №1
Найдите область определения рациональной дроби:
Решение:
а) Областью определения рациональной дроби 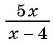
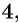
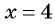
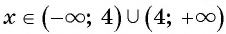
б) Найдем, при каких значениях переменной знаменатель дроби 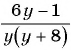
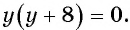
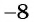
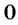
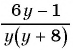
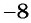
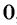
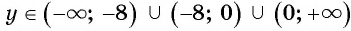
в) Поскольку выражение 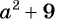
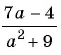
Рациональные выражения:
Пример №2
Какие из следующих выражений:
а)
б)
в)
г)
д) 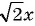
Решение:
Выражения а), в), г) и д) являются рациональными, так как составлены из чисел, переменных и содержат действия сложения, вычитания, умножения и деления. Выражение б) не является рациональным, так как содержит действие извлечения корня из выражения с переменными.
Пример №3
Какие из следующих выражений:
а)
б)
в)
г)
д) 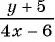
Решение:
Выражения б), в), д) являются дробными рациональными, так как составлены из чисел, переменных, натуральных степеней переменных с помощью действий сложения, вычитания, умножения и содержат действие деления на рациональное выражение с переменными.
Пример №4
Какие из следующих выражений:
а)
б)
в)
г)
д) 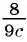
Решение:
Выражения а) — д) являются рациональными дробями, так как каждое из них представляет собой дробь, числитель и знаменатель которой являются многочленами.
Пример №5
Найдите значение выражения:
а) 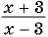
б) 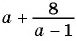
в) 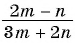
Решение:
а) Подставим 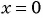
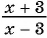
б) При 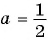
в) Если 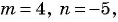
Область определения рациональной дроби
Пример №6
Найдите область определения рациональной дроби:
а)
б)
в)
Решение:
а) Найдем, при каком значении переменной знаменатель дроби обращается в нуль. Для этого решим уравнение 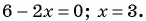
б) 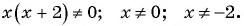
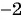
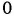
в) 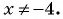
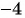
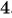
Пример №7
Найдите область определения рационального выражения:
а)
б)
Решение:
а) Выражение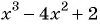
б) Знаменатель первой дроби обращается в нуль при 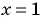
Основное свойство рациональной дроби
Действия с рациональными дробями выполняются по тем же правилам, что с обыкновенными дробями. Так, согласно основному свойству обыкновенных дробей, если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
Например,
Аналогичное свойство можно сформулировать для рациональных дробей.
Если числитель и знаменатель дроби умножить или разделить на одно и то же выражение, не равное нулю, то получится дробь, тождественно равная данной.
Это свойство называют основным свойством дроби.
Для любой рациональной дроби 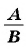
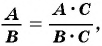
Умножим числитель и знаменатель дроби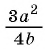
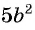
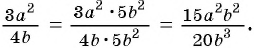
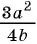
Пример №8
Приведите дробь:
а) 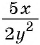
б) 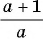
в) 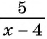
Решение:
а)
б)
в)
Если основное свойство дроби записать справа налево, то получится равенство
Это равенство позволяет дробь 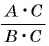
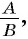
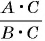
Например, разделим числитель и знаменатель дроби 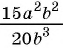
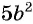
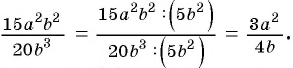
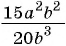
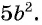
Сократить рациональную дробь — это значит числитель и знаменатель дроби разделить на их общий множитель.
Например, сократим дробь 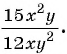
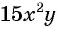
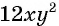
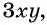
Чтобы сократить рациональную дробь, нужно:
- Разложить (если возможно) числитель и знаменатель дроби на множители.
- Определить общий множитель числителя и знаменателя дроби.
- Разделить числитель и знаменатель данной дроби на общий множитель.
Сократите дробь
(1)
(2) 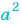
(3)
Пример №9
Сократите дробь:
а)
б)
Решение:
а)
б)
Из основного свойства дроби следует, что 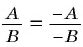
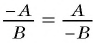
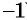
Пример №10
Приведите дробь 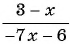
Решение:
Воспользуемся равенством 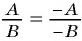
Пример №11
Сократите дробь:
а)
б)
Решение:
а) Разложим знаменатель дроби на множители и получим:
Выражения 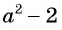
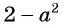
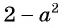
Полученный ответ можно записать в виде 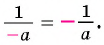
б) Разложим числитель и знаменатель дроби на множители и получим:
Поменяем знаки одного из множителей 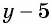
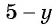
Пример №12
Приведите дробь 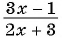
а)
б)
Решение:
а) Умножим числитель и знаменатель дроби на 2 и получим:
б) Умножим числитель и знаменатель дроби на 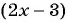
Разберём лекцию подробно:
Вспомним основное свойство обыкновенной дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получим дробь, равную данной. Иначе говоря, для любых натуральных чисел 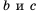
Докажем, что эти равенства являются верными не только для натуральных значений 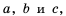
Докажем сначала, что
Пусть 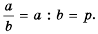
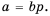
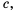
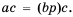
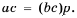
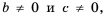
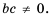
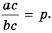
Это равенство является тождеством, следовательно, можем поменять в нем левую и правую части местами:
Это тождество дает возможность заменить дробь 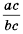
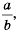
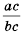
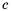
Свойство дроби, выраженное равенствами 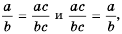
Если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля выражение, то получим дробь, равную данной.
Рассмотрим примеры применения этого свойства для дробей на их области допустимых значений переменной.
Пример №13
Сократите дробь
Решение:
Представим числитель и знаменатель этой дроби в виде произведений, содержащих одинаковый (общий) множитель 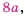
Ответ:
Пример №14
Сократите дробь
Решение:
Разложим на множители числитель и знаменатель дроби: 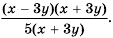
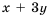
Ответ:
Таким образом, чтобы сократить дробь, нужно:
- разложить на множители числитель и знаменатель дроби, если это необходимо;
- выполнить деление числителя и знаменателя на их общий множитель и записать ответ.
Тождество 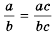
Пример №15
Приведите дробь 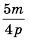
Решение:
Поскольку 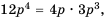
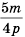
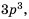
Множитель 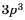
Ответ:
Пример №16
Приведите дробь 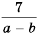
Решение:
Поскольку 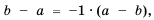
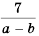
Дробь 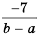
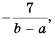
Поэтому
Ответ.
Аналогично, например, 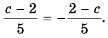
- если изменить знак в числителе (или знаменателе) дроби одновременно со знаком перед дробью, то получим дробь, тождественно равную данной.
Это правило можно записать с помощью тождества:
Пример №17
Найдите область определения функции 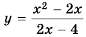
Решение:
Область определения функции — все числа, кроме тех, которые обращают знаменатель 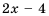
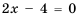
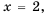
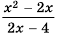
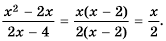
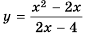
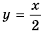
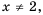
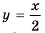
График функции 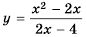
Сокращение рациональных дробей
Пример №18
Сократите дробь
Решение:
Дробь можно сократить на 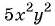
Пример №19
Сократите дробь:
а)
б)
в)
г)
Решение:
а) Разложим на множители числитель дроби и сократим дробь:
б) С помощью формул сокращенного умножения разложим на множители числитель и знаменатель дроби и получим:
в) Разложим на множители числитель и знаменатель дроби:
Множители 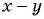
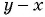
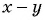
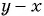
г) После разложения на множители числителя дроби имеем:
Воспользуемся тем, что 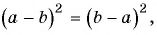
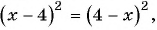
Пример №20
Сократите дробь:
а)
б)
Решение:
а) С помощью способа группировки разложим числитель и знаменатель дроби на множители и сократим дробь:
б)
Пример №21
Сократите дробь:
Решение:
Для разложения на множители знаменателя дроби воспользуемся формулой разложения квадратного трехчлена на множители: 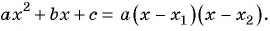
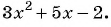
тогда
Сократим дробь:
Пример №22
Упростите выражение 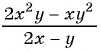
Решение:
Упростим выражение, сократив дробь:
Подставим 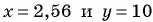
Пример №23
Из данных рациональных дробей выберите дробь, тождественно равную дроби
а)
б)
в)
Решение:
Выполним преобразования:
Дроби 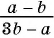
Пример №24
Приведите дробь:
а) 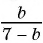
б) 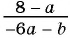
Решение:
Умножим числитель и знаменатель дроби на 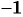
а)
б)
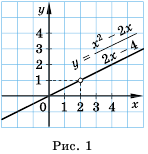
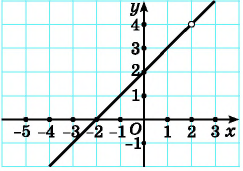
Пример №25
Постройте график функции
Решение:
Областью определения данной функции является множество всех действительных чисел, кроме числа 2.
Сократим дробь 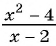
Необходимо построить график функции 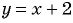
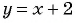
Сложение и вычитание рациональных дробей
Вспомним, как складывают и вычитают обыкновенные дроби. Например:
Сложение и вычитание рациональных дробей выполняются по таким же правилам, что сложение и вычитание обыкновенных дробей.
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.
Затем, если возможно, следует сократить полученную дробь.
Пример №26
Найдите сумму рациональных дробей:
а)
б)
Решение:
а)
б)
Чтобы вычесть дроби с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же. Затем, если возможно, следует сократить полученную дробь.
Пример №27
Найдите разность рациональных дробей:
а)
б)
Решение:
а)
б)
При сложении и вычитании обыкновенных дробей с разными знаменателями их приводят к общему знаменателю (например, 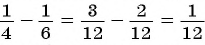
Для того чтобы выполнить сложение или вычитание рациональных дробей с разными знаменателями, их также нужно привести к общему знаменателю.
Чтобы привести рациональные дроби к общему знаменателю, нужно:
- Разложить знаменатель каждой дроби на множители (если это необходимо) и определить общий знаменатель дробей.
- Умножить числитель и знаменатель каждой дроби на недостающие множители из общего знаменателя дробей.
Приведите к общему знаменателю рациональные дроби 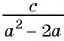
(1) 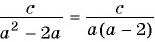
Общий знаменатель
(2)
Пример №28
Приведите к общему знаменателю дроби: а)
б)
Решение:
а) Общим знаменателем данных дробей является одночлен 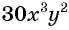
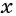
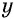
Умножим числитель и знаменатель первой дроби на 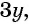
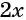
б) Разложим на множители знаменатель каждой дроби и получим:
Умножим числитель и знаменатель первой дроби на 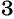
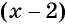
и
Чтобы выполнить сложение (вычитание) рациональных дробей с разными знаменателями, нужно:
- Привести дроби к общему знаменателю.
- Применить правила сложения (вычитания) дробей с одинаковыми знаменателями.
Найдите сумму рациональных дробей
(1)
(2)
Пример №29
Найдите разность рациональных дробей
Решение:
Сложение и вычитание дробей с одинаковыми знаменателями
Вспомним, как сложить дроби с одинаковыми знаменателями. Нужно сложить их числители, а знаменатель оставить тот же. Например:
Запишем это правило в виде формулы:
Это равенство справедливо для любых дробей. Докажем его (при условии
Пусть 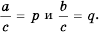
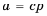
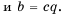
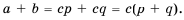
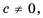
следовательно,
Сформулируем правило сложения дробей с одинаковыми знаменателями:
чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Пример №30
Аналогично можно доказать тождество
при помощи которого записывают правило вычитания дробей с одинаковыми знаменателями.
Сформулируем правило вычитания дробей с одинаковыми знаменателями:
чтобы вычесть дроби с одинаковыми знаменателями, нужно от числителя уменьшаемого отнять числитель вычитаемого, а знаменатель оставить тот же.
Пример №31
Рассмотрим еще несколько примеров.
Пример №32
Найдите сумму и разность дробей
Решение:
Ответ.
Пример №33
Упростите выражение
Решение:
Ответ:
Пример №34
Найдите сумму
Решение:
Так как 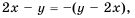
Тогда
Ответ:
Если в тождествах 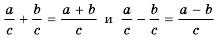
С помощью этих тождеств дробь, числитель которой является суммой или разностью нескольких выражений, можно записать в виде суммы или разности нескольких дробей.
Пример №35
Пример №36
Запишите дробь в виде суммы или разности целого выражения и дроби:
Решение:
Ответ.
Пример №37
Выполните сложение рациональных дробей:
а)
б)
Решение:
а)
б)
Пример №38
Найдите разность рациональных дробей:
а)
б)
в)
Решение:
а)
б)
в)
Пример №39
Выполните действия:
а)
б)
Решение:
а) Знаменатели дробей отличаются только знаком. Поменяем знак в знаменателе второй дроби и перед этой дробью и получим:
б)
Пример №40
Выполните действия:
а)
б)
Решение:
а)
б)
Разложим на множители квадратный трехчлен в числителе дроби и сократим дробь:
Сложение и вычитание дробей с разными знаменателями
Если дроби имеют разные знаменатели, то их, как и обычные дроби, сначала приводят к общему знаменателю, а потом складывают или вычитают по правилу сложения или вычитания дробей с одинаковыми знаменателями.
Рассмотрим, как прибавить дроби 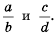
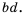
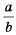
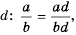
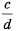
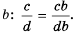
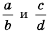
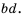
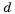
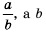
Описанную последовательность действий для сложения дробей с разными знаменателями можно записать так:
или сокращенно:
Аналогично выполняют и вычитание дробей с разными знаменателями:
Пример №41
Выполните действие:
Решение:
Общим знаменателем двух или более дробей может быть не только произведение их знаменателей. Вообще у дробей есть бесконечно много общих знаменателей. Часто при сложении и вычитании дробей с разными знаменателями удается найти более простой общий знаменатель, чем произведение знаменателей этих дробей. В таком случае говорят о простейшем общем знаменателе (аналогично наименьшему общему знаменателю числовых дробей).
Рассмотрим пример, где знаменатели дробей — одночлены.
Пример №42
Выполните сложение
Решение. Общим знаменателем данных дробей можно считать одночлен 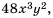
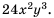
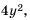
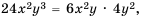
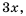
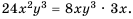
Ответ:
Обратите внимание, что в примере 2 при приведении дробей к общему знаменателю дополнительные множители 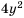
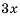
Рассмотрим пример, в котором знаменателями дробей являются многочлены.
Пример №43
Выполните вычитание
Решение:
Чтобы найти общий знаменатель, разложим знаменатели на множители:
Простейшим общим знаменателем дробей будет выражение 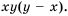
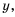
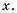
Ответ.
Таким образом, чтобы выполнить сложение или вычитание дробей с разными знаменателями, нужно:
- разложить на множители знаменатели дробей, если это необходимо;
- найти общий знаменатель, лучше простейший;
- записать дополнительные множители;
- найти дробь, которая является суммой или разницей данных дробей;
- упростить эту дробь и получить ответ.
Аналогично выполняют сложение и вычитание целого выражения и дроби.
Пример №44
Упростите выражение
Решение:
Запишем выражение 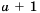
Ответ:
Пример №45
Выполните сложение рациональных дробей:
а)
б)
в)
г)
Решение:
а)
б)
в)
г)
Пример №46
Выполните вычитание:
а)
б)
в)
г)
д)
Решение:
а)
б)
в)
г)
д) Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
Пример №47
Представьте в виде дроби выражение
Решение:
Умножение и деление рациональных дробей
Вспомним, как умножают и делят обыкновенные дроби.
Правила умножения и деления рациональных дробей аналогичны правилам умножения и деления обыкновенных дробей.
Произведение рациональных дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению знаменателей данных дробей.
Чтобы найти произведение рациональных дробей, нужно:
- Произведение числителей данных дробей записать в числителе новой дроби, а произведение знаменателей данных дробей записать в знаменателе новой дроби.
- Сократить полученную дробь, если это возможно.
Найдите произведение рациональных дробей
(1)
(2)
Пример №48
Найдите произведение рациональных дробей:
а)
б)
Решение:
а)
б)
Правило умножения рациональных дробей можно использовать при возведении рациональной дроби в степень. Например:
Обобщим этот прием и получим правило:
Чтобы возвести рациональную дробь в степень, нужно возвести в эту степень числитель дроби и полученный результат записать в числителе новой дроби, возвести в эту степень знаменатель дроби и полученный результат записать в знаменателе новой дроби.
Пример №49
Возведите в степень дробь:
а)
б)
Решение:
а)
б)
Чтобы разделить одну рациональную дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Пример №50
Найдите частное:
а)
б)
Решение:
а)
б)
Пример №51
Представьте в виде дроби рациональное выражение:
а)
б)
Решение:
а) Представим множитель 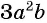
Выполним умножение дробей:
б) Представим выражение 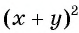
Пример №52
Выполните умножение рациональных дробей:
а)
б)
Решение:
а)
б)
Пример №53
Представьте в виде рациональной дроби произведение:
а)
б)
в)
Решение:
а)
б)
в)
Пример №54
Представьте в виде рациональной дроби выражение:
а)
б)
в)
Решение:
а)
б)
в)
Пример №55
Представьте в виде степени рациональную дробь:
а)
б)
Решение:
а)
б)
Пример №56
Выполните деление рациональных дробей:
а)
б)
в)
г)
д)
Решение:
а)
б)
в)
г)
д) Воспользуемся формулой разложения квадратного трехчлена на множители и получим:
Тогда
Пример №57
Выполните действия:
а)
б)
в)
Решение:
а)
б)
в) Разложим на множители многочлен, применив способ группировки:
Тогда
Пример №58
Найдите значение выражения
при
Решение:
Выполним деление:
При 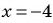
Пример №59
Найдите значение выражения
при
Решение:
Выполним умножение:
При 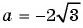
Умножение дробей
Напомним, что произведением двух обыкновенных дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей данных дробей:
Докажем, что это равенство является тождеством для любых значений 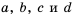
Пусть 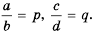
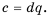
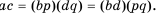
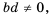
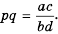
Сформулируем правило умножения дробей.
Чтобы умножить дробь на дробь, нужно перемножить отдельно числители и отдельно знаменатели сомножителей и записать первый результат в числителе, а второй — в знаменателе произведения дробей.
Пример №60
Выполните умножение
Решение:
Ответ:
Пример №61
Найдите произведение
Решение.
Используем правило умножения дробей и разложим на множители числитель первой дроби и знаменатель второй:
Ответ.
Обратите внимание, что в примерах 1 и 2 при умножении дробей мы не находили сразу же результат умножения числителей и знаменателей. Сначала мы записали произведения в числителе и в знаменателе по правилу умножения дробей, потом сократили полученную дробь, так как она оказалась сократимой, а уже затем выполнили умножение в числителе и в знаменателе и записали ответ. Целесообразно это учитывать и в дальнейшем.
Пример №62
Умножить дробь 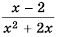
Решение:
учитывая, что 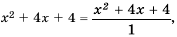
Ответ.
Правило умножения дробей можно распространить на произведение трех и более множителей.
Пример №63
Возведение дроби в степень
Рассмотрим возведение дроби 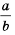
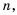
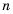
По определению степени и правилу умножения дробей имеем:
Следовательно:
Сформулируем правило возведения дроби в степень.
Чтобы возвести дробь в степень, нужно возвести в эту степень числитель и знаменатель и первый результат записать в числитель, а второй — в знаменатель дроби.
Пример №64
Пример №65
Представьте выражение 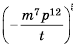
Решение:
Ответ:
Деление дробей
Напомним, чтобы найти частное двух обыкновенных дробей, нужно делимое умножить на дробь, обратную делителю:
Формулой это можно записать так:
Докажем, что это равенство является тождеством для любых значений 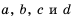
Так как:
то по определению частного имеем:
Следовательно, если
Дробь 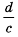
Сформулируем правило деления дробей.
Чтобы разделить одну дробь на другую, нужно первую дробь у множить на дробь, обратную второй.
Пример №66
Разделите дробь 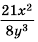
Решение:
Ответ.
Пример №67
Выполните деление
Решение:
Ответ:
Пример №68
Упростите выражение:
Решение:
Так как 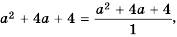
Ответ:
Преобразования рациональных выражений
При решении многих задач требуется упрощать рациональные выражения, приводя их к рациональным дробям. Для этого выполняют преобразования рациональных выражений.
Чтобы преобразовать рациональное выражение, нужно:
- Установить порядок действий в выражении.
- Выполнить действия по порядку, используя правила сложения, вычитания, умножения и деления рациональных дробей.
Упростите выражение:
(1)
(2)
Пример №69
Представьте выражение 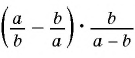
Решение:
(1) Сначала необходимо выполнить вычитание выражений, стоящих в скобках, а затем выполнить умножение.
(2)
Преобразование рационального выражения можно выполнить не по действиям, а «цепочкой». В данном случае получим:
Пример №70
Найдите значение выражения
Решение:
Упростим выражение, выполнив действия по порядку:
1)
2)
3)
При 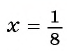
Преобразования рациональных выражений можно выполнять наряду с другими, ранее изученными преобразованиями.
Пример №71
Упростите выражение 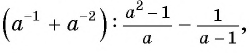
Решение:
1)
2)
3)
Правила преобразования рациональных выражений можно использовать и для преобразования выражений, содержащих корни.
Пример №72
Сократите дробь:
а)
б)
в)
Решение:
а)
б)
в)
Пример №73
Упростите выражение
Решение:
1)
2)
3)
Пример №74
Представьте выражение 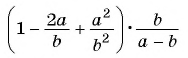
Решение:
1)
2)
Пример №75
Найдите значение выражения 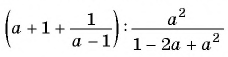
Решение:
Преобразуем данное выражение «цепочкой»:
При 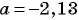
Пример №76
Упростите выражение
Решение:
1) Корнями квадратного трехчлена 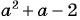
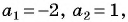
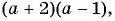
2)
Пример №77
Докажите, что значение выражения
не зависит от значений переменных.
Решение:
Значение выражения при различных значениях переменных из области его определения можно найти, предварительно упростить его:
1)
2)
Получили, что результат упрощения равен числу 1, значит при любых значениях переменных из области определения значение данного выражения равно 1, т. е. не зависит от значений переменных.
Пример №78
Упростите выражение
Решение:
Запишем дробь в виде частного и получим:
Пример №79
Упростите выражение
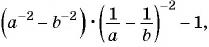
Решение:
1)
2)
3)
4)
Пример №80
Примените к выражению алгоритм сокращения рациональной дроби:
а)
б)
Решение:
а)
б)
Пример №81
Упростите выражение
Решение:
1)
2)
Пример №82
Найдите значение выражения 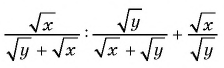
Решение:
Упростим данное выражение:
При 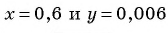
- Заказать решение задач по высшей математике
Тождественные преобразования рациональных выражений
Рассмотрим примеры преобразований рациональных выражений.
Пример №83
Докажите тождество
Решение:
Упростим левую часть равенства:
С помощью тождественных преобразований мы привели левую часть равенства к правой. Следовательно, равенство является тождеством.
Пример №84
Упростите выражение
Решение:
Сначала выполним действие в каждой из скобок, а потом — действие деления:
Ответ:
Решение можно было записать и в виде «цепочки»:
Каждое выражение, содержащее сумму, разность, произведение и частное рациональных дробей, можно представить в виде рациональной дроби.
Пример №85
Докажите, что при всех допустимых значениях переменных значение дроби 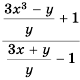
Решение:
Можно представить эту дробь в виде частного 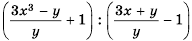
А можно, используя основное свойство дроби, умножить числитель и знаменатель данной дроби на их общий знаменатель, то есть на
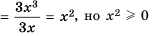
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Система показательных уравнений
- Непрерывные функции и их свойства
- Правило Лопиталя
- Вычисления в Mathematica с примерами
Рациональные дроби и их свойства. Основное свойство дроби. Сокращение дробей.
Целые выражения – это выражения, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения 7а2b, m3+n3, a+58 и т.д.
В отличие от них выражения 4a-b2a+1, x+yx2-3xy+y2, помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение 10+1a не имеет смысла при а = 0. При всех остальных значениях а это выражение имеет смысл. Выражение xx-y имеет смысл при тех значениях х и у, когда x ≠ y.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Выражение вида ab называется, как известно, дробью.
Дробь, числитель и знаменатель которой – многочлены, называют рациональной дробью.
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Пример 1. Найдем допустимые значения переменной в дроби 5a(a-9).
Чтобы найти, при каких значениях а знаменатель дроби обращается в нуль, нужно решить уравнение а(а — 9) = 0.
Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.
Пример 2. При каком значении х значение дроби x-22-252x+6 равно нулю?
Дробь ab равна нулю тогда и только тогда, когда a = 0 и b ≠ 0.
Числитель дроби равен нулю при x = 7 и x= -3. Знаменатель данной дроби не равен нулю, если x ≠ -3. Значит, данная дробь равна нулю при x = 7.
Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство ab=a∙cb∙c.
Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т.е. при b ≠ 0 и с ≠ 0.
Пусть ab=m. Тогда по определению частного a=bm. Умножим обе части этого равенства на с:
ac=bmc
На основании сочетательного и переместительного свойств умножения имеем:
ac=bcm
Так как bс ≠ 0, то по определению частного
acbc=m
Значит,
ab=acbc.
Мы показали, что для любых числовых значений переменных b и с, где b ≠ 0 и с ≠ 0, верно равенство ab=acbc.
Равенство сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.
Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Например, x+2x-3=(x+2)(x+y)(x-3)(x+y).
Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.
Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.
Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.
Пример 3. Приведем дробь 2x7y к знаменателю 35у3.
Так как 35у3 = 7у·5у2, то, умножив числитель и знаменатель дроби 2x7y на 5у2, получим:
2x7y=2x·5y27y∙5y2=10xy235y3
Множитель 5у2 называют дополнительным множителем к числителю и знаменателю дроби 2x7y.
Пример 4. Приведем дробь 52y-x к знаменателю x-2y.
Для этого числитель и знаменатель данной дроби умножим на -1:
52y-x=5·(-1)(2y-x)·(-1)=-5x-2y
Дробь -5x-2y можно заменить тождественно равным выражением -5x-2y, поставив знак «минус» перед дробью и заменив знак в числителе.
Если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.