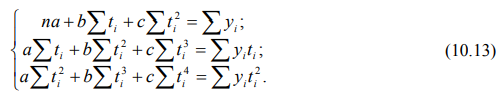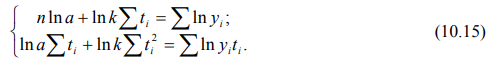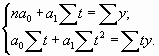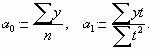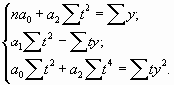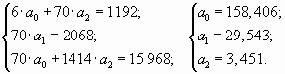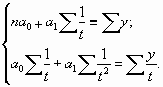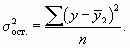Одной
из задач, возникающих при анализе рядов
динамики, является установление
закономерности изменения уровней
изучаемого показателя во времени. Для
этого необходимо выделить такие периоды
(этапы) развития, которые достаточно
однородны в отношении взаимосвязи
данного явления с другими и в отношении
условий его развития.
Выделение
этапов
развития –
это задача, находящаяся на стыке науки,
изучающей данное явление (экономики,
социологии и т. п.), и статистики. Решение
этой задачи осуществляется не только
и даже не столько с помощью статистических
методов (хотя и они могут принести
определенную пользу), сколько на базе
содержательного анализа сущности,
природы явления и общих законов его
развития.
Для
каждого этапа развития нужно выявить
и численно охарактеризовать основную
тенденцию изменения уровня явления.
Под тенденцией понимается общее
направление к росту, снижению или
стабилизации уровня явления с течением
времени. Если уровень непрерывно растет
или непрерывно снижается, то тенденция
к росту или снижению является явной и
отчетливой: она легко обнаруживается
визуально по графику временного ряда.
Следует, однако, иметь в виду, что и рост,
и снижение уровня могут происходить
по-разному: либо равномерно, либо
ускоренно, либо замедленно. Под равномерным
ростом (или снижением) здесь понимается
рост (снижение) с постоянной абсолютной
скоростью, когда цепные абсолютные
приросты (4) одинаковы. При ускоренном
росте или снижении цепные приросты
систематически увеличиваются по
абсолютной величине, а при замедленном
росте или снижении – уменьшаются (тоже
по модулю). Практически уровни ряда
динамики очень редко растут (или
снижаются) строго равномерно. Нечасто
встречается и систематическое – без
единого отклонения – увеличение или
снижение цепных приростов.
Такие
отклонения объясняются либо изменением
с течением времени всего комплекса
основных причин и факторов, от которых
зависит уровень явления, либо изменением
направления и силы действия второстепенных
(в том числе случайных) обстоятельств
и факторов. Поэтому при анализе динамики
речь идет не просто о тенденции развития,
а об основной тенденции, достаточно
стабильной (устойчивой) на протяжении
данного этапа развития. В некоторых
случаях эта закономерность, общая
тенденция развития объекта вполне ясно
отображается уровнями динамического
ряда.
5. Основной тенденцией (трендом)
Основной
тенденцией (трендом) называется
достаточно плавное и устойчивое изменение
уровня явления во времени, более или
менее свободное от случайных колебаний.
Основную тенденцию можно представить
либо аналитически – в виде уравнения
модели) тренда, либо графически. Выявление
основной тенденции развития (тренда)
называется в статистике также выравниваем
временного ряда, а методы выявления
основной тенденции – методами
выравнивания.
Одними
из самых распространенных способов
выявления основных тенденций (тренда)
ряда динамики являются:
1)
метод укрупнения интервалов основан
на укрупнении периодов времени, к которым
относятся уровни. Например, ряд недельных
данных можно преобразовать в ряд
помесячной динамики, ряд квартальных
данных заменить годовыми уровнями.
Уровни нового ряда могут быть получены
путем суммирования уровней исходного
ряда, либо могут представлять средние
уровни. Распространенным приемом при
выявлении тенденции развития является
сглаживание
ряда динамики.
Суть различных приемов сглаживания
сводится к замене фактических уровней
ряда расчетными уровнями, которые в
меньшей степени подвержены колебаниям.
Это способствует более четкому проявлению
тенденции развития.
2)
метод скользящей средней (суть метода
состоит в замене абсолютных данных
средними арифметическими за определенные
периоды). Расчет средних ведется способом
скольжения, т. е. постепенным исключением
из принятого периода первого уровня и
включением следующего. Сглаживание
ряда динамики с помощью скользящей
средней заключается в том, что вычисляется
средний уровень из определенного числа
первых по порядку уровней ряда, затем
средний уровень из такого же числа
уровней, начиная со второго, далее –
начиная с третьего и т.д. Таким образом,
при расчете средних уровней они как бы
«скользят» по ряду динамики от его
начала к концу, каждый раз отбрасывая
один уровень вначале и добавляя один
следующий. Отсюда название – скользящая
средняя.
Каждое
звено скользящей средней – это средний
уровень за соответствующий период,
который относится к середине
выбранного периода,
если число уровней ряда динамики
нечетное.
Нахождение
скользящей средней по четному числу
членов рядов динамики несколько сложнее,
так как средняя может быть отнесена
только к середине между двумя датами,
находящимся в середине интервала
сглаживания. Например, средняя, найденная
для четырех уровней, относится к середине
между вторым и третьим, третьим и
четвертым уровнями и так далее. Чтобы
ликвидировать такой сдвиг, применяют
так называемый способ
центрирования. Центрирование заключается
в нахождении средней из двух смежных
скользящих средних для отнесения
полученного уровня к определенной дате.
При центрировании необходимо находить
скользящие суммы, скользящие средние
нецентрированные по этим суммам и
средние из двух смежных нецентрированных
скользящих средних.
Недостаток
метода простой скользящей средней
состоит в том, что сглаженный ряд динамики
сокращается ввиду невозможности получить
сглаженные уровни для начала и конца
ряда. Этот недостаток устраняется
применением метода аналитического
выравнивания для анализа основной
тенденции.
;
3)
метод аналитического выравнивания. При
этом уровни ряда динамики выражаются
в виде функций времени:
а)
f(t)=
a0+
ajt–
линейная зависимость;
б)
f(t)
= a + cijt + a2t2–
параболическая зависимость.
Способ
укрупнения интервалов и их характеристики
средними уровнями заключается в переходе
от интервалов менее продолжительных к
более продолжительным, например от
суток – к неделям или декадам, от декад
– к месяцам, от месяцев – к кварталам
или годам, от годовых интервалов – к
многолетним. Если уровни ряда динамики
колеблются с более или менее определенной
периодичностью (волнообразно), то
укрупненный интервал целесообразно
взять равным периоду колебаний (длине
«волны» цикла). Если же такая периодичность
отсутствует, то укрупнение производят
постепенно от малых интервалов к все
более крупным, пока общее направление
тренда не станет достаточно отчетливым.
Если
ряд динамики является моментным, а также
в тех случаях, когда уровень ряда является
относительной или средней величиной,
суммирование уровней не имеет смысла,
и следует охарактеризовать укрупненные
периоды средними уровнями.
При
укрупнении интервалов число членов
динамического ряда сильно сокращается,
в результате чего движение уровня внутри
укрупненного интервала выпадает из
поля зрения. В связи с этим для выявления
основной тенденции и более детальной
ее характеристики используется
сглаживание ряда с помощью скользящей
средней.
Сглаживание
ряда динамики с помощью скользящей
средней заключается в том, что вычисляется
средний уровень из определенного числа
первых по порядку уровней ряда, затем
– средний уровень из такого же числа
уровней, начиная со второго, далее –
начиная с третьего, и т. д. Таким образом,
при расчетах среднего уровня как бы
скользят по временному ряду от его
начала к концу, каждый раз отбрасывая
один уровень в начале и добавляя один
следующий. Отсюда название – скользящая
средняя.
Каждое
звено скользящей средней – это средний
уровень за соответствующий период. При
графическом изображении и при некоторых
расчетах каждое звено принято условно
относить к центральному интервалу того
периода, за который сделан расчет (для
моментального ряда – к центральной
дате).
Вопрос
о том, за какой период следует вычислять
звенья скользящей средней, решается в
зависимости от конкретных особенностей
динамики. Как и при укрупнении интервалов,
если в колебаниях уровня есть определенная
периодичность, то период сглаживания
целесообразно принять равным периоду
колебаний или кратной его величине.
Так, при наличии квартальных уровней,
испытывающих ежегодно сезонные спады
и повышения, целесообразно применять
четырех– или восьмиквартальную среднюю
и т. п. Если же колебания уровней являются
беспорядочными, то целесообразно
постепенно укрупнять интервал сглаживания,
пока не выявится отчетливая картина
тренда.
Аналитическое
выравнивание ряда динамики позволяет
получить аналитическую модель тренда.
Оно производится следующим образом.
1.
На основе содержательного анализа
выделяется этап развития и устанавливается
характер динамики на этом этапе.
2.
Исходя из предположения о той или иной
закономерности роста и из характера
динамики выбираются форма аналитического
выражения тренда, вид аппроксимирующей
функции, которой графически соответствует
определенная линия – прямая, парабола,
показательная кривая и т. п. Эта линия
(функция) выражает предполагаемую
закономерность плавного изменения
уровня во времени, т. е. основную тенденцию.
При этом каждый уровень ряда динамики
условно рассматривается как сумма двух
составляющих (компонент): yt
= f(t) + ε. Одна из них (yt
=
f(t)),
выражающая тренд, характеризует влияние
постоянно действующих основных факторов
и называется систематической регулярной
компонентой. Другая составляющая (е!)
отражает влияние случайных факторов и
обстоятельств и называется случайной
компонентой. Эту компоненту называют
также остаточной (или просто остатком),
так как она равна отклонению фактического
уровня от тренда. Таким образом,
допускается (условно предполагается),
что основная тенденция (тренд) формируется
под влиянием постоянно действующих
главных факторов, а второстепенные,
случайные факторы вызывают отклонение
уровня от тренда.
Выбор
формы кривой во многом определяет
результаты экстраполяции тренда.
Основанием для выбора вида кривой может
быть содержательный анализ сущности
развития данного явления. Можно опираться
также на результаты предыдущих
исследований в данной области. Наиболее
простой эмпирический прием – визуальный:
выбор формы тренда на основе графического
изображения ряда – ломаной линии. На
практике линейная зависимость используется
чаще, чем параболическая, в силу ее
простоты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Выявление основной тенденции развития и формирование моделей для анализа и прогнозирования.
При изучении и прогнозировании рядов динамики важной задачей является определение основной тенденции развития, для определения которой используются различные приемы и методы.
Одним из приемов выявления тенденции является метод скользящей средней. Суть метода состоит в замене абсолютных данных средними арифметическими за отдельные периоды. Расчет средних ведется способом скольжения, то есть постепенным исключением из принятого периода скольжения первого уровня и включением следующего.
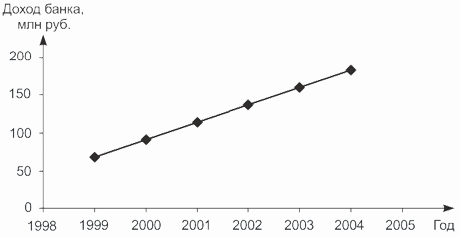
В таблице 6.2 приведены результаты сглаживания временного ряда методом трехчленной и четырехчленной скользящей средней (на основе данных об экспорте товаров).
Таблица 2
Динамика экспорта Российской Федерации в 2009 г.
и расчет скользящих средних
|
Месяц |
Экспорт товаров, млн. долл. США |
Трехчленные скользящие суммы |
Трехчленные скользящие средние |
Четырехчленные скользящие средние |
Четырехчленные скользящие средние (нецентрированные) |
Четырехчленные скользящие средние (центрированные) |
|
1 |
17786 |
– |
– |
– |
– |
– |
|
2 |
18373 |
– |
18946,3 |
– |
19438,3 |
|
|
3 |
20680 |
56839 |
19989,0 |
77753 |
20622,5 |
20030,4 |
|
4 |
20914 |
59967 |
21372,3 |
82490 |
22128,3 |
21375,4 |
|
5 |
22523 |
64117 |
22611,0 |
88513 |
23510,8 |
22819,5 |
|
6 |
24396 |
67833 |
24376,3 |
94043 |
25047,8 |
24279,3 |
|
7 |
26210 |
73129 |
25889,3 |
100191 |
26571,8 |
25809,8 |
|
8 |
27062 |
77668 |
27297,0 |
106287 |
28071,0 |
27321,4 |
|
9 |
28619 |
81891 |
28691,3 |
112284 |
29203,0 |
28637,0 |
|
10 |
30393 |
86074 |
29916,7 |
116812 |
30964,3 |
30083,6 |
|
11 |
30738 |
89750 |
31746,0 |
– |
– |
– |
|
12 |
34107 |
95238 |
– |
– |
– |
– |
Взяв данные за три месяца, исчисляем трехчленные суммы, затем среднюю:
;
и т.д.
Интервал скольжения можно брать четный (четыре, шесть и т.д.). Нахождение скользящей средней по четному числу членов осложняется тем, что средняя может быть отнесена только к середине между двумя датами. Чтобы ликвидировать этот сдвиг, применяется центрирование, то есть нахождение средней из средних за два периода для отнесения полученного уровня к определенной дате. При центрировании также необходимо находить скользящие суммы.
Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание.
При этом уровни ряда динамики выражаются в виде функции времени:
.
При таком подходе изменение исследуемого показателя связывают лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени.
Правильно выбранная модель кривой роста должна соответствовать характеру изменения тенденции исследуемого явления. Кривая роста позволяет получить выровненные или теоретические значения уровней динамического ряда. Это те уровни, которые наблюдались бы в случае полного совпадения динамики явления с кривой.
Прогнозирование на основе модели кривой роста базируется на экстраполяции, т. е. на продлении в будущее тенденции, наблюдавшейся в прошлом. При этом предполагается, что во временном ряду присутствует тренд, характер развития показателя обладает свойством инерционности, сложившаяся тенденция не должна претерпевать существенных изменений в течение периода упреждения.
В настоящее время в литературе описано несколько десятков кривых роста, многие из которых широко применяются для выравнивания экономических временных рядов: линейная модель, полиномиальная модель второй, третьей степени, логарифмическая, экспоненциальная модели и др.
Существует несколько практических подходов, облегчающих процесс выбора формы кривой роста.
Наиболее простой путь — визуальный анализ, опирающийся на изучение графического изображения временного ряда. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если на графике исходного ряда тенденция развития недостаточно четко просматривается, то можно провести некоторые стандартные преобразования ряда (например, сглаживание), а потом подобрать функцию, отвечающую графику преобразованного ряда. В современных пакетах статистической обработки имеется богатый арсенал стандартных преобразований данных и широкие возможности для графического изображения, в том числе в различных масштабах. Все это позволяет существенно упростить для исследователя проведение данного этапа.
В табличном процессоре Microsoft Excel выбор кривой можно осуществить на основании сравнения величины достоверности аппроксимации выбранных моделей: для анализа и прогнозирования необходимо выбрать такую модель, где данная величина будет наибольшей.
Рассмотрим применение метода аналитического выравнивания по прямой ля выражения основной тенденции на следующем примере.
А таблице 2 приведены уже известные данные об экспорте Российской Федерации в 2009 году. Для выравнивания ряда динамики по прямой воспользуемся уравнением .
Способ наименьших квадратов дает систему нормальных уравнений для нахождения параметров и
:
;
,
где – исходный уровень ряда динамики;
– число членов ряда;
– показатель времени, который обозначается порядковым номером, начиная от низшего (1, 2, 3 и т.д.).
Решение системы позволяет получить выражение для параметров и
:
; (15)
. (16)
Расчет необходимых значений приведен в таблице 6.2. По итоговым данным определяем параметры уравнения: =15 769,
=1 443,2.
В результате получаем следующее уравнение основной тенденции экспорта России в 2009 году:
Таблица 3
Исходные и расчетные данные для определения параметров уравнения
|
Месяц |
Порядковый номер, t |
Экспорт, млн. долл. США, y |
|
|
|
|
|
Январь |
1 |
17786 |
1 |
17786 |
17212,2 |
573,8 |
|
Февраль |
2 |
18373 |
4 |
36746 |
18655,4 |
-282,4 |
|
Март |
3 |
20680 |
9 |
62040 |
20098,6 |
581,4 |
|
Апрель |
4 |
20914 |
16 |
83656 |
21541,8 |
-627,8 |
|
Май |
5 |
22523 |
25 |
112615 |
22985 |
-462 |
|
Июнь |
6 |
24396 |
36 |
146376 |
24428,2 |
-32,2 |
|
Июль |
7 |
26210 |
49 |
183470 |
25871,4 |
338,6 |
|
Август |
8 |
27062 |
64 |
216496 |
27314,6 |
-252,6 |
|
Сентябрь |
9 |
28619 |
81 |
257571 |
28757,8 |
-138,8 |
|
Октябрь |
10 |
30393 |
100 |
303930 |
30201 |
192 |
|
Ноябрь |
11 |
30738 |
121 |
338118 |
31644,2 |
-906,2 |
|
Декабрь |
12 |
34107 |
144 |
409284 |
33087,4 |
1019,6 |
|
Итого |
78 |
301 801 |
650 |
2 168 088 |
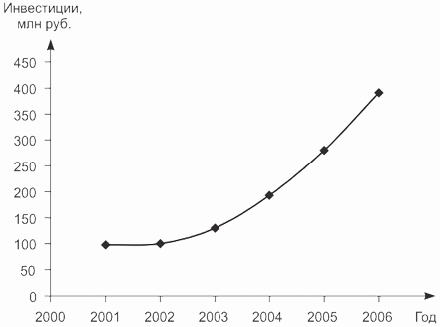
По окончании расчета целесообразно построить график с изображением исходных данных и теоретических значений ряда (рис. 1).
Рис. 1. Графическое изображение исходных данных и теоретических значений по линейной модели
Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колеблемость уровней около тренда служит мерой воздействия остаточных факторов.
Оценка качества модели сводится к оценке ее точности и адекватности.
Проверка адекватности выбранных моделей реальному процессу (в частности, адекватности полученной кривой роста) строится на анализе остаточной компоненты. Остаточная компонента получается после выделения из исследуемого ряда систематической составляющей (тренда и периодической составляющей, если она присутствует во временном ряду). В нашем случае исходный временной ряд описывает процесс, не подверженный сезонным колебаниям. Ряд остатков получается как отклонение фактических значений временного ряда от теоретических, полученных по модели (табл. 3):
. (17)
Теоретические значения за каждый период рассчитываются путем подстановки в полученную функцию последовательных значений t.
Принято считать, что модель адекватна описываемому процессу, если остаточная последовательность (ряд остатков) представляет собой случайную компоненту ряда.
Поэтому при оценке «качества» модели проверяют, удовлетворяет ли остаточная последовательность следующим свойствам:
-
случайности колебаний уровней ряда;
-
соответствию распределения остаточной компоненты нормальному закону с нулевым математическим ожиданием;
-
независимости значений уровней ряда остатков между собой.
При проверке первого свойства исследователю полезно провести графический анализ остаточной последовательности.
В современных эконометрических пакетах имеется набор графических средств, позволяющих судить о том, насколько распределение остатков согласуется с нормальным распределением. Например, полезным может оказаться график гистограммы остатков с наложенной нормальной плотностью, позволяющей исследователю оценить симметричность распределения остатков и близость к нормальному закону.
Кроме графических средств, в современных пакетах прикладных программ представлены и статистические критерии, позволяющие проводить проверку гипотезы о нормальности распределения остатков, например, критерий Пирсона и др. Однако на практике использование этих средств зачастую затруднено из-за небольшой длины временных рядов экономических показателей (n < 50). Поэтому проверка на нормальность может быть произведена приближенно, например, на основе подхода, опирающегося на рассмотрение показателей асимметрии и эксцесса.
Как известно, при нормальном распределении показатели асимметрии и эксцесса равны нулю. Так как мы предполагаем, что отклонения от тренда представляют собой выборку из некоторой генеральной совокупности, то можно определить выборочные характеристики асимметрии (А) и эксцесса (Э), а также оценить их среднеквадратические ошибки, зависящие от длины ряда n:
,
. (18)
Если одновременно выполняются следующие неравенства:
, (19)
, (20)
то гипотеза о нормальном характере распределения случайной компоненты не отвергается.
Если выполняется хотя бы одно из неравенств:
, (21)
, (22)
то гипотеза о нормальном характере распределения отвергается.
Другие случаи требуют дополнительной проверки с помощью более мощных критериев.
Рассмотрим подробнее последнее свойство. Если вид функции, описывающей систематическую составляющую, выбран неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, т.к. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция остатков.
Существует несколько приемов обнаружения автокорреляции. Наиболее распространенным является подход, опирающийся на критерий Дарбина-Уотсона. Тест Дарбина-Уотсона связан с проверкой гипотезы об отсутствии автокорреляции первого порядка, т.е. автокорреляции между соседними остаточными членами ряда. При этом критическая статистика определяется по формуле:
. (23)
Можно показать, что величина d приближенно равна:
, (24)
где — коэффициент автокорреляции первого порядка (то есть парный коэффициент корреляции между двумя последовательностями остатков
,
,…,
и
,
, …,
. Близость значения статистики d к нулю означает наличие высокой положительной автокорреляции (коэффициент
близок к единице); близость значения статистики d к четырем означает наличие высокой отрицательной автокорреляции (коэффициент
близок к минус единице). Естественно, в случае отсутствия автокорреляции значение статистики d будет близким к двум (коэффициент
не сильно отличается от нуля).
Применение на практике критерия Дарбина-Уотсона основано на сравнении расчетного значения статистики d с пороговыми, граничными значениями и
.
Граничные значения и
, зависящие от числа наблюдений n, количества объясняющих переменных в модели, уровня значимости α, находятся по таблицам (авторами критерия составлены таблицы для α = 0,05, α = 0,025 и α = 0,01). Фрагмент таблицы Дарбина-Уотсона с критическими значениями
и
при 5% уровне значимости представлен ниже (см. табл. 3).
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза об отсутствии автокорреляции остатков. Пусть альтернативная гипотеза состоит в наличии в остатках положительной автокорреляции первого порядка.
Тогда при сравнении расчетного значения статистики d ( d < 2) с и
возможны следующие варианты.
1) если d < , то гипотеза
об отсутствии автокорреляции отвергается (с вероятностью ошибки, равной α ) в пользу гипотезы о положительной автокорреляции;
2) если d > , то гипотеза
не отвергается;
3) если , то нельзя сделать определенный вывод по имеющимся исходным данным (значение d попало в область неопределенности).
Если альтернативной является гипотеза о наличии в остатках отрицательной автокорреляции первого порядка, то с пороговыми, граничными значениями и
сравнивается величина 4 − d (при d >2).
При этом возможны следующие варианты.
1) если 4 − d < , то гипотеза
об отсутствии автокорреляции отвергается (с вероятностью ошибки, равной α) в пользу гипотезы об отрицательной автокорреляции;
2) если 4 − d > , то гипотеза
не отвергается;
3) если , то нельзя сделать определенный вывод по имеющимся исходным данным.
Таблица 3
Значения и
критерия Дарбина-Уотсона при 5% уровне значимости ( n – длина временного ряда, К – число объясняющих переменных в модели)
|
n |
К=1 |
К=2 |
К=3 |
|||
|
|
|
|
|
|
|
|
|
15 |
1,08 |
1,36 |
0,95 |
1,54 |
0,82 |
1,75 |
|
16 |
1,1 |
1,37 |
0,98 |
1,54 |
0,86 |
1,73 |
|
17 |
1,13 |
1,38 |
1,02 |
1,54 |
0,9 |
1,71 |
|
18 |
1,16 |
1,39 |
1,05 |
1,53 |
0,93 |
1,69 |
|
19 |
1,18 |
1,4 |
1,08 |
1,53 |
0,97 |
1,68 |
|
20 |
1,2 |
1,41 |
1,1 |
1,54 |
1 |
1,68 |
|
21 |
1,22 |
1,42 |
1,13 |
1,54 |
1,03 |
1,67 |
|
22 |
1,”4 |
1,43 |
1,15 |
1,54 |
1,05 |
1,66 |
|
23 |
1,26 |
1,44 |
1,17 |
1,54 |
1,08 |
1,66 |
|
24 |
1,27 |
1,45 |
1,19 |
1,55 |
1,1 |
1,66 |
|
25 |
1,29 |
1,45 |
1,21 |
1,55 |
1,12 |
1,66 |
|
26 |
1,3 |
1,46 |
1,22 |
1,55 |
1,14 |
1,65 |
|
27 |
1,32 |
1,47 |
1,24 |
1,56 |
1,16 |
1,65 |
|
28 |
1,33 |
1,48 |
1,26 |
1,56 |
1,18 |
1,65 |
|
29 |
1,34 |
1,48 |
1,27 |
1,56 |
1,2 |
1,65 |
|
30 |
1,35 |
1,49 |
1,28 |
1,57 |
1,21 |
1,65 |
|
31 |
1,36 |
1,5 |
1,3 |
1,57 |
1,23 |
1,65 |
|
32 |
1,37 |
1,5 |
1,31 |
1,57 |
1,24 |
1,65 |
|
33 |
1,38 |
1,51 |
1,32 |
1,58 |
1,26 |
1,65 |
|
34 |
1,49 |
1,51 |
1,33 |
1,58 |
1,27 |
1,65 |
|
35 |
1,4 |
1,52 |
1,34 |
1,58 |
1,28 |
1,65 |
|
36 |
1,41 |
1,52 |
1,35 |
1,59 |
1,29 |
1,65 |
Таким образом, можно считать, что в случае отсутствия автокорреляции в остатках расчетное значение статистики «не слишком отличается» от 2.
Важнейшими характеристиками качества модели, выбранной для прогнозирования, являются показатели ее точности. Они описывают величины случайных ошибок, полученных при использовании модели. Таким образом, чтобы судить о качестве выбранной модели, необходимо проанализировать систему показателей, характеризующих как адекватность модели, так и ее точность.
О точности прогноза можно судить по величине ошибки (погрешности) прогноза. Ошибка прогноза — величина, характеризующая расхождение между фактическим и прогнозным значением показателя.
Абсолютная ошибка прогноза определяется по формуле:
, (25)
где – прогнозное значение показателя,
– фактическое значение.
Эта характеристика имеет ту же размерность, что и прогнозируемый показатель, и зависит от масштаба измерения уровней временного ряда.
На практике широко используется относительная ошибка прогноза, выраженная в процентах относительно фактического значения показателя:
(26)
При проведении сравнительной оценки моделей могут использоваться такие характеристики качества как дисперсия (S2) или среднеквадратическая ошибка (S):
;
. (27)
Чем меньше значения этих характеристик, тем выше точность модели.
В указанном выше примере коэффициенты асимметрии и эксцесса равны соответственно 0,0047 и (-0,77), гипотеза о нормальном характере распределения случайной компоненты не отвергается.
Проверив остатки на автокорреляцию, получаем критерий Дарбина – Уотсона ; d >
, гипотеза
об отсутствии автокорреляции не отвергается, можно сделать вывод о независимости значений уровней ряда остатков между собой. Следовательно, выбранная модель адекватна по рассмотренным критериям.
Среднеквадратическая ошибка прогноза составляет 536 млн. долл. США или 3 % от среднего значения экспорта Российской Федерации. Модель является достаточно точной и может быть использована для описания основной тенденции и прогнозирования.
В случае если исследователь рассматривает в качестве альтернативы другие модели, для экстраполяции тенденции на будущие периоды необходимо выбрать адекватную модель с наименьшими значениями ошибок.
Одной из задач, возникающих при анализе рядов
динамики, является установление закономерности изменения уровней изучаемого
показателя во времени. В некоторых случаях эта закономерность, общая тенденция
развития объекта вполне ясно отображается уровнями динамического ряда. Но часто
приходится встречаться с такими рядами динамики, когда уровни ряда претерпевают
самые различные изменения (то возрастают, то убывают) и можно говорить лишь об
общей тенденции развития явления, либо о тенденции к росту, либо к снижению. В
этих случаях для определения основной тенденции развития явления, достаточно
устойчивой на протяжении данного периода, используют особые приемы обработки
рядов динамики.
Уровни ряда динамики формируются под совокупным
влиянием множества длительно и кратковременно действующих факторов и в том
числе различного рода случайных обстоятельств.
Выявление основной закономерности изменения уровней
ряда предполагает ее количественное выражение, в некоторой мере свободное от случайных
воздействий. Выявление основной тенденции развития (тренда) называется в
статистике также выравниванием временного ряда, а методы выявления основной
тенденции — методами выравнивания. Выравнивание позволяет характеризовать
особенность изменения во времени данного динамического ряда в наиболее общем
виде как функцию времени, предполагая, что через время можно выразить влияние
всех основных факторов.
Приемы сглаживания динамических рядов (укрупнение
интервала и метод скользящей средней) могут рассматриваться как важное
вспомогательное средство, облегчающее применение других методов и, в частности,
более строгих методов выявления тенденции. Для того чтобы представить
количественную модель, выражающую общую тенденцию изменений уровней
динамического ряда во времени, используется аналитическое выравнивание ряда
динамики.
В этом случае фактические уровни заменяются
уровнями, вычисленными на основе определенной кривой.
Предполагается, что она отражает общую тенденцию изменения во времени
изучаемого показателя.
При аналитическом выравнивании ряда динамики
закономерно изменяющийся уровень изучаемого показателя оценивается как функция
времени
,
Где
—
уровни динамического ряда, вычисленные по соответствующему аналитическому
уравнению на момент времени t.
При выборе формы уравнения следует исходить и из
объема имеющейся информации. Чем больше параметров содержит уравнение тренда,
тем больше должно быть наблюдений при одной и той же степени надежности
оценивания. Выбор формы кривой может осуществляться: и на основе принятого
критерия, в качестве которого может служить сумма квадратов отклонений
фактических значений от значений, рассчитанных по уравнению тренда. Из
совокупности кривых выбирается та, которой соответствует минимальное значение
критерия. Рассмотрим аналитическое выравнивание ряда динамики
по прямой, т.е. аналитическое уравнение вида:
где
-порядковый номер
периодов или моментов времени.
Параметры
и
прямой рассчитываются
по методу наименьших квадратов (МНК).
Система нормальных уравнений в данном
случае имеет вид:
Поиск параметров уравнения можно упростить, если
отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда
динамики была равна нулю
.
При нечетном числе уровней ряда динамики уровень, находящийся в середине ряда, принимается за условное начало отчета времени
(этому периоду или моменту времени придается нулевое значение). Даты времени,
стоящие выше этого уровня, обозначаются натуральными числами со знаками минус,
а ниже -натуральными числами со знаками плюс.
При условии
получим:
Правильность расчета уровней выравниваемого ряда
динамики может быть проверена следующим образом: сумма значений эмпирического
ряда должна совпадать с суммой вычисленных уровней выровненного ряда, т.е.
Аналитическое уравнение представляет собой математическую
модель развития явления и дает выражение статистической закономерности,
проявляющейся в рядах динамики. Следует помнить, что прием аналитического
выравнивания содержит в себе ряд условностей, связанных
прежде всего с тем, что уровни, характеризующие тот или иной динамический ряд,
рассматриваются как функция времени. В действительности же развитие явлений
обусловлено не тем, сколько времени прошло с отправного момента, а тем, какие
факторы влияли на развитие, в каком направлении и с какой интенсивностью. Развитие явлений во времени выступает
как внешнее выражение этих факторов, как их суммарное действие; оказывающее
влияние на изменение уровня в отдельно взятые промежутки или моменты времени.
Выявить основную тенденцию развития явления методом наименьших квадратов можно
лишь тогда, когда выяснено, что изменяющиеся во времени процессы протекают на
всем рассматриваемом промежутке времени одинаково, что их количественное и
качественное изменение происходит под действием одного и того же комплекса основных
факторов, определяющих движение данного ряда динамики.
Модели, учитывающие общие закономерности изменения
экономического явления в изучаемый интервал времени и изменения во времени
влияния комплекса факторов, называют многофакторными динамическими моделями.
Выделим особенности моделей аналитического
выравнивания уровней динамического ряда, накладывающие ограничения на их
использование. Во-первых, динамические ряды, к которым применяется
аппроксимация, должны быть достаточно длинными. Во-вторых, применение
аппроксимации наиболее целесообразно в случае медленно и плавно меняющегося
уровня. В-третьих, аппроксимация как метод моделирования практически не
адаптируется к изменяющимся условиям формирования уровней ряда; при появлении
новых данных построение модели должно быть проведено заново. В-четвертых, при
использовании для расчета параметров уравнения метода наименьших квадратов
(МНК) считается, что значимость информации в пределах отрезка аппроксимации
одинакова независимо от давности полученных данных, в то время как более
поздние данные имеют большую ценность.
Помимо этого, динамические ряды экономических
показателей часто имеют небольшую длину и подвержены значительным колебаниям,
которые аппроксимация предвидеть не может.
Задача
В таблице приведены готовые данные о
трудоемкости производства:
| Год | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|
Трудоемкость производства, человек-часов |
8 | 8.4 | 7.6 | 7 | 7.3 | 6.6 | 5.9 | 5 | 5.2 |
-
Провести аналитическое выравнивание ряда динамики по прямой.
Построить точечный и интервальный
прогноз на 2018 год.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
1) Произведем аналитическое выравнивание ряда по прямой.
Составим расчетную таблицу:
Расчетная вспомогательная таблица 1
| Годы |
|
|
|
|
| 2009 | -4 | 8 | 16 | -32 |
| 2010 | -3 | 8,4 | 9 | -25,2 |
| 2011 | -2 | 7,6 | 4 | -15,2 |
| 2012 | -1 | 7 | 1 | -7 |
| 2013 | 0 | 7,3 | 0 | 0,0 |
| 2014 | 1 | 6,6 | 1 | 6,6 |
| 2015 | 2 | 5,9 | 4 | 11,8 |
| 2016 | 3 | 5 | 9 | 15 |
| 2017 | 4 | 5,2 | 16 | 20,8 |
| Итого | 0 | 61,0 | 60 | -25,2 |
Коэффициенты уравнения линейного тренда найдем по формулам:
Уравнение линейного тренда имеет вид:
2) Составим расчетную таблицу:
Расчетная вспомогательная таблица 2
| Годы |
|
|
Теоретические значения |
|
| 2009 | -4 | 8 | 8,48 | 0,2304 |
| 2010 | -3 | 8,4 | 8,06 | 0,1156 |
| 2011 | -2 | 7,6 | 7,64 | 0,0016 |
| 2012 | -1 | 7 | 7,22 | 0,0484 |
| 2013 | 0 | 7,3 | 6,8 | 0,25 |
| 2014 | 1 | 6,6 | 6,38 | 0,0484 |
| 2015 | 2 | 5,9 | 5,96 | 0,0036 |
| 2016 | 3 | 5 | 5,54 | 0,2916 |
| 2017 | 4 | 5,2 | 5,12 | 0,0064 |
| Итого | — | — | — | 0,996 |
Среднеквадратическая ошибка:
Точечный прогноз на 2018 год (t=5):
Ошибка
прогноза составит:
По таблице критерия Стьюдента,
для доверительной вероятности
(уровня значимости
) находим:
Вывод к задаче
Таким образом
тренд для трудоемкости производства выражается линейным уравнением
.
Согласно прогнозу, в 2018 году трудоемкость производства с вероятностью 0,95
будет лежать в пределах от 3,6 до 5,8 человеко-часов.
Методы выявления основной тенденции (тренда) в рядах динамики
При анализе рядов динамики необходимо решить одну из важнейших задач статистики – определить основную тенденцию развития (тренд).
Основная тенденция развития (тренд ряда динамики) – это общее направление в изменении уровней ряда.
Уровни ряда динамики формируются под влиянием многих факторов, которые неоднородны по силе, направлению и времени действия.
Среди действующих факторов выделяются факторы:
§ основные (главные) – определяют закономерность (тенденцию) развития;
§ случайные – вызывают колебания уровней.
Таким образом, при анализе рядов динамики различают три компоненты:
• основная тенденция развития, или тренд (изменения, определяющие общее направление развития);
• периодически повторяющиеся колебания (сезонные колебания);
• случайные колебания (возникают под влиянием внешних факторов и вызывают колебания уровней относительно тренда).
При изучении рядов динамики необходимо разделить эти компоненты и выявить основную закономерность развития явления, т.е. выявить общую тенденцию в изменении уровней, освобожденную от действия случайных факторов. Выявление основной тенденции развития в статистике называется выравниванием ряда динамики.
Таким образом, при изучении основной тенденции ряда динамики решаются следующие задачи:
1. выявление основной тенденции развития;
2. измерение выявленного тренда, т.е. его обобщающая количественная оценка.
Эти задачи решаются с помощью следующих методов выравнивания (сглаживания) рядов динамики:
§ метод укрупнения интервалов;
§ метод скользящей средней (механическоесглаживание);
§ метод аналитического выравнивания.
В этих методах при обработке вместо фактических уровней ряда определяются расчетные уровни, освобожденные от действия случайных факторов. В результате уменьшается колеблемость уровней. Они становятся как бы «выровненными», «сглаженными» по отношению к исходным данным.
Метод укрупнения интервалов – основан на укрупнении периодов времени, к которым относятся уровни ряда. Происходит переход от первоначального ряда к ряду с 
Замечание. Если ряд является моментным или уровни выражены относительной (средней) величиной, то суммирование уровней не имеет смысла. Тогда по укрупненным интервалам рассчитывают средние показатели.
При использовании этого метода число уровней ряда существенно сокращается. Не учитывается изменение уровней внутри укрупненных интервалов. Поэтому для более детальной характеристики тенденции используют выравнивание ряда с помощью скользящей (подвижной) средней.
Метод скользящей средней– последовательный расчет средних величин постепенно охватывающих последующие периоды времени. Состоит в замене абсолютных данных средними арифметическими величинами за отдельные периоды. Расчет средних ведется способом скольжения: последовательно смещают начало отсчета на единицу времени, т.е. постепенно исключают из интервала первые уровни и включают последующие. В результате получается средняя, относящаяся к середине укрупненного интервала.
Например, трехлетняя скользящая средняя имеет вид:
§ для первого интервала —
§ для второго интервала —
§ для третьего интервала — 
В результате сглаживания получается ряд динамики, количество уровней которого меньше, чем у исходного. Фактические уровни заменяются расчетными, которые имеют меньшую колеблемость. Случайные колебания погашаются, и основная тенденция выражается в виде плавной линии.
Таким образом, методы укрупнения интервалов и скользящей средней позволяют выявить тренд, но не помогают его измерить. В этом случае применяется метод аналитического выравнивания, который позволяет измерить тренд, т.е. дать его обобщенную статистическую оценку.
Метод аналитического выравнивания –наиболее эффективный метод выявления основной тенденции. Заключается в построении аналитической функции, характеризующей зависимость уровней ряда от времени 
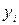
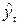
Каждый фактический уровень 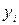
— 
— 
Задачи аналитического выравнивания:
§ определение на основе фактических данных вида функции 
§ нахождение параметров указанной функции (уравнения) по фактическим (эмпирическим) данным;
§ расчет теоретических (выровненных) уровней по найденному уравнению.
Определение теоретических (расчетных) уровней 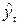
Проблемой, требующей своего решения при применении этого метода, является подбор математической функции, по которой рассчитываются теоретические уровни тренда.
От правильности решения данной проблемы зависят выводы о закономерностях тренда изучаемого явления. Если выбранный тип математической функции адекватен основной тенденции развития, то модель тренда может иметь практическое применение при изучении сезонных колебаний, прогнозировании и других целях.
Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Выбор функции определяется характером динамики развития конкретного явления.
Наиболее приемлемой для выравнивания является функция, соответствующая тенденции основных показателей динамики (абсолютный прирост, темпы роста и прироста).
Выбор вида уравнения зависит от показателей динамики:
1) равномерное развитие — если относительно стабильны абсолютные приросты 

где 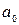

Параметр 


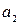
Тенденции развития и колебания
Методические основы изучения основной тенденции развития
Уровни ряда динамики формируются под совокупным влиянием множества долговременных и краткосрочных факторов, и, в том числе, различного рода случайных обстоятельств. В связи с чем, при статистическом изучении динамики необходимо четко разделить ее на два основных элемента – тенденцию и колеблемость.
Тенденция развития динамического ряда к увеличению либо снижению его уровней – основная закономерность изменения уровней ряда. В отдельные же годы уровни испытывают колебания, отклоняясь от основной тенденции.
Тенденция динамики связана с действием долговременно существующих причин и условий развития. Однако после какого-то периода времени эти причины и условия тоже могут измениться и породить уже другую тенденцию развития изучаемого явления. Основная тенденция развития ряда динамики выражается в форме уравнения, называемого трендом.
Колебания, напротив, связаны с действием краткосрочных или циклических (конъюнктурных) факторов, влияющих на отдельные уровни динамического ряда, и отклоняющих уровни от тенденции то в одну, то в другую сторону. Например, положительная тенденция динамики урожайности связана с прогрессом агротехники, с укреплением экономического положения определенной совокупности хозяйств, совершенствованием организации производства. Колеблемость урожайности может быть вызвана, например, чередованием благоприятных по погоде и неблагоприятных лет, колебаниями в развитии вредных насекомых и болезней растений, и т.п.
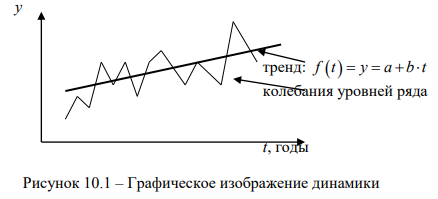
Тенденцию и колебания наглядно показывает график (рис. 10.1). По оси абсцисс на графике всегда отражается время, по оси ординат – уровни ряда динамики. По обеим осям строго соблюдается масштаб, иначе характер динамики будет искажен.
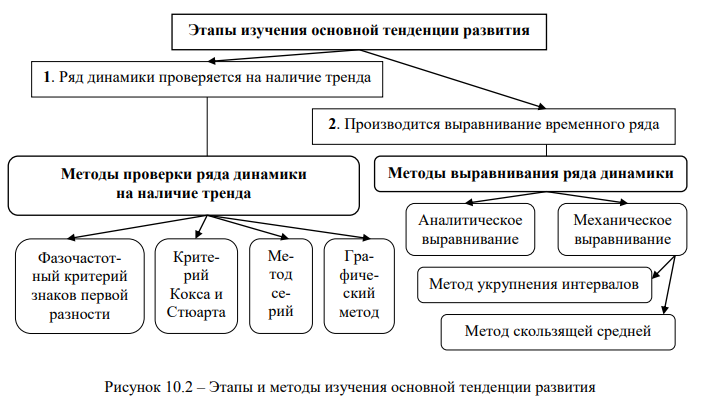
Изучение основной тенденции развития осуществляется в два этапа (рис. 10.2):
- на первом этапе ряд динамики проверяется на наличие тренда;
- на втором этапе проводится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
Проверка на наличие тренда в ряду динамики может быть осуществлена различными методами, в частности, приведенными на рис. 10.2.
Суть фазочастотного критерия знаков первой разности (Валлиса и Мура) заключается в том, что наличие тренда в динамическом ряду утверждается в том случае, если этот ряд не содержит или содержит в приемлемом количестве фазы – изменения знака разности первого порядка.
Суть критерия Кокса и Стюарта сводится к тому, что весь анализируемый ряд динамики разбивается на три равные по числу уровней группы и сравнивают между собой суммарные или средние уровни первой и последней групп. Существенное различие между ними позволяет сделать вывод о наличии тренда. Если количество уровней ряда динамики не делится на три, то недостающие уровни можно добавить, например, используя для этого условные уровни, повторив значения стоящие крайними в ряду, или фактические уровни смежных с крайними периодов.
В соответствии с методом серий каждый конкретный уровень временного ряда считается принадлежащим к одному из двух типов: например, если, уровень ряда меньше медианного значения, то считается, что он имеет тип А, в противном случае – тип В. После замены числовых значений уровней ряда буквами А и В последовательность уровней временного ряда выступает как последовательность типов. В образовавшейся последовательности типов определяется число серий (R). Серией называется любая последовательность элементов одинакового типа, граничащая с элементами другого типа. Если во временном ряду общая тенденция к росту или снижению отсутствует, то количество серий является случайной величиной (для n >10) и оказывается в доверительном интервале, характеризуемом неравенством:
где R – среднее число серий, определяемое по формуле:
n – число уровней ряда; t – нормированное отклонение – параметр, назначаемый в соответствии с принятым уровнем доверительной вероятности Р (вероятности, с которой число серий может оказаться в доверительном интервале). Значения t приводятся в таблицах нормального распределения вероятностей.
Наиболее часто используемые сочетания t и Р приведены в таблице 6.3; σR – среднее квадратическое отклонение числа серий, которое рассчитывается по формуле:
Полученные границы доверительного интервала округляют до целых чисел, уменьшая нижнюю границу и увеличивая верхнюю.
При графическом методе тип тренда устанавливают путем размещения на поле графика эмпирических уровней. Концентрированное вокруг определенной кривой или хаотическое размещение эмпирических уровней ряда позволяет сделать вывод о наличии или отсутствии основной тенденции развития.
Пример проверки ряда динамики на наличие тренда
По данным таблицы 10.1 необходимо определить наличие тренда в ряду динамики числа браков на 1000 человек населения Российской Федерации в 2005-2018 гг.
Число браков на 1000 человек населения Российской Федерации в 2005-2018 гг., ‰
| Годы | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Браки | 7,4 | 7,8 | 8,8 | 8,3 | 8,4 | 8,5 | 9,2 | 8,5 | 8,5 | 8,4 | 7,9 | 6,7 | 7,1 | 6,1 |
Для применения фазочастотного критерия знаков первой разности необходимо определить наличие роста или уменьшение рассматриваемого показателя от года к году рассматриваемого периода, т.е. знак «+» или «-» цепного абсолютного прироста (формула 9.2, с. 154), для наглядности представив результаты в таблице 10.2.
Знаки первой разности числа браков на 1000 человек населения Российской Федерации в 2005-2018 гг.
| Годы | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Знак | … | + | + | — | + | + | + | — | 0 | — | — | — | + | — |
Количество «+» и « — « оказалось одинаковым, что, на первый взгляд, однозначно свидетельствует об отсутствии какой-либо закономерности динамики браков в России в рассматриваемом периоде.
Для применения критерия Кокса и Стюарта необходимо представленный ряд динамики разбить на три равные части, для чего к нему добавим имеющиеся на период исследования в официальной статистике данные о числе браков на 1000 человек населения в 2004 году – 6,8‰.
Первая треть добавленного ряда будет охватывать данные 2004-2008 гг., а последняя – 2014- 2018 гг., соответственно: (6,8+7,4+7,8+8,8+8,3=39,1) и (8,4+7,9+6,7+7,1+6,1=36,2). Средний уровень числа браков на 1000 человек населения страны в 2004-2008 гг. и 2014-2018 гг. составил, соответственно: 39,1:5=7,82‰ и 36,2:5=7,24‰.
Численные различия рассматриваемого показателя по выделенным периодам не велики, что также не позволяет утверждать наличие определенного тренда заключения браков в Российской Федерации.
Для применения метода серий рассчитаем медианное значение числа браков на 1000 человек населения страны в 2005-2018 гг.
Упорядоченная по возрастанию последовательность числа браков на 1000 человек населения в 2005-2018 гг. приведена в таблице 10.3.
Число браков на 1000 человек населения Российской Федерации в 2005-2018 гг. в порядке возрастания, ‰
| № п./п. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Браки | 6,1 | 6,7 | 7,1 | 7,4 | 7,8 | 7,9 | 8,3 | 8,4 | 8,4 | 8,5 | 8,5 | 8,5 | 8,8 | 9,2 |
Так как ряд имеет четырнадцать значений уровней, то медиана будет равна половине суммы значений уровней седьмого и восьмого элемента упорядоченного ряда: Ме = 8,35 ‰.
К типу А относятся значения уровней рассматриваемого ряда динамики которые меньше медианного значения, к типу В – больше и ряд типов выглядит как ААВАВВВВВВАААА, отсюда число серий R = 5.
С вероятностью 0,954 найдем доверительный интервал, в котором может оказаться R, если количество серий является случайной величиной. Для этого предварительно найдем следующие показатели:
– с вероятностью 0,954 нормированное отклонение: t = 2 (см. табл. 10.1);
– среднее число серий: 7,5 (формула 10.2);
– среднее квадратическое отклонение числа серий: 1,803 (формула 10.3).
С вероятностью 0,954 можно утверждать, что количество серий случайная величина, если оно попадает в доверительный интервал 3 Исходный и выровненные методом скользящей средней ряды динамики выпуска продукции в течение месяца
Рабочие дни месяцаВыпуск продукции, млн. руб.Скользящая сумма, млн. руб.Скользящая средняя, млн. руб.ИнтервалыИнтервалытрехдневныепятидневныетрехдневныепятидневные123456137––––242112–37,3–333120215404344513623345,346,655815824752,749,465516928456,356,875618130860,361,68701953246564,89692133407164,8107421437071,36811712313707774128622739375,774137024838782,778,6149223040976,777,4156825340484,380,8169324242380,784,6178126342587,7851889264460889219942864769595,22010330649410298,821109311516103,7103,22299319–106,3–23111––––
Результаты расчетов скользящих сумм и скользящих средних приведены в 3-6 колонках таблицы 10.4.
Данные колонок 5 и 6 таблицы 10.4 показывают устойчивую тенденцию роста ежедневного выпуска продукции в течение месяца.
Аналитическое выравнивание рядов динамики
Под аналитическим выравниванием понимают определение основной проявляющейся во времени тенденции развития изучаемого явления, выраженной соответствующим уравнением регрессии. При этом развитие предстает как бы в зависимости только от течения времени, т.е. одного фактора — времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющий во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически.
На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции.
Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса. Чаще всего при выравнивании используются следующие зависимости:
– линейная, выраженная уравнением:
f(t) = y = a + b×t; (10.4)
– параболическая, выраженная уравнением:
f(t) = y = a + b×t + c×t 2 ; (10.5)
– экспоненциальная, выраженная уравнением:
f(t) = y = a×k t ; (10.4)
где y – уровни, освобожденные от колебаний;
а – начальный уровень тренда в момент или период, принятый за начало отсчета времени t (t = 0);
t – номер периода;
b – среднегодовой абсолютный прирост; константа линейного тренда (параметр, показывающий, на сколько изменится результат при изменении времени на единицу);
с – квадратический параметр, равный половине ускорения; константа параболического тренда. Ускорение (Δ’i) как разность между абсолютным приростом за данный период и абсолютным приростом за предыдущий период одинаковой длительности рассчитывается по формуле:
Δ’i = Δi — Δ’i-1. (10.7)
k – коэффициент роста; константа экспоненциального тренда.
Выравнивать динамические ряды по уравнению прямой линии целесообразно тогда, когда более или менее постоянны цепные абсолютные приросты, т.е. тогда, когда уровни ряда изменяются приблизительно в арифметической прогрессии.
Выравнивание динамических рядов по уравнению квадратической параболы необходимо применять в тех случаях, когда изменение уровней ряда происходит с приблизительно равномерным ускорением или замедлением цепных абсолютных приростов.
Выравнивание по экспоненциальной функции целесообразно использовать тогда, когда уровни ряда динамики выявляют тенденцию постоянства цепных темпов роста, т.е. в случае изменения уровней ряда динамики в геометрической прогрессии.
Кроме выше рассмотренных существуют логарифмическая, гиперболическая, логистическая и др. формы тренда.
Для расчета параметров уравнения тренда обычно используют метод наименьших квадратов.
Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую вычисляют параметры тренда.
Для линейного тренда нормальные уравнения МНК имеют вид:
где yi – уровни исходного ряда динамики;
ti – номера периодов или моментов времени;
n – число уровней ряда.
Систему можно упростить, перенеся начало отсчета времени ti в середину ряда. Тогда Σti будет равна 0 и система приобретет вид:
Отметим, что значение Σt 2 при четном числе n можно определить по формуле:
Для того, чтобы выйти на значение Σt 2 , полученное по формуле, при четном числе n шаг между ti и ti-1 или ti+1 принимается равным 2 года.
Для тренда, выраженного квадратической параболой, нормальные уравнения МНК имеют вид:
После переноса начала отсчета ti в середину ряда получим:
Для экспоненциального тренда нормальные уравнения МНК имеют вид:
После переноса начала отсчета ti в середину ряда получим:
Построив уравнение регрессии, проводят оценку его надежности. Это делается посредством F-критерия Фишера, рассчитываемого по формуле 8.15. Если Fфакт > Fтеор, то уравнение регрессии значимо, т.е. построенная модель адекватна фактической временной тенденции.
Пример аналитического выравнивания ряда динамики
По данным таблицы 9.11 необходимо провести аналитическое выравнивание ряда динамики среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом за 2000-2018 гг.
Проверку ряда динамики среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации за 2000-2018 гг. на наличие тренда проведем с помощью фазочастотного критерия знаков первой разности.
Данные таблицы 9.12 свидетельствуют о неуклонном росте среднемесячной заработной платы в стране и, соответственно, о положительных значениях знаков первой разности на протяжении всего исследованного периода.
Тенденция к росту уровней рассматриваемого ряда динамики очевидна.
Для определения тренда, наиболее точно отражающего закономерность изменения среднего уровня месячной заработной платы работников организаций по экономике Российской Федерации во времени, рассчитаем параметры уравнений линейной, параболической и экспоненциальной зависимостей, оценив их надежность с помощью F-критерия Фишера.
Результаты вспомогательных действий для расчета параметров уравнений регрессии приведены в таблице 10.5. Для упрощения расчетов начало отсчета времени ti перенесено в середину ряда.
| Годы | Среднемесячная зарплата, тыс. руб., уi, | Условное время, годы, ti | уiti | ti 2 | уiti 2 | ti 4 | Ln уiti | (Ln уiti)×ti | Уровни трендов | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| линейного | параболы II порядка | экспоненциального | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2000 | 2,2 | -9 | -19,8 | 81 | 178,2 | 6561 | 0,8 | -7,1 | -1,3 | -2,0 | 3,5 |
| 2001 | 3,2 | -8 | -25,6 | 64 | 204,8 | 4096 | 1,2 | -9,3 | 1,0 | 0,5 | 4,1 |
| 2002 | 4,4 | -7 | -30,8 | 49 | 215,6 | 2401 | 1,5 | -10,4 | 3,4 | 3,1 | 4,8 |
| 2003 | 5,5 | -6 | -33,0 | 36 | 198,0 | 1296 | 1,7 | -10,2 | 5,7 | 5,6 | 5,7 |
| 2004 | 6,7 | -5 | -33,5 | 25 | 167,5 | 625 | 1,9 | -9,5 | 8,1 | 8,2 | 6,6 |
| 2005 | 8,6 | -4 | -34,4 | 16 | 137,6 | 256 | 2,2 | -8,6 | 10,4 | 10,6 | 7,8 |
| 2006 | 10,6 | -3 | -31,8 | 9 | 95,4 | 81 | 2,4 | -7,1 | 12,8 | 13,1 | 9,1 |
| 2007 | 13,6 | -2 | -27,2 | 4 | 54,4 | 16 | 2,6 | -5,2 | 15,2 | 15,5 | 10,6 |
| 2008 | 17,3 | -1 | -17,3 | 1 | 17,3 | 1 | 2,9 | -2,9 | 17,5 | 17,9 | 12,4 |
| 2009 | 18,6 | 0 | 0 | 0 | 0 | 0 | 2,9 | 0,0 | 19,9 | 20,3 | 14,5 |
| 2010 | 21,0 | 1 | 21,0 | 1 | 21,0 | 1 | 3,0 | 3,0 | 22,2 | 22,6 | 17,0 |
| 2011 | 23,4 | 2 | 46,8 | 4 | 93,6 | 16 | 3,2 | 6,3 | 24,6 | 24,9 | 19,9 |
| 2012 | 26,6 | 3 | 79,8 | 9 | 239,4 | 81 | 3,3 | 9,8 | 26,9 | 27,2 | 23,3 |
| 2013 | 29,8 | 4 | 119,2 | 16 | 476,8 | 256 | 3,4 | 13,6 | 29,3 | 29,5 | 27,3 |
| 2014 | 32,5 | 5 | 162,5 | 25 | 812,5 | 625 | 3,5 | 17,4 | 31,7 | 31,7 | 31,9 |
| 2015 | 34,0 | 6 | 204,0 | 36 | 1224,0 | 1296 | 3,5 | 21,2 | 34,0 | 33,9 | 37,4 |
| 2016 | 36,7 | 7 | 256,9 | 49 | 1798,3 | 2401 | 3,6 | 25,2 | 36,4 | 36,1 | 43,7 |
| 2017 | 39,2 | 8 | 313,6 | 64 | 2508,8 | 4096 | 3,7 | 29,3 | 38,7 | 38,3 | 51,2 |
| 2018 | 43,7 | 9 | 393,3 | 81 | 3539,7 | 6561 | 3,8 | 34,0 | 41,1 | 40,4 | 59,9 |
| Всего | 377,6 | 0 | 1343,7 | 570 | 11982,9 | 30666 | 50,9 | 89,6 | 377,6 | 377,6 | 390,8 |
Данные для расчета параметров уравнений регрессии, характеризующих динамику среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом за 2000-2018 гг.
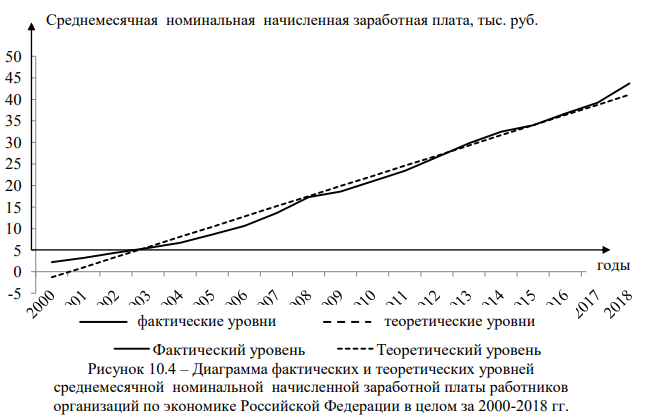
Рассчитаем параметры линейного тренда:
– начальный уровень тренда а в момент, принятый за начало отсчета времени (t = 0), по формуле 10.10 равен: 19,874 тыс. руб.;
– константа линейного тренда b по формуле 10.11 равна: 2,357 тыс. руб.
Уравнение линейного тренда имеет вид (формула 10.4): y = 19,874 + 2,357×t.
Параметры линейного уравнения означают, что среднемесячный уровень номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом и его выровненный уровень, отнесенный к середине периода, т.е. к 2009 г., равняются 19,874 тыс. руб., а среднегодовой абсолютный прирост среднемесячной заработной платы за рассмотренный период составил 2,357 тыс. руб.
Рассчитаем параметры параболического тренда с помощью системы уравнений 10.14, установив начало отсчета времени (t = 0) в середине ряда, и осуществив соответствующую подстановку данных из столбцов 2-7 таблицы 10.5.
Полученная система имеет уравнений вид:
19a + 570c = 377,6;
570b = 1343,7;
570a + 30666c = 11982,9.
Решив эту систему уравнений имеем: a = 20,285, b = 2,357, c = -0,014.
Уравнение параболического тренда имеет вид (формула 10.5):
y = 20,285 + 2,357t + 0,014t 2 .
Значение параметра с (константы параболического тренда, равной половине ускорения изменения абсолютного цепного прироста) означает, что абсолютный прирост среднемесячной номинальной начисленной заработной работников организаций по экономике страны в рассматриваемом периоде замедлялся в среднем на 28 рубля (2×0,014×1000) в год. Сам же абсолютный прирост уже не является константой параболического тренда, а является средней величиной за период. В год, принятый за начало отсчета, т.е. 2009 г., тренд проходит через точку с ординатой 20,285 тыс. руб. Свободный член параболического тренда не является средним уровнем за период.
Рассчитаем параметры экспоненциального тренда, используя данные колонок 8 и 9 таблицы 10.5:
- по формуле 10.17 ln a = 2,679, отсюда, а = 14,543;
- по формуле 10.18 ln k = 0,157, отсюда k = 1,170.
Уравнение экспоненциального тренда имеет вид (формула 10.6): y = 14,543×1,17 t .
Значение параметра k (константы экспоненциального тренда) означает, что среднегодовой темп роста среднемесячной номинальной начисленной зарплаты работников организаций по экономике Российской Федерации в целом в 2000-2018 гг. составлял 117,0 %. В точке, принятой за начало отчета, тренд проходит точку с ординатой 14,543 тыс. руб.
Отметим, что суммы теоретических уровней линейного и параболического трендов (колонки 10 и 11 таблицы 10.5) совпадают с суммой фактических уровней среднемесячной заработной платы за 2000-2018 гг. (колонка 2 таблицы 10.5). Это свидетельствует не только о том, что параметры трендов рассчитаны правильно, но и позволяет предположить, что полученные уравнения регрессии адекватно характеризуют сложившуюся тенденцию.
Для составления прогнозов на будущее, рассмотренные тренды неравнозначны по степени адекватности отражения формы прогрессии уровней ряда динамики, поэтому проведем оценку надежности уравнений регрессии с помощью критерия Фишера при α = 0,05 (с вероятностью 0,95).
Рассчитаем теоретические и фактические значения F-критерия для линейного, параболического и экспоненциального трендов.
Для расчета общей и факторных дисперсий для всех видов трендов среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом за 2000-2018 гг. построим вспомогательную таблицу 10.6.
| Годы | Среднемесячная зарплата, тыс. руб., уi, | уi 2 | Линейный тренд | Параболический тренд | Экспоненциальный тренд | |||
|---|---|---|---|---|---|---|---|---|
| y’i | (y’i— y ) 2 | y’i | (y’i— y ) 2 | y’i | (y’i— y ) 2 | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2000 | 2,2 | 4,84 | -1,3 | 450,13 | -2,0 | 480,29 | 3,5 | 267,04 |
| 2001 | 3,2 | 10,24 | 1,0 | 355,66 | 0,5 | 373,46 | 4,1 | 247,74 |
| 2002 | 4,4 | 19,36 | 3,4 | 272,30 | 3,1 | 280,97 | 4,8 | 226,08 |
| 2003 | 5,5 | 30,25 | 5,7 | 200,06 | 5,6 | 202,39 | 5,7 | 201,99 |
| 2004 | 6,7 | 44,89 | 8,1 | 138,93 | 8,2 | 137,32 | 6,6 | 175,51 |
| 2005 | 8,6 | 73,96 | 10,4 | 88,91 | 10,6 | 85,33 | 7,8 | 146,89 |
| 2006 | 10,6 | 112,36 | 12,8 | 50,01 | 13,1 | 46,03 | 9,1 | 116,63 |
| 2007 | 13,6 | 184,96 | 15,2 | 22,23 | 15,5 | 18,99 | 10,6 | 85,65 |
| 2008 | 17,3 | 299,29 | 17,5 | 5,56 | 17,9 | 3,84 | 12,4 | 55,45 |
| 2009 | 18,6 | 345,96 | 19,9 | 0,00 | 20,3 | 0,17 | 14,5 | 28,41 |
| 2010 | 21,0 | 441,00 | 22,2 | 5,56 | 22,6 | 7,59 | 17,0 | 8,14 |
| 2011 | 23,4 | 547,56 | 24,6 | 22,23 | 24,9 | 25,72 | 19,9 | 0,00 |
| 2012 | 26,6 | 707,56 | 26,9 | 50,01 | 27,2 | 54,17 | 23,3 | 11,81 |
| 2013 | 29,8 | 888,04 | 29,3 | 88,91 | 29,5 | 92,57 | 27,3 | 54,84 |
| 2014 | 32,5 | 1056,25 | 31,7 | 138,93 | 31,7 | 140,55 | 31,9 | 145,20 |
| 2015 | 34,0 | 1156,00 | 34,0 | 200,06 | 33,9 | 197,74 | 37,4 | 305,76 |
| 2016 | 36,7 | 1346,89 | 36,4 | 272,30 | 36,1 | 263,77 | 43,7 | 568,71 |
| 2017 | 39,2 | 1536,64 | 38,7 | 355,66 | 38,3 | 338,29 | 51,2 | 979,22 |
| 2018 | 43,7 | 1909,69 | 41,1 | 450,13 | 40,4 | 420,95 | 59,9 | 1600,40 |
| Всего | 377,6 | 10715,74 | 377,6 | 3167,60 | 377,6 | 3170,15 | 390,8 | 5225,47 |
Данные для расчета дисперсий среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом за 2000-2018 гг.
Общую дисперсию рассчитываем по данным колонок 2 и 3 таблицы 10.6, используя способ разности (формула 5.12),
169,0. Факторную дисперсию по теоретическим значениям рассчитываем по формуле 8.9, а остаточную дисперсию – по формуле 8.11. Напомним, что у = 19,874 тыс. руб.
Для линейного тренда:
- факторная дисперсия по данным столбца 5 таблицы 10.6 равна: 166,7;
- остаточная дисперсия: = 169,0 – 166,7 = 2,3.
Для тренда, характеризуемого параболой второго порядка:
- факторная дисперсия по данным столбца 7 таблицы 10.6 равна: 166,9;
- остаточная дисперсия: = 169,0 – 166,9 = 2,1.
Для экспоненциального тренда:
- факторная дисперсия по данным столбца 9 таблицы 10.6 равна: 275,0;
- остаточная дисперсия: 169,0 – 275,0 = -106,0.
Фактическое значение критерия Фишера для каждого типа тренда определим по формуле 8.15, а значения степеней свободы k1 и k2 дисперсий – по формулам 8.16 и 8.17.
Итак, для линейного тренда при k1 = 2 – 1 = 1 и k2 = 19 – 2 = 17 фактическое значение критерия Фишера равно: 1232,1; теоретическое значение критерия Фишера по данным таблицы 7.10 равно: Fт ≈ 4,4. Так как Fф > Fт (1232,1 > 4,4), то с вероятностью 0,95 можно утверждать, что линейная регрессия адекватно отражает динамику среднемесячной номинальной начисленной заработной платы работников организаций по экономике Российской Федерации в целом в 2000-2018 гг.
Для тренда, характеризуемого параболой второго порядка, при k1 = 3 – 1 = 2 и k2 = 19 – 3 = 16 фактическое значение критерия Фишера равно: 635,8; теоретическое значение критерия Фишера по данным таблицы 7.10 равно: Fт = 3,6. Так как Fф > Fт (635,8 > 3,6), то с вероятностью 0,95 можно утверждать, что и параболическая регрессия адекватно отражает динамику номинальной среднемесячной заработной платы работников организаций России в 2000-2018 гг.
Для экспоненциального тренда фактическое значение критерия Фишера равно отрицательной величине, что не позволяет рассматривать данный тренд на предмет адекватности.
Наиболее адекватно сложившуюся в исследуемом ряду динамики тенденцию отражает линейный тренд (рис. 10.4).
Понятие о колеблемости
При изучении и измерении тенденции динамики колебания уровней играли лишь роль помех, «информационного шума», от которого следовало по возможности абстрагироваться. Однако факторы, обусловливающие колебания уровней временного ряда, как правило, объективны, что предопределяет самостоятельное исследование колеблемости.
Значение изучения колебаний уровней динамического ряда определяется, в первую очередь, тем, что регулирование рыночной экономики, как со стороны государства, так и производителей в значительной мере состоит в регулировании колебаний экономических процессов. Например, колебания урожайности, продуктивности скота, производства сельхозпродукции экономически нежелательны, так как потребность в продукции агрокомплекса постоянна. Эти колебания следует уменьшать, применяя прогрессивную технологию и другие меры. Напротив, сезонные колебания объемов производства зимней и летней одежды, обуви, мороженного, прохладительных напитков и т.п. – необходимы и закономерны, так как спрос на эти товары тоже колеблется по сезонам и равномерное производство требует лишних затрат на хранение запасов.
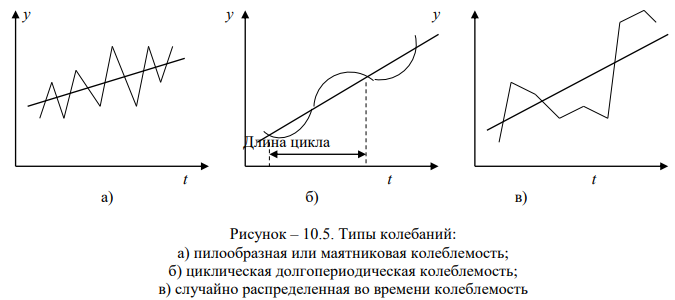
Типы колебаний статистических показателей весьма разнообразны. Три основных типа колебаний: пилообразная или маятниковая колеблемость, циклическая долгопериодическая колеблемость и случайно распределенная во времени колеблемость показаны на рис. 10.5, на котором хорошо видны их свойства и отличия друг от друга.
Пилообразная или маятниковая колеблемость состоит в попеременных отклонениях уровней ряда от тренда то в одну, то в другую сторону. Такие колебания можно наблюдать в динамике урожайности при невысоком уровне агротехники: высокий урожай при благоприятных условиях погоды выносит из почвы больше питательных веществ, чем их образуется естественным путем за год, следовательно, почва обедняется, что вызывает снижение следующего урожая ниже тренда, который выносит меньше питательных веществ, чем образуется за год и плодородие возрастает, и т.д.
Циклическая долгопериодическая колеблемость свойственна, например, солнечной активности (10-летние циклы), а, значит, и связанным с ней на Земле процессами – урожайности отдельных культур в ряде районов, некоторым заболеваниям людей, растений и т.п. Для этого типа колеблемости характерны редкая смена знаков отклонений от тренда и кумулятивный эффект отклонений одного знака, который может тяжело отражаться на экономике. Зато эти колебания хорошо прогнозируются.
Случайно распределенная во времени колеблемость – нерегулярная, хаотическая. Она может возникнуть при наложении множества колебаний с разными по длительности циклами. Но может возникать и в результате столь же хаотической колеблемости главной причины существования колебаний, например суммы осадков за летний период, температуры воздуха в среднем за месяц в разные годы.
На предположении, что параметры тренда и колебаний сохраняются до прогнозируемого периода, т.е. на экстраполяции, основана методика статистического прогноза по тренду и колеблемости. Экстраполяция справедлива, если система развивается эволюционно в достаточно стабильных условиях.
Сезонные колебания
Особого внимания при изучении колеблемости заслуживают сезонные колебания. Сезонные колебания строго цикличны – повторяются через каждый год.
Сезонными колебаниями называют периодические колебания уровней, возникающие под влиянием смены времени года.
Роль сезонных колебаний велика в агропромышленном комплексе, торговле многими товарами, заболеваемости, строительстве, деятельности рекреационных учреждений, на транспорте.
Сезонность наносит большой ущерб народному хозяйству, связанный с неравномерным использованием оборудования и рабочей силы, с неравномерной загрузкой транспорта и т.д.
Для изучения сезонных колебаний необходимо иметь уровни за каждый месяц (квартал) года, а, чтобы сгладить случайные колебания и точнее измерить сезонные, их изучают за несколько лет.
Уровень сезонности и форма «сезонной волны» изучаются с помощью индексов сезонности.
Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции.
Индивидуальные индексы сезонности показывают, во сколько раз фактический уровень ряда в момент (интервал) времени t больше или меньше среднего уровня, соответствующего данному моменту (интервалу) времени, либо уровня, вычисляемого по уравнению тенденции f(t).
Индекс сезонности (It,сез), если тренда нет или он незначителен, рассчитывают по формуле:
где y t – средний уровень показателя по одноименным месяцам (кварталам) за ряд лет;
t – номер месяца (квартала);
y o – общий средний уровень показателя за период исследования.
При наличии тренда индекс сезонности определяется на основе методов, исключающих влияние тенденции. Порядок расчета индекса сезонности при наличии тренда следующий:
1) для каждого уровня (yt,i) определяются выровненные значения по тренду f(t) = yt,i;
2) рассчитываются индивидуальные индексы уровней исследуемых показателей для каждого месяца (квартала) каждого года по формуле:

где n – число лет (i = 1, …, n).
Совокупность исчисленных для каждого месяца годового цикла индексов сезонности характеризует «сезонную волну» развития изучаемого явления во внутригодовой динамике.
Пример расчета индексов сезонности при условии отсутствия четко выраженной тенденции изменения уровней ряда динамики
По данным таблицы 10.7 необходимо проанализировать внутригодовую динамику потерь рабочего времени на предприятиях города N по причине неявок персонала на работу в 2016-2018 гг.
| Годы | Месяцы | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь | |
| 2016 | 186 | 165 | 192 | 80 | 48 | 54 | 52 | 78 | 35 | 64 | 221 | 175 |
| 2017 | 174 | 180 | 204 | 123 | 50 | 46 | 68 | 84 | 43 | 58 | 179 | 198 |
| 2018 | 182 | 174 | 165 | 126 | 68 | 42 | 47 | 65 | 54 | 74 | 187 | 170 |
Данные о потерях рабочего времени на предприятиях города N по причине неявок персонала на работу в 2016-2018 гг., чел.-дн. (данные условные)
Проверим ряд динамики потерь рабочего времени на предприятиях города N в 2016-2018 гг. на наличие тренда. Для этого рассчитаем годовые потери рабочего времени, т.е. проведем укрупнение месячных уровней в годовые, и определим темпы роста. Расчет базисных темпов роста в данном примере соответствует методике проверки ряда динамики на наличие тренда с помощью критерия Кокса и Стюарта.
Просуммировав месячные уровни, получили потери рабочего времени в 2016 г. – 1350 чел.- дн.; в 2017 г. – 1407 чел.-дн.; в 2018 г. – 1354 чел.-дн.
Базисные темпы роста потерь рабочего времени на предприятиях города N в 2016-2018 гг., рассчитанные по формуле 9.5, составили 100,3 % (1354 : 1350 × 100); цепные темпы роста потерь рабочего времени внутри этого периода, рассчитанные по формуле 9.6, составили в 2017 г. по сравнению с 2016 г. 104,2 % (1407 : 1350 × 100), а в 2018 г. по сравнению с 2017 г. – 96,2 % (1354 : 1407 × 100).
Рассчитанные значения темпов роста годовых уровней ряда динамики потерь рабочего времени на предприятиях города N в 2016-2018 гг., позволяют сделать вывод, что изучаемое явление не имеет четко выраженной тенденции к росту, поэтому индексы сезонности рассчитываются по формуле 10.19.
Средние уровни потерь рабочего времени по одноименным месяцам за три года ( y t) и их общий среднемесячный уровень за период исследования ( y o) найдем по формуле 4.21.
Результаты расчетов соответствующих индексов сезонности представим в таблице 10.8.
| Годы | Месяцы | Всего, чел.-дн. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | ||
| 2016 | 186 | 165 | 192 | 80 | 48 | 54 | 52 | 78 | 35 | 64 | 221 | 175 | 1350 |
| 2017 | 174 | 180 | 204 | 123 | 50 | 46 | 68 | 84 | 43 | 58 | 179 | 198 | 1407 |
| 2018 | 182 | 174 | 165 | 126 | 68 | 42 | 47 | 65 | 54 | 74 | 187 | 170 | 1354 |
| Итого, чел.-дн. | 542 | 519 | 561 | 329 | 166 | 142 | 167 | 227 | 132 | 196 | 587 | 543 | 4111 |
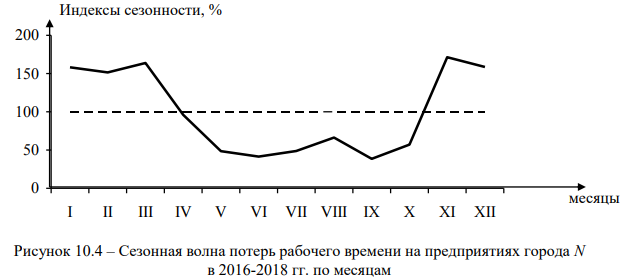
| y t, чел.-дн. | 180,7 | 173,0 | 187,0 | 109,7 | 55,3 | 47,3 | 55,7 | 75,7 | 44,0 | 65,3 | 195,3 | 181,0 | х |
| It,сез, % | 158,2 | 151,5 | 163,8 | 96,0 | 48,5 | 41,4 | 48,7 | 66,3 | 38,5 | 57,2 | 171,3 | 158,5 | х |
Результаты расчета индексов сезонности внутригодовой динамики потерь рабочего времени на предприятиях города N по причине неявок персонала на работу в 2016-2018 гг.
Расчеты y t проводились следующим образом: y I = 542 : 3 = 180,7 чел.-дн.; y II = 519 : 3 = 151,5 чел.-дн.; и т.д.; y o = 4111 : 36 = 114,2 чел.-дн.
Наглядное представление о сезонной волне потерь рабочего времени на предприятиях города N дает график на рис. 10.4.
На рис. 10.4 четко видно, что наибольшие потери рабочего времени на предприятиях города N по причине неявок персонала на работу в 2016-2018 гг. приходились на март и ноябрь – пик сезонной заболеваемости острыми респираторными заболеваниями. Ярко выраженный спад потерь рабочего времени по причине неявок работников на предприятия города N приходился на период с мая по октябрь, что соответствует общей тенденции динамики потерь рабочего времени в экономике страны.
Пример расчета индексов сезонности при условии наличия тренда
По данным таблицы 10.9 необходимо проанализировать внутригодовую динамику потерь рабочего времени на предприятиях города К по причине неявок персонала на работу в 2016- 2018 гг.
Просуммировав внутригодовые уровни потерь рабочего времени на предприятиях города К по годам (2016 г. – 3010 чел.-дн.; 2017 г. – 2760 чел.-дн.; 2018 г. – 2510 чел.-дн.), видим наличие ярко выраженной тенденции их снижениях их уровня.
| Годы | Месяцы | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь | |
| 2016 | 420 | 560 | 300 | 270 | 110 | 20 | 50 | 240 | 180 | 180 | 380 | 300 |
| 2017 | 340 | 480 | 250 | 260 | 180 | 70 | 40 | 170 | 130 | 220 | 370 | 250 |
| 2018 | 400 | 290 | 360 | 240 | 90 | 30 | 40 | 110 | 150 | 210 | 350 | 240 |
Данные о потерях рабочего времени на предприятиях города К по причине неявок персонала на работу в 2016-2018 гг., чел.-дн. (данные условные)
Для исключения влияния выявленной тенденции при анализе внутригодовой динамики потерь рабочего времени на предприятиях города К используем метод, основанный на аналитическом выравнивании уровней ряда.
Выравнивание уровней рассматриваемого ряда динамики по месяцам 2016-2018 гг. проведем, используя уравнение прямой (формула 10.4). Параметры линейного тренда рассчитаем по данным таблицы 10.10 упрощенным способом, выбрав начало отсчета t таким образом, чтобы было выполнено условие Σt = 0.
| Период | yt,i, чел.-дн. | t | yt,i×t | t 2 | y’t,i, чел.-дн. | it,i, % |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Январь 2016 г. | 420 | -35 | -14700 | … | 279 | 150,5 |
| Февраль 2016 г. | 560 | -33 | -18480 | … | 276 | 202,8 |
| Март 2016 г. | 300 | -31 | -9300 | … | 273 | 109,7 |
| Апрель 2016 г. | 270 | -29 | -7830 | … | 271 | 99,8 |
| Май 2016 г. | 110 | -27 | -2970 | … | 268 | 41,1 |
| Июнь 2016 г. | 20 | -25 | -500 | … | 265 | 7,5 |
| Июль 2016 г. | 50 | -23 | -1150 | … | 262 | 19,1 |
| Август 2016 г. | 240 | -21 | -5040 | … | 259 | 92,5 |
| Сентябрь 2016 г. | 180 | -19 | -3420 | … | 257 | 70,1 |
| Октябрь 2016 г. | 180 | -17 | -3060 | … | 254 | 70,9 |
| Ноябрь 2016 г. | 380 | -15 | -5700 | … | 251 | 151,4 |
| Декабрь 2016 г. | 300 | -13 | -3900 | … | 248 | 120,9 |
| Январь 2017 г. | 340 | -11 | -3740 | … | 245 | 138,5 |
| Февраль 2017 г. | 480 | -9 | -4320 | … | 243 | 197,9 |
| Март 2017 г. | 250 | -7 | -1750 | … | 240 | 104,3 |
| Апрель 2017 г. | 260 | -5 | -1300 | … | 237 | 109,7 |
| Май 2017 г. | 180 | -3 | -540 | … | 234 | 76,9 |
| Июнь 2017 г. | 70 | -1 | -70 | … | 231 | 30,3 |
| Июль 2017 г. | 40 | 1 | 40 | … | 229 | 17,5 |
| Август 2017 г. | 170 | 3 | 510 | … | 226 | 75,3 |
| Сентябрь 2017 г. | 130 | 5 | 650 | … | 223 | 58,3 |
| Октябрь 2017 г. | 220 | 7 | 1540 | … | 220 | 100,0 |
| Ноябрь 2017 г. | 370 | 9 | 3330 | … | 217 | 170,2 |
| Декабрь 2017 г. | 250 | 11 | 2750 | … | 215 | 116,5 |
| Январь 2018 г. | 400 | 13 | 5200 | … | 212 | 188,9 |
| Февраль 2018 г. | 290 | 15 | 4350 | … | 209 | 138,8 |
| Март 2018 г. | 360 | 17 | 6120 | … | 206 | 174,6 |
| Апрель 2018 г. | 240 | 19 | 4560 | … | 203 | 118,0 |
| Май 2018 г. | 90 | 21 | 1890 | … | 201 | 44,9 |
| Июнь 2018 г. | 30 | 23 | 690 | … | 198 | 15,2 |
| Июль 2018 г. | 40 | 25 | 1000 | … | 195 | 20,5 |
| Август 2018 г. | 110 | 27 | 2970 | … | 192 | 57,2 |
| Сентябрь 2018 г. | 150 | 29 | 4350 | … | 189 | 79,2 |
| Октябрь 2018 г. | 210 | 31 | 6510 | … | 187 | 112,5 |
| Ноябрь 2018 г. | 350 | 33 | 11550 | … | 184 | 190,4 |
| Декабрь 2018 г. | 240 | 35 | 8400 | … | 181 | 132,6 |
| Всего | 8280 | 0 | -21360 | 15540 | 8280 | х |
Данные для расчета параметров линейного тренда потерь рабочего времени на предприятиях города К по причине неявок персонала на работу по месяцам 2016-2018 гг.
По формуле 10.10 и данным столбца 2 таблицы 10.10: а = 8280 : 36 = 230 чел.-дн.
По формуле 10.11 и данным столбцов 3 и 4 таблицы 10.10: b = -21360 : 15540 = -1,4 чел.-дн.
В соответствии с формулой 10.4 уравнение прямой выровненного ряда динамики потерь рабочего времени на предприятиях города К по причине неявок персонала на работу за 2016-2018 гг. имеет вид: y’t = 230 — 1,4×t.
На основании этого уравнения рассчитаем значения уровней выровненного ряда динамики y’t,i (см. столбец 6 табл. 10.10) и сопоставим с ними исходные уровни ряда yt,i, т. е. найдем индивидуальные индексы уровней исследуемых показателей для каждого квартала каждого года it,i, (см. столбец 7 табл. 10.10).
Индексы сезонности для каждого квартала определяем по формуле 10.21.
Так, для января индекс сезонности равен: 1,593 (159,3%); для февраля – 1,798 (179,8%); и т.д. Результаты расчетов индексов сезонности сведены в таблице 10.11.
| Месяцы | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| It,сез, % | 159,3 | 179,8 | 129,5 | 109,2 | 54,3 | 17,7 | 19,0 | 75,0 | 69,2 | 94,5 | 170,7 | 123,3 |
Результаты расчета индексов сезонности внутригодовой динамики потерь рабочего времени на предприятиях города К по причине неявок персонала на работу в 2016-2018 гг.
Наглядное представление о внутригодовой динамике потерь рабочего времени на предприятиях города К по месяцам рассмотренного периода дает графическое изображение «сезонной волны» (рис. 10.4), отражающее наиболее высокие уровни потерь рабочего времени в феврале и ноябре.
Методы выявления тенденции рядов динамики.
1. Укрупнение интервалов — наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней.
2. Скользящая средняя — это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода.
3. Аналитическое выравнивание ряда динамики позволяет получить описание плавной линии развития ряда. Задача: определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами.
Определение основной тенденции динамики на основе укрупнения интервалов и скользящей средней.
Уровни ряда динамики формируются под вниманием 3-х групп факторов:
1. Факторов определяющих основное направление, т.е. тенденцию развития изучаемого явления.
2. Факторов действующих периодически, т.е. направленных колебаний по неделям месяца, месяцам года и т.д.
3. Факторов действующих в разных, иногда в противоположных направлениях и не оказывающих существенного влияния на уровень данного ряда динамики.
Основной задачей статистического изучения данамики является выявление тенденции.
Основными методами выявления тенденции рядов динамики являются:
— метод укрупнения интервалов
— метод скользящей средней
— метод аналитического выравнивания
1. Сущность метода укрупнения интервалов заключается в следующем:
Исходный ряд динамики преобразуется и заменяется другими состоящими из других уровней, относящихся к укрупненным периодам или моментам времени.
Например: ряд динамики прибыли малого предприятия за 1997 год по кварталам того же года. При этом уровни ряда за укрупненные периоды или моменты времени могут представлять собой либо суммарные, либо средние показатели. Однако в любом случае рассчитанные таким образом уровни ряда более отчетливо выявляют тенденции, поскольку сезонные и случайные колебания при суммировании или определении средних взаимопогашаются и уравновешиваются.
2. Метод скользящей средней, как и предыдущий предполагает преобразование исходного ряда динамики. Для выявления тенденции формируются интервал, состоящий из одинакового числа уровней. При этом каждый последующий интервал получается путем смещения на 1 уровень от начального. По образованным таким образом интервалам определяются в начале сумма, а затем средние. Технически удобнее определять скользящие средние для нечетного интервала. В этом случае рассчитанная средняя величина будет относиться к конкретному уровню ряда динамики, т.е. к середине интервала скольжения.
При определении скользящей средней по четному интервалу, расчетное значение средней величины относится к промежутку между двумя уровнями, и таким образом теряют экономический смысл. Это делает необходимыми дополнительные расчеты связанные с центрированием по формуле арифметической простой из двух соседних не центрированных средних.
Определение основной тенденции методом аналитического выравнивания.
Основными методами выявления тенденции рядов динамики являются:
— метод укрупнения интервалов
— метод скользящей средней
— метод аналитического выравнивания
Более совершенным приемом изучения общей тенденции в рядах динамики является аналитическое выравнивание. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Вид уравнения определяется характером динамики развития конкретного явления. Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики, а именно:
· если относительно стабильны абсолютные приросты (первые разности уровней приблизительно равны), , сглаживание может быть выполнено по прямой;
· если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны), можно принять параболу второго порядка;
· при ускоренно возрастающих или замедляющихся абсолютных приростах — параболу третьего порядка;
· при относительно стабильных темпах роста- показательную функцию.
Для аналитического выравнивания наиболее часто используются следующие виды трендовых моделей: прямая (линейная), парабола второго порядка, показательная (логарифмическая) кривая, гиперболическая.
Цель аналитического выравнивания- определение аналитической или графической зависимости.
После выяснения характера кривой развития необходимо определить ее параметры, что можно сделать различными методами:
1) решением системы уравнений по известным уровням ряда динамики;
2) методом средних значений (линейных отклонений), который заключается в следующем: ряд расчленяется на две примерно равные части, и вводятся преобразования, чтобы сумма выровненных значений в каждой части совпала с суммой фактических значений, например, в случае выравнивания прямой линии ;
3) выравниванием ряда динамики с помощью метода конечных разностей;
4) методом наименьших квадратов: это некоторый прием получения оценки детерминированной компоненты , характеризующих тренд или ряд изучаемого явления.
Понятие и виды населения.
Население, как предмет изучения в статистике, представляет собой совокупность людей, проживающих на определенной территории и непрерывно возобновляющихся за счет рождений и смертей. Население любого государства весьма неоднородно по своему составу и изменчиво во времени, поэтому закономерности развития населения, изменение его состава и многие другие характеристики должны изучаться с учетом конкретных исторических условий.
Показатели, характеризующие население:
· численность и его динамика
· интенсивность демографических процессов: рождаемость, смертность, естественный прирост, брачность
· расселение, плотность, урбанизация, миграция
· возрастно-половой состав и семейное состояние
· расовый, языковой, этнический и религиозный состав
· уровень социально-экономического развития, уровень жизни.
Виды и модели населения
В демографии выделяются следующие категории населения:
Постоянное население — обычное население, основная категоря, объединяющая совокупность людей, для которых данная территория представляет собой место обычного проживания в данное время
Стабильное население — теоретическая модель населения с неизменными во времени интенсивностями рождаемости, смертности и возрастной структурой
Стационарное население — теоретическое население, частный случай стабильного населения при истинном коэффециенте естественного прироста r = 0 и неизменной численности населения P(t) = P(0)
В статистике населения (демостатистике), занимающейся сбором эмпирических данных и учетом населения, различаются также следующие категории:
Наличное население — часть населения, которая находится на момент учета в данном населенном пункте, независимо от места постоянного проживания.
Постоянное население— часть населения, которая постоянно проживает в данном населенном пункте, независимо от фактического местонахождения на момент учета.
Временно отсутствующие — лица, которые на момент учета временно отсутствовали в месте постоянного проживания (на срок не более 6 месяцев).
Временно присутствующие — лица, которые временно находились в данном населенном пункте на момент учета (на срок не более 6 месяцев).
Перепись населения.
Основные понятия переписи населения
Программа переписи населения — перечень сведений, собираемых при переписи. В переписной лист включается ряд вопросов, позволяющих получить необходимую информацию. Например, адрес, демографические признаки — (пол, возраст, состояние в браке), гражданство, этнические характеристики, религия, образование и т.д.
Перепись срочная — перепись, организованная в короткие сроки (от 2 до 11 дней). Для неё характерны централизованное руководство сбором и разработкой данных, строго ограниченная цель и краткая программа наблюдения (1-5 вопросов), а также оперативный способ передачи данных.
источники:
http://be5.biz/ekonomika/s015/10.html
http://lektsia.com/5×3756.html
9.3. Методы анализа основной тенденции в рядах динамики
Комплексный анализ динамических рядов, как правило, включает не только расчет характеристик интенсивности изменения уровней ряда при переходе от одного момента или промежутка времени к другому (абсолютных приростов, коэффициентов и темпов роста и прироста), а также нахождение обобщенных средних характеристик (среднего уровня ряда, средних темпов роста и прироста), но и выявление основных закономерностей в развитии динамического ряда. Определение тенденции развития, построение модели, описывающей изменение явления во времени, прогнозирование явления — все это важнейшие задачи при изучении динамических рядов экономических и социальных показателей.
На формирование уровней динамического ряда влияет множество различных факторов, которые по характеру воздействия можно объединить в три группы:
- действующие долговременно и определяющие основную тенденцию развития явления;
- действующие периодически — сезонные и циклические колебания;
- вызывающие случайные колебания уровней динамического ряда.
Соответственно, для анализа закономерности изменения уровней ряда динамики во времени применяют следующую модель:
где Тt — основная тенденция ряда (тренд);
St — циклические (в частности, сезонные) колебания;
еt — случайные колебания.
В аддитивной модели ряд динамики представлен как сумма перечисленных компонент [yt = Tt + St + et], в мультипликативной модели — как их произведение [
Тенденцией развития, или трендом, называется сформировавшееся направление развития явления во времени под воздействием постоянно действующих факторов. Судить о наличии тенденции в динамическом ряду на основе его визуального анализа можно лишь тогда, когда четко видно, что при переходе от одного момента времени к другому уровни ряда возрастают или убывают. Однако, как правило, нельзя сразу сказать, есть или нет тенденция в изменении уровней динамического ряда. Для этого применяются специальные методы.
К методам выявления основной тенденции развития динамического ряда (Тt) относятся:
- метод укрупнения интервалов;
- метод скользящей средней;
- аналитическое выравнивание динамических рядов.
Рассмотрим их подробнее.
9.3.1. Метод укрупнения интервалов
Применение метода укрупнения интервалов рассмотрим на основе данных табл. 9.13.
| Месяц | Поставка товаров, млн руб. |
|---|---|
| Январь | 80 |
| Февраль | 78 |
| Март | 75 |
| Апрель | 80 |
| Май | 82 |
| Июнь | 85 |
| Июль | 87 |
| Август | 82 |
| Сентябрь | 85 |
| Октябрь | 84 |
| Ноябрь | 86 |
| Декабрь | 88 |
Как видим, визуальный анализ данных не позволяет сделать какие-либо выводы о наличии тенденции в данном динамическом ряду: в отдельные месяцы, например, в феврале, марте, августе, октябре и декабре, поставки товаров снижались по сравнению с предыдущими месяцами, в остальные периоды — возрастали.
Применим к исходным данным метод укрупнения интервалов, образовав новый динамический ряд с более крупными временными периодами — кварталами, и рассчитаем средний месячный объем поставок в каждом квартале (табл. 9.14).
| Квартал | Среднемесячные поставки товаров, млн руб. |
|---|---|
| I | 77.7 |
| II | 82.3 |
| III | 84.0 |
| IV | 84.7 |
Итак, по новым, более крупным интервалам уже четко видно, что значения исследуемого признака во временном аспекте имеют тенденцию к возрастанию.
Применение рассмотренного метода в основном ограничивается теми ситуациями, когда исходные данные относятся к дням, неделям или месяцам года, так как значения исследуемого признака по более мелким временным интервалам больше подвержены случайным колебаниям. Если временные промежутки представляют собой годы, то укрупнение интервалов становится малоэффективным.
9.3.2. Метод скользящей средней
Следующий способ выявления тенденции в динамическом ряду основан на расчете и анализе так называемых скользящих (подвижных) средних.
Скользящими (подвижными) средними называются средние арифметические значения показателя, исчисленные по новым m-членным укрупненным интервалам. Правила построения этих интервалов следующие. Первый из интервалов включает первые m уровней ряда динамики, второй интервал образуется путем исключения первого члена укрупненного интервала и замены его последующим элементом ряда динамики, имеющим номер (m + 1) и т.д. — до включения в интервал последнего уровня ряда. По вычисленным подобным путем подвижным средним делают вывод о существовании тенденции в динамическом ряду.
Если в качестве укрупненного интервала используют период в три месяца, то первая подвижная трехчленная средняя вычисляется как средняя арифметическая из данных за январь, февраль и март, вторая — как средняя арифметическая из данных за февраль, март, апрель и т.д. Значения подвижных средних относят к конкретному временному периоду, соответствующему середине укрупненного интервала.
Проведем сглаживание ряда методом скользящей средней по трем членам (табл. 9.15).
 |
В нашем примере первая скользящая средняя относится к февралю, вторая — к марту и т. д.
В тех случаях, когда сглаживание проводится по четному числу уровней ряда динамики, середина временного интервала сглаживания будет находиться между двумя моментами (периодами) времени. Например, если проводить сглаживание по четырем членам, середина первого интервала будет находиться между февралем и мартом, второго интервала — между мартом и апрелем и т.д. В таких случаях возникает необходимость центрирования полученных результатов для отнесения сглаженных значений показателя к конкретным периодам или моментам времени. Расчет центрированных скользящих средних может проводиться в два этапа:
- определение скользящих сумм и нецентрированных скользящих средних по четному числу уровней ряда динамики;
- исчисление центрированных скользящих средних из двух смежных ранее исчисленных нецентрированных скользящих средних и отнесение их к соответствующим периодам или моментам времени.
Методика расчета центрированных скользящих средних показана ниже (табл. 9.16).
 |
9.3.3. Аналитическое сглаживание (выравнивание) рядов динамики
Аналитическое выравнивание динамических рядов — это нахождение определенной модели (уравнения тренда), которая математически описывает тенденцию развития явления во времени. При этом уровни показателя рассматриваются только как функция от времени. В отличие от рассмотренных выше методов, таких, как укрупнение интервалов, скользящих средних, направленных в основном на то, чтобы ответить на вопрос: есть ли тенденция в динамическом ряду или нет, и определить ее направление, аналитическое выравнивание позволяет более точно установить характер развития явления, а главное — описать его математически, уловить все нюансы и направления развития и, что, пожалуй, наиболее интересно, использовать в дальнейшем полученную модель для прогнозирования.
Первым шагом в проведении аналитического выравнивания является выбор вида математической функции, которую предполагается использовать в качестве модели тренда. При этом можно руководствоваться формой кривой, полученной на основе отображения на графике эмпирических данных. Схема построения графика достаточно проста: по оси абсцисс откладываются временные периоды (даты), по оси ординат — значения уровней динамического ряда.
При анализе рядов динамики в качестве линии тренда чаще всего используются следующие функции:
- линейная:
yt= a0 + a1t;
- парабола 2-го порядка:
yt= a0 + a1t + a2t2;
- показательная:
- гиперболическая:
Кроме того, возможности современного программного обеспечения (например, система STATISTICA) позволяют использовать в качестве модели тренда математическую функцию любого (задаваемого пользователем) произвольного вида.
Выравнивание по линейной функции (прямой). Выбор в пользу выравнивания по линейной функции производят либо по результатам графического анализа эмпирических данных, либо если уровни ряда меняются в арифметической прогрессии (в этом случае рассчитанные цепные абсолютные приросты уровней приблизительно одинаковы).
При выравнивании по линейной функции (прямой) используется уравнение вида
yt= a0 + a1t,
где t — условный показатель времени.
Параметры уравнения определяются на основе метода наименьших квадратов путем решения системы нормальных линейных уравнений
В качестве примера рассмотрим динамический ряд, представленный в табл. 9.17.
| Год | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
|---|---|---|---|---|---|---|
| Доход банков от операций с ценными бумагами, млн руб. | 70 | 92 | 112 | 135 | 159 | 185 |
| Цепные абсолютные приросты | — | 22 | 20 | 23 | 24 | 26 |
Итак, рассчитанные нами цепные абсолютные приросты относительно постоянны, поэтому можно говорить о целесообразности выбора в качестве аналитической функции уравнения прямой.
При нахождении параметров уравнения показатель времени удобно обозначить так, чтобы выполнялось следующее равенство: ![[sum_t = 0]](https://intuit.ru/sites/default/files/tex_cache/028883db35624326b97512540cfa51a0.png)
Предположим, что мы рассматриваем динамический ряд, имеющий пять уровней (за период с 2002 по 2006 г.), тогда условный показатель времени обозначим так, как это показано в табл. 9.18.
| Год | 2002 | 2003 | 2004 | 2005 | 2006 |
|---|---|---|---|---|---|
| Доход банков от операций с ценными бумагами, млн руб. | 52 | 112 | 135 | 159 | 185 |
| Условный показатель времени t | -2 | -1 | 0 | 1 | 2 |
При четном количестве уровней в середине ряда находятся два момента (периода) времени. Одному из них присваивают значение t = -1, а другому t = +1. Тогда предыдущие моменты времени получают значения -3, -5 и т.д., а последующие значения — +3, +5 и т.д. (т.е. с шагом 2 в одну и другую сторону от центра).
При подобном способе обозначения времени система уравнений упрощается
Тогда коэффициенты уравнения а0 и а1 находят следующим образом:
Определим по данным табл. 9.17, в которой представлен ряд динамики с четным числом уровней, параметры уравнения прямой (табл. 9.19).
| Год | Доход банков от операций с ценными бумагами, млн руб., y | t | t2 | yt | Выравненные значения, yt |
|---|---|---|---|---|---|
| 2001 | 70 | -5 | 25 | -350 | 68,43 |
| 2002 | 92 | -3 | 9 | -276 | 91,258 |
| 2003 | 112 | -1 | 1 | -112 | 114,086 |
| 2004 | 135 | 1 | 1 | 135 | 136,914 |
| 2005 | 159 | 3 | 9 | 477 | 159,742 |
| 2006 | 185 | 5 | 25 | 925 | 182,57 |
| Сумма | 753 | 0 | 70 | 799 | 753 |
Тогда
Искомое уравнение прямой имеет вид: yt= 125,5 + 11,414t.
Подставляя в полученное уравнение соответствующее значение t, рассчитаем выравненные теоретические значения показателя (см. последнюю графу табл. 9.11). При этом сумма выравненных значений должна равняться сумме эмпирических значений (753), если это не так, то параметры уравнения определены неверно.
График, построенный по выравненным значениям показателя, будет отражать тенденцию развития явления во времени (рис. 9.1).
Рис.
9.1.
Уравнение прямой, описывающее изменение во времени дохода банков от операций с ценными бумагами
На основе полученного уравнения тренда можно строить прогнозные значения показателя для разных периодов времени путем подстановки в полученное уравнение значений временной компоненты. Например, для 2007 г. получим следующую ожидаемую величину дохода:
yi= 125,5 + 11,414t = 125,5 + 11,414 * 7 = 205,398 (млн руб.).
Выравнивание по параболе второго порядка. При ускоренном или замедленном изменении уровней динамического ряда, когда постоянны рассчитанные вторые разности уровней (цепные абсолютные приросты цепных абсолютных приростов), для аналитического выравнивания применяют параболу второго порядка:
yi= a0 + a1t + a2t2.
Параметры уравнения находят на основе метода наименьших квадратов, при этом обозначение условного показателя времени t абсолютно аналогично обозначению времени при построении прямой.
Система нормальных уравнений для нахождения параметров уравнения параболы имеет вид:
Если принять обозначение времени, при котором выполняется равенство 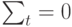
Проведем аналитическое выравнивание данных, характеризующих динамику инвестиций за период 2001-2006 гг. (табл. 9.20).
| Показатель | Год | |||||
|---|---|---|---|---|---|---|
| 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | |
| Инвестиции, млн руб., yi | 98 | 100 | 130 | 193 | 280 | 391 |
Первые разности (цепные абсолютные приросты) 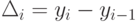
|
— | 2 | 30 | 63 | 87 | 111 |
Вторые разности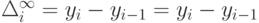
|
— | — | 28 | 33 | 24 | 24 |
Рассчитанные вторые разности демонстрируют относительное постоянство, поэтому в качестве аналитической функции для выравнивания возьмем уравнение параболы второго порядка. Наш выбор подтверждает и графический анализ данных (рис. 9.2).
Рис.
9.2.
Динамика инвестиций за 2001-2006 гг.
Проведем необходимые расчеты для определения параметров уравнения в табл. 9.21.
| Год | Вложение в уставные капиталы, млн руб., y | Условное обозначение времени, t | t2 | t4 | y-t | y-t2 | Выравненные значения, yi |
|---|---|---|---|---|---|---|---|
| 1999 | 98 | -5 | 25 | 625 | -490 | 2 450 | 97 |
| 2000 | 100 | -3 | 9 | 81 | -300 | 900 | 101 |
| 2001 | 130 | -1 | 1 | 1 | -130 | 130 | 132 |
| 2002 | 193 | 1 | 1 | 1 | 193 | 193 | 191 |
| 2003 | 280 | 3 | 9 | 81 | 840 | 2 520 | 278 |
| 2004 | 391 | 5 | 25 | 625 | 1 955 | 9 775 | 392 |
| Сумма | 1 192 | 0 | 70 | 1 414 | 2 068 | 15 968 | 1 192 |
Построим и решим систему уравнений (табл. 9.15):
Таким образом, искомое уравнение параболы имеет вид
yi =158,406 + 29,543t + 3,451t2.
Выравнивание по показательной функции. Если уровни ряда меняются в геометрической прогрессии, т.д. рассчитанные цепные коэффициенты роста относительно постоянны, то для выравнивания используют показательную функцию вида
Параметры показательного уравнения определяются путем решения следующей системы нормальных уравнений:
Если принять обозначении времени t, при котором выполняется условие 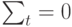
Проведем аналитическое выравнивание данных, характеризующих изменение числа страховых компаний региона за период 2000-2006 гг. (табл. 9.22).
| Год | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
|---|---|---|---|---|---|---|---|
| Число страховых компаний, yi | 215 | 220 | 223 | 229 | 235 | 241 | 248 |
Цепные коэффициенты роста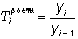 |
— | 1,023 | 1,014 | 1,027 | 1,026 | 1,026 | 1,029 |
Относительно постоянные цепные коэффициенты роста позволяют в качестве аналитического выражения тренда выбрать показательную функцию.
Проведем необходимые расчеты для определения параметров выбранного уравнения в табл. 9.23.
| Год | Число страховых компаний, y | Условное обозначение времени, t | t2 | lgy | t – lgy | Выравненные значения, yt |
|---|---|---|---|---|---|---|
| 2000 | 215 | -3 | 9 | 2,332438 | -6,99732 | 210 |
| 2001 | 220 | -2 | 4 | 2,342423 | -4,68485 | 217 |
| 2002 | 223 | -1 | 1 | 2,348305 | -2,3483 | 223 |
| 2003 | 229 | 0 | 0 | 2,359835 | 0 | 230 |
| 2004 | 241 | 1 | 1 | 2,371068 | 2,371068 | 237 |
| 2005 | 241 | 2 | 4 | 2,382017 | 4,764034 | 244 |
| 2006 | 248 | 3 | 9 | 2,394452 | 7,183355 | 251 |
| Сумма | 1 611 | 0 | 28 | 16,53054 | 0,287991 | 1 611 |
Составим и решим систему нормальных уравнений:
Показательное уравнение будет иметь вид
yi= 229,8 * 1,03t
Подставляя в полученное уравнение значения условного показателя времени t, рассчитаем выравненные значения `yi.
Выравнивание по гиперболе. Если уровни динамического ряда снижаются, постепенно замедляя свою скорость, но по логике никогда не смогут достичь нуля, то для проведения аналитического выравнивания выбирают уравнение гиперболы:
Параметры этого уравнения определяются на основе решения следующей системы нормальных уравнений:
При нахождении параметров гиперболы применение принципа «отсчета от условного нуля», который использовался при нахождении параметров прямой, параболы и показательной функции, становится невозможным из-за выражения 1/t при котором 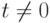
Произведем аналитическое выравнивание данных, характеризующих изменение себестоимости единицы продукции вида «А» в течение года (табл. 9.24).
| Месяц | Себестоимость единицы продукции вида «А», руб., y | Условное обозначение времени, t | 1/t | t2 | 1/t2 | y/t | Выравнивание значения, `yi |
|---|---|---|---|---|---|---|---|
| Январь | 58 | 1 | 1,00000 | 1 | 1,000000 | 58,000 | 59 |
| Февраль | 52 | 2 | 0,50000 | 4 | 0,25000 | 26,000 | 50 |
| Март | 48 | 3 | 0,33333 | 9 | 0,11111 | 16,000 | 47 |
| Апрель | 45 | 4 | 0,25000 | 16 | 0,06250 | 11,250 | 45 |
| Май | 44 | 5 | 0,20000 | 25 | 0,04000 | 8,800 | 44 |
| Июнь | 43 | 6 | 0,16667 | 36 | 0,02778 | 7,167 | 43 |
| Июль | 43 | 7 | 0,14286 | 49 | 0,02041 | 6,143 | 43 |
| Август | 42 | 8 | 0,12500 | 64 | 0,01563 | 5,250 | 43 |
| Сентябрь | 42 | 9 | 0,11111 | 81 | 0,01235 | 4,667 | 42 |
| Октябрь | 42 | 10 | 0,10000 | 100 | 0,01000 | 4,200 | 42 |
| Ноябрь | 42 | 11 | 0,09091 | 121 | 0,00826 | 3,818 | 42 |
| Декабрь | 41 | 12 | 0,08333 | 144 | 0,00694 | 3,417 | 42 |
| Сумма | 542 | — | 3,10321 | — | 1,56498 | 154,711 | 542 |
Составим систему уравнений
откуда находим значения параметров
Уравнение гиперболы примет вид
Подставив в полученное уравнение значения условного показателя времени t, рассчитаем выравненные значения yi и поместим их в расчетную таблицу. Как видим, выравненные значения достаточно близки к эмпирическим данным, что позволяет надеяться на получение достоверных прогнозов на основе построенной модели.
При проведении аналитического выравнивания зачастую бывает трудно заранее определить подходящий вид уравнения тренда, особенно если эмпирические данные графически явно не демонстрируют относимость к какой-либо аналитической функции. Тогда поступают следующим образом: строят несколько уравнений тренда. Затем для каждого из них вычисляют остаточную дисперсию и модель с наименьшей величиной остаточной дисперсии признают лучшей из имеющихся на данный момент.
Остаточная дисперсия исчисляется по формуле
Это более простой метод, но есть и другие, более сложные методы.