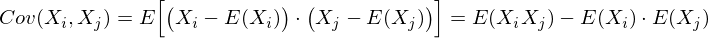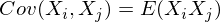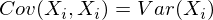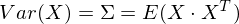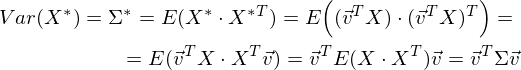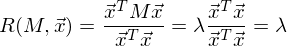В этой статье я бы хотел рассказать о том, как именно работает метод анализа главных компонент (PCA – principal component analysis) с точки зрения интуиции, стоящей за ее математическим аппаратом. Максимально просто, но подробно.
Математика вообще очень красивая и изящная наука, но порой ее красота скрывается за кучей слоев абстракции. Показать эту красоту лучше всего на простых примерах, которые, так сказать, можно покрутить, поиграть и пощупать, потому что в конце концов все оказывается гораздо проще, чем кажется на первый взгляд – самое главное понять и представить.
В анализе данных, как и в любом другом анализе, порой бывает нелишним создать упрощенную модель, максимально точно описывающую реальное положение дел. Часто бывает так, что признаки довольно сильно зависят друг от друга и их одновременное наличие избыточно.
К примеру, расход топлива у нас меряется в литрах на 100 км, а в США в милях на галлон. На первый взгляд, величины разные, но на самом деле они строго зависят друг от друга. В миле 1600м, а в галлоне 3.8л. Один признак строго зависит от другого, зная один, знаем и другой.
Но гораздо чаще бывает так, что признаки зависят друг от друга не так строго и (что важно!) не так явно. Объем двигателя в целом положительно влияет на разгон до 100 км/ч, но это верно не всегда. А еще может оказаться, что с учетом не видимых на первый взгляд факторов (типа улучшения качества топлива, использования более легких материалов и прочих современных достижений), год автомобиля не сильно, но тоже влияет на его разгон.
Зная зависимости и их силу, мы можем выразить несколько признаков через один, слить воедино, так сказать, и работать уже с более простой моделью. Конечно, избежать потерь информации, скорее всего не удастся, но минимизировать ее нам поможет как раз метод PCA.
Выражаясь более строго, данный метод аппроксимирует n-размерное облако наблюдений до эллипсоида (тоже n-мерного), полуоси которого и будут являться будущими главными компонентами. И при проекции на такие оси (снижении размерности) сохраняется наибольшее количество информации.
Шаг 1. Подготовка данных
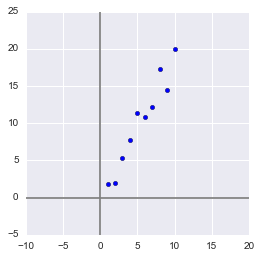
Здесь для простоты примера я не буду брать реальные обучающие датасеты на десятки признаков и сотни наблюдений, а сделаю свой, максимально простой игрушечный пример. 2 признака и 10 наблюдений будет вполне достаточно для описания того, что, а главное – зачем, происходит в недрах алгоритма.
Сгенерируем выборку:
x = np.arange(1,11)
y = 2 * x + np.random.randn(10)*2
X = np.vstack((x,y))
print X
OUT:
[[ 1. 2. 3. 4. 5.
6. 7. 8. 9. 10. ]
[ 2.73446908 4.35122722 7.21132988 11.24872601 9.58103444
12.09865079 13.78706794 13.85301221 15.29003911 18.0998018 ]]
В данной выборке у нас имеются два признака, сильно коррелирующие друг с другом. С помощью алгоритма PCA мы сможем легко найти признак-комбинацию и, ценой части информации, выразить оба этих признака одним новым. Итак, давайте разбираться!
Для начала немного статистики. Вспомним, что для описания случайной величины используются моменты. Нужные нам – мат. ожидание и дисперсия. Можно сказать, что мат. ожидание – это «центр тяжести» величины, а дисперсия – это ее «размеры». Грубо говоря, мат. ожидание задает положение случайной величины, а дисперсия – ее размер (точнее, разброс).
Сам процесс проецирования на вектор никак не влияет на значения средних, так как для минимизации потерь информации наш вектор должен проходить через центр нашей выборки. Поэтому нет ничего страшного, если мы отцентрируем нашу выборку – линейно сдвинем ее так, чтобы средние значения признаков были равны 0. Это очень сильно упростит наши дальнейшие вычисления (хотя, стоит отметить, что можно обойтись и без центрирования).
Оператор, обратный сдвигу будет равен вектору изначальных средних значений – он понадобится для восстановления выборки в исходной размерности.
Xcentered = (X[0] - x.mean(), X[1] - y.mean())
m = (x.mean(), y.mean())
print Xcentered
print "Mean vector: ", m
OUT:
(array([-4.5, -3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5]),
array([-8.44644233, -8.32845585, -4.93314426, -2.56723136, 1.01013247,
0.58413394, 1.86599939, 7.00558491, 4.21440647, 9.59501658]))
Mean vector: (5.5, 10.314393916)
Дисперсия же сильно зависит от порядков значений случайной величины, т.е. чувствительна к масштабированию. Поэтому если единицы измерения признаков сильно различаются своими порядками, крайне рекомендуется стандартизировать их. В нашем случае значения не сильно разнятся в порядках, так что для простоты примера мы не будем выполнять эту операцию.
Шаг 2. Ковариационная матрица
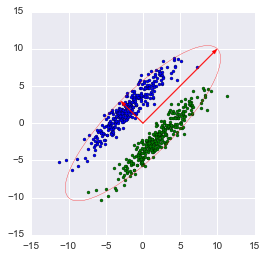
В случае с многомерной случайной величиной (случайным вектором) положение центра все так же будет являться мат. ожиданиями ее проекций на оси. А вот для описания ее формы уже недостаточно толькое ее дисперсий по осям. Посмотрите на эти графики, у всех трех случайных величин одинаковые мат.ожидания и дисперсии, а их проекции на оси в целом окажутся одинаковы!
Для описания формы случайного вектора необходима ковариационная матрица.
Это матрица, у которой (i,j)-элемент является корреляцией признаков (Xi, Xj). Вспомним формулу ковариации:
В нашем случае она упрощается, так как
E(Xi) = E(Xj) = 0:
Заметим, что когда Xi = Xj:
и это справедливо для любых случайных величин.
Таким образом, в нашей матрице по диагонали будут дисперсии признаков (т.к. i = j), а в остальных ячейках – ковариации соответствующих пар признаков. А в силу симметричности ковариации матрица тоже будет симметрична.
Замечание: Ковариационная матрица является обобщением дисперсии на случай многомерных случайных величин – она так же описывает форму (разброс) случайной величины, как и дисперсия.
И действительно, дисперсия одномерной случайной величины – это ковариационная матрица размера 1×1, в которой ее единственный член задан формулой Cov(X,X) = Var(X).
Итак, сформируем ковариационную матрицу Σ для нашей выборки. Для этого посчитаем дисперсии Xi и Xj, а также их ковариацию. Можно воспользоваться вышенаписанной формулой, но раз уж мы вооружились Python’ом, то грех не воспользоваться функцией numpy.cov(X). Она принимает на вход список всех признаков случайной величины и возвращает ее ковариационную матрицу и где X – n-мерный случайный вектор (n-количество строк). Функция отлично подходит и для расчета несмещенной дисперсии, и для ковариации двух величин, и для составления ковариационной матрицы.
(Напомню, что в Python матрица представляется массивом-столбцом массивов-строк.)
covmat = np.cov(Xcentered)
print covmat, "n"
print "Variance of X: ", np.cov(Xcentered)[0,0]
print "Variance of Y: ", np.cov(Xcentered)[1,1]
print "Covariance X and Y: ", np.cov(Xcentered)[0,1]
OUT:
[[ 9.16666667 17.93002811]
[ 17.93002811 37.26438587]]
Variance of X: 9.16666666667
Variance of Y: 37.2643858743
Covariance X and Y: 17.9300281124
Шаг 3. Собственные вектора и значения (айгенпары)
О’кей, мы получили матрицу, описывающую форму нашей случайной величины, из которой мы можем получить ее размеры по x и y (т.е. X1 и X2), а также примерную форму на плоскости. Теперь надо найти такой вектор (в нашем случае только один), при котором максимизировался бы размер (дисперсия) проекции нашей выборки на него.
Замечание: Обобщение дисперсии на высшие размерности — ковариационная матрица, и эти два понятия эквивалентны. При проекции на вектор максимизируется дисперсия проекции, при проекции на пространства больших порядков – вся ее ковариационная матрица.
Итак, возьмем единичный вектор на который будем проецировать наш случайный вектор X. Тогда проекция на него будет равна vTX. Дисперсия проекции на вектор будет соответственно равна Var(vTX). В общем виде в векторной форме (для центрированных величин) дисперсия выражается так:
Соответственно, дисперсия проекции:
Легко заметить, что дисперсия максимизируется при максимальном значении vT Σv. Здесь нам поможет отношение Рэлея. Не вдаваясь слишком глубоко в математику, просто скажу, что у отношения Рэлея есть специальный случай для ковариационных матриц:
и
Последняя формула должна быть знакома по теме разложения матрицы на собственные вектора и значения. x является собственным вектором, а λ – собственным значением. Количество собственных векторов и значений равны размеру матрицы (и значения могут повторяться).
Кстати, в английском языке собственные значения и векторы именуются eigenvalues и eigenvectors соответственно.
Мне кажется, это звучит намного более красиво (и кратко), чем наши термины.
Таким образом, направление максимальной дисперсии у проекции всегда совпадает с айгенвектором, имеющим максимальное собственное значение, равное величине этой дисперсии.
И это справедливо также для проекций на большее количество измерений – дисперсия (ковариационная матрица) проекции на m-мерное пространство будет максимальна в направлении m айгенвекторов, имеющих максимальные собственные значения.
Размерность нашей выборки равна двум и количество айгенвекторов у нее, соответственно, 2. Найдем их.
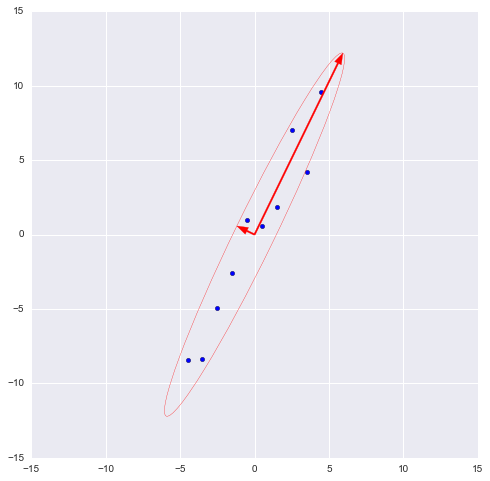
В библиотеке numpy реализована функция numpy.linalg.eig(X), где X – квадратная матрица. Она возвращает 2 массива – массив айгензначений и массив айгенвекторов (векторы-столбцы). И векторы нормированы — их длина равна 1. Как раз то, что надо. Эти 2 вектора задают новый базис для выборки, такой что его оси совпадают с полуосями аппроксимирующего эллипса нашей выборки.
На этом графике мы апроксимировали нашу выборку эллипсом с радиусами в 2 сигмы (т.е. он должен содержать в себе 95% всех наблюдений – что в принципе мы здесь и наблюдаем). Я инвертировал больший вектор (функция eig(X) направляла его в обратную сторону) – нам важно направление, а не ориентация вектора.
Шаг 4. Снижение размерности (проекция)
Наибольший вектор имеет направление, схожее с линией регрессии и, спроецировав на него нашу выборку, мы потеряем информацию, сравнимую с суммой остаточных членов регрессии (только расстояние теперь евклидово, а не дельта по Y). В нашем случае зависимость между признаками очень сильная, так что потеря информации будет минимальна. «Цена» проекции — дисперсия по меньшему айгенвектору — как видно из предыдущего графика, очень невелика.
Замечание: диагональные элементы ковариационной матрицы показывают дисперсии по изначальному базису, а ее собственные значения – по новому (по главным компонентам).
Часто требуется оценить объем потерянной (и сохраненной) информации. Удобнее всего представить в процентах. Мы берем дисперсии по каждой из осей и делим на общую сумму дисперсий по осям (т.е. сумму всех собственных чисел ковариационной матрицы).
Таким образом, наш больший вектор описывает 45.994 / 46.431 * 100% = 99.06%, а меньший, соответственно, примерно 0.94%. Отбросив меньший вектор и спроецировав данные на больший, мы потеряем меньше 1% информации! Отличный результат!
Замечание: На практике, в большинстве случаев, если суммарная потеря информации составляет не более 10-20%, то можно спокойно снижать размерность.
Для проведения проекции, как уже упоминалось ранее на шаге 3, надо провести операцию vTX (вектор должен быть длины 1). Или, если у нас не один вектор, а гиперплоскость, то вместо вектора vT берем матрицу базисных векторов VT. Полученный вектор (или матрица) будет являться массивом проекций наших наблюдений.
_, vecs = np.linalg.eig(covmat)
v = -vecs[:,1])
Xnew = dot(v,Xcentered)
print Xnew
OUT:
[ -9.56404107 -9.02021624 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
dot(X,Y) — почленное произведение (так мы перемножаем векторы и матрицы в Python)
Нетрудно заметить, что значения проекций соответствуют картине на предыдущем графике.
Шаг 5. Восстановление данных
С проекцией удобно работать, строить на ее основе гипотезы и разрабатывать модели. Но не всегда полученные главные компоненты будут иметь явный, понятный постороннему человеку, смысл. Иногда полезно раскодировать, к примеру, обнаруженные выбросы, чтобы посмотреть, что за наблюдения за ними стоят.
Это очень просто. У нас есть вся необходимая информация, а именно координаты базисных векторов в исходном базисе (векторы, на которые мы проецировали) и вектор средних (для отмены центровки). Возьмем, к примеру, наибольшее значение: 10.596… и раскодируем его. Для этого умножим его справа на транспонированный вектор и прибавим вектор средних, или в общем виде для всей выборки: XTvT+m
n = 9 #номер элемента случайной величины
Xrestored = dot(Xnew[n],v) + m
print 'Restored: ', Xrestored
print 'Original: ', X[:,n]
OUT:
Restored: [ 10.13864361 19.84190935]
Original: [ 10. 19.9094105]
Разница небольшая, но она есть. Ведь потерянная информация не восстанавливается. Тем не менее, если простота важнее точности, восстановленное значение отлично аппроксимирует исходное.
Вместо заключения – проверка алгоритма
Итак, мы разобрали алгоритм, показали как он работает на игрушечном примере, теперь осталось только сравнить его с PCA, реализованным в sklearn – ведь пользоваться будем именно им.
from sklearn.decomposition import PCA
pca = PCA(n_components = 1)
XPCAreduced = pca.fit_transform(transpose(X))
Параметр n_components указывает на количество измерений, на которые будет производиться проекция, то есть до скольки измерений мы хотим снизить наш датасет. Другими словами – это n айгенвекторов с самыми большими собственными числами. Проверим результат снижения размерности:
print 'Our reduced X: n', Xnew
print 'Sklearn reduced X: n', XPCAreduced
OUT:
Our reduced X:
[ -9.56404106 -9.02021625 -5.52974822 -2.96481262 0.68933859
0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
Sklearn reduced X:
[[ -9.56404106]
[ -9.02021625]
[ -5.52974822]
[ -2.96481262]
[ 0.68933859]
[ 0.74406645]
[ 2.33433492]
[ 7.39307974]
[ 5.3212742 ]
[ 10.59672425]]
Мы возвращали результат как матрицу вектор-столбцов наблюдений (это более канонический вид с точки зрения линейной алгебры), PCA в sklearn же возвращает вертикальный массив.
В принципе, это не критично, просто стоит отметить, что в линейной алгебре канонично записывать матрицы через вектор-столбцы, а в анализе данных (и прочих связанных с БД областях) наблюдения (транзакции, записи) обычно записываются строками.
Проверим и прочие параметры модели – функция имеет ряд атрибутов, позволяющих получить доступ к промежуточным переменным:
— Вектор средних: mean_
— Вектор(матрица) проекции: components_
— Дисперсии осей проекции (выборочная): explained_variance_
— Доля информации (доля от общей дисперсии): explained_variance_ratio_
Замечание: explained_variance_ показывает выборочную дисперсию, тогда как функция cov() для построения ковариационной матрицы рассчитывает несмещенные дисперсии!
Сравним полученные нами значения со значениями библиотечной функции.
print 'Mean vector: ', pca.mean_, m
print 'Projection: ', pca.components_, v
print 'Explained variance ratio: ', pca.explained_variance_ratio_, l[1]/sum(l)
OUT:
Mean vector: [ 5.5 10.31439392] (5.5, 10.314393916)
Projection: [[ 0.43774316 0.89910006]] (0.43774316434772387, 0.89910006232167594)
Explained variance: [ 41.39455058] 45.9939450918
Explained variance ratio: [ 0.99058588] 0.990585881238
Единственное различие – в дисперсиях, но как уже упоминалось, мы использовали функцию cov(), которая использует несмещенную дисперсию, тогда как атрибут explained_variance_ возвращает выборочную. Они отличаются только тем, что первая для получения мат.ожидания делит на (n-1), а вторая – на n. Легко проверить, что 45.99 ∙ (10 — 1) / 10 = 41.39.
Все остальные значения совпадают, что означает, что наши алгоритмы эквивалентны. И напоследок замечу, что атрибуты библиотечного алгоритма имеют меньшую точность, поскольку он наверняка оптимизирован под быстродействие, либо просто для удобства округляет значения (либо у меня какие-то глюки).
Замечание: библиотечный метод автоматически проецирует на оси, максимизирующие дисперсию. Это не всегда рационально. К примеру, на данном рисунке неаккуратное снижение размерности приведет к тому, что классификация станет невозможна. Тем не менее, проекция на меньший вектор успешно снизит размерность и сохранит классификатор.
Итак, мы рассмотрели принципы работы алгоритма PCA и его реализации в sklearn. Я надеюсь, эта статья была достаточно понятна тем, кто только начинает знакомство с анализом данных, а также хоть немного информативна для тех, кто хорошо знает данный алгоритм. Интуитивное представление крайне полезно для понимания того, как работает метод, а понимание очень важно для правильной настройки выбранной модели. Спасибо за внимание!
P.S.: Просьба не ругать автора за возможные неточности. Автор сам в процессе знакомства с дата-анализом и хочет помочь таким же как он в процессе освоения этой удивительной области знаний! Но конструктивная критика и разнообразный опыт всячески приветствуются!
Анализ главных компонент – это метод понижения размерности Датасета (Dataset), который преобразует больший набор переменных в меньший с минимальными потерями информативности.
Уменьшение количества переменных в наборе данных происходит в ущерб точности, но хитрость здесь заключается в том, чтобы потерять немного в точности, но обрести простоту. Поскольку меньшие наборы данных легче исследовать и визуализировать, анализ данных становится намного проще и быстрее для Алгоритмов (Algorithm) Машинного обучения (ML).
Идея PCA проста: уменьшить количество переменных в наборе данных, сохранив при этом как можно больше информации.
Шаг первый. Стандартизация
Мы осуществляем Стандартизацию (Standartization) исходных переменных, чтобы каждая из них вносила равный вклад в анализ. Почему так важно выполнить стандартизацию до PCA? Метод очень чувствителен к Дисперсиям (Variance) исходных Признаков (Feature). Если есть больши́е различия между диапазонами исходных переменных, те переменные с бо́льшими диапазонами будут преобладать над остальными (например, переменная, которая находится в диапазоне от 0 до 100, будет преобладать над переменной, которая находится в диапазоне от 0 до 1), что приведет к необъективным результатам. Преобразование данных в сопоставимые масштабы может предотвратить эту ситуацию.
Математически это можно сделать путем вычитания Среднего значения (Mean) из каждого значения и деления полученной разности на Стандартное отклонение (Standard Deviation). После стандартизации все переменные будут преобразованы в исходные значения.
Шаг второй. Матрица ковариации
Цель этого шага – понять, как переменные отличаются от среднего по отношению друг к другу, или, другими словами, увидеть, есть ли между ними какая-либо связь. Порой переменные сильно коррелированы и содержат избыточную информацию, и чтобы идентифицировать эти взаимосвязи, мы вычисляем Ковариационную матрицу (Covariance Matrix).
Ковариационная матрица представляет собой симметричную матрицу размера p × p (где p – количество измерений), где в качестве ячеек пребывают коэффициенты ковариации, связанные со всеми возможными парами исходных переменных. Например, для трехмерного набора данных с 3 переменными x, y и z ковариационная матрица представляет собой следующее:
Поскольку ковариация переменной с самой собой – это ее дисперсия, на главной диагонали (от верхней левой ячейки к нижней правой), у нас фактически есть дисперсии каждой исходной переменной. А поскольку ковариация коммутативна (в ячейке XY значение равно YX), элементы матрицы симметричны относительно главной диагонали.
Что коэффициенты ковариации говорят нам о корреляциях между переменными? На самом деле, имеет значение знак ковариации. Если коэффициент – это:
- положительное число, то две переменные прямо пропорциональны, то есть второй увеличивается или уменьшается вместе с первым.
- отрицательное число, то переменные обратно пропорциональны, то есть второй увеличивается, когда первый уменьшается, и наоборот.
Теперь, когда мы знаем, что ковариационная матрица – это не более чем таблица, которая отображает корреляции между всеми возможными парами переменных, давайте перейдем к следующему шагу.
Шаг третий. Вычисление собственных векторов
Собственные векторы (Eigenvector) и Собственные значения (Eigenvalues) – это понятия из области Линейной алгебры (Linear Algebra), которые нам нужно экстраполировать из ковариационной матрицы, чтобы определить так называемые главные компоненты данных. Давайте сначала поймем, что мы подразумеваем под этим термином.
Главная компонента – это новая переменная, смесь исходных. Эти комбинации выполняются таким образом, что новые переменные (то есть главные компоненты) не коррелированы, и большая часть информации в исходных переменных помещается в первых компонентах. Итак, идея состоит в том, что 10-мерный датасет дает нам 10 главных компонент, но PCA пытается поместить максимум возможной информации в первый, затем максимум оставшейся информации во второй и так далее, пока не появится что-то вроде того, что показано на графике ниже:
Такая организация информации в главных компонентах позволит нам уменьшить размерность без потери большого количества информации за счет отбрасывания компонент с низкой информативностью.
Здесь важно понимать, что главные компоненты менее интерпретируемы и не имеют никакого реального значения, поскольку они построены как линейные комбинации исходных переменных.
С геометрической точки зрения, главные компоненты представляют собой Векторы (Vector) данных, которые объясняют максимальное количество отклонений. Главные компоненты – новые оси, которые обеспечивают лучший угол для оценки данных, чтобы различия между наблюдениями были лучше видны.
Поскольку существует столько главных компонент, сколько переменных в наборе, главные компоненты строятся таким образом, что первый из них учитывает наибольшую возможную дисперсию в наборе данных. Например, предположим, что диаграмма рассеяния нашего набора данных выглядит так:
Можем ли мы проецировать первый главный компонент? Да, это линия, которая соответствует фиолетовым отметкам, потому что она проходит через начало координат, и проекции точек на компонент наиболее короткие. Говоря математически, это линия, которая максимизирует дисперсию (среднее квадратов расстояний от проецируемых красных точек до начала координат).
Второй главный компонент рассчитывается таким же образом, при условии, что он не коррелирован (т.е. перпендикулярен) первому главному компоненту и учитывает следующую по величине дисперсию. Это продолжается до тех пор, пока не будет вычислено p главных компонент, равное исходному количеству переменных.
Теперь, когда мы поняли, что подразумевается под главными компонентами, давайте вернемся к собственным векторам и собственным значениям. Прежде всего, нам нужно знать, что они всегда «ходят парами», то есть каждый собственный вектор имеет собственное значение. И их количество равно количеству измерений данных. Например, для 3-мерного набора данных есть 3 переменных, следовательно, есть 3 собственных вектора с 3 соответствующими собственными значениями.
За всей магией, описанной выше, стоят собственные векторы и собственные значения, потому что собственные векторы матрицы ковариации на самом деле являются направлениями осей, где наблюдается наибольшая дисперсия (большая часть информации) и которые мы называем главными компонентами. А собственные значения – это просто коэффициенты, прикрепленные к собственным векторам, которые дают величину дисперсии, переносимую в каждом основном компоненте.
Ранжируя собственные векторы в порядке от наибольшего к наименьшему, мы получаем главные компоненты в порядке значимости.
Шаг четвертый. Вектор признака
Как мы видели на предыдущем шаге, вычисляя собственные векторы и упорядочивая их по собственным значениям в в порядке убывания, мы можем ранжировать основные компоненты в порядке значимости. На этом этапе мы выбираем, оставить ли все эти компоненты или отбросить те, которые имеют меньшее значение, и сформировать с оставшимися матрицу векторов, которую мы называем Вектором признака (Feature Vector).
Итак, вектор признаков – это просто матрица, в столбцах которой есть собственные векторы компонент, которые мы решили оставить. Это первый шаг к уменьшению размерности, потому что, если мы решим оставить только p собственных векторов (компонент) из n, окончательный набор данных будет иметь только p измерений.
Шаг 5. Трансформирование данных по осям главных компонент
На предыдущих шагах, помимо стандартизации, мы не вносили никаких изменений в данные, а просто выбирали основные компоненты и формировали вектор признаков, но исходной набор данных всегда остается.
На этом последнем этапе цель состоит в переориентации данных с исходных осей на оси, представленные главными компонентами (отсюда и название «Анализ главных компонент»). Это можно сделать, перемножив транспонированный исходный набор данных на транспонированный вектор признаков.
PCA и Scikit-learn
PCA можно реализовать с помощью SkLearn. Для начала импортируем необходимые библиотеки:
import numpy as np
import pandas as pd
import sklearn
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScalerМы будем использовать датасет банка, автоматизирующего выдачу кредитных продуктов своим клиентам:
df = pd.read_csv('https://www.dropbox.com/s/9t04t1haanbdvvt/bank-data-for-pca.csv?dl=1')
dfСоздадим список признаков, подлежащих уменьшению. Это макроэкономические показатели с невысоким уровнем важности, которые почти не попали в список выше. Выберем сокращаемые и Целевую переменные (Target Variable):
X = df[['Возраст', 'Длительность', 'Кампания', 'День недели', 'Предыдущий контакт', 'Индекс потребительских цен', 'Европейская межбанковская ставка', 'Количество сотрудников в компании']]
y = df.iloc[:, -1]Выберем cамые важные признаки с помощью функции SelectKBest, которая использует критерий Хи-квадрат (Chi Square):
bestfeatures = SelectKBest(score_func = chi2, k = 'all')
fit = bestfeatures.fit(X, y)Создадим объект dfscores, куда отправим, соответственно, очки важности всех признаков датасета:
dfscores = pd.DataFrame(fit.scores_)
dfcolumns = pd.DataFrame(X.columns)Создадим для коэффициентов отдельный объект, соединив названия столбцов и очки, и отобразим пять признаков, набравших наибольшее количество очков:
featureScores = pd.concat([dfcolumns, dfscores], axis = 1)
featureScores.columns = ['Specs', 'Score']
print(featureScores.nlargest(5, 'Score'))Неожиданно, но самыми важными признаками оказались количество сотрудников в компании и порядковый номер рекламной кампании, в которой участвует клиент:
Specs Score
1 Длительность 1.760568e+06
7 Количество сотрудников в компании 5.251380e+03
6 Европейская межбанковская ставка 3.239336e+03
4 Предыдущий контакт 3.089714e+03
2 Кампания 5.419261e+02Создадим список признаков, подлежащих понижению. Это макроэкономические показатели с невысоким уровнем важности, которые почти не попали в список выше:
features = ['Колебание уровня безработицы', 'Индекс потребительских цен', 'Индекс потребительской уверенности', 'Европейская межбанковская ставка']
x = df.loc[:, features].valuesВыполним стандартизацию объекта X. StandardScaler() на месте заменяет данные на их стандартизированную версию, и мы получаем признаки, где все значения как бы центрированы относительно нуля. Такое преобразование необходимо, чтобы правильно объединить признаки между собой.
x = StandardScaler().fit_transform(x)
pd.DataFrame(data = x, columns = features).head()Результат выглядит следующим образом:
Мы хотим получить один главный компонент. Передадим функции обучающие данные:
pca = PCA(n_components = 1)
principalComponents = pca.fit_transform(x)
principalDf = pd.DataFrame(data = principalComponents, columns = ['principal component 1'])
principalDf.head()Мы получили вот такой главный компонент:
Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: Zakaria Jaadi
Фото: @codyrs
Анализ главных компонентов (PCA) — это популярный и мощный непараметрический неконтролируемый инструмент, используемый для анализа многомерных данных. PCA можно использовать в качестве метода уменьшения размерности, исследовательского инструмента для выявления скрытых закономерностей и т. д. Но, как всегда, не существует единого решения для всех имеющихся проблем. Конечно, PCA не является исключением из этого правила. Прежде чем мы углубимся в PCA, полезно изучить мотивы использования таких методов, как PCA, в многомерном анализе.
Прежде чем мы приступим к работе с PCA, давайте рассмотрим концепцию под названием ортогонализация. Ортогонализация дает интуитивное представление о том, почему PCA имеет смысл в линейных параметрах данных.
Ортогонализация
Представьте, что вы находитесь в магазине игрушек и вам нравится машинка с дистанционным управлением. Однако игрушечная машинка работает с двумя пультами дистанционного управления, настроенными по-разному, и вы можете использовать один из них. Ниже приводится описание конфигурации каждого из пультов дистанционного управления.
Давайте сравним два контроллера. Что, если вы хотите направить свою машину влево? На контроллере 1 все довольно просто. Просто нажмите Кнопку X влево. Как бы вы сделали это, используя Controller 2? Это невозможно? Нет, однозначно можно! Чтобы повернуть налево, оператор должен использовать обе кнопки таким образом, чтобы нежелательные движения вперед/назад кнопки X блокировались кнопкой Y.
Что бы вы выбрали? Контроллер 1, очевидно же! Почему? Самый простой ответ: «Потому что каждое атомарное движение управляется с помощью независимого ключа, что упрощает управление». Благодаря специальному нажатию клавиши для основных движений, таких как движение вперед, назад, влево и вправо, мы устранили любую зависимость между этими движениями. Это делает Контроллер 1 ортогонализированнымконтроллером, где каждая клавиша выполняет движение, отличное от движений, выполняемых остальными клавишами.
Почти все машины, которые мы видим, следуют принципу ортогонализации. Посмотрите на свою машину: педаль акселератора разгоняет ее и больше ничего не делает. Термостат в вашем доме имеет специальные клавиши для установки температуры, включения/выключения вентилятора и т. д.
Здорово! Ортогонализация повсюду. Но какое отношение ортогонализация имеет к PCA? Хм, интересный вопрос! Продолжай читать.
Функции педали акселератора и педали тормоза в автомобиле независимы, т.е. нажатием на педаль тормоза вы выполняете торможение и ничего больше. Другими словами, ортогональные управления имеют взаимно независимые функции. Концепция взаимно независимых элементов управления приводит нас к PCA.
Учитывая некоторые данные с функциями d, цель PCA состоит в том, чтобы преобразовать данные в новое пространство функций таким образом, чтобы новые функции kвзаимно независимы, т.е. имеют диагональную ковариационную матрицу. Это преобразование также является формой ортогонализации.
Ждать! Итак, PCA преобразует данные в новое функциональное пространство?Разве PCA не должен уменьшать размеры исходных данных? В чем суть этого нового функционального пространства?
Да, PCA — это метод уменьшения размеров. Но уменьшение размерностей не выполняется на исходных данных. По мере чтения этой статьи вы получите четкое представление о том, что происходит на заднем плане. В следующих разделах мы рассмотрим, как работает PCA, а также его плюсы и минусы.
Что такое ПСА?
Анализ основных компонентов — это непараметрический, неконтролируемый статистический метод для анализа многомерных данных. Как PCA выполняет многомерный анализ?
В реальном мире невозможно собрать набор данных с независимыми функциями. Часто мы записываем функции, связанные друг с другом, либо потому, что мы не знаем, что они связаны друг с другом, либо потому, что мы не хотим потерять какую-либо важную информацию, отбрасывая их. Таким образом, у нас есть многомерные данные с множеством признаков и возможными корреляциями между некоторыми признаками. Имея набор данных с функциями d, непросто анализировать данные в их исходной форме. Это может быть связано с:
- большие размерности данных, приводящие к избыточности информации
- Шумные функции из-за перекрестных помех между функциями (отсутствие ортогональных данных). Это зависит от того, как записываются данные.
- тот факт, что мы не можем полностью просматривать более 3–4 измерений данных одновременно
Итак, не было бы здорово удалить избыточность в функциях наших данных? Да, это именно то, что делает PCA. Цель PCA – найти ‘d’ ортогональных базисных векторов, которые лучше всего выражают исходные данные, так что никакие два признака не коррелированы, т. е. ковариация данных в новом пространстве признаков представляет собой тождество. матрица. Новые ортогональные базисные векторы также называютсяглавными компонентами.
Каков критерий выбора этих новых ортогональных базисных векторов? Помня об ортогонализации, мы хотим, чтобы эти новые векторы были независимы друг от друга. Следовательно, в новом пространстве признаков каждый признак должен быть независим от другого. Таким образом, первое предположение PCA состоит в том, чтобы иметь ортогональные базисные векторы.
Теперь, когда отношения между новыми базисными векторами установлены, как объекты в этом новом пространстве признаков связаны с исходными объектами? Это приводит нас к второму допущению,линейности. Базисные векторы в новом пространстве признаков представляют собой линейную комбинацию исходных базисных векторов (признаков).
Итак, новые базисные векторы взаимно ортогональны и представляют собой линейную комбинацию исходных базисных векторов (исходных признаков). Эти два предположения сужают пространство поиска. Но как нам узнать эти взаимно ортогональные базисные векторы? По какому критерию выбираются базисные векторы? Выбор подходящих базисных векторов осуществляется на основе третьего предположения:направление высокой дисперсии.
Предположения PCA:
- Новое пространство признаков имеет ортонормальные базисные векторы
- Новые базисные векторы представляют собой линейную комбинациюn исходных базисных векторов.
- Высокая дисперсия объясняет базовые данные
Наряду с этими основными предположениями существует условие, которое должно быть выполнено для правильной работы алгоритма. Все функции в данных должны быть центрированы по нулю.
Здорово! Мы знаем все предположения, сделанные PCA. Как определяется направление максимальной дисперсии? Как получаются базисные векторы? Ждать! Прежде чем мы погрузимся в математику, не было бы неплохо взглянуть на пример использования PCA, чтобы получить представление о его использовании?
В следующем разделе игрушечный пример используется для иллюстрации варианта использования PCA.
PCA: показано на примере
В этом разделе придумана игрушечная задача, чтобы продемонстрировать вариант использования PCA. Данные для задачи об игрушках моделируются путем добавления некоторого шума к точкам на перпендикулярных линиях.
Линии имеют наклоны 1 и -1, взаимно перпендикулярные. Обе линии имеют разные точки пересечения оси Y. Гауссовский шум добавляется как к линиям с нулевым средним значением, так и к разным дисперсиям. Декартова плоскость простирается от -12 доo 12. Ненулевое пересечение выбрано, чтобы отразить свойства реальных наборов данных и проиллюстрировать важность нулевого центрирования данных. Данные игрушки выглядят так, как показано на следующем рисунке:
Вы можете видеть, что центр находится далеко от нуля, а в наборе данных много шума. Теперь примените PCA к этому набору данных. В этом примере используется реализация PCA от Scikit-learn.
Главные компоненты (векторы, выделенные красным), полученные при нецентрировании, показаны выше. Здесь происходит кое-что интересное, главный компонент указывает не в том направлении, в котором мы собираемся видеть. Почему? Нецентрированные данные имеют другое распределение по пространству по сравнению с данными с нулевым центром, и PCA ищет вектор направления максимальной дисперсии, который проходит через начало координат.
Что!? Почему PCA ищет векторы, проходящие только через начало координат? Почему он не выбирает другие векторы? Ответ на вопрос, почему PCA просматривает данные из источника, заключается в предположении 2, а именно: «новые базисные векторы представляют собой линейную комбинацию исходных базисных векторов». Линейный комбинация исходных базисных векторов не включает компонент пересечения. Не включая явно компонент перехвата, PCA делает неявное предположение, что данные сосредоточены в источнике. Вот почему абсолютно необходимо иметь нулевое среднее значение.
В следующей реализации данные центрированы и нормализованы по стандартному отклонению каждого признака. На рис. 6 показаны основные компоненты данных с нулевым центром.
Ну наконец то! Похоже, что PCA захватила фактический базисный вектор, из которого был сгенерирован игрушечный набор данных. Что дальше? Как только основные компоненты получены, исходные данные должны быть преобразованы в новое пространство признаков, определяемое основными компонентами. На рис. 8 показано, как набор данных будет выглядеть в новом функциональное пространство.
- Что вы думаете о распространении преобразованных данных?
Похоже, что оси x и оси y не коррелированы друг с другом, т.е. их корреляция приблизительно равна нулю. Проверим это математически (см. рис. 10). В следующем фрагменте показаны недиагональные элементы, установленные на ноль. Ура! мы достигли ортогонализации. Новые функции не зависят друг от друга, и мы можем анализировать их по отдельности.
- Почему важна диагональная ковариационная матрица?
Представьте, что вы имеете дело с набором данных, который содержит более 10 признаков, и некоторые из них коррелированы, что часто верно для реальных наборов данных. В таком случае трудно определить признаки, важные для решения поставленной задачи. Рассмотрим функцию с именем X1. Даже если X1 коррелирует с целевой переменной, мы не можем быть уверены в корреляции из-за возможного шума в признаке из-за его взаимодействия с другими признаками. Но если мы знаем, что эта функция не коррелирует с другими функциями, мы можем быть уверены в ее предсказательной силе. - Вы заметили метки на оси x и оси y?
Оси x и y больше не называются x и y, так как данные теперь новое функциональное пространство. Функции будут называться PC1, PC2и т. д..
Это отличный пример того, как PCA может помочь в наших начинаниях по науке о данных. В следующем разделе мы рассмотрим приложения PCA как инструмента уменьшения размерности и многомерного анализа.
Где уменьшение размера? Разве PCA не об уменьшении размера?
Разве отклонение PCA не простое? PCA, основанный на его скромных предположениях, является мощным инструментом в многомерном анализе. В этом разделе мы рассмотрим использование PCA в качестве метода fэлементного извлечения. Извлечение признаков – это один из доступных подходов к уменьшению размерности. Сокращение размеров имеет два подхода: выбор признаков и извлечение признаков.
Выбор признаков — это подход, заключающийся в уменьшении исходного пространства признаков до подмножества исходных признаков. Сокращенный набор функций состоит из исходных функций, и выбор основан на некоторой оценке пригодности. Оценка пригодности может быть предсказательной силой функции по отношению к целевой переменной, такой как прирост информации и т. д. Предположение, сделанное методами выбора функций, таково: «некоторые функции являются избыточными и могут быть удалены без потери информации» (Источник: Википедия)
Другой подход к уменьшению размеров — это извлечение признаков. Извлечение признаков, с другой стороны, преобразует данные в новое пространство признаков. Мы можем свободно выбирать количество измерений в новом пространстве признаков. PCA — это метод извлечения линейных признаков. Важно помнить, что функции в более низком измерении не совпадают с исходными функциями.
Теперь, когда мы знаем, на что способен PCA, давайте выполним уменьшение размерности набора данных Iris с помощью PCA. Набор данных Iris имеет четыре характеристики (ширина чашелистика, длина чашелистика, ширина лепестка, длина лепестка), описывающие три вида растения Iris. На следующем рисунке показано распределение набора данных с использованием парного графика.
В этом примере используется реализация PCA от Scikit-learn. Конечно, после масштабирования признаков до нулевого среднего и единичной дисперсии. После преобразования данных как выбрать количество сохраняемых функций? Есть ли эффективный способ выбрать количество функций?
Да, вам следует обратить внимание на различия, объясняемые функциями. Реализация PCA от Scikit-learn имеет свойства, называемые explained_variance_ и explained_variance_ratio_. Каждый принципиальный компонент объясняет некоторую дисперсию исходных данных. В зависимости от количества информации, которую мы можем позволить себе потерять, выбирается количество основных компонентов. В случае набора данных Iris в исходном подпространстве есть четыре объекта. Сколько главных компонент необходимо выбрать для представления данных? Ниже приведен график дисперсии, объясняющий соотношение каждого главного компонента.
Первая главная компонента объясняет около 72,7% дисперсии исходных данных. Это означает, что если мы сохраним только одно измерение в новом пространстве признаков, сохранится 72,7% исходной информации. Первые два основных компонента вместе объясняют 95,8% дисперсии исходных данных. Потеря ~4% дисперсии для двумерного представления того стоит. Сложность вычислений 2D меньше по сравнению с данными 3D или 4D. Более того, мы можем легко визуализировать распределение данных в двухмерном пространстве.
Разве не здорово иметь параметр, показывающий потерянную информацию! Мы можем использовать кумулятивный график коэффициента объясненной дисперсии, чтобы понять компромисс между количеством выбранных основных компонентов и объемом сохраненной информации (дисперсией).
Многомерный анализ с использованием ПК-загрузок
Мы видели, как PCA можно использовать в качестве метода извлечения признаков. PCA также используется для анализа взаимосвязи между исходными функциями и основными компонентами.
Как описано ранее, основные компоненты набора данных представляют собой линейную комбинацию исходных признаков. Коэффициенты линейной комбинации называются нагрузками. Загрузки основного компонента можно использовать, чтобы понять, что представляет собой главный компонент, и понять (расплывчато) многомерное распределение данных.
На следующем рисунке показаны основные компоненты, полученные для масштабированного набора данных Iris. Каждая строка представляет главный компонент. Первые нагрузки главного компонента присутствуют в первой строке и так далее.
В предыдущем разделе я решил ограничить количество основных компонентов двумя (на основе объясненного коэффициента дисперсии). Итак, рассмотрим нагрузки первых двух основных компонентов. Но эти концепции применимы и к другим основным компонентам.
Первая главная компонента (PC) имеет положительные нагрузки для длины чашелистика, длины лепестка и ширины лепестка; отрицательная нагрузка на длину чашелистика. Глядя на величину, мы можем сказать, что на первый PC больше повлияли другие характеристики, а не длина чашелистика. Второй ПК имеет положительные нагрузки по всем характеристикам. Но величина нагрузки на ширину чашелистика преобладает над другими нагрузками. Я знаю, это похоже на сравнение набора чисел. Но когда мы наносим эти векторы нагрузки рядом с преобразованными данными, мы можем увидеть интересные закономерности.
На следующем рисунке мы можем видеть векторы нагрузки, нанесенные рядом с преобразованными данными, с PC1 в качестве оси X и PC2 в качестве оси Y. Этот тип графика называется двойной график.
Вектор загрузки sepal_width рисуется следующим образом:
- Координата x вектора загрузки — это загрузка объекта sepal_width на ПК 1 (ось x).
- Координата Y вектора загрузки — это загрузка функции sepal_width на ПК 2 (ось Y).
- Нарисуйте вектор, проходящий через начало координат и точку, описанную выше.
Из приведенного выше побочного графика для заданной точки (x, y) мы можем легко сделать вывод:
- Высокое положительное значение y подразумевает большую ширину чашелистика.
- По мере продвижения от -4 до +4 по оси x значения длины чашелистика, длины лепестка, ширины лепестка увеличиваются, тогда как значение ширины чашелистика уменьшается.
Еще одно наблюдение на участке: Iris Setosa имеет меньшую длину чашелистика, длину лепестка и ширину лепестка по сравнению с другими классами. То же наблюдение можно сделать из парного графика. Однако нам нужно увидеть d * (d-1)графики, чтобы прийти к такому выводу [d — количество признаков]. Но один побочный сюжет может отображать всю информацию/шаблоны одновременно.
До сих пор мы рассматривали применение PCA в анализе и извлечении признаков. В следующем разделе мы рассмотрим подводные камни использования PCA.
Нет бесплатного обеда!
Теперь, когда мы установили сильные стороны PCA, пришло время взглянуть на его слабые стороны. Предположения, сделанные PCA, являются контрольными точками PCA. Давайте разберем каждое предположение, чтобы найти, где эти предположения неверны.
- Ортонормированные базисные векторы
Предполагается, что основные направления отклонений перпендикулярны. Если лежащие в основе направления дисперсии неортогональны, полученные главные компоненты не смогут отразить фактические направления дисперсии.
- Основные компоненты представляют собой линейную комбинацию исходных функций
На следующем рисунке точно представлен случай, когда предположение о линейной комбинации не выполняется. В этом случае направление отклонения точно представлено в полярных координатах.
Другим недостатком методов PCA и извлечения признаков в целом является то, что новое пространство признаков строится неконтролируемым образом. Это так, даже когда у нас есть целевая переменная. Иногда это оказывается проклятием, поскольку целевая переменная не влияет на основные компоненты. Вполне возможно, что новые данные более низкого измерения могут быть такими же плохими, как и исходные данные с точки зрения анализа.
Дело не в том, что PCA прекращает вычисление основных компонентов, когда предположения не выполняются. Мы все еще можем вычислить основные компоненты, и сумма объясненных коэффициентов дисперсии всех компонентов будет равна единице. Единственная проблема заключается в том, что вновь вычисленные главные компоненты не будут точным представлением исходных данных, если какое-либо из этих предположений будет нарушено.
PCA имеет свою долю сильных и слабых сторон. Предположения, которые мы сделали, настолько сильны, что метод уязвим для некоторых видов данных. Существуют ли какие-либо другие методы, которые могут работать в случае сбоя PCA? Конечно! Есть много.
Но здесь возникает важный вопрос: как узнать, нарушаются ли допущения в многомерной обстановке? Откровенно говоря, я не знаю!
Мы можем поискать какие-то зацепки, но, как говорится: бесплатных обедов не бывает!
Вот некоторые подсказки, которые мы можем искать:
- Нелинейное распределение на парных участках
- сравнить результаты других методов уменьшения размерности (многократное обучение, Kernel PCA и т. д.)
- Базовые знания! Ничто не может победить это.
Альтернативные методы
Как упоминалось ранее, PCA подходит не для всех параметров. Некоторые другие популярные методы уменьшения размеров:
- Анализ независимых компонентов (ICA)
- Неотрицательная матричная факторизация (NMF)
- ИЗОМАП
- Ядро PCA
- Локально-линейное вложение
- Многомерное масштабирование
- t-распределенное стохастическое встраивание соседей (t-SNE)
Читателям предлагается ознакомиться и с другими методами.
Вывод
PCA, как описано ранее, является мощным инструментом анализа больших размерностей. При рассмотрении PCA следует помнить о следующих вещах:
- Уменьшенные размеры находятся в другом пространстве функций и НЕ являются подмножеством исходных функций.
- предположение о линейности и ортогональности
Наконец, используйте PCA осторожно!
использованная литература
- Введение в статистическое обучение — Роберт Тибширани и Тревор Хасти
- Учебник по PCA [https://arxiv.org/abs/1404.1100]
- Слайды уменьшения размерности — Миндже Ким, Университет Индианы
8 июля 2021 г.
Компании и организации могут использовать метод уменьшения размерности, такой как анализ основных компонентов, чтобы сжать большой набор данных в более управляемый и простой в использовании. Этот процесс может служить различным целям в технологической и программной отраслях, включая использование программного обеспечения для распознавания лиц и сжатия изображений. Изучение того, что такое анализ основных компонентов, может помочь вам лучше понять, как его используют профессионалы и как проводить его самостоятельно. В этой статье мы даем определение анализу основных компонентов, перечисляем шаги для его выполнения и приводим пример, который поможет вам в его проведении.
Что такое анализ главных компонентов?
Анализ главных компонентов (PCA) — это математический метод, используемый для уменьшения большого набора данных до меньшего при сохранении большей части информации о его вариациях. Хотя это сокращение может сделать набор данных менее точным, оно также может сделать его более управляемым и простым в использовании. Меньшие наборы данных без лишних переменных могут упростить как людям, так и машинам просмотр и анализ данных. Этот метод подчеркивает изменчивость в наборе данных и помогает выявить закономерности.
Специалисты по данным могут работать с набором данных с большим количеством переменных, а это означает, что между переменными также существует множество взаимосвязей. Если ученый хочет свести к минимуму количество взаимосвязей переменных для идентификации, управления и контроля, он может рассмотреть возможность внедрения АПК. Уменьшая размеры их пространства признаков с помощью PCA, нужно учитывать меньше взаимосвязей.
Как провести анализ основных компонентов
Вот несколько шагов для проведения анализа основных компонентов:
1. Стандартизируйте данные
Первым шагом анализа основных компонентов является стандартизация данных, преобразование исходных значений набора данных в сравнительные шкалы. Этот процесс гарантирует, что каждое значение имеет равную роль в анализе и что различные диапазоны между вашими исходными переменными не искажают ваши результаты. Чтобы стандартизировать ваши данные, вычтите среднее значение и разделите на стандартное отклонение для каждого значения каждой переменной. Вот уравнение:
Z = (значение — среднее) / стандартное отклонение
2. Вычислите ковариационную матрицу
Вычислив ковариационную матрицу, вы можете определить, есть ли какая-либо связь между переменными вашего набора данных. Это может позволить вам определить, содержат ли сильно коррелированные переменные, т. е. переменные, связанные с другими, избыточную информацию, которую вы можете удалить. Ковариационная матрица — это таблица, в которой отображаются корреляции между всеми возможными парами переменных в вашем наборе данных.
Это симметричная матрица, включающая все возможные пары исходных переменных. Если ваша ковариация положительна, это означает, что переменные увеличиваются и уменьшаются вместе, что означает корреляцию между ними. Если верно и обратное, это означает, что если ковариация отрицательна, между двумя переменными нет корреляции. Например, ковариационная матрица с переменными a и b может включать:
Cov(a,b)Cov(b,a)Cov(a,a)Cov(b,b)
3. Рассчитайте собственные векторы и собственные значения, чтобы определить главные компоненты.
Собственные векторы и собственные значения — это понятия из линейной алгебры, которые можно использовать для определения главных компонентов из матрицы ковариаций. Главные компоненты — это новые переменные, являющиеся комбинациями исходных переменных. Они являются результатом сжатия исходных переменных в новые, некоррелированные переменные, что позволяет избавиться от корреляций в вашем наборе данных.
Основные компоненты представляют данные, отображающие максимальное количество отклонений, и их использование в качестве репрезентативных иллюстрирует, как PCA может позволить вам включить максимальное количество информации в каждый компонент и уменьшить размеры ваших данных. Вы можете определить свои основные компоненты, вычислив собственные векторы (????) и перечислив их в порядке убывания в соответствии с их собственными значениями. Это показывает вам основные компоненты в порядке значимости. Например:
У вас есть двумерный набор данных с переменными a и b, а собственные векторы и собственные значения ковариационной матрицы:
*v1 =*
0,6780,735????1 = 1,284
v2 =
-0,7350,678????2 = 0,049
Затем вы можете расположить собственные значения (1,284 и 0,049) в порядке убывания и заметить, что ????1 > ????2. Это означает, что v1 — собственный вектор, соответствующий первой главной компоненте, а v2 — второй главной компоненте. Затем вы можете вычислить процент дисперсии для каждого компонента, разделив собственное значение каждого компонента на сумму его собственных значений.
4. Создайте вектор признаков
Когда у вас есть список основных компонентов, вы можете решить, хотите ли вы сохранить их все или отбросить те, у которых собственные значения меньше и, следовательно, они менее значимы. Остальные компоненты, которые вы решите использовать, могут составить вектор признаков. Это означает, что в векторе признаков перечислены собственные значения компонентов, которые вы решили сохранить, что позволяет уменьшить размерность, если это ваша цель. Если вы не надеетесь уменьшить размерность ваших данных, вектор признаков все равно может быть полезен для перечисления ваших данных в соответствии с новыми переменными, вашими основными компонентами.
Обратитесь к предыдущим числам в качестве примера и предположим, что вы решили отбросить собственный вектор v2, потому что он имеет меньшее значение, чем v1. Это означает, что вы можете сформировать вектор признаков, используя только переменные из v1. Ваш вектор признаков будет выглядеть так:
0,6780,735
5. Реконструируйте данные
Этот последний шаг включает в себя получение информации, которую вы вычислили из собственных векторов вашей ковариационной матрицы, и переориентацию ваших данных, чтобы они включали только выбранные вами основные компоненты. Во время этого процесса вы не изменили исходную информацию, и набор входных данных остался прежним. Теперь вы можете просто применить свои новые переменные к исходным осям исходного набора данных, реконструируя ваши данные в соответствии с новым диапазоном дисперсии.
Формула для ремоделирования данных:
Окончательный набор данных = (вектор признаков) tx (стандартизированный исходный набор данных) t
Пример анализа главных компонентов
Исследователь данных изучает корреляцию между ростом и весом среди студентов Северо-Южного университета. Два ее измерения, рост и вес, являются осями графика, на котором она наносит точки данных для индивидуального представления учеников. Однако ей требуется меньшая размерность для ее набора данных. Чтобы свести к минимуму вариации, она использует PCA для создания новой системы координат, в которой каждый компонент имеет новое значение (x,y).
После стандартизации своих данных и создания ковариационных матриц она вычисляет два основных компонента, v1 и v2. Она находит, что v1 дает значение 0,429, а v2 дает значение 0,251. Это означает, что после перечисления их в порядке убывания v1 ≥ v2. Чтобы свести к минимуму дисперсию, она собирается отказаться от одного из основных компонентов. Она решает отказаться от версии 2, так как она меньше, чем версия 1. Оси теперь являются двумя основными компонентами роста (pc1) и веса (pc2), которые позволяют ей отображать новые точки данных на втором графике и реконструировать данные.
Анализ основных компонентов, часто сокращенно PCA, представляет собой метод машинного обучения без учителя , который направлен на поиск основных компонентов — линейных комбинаций исходных предикторов — которые объясняют большую часть вариаций в наборе данных.
Цель PCA состоит в том, чтобы объяснить большую часть изменчивости в наборе данных с меньшим количеством переменных, чем в исходном наборе данных.
Для заданного набора данных с переменными p мы могли бы изучить диаграммы рассеяния каждой попарной комбинации переменных, но само количество диаграмм рассеяния может очень быстро стать большим.
Для предикторов p существуют диаграммы рассеяния p(p-1)/2.
Итак, для набора данных с p = 15 предикторов будет 105 различных диаграмм рассеяния!
К счастью, PCA предлагает способ найти низкоразмерное представление набора данных, которое фиксирует как можно больше вариаций данных.
Если мы сможем зафиксировать большую часть изменений всего в двух измерениях, мы сможем спроецировать все наблюдения в исходном наборе данных на простую диаграмму рассеяния.
Находим главные компоненты следующим образом:
Учитывая набор данных с предикторами p : X 1 , X 2 , …, X p, , рассчитайте Z 1 , … , Z M как M линейных комбинаций исходных предикторов p , где:
- Z m = ΣΦ jm X j для некоторых констант Φ 1m , Φ 2m , Φ pm , m = 1, …, M.
- Z 1 — это линейная комбинация предикторов, которая фиксирует максимально возможную дисперсию.
- Z 2 является следующей линейной комбинацией предикторов, которая фиксирует наибольшую дисперсию, будучи ортогональной (т.е. некоррелированной) с Z 1 .
- Тогда Z 3 является следующей линейной комбинацией предикторов, которая захватывает наибольшую дисперсию, будучи ортогональной Z 2 .
- И так далее.
На практике мы используем следующие шаги для вычисления линейных комбинаций исходных предикторов:
1. Масштабируйте каждую из переменных так, чтобы среднее значение равнялось 0, а стандартное отклонение равнялось 1.
2. Рассчитайте ковариационную матрицу для масштабированных переменных.
3. Вычислите собственные значения ковариационной матрицы.
Используя линейную алгебру, можно показать, что собственный вектор, соответствующий наибольшему собственному значению, является первой главной компонентой. Другими словами, эта конкретная комбинация предикторов объясняет наибольшую дисперсию данных.
Собственный вектор, соответствующий второму по величине собственному значению, является вторым главным компонентом и так далее.
В этом руководстве представлен пошаговый пример того, как выполнить этот процесс в R.
Шаг 1: Загрузите данные
Сначала мы загрузим пакет tidyverse , который содержит несколько полезных функций для визуализации и управления данными:
library (tidyverse)
В этом примере мы будем использовать набор данных USArrests , встроенный в R, который содержит количество арестов на 100 000 жителей в каждом штате США в 1973 году за убийство , нападение и изнасилование .
Он также включает процент населения в каждом штате, проживающего в городских районах, UrbanPop .
Следующий код показывает, как загрузить и просмотреть первые несколько строк набора данных:
#load data
data ("USArrests")
#view first six rows of data
head(USArrests)
Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7
Шаг 2: Расчет основных компонентов
После загрузки данных мы можем использовать встроенную функцию R prcomp() для вычисления основных компонентов набора данных.
Обязательно укажите масштаб = TRUE , чтобы каждая из переменных в наборе данных была масштабирована так, чтобы иметь среднее значение 0 и стандартное отклонение 1 перед вычислением основных компонентов.
Также обратите внимание, что собственные векторы в R по умолчанию указывают в отрицательном направлении, поэтому мы умножим на -1, чтобы поменять знаки.
#calculate principal components
results <- prcomp(USArrests, scale = TRUE )
#reverse the signs
results$rotation <- -1*results$rotation
#display principal components
results$rotation
PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432
Мы можем видеть, что первая главная компонента (PC1) имеет высокие значения для Убийства, Нападения и Изнасилования, что указывает на то, что эта главная компонента описывает наибольшую вариацию этих переменных.
Мы также можем видеть, что второй основной компонент (PC2) имеет высокое значение для UrbanPop, что указывает на то, что этот основной компонент уделяет наибольшее внимание городскому населению.
Обратите внимание, что оценки основных компонентов для каждого состояния хранятся в results$x.Мы также умножим эти оценки на -1, чтобы поменять местами знаки:
#reverse the signs of the scores
results$x <- -1*results$x
#display the first six scores
head(results$x)
PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164
Шаг 3. Визуализируйте результаты с помощью биплота
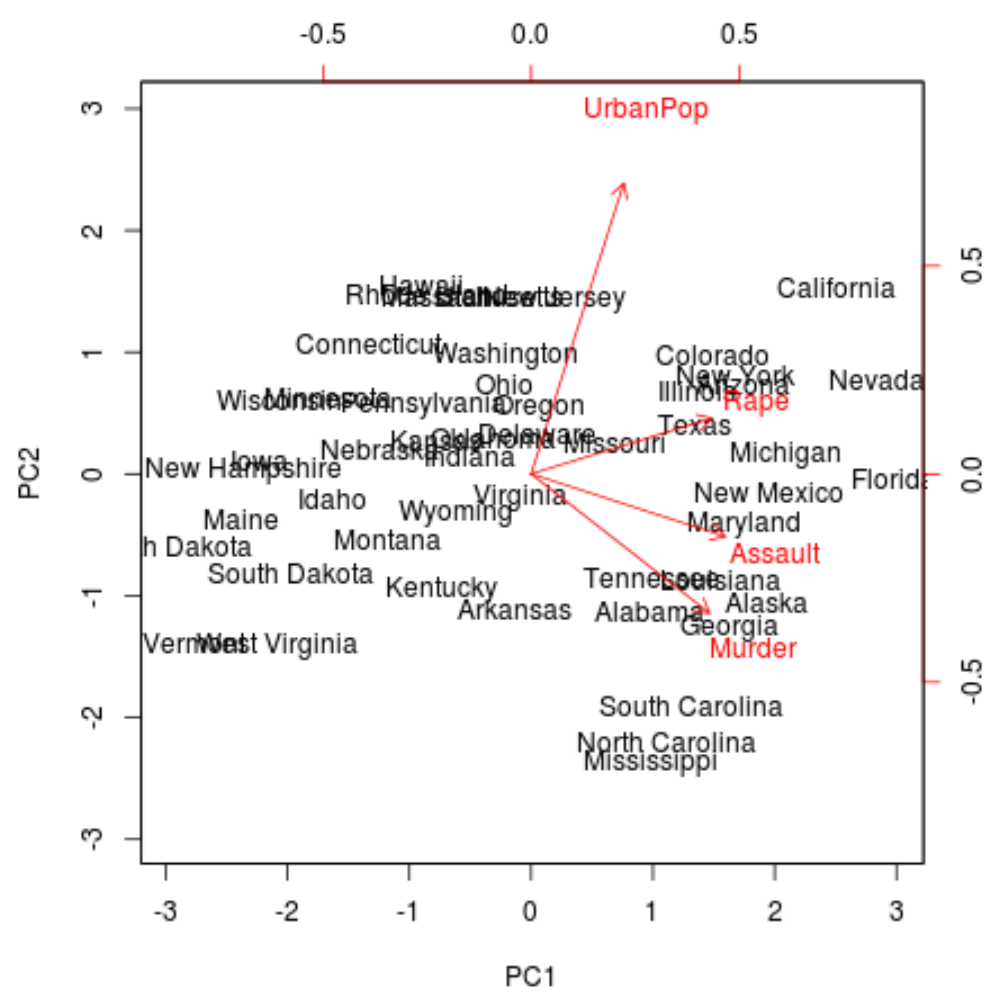
Затем мы можем создать двойную диаграмму — график, который проецирует каждое из наблюдений в наборе данных на диаграмму рассеяния, которая использует первый и второй главные компоненты в качестве осей:
Обратите внимание, что масштаб = 0 гарантирует, что стрелки на графике масштабируются для представления нагрузок.
biplot(results, scale = 0 )
На графике мы можем видеть каждое из 50 состояний, представленных в простом двумерном пространстве.
Состояния, которые находятся близко друг к другу на графике, имеют схожие шаблоны данных в отношении переменных в исходном наборе данных.
Мы также можем видеть, что определенные состояния более тесно связаны с одними преступлениями, чем с другими. Например, штат Джорджия ближе всего к переменной Убийство в сюжете.
Если мы посмотрим на штаты с самым высоким уровнем убийств в исходном наборе данных, мы увидим, что Грузия на самом деле находится в верхней части списка:
#display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])
Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2
Шаг 4: Найдите дисперсию, объясненную каждым основным компонентом
Мы можем использовать следующий код для расчета общей дисперсии в исходном наборе данных, объясненной каждым основным компонентом:
#calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)
[1] 0.62006039 0.24744129 0.08914080 0.04335752
По результатам мы можем наблюдать следующее:
- Первый главный компонент объясняет 62% общей дисперсии в наборе данных.
- Второй главный компонент объясняет 24,7% общей дисперсии в наборе данных.
- Третий главный компонент объясняет 8,9% общей дисперсии в наборе данных.
- Четвертый главный компонент объясняет 4,3% общей дисперсии в наборе данных.
Таким образом, первые два основных компонента объясняют большую часть общей дисперсии данных.
Это хороший знак, потому что предыдущая побочная диаграмма проецировала каждое из наблюдений из исходных данных на диаграмму рассеяния, которая учитывала только первые два основных компонента.
Таким образом, можно смотреть на шаблоны в побочной диаграмме, чтобы идентифицировать состояния, которые похожи друг на друга.
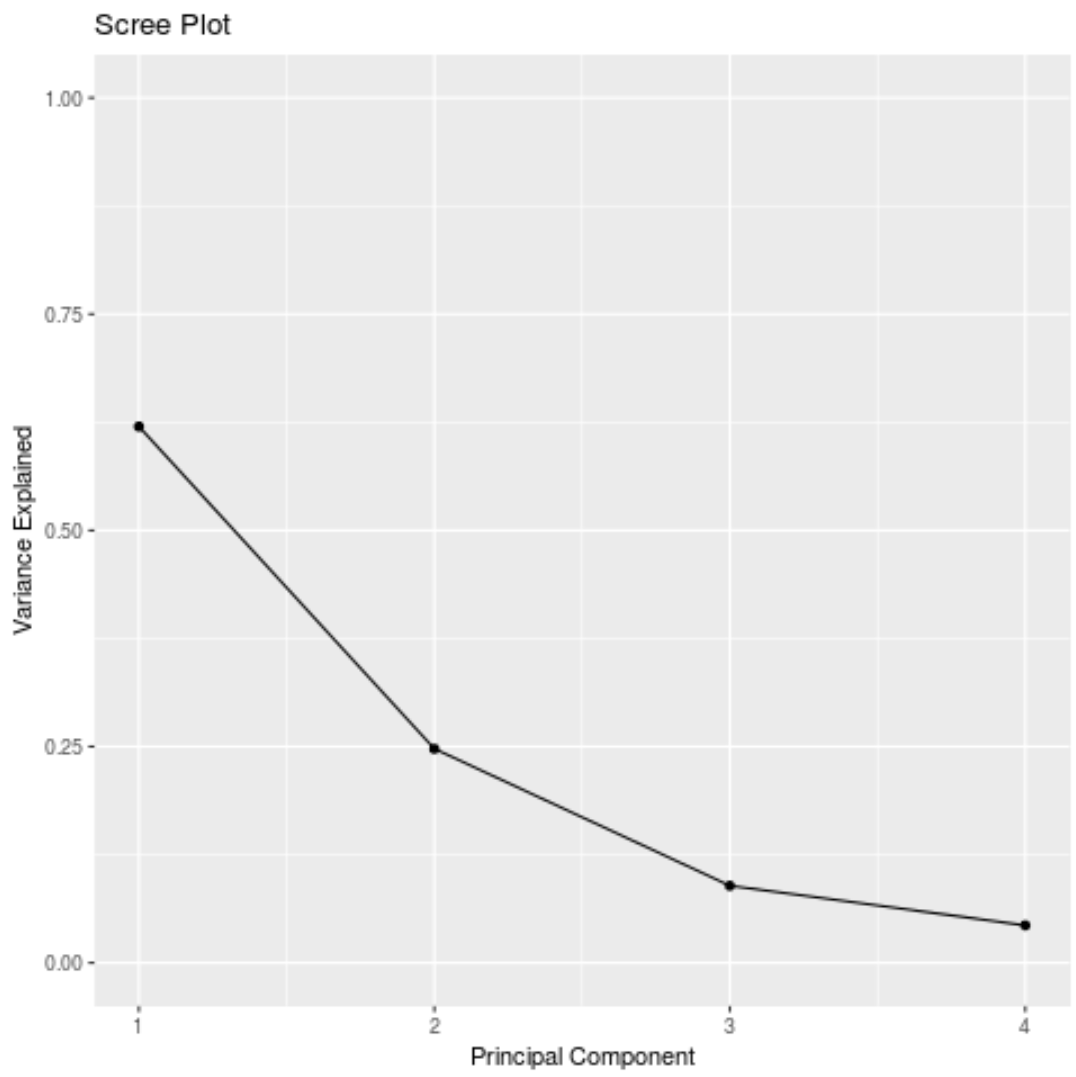
Мы также можем создать график осыпи — график, который отображает общую дисперсию, объясненную каждым основным компонентом, — чтобы визуализировать результаты PCA:
#calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)
#create scree plot
qplot(c(1:4), var_explained) +
geom_line() +
xlab(" Principal Component ") +
ylab(" Variance Explained ") +
ggtitle(" Scree Plot ") +
ylim(0, 1)
Анализ основных компонентов на практике
На практике PCA используется чаще всего по двум причинам:
1. Исследовательский анализ данных. Мы используем PCA, когда впервые изучаем набор данных и хотим понять, какие наблюдения в данных наиболее похожи друг на друга.
2. Регрессия основных компонентов.Мы также можем использовать PCA для расчета основных компонентов, которые затем можно использовать в регрессии основных компонентов.Этот тип регрессии часто используется, когда между предикторами в наборе данных существует мультиколлинеарность .
Полный код R, использованный в этом руководстве, можно найти здесь .